⧼exchistory⧽
24 exercise(s) shown, 0 hidden
SORT:
BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

Consider the Markov chain with transition matrix

[[math]] \mat {P} = \pmatrix{ 1/2 & 1/2 \cr 1/4 & 3/4}\ . [[/math]]

Find the fundamental matrix [math]\mat{Z}[/math] for this chain. Compute the mean first passage matrix using [math]\mat{Z}[/math].

BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

A study of the strengths of Ivy League football teams

shows that if a school has a strong team one year it is equally likely to have a strong team or average team next year; if it has an average team, half the time it is average next year, and if it changes it is just as likely to become strong as weak; if it is weak it has 2/3 probability of remaining so and 1/3 of becoming average.

  • A school has a strong team. On the average, how long will it be before it has another strong team?
  • A school has a weak team; how long (on the average) must the alumni wait for a strong team?
BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

Consider Example with [math]a = .5[/math] and [math]b = .75[/math]. Assume that the President says that he or she will run. Find the expected length of time before the first time the answer is passed on incorrectly.

BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

Find the mean recurrence time for each state of Example for [math]a = .5[/math] and [math]b = .75[/math]. Do the same for general [math]a[/math] and [math]b[/math].

BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

A die is rolled repeatedly. Show by the results of this section that the mean time between occurrences of a given number is 6.

BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

For the Land of Oz example (Example), make rain into an absorbing state and find the fundamental matrix [math]\mat{N}[/math]. Interpret the results obtained from this chain in terms of the original chain.

BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

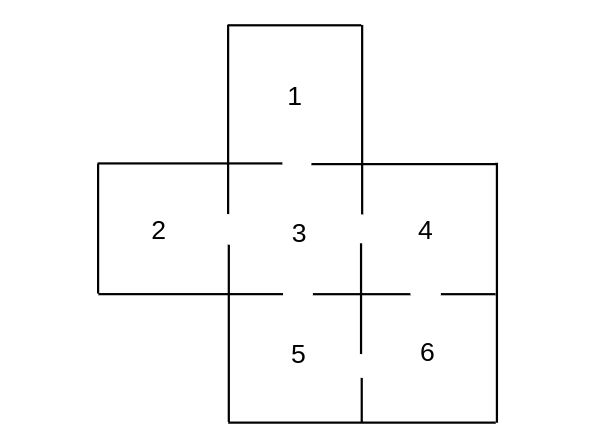
A rat runs through the maze shown in Figure. At each step it leaves the room it is in by choosing at random one of the doors out of the room.

  • Give the transition matrix [math]\mat{P}[/math] for this Markov chain.
  • Show that it is an ergodic chain but not a regular chain.
  • Find the fixed vector.
  • Find the expected number of steps before reaching Room 5 for the first time, starting in Room 1.
BBy Bot
Jun 09'24

Modify the program ErgodicChain so that you can compute the basic quantities for the queueing example of Exercise. Interpret the mean recurrence time for state 0.

BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

Consider a random walk on a circle of circumference [math]n[/math].

The walker takes one unit step clockwise with probability [math]p[/math] and one unit counterclockwise with probability [math]q = 1 - p[/math]. Modify the program ErgodicChain to allow you to input [math]n[/math] and [math]p[/math] and compute the basic quantities for this chain.

  • For which values of [math]n[/math] is this chain regular? ergodic?
  • What is the limiting vector [math]\mat{w}[/math]?
  • Find the mean first passage matrix for [math]n = 5[/math] and [math]p = .5[/math]. Verify that [math]m_{ij} = d(n - d)[/math], where [math]d[/math] is the clockwise distance from [math]i[/math] to [math]j[/math].
BBy Bot
Jun 09'24
[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

Two players match pennies and have between them a total of 5 pennies. If at any time one player has all of the pennies, to keep the game going, he gives one back to the other player and the game will continue. Show that this game can be formulated as an ergodic chain. Study this chain using the program ErgodicChain.