exercise:58957e3826: Difference between revisions

Latest revision as of 17:01, 14 June 2024

Consider the ESP problem as described in Exercise. You are again guessing with information, and you are using the optimal guessing strategy of guessing star if the remaining deck has more stars, circle if more circles, and tossing a coin if the number of stars and circles are equal. Assume that [math]S \geq C[/math], where [math]S[/math] is the number of stars and [math]C[/math] the number of circles.

We can plot the results of a typical game on a graph, where the horizontal axis represents the number of steps and the vertical axis represents the difference between the number of stars and the number of circles that have been turned up. A typical game is shown in Figure. In this particular game, the order in which the cards were turned up is [math](C,S,S,S,S,C,C,S,S,C)[/math]. Thus, in this particular game, there were six stars and four circles in the deck. This means, in particular, that every game played with this deck would have a graph which ends at the point [math](10, 2)[/math]. We define the line [math]L[/math] to be the horizontal line which goes through the ending point on the graph (so its vertical coordinate is just the difference between the number of stars and circles in the deck).

Show that, when the random walk is below the line [math]L[/math], the player guesses right when the graph goes up (star is turned up) and, when the walk is above the line, the player guesses right when the walk goes down (circle turned up). Show from this property that the subject is sure to have at least [math]S[/math] correct guesses.
When the walk is at a point [math](x,x)[/math] on the line [math]L[/math] the number of stars and circles remaining is the same, and so the subject tosses a coin. Show that the probability that the walk reaches [math](x,x)[/math] is
[[math]] \frac{{S \choose x}{C \choose x}}{{{S + C} \choose {2x}}}\ . [[/math]]
Hint: The outcomes of [math]2x[/math] cards is a hypergeometric distribution (see Important Distributions).
Using the results of (a) and (b) show that the expected number of correct guesses under intelligent guessing is
[[math]] S + \sum_{x = 1}^C \frac12 \frac{{S \choose x}{C \choose x}}{{{S + C} \choose {2x}}}\ . [[/math]]

@@ Line 1: / Line 1: @@
-<div class="d-none"><math>
+Consider the ESP problem as described in [[exercise:F66abbb0e8|Exercise]].  You are again guessing with information, and you are using the optimal
-\newcommand{\NA}{{\rm NA}}
+guessing strategy of guessing ''star'' if the remaining deck has more stars, '' circle'' if more circles, and tossing a coin if the number of stars and circles are
-\newcommand{\mat}[1]{{\bf#1}}
+equal.  Assume that <math>S \geq C</math>, where <math>S</math> is the number of stars and <math>C</math> the number of circles.
-\newcommand{\exref}[1]{\ref{##1}}
-\newcommand{\secstoprocess}{\all}
-\newcommand{\NA}{{\rm NA}}
-\newcommand{\mathds}{\mathbb}</math></div> Consider the ESP problem as described in Exercise \ref{exer
-.1.25}.  You are again guessing with information, and you are using the optimal
-guessing strategy of guessing ''star'' if the remaining deck has more stars, ''
-circle'' if more circles, and tossing a coin if the number of stars and circles are
-equal.  Assume that <math>S \geq C</math>, where <math>S</math> is the number of stars and <math>C</math> the number
-of circles.
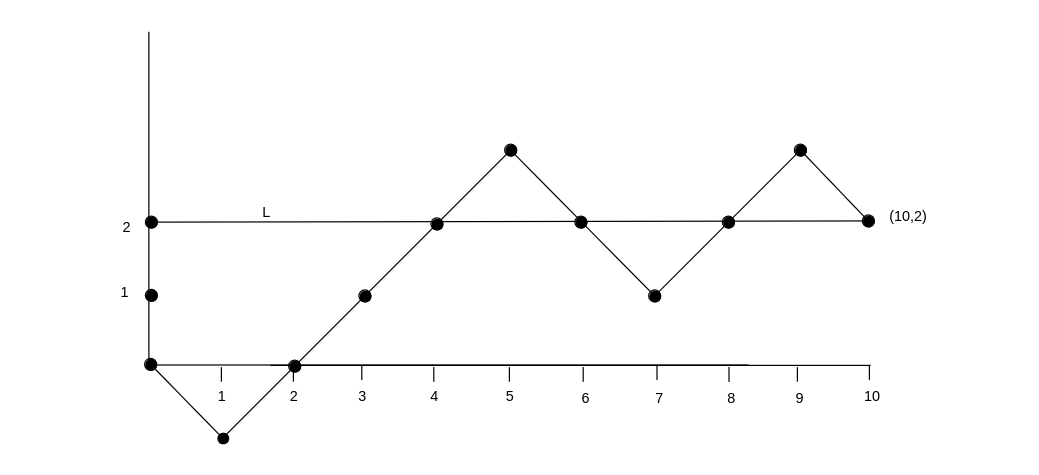
+We can plot the results of a typical game on a graph, where the horizontal axis represents the number of steps and the vertical axis represents the ''difference'' between the number of stars and the number of circles that have been turned up.  A typical game is shown in [[#fig 6.4|Figure]].  In this particular game, the order in which the cards were turned up is <math>(C,S,S,S,S,C,C,S,S,C)</math>.  Thus, in this particular
-We can plot the results of a typical game on a graph, where the horizontal axis
+game, there were six stars and four circles in the deck.  This means, in particular, that every game played with this deck would have a graph which ends at the point
-represents the number of steps and the vertical axis represents the ''difference''
-between the number of stars and the number of circles that have been turned up.  A
-typical game is shown in Figure \ref{fig 6.4}.  In this particular game, the order in
-which the cards were turned up is <math>(C,S,S,S,S,C,C,S,S,C)</math>.  Thus, in this particular
-game, there were six stars and four circles in the deck.  This means, in particular,
-that every game played with this deck would have a graph which ends at the point
 <math>(10, 2)</math>.  We define the line <math>L</math> to be the horizontal line which goes through the
 ending point on the graph (so its vertical coordinate is just the difference between
 the number of stars and circles in the deck).
-<div id="PSfig6-4" class="d-flex justify-content-center">
-[[File:guide_e6d15_PSfig6-4.ps | 400px | thumb |  ]]
+<div id="fig 6.4" class="d-flex justify-content-center">
+[[File:guide_e6d15_PSfig6-4.png | 400px | thumb | Random walk for ESP. ]]
 </div>
-<ul><li> Show that, when the random walk is below the line <math>L</math>, the player guesses right
-when the graph goes up (star is turned up) and, when the walk is above the line, the
+<ul style="list-style-type:lower-alpha"><li> Show that, when the random walk is below the line <math>L</math>, the player guesses right when the graph goes up (star is turned up) and, when the walk is above the line, the player guesses right when the walk goes down (circle turned up).  Show from this property that the subject is sure to have at least <math>S</math> correct guesses.
-player guesses right when the walk goes down (circle turned up).  Show from this
-property that the subject is sure to have at least <math>S</math> correct guesses.
 </li>
 <li> When the walk is at a point <math>(x,x)</math> ''on'' the line <math>L</math> the number of stars
@@ Line 38: / Line 22: @@
 \frac{{S \choose x}{C \choose x}}{{{S + C} \choose {2x}}}\ .
 </math>
-'' Hint'': The outcomes of <math>2x</math> cards is a hypergeometric distribution (see
-Section \ref{sec 5.1}).
+'' Hint'': The outcomes of <math>2x</math> cards is a hypergeometric distribution (see [[guide:A618cf4c07|Important Distributions]]).
 </li>
 <li> Using the results of (a) and (b) show that the expected number of correct