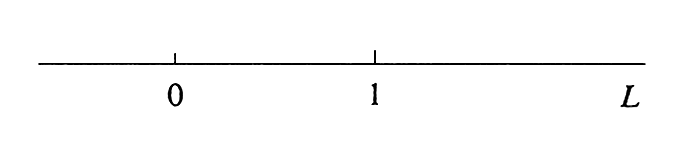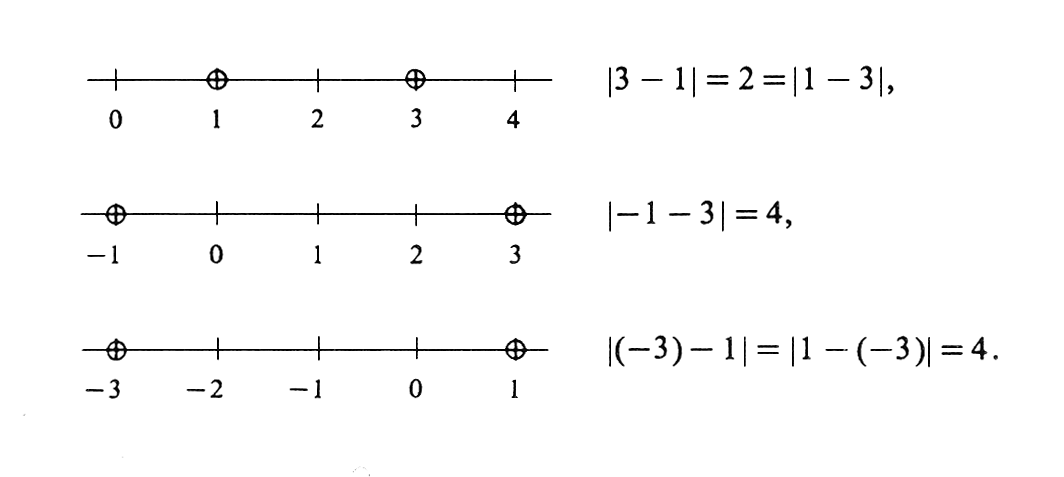guide:A5dd35d44b: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
==<span id="sec 1.1"></span>Real Numbers, Inequalities, Absolute Values.== | |||
Calculus deals with numerical-valued quantities and, | |||
in the beginning, with quantities whose values are real numbers. | |||
Some understanding of the basic set <math>\R</math> of all real numbers | |||
is therefore essential. | |||
A '''real number''' is one that can be written as a decimal: | |||
positive or negative or zero, terminating or nonterminating. | |||
Examples are | |||
<math display="block"> | |||
1, \;-5, \;0, \;14, | |||
</math> | |||
<math display="block"> | |||
\frac{2}{3} = 0.666666 \ldots, \; \frac{3}{8} = 0.375, | |||
</math> | |||
<math display="block"> | |||
\sqrt{2} = 1.4142 \ldots, | |||
</math> | |||
<math display="block"> | |||
-\pi = -3.141592\ldots, | |||
</math> | |||
<math display="block"> | |||
176355.14233333 \ldots | |||
. | |||
</math> | |||
The most familiar subset of <math>R</math> is the set <math>\Z</math> of '''integers'''. | |||
These are the numbers | |||
<span id{{=}}"eq1.1.1"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\ldots, -3, -2, -1, 0, 1, 2, 3,\ldots . | |||
\label{eq1.1.1} | |||
\end{equation} | |||
</math> | |||
Another subset is the set <math>\Q</math> of all rational numbers. | |||
A real number <math>r</math> is \dt {rational} | |||
if it can be expressed as the ratio of two integers, | |||
more precisely, | |||
if <math>r = \frac{m}{n}</math>, | |||
where <math>m</math> and <math>n</math> are integers and <math>n \neq 0</math>. | |||
Since every integer <math>m</math> can be written <math>\frac{m}{1}</math>, | |||
it follows that every integer is also a rational number. | |||
A scheme, analogous [[#eq1.1.1 |to]], | |||
which lists all the positive rational | |||
numbers is the following: | |||
<span id{{=}}"eq1.1.2"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{eq1.1.2} | |||
\begin{array}{ccccc} | |||
\frac{1}{1}, & \frac{2}{1}, & \frac{3}{1}, & \frac{4}{1}, & \ldots\\ | |||
\frac{1}{2}, & \frac{2}{2}, & \frac{3}{2}, & \frac{4}{2}, & \ldots\\ | |||
\frac{1}{3}, & \frac{2}{3}, & \frac{3}{3}, & \frac{4}{3}, & \ldots\\ | |||
\vdots | |||
\end{array} | |||
\end{equation} | |||
</math> | |||
Of course there are infinitely many repetitions in this presentation since, | |||
for example, | |||
<math>\frac{2}{1} = \frac{4}{2} = \frac{6}{3} = \ldots.</math> | |||
An unsophisticated guess would be that all real numbers are rational. | |||
There are, however, many famous proofs that this is not so. | |||
For example, | |||
a very simple and beautiful argument shows that <math>\sqrt 2</math> is not rational. | |||
(See Problem [[exercise:8162304386 |Exercise]] at the end of this section.) | |||
It is not hard to prove that a real number is rational | |||
if and only if its decimal expansion beyond some digit | |||
consists of a finite sequence of digits repeated forever. | |||
Thus the numbers | |||
<math display="block"> | |||
1.71349213213213213213 \ldots \mbox{(forever)} , | |||
</math> | |||
<math display="block"> | |||
1.500000000 \ldots \mbox{(forever)} | |||
</math> | |||
are rational, but | |||
<math display="block"> | |||
0.101001000100001000001 \ldots \mbox{(etc.)} | |||
</math> | |||
is not. | |||
The fundamental algebraic operations on real numbers | |||
are addition and multiplication: | |||
For any two elements <math>a</math> and <math>b</math> in <math>\R</math>, | |||
two elements <math>a + b</math> and <math>ab</math> in <math>\R</math> are uniquely determined. | |||
These elements, | |||
called the '''sum''' and '''product''' of <math>a</math> and <math>b</math>, respectively, | |||
are defined so that the following six facts are true: | |||
\begin{axiom}[Associative Laws] | |||
\label{axiom.i} | |||
<math display="block"> | |||
a + (b + c) = (a + b) + c, | |||
</math> | |||
<math display="block"> | |||
a(bc) = (ab)c. | |||
</math> | |||
\end{axiom} | |||
\begin{axiom}[Commutative Laws] | |||
\label{axiom.ii} | |||
<math display="block"> | |||
a + b = b + a, | |||
</math> | |||
<math display="block"> | |||
ab= ba. | |||
</math> | |||
\end{axiom} | |||
\begin{axiom}[Distributive Law] | |||
\label{axiom.iii} | |||
<math display="block"> | |||
(a + b) c = ac + bc. | |||
</math> | |||
\end{axiom} | |||
\begin{axiom}[Existence of Identities] | |||
\label{axiom.iv} | |||
<math>\R</math> contains two distinct elements <math>0</math> and <math>1</math> | |||
with the properties that <math>0 + a = a</math> and <math>1 \cdot a = a</math> | |||
for every <math>a</math> in <math>\R</math>. | |||
\end{axiom} | |||
\begin{axiom}[Existence of Subtraction] | |||
\label{axiom.v} | |||
For every <math>a</math> in <math>\R</math>, | |||
there is an element in <math>\R</math> denoted by <math>-a</math> | |||
such that <math>a + (-a) = 0</math>. | |||
\begin{note} | |||
<math>a - b</math> is an abbreviation of <math>a + (-b)</math>. | |||
\end{note} | |||
\end{axiom} | |||
\begin{axiom}[Existence of Division] | |||
\label{axiom.vi} | |||
For every <math>a \neq 0</math> in <math>\R</math>, | |||
there is an element in <math>\R</math> denoted by <math>a^{-1}</math> or <math>\frac{1}{a}</math> | |||
such that <math>aa^{-1} = 1</math>. | |||
\begin{note} | |||
<math>\frac{a}{b}</math> is an abbreviation of <math>ab^{-1}</math>. | |||
\end{note} | |||
\end{axiom} | |||
Addition and multiplication are here introduced as binary operations. | |||
However, as a result of the associative law of addition, | |||
<math>a + b + c</math> is defined to be the | |||
common value of <math>(a + b) + c</math> and <math>a + (b + c)</math>. | |||
In a like manner we may define the triple product <math>abc</math> and, | |||
more generally, | |||
<math>a_{1} + \ldots + a_{n}</math> and <math>a_{1} \ldots a_{n}</math>. | |||
Many theorems of algebra are consequences of the above six facts, | |||
and we shall assume them without proof. | |||
They are, in fact, | |||
frequently taken as part of a set of axioms for <math>\R</math>. | |||
Another essential property of the real numbers is that of order. | |||
We write <math>a < b</math> | |||
as an abbreviation of the statement that <math>a</math> is less than <math>b</math>. | |||
Presumably the reader, given two decimals, | |||
knows how to tell which one is the smaller. | |||
The following four facts simply recall | |||
the basic properties governing inequalities. | |||
On the other hand, | |||
they may also be taken as axioms for an abstractly defined relation | |||
between elements of <math>\R</math>, | |||
which we choose to denote by <math> < </math>. | |||
\begin{axiom}[Transitive Law] | |||
\label{axiom.vii} | |||
If <math>a < b</math> and <math>b < c</math>, then <math>a < c</math>. | |||
\end{axiom} | |||
\begin{axiom}[Law of Trichotomy] | |||
\label{axiom.viii} | |||
For every real number <math>a</math>, | |||
one and only one of the following alternatives holds: | |||
<math>a = 0</math>, or <math>a < 0</math>, or <math>0 < a</math>. | |||
\end{axiom} | |||
\begin{axiom} | |||
\label{axiom.ix} | |||
If <math>a < b</math>, then <math>a + c < b + c</math>. | |||
\end{axiom} | |||
\begin{axiom} | |||
\label{axiom.x} | |||
''If <math>a < b</math> and <math>0 < c</math>, then <math>ac < bc</math>.'' | |||
\end{axiom} | |||
Note that each of the above Axioms [[#axiom.vi |except]] | |||
remains true when restricted to the set <math>\Z</math> of integers. | |||
Moreover, | |||
all the axioms are true for the set <math>\Q</math> of rational numbers. | |||
Hence as a set of axioms for <math>\R</math>, | |||
they fail to distinguish between two very different sets: | |||
<math>\R</math> and its subset <math>\Q</math>. | |||
Later in this section we shall add one more item to the list, | |||
which will complete the algebraic description of <math>\R</math>. | |||
A real number <math>a</math> is if '''positive''' <math>0 < a</math> | |||
and '''negative''' if <math>a < 0</math>. | |||
Since the relation “greater than” is just as useful as “less than,” | |||
we adopt a symbol for it, too, | |||
and abbreviate the statement that <math>a</math> is greater than <math>b</math> | |||
by writing <math>a > b</math>. | |||
Clearly <math>a > b</math> if and only if <math>b < a</math>. | |||
[[#axiom.x |Axiom]], | |||
when translated into English, | |||
says that the direction of an inequality is preserved | |||
if both sides are multiplied by the same positive number. | |||
Just the opposite happens if the number is negative: | |||
The inequality is reversed. | |||
That is, | |||
{{proofcard|Proposition|thm_1.1.1|If <math>a < b</math> and <math>c < 0</math>, then <math>ac > bc</math>. | |||
|Since <math>c < 0</math>, [[#axiom.iv [[#axiom.v ||Axioms]],]], | |||
[[#axiom.ix |and]] | |||
imply | |||
<math display="block"> | |||
0 = c + (-c) < 0 + (- c) = - c | |||
. | |||
</math> | |||
So <math>-c</math> is positive. | |||
Hence by <math>(x)</math>, we get <math>-ac < -bc</math>. | |||
By [[#axiom.ix |Axiom]] | |||
again, | |||
<math display="block"> | |||
-ac + (bc + ac) < -bc + (bc + ac). | |||
</math> | |||
Hence <math>bc < ac</math>, | |||
and this is equivalent to <math>ac > bc</math>.}} | |||
Two more abbreviations complete the mathematician's array of symbols | |||
for writing inequalities: | |||
<math>a \leq b</math> means <math>a < b</math> or <math>a=b</math>, | |||
<math>a \geq b</math> means <math>a > b</math> or <math>a=b</math>. | |||
The geometric interpretation of the set <math>\R</math> of all real numbers | |||
as a straight line is familiar to anyone who has ever used a ruler, | |||
and it is essential to an understanding of calculus. | |||
To describe the assignment of points to numbers, | |||
consider an arbitrary straight line <math>L</math>, | |||
and choose on it two distinct points, | |||
one of which we assign to, or identify with, the number <math>0</math>, | |||
and the other to the number <math>1</math>. | |||
(See [[#fig 1.1|Figure]].) | |||
<div id="fig 1.1" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_1.png | 400px | thumb | ]] | |||
</div> | |||
The rest is automatic. | |||
The scale on <math>L</math> is chosen so that the unit of distance is | |||
the length of the line segment between the points <math>0</math> and <math>1</math>. | |||
Every positive number <math>a</math> is assigned the point on the side of <math>0</math> | |||
containing <math>1</math> which is <math>a</math> units of distance from <math>0</math>. | |||
Every negative number <math>a</math> is assigned the point on the side of <math>0</math> | |||
not containing <math>1</math> which is <math>-a</math> units of distance from <math>0</math>. | |||
Note that if <math>L</math> is oriented so that <math>1</math> lies to the right of <math>0</math>, | |||
then | |||
'' | |||
for any two numbers <math>a</math> and <math>b</math> (positive, negative, or zero), | |||
<math>a < b</math> if and only if <math>a</math> lies to the left of <math>b</math>.'' | |||
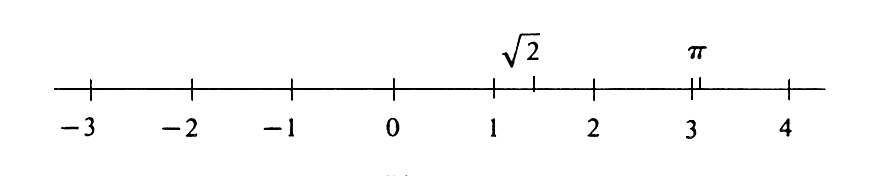
A line which has been identified with <math>\R</math> under a correspondence | |||
such as the one just described is called a '''real number line'''. | |||
(See [[#fig 1.2|Figure]].) | |||
<div id="fig 1.2" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_2.png | 400px | thumb | ]] | |||
</div> | |||
An '''interval''' | |||
is a subset <math>I</math> of <math>\R</math> with the property that | |||
whenever <math>a</math> and <math>c</math> belong to <math>I</math> and <math>a \leq b \leq c</math>, | |||
then <math>b</math> also belongs to <math>I</math>. | |||
Geometrically an interval is a connected piece of a real number line. | |||
A number d is called a '''lower bound''' of a set <math>S</math> of real numbers | |||
if <math>d \leq s</math> for every <math>s</math> in <math>S</math>. | |||
It is an '''upper bound''' of <math>S</math> if <math>s \leq d</math> for every <math>s</math> in <math>S</math>. | |||
A given subset of <math>\R</math>, and in particular an interval, | |||
is called '''bounded''' if it has both an upper and lower bound. | |||
There are four different kinds of bounded intervals: | |||
<math>(a, b)</math>, the set of all numbers <math>x</math> such that <math>a < x < b</math>; | |||
<math>[a, b]</math>, the set of all numbers <math>x</math> such that <math>a \leq x \leq b</math>; | |||
<math>[a, b)</math>, the set of all numbers <math>x</math> such that <math>a \leq x < b</math>; | |||
<math>(a, b]</math>, the set of all numbers <math>x</math> such that <math>a < x \leq b</math>. | |||
In each case the numbers <math>a</math> and <math>b</math> | |||
are called the '''endpoints''' of the interval. | |||
The set <math>[a, b]</math> contains both its endpoints, | |||
whereas <math>(a, b)</math> contains neither one. | |||
Clearly <math>[a, b)</math> contains its left endpoint but not its right one, | |||
and an analogous remark holds for <math>(a, b]</math>. | |||
It is important to realize that | |||
there is no element <math>\infty</math> (infinity) in the set <math>\R</math>. | |||
Nevertheless, the symbols <math>\infty</math> and <math>-\infty</math> are commonly used | |||
in denoting unbounded intervals. | |||
Thus | |||
<math>(a, \infty)</math> is the set of all numbers <math>x</math> such that <math>a < x</math>; | |||
<math>[a, \infty)</math> is the set of all numbers <math>x</math> such that <math>a \leq x</math>; | |||
<math>(-\infty, a)</math> is the set of all numbers <math>x</math> such that <math>x < a</math>; | |||
<math>(-\infty, a]</math> is the set of all numbers <math>x</math> such that <math>x \leq a</math>; | |||
<math>(-\infty, \infty)</math> is the entire set <math>\R</math>. | |||
The symbols <math>\infty</math> and <math>-\infty</math> also appear frequently | |||
in inequalities although they are really unnecessary, | |||
because, for example, | |||
<math display="block"> | |||
\begin{array}{r} | |||
-\infty < x < a \;\;\; \mbox{is equivalent to $x < a$}, \\ | |||
a \leq x < \infty \;\;\;\mbox{is equivalent to <math>a \leq x</math>}, | |||
\end{array} | |||
</math> | |||
etc. | |||
Since <math>\infty</math> is not an element of <math>\R</math>, | |||
we shall never use the notations <math>[a, \infty], x \leq \infty</math>, etc. | |||
An unbounded interval has either one endpoint or none; | |||
in each of the above cases it is the number <math>a</math>. | |||
We call an interval '''open''' if it contains none of its endpoints, | |||
and '''closed''' if it contains them all. | |||
Thus, for example, <math>(a, b)</math> and <math>(-\infty, a)</math> are open, | |||
but <math>[a, b]</math> and <math>[a, \infty)</math> are closed. | |||
The intervals <math>[a, b)</math> and <math>(a, b]</math> are neither open nor closed, | |||
although they are sometimes called half-open or half-closed. | |||
Since <math>(-\infty, \infty)</math> has no endpoints, | |||
it vacuously both does and does not contain them. | |||
Hence <math>(-\infty, \infty)</math> has the dubious distinction | |||
of being both open and closed. | |||
<div id="fig 1.3" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_3.png | 400px | thumb | ]] | |||
</div> | |||
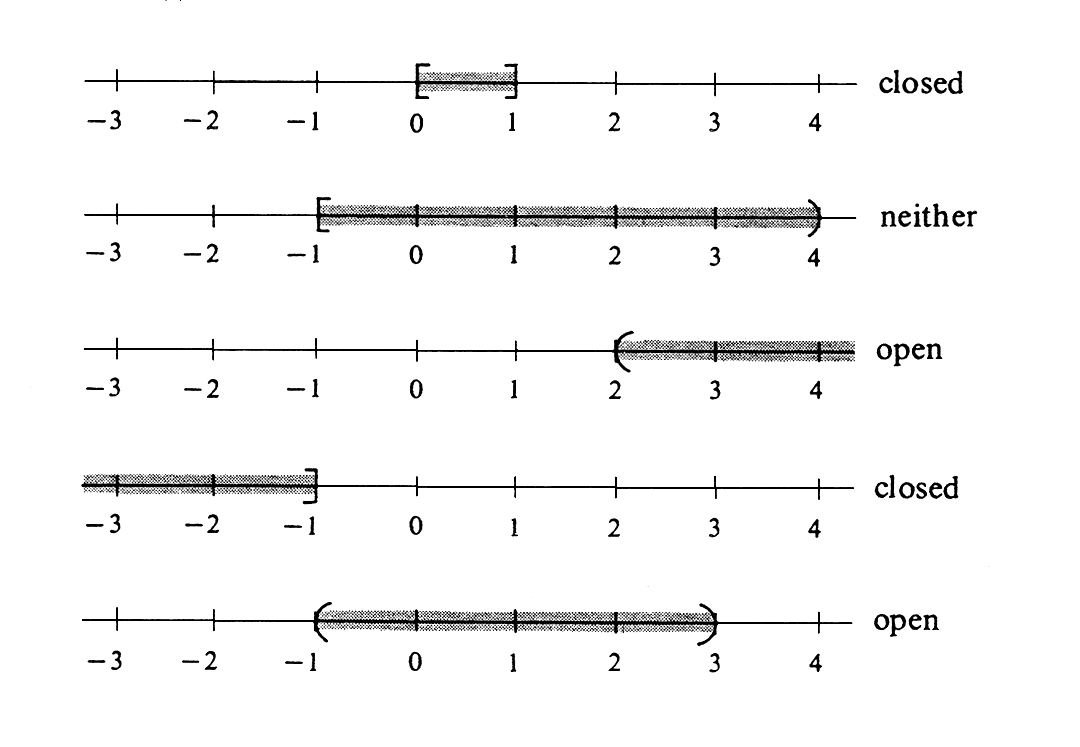
<span id="exam 1.1.1"/> | |||
'''Example''' | |||
\label{exam 1.1.1} | |||
Draw the intervals | |||
<math>[0, 1]</math>, <math>[-1, 4)</math>, <math>(2, \infty</math>), <math>(-\infty, -1]</math>, <math>(-1, 3)</math>, | |||
and identify them as open, closed, neither, | |||
or both (see [[#fig 1.3|Figure]]). | |||
It is frequently necessary to talk about the size of a real number | |||
without regard to its sign, not caring whether it is positive or negative. | |||
This happens often enough to warrant a definition and special notation: | |||
The '''absolute value''' of a real number <math>a</math> is denoted by <math>|a|</math> | |||
and defined by | |||
<math display="block"> | |||
|a| = \left \{ \begin{array}{rl} | |||
a & \mbox{if $a \geq 0$}, \\ | |||
-a & \mbox{if <math>a < 0</math>}. | |||
\end{array} | |||
\right. | |||
</math> | |||
Thus <math>|3| = 3</math>, <math>|0| = 0</math>, <math>|- 3| = 3</math>. | |||
Obviously, | |||
''the absolute value of a real number cannot be negative.'' | |||
Geometrically, | |||
<math>|a|</math> is the distance between the points <math>0</math> and <math>a</math> | |||
on the real number line. | |||
A generalization that is of extreme importance is the fact that <math>|a - b|</math> | |||
''is the distance between the | |||
points <math>a</math> and <math>b</math> on the real number line for any two numbers | |||
<math>a</math> and <math>b</math> whatsoever.'' | |||
Probably the best way to convince oneself that this is true | |||
is to look at a few illustrations (see [[#fig 1.4|Figure]]). | |||
<div id="fig 1.4" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_4.png | 400px | thumb | ]] | |||
</div> | |||
<span id="exam 1.1.2"/> | |||
'''Example''' | |||
\label{exam 1.1.2} | |||
Describe the set <math>I</math> of all real numbers <math>x</math> | |||
such that <math>|x - 5| < 3</math>. | |||
For any number <math>x</math>, | |||
the number <math>|x - 5|</math> is the distance between <math>x</math> and <math>5</math> | |||
on a real number line (see [[#fig 1.5|Figure]]). | |||
<div id="b^2" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_5.png | 400px | thumb | fig 1.5} | |||
That distance will be less than <math>3</math> | |||
if and only if <math>x</math> satisfies the inequalities <math>2 < x < 8</math>. | |||
We conclude that <math>I</math> is the open interval <math>(2, 8)</math>. | |||
There is an alternative way of writing the definition | |||
of the absolute value of a number <math>a</math> | |||
which requires only one equation: | |||
We do not have to give separate definitions for positive and negative <math>a</math>. | |||
This definition uses a square root, | |||
and before proceeding to it, | |||
we call attention to the following mathematical custom: | |||
Although every positive real number a has two square roots, | |||
in this book | |||
''the expression <math>\sqrt a</math> always denotes the positive root''. | |||
Thus the two solutions of the equation <math>x^2 = 5</math> are | |||
<math>\sqrt 5</math> and <math>-\sqrt 5</math>. | |||
Note that the two equations | |||
<math display="block"> | |||
x^2 = a | |||
</math> | |||
and | |||
<math display="block"> | |||
x = \sqrt a | |||
</math> | |||
are not equivalent. | |||
The second implies the first, but not conversely. | |||
On the other hand, | |||
<math display="block"> | |||
x^2 = a | |||
</math> | |||
and | |||
<math display="block"> | |||
|x| = \sqrt a | |||
</math> | |||
are equivalent. | |||
Having made these remarks, we observe that | |||
\begin{prop ]] | |||
</div></math> | |||
and since the positive square root of a product of two positive numbers | |||
is the product of their positive square roots, | |||
we get | |||
<math display="block"> | |||
|ab| = \sqrt {(ab)^2} = \sqrt {{a^2}{b^2}} = \sqrt{a^2} \sqrt{b^2} = |a| |b|. | |||
</math> | |||
To [[#thm 1.1.4 |prove]], | |||
we observe, first of all, that <math>ab \leq |ab|</math>. | |||
Hence | |||
<math display="block"> | |||
a^2 + 2ab + b^2 \leq a^2 + 2|ab| + b^{2} = |a|^2 + 2|a| |b| + |b|^2. | |||
</math> | |||
Thus, | |||
<math display="block"> | |||
|a + b|^{2} = (a + b)^{2} \leq (|a| + |b|)^{2}. | |||
</math> | |||
By taking the positive square root of each side of the inequality | |||
(see Problem [[exercise:C24f7adcb0 |Exercise]]), we [[#thm 1.1.4 |get]]. | |||
\end{proof} | |||
As remarked above, our list of [[#axiom.i |Axioms]] [[#axiom.x |through]] | |||
about the set <math>\R</math> of real numbers is incomplete. | |||
One important property of real numbers | |||
that together with the others gives a complete characterization | |||
is the following: | |||
\begin{axiom}[Least Upper Bound Property] | |||
\label{axiom.xi} | |||
Every nonempty subset of <math>\R</math> which has an upper bound | |||
has a least upper bound. | |||
\end{axiom} | |||
Suppose <math>S</math> is a nonempty subset of <math>\R</math> which has an upper bound. | |||
What [[#axiom.xi |Axiom]] says | |||
is that there is some number <math>b</math> which | |||
(1) is an upper bound, i.e., <math>s \leq b</math> for every <math>s</math> in <math>S</math>, and | |||
(2) if <math>c</math> is any other upper bound of <math>S</math>, then <math>b \leq c</math>. | |||
It is hard to see at first how such a statement can be so significant. | |||
Intuitively it says nothing more than this: | |||
If you cannot go on forever, you have to stop somewhere. | |||
Note, however, that the rational numbers do ''not'' have this property. | |||
The set of all rational numbers less than the irrational number <math>\sqrt2</math> | |||
certainly has an upper bound. | |||
In fact, each of the numbers | |||
<math>2</math>, <math>1.5</math>, <math>1.42</math>, <math>1.415</math>, <math>1.4143</math>, and <math>1.41422</math> is an upper bound. | |||
However, for every rational upper bound, | |||
there will always exist a smaller one. | |||
Hence there is no rational least upper bound. | |||
\end{exercise} | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Revision as of 01:06, 3 November 2024
Real Numbers, Inequalities, Absolute Values.
Calculus deals with numerical-valued quantities and, in the beginning, with quantities whose values are real numbers. Some understanding of the basic set [math]\R[/math] of all real numbers is therefore essential. A real number is one that can be written as a decimal: positive or negative or zero, terminating or nonterminating. Examples are
The most familiar subset of [math]R[/math] is the set [math]\Z[/math] of integers. These are the numbers
Another subset is the set [math]\Q[/math] of all rational numbers. A real number [math]r[/math] is \dt {rational} if it can be expressed as the ratio of two integers, more precisely, if [math]r = \frac{m}{n}[/math], where [math]m[/math] and [math]n[/math] are integers and [math]n \neq 0[/math]. Since every integer [math]m[/math] can be written [math]\frac{m}{1}[/math], it follows that every integer is also a rational number. A scheme, analogous to, which lists all the positive rational numbers is the following:
Of course there are infinitely many repetitions in this presentation since, for example, [math]\frac{2}{1} = \frac{4}{2} = \frac{6}{3} = \ldots.[/math] An unsophisticated guess would be that all real numbers are rational. There are, however, many famous proofs that this is not so. For example, a very simple and beautiful argument shows that [math]\sqrt 2[/math] is not rational. (See Problem Exercise at the end of this section.) It is not hard to prove that a real number is rational if and only if its decimal expansion beyond some digit consists of a finite sequence of digits repeated forever. Thus the numbers
are rational, but
is not. The fundamental algebraic operations on real numbers are addition and multiplication: For any two elements [math]a[/math] and [math]b[/math] in [math]\R[/math], two elements [math]a + b[/math] and [math]ab[/math] in [math]\R[/math] are uniquely determined. These elements, called the sum and product of [math]a[/math] and [math]b[/math], respectively, are defined so that the following six facts are true:
\begin{axiom}[Associative Laws] \label{axiom.i}
\end{axiom} \begin{axiom}[Commutative Laws] \label{axiom.ii}
\end{axiom} \begin{axiom}[Distributive Law] \label{axiom.iii}
\end{axiom} \begin{axiom}[Existence of Identities] \label{axiom.iv} [math]\R[/math] contains two distinct elements [math]0[/math] and [math]1[/math] with the properties that [math]0 + a = a[/math] and [math]1 \cdot a = a[/math] for every [math]a[/math] in [math]\R[/math]. \end{axiom}
\begin{axiom}[Existence of Subtraction] \label{axiom.v} For every [math]a[/math] in [math]\R[/math], there is an element in [math]\R[/math] denoted by [math]-a[/math] such that [math]a + (-a) = 0[/math]. \begin{note} [math]a - b[/math] is an abbreviation of [math]a + (-b)[/math]. \end{note} \end{axiom}
\begin{axiom}[Existence of Division] \label{axiom.vi} For every [math]a \neq 0[/math] in [math]\R[/math], there is an element in [math]\R[/math] denoted by [math]a^{-1}[/math] or [math]\frac{1}{a}[/math] such that [math]aa^{-1} = 1[/math]. \begin{note} [math]\frac{a}{b}[/math] is an abbreviation of [math]ab^{-1}[/math]. \end{note} \end{axiom} Addition and multiplication are here introduced as binary operations. However, as a result of the associative law of addition, [math]a + b + c[/math] is defined to be the common value of [math](a + b) + c[/math] and [math]a + (b + c)[/math]. In a like manner we may define the triple product [math]abc[/math] and, more generally, [math]a_{1} + \ldots + a_{n}[/math] and [math]a_{1} \ldots a_{n}[/math]. Many theorems of algebra are consequences of the above six facts, and we shall assume them without proof. They are, in fact, frequently taken as part of a set of axioms for [math]\R[/math]. Another essential property of the real numbers is that of order. We write [math]a \lt b[/math] as an abbreviation of the statement that [math]a[/math] is less than [math]b[/math]. Presumably the reader, given two decimals, knows how to tell which one is the smaller. The following four facts simply recall the basic properties governing inequalities. On the other hand, they may also be taken as axioms for an abstractly defined relation between elements of [math]\R[/math], which we choose to denote by [math] \lt [/math].
\begin{axiom}[Transitive Law] \label{axiom.vii} If [math]a \lt b[/math] and [math]b \lt c[/math], then [math]a \lt c[/math]. \end{axiom} \begin{axiom}[Law of Trichotomy] \label{axiom.viii} For every real number [math]a[/math], one and only one of the following alternatives holds: [math]a = 0[/math], or [math]a \lt 0[/math], or [math]0 \lt a[/math]. \end{axiom} \begin{axiom} \label{axiom.ix} If [math]a \lt b[/math], then [math]a + c \lt b + c[/math]. \end{axiom} \begin{axiom} \label{axiom.x} If [math]a \lt b[/math] and [math]0 \lt c[/math], then [math]ac \lt bc[/math]. \end{axiom}
Note that each of the above Axioms except remains true when restricted to the set [math]\Z[/math] of integers. Moreover, all the axioms are true for the set [math]\Q[/math] of rational numbers. Hence as a set of axioms for [math]\R[/math], they fail to distinguish between two very different sets: [math]\R[/math] and its subset [math]\Q[/math]. Later in this section we shall add one more item to the list, which will complete the algebraic description of [math]\R[/math]. A real number [math]a[/math] is if positive [math]0 \lt a[/math] and negative if [math]a \lt 0[/math]. Since the relation “greater than” is just as useful as “less than,” we adopt a symbol for it, too, and abbreviate the statement that [math]a[/math] is greater than [math]b[/math] by writing [math]a \gt b[/math]. Clearly [math]a \gt b[/math] if and only if [math]b \lt a[/math]. Axiom, when translated into English, says that the direction of an inequality is preserved if both sides are multiplied by the same positive number. Just the opposite happens if the number is negative: The inequality is reversed. That is,
If [math]a \lt b[/math] and [math]c \lt 0[/math], then [math]ac \gt bc[/math].
Since [math]c \lt 0[/math], [[#axiom.iv |Axioms,]], and imply
Two more abbreviations complete the mathematician's array of symbols for writing inequalities: [math]a \leq b[/math] means [math]a \lt b[/math] or [math]a=b[/math], [math]a \geq b[/math] means [math]a \gt b[/math] or [math]a=b[/math]. The geometric interpretation of the set [math]\R[/math] of all real numbers as a straight line is familiar to anyone who has ever used a ruler, and it is essential to an understanding of calculus. To describe the assignment of points to numbers, consider an arbitrary straight line [math]L[/math], and choose on it two distinct points, one of which we assign to, or identify with, the number [math]0[/math], and the other to the number [math]1[/math]. (See Figure.)
The rest is automatic. The scale on [math]L[/math] is chosen so that the unit of distance is the length of the line segment between the points [math]0[/math] and [math]1[/math]. Every positive number [math]a[/math] is assigned the point on the side of [math]0[/math] containing [math]1[/math] which is [math]a[/math] units of distance from [math]0[/math]. Every negative number [math]a[/math] is assigned the point on the side of [math]0[/math] not containing [math]1[/math] which is [math]-a[/math] units of distance from [math]0[/math]. Note that if [math]L[/math] is oriented so that [math]1[/math] lies to the right of [math]0[/math], then for any two numbers [math]a[/math] and [math]b[/math] (positive, negative, or zero), [math]a \lt b[/math] if and only if [math]a[/math] lies to the left of [math]b[/math]. A line which has been identified with [math]\R[/math] under a correspondence such as the one just described is called a real number line. (See Figure.)
An interval is a subset [math]I[/math] of [math]\R[/math] with the property that whenever [math]a[/math] and [math]c[/math] belong to [math]I[/math] and [math]a \leq b \leq c[/math], then [math]b[/math] also belongs to [math]I[/math]. Geometrically an interval is a connected piece of a real number line. A number d is called a lower bound of a set [math]S[/math] of real numbers if [math]d \leq s[/math] for every [math]s[/math] in [math]S[/math]. It is an upper bound of [math]S[/math] if [math]s \leq d[/math] for every [math]s[/math] in [math]S[/math]. A given subset of [math]\R[/math], and in particular an interval, is called bounded if it has both an upper and lower bound. There are four different kinds of bounded intervals: [math](a, b)[/math], the set of all numbers [math]x[/math] such that [math]a \lt x \lt b[/math]; [math][a, b][/math], the set of all numbers [math]x[/math] such that [math]a \leq x \leq b[/math]; [math][a, b)[/math], the set of all numbers [math]x[/math] such that [math]a \leq x \lt b[/math]; [math](a, b][/math], the set of all numbers [math]x[/math] such that [math]a \lt x \leq b[/math]. In each case the numbers [math]a[/math] and [math]b[/math] are called the endpoints of the interval. The set [math][a, b][/math] contains both its endpoints, whereas [math](a, b)[/math] contains neither one. Clearly [math][a, b)[/math] contains its left endpoint but not its right one, and an analogous remark holds for [math](a, b][/math]. It is important to realize that there is no element [math]\infty[/math] (infinity) in the set [math]\R[/math]. Nevertheless, the symbols [math]\infty[/math] and [math]-\infty[/math] are commonly used in denoting unbounded intervals. Thus [math](a, \infty)[/math] is the set of all numbers [math]x[/math] such that [math]a \lt x[/math]; [math][a, \infty)[/math] is the set of all numbers [math]x[/math] such that [math]a \leq x[/math]; [math](-\infty, a)[/math] is the set of all numbers [math]x[/math] such that [math]x \lt a[/math]; [math](-\infty, a][/math] is the set of all numbers [math]x[/math] such that [math]x \leq a[/math]; [math](-\infty, \infty)[/math] is the entire set [math]\R[/math]. The symbols [math]\infty[/math] and [math]-\infty[/math] also appear frequently in inequalities although they are really unnecessary, because, for example,
}, \end{array} </math> etc. Since [math]\infty[/math] is not an element of [math]\R[/math], we shall never use the notations [math][a, \infty], x \leq \infty[/math], etc. An unbounded interval has either one endpoint or none; in each of the above cases it is the number [math]a[/math]. We call an interval open if it contains none of its endpoints, and closed if it contains them all. Thus, for example, [math](a, b)[/math] and [math](-\infty, a)[/math] are open, but [math][a, b][/math] and [math][a, \infty)[/math] are closed. The intervals [math][a, b)[/math] and [math](a, b][/math] are neither open nor closed, although they are sometimes called half-open or half-closed. Since [math](-\infty, \infty)[/math] has no endpoints, it vacuously both does and does not contain them. Hence [math](-\infty, \infty)[/math] has the dubious distinction of being both open and closed.
Example
\label{exam 1.1.1} Draw the intervals [math][0, 1][/math], [math][-1, 4)[/math], [math](2, \infty[/math]), [math](-\infty, -1][/math], [math](-1, 3)[/math], and identify them as open, closed, neither, or both (see Figure).
It is frequently necessary to talk about the size of a real number without regard to its sign, not caring whether it is positive or negative. This happens often enough to warrant a definition and special notation: The absolute value of a real number [math]a[/math] is denoted by [math]|a|[/math] and defined by
}.
\end{array}
\right. </math> Thus [math]|3| = 3[/math], [math]|0| = 0[/math], [math]|- 3| = 3[/math]. Obviously, the absolute value of a real number cannot be negative. Geometrically, [math]|a|[/math] is the distance between the points [math]0[/math] and [math]a[/math] on the real number line. A generalization that is of extreme importance is the fact that [math]|a - b|[/math] is the distance between the points [math]a[/math] and [math]b[/math] on the real number line for any two numbers [math]a[/math] and [math]b[/math] whatsoever. Probably the best way to convince oneself that this is true is to look at a few illustrations (see Figure).
Example
\label{exam 1.1.2} Describe the set [math]I[/math] of all real numbers [math]x[/math] such that [math]|x - 5| \lt 3[/math]. For any number [math]x[/math], the number [math]|x - 5|[/math] is the distance between [math]x[/math] and [math]5[/math] on a real number line (see Figure).
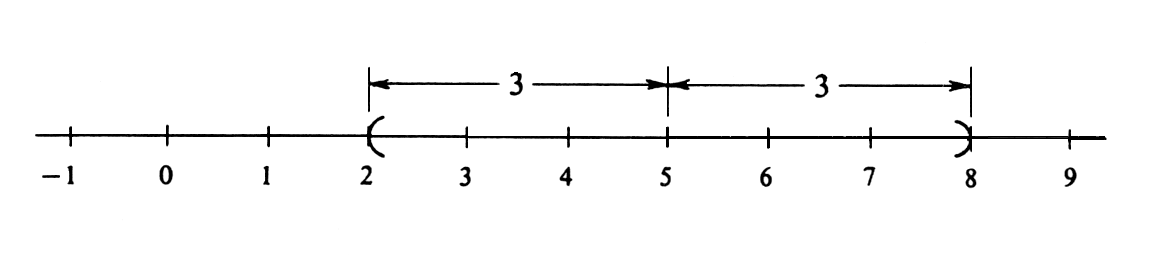
</math>
and since the positive square root of a product of two positive numbers is the product of their positive square roots, we get
To prove, we observe, first of all, that [math]ab \leq |ab|[/math]. Hence
Thus,
By taking the positive square root of each side of the inequality (see Problem Exercise), we get. \end{proof} As remarked above, our list of Axioms through about the set [math]\R[/math] of real numbers is incomplete. One important property of real numbers that together with the others gives a complete characterization is the following:
\begin{axiom}[Least Upper Bound Property] \label{axiom.xi} Every nonempty subset of [math]\R[/math] which has an upper bound has a least upper bound. \end{axiom} Suppose [math]S[/math] is a nonempty subset of [math]\R[/math] which has an upper bound. What Axiom says is that there is some number [math]b[/math] which (1) is an upper bound, i.e., [math]s \leq b[/math] for every [math]s[/math] in [math]S[/math], and (2) if [math]c[/math] is any other upper bound of [math]S[/math], then [math]b \leq c[/math]. It is hard to see at first how such a statement can be so significant. Intuitively it says nothing more than this: If you cannot go on forever, you have to stop somewhere. Note, however, that the rational numbers do not have this property. The set of all rational numbers less than the irrational number [math]\sqrt2[/math] certainly has an upper bound. In fact, each of the numbers [math]2[/math], [math]1.5[/math], [math]1.42[/math], [math]1.415[/math], [math]1.4143[/math], and [math]1.41422[/math] is an upper bound. However, for every rational upper bound, there will always exist a smaller one. Hence there is no rational least upper bound. \end{exercise}
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.