guide:3c6a2362c1: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
==<span id="sec 2.6"></span>The Differential.== | |||
If <math>y = f(x)</math>, we have denoted the derivative of <math>f</math> by <math>f'</math>, or <math>\frac{df}{dx}</math>, or <math>\frac{dy}{dx}</math>. The value of the derivative at a number a is written <math>f'(a)</math>, or <math>\frac{df}{dx} (a)</math>, or <math>\frac{dy}{dx} (a)</math>. Up to this point, the expressions <math>df</math>, <math>dy</math>, and <math>dx</math> by themselves have had no meaning other than as parts of notations for the derivative. However, the cancellation suggested by the Chain Rule | |||
<math display="block"> | |||
\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} | |||
</math> | |||
indicates that the derivative behaves like a ratio and suggests that it may be possible to sensibly regard it as such. In this section we shall define a mathematical object called the differential of a function, examples of which are <math>df</math>, <math>dy</math>, and <math>dx</math>. The ratio of <math>df</math>, or <math>dy</math>, to <math>dx</math> will be equal to the derivative. | |||
<div id="fig 2.20" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig2_20.png | 400px | thumb | ]] | |||
</div> | |||
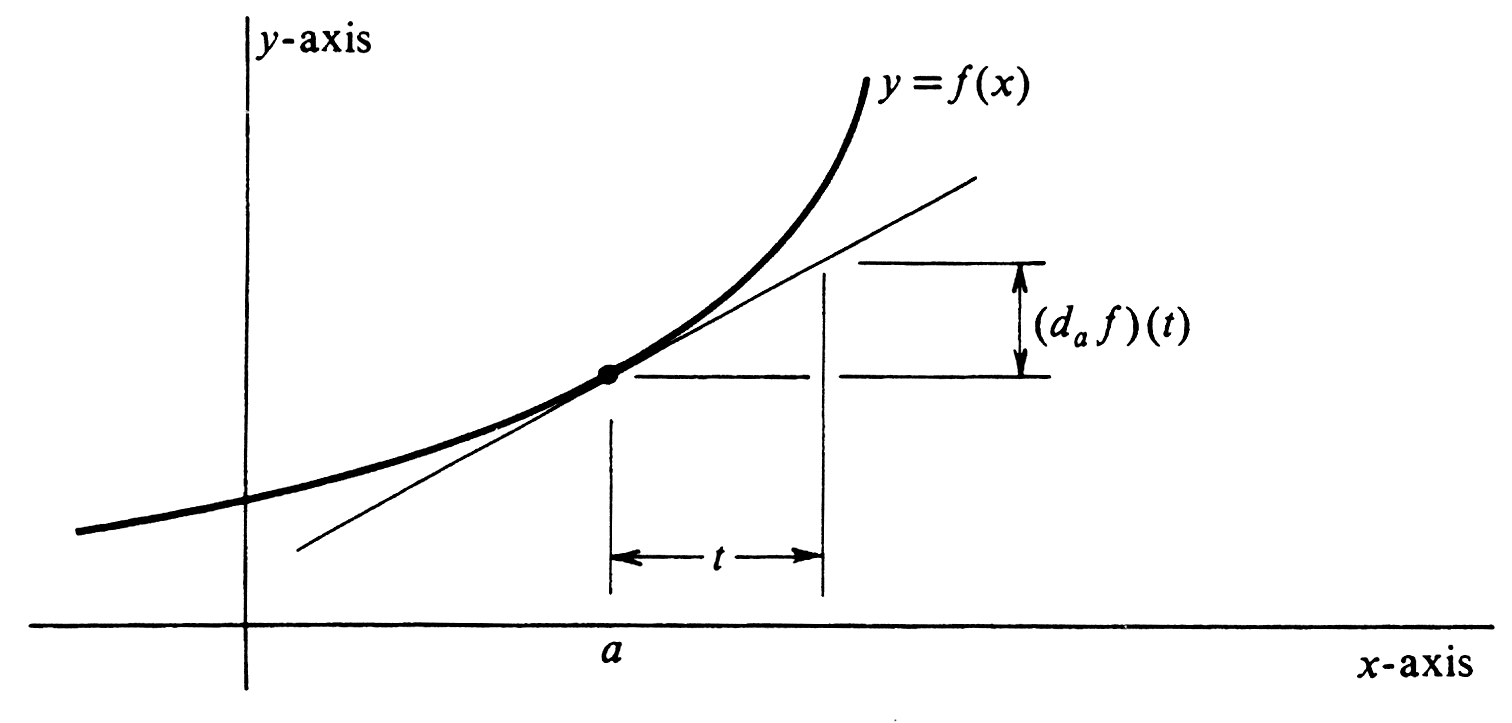
If <math>f</math> is a function having a derivative at <math>a</math>, we define its '''differential at''' <math>a</math>, denoted by <math>d_{a}f</math>, to be the linear function whose value for any number <math>t</math> is | |||
<math display="block"> | |||
(d_{a}f)(t) = f'(a)t. | |||
</math> | |||
For example, if <math>f(x) = x^2 - 2x</math>, then the differential <math>d_{a}f</math> is the function of <math>t</math> defined by <math>f'(a)t = (2a - 2)t</math>. In particular, | |||
<math display="block"> | |||
(d_{3}f)(t)= [2 \cdot 3 - 2]t = 4t. | |||
</math> | |||
The value of the differential for a typical function <math>f</math> is illustrated in [[#fig 2.20|Figure]]. | |||
By simply <math>df</math> we mean the rule (or function) that assigns the linear function <math>d_{x}f</math> to each number <math>x</math> in the domain of <math>f'</math>. | |||
{{proofcard|Theorem|eq2.6.1|If <math>f</math> and <math>u</math> are differentiablefunctions, then | |||
<math display="block"> | |||
\begin{equation} | |||
df(u) = f'(u)du. | |||
\end{equation} | |||
</math> | |||
|This formula is an abbreviation of the equation | |||
<span id{{=}}"eq2.6.2"/> | |||
<math display="block"> | |||
\begin{equation} | |||
d_{x} f(u) = f'(u(x)) d_{x}u. | |||
\label{eq2.6.2} | |||
\end{equation} | |||
</math> | |||
The proof is an application of the Chain Rule. | |||
We first write down the two linear functions <math>d_{x}f(u)</math> and <math>d_{x}u</math>. By the definition of the differential they are | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
(d_{x}u)(t) &=& u'(x)t,\\ | |||
(d_{x}f(u))(t) &=& [[f(u)]'(x)]t. | |||
\end{eqnarray*} | |||
</math> | |||
The Chain Rule says that <math>[f(u)]'(x) = f'(u(x))u'(x)</math>. Hence | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
(d_{x} f(u) )(t) &=& [f'(u(x) )u'(x)]t \\ | |||
&=& f'(u(x))(d_{x}u)(t). | |||
\end{eqnarray*} | |||
</math> | |||
Thus (2) appears as an equality between linear functions, | |||
and the proof is complete.}} | |||
If <math>u</math> is the independent variable <math>x</math>, then (6.1) reduces to the formula | |||
<span id{{=}}"eq2.6.3"/> | |||
<math display="block"> | |||
\begin{equation} | |||
df(x) = f'(x)dx. | |||
\label{eq2.6.3} | |||
\end{equation} | |||
</math> | |||
<span id="thm drules"/> | |||
'''Example''' | |||
Evaluate the following differentials: | |||
\item[a] <math>d(x^2 + 2)</math>, | |||
\item[b] <math>d\sqrt{x^2 + 3}</math>, | |||
\item[c] <math>d(2x^2-x)^7</math>.] | |||
Using formula (3), we get immediately | |||
\item[(a') <math>d(x^2 + 2) = 2xdx</math> | |||
\item[(b') <math>d\sqrt{x^2 + 3} = x(x^2 + 3)^{-1/2} dx</math>] | |||
\item[(c') <math>d(2x^2-x)^7 = 7(2x^2-x)^6(4x-1)dx</math>.] | |||
It is worthwhile learning to use the stronger formula (1). In problem (b), let <math>f</math> be the function <math>f(u) = \sqrt{u}</math>. If we set <math>u = x^2 + 3</math>, then <math>du = 2x dx</math> and | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
d\sqrt{x^2 + 3} &=& df(u) = f'(u) du\\ | |||
&=& \frac{1}{2}u^{-1/2}du\\ | |||
&=& \frac{1}{2}(x^2 + 3)^{-1/2}2x dx. | |||
\end{eqnarray*} | |||
</math> | |||
Let us also do problem (c) using (1), but without explicitly making the substitution <math>u = 2x^2 - x</math>. We get | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
d(2x^2 - x)^7 &=& 7(2x^2 - x)^{6} d(2x^2 - x)\\ | |||
&=& 7(2x^2 - x)^{6} (4x - 1) dx. | |||
\end{eqnarray*} | |||
</math> | |||
Formula (3) establishes the fact that the ratio of <math>df</math> to <math>dx</math> is equal to the derivative <math>f'</math>. We can see this in greater detail by going back to the definitions: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
(d_{a}f)(t) &=& f'(a)t, \\ | |||
(d_{a}x)(t) &=& x'(a)t. | |||
\end{eqnarray*} | |||
</math> | |||
Since <math>x</math> is the identity function, its derivative is the constant function 1. Hence <math>(d_{a}x)(t) = t.</math> The ratio of the two linear functions <math>d_{a}f</math> and <math>d_{a}x</math> is thus the constant function | |||
<math display="block"> | |||
\frac{d_{a}f}{d_{a}x} = \frac{f'(a)t}{t} = f'(a). | |||
</math> | |||
Having proved this formula for every a in the domain of <math>f'</math>, we can write it simply as | |||
<math display="block"> | |||
\frac{df}{dx} (a) = f'(a) \;\;\; \mbox{or} \;\;\; \frac{df}{dx} = f'. | |||
</math> | |||
If <math>f</math> and <math>g</math> are differentiable functions, then it is easy to show that <math>d_{a}(f + g) = d_{a}f + d_{a}g</math>. The proof involves only the definition of the differential plus the fact that the derivative of a sum is the sum of the derivatives. In detail: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
[d_{a}(f + g)](t) &=& [(f + g)'(a)] t = [f' (a) + g'(a)] t\\ | |||
&=& f'(a)t + g'(a)t = (d_{a}f)(t) + (d_{a}g)(t)\\ | |||
&=& [d_{a}f + d_{a}g](t) . | |||
\end{eqnarray*} | |||
</math> | |||
The result is simply the equation | |||
<math display="block"> | |||
d(f + g) = df + dg. | |||
</math> | |||
An analogous argument using the Product Rule for differentiation shows that <math>d_{a}(fg) = f(a)d_{a}g + g(a)d_{a}f</math>, or, more simply, | |||
<math display="block"> | |||
d(fg) = f dg + g df. | |||
</math> | |||
For each one of the six differentiation [[guide:0115c430d0#thm ddxrules |rules]] | |||
proved in Section \secref{1.7} of Chapter \ref{chp 1}, | |||
there is an analogous rule in terms of differentials: | |||
Let <math>u</math> and <math>v</math> be differentiable functions, and <math>c</math> a constant. Then | |||
{{proofcard|Proposition|thm_drules|\item [(i)] <math>d(u + v) = du + dv</math>, | |||
\item [(ii)] <math>d(cu)= cdu</math>, | |||
\item [(iii)] <math>dc= 0</math>, | |||
\item [(iv)] <math>d(uv) = u dv + v du</math>, | |||
\item [(v)] | |||
<math>du^r = ru^{r-1}du, \provx{where </math>r<math> is any rational number,}</math> | |||
\item [(vi)] <math>d \biggl(\frac{u}{v} \biggr) = \frac{vdu - udv}{v^2}</math>.|}} | |||
Note that we have replaced the analogue of (v) | |||
in the list in Section \secref{1.7} of Chapter \ref{chp 1} | |||
by the formula corresponding to the more powerful [[guide:Fee760f50f#thm 1.8.2 |theorem]] of Chapter \ref{chp 1}. | |||
'''Example''' | |||
Find the differential <math>d(x^3 + \sqrt{x^2 + 2x})^7</math>. Applying the above formulas successively, we get | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
d(x^3 + \sqrt{x^2 + 2x})^7 | |||
&=& 7(x^3 + \sqrt{x^2 + 2x})^6 d(x^3 + \sqrt{x^2 + 2x}) \;\;\;\mbox{by (v)}\\ | |||
&=& 7(x^3 + \sqrt{x^2 + 2x})^6 (dx^3 + d\sqrt{x^2 + 2x}) \;\;\;\mbox{by (i)}\\ | |||
&=& 7(x^3 + \sqrt{x^2 + 2x})^6 [3x^2 dx + \frac{1}{2}(x^2 + 2x)^{-1/2} d(x^2 + 2x)] \\ | |||
& & \mbox{by (v)}\\ | |||
&=& 7(x^3 + \sqrt{x^2 + 2x})^6 [3x^2 dx + \frac{1}{2}(x^2 + 2x)^{-1/2} (2x dx + 2 dx)] \\ | |||
& & \mbox{by (i) and (ii)} \\ | |||
&=& 7(x^3 + \sqrt{x^2 + 2x})^6 \biggl( 3x^2 +\frac{x+1}{\sqrt{x^2 + | |||
2x}}\biggr) dx. | |||
\end{eqnarray*} | |||
</math> | |||
The derivative is therefore given by | |||
<math display="block"> | |||
\frac{d(x^3 + \sqrt{x^2 + 2x})^7}{dx} = 7(x^3 + \sqrt{x^2 + 2x})^6 \biggl(3x^2 + \frac{x + | |||
1}{\sqrt{x^2 + 2x}}\biggr). | |||
</math> | |||
The task of computing the differential of a complicated function of <math>x</math> amounts to successively working the differential operator d through the given expression from left to right. At each stage one uses the correct one of formulas (i) through (vi), or formula (1), until one finally reaches <math>dx</math>, and the process stops. The derivative can then be obtained by dividing the resulting equation by <math>dx</math>. Note that an equation of the form <math>df(x) = ...</math> will always contain the symbol <math>d</math> on the right side. Equations such as <math>dx^5 = 5x^4</math> are not only false; they are nonsense. (Correct version: <math>dx^5 = 5x^4 dx</math>.) | |||
'''Example''' | |||
Consider the functions | |||
\item [(a) <math>y = (4x^3 + 3x^2 + 1)^2,</math>] | |||
\item [(b) <math>y = \frac{x^2 -1}{x^2 + 1}</math>] | |||
\item [(c) <math>z = 3y^{5/3}.</math>] | |||
Find the differential of each: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\mbox{(a')}\; dy &=& 2(4x^3 + 3x^2 + 1) d(4x^3 + 3x^2 + 1) \\ | |||
&=& 2(4x^3 + 3x^2 + 1)(12x^2 dx + 6x dx) \\ | |||
&=& 12x(4x^3 + 3x^2 + 1)(2x + 1) dx, | |||
\end{eqnarray*} | |||
</math> | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\mbox{(b')}\; dy &=& \frac{(x^2 + 1 ) d(x^2 - 1 ) - (x^2 - 1 ) d(x^2 + 1 )}{(x^2 + 1 )^2}\\ | |||
&=& \frac{(x^2 + 1)2xdx - (x^2 - 1)2xdx}{(x^2 + 1)^2} = \frac{4x dx}{(x^2 + 1)^2}, | |||
\end{eqnarray*} | |||
</math> | |||
<math display="block"> | |||
\mbox{(c')}\; dz = (3)(\frac{5}{3})y^{2/3}dy= 5y^{2/3}dy. | |||
</math> | |||
If we consider the composition of the function <math>y</math> in (b) with the function <math>z</math> in (c), we get for the differential of the composition | |||
<math display="block"> | |||
dz = 5y^{2/3} \frac{4x dx}{(x^2 + 1)^2} = 5 \biggl(\frac{x^2 - 1}{x^2 + 1} \biggr)^{2/3} \frac{4x}{(x^2 + 1)^2} dx. | |||
</math> | |||
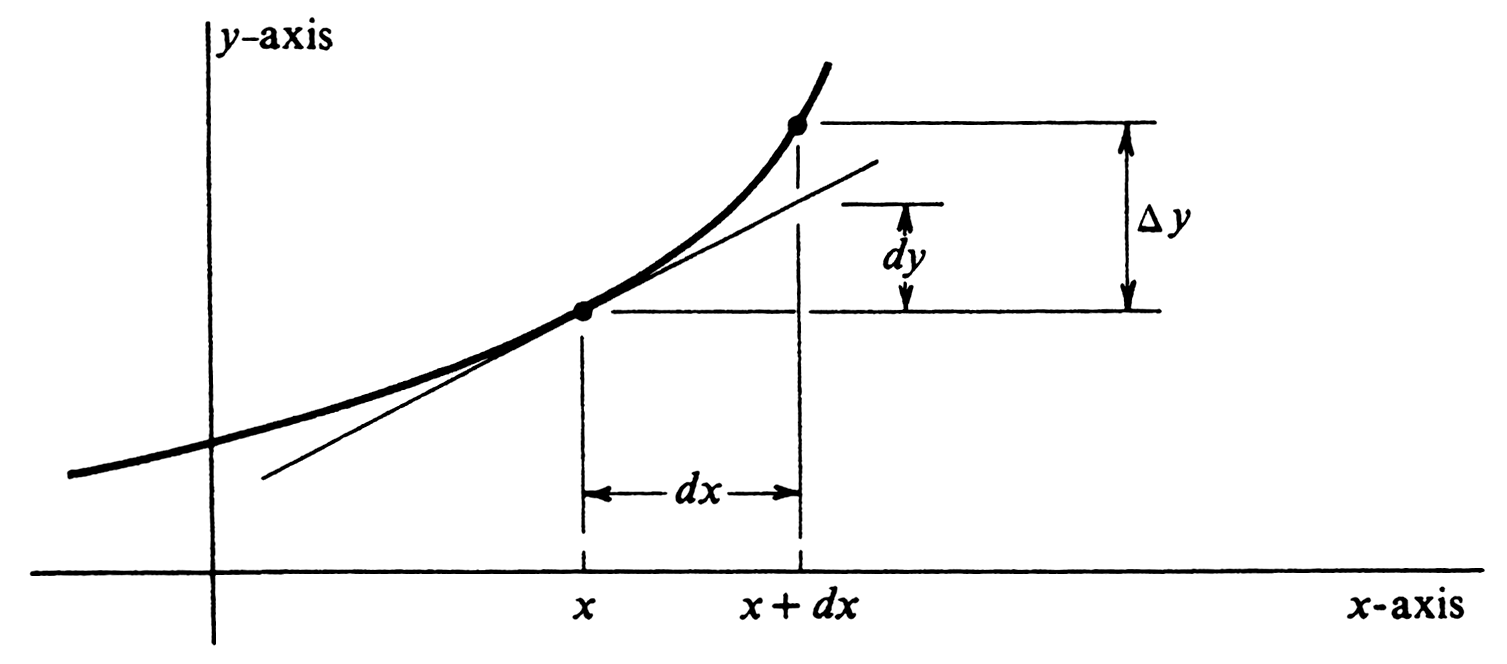
One traditional interpretation of the differential, which is especially useful in physics, is that of an “infinitesimal.” If <math>y = f(x)</math>, we know that <math>dy = f'(x) dx</math>. Now <math>dx</math> is the function that assigns to every real number a the linear function defined by <math>(d_{a}x)(t) = x'(a)t = t</math>; i.e., it assigns the identity function. Hence we can interpret <math>dx</math> as simply another independent variable. Then <math>dy</math> is the variable whose value for a given <math>x</math> and <math>dx</math> is shown in [[#fig 2.21|Figure]]. (Compare this illustration with [[#fig 2.20|Figure]].) The difference between the value of <math>f</math> at <math>x</math> and at <math>x + dx</math> is denoted by <math>\Delta y</math> in the figure. If <math>dx</math> is chosen <math>y</math>-axis very small, then the difference between <math>dy</math> and <math>\Delta y</math> is relatively negligible. Hence <math>dy</math> measures the resulting change in the value of <math>y = f(x)</math> corresponding to an infinitesimal change <math>dx</math> in the variable <math>x</math>. | |||
<div id="fig 2.21" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig2_21.png | 400px | thumb | ]] | |||
</div> | |||
'''Example''' | |||
The height <math>h</math> of a square pyramid is found to be 100 feet, and the length <math>x</math> of one edge of its base is measured to be 160 feet. The volume <math>V</math> of the pyramid is given by the formula <math>V = \frac{1}{3}hx^2</math>. What error in the computed | |||
volume will result from an error of 4 inches in the measurement of <math>x</math>? If we consider <math>h</math> as fixed, and <math>V</math> as a function of <math>x</math>, then | |||
<math display="block"> | |||
dV = \frac{1}{3}h dx^2 = \frac{2}{3}hx dx. | |||
</math> | |||
Since 4 inches is small compared with 160 feet, we set <math>dx</math> = 4 inches = <math>\frac{1}{3}</math> foot. The resulting change in volume is then approximately | |||
<math display="block"> | |||
dV = \frac{2}{3}(100)(160)\frac{1}{3} = \frac{32}{9} 1000 = 3555 \;\mbox{feet}^3. | |||
</math> | |||
The percentage error in volume is | |||
<math display="block"> | |||
\frac{dV}{V} = \frac{ {\frac{2}{3}} hx dx}{{\frac{1}{3}}hx^2} = 2 \frac{dx}{x}. | |||
</math> | |||
We compute <math>\frac{dx}{x} = \frac{\frac{1}{3}}{160} = 0.0021 = 0.21\%</math>, and so the percentage error in volume is only <math>0.42\%</math>. | |||
\end{exercise} | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Latest revision as of 01:07, 3 November 2024
The Differential.
If [math]y = f(x)[/math], we have denoted the derivative of [math]f[/math] by [math]f'[/math], or [math]\frac{df}{dx}[/math], or [math]\frac{dy}{dx}[/math]. The value of the derivative at a number a is written [math]f'(a)[/math], or [math]\frac{df}{dx} (a)[/math], or [math]\frac{dy}{dx} (a)[/math]. Up to this point, the expressions [math]df[/math], [math]dy[/math], and [math]dx[/math] by themselves have had no meaning other than as parts of notations for the derivative. However, the cancellation suggested by the Chain Rule
indicates that the derivative behaves like a ratio and suggests that it may be possible to sensibly regard it as such. In this section we shall define a mathematical object called the differential of a function, examples of which are [math]df[/math], [math]dy[/math], and [math]dx[/math]. The ratio of [math]df[/math], or [math]dy[/math], to [math]dx[/math] will be equal to the derivative.
If [math]f[/math] is a function having a derivative at [math]a[/math], we define its differential at [math]a[/math], denoted by [math]d_{a}f[/math], to be the linear function whose value for any number [math]t[/math] is
For example, if [math]f(x) = x^2 - 2x[/math], then the differential [math]d_{a}f[/math] is the function of [math]t[/math] defined by [math]f'(a)t = (2a - 2)t[/math]. In particular,
The value of the differential for a typical function [math]f[/math] is illustrated in Figure. By simply [math]df[/math] we mean the rule (or function) that assigns the linear function [math]d_{x}f[/math] to each number [math]x[/math] in the domain of [math]f'[/math].
If [math]f[/math] and [math]u[/math] are differentiablefunctions, then
This formula is an abbreviation of the equation
If [math]u[/math] is the independent variable [math]x[/math], then (6.1) reduces to the formula
Example
Evaluate the following differentials:
\item[a] [math]d(x^2 + 2)[/math], \item[b] [math]d\sqrt{x^2 + 3}[/math], \item[c] [math]d(2x^2-x)^7[/math].]
Using formula (3), we get immediately
\item[(a') [math]d(x^2 + 2) = 2xdx[/math] \item[(b') [math]d\sqrt{x^2 + 3} = x(x^2 + 3)^{-1/2} dx[/math]] \item[(c') [math]d(2x^2-x)^7 = 7(2x^2-x)^6(4x-1)dx[/math].]
It is worthwhile learning to use the stronger formula (1). In problem (b), let [math]f[/math] be the function [math]f(u) = \sqrt{u}[/math]. If we set [math]u = x^2 + 3[/math], then [math]du = 2x dx[/math] and
Let us also do problem (c) using (1), but without explicitly making the substitution [math]u = 2x^2 - x[/math]. We get
Formula (3) establishes the fact that the ratio of [math]df[/math] to [math]dx[/math] is equal to the derivative [math]f'[/math]. We can see this in greater detail by going back to the definitions:
Since [math]x[/math] is the identity function, its derivative is the constant function 1. Hence [math](d_{a}x)(t) = t.[/math] The ratio of the two linear functions [math]d_{a}f[/math] and [math]d_{a}x[/math] is thus the constant function
Having proved this formula for every a in the domain of [math]f'[/math], we can write it simply as
If [math]f[/math] and [math]g[/math] are differentiable functions, then it is easy to show that [math]d_{a}(f + g) = d_{a}f + d_{a}g[/math]. The proof involves only the definition of the differential plus the fact that the derivative of a sum is the sum of the derivatives. In detail:
The result is simply the equation
An analogous argument using the Product Rule for differentiation shows that [math]d_{a}(fg) = f(a)d_{a}g + g(a)d_{a}f[/math], or, more simply,
For each one of the six differentiation rules proved in Section \secref{1.7} of Chapter \ref{chp 1}, there is an analogous rule in terms of differentials: Let [math]u[/math] and [math]v[/math] be differentiable functions, and [math]c[/math] a constant. Then
\item [(i)] [math]d(u + v) = du + dv[/math], \item [(ii)] [math]d(cu)= cdu[/math], \item [(iii)] [math]dc= 0[/math], \item [(iv)] [math]d(uv) = u dv + v du[/math], \item [(v)] [math]du^r = ru^{r-1}du, \provx{where [/math]r[math] is any rational number,}[/math] \item [(vi)] [math]d \biggl(\frac{u}{v} \biggr) = \frac{vdu - udv}{v^2}[/math].
Note that we have replaced the analogue of (v) in the list in Section \secref{1.7} of Chapter \ref{chp 1} by the formula corresponding to the more powerful theorem of Chapter \ref{chp 1}.
Example
Find the differential [math]d(x^3 + \sqrt{x^2 + 2x})^7[/math]. Applying the above formulas successively, we get
The derivative is therefore given by
The task of computing the differential of a complicated function of [math]x[/math] amounts to successively working the differential operator d through the given expression from left to right. At each stage one uses the correct one of formulas (i) through (vi), or formula (1), until one finally reaches [math]dx[/math], and the process stops. The derivative can then be obtained by dividing the resulting equation by [math]dx[/math]. Note that an equation of the form [math]df(x) = ...[/math] will always contain the symbol [math]d[/math] on the right side. Equations such as [math]dx^5 = 5x^4[/math] are not only false; they are nonsense. (Correct version: [math]dx^5 = 5x^4 dx[/math].) Example
Consider the functions
\item [(a) [math]y = (4x^3 + 3x^2 + 1)^2,[/math]] \item [(b) [math]y = \frac{x^2 -1}{x^2 + 1}[/math]] \item [(c) [math]z = 3y^{5/3}.[/math]]
Find the differential of each:
If we consider the composition of the function [math]y[/math] in (b) with the function [math]z[/math] in (c), we get for the differential of the composition
One traditional interpretation of the differential, which is especially useful in physics, is that of an “infinitesimal.” If [math]y = f(x)[/math], we know that [math]dy = f'(x) dx[/math]. Now [math]dx[/math] is the function that assigns to every real number a the linear function defined by [math](d_{a}x)(t) = x'(a)t = t[/math]; i.e., it assigns the identity function. Hence we can interpret [math]dx[/math] as simply another independent variable. Then [math]dy[/math] is the variable whose value for a given [math]x[/math] and [math]dx[/math] is shown in Figure. (Compare this illustration with Figure.) The difference between the value of [math]f[/math] at [math]x[/math] and at [math]x + dx[/math] is denoted by [math]\Delta y[/math] in the figure. If [math]dx[/math] is chosen [math]y[/math]-axis very small, then the difference between [math]dy[/math] and [math]\Delta y[/math] is relatively negligible. Hence [math]dy[/math] measures the resulting change in the value of [math]y = f(x)[/math] corresponding to an infinitesimal change [math]dx[/math] in the variable [math]x[/math].
Example
The height [math]h[/math] of a square pyramid is found to be 100 feet, and the length [math]x[/math] of one edge of its base is measured to be 160 feet. The volume [math]V[/math] of the pyramid is given by the formula [math]V = \frac{1}{3}hx^2[/math]. What error in the computed volume will result from an error of 4 inches in the measurement of [math]x[/math]? If we consider [math]h[/math] as fixed, and [math]V[/math] as a function of [math]x[/math], then
Since 4 inches is small compared with 160 feet, we set [math]dx[/math] = 4 inches = [math]\frac{1}{3}[/math] foot. The resulting change in volume is then approximately
The percentage error in volume is
We compute [math]\frac{dx}{x} = \frac{\frac{1}{3}}{160} = 0.0021 = 0.21\%[/math], and so the percentage error in volume is only [math]0.42\%[/math].
\end{exercise}
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.