guide:5103dec63d: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
==<span id="sec 5.1"></span>The Natural Logarithm.== | |||
If <math>f</math> is any real-valued function of a real variable which is continuous on some interval, we have seen that there exists an antiderivative, or indefinite integral, <math>F</math> such that <math>F'(x) = f(x)</math> for every <math>x</math> in the interval. For some functions we have been able to write their antiderivatives explicitly. For example, if <math>f(x) = x^r</math> and <math>r</math> is a rational number different from -1, then the general antiderivative is | |||
<math display="block"> | |||
\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + c, | |||
</math> | |||
where <math>c</math> is an arbitrary constant. This formula is not applicable if <math>r = - 1</math>. Nevertheless, <math>\frac{1}{x}</math> is certainly continuous on the interval <math>(0, \infty)</math>, and therefore some function has it for a derivative. For every positive number <math>a</math>, we can define such a function by writing | |||
<math display="block"> | |||
F(x) = \int_{a}^{x} \frac{dt}{t}, \;\;\;\mbox{for every}\; x > 0. | |||
</math> | |||
For then by the Fundamental Theorem of Calculus [see Theorem (5.2), page 200], | |||
<math display="block"> | |||
F'(x)= \frac{1}{x}. | |||
</math> | |||
To be specific, we choose <math>a = 1</math> and select <math>\int_{1}^{x} \frac{dt}{t}</math> for a particular antiderivative of <math>\frac{1}{x}</math>. As we shall see, this function is interesting enough to have a special name and a special notation. The notation we shall use is <math>\ln\;(x)</math>, or, more briefly, <math>\ln\; x</math>, and we shall save the name and reason for its choice until we have investigated its properties. | |||
For now, we define | |||
<math display="block"> | |||
\ln\; x = \int_{1}^{x} \frac{dt}{t}, \;\;\;\mbox{ for every}\; x > 0. | |||
</math> | |||
The reason that <math>x</math> must be positive in this definition is that the function <math>\frac{1}{t}</math> has a discontinuity at <math>t = 0</math>. If <math>x</math> is negative, the integral does not exist and <math>\ln x</math> is not defined. | |||
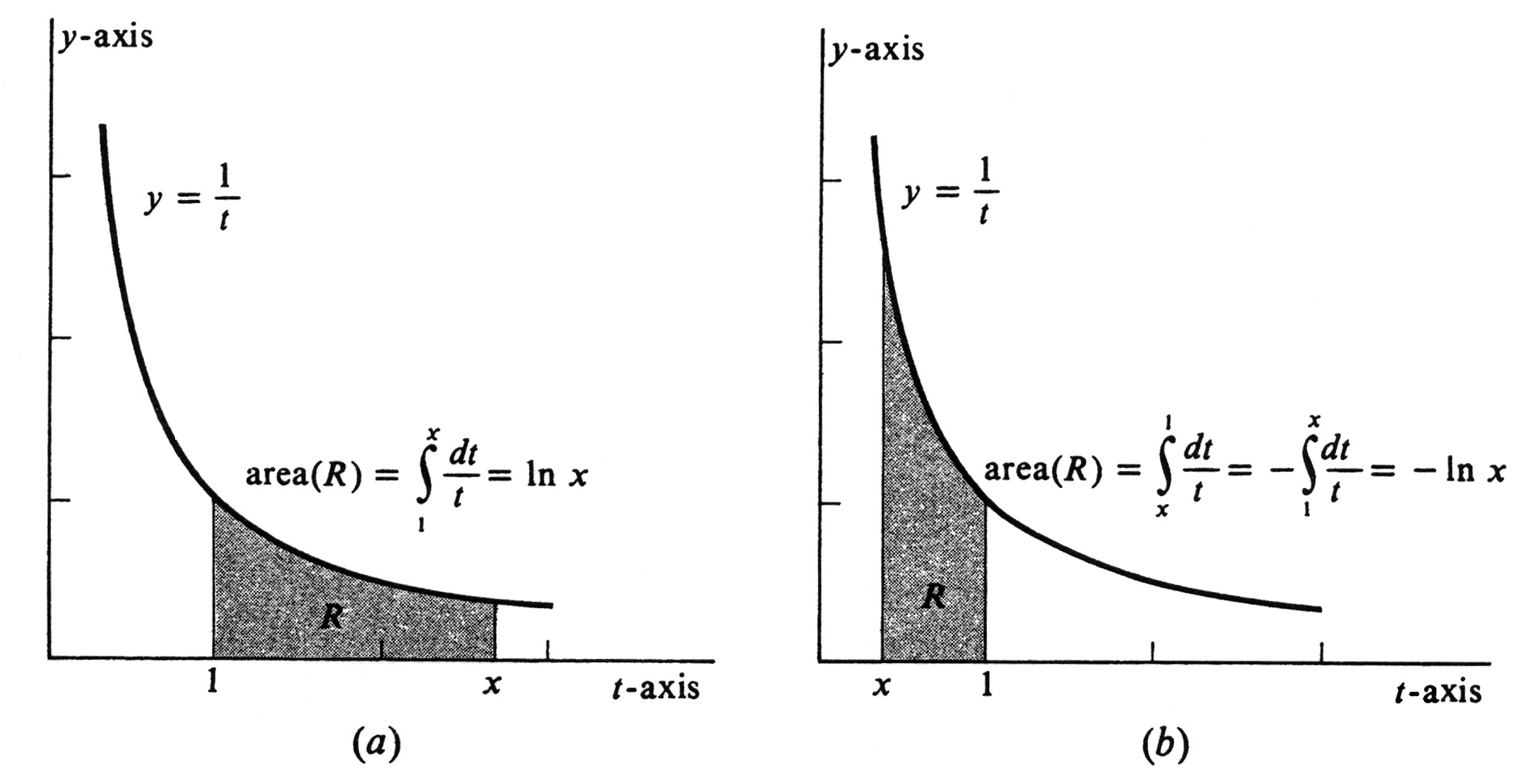
Geometrically, In <math>x</math> is an area or the negative of an area. If <math>x > 1</math>, then <math>\ln x</math> is the area of the region bounded by the hyperbola <math>y = \frac{1}{t}</math>, the <math>t</math>-axis, and the lines <math>t = 1</math> and <math>t = x</math> [see [[#fig 5.1|Figure]](a)]. On the other hand, if <math>0 < x < 1</math>, we have | |||
<math display="block"> | |||
\ln\; x = \int_{1}^{x} \frac{dt}{t} = -\int_{x}^{1} \frac{dt}{t}, | |||
</math> | |||
and <math>\ln x</math> is the negative of the area shown in [[#fig 5.1|Figure]](b). Thus we have the following properties of the function <math>\ln</math>. | |||
{{proofcard|Theorem|theorem-1| | |||
<math display="block"> | |||
\left \{ \begin{array}{l} | |||
\ln\; 1 = 0,\\ | |||
\ln\; x > 0, \;\;\;\mbox{if} \;x > 1, \\ | |||
\ln\; x < 0, \;\;\;\mbox{if} \;0 < x < 1. | |||
\end{array} | |||
\right. | |||
</math>|}} | |||
<div id="fig 5.1" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig5_1.png | 400px | thumb | ]] | |||
</div> | |||
Another interesting property is obtained by taking the derivative <math>\frac{d}{dx} \ln\; kx</math>, where <math>k</math> is an arbitrary positive constant. By the Chain Rule, | |||
<math display="block"> | |||
\frac{d}{dx} \ln\; kx = \frac{1}{kx} \frac{d}{dx} kx = \frac{1}{kx} \cdot k = \frac{1}{x}. | |||
</math> | |||
Hence the functions <math>\ln kx</math> and <math>\ln x</math> have the same derivative. | |||
We know that two functions which have the same derivative over an interval, in this case | |||
all positive real numbers, differ by a constant. Hence | |||
<math display="block"> | |||
\ln\; kx - \ln\; x = c, | |||
</math> | |||
for some real number <math>c</math> and all positive <math>x</math>. We evaluate <math>c</math> by substituting a particular value for <math>x</math>. Since the value of <math>\ln 1</math> is known, we let <math>x = 1</math>, getting | |||
<math display="block"> | |||
\ln\; k - \ln\; 1 = c. | |||
</math> | |||
Since <math>\ln 1 = 0</math>, we know that <math>c = \ln\; k</math>. Hence <math>\ln kx - \ln x = \ln k</math>, or, equivalently, | |||
<math display="block"> | |||
\ln\; kx = \ln\; k + \ln\; x. | |||
</math> | |||
In deriving this equation we have used the fact that <math>k</math> is a constant and <math>x</math> a variable. Once we have derived it, and know that it is valid for every positive <math>k</math> and <math>x</math>, we can forget the distinction and write | |||
{{proofcard|Theorem|theorem-2| | |||
<math display="block"> | |||
\ln\; ab = \ln\; a + \ln\; b, \;\;\;\mbox{for all positioe real numbers $a$ and <math>b</math>}. | |||
</math>|}} | |||
If <math>a</math> is positive, then <math>\frac{1}{a}</math> is also positive and a substitution of <math>\frac{1}{a}</math> for <math>b</math> in (1.2) gives the equation <math>\ln\; 1 = \ln\; a + \ln\; \frac{1}{a} </math>. Since <math>\ln 1 = 0</math>, we have | |||
{{proofcard|Theorem|theorem-3| | |||
<math display="block"> | |||
\ln\; \frac{1}{a} = - \ln\; a, \;\;\;a > 0. | |||
</math>|}} | |||
Applying (1.2) to the product of the two numbers <math>a</math> and <math>\frac{1}{b}</math>, and using (1.3), we obtain | |||
<math>\ln\; \frac{a}{b} = \ln\; \Bigl( a \cdot \frac{1}{b} \Bigr) = \ln\; a + \ln\; \frac{1}{b} | |||
= \ln\; a - \ln\; b</math>. That is, | |||
{{proofcard|Theorem|theorem-4| | |||
<math display="block"> | |||
\ln\;\frac{a}{b} = \ln\; a - \ln\; b, \;\;\; a > 0 \; \mbox{and} \;b > 0. | |||
</math>|}} | |||
In summary: The function <math>\ln</math> applied to a product is equal to the sum of the values obtained when the function is applied to the factors. Applied to the quotient, the value of In is the difference between the values of the function applied to the numerator and to the denominator. | |||
Let <math>r</math> be any rational number, and consider the derivative <math>\frac{d}{dx} \ln\; x^r</math>. | |||
By the Chain Rule again, | |||
<math display="block"> | |||
\frac{d}{dx} \ln\; x^r = \frac{1}{x^r} \frac{d}{dx} x^r = \frac{1}{x^r} r x^{r-1} = r \frac{1}{x}. | |||
</math> | |||
Moreover, | |||
<math display="block"> | |||
\frac{d}{dx} r \ln\; x = r \frac{d}{dx} \ln\; x = r \frac{1}{x}. | |||
</math> | |||
Thus <math>\ln\; x^r</math> and <math>r \ln\; x</math> have the same derivative and so must differ by a constant: | |||
<math display="block"> | |||
\ln\; x^r - r \ln\; x = c. | |||
</math> | |||
Substitution of 1 for <math>x</math> tells us that <math>c = 0</math>, and therefore <math>\ln\; x^r = r \ln\; x</math> for every positive number <math>x</math>. For uniformity in appearance with properties (1.2), (1.3), and (1.4), we set <math>x = a</math> and obtain | |||
{{proofcard|Theorem|theorem-5| | |||
<math display="block"> | |||
\ln\; a^r = r \ln\; a, \;\mbox{for every rational number $r$ and every positive real number <math>a</math>.} | |||
</math>|}} | |||
The properties we have derived for the function In should be recognized by anyone who has been exposed to logarithms. However, <math>\ln</math> is not the same as the function <math>\log_{10}</math> or the function <math>\log_{2}</math>, which the student may have seen earlier. It has many of the same properties though and is called the '''natural logarithm''', hence the abbreviation <math>\ln</math>. | |||
We next draw the graph of the function <math>\ln</math>. Since <math>\frac{d}{dx} \ln\; x = \frac{1}{x}</math> and since <math>\frac{1}{x}</math> is positive for all <math>x</math> for which <math>\ln\; x</math> is defined, the slope of the tangent line to the graph is always positive. From this we can see that <math>\ln\; x</math> always increases as <math>x</math> increases; that is, the function <math>\ln</math> is strictly increasing. To prove this analytically, we use the Mean Value Theorem, page 113. Suppose that <math>0 < a < b</math>. By the Mean Value Theorem there exists a number <math>c</math> such that <math>a < c < b</math> and | |||
<math display="block"> | |||
\ln\; b - \ln\; a = (b - a) \Bigl( \frac{d}{dx} \ln\; x \Bigr) (c) = (b - a) \frac{1}{c} > 0. | |||
</math> | |||
<div id="fig 5.2" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig5_2.png | 400px | thumb | ]] | |||
</div> | |||
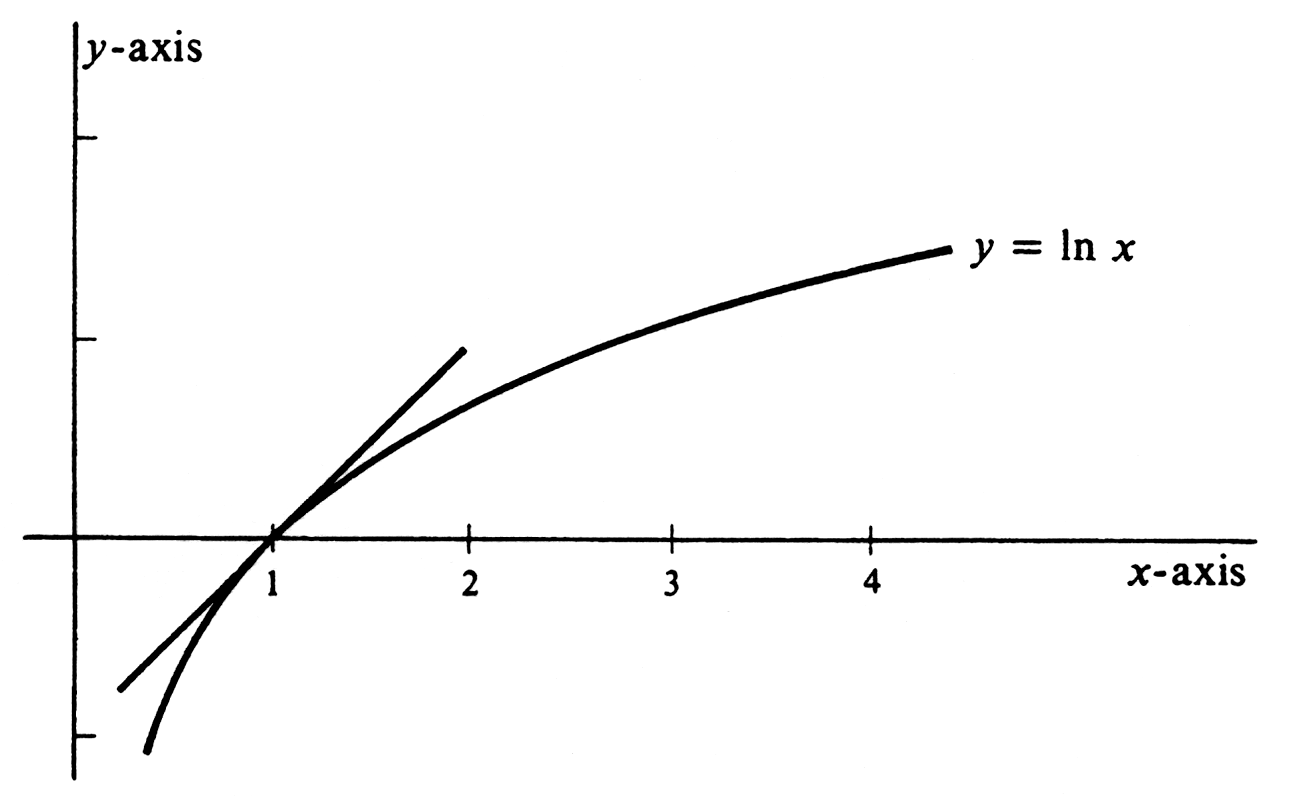
Hence <math>\ln\; a < \ln\; b</math>, and the monotonicity of the natural logarithm is proved. Since <math>\frac{d^2}{dx^2} \ln\; x = - \frac{1}{x^2}</math>, the graph of <math>\ln x</math> is concave downward for all <math>x</math>. With this information and the fact that <math>\ln 1 = 0</math>, we can make a reasonable sketch of the graph. This appears in [[#fig 5.2|Figure]]. Note that the graph is steep and the values of the function negative for very small values of <math>x</math>. The values increase and the curve goes up to the right, passing through (1, 0) with a | |||
slope of 1. Since <math>\frac{d}{dx} \ln\; x = \frac{1}{x}</math>, the slope decreases as <math>x</math> increases. This raises the question of whether <math>\ln x</math> becomes arbitrarily large as <math>x</math> increases without bound, or possibly tends toward some limiting value. However, it is obvious that the inequality <math>\frac{1}{t} \geq \frac{1}{2}</math> is true for every real number in the closed interval [1, 2]. It follows from one of the fundamental properties of the integral [specifically, from (4.3) on page 191] that | |||
<math display="block"> | |||
\int_{1}^{2} \frac{1}{ t} dt \geq \int_{1}^{2} \frac{1}{2} dt. | |||
</math> | |||
The left side of this inequality is equal to <math>\ln 2</math>, and the right side to <math>\frac{1}{2}</math>. Thus we have proved that | |||
<math display="block"> | |||
\ln\; 2 \geq \frac{1}{2}, | |||
</math> | |||
[a fact which can also be obtained geometrically by looking at [[#fig 5.1|Figure]](a) and considering the area under the curve <math>y = \frac{1}{t}</math> between <math>t = 1</math> and <math>t = 2</math>]. Hence for every rational number <math>r</math>, we have <math>\ln\; 2^r = r \ln\; 2 \geq \frac{r}{2}</math> . By taking <math>r</math> large enough, we can make <math>\frac{r}{2}</math> and, consequently <math>\ln\; 2^r</math>, as large as we like. We conclude that | |||
<math display="block"> | |||
\lim_{x \rightarrow \infty} \ln\; x = \infty. | |||
</math> | |||
'''Example''' | |||
If <math>\ln\; 2 = a</math> and <math>\ln\; 3 = b</math>, evaluate each of the following in terms of <math>a</math> and <math>b</math>. | |||
<math display="block"> | |||
\begin{array}{lll} | |||
(a)\;\;\; \ln\; 4, \;\;\;&(c)\;\;\; \ln\; \frac{1}{6}, \;\;\;&(e)\;\;\; \ln\; \frac{2}{9},\\ | |||
(b)\;\;\; \ln\; 6, \;\;\;&(d)\;\;\; \ln\; 24, \;\;\;&(f)\;\;\; \ln\; 2^{m}3^{n}. | |||
\end{array} | |||
</math> | |||
Using the various properties of logarithms developed above, we find | |||
\item[a]] <math>\ln 4 = \ln 2^{2} = 2 \ln 2 = 2a,</math> | |||
\item[(b)] <math>\ln 6 = \ln (2 \cdot 3) = \ln 2 + \ln 3 = a + b,</math> | |||
\item[(c)] <math>\ln 6 = - \ln 6 = - (a + b) = - a - b,</math> | |||
\item[(d)] <math>\ln 24 = \ln (8 \cdot 3) = \ln 8 + \ln 3 = \ln 2^{3} + \ln 3 = 3 \ln 2 + \ln 3 = 3a + b,</math> | |||
\item[(e)] <math>\ln \frac{2}{9} = \ln 2 - \ln 9 = \ln 2 - \ln 3^{2} = \ln 2 - 2 \ln 3 = a - 2b,</math> | |||
\item[(f)] <math>\ln 2^{m}3^{n} = \ln 2^{m} + \ln 3^{n} = m \ln 2 + n \ln 3 = ma + nb.</math> | |||
The derivative of the natural logarithm of a differentiable function is found by means of the Chain Rule. Thus ''if'' <math>F(x) = \ln(f(x))</math>, ''then'' <math>F'(x) = \ln'\; (f(x))f' (x) = \frac{1}{f(x)} f'(x) = \frac{f'(x)}{f(x)}</math>. If the variable <math>u</math> is used to denote a differentiable function of <math>x</math>, then the same result can be written | |||
<math display="block"> | |||
\frac{d}{dx} \ln\; u = \frac{1}{u} \cdot \frac{du}{dx}. | |||
</math> | |||
\medskip | |||
'''Example''' | |||
Find the derivatives of (a) <math>\ln (x^2 - 3)</math>, (b) <math>\ln \sqrt{4x + 7}</math>. Using the Chain Rule in (a), we obtain | |||
<math display="block"> | |||
\frac{d}{dx} \ln(x^2 - 3) = \frac{1}{x^2 - 3} \cdot 2x = \frac{2x}{x^2 - 3}. | |||
</math> | |||
Note that the original function, <math>\ln (x^2 - 3)</math>, is defined only for <math>|x| > \sqrt{3}</math>, although the function which is its derivative can be defined for all <math>x</math> except <math>\pm \sqrt{3}</math>. We can do (b) either by use of the Chain Rule directly, as | |||
<math display="block"> | |||
\frac{d}{dx} \ln \sqrt{4x + 7} = \frac{1}{\sqrt (4x + 7)} \cdot \frac{1}{2} (4x + 7)^{-1/2} \cdot 4 = \frac{2}{4x + 7}, | |||
</math> | |||
or more simply by noting that <math>\ln \sqrt{4x + 7} = \frac{1}{2} \ln(4x + 7)</math>. Then | |||
<math display="block"> | |||
\frac{d}{dx} \ln \sqrt{4x + 7} = \frac{1}{2} \frac{d}{dx} \ln(4x + 7) = \frac{1}{2} \frac{1}{4x + 7} \cdot 4 = \frac{2}{4x + 7}. | |||
</math> | |||
The latter method would be much shorter for finding the derivative of <math>\ln(x^2 + 2)(x - 3)(x + 5)^3</math>. The expanded form <math>\ln (x^2 + 2) + \ln (x - 3) + 3 \ln (x + 5)</math> is certainly simpler to differentiate. | |||
\medskip | |||
Since the natural logarithm is defined only for positive numbers, it follows that the function In <math>x</math> is an antiderivative of <math>\frac{1}{x}</math> only for <math>x > 0</math>. It is natural to ask whether or not <math>\frac{1}{x}</math>, which is defined and continuous for all <math>x</math> except 0, has an antiderivative for <math>x < 0</math>. The answer is yes; <math>\ln (-x)</math> is an antiderivative. Of course, if <math>x</math> is negative, then <math>-x</math> is positive and so <math>\ln (-x)</math> is defined. By the Chain Rule, | |||
<math display="block"> | |||
\frac{d}{dx} \ln\;(-x) = \frac{1}{(-x)} \frac{d}{dx} (-x) = \frac{1}{(-x)} \cdot (-1) = \frac{1}{x} . | |||
</math> | |||
This equation may be combined with the equation <math>\frac{d}{dx} \ln x = \frac{1}{x}</math>, which holds for all positive <math>x</math>, into the single equation | |||
<math display="block"> | |||
\frac{d}{dx} \ln |x| = \frac{1}{x}, \;\;\;\mbox{for all $x$ except 0}. | |||
</math> | |||
The corresponding formula for the indefinite integral is | |||
{{proofcard|Theorem|theorem-6| | |||
<math display="block"> | |||
\int \frac{dx}{x} dx = \ln | x | + c. | |||
</math>|}} | |||
If <math>f</math> is a differentiable function, the Chain Rule implies that | |||
<math display="block"> | |||
\frac{d}{dx} \ln | f(x) | = \frac{1}{f(x)} \cdot f'(x) = \frac{f'(x)}{f(x)}. | |||
</math> | |||
Hence, we have the integration formula | |||
{{proofcard|Theorem|theorem-7| | |||
<math display="block"> | |||
\int \frac{f'(x)}{f(x)}dx = \ln |f(x)| + c. | |||
</math>|}} | |||
'''Example''' | |||
Integrate (a) <math>\int \frac{dx}{3x}</math>, (b) <math>\int \frac{x + 7}{x^2 + 14x + 5} dx</math>. To do (a), we use (1.6) and the fact that the integral of a constant times a function is the constant times the integral of the function. | |||
<math display="block"> | |||
\int \frac{dx}{3x} = \frac{1}{3} \int \frac{dx}{x} = \frac{1}{3} \ln |x| + c. | |||
</math> | |||
For (b), formula (1.7) is applicable because the numerator is <math>\frac{1}{2}</math> times the derivative of the denominator. | |||
<math display="block"> | |||
\int \frac{x + 7}{x^2 + 14x + 5} dx = \frac{1}{2} \int \frac{2x + 14}{x^2 + 14x + 5} dx = \frac{1}{2} \ln |x^2 + 14x + 5| + c. | |||
</math> | |||
Alternative ways of writing the integration formula (1.7) are obtained by letting <math>u = f(x)</math>. We then get | |||
<math display="block"> | |||
\int \frac{1}{u} \frac{du}{dx} dx = \ln |u| + c . | |||
</math> | |||
Using the theory of differentials, we have <math>du = \frac{du}{dx}dx</math>, and the formula becomes | |||
<math display="block"> | |||
\int \frac{u}{du} = \ln |u| + c. | |||
</math> | |||
'''Example''' | |||
Compute the definite integral <math>\int_{0}^{2} \frac{x^{2}dx}{x^3 - 17}</math> . Let <math>u = x^3 - 17</math>. Then <math>du = 3x^{2}dx</math>, or, equivalently, <math>x^2dx = \frac{du}{3}</math>. Hence | |||
<math display="block"> | |||
\frac{x^2 dx}{x^3 - 17} = \frac{1}{u} \frac{du}{3} = \frac{1}{3} \frac{du}{u}, | |||
</math> | |||
and so | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\int \frac{x^2 dx}{x^3 - 17} &=& \frac{1}{3} \int \frac{du}{u} = \frac{1}{3} \ln |u| + c\\ | |||
&=& \frac{1}{3} \ln | x^3 - 17 | + c. | |||
\end{eqnarray*} | |||
</math> | |||
Finally, therefore, | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\int_{0}^{2} \frac{x^{2}dx}{x^{3} - 17} | |||
&=& \frac{1}{3} \ln |x^3 - 17| \Big|_{0}^{2} | |||
= \frac{1}{3} \ln |8 - 17| - \frac{1}{3} \ln |-17| \\ | |||
&=& \frac{1}{3} \ln 9 - \frac{1}{3} \ln 17 = \frac{1}{3} \ln \frac{9}{17}. | |||
\end{eqnarray*} | |||
</math> | |||
Note that, if we had neglected the absolute value, we would have encountered the undefined quantities <math>\ln(- 9)</math> and <math>\ln( - 17)</math>. | |||
\medskip | |||
Since <math>\log_{10} 10 = 1</math> and <math>\log_{2}2 = 1</math>, it is reasonable to ask for that value of <math>x</math> for which <math>\ln x = 1</math> and to call this number the base for natural logarithms. We know that such a number exists, since <math>\ln x</math> increases as <math>x</math> increases and since the graph of <math>y = \ln x</math> crosses the line <math>y = 1</math>. An accurate graph would show that the abscissa of the point where they cross is between 2.7 and 2.8, more accurately between 2.71 and 2.72, and more accurately still between 2.718 and 2.719. Although this number is irrational, we can find better and better decimal approximations to it. They start out 2.71828.... This number, denoted by <math>e</math>, is | |||
therefore defined by the equation <math>\ln e = 1</math>. | |||
The sequence of rational numbers <math>1 + 1, 1 + \frac{1}{2}, 1 + \frac{1}{3}, 1 + \frac{1}{4}, ... , 1 + \frac{1}{n}, . . .</math> approaches 1 as a limit. The chord connecting points (1, 0) and <math>\Bigl( 1 + \frac{1}{n}, \ln \Bigl( 1 + \frac{1}{n} \Bigr) \Bigr)</math> on the graph of <math>y = \ln x</math> has a slope equal to | |||
<math display="block"> | |||
\frac{\ln \Bigl( 1 + \frac{1}{n} \Bigr) - 0}{\Bigl( 1 + \frac{1}{n} \Bigr) - 1} = n \ln \Bigl( 1 + \frac{1}{n} \Bigr). | |||
</math> | |||
Hence, by (1.5), the slope is <math>\ln \Bigl( 1 + \frac{1}{n} \Bigr)^n</math>. As <math>n \rightarrow \infty</math>, we have <math>\frac{1}{n} \rightarrow 0</math>, and the chord approaches the tangent to the curve at (1, 0), which has slope equal to 1. Hence | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} \ln \Bigl (1 + \frac{1}{n} \Bigr)^{n} = 1 | |||
</math> | |||
\medskip | |||
<span id="table 5.1"/> | |||
{|class="table" | |||
|- | |||
|n || <math>(1 + \frac{1}{n})^n</math> | |||
|- | |||
|1 || 2. | |||
|- | |||
|2 || 2.25 | |||
|- | |||
|10 || 2.594 | |||
|- | |||
|50 || 2.692 | |||
|- | |||
|1000 || 2.717 | |||
|- | |||
|<math>e</math> || 2.71828 ... | |||
|} | |||
\medskip | |||
<div id="fig 5.3" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig5_3.png | 400px | thumb | ]] | |||
</div> | |||
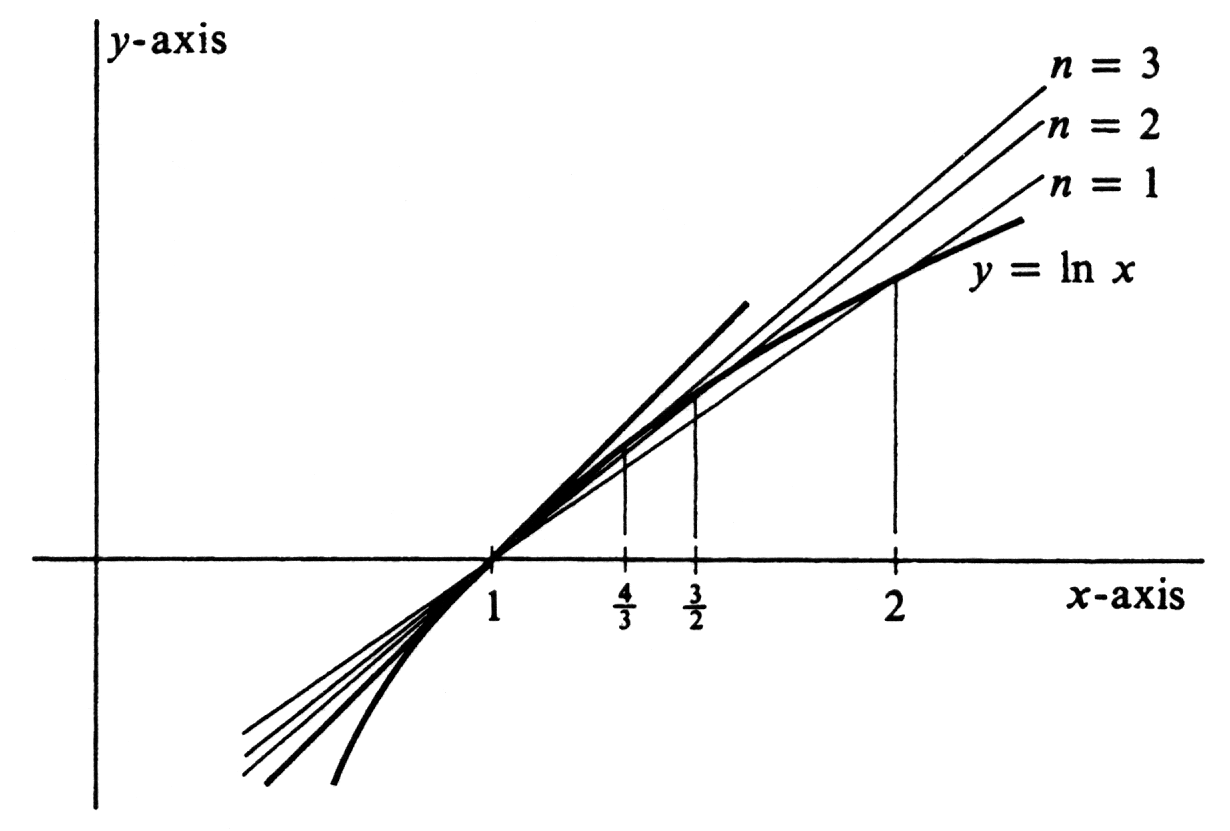
Furthermore, as can be seen from [[#fig 5.3|Figure]], the slope of the chord increases as <math>n</math> increases. Hence <math>\ln \Bigl(1 + \frac{1}{n} \Bigr)^{n}</math> increases, and because <math>\ln</math> is an increasing function, it follows that the numbers <math>\Bigl( 1 + \frac{1}{n} \Bigr)^{n}</math> also increase. Since | |||
<math display="block"> | |||
\ln \Bigl(1 + \frac{1}{n} \Bigr)^{n} < 1 = \ln e, | |||
</math> | |||
we know that | |||
<math display="block"> | |||
\Bigl(1 + \frac{1}{n} \Bigr)^{n} < e. | |||
</math> | |||
It follows immediately from the least upper bound property of the real numbers that a bounded sequence of increasing real numbers must have a limit. Hence | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} \Bigl(1 + \frac{1}{n} \Bigr)^{n}\;\mbox{exists}. | |||
</math> | |||
Since <math>\ln</math> is a continuous function, the limit of a natural logarithm approaches the natural logarithm of the limit, and so | |||
<math display="block"> | |||
1 = \lim_{n \rightarrow \infty} \ln \Bigl( 1 +\frac{1}{n} \Bigr)^n = \ln | |||
[\lim_{n \rightarrow \infty} \Bigl(1 + \frac{1}{n} \Bigr)^n ]. | |||
</math> | |||
Since <math>1 = \ln e</math> and since there is only one number whose logarithm is 1, we conclude that | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} \Bigl( 1 + \frac{1}{n} \Bigr)^n = e. | |||
</math> | |||
In Table 1 values of <math>\Bigl( 1 + \frac{1}{n} \Bigr)^n</math> for several values of <math>n</math> are compared with the limiting value <math>e</math>. | |||
\end{exercise} | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Revision as of 01:08, 3 November 2024
The Natural Logarithm.
If [math]f[/math] is any real-valued function of a real variable which is continuous on some interval, we have seen that there exists an antiderivative, or indefinite integral, [math]F[/math] such that [math]F'(x) = f(x)[/math] for every [math]x[/math] in the interval. For some functions we have been able to write their antiderivatives explicitly. For example, if [math]f(x) = x^r[/math] and [math]r[/math] is a rational number different from -1, then the general antiderivative is
where [math]c[/math] is an arbitrary constant. This formula is not applicable if [math]r = - 1[/math]. Nevertheless, [math]\frac{1}{x}[/math] is certainly continuous on the interval [math](0, \infty)[/math], and therefore some function has it for a derivative. For every positive number [math]a[/math], we can define such a function by writing
For then by the Fundamental Theorem of Calculus [see Theorem (5.2), page 200],
To be specific, we choose [math]a = 1[/math] and select [math]\int_{1}^{x} \frac{dt}{t}[/math] for a particular antiderivative of [math]\frac{1}{x}[/math]. As we shall see, this function is interesting enough to have a special name and a special notation. The notation we shall use is [math]\ln\;(x)[/math], or, more briefly, [math]\ln\; x[/math], and we shall save the name and reason for its choice until we have investigated its properties. For now, we define
The reason that [math]x[/math] must be positive in this definition is that the function [math]\frac{1}{t}[/math] has a discontinuity at [math]t = 0[/math]. If [math]x[/math] is negative, the integral does not exist and [math]\ln x[/math] is not defined. Geometrically, In [math]x[/math] is an area or the negative of an area. If [math]x \gt 1[/math], then [math]\ln x[/math] is the area of the region bounded by the hyperbola [math]y = \frac{1}{t}[/math], the [math]t[/math]-axis, and the lines [math]t = 1[/math] and [math]t = x[/math] [see Figure(a)]. On the other hand, if [math]0 \lt x \lt 1[/math], we have
and [math]\ln x[/math] is the negative of the area shown in Figure(b). Thus we have the following properties of the function [math]\ln[/math].
Another interesting property is obtained by taking the derivative [math]\frac{d}{dx} \ln\; kx[/math], where [math]k[/math] is an arbitrary positive constant. By the Chain Rule,
Hence the functions [math]\ln kx[/math] and [math]\ln x[/math] have the same derivative. We know that two functions which have the same derivative over an interval, in this case all positive real numbers, differ by a constant. Hence
for some real number [math]c[/math] and all positive [math]x[/math]. We evaluate [math]c[/math] by substituting a particular value for [math]x[/math]. Since the value of [math]\ln 1[/math] is known, we let [math]x = 1[/math], getting
Since [math]\ln 1 = 0[/math], we know that [math]c = \ln\; k[/math]. Hence [math]\ln kx - \ln x = \ln k[/math], or, equivalently,
In deriving this equation we have used the fact that [math]k[/math] is a constant and [math]x[/math] a variable. Once we have derived it, and know that it is valid for every positive [math]k[/math] and [math]x[/math], we can forget the distinction and write
If [math]a[/math] is positive, then [math]\frac{1}{a}[/math] is also positive and a substitution of [math]\frac{1}{a}[/math] for [math]b[/math] in (1.2) gives the equation [math]\ln\; 1 = \ln\; a + \ln\; \frac{1}{a} [/math]. Since [math]\ln 1 = 0[/math], we have
Applying (1.2) to the product of the two numbers [math]a[/math] and [math]\frac{1}{b}[/math], and using (1.3), we obtain [math]\ln\; \frac{a}{b} = \ln\; \Bigl( a \cdot \frac{1}{b} \Bigr) = \ln\; a + \ln\; \frac{1}{b} = \ln\; a - \ln\; b[/math]. That is,
In summary: The function [math]\ln[/math] applied to a product is equal to the sum of the values obtained when the function is applied to the factors. Applied to the quotient, the value of In is the difference between the values of the function applied to the numerator and to the denominator. Let [math]r[/math] be any rational number, and consider the derivative [math]\frac{d}{dx} \ln\; x^r[/math]. By the Chain Rule again,
Moreover,
Thus [math]\ln\; x^r[/math] and [math]r \ln\; x[/math] have the same derivative and so must differ by a constant:
Substitution of 1 for [math]x[/math] tells us that [math]c = 0[/math], and therefore [math]\ln\; x^r = r \ln\; x[/math] for every positive number [math]x[/math]. For uniformity in appearance with properties (1.2), (1.3), and (1.4), we set [math]x = a[/math] and obtain
The properties we have derived for the function In should be recognized by anyone who has been exposed to logarithms. However, [math]\ln[/math] is not the same as the function [math]\log_{10}[/math] or the function [math]\log_{2}[/math], which the student may have seen earlier. It has many of the same properties though and is called the natural logarithm, hence the abbreviation [math]\ln[/math]. We next draw the graph of the function [math]\ln[/math]. Since [math]\frac{d}{dx} \ln\; x = \frac{1}{x}[/math] and since [math]\frac{1}{x}[/math] is positive for all [math]x[/math] for which [math]\ln\; x[/math] is defined, the slope of the tangent line to the graph is always positive. From this we can see that [math]\ln\; x[/math] always increases as [math]x[/math] increases; that is, the function [math]\ln[/math] is strictly increasing. To prove this analytically, we use the Mean Value Theorem, page 113. Suppose that [math]0 \lt a \lt b[/math]. By the Mean Value Theorem there exists a number [math]c[/math] such that [math]a \lt c \lt b[/math] and
Hence [math]\ln\; a \lt \ln\; b[/math], and the monotonicity of the natural logarithm is proved. Since [math]\frac{d^2}{dx^2} \ln\; x = - \frac{1}{x^2}[/math], the graph of [math]\ln x[/math] is concave downward for all [math]x[/math]. With this information and the fact that [math]\ln 1 = 0[/math], we can make a reasonable sketch of the graph. This appears in Figure. Note that the graph is steep and the values of the function negative for very small values of [math]x[/math]. The values increase and the curve goes up to the right, passing through (1, 0) with a slope of 1. Since [math]\frac{d}{dx} \ln\; x = \frac{1}{x}[/math], the slope decreases as [math]x[/math] increases. This raises the question of whether [math]\ln x[/math] becomes arbitrarily large as [math]x[/math] increases without bound, or possibly tends toward some limiting value. However, it is obvious that the inequality [math]\frac{1}{t} \geq \frac{1}{2}[/math] is true for every real number in the closed interval [1, 2]. It follows from one of the fundamental properties of the integral [specifically, from (4.3) on page 191] that
The left side of this inequality is equal to [math]\ln 2[/math], and the right side to [math]\frac{1}{2}[/math]. Thus we have proved that
[a fact which can also be obtained geometrically by looking at Figure(a) and considering the area under the curve [math]y = \frac{1}{t}[/math] between [math]t = 1[/math] and [math]t = 2[/math]]. Hence for every rational number [math]r[/math], we have [math]\ln\; 2^r = r \ln\; 2 \geq \frac{r}{2}[/math] . By taking [math]r[/math] large enough, we can make [math]\frac{r}{2}[/math] and, consequently [math]\ln\; 2^r[/math], as large as we like. We conclude that
Example
If [math]\ln\; 2 = a[/math] and [math]\ln\; 3 = b[/math], evaluate each of the following in terms of [math]a[/math] and [math]b[/math].
Using the various properties of logarithms developed above, we find
\item[a]] [math]\ln 4 = \ln 2^{2} = 2 \ln 2 = 2a,[/math]
\item[(b)] [math]\ln 6 = \ln (2 \cdot 3) = \ln 2 + \ln 3 = a + b,[/math]
\item[(c)] [math]\ln 6 = - \ln 6 = - (a + b) = - a - b,[/math]
\item[(d)] [math]\ln 24 = \ln (8 \cdot 3) = \ln 8 + \ln 3 = \ln 2^{3} + \ln 3 = 3 \ln 2 + \ln 3 = 3a + b,[/math]
\item[(e)] [math]\ln \frac{2}{9} = \ln 2 - \ln 9 = \ln 2 - \ln 3^{2} = \ln 2 - 2 \ln 3 = a - 2b,[/math]
\item[(f)] [math]\ln 2^{m}3^{n} = \ln 2^{m} + \ln 3^{n} = m \ln 2 + n \ln 3 = ma + nb.[/math]
The derivative of the natural logarithm of a differentiable function is found by means of the Chain Rule. Thus if [math]F(x) = \ln(f(x))[/math], then [math]F'(x) = \ln'\; (f(x))f' (x) = \frac{1}{f(x)} f'(x) = \frac{f'(x)}{f(x)}[/math]. If the variable [math]u[/math] is used to denote a differentiable function of [math]x[/math], then the same result can be written
\medskip Example
Find the derivatives of (a) [math]\ln (x^2 - 3)[/math], (b) [math]\ln \sqrt{4x + 7}[/math]. Using the Chain Rule in (a), we obtain
Note that the original function, [math]\ln (x^2 - 3)[/math], is defined only for [math]|x| \gt \sqrt{3}[/math], although the function which is its derivative can be defined for all [math]x[/math] except [math]\pm \sqrt{3}[/math]. We can do (b) either by use of the Chain Rule directly, as
or more simply by noting that [math]\ln \sqrt{4x + 7} = \frac{1}{2} \ln(4x + 7)[/math]. Then
The latter method would be much shorter for finding the derivative of [math]\ln(x^2 + 2)(x - 3)(x + 5)^3[/math]. The expanded form [math]\ln (x^2 + 2) + \ln (x - 3) + 3 \ln (x + 5)[/math] is certainly simpler to differentiate. \medskip Since the natural logarithm is defined only for positive numbers, it follows that the function In [math]x[/math] is an antiderivative of [math]\frac{1}{x}[/math] only for [math]x \gt 0[/math]. It is natural to ask whether or not [math]\frac{1}{x}[/math], which is defined and continuous for all [math]x[/math] except 0, has an antiderivative for [math]x \lt 0[/math]. The answer is yes; [math]\ln (-x)[/math] is an antiderivative. Of course, if [math]x[/math] is negative, then [math]-x[/math] is positive and so [math]\ln (-x)[/math] is defined. By the Chain Rule,
This equation may be combined with the equation [math]\frac{d}{dx} \ln x = \frac{1}{x}[/math], which holds for all positive [math]x[/math], into the single equation
The corresponding formula for the indefinite integral is
If [math]f[/math] is a differentiable function, the Chain Rule implies that
Hence, we have the integration formula
Example Integrate (a) [math]\int \frac{dx}{3x}[/math], (b) [math]\int \frac{x + 7}{x^2 + 14x + 5} dx[/math]. To do (a), we use (1.6) and the fact that the integral of a constant times a function is the constant times the integral of the function.
For (b), formula (1.7) is applicable because the numerator is [math]\frac{1}{2}[/math] times the derivative of the denominator.
Alternative ways of writing the integration formula (1.7) are obtained by letting [math]u = f(x)[/math]. We then get
Using the theory of differentials, we have [math]du = \frac{du}{dx}dx[/math], and the formula becomes
Example Compute the definite integral [math]\int_{0}^{2} \frac{x^{2}dx}{x^3 - 17}[/math] . Let [math]u = x^3 - 17[/math]. Then [math]du = 3x^{2}dx[/math], or, equivalently, [math]x^2dx = \frac{du}{3}[/math]. Hence
and so
Finally, therefore,
Note that, if we had neglected the absolute value, we would have encountered the undefined quantities [math]\ln(- 9)[/math] and [math]\ln( - 17)[/math].
\medskip
Since [math]\log_{10} 10 = 1[/math] and [math]\log_{2}2 = 1[/math], it is reasonable to ask for that value of [math]x[/math] for which [math]\ln x = 1[/math] and to call this number the base for natural logarithms. We know that such a number exists, since [math]\ln x[/math] increases as [math]x[/math] increases and since the graph of [math]y = \ln x[/math] crosses the line [math]y = 1[/math]. An accurate graph would show that the abscissa of the point where they cross is between 2.7 and 2.8, more accurately between 2.71 and 2.72, and more accurately still between 2.718 and 2.719. Although this number is irrational, we can find better and better decimal approximations to it. They start out 2.71828.... This number, denoted by [math]e[/math], is
therefore defined by the equation [math]\ln e = 1[/math].
The sequence of rational numbers [math]1 + 1, 1 + \frac{1}{2}, 1 + \frac{1}{3}, 1 + \frac{1}{4}, ... , 1 + \frac{1}{n}, . . .[/math] approaches 1 as a limit. The chord connecting points (1, 0) and [math]\Bigl( 1 + \frac{1}{n}, \ln \Bigl( 1 + \frac{1}{n} \Bigr) \Bigr)[/math] on the graph of [math]y = \ln x[/math] has a slope equal to
Hence, by (1.5), the slope is [math]\ln \Bigl( 1 + \frac{1}{n} \Bigr)^n[/math]. As [math]n \rightarrow \infty[/math], we have [math]\frac{1}{n} \rightarrow 0[/math], and the chord approaches the tangent to the curve at (1, 0), which has slope equal to 1. Hence
\medskip
| n | [math](1 + \frac{1}{n})^n[/math] |
| 1 | 2. |
| 2 | 2.25 |
| 10 | 2.594 |
| 50 | 2.692 |
| 1000 | 2.717 |
| [math]e[/math] | 2.71828 ... |
\medskip
Furthermore, as can be seen from Figure, the slope of the chord increases as [math]n[/math] increases. Hence [math]\ln \Bigl(1 + \frac{1}{n} \Bigr)^{n}[/math] increases, and because [math]\ln[/math] is an increasing function, it follows that the numbers [math]\Bigl( 1 + \frac{1}{n} \Bigr)^{n}[/math] also increase. Since
we know that
It follows immediately from the least upper bound property of the real numbers that a bounded sequence of increasing real numbers must have a limit. Hence
Since [math]\ln[/math] is a continuous function, the limit of a natural logarithm approaches the natural logarithm of the limit, and so
Since [math]1 = \ln e[/math] and since there is only one number whose logarithm is 1, we conclude that
In Table 1 values of [math]\Bigl( 1 + \frac{1}{n} \Bigr)^n[/math] for several values of [math]n[/math] are compared with the limiting value [math]e[/math].
\end{exercise}
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.