guide:3cc850dbe4

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

Area and Arc Length in Polar Coordinates.

This section is divided into two parts. In the first, which is the longer of the two, we shall study the problem of finding the areas of regions bounded by curves defined by equations in polar coordinates. To solve this problem, an integral formula for area in polar coordinates will be derived. The second part is concerned with the computation of the arc lengths of polar curves by applying the methods developed in Section 2. Let [math]f[/math] be a continuous function which contains the closed interval [math][a, b][/math] in its domain. We have already observed that the polar graph of the equation

[[math]] \begin{equation} r = f(\theta), \label{eq10.7.1} \end{equation} [[/math]]

where [math]\theta[/math] takes on all values in the interval [math][a, b][/math], is the parametrized curve defined by the equations

[[math]] \begin{equation} \left \{ \begin{array}{ll} x(\theta) = r \cos \theta = f(\theta) \cos \theta, &\\ y(\theta) = r \sin \theta = f(\theta) \sin \theta, \;\;\; &a \leq \theta \leq b. \end{array} \right . \label{eq10.7.2} \end{equation} [[/math]]

For the area problem, we shall assume to begin with that the interval [math][a, b][/math] has length no greater than [math]2\pi[/math], i.e., that

[[math]] \begin{equation} b - a \leq 2\pi, \label{eq10.7.3} \end{equation} [[/math]]

and also that [math]f[/math] is nonnegative on [math][a, b][/math]:

[[math]] \begin{equation} f(\theta) \geq 0, \;\;\;\mbox{for every number $\theta$ in \ltmath\gt[a, b][[/math]]

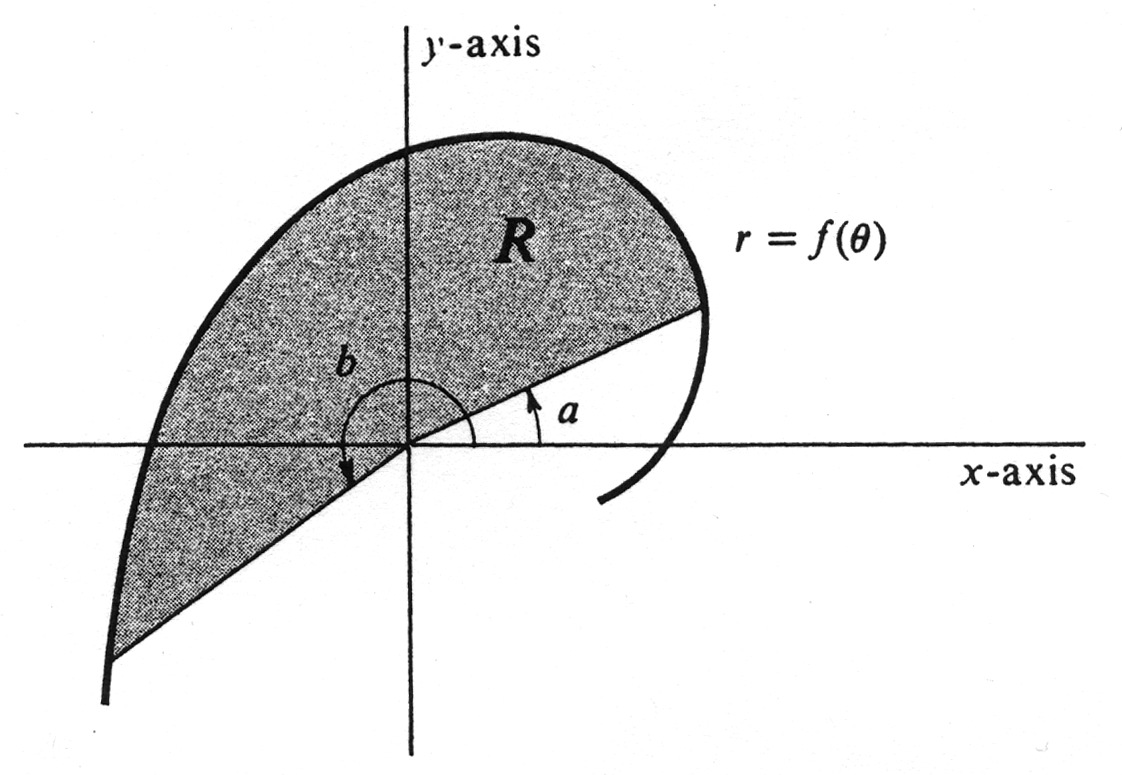
.} \label{eq10.7.4} \end{equation} </math> Let [math]R[/math] be the subset of the plane consisting of all points which have polar coordinates [math](r, \theta)[/math] such that [math]a \leq \theta \leq b[/math] and [math]0 \leq r \leq f(\theta)[/math]. An example is the shaded region [math]R[/math] shown in Figure 30. The problem is to compute the area of [math]R[/math]. The effect of the two assumptions (3) and (4) is that every point of [math]R[/math] has precisely one pair of polar coordinates [math](r, \theta)[/math] with [math]a \leq \theta \leq b[/math] (except, if [math]b - a = 2\pi[/math], for those points of [math]R[/math] along the line defined by [math]\theta = a[/math]).

File:Guide c5467 scanfig10 30.png

To derive a formula for the area of [math]R[/math], we consider an arbitrary partition [math]\sigma = \{ \theta_0, . . . ,\theta_n \}[/math] of [math][a, b][/math] with the property that

[[math]] a = \theta_0 \leq \theta_1 \leq ... \leq \theta_n = b . [[/math]]

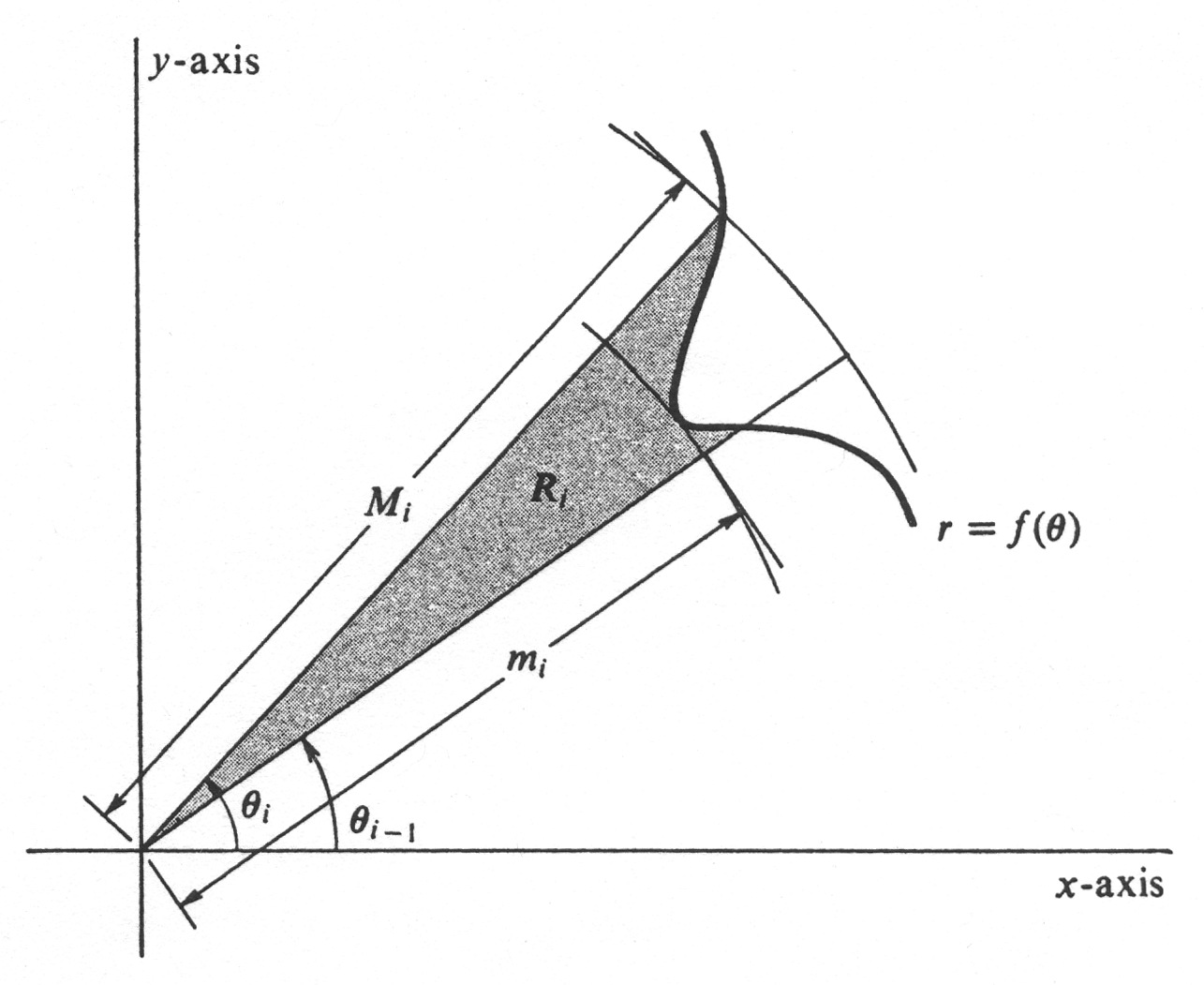
For each [math]i = 1, . . . ,n[/math], let [math]m_i[/math] and [math]M_i[/math] be, respectively, the minimum and maximum values of the function [math]f[/math] in the subinterval [math][\theta_{i-1}, \theta_i][/math]. In addition, let [math]R_i[/math] be the subset of [math]R[/math] consisting of all points with polar coordinates [math](r, \theta)[/math] such that [math]\theta_{i-1} \leq \theta \leq \theta_i[/math] and [math]0 \leq r \leq f(\theta)[/math], as illustrated in Figure 31. It follows from the preceding paragraph that except for their boundaries the sets [math]R_1, . . ., R_n[/math] are pairwise disjoint. Hence

[[math]] \begin{equation} area(R) = area(R_1) + + area(R_n). \label{eq10.7.5} \end{equation} [[/math]]

File:Guide c5467 scanfig10 31.png

Each set [math]R_i[/math] is contained in a sector of the circle of radius [math]M_i[/math] and center the origin with angle equal to [math]\theta_i - \theta_{i-1}[/math] radians, and it contains a sector of the circle of radius [math]m_i[/math] with the same center and the same angle. Since any sector of a circle of radius [math]\rho[/math] and angle [math]\alpha[/math] radians has area equal to [math]\frac{1}{2}\rho^2 \alpha[/math], we conclude that

[[math]] \frac{1}{2} m_i^2 (\theta_i - \theta_{i - 1}) \leq area(R_i) \leq \frac{1}{2}M_i^2 (\theta_i - \theta_{i-1}), [[/math]]

for each [math]i = 1, . . ., n[/math]. Adding inequalities and using equation (5), we get

[[math]] \sum_{i=1}^n (\frac{m_i^2}{2}(\theta_i - \theta_{i-1}) \leq area(R) \leq \sum_{i=1}^n \frac{M_i^2}{2} (\theta_i - \theta_{i-1}). [[/math]]

However, [math]\sum_{i=1}^n (\frac{m_i^2}{2}(\theta_i - \theta_{i-1})[/math] and [math]\sum_{i=1}^n \frac{M_i^2}{2} (\theta_i - \theta_{i-1})[/math] are, respectively, the lower and upper sums for the function [math]\frac{f^2}{2}[/math] relative to the partition [math]\sigma[/math] (see page 165). Denoting them by [math]L_\sigma \Big(\frac{f^2}{2}\Big)[/math] and [math]U_\sigma \Big(\frac{f^2}{2}\Big)[/math] respectively, we have proved

[[math]] \begin{equation} L_\sigma \Big( \frac{f^2}{2} \Big) \leq area(R) \leq U_\sigma \Big( \frac{f^2}{2} \Big), \label{eq10.7.6} \end{equation} [[/math]]

for every partition [math]\sigma[/math] of [math][a, b][/math]. Since [math]f[/math] is continuous, so is [math]\frac{f^2}{2}[/math], and every function which is continuous on a closed bounded interval is integrable over that interval [see Theorem (5.1), page 1991. Hence the function [math]\frac{f^2}{2}[/math] is integrable over [math][a, b][/math], and it therefore follows immediately from the inequalities (6) and the definition of integrability on page 168 that

[[math]] area(R)= \int_a^b \frac{f^2}{2} . [[/math]]

Summarizing, we have proved:

Theorem

lf the function [math]f[/math] is continuous and nonnegative at every point of the closed interval [math][a, b][/math] and if [math]b - a \leq 2\pi[/math], then the area of the region [math]R[/math] bounded by the polar graphs of the equations [math]r = f (\theta), \theta = a[/math], and [math]\theta = b[/math] is given by

[[math]] area(R) = \frac{1}{2} \int_a^b f (\theta)^2 d\theta = \frac{1}{2} \int_a^b r^2 d\theta . [[/math]]

File:Guide c5467 scanfig10 32.png

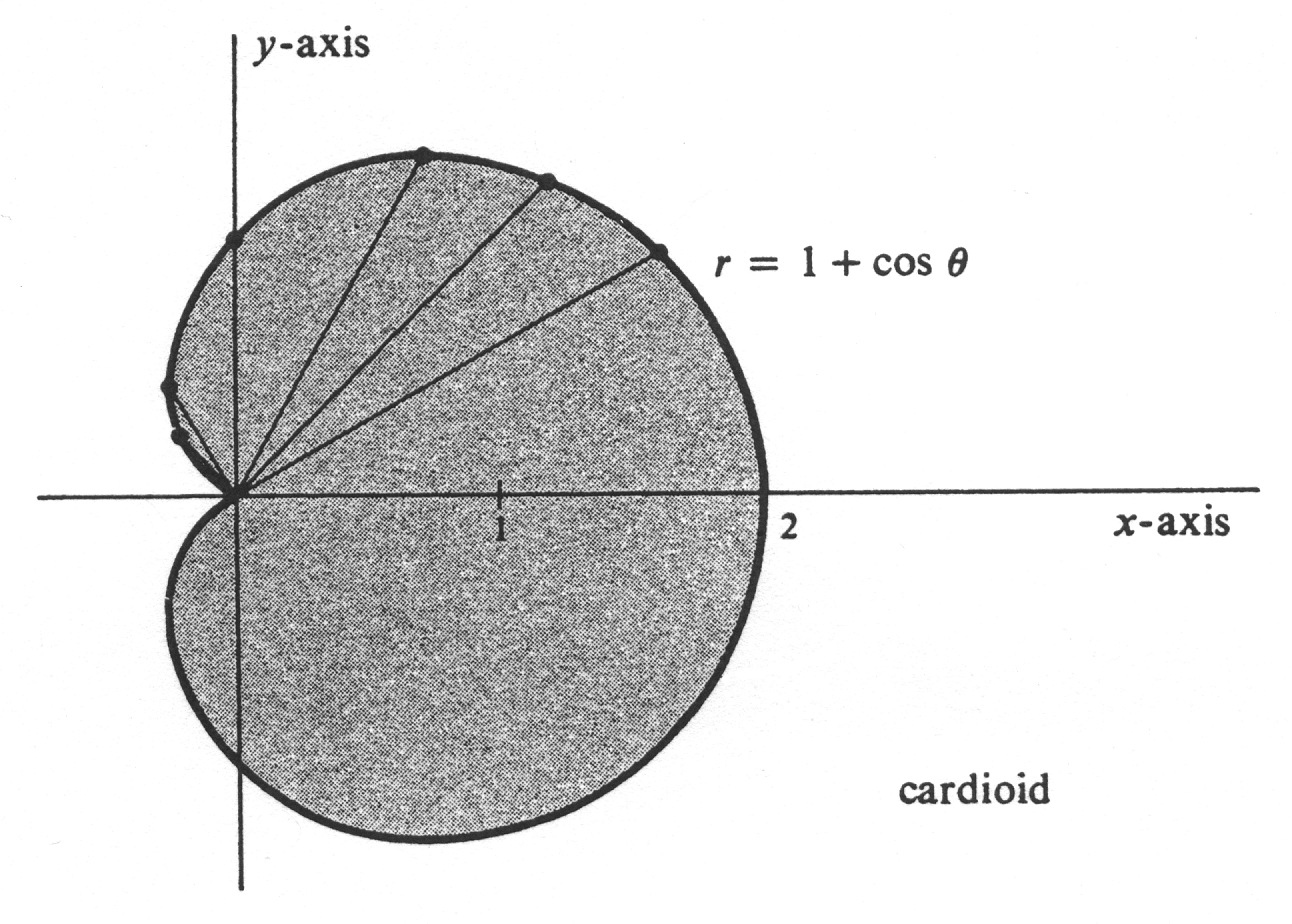
Example The curve defined by the equation [math]r = 1 + \cos \theta[/math] in polar coordinates, and drawn in Figure 32, is a cardioid. Compute the area of the region [math]R[/math] which it bounds. Since this curve is symmetric about the [math]x[/math]-axis, it is sufficient (but in this example no easier) to find the area of that part of [math]R[/math] lying on or above the [math]x[/math]-axis and to multiply the result by 2. The function [math]f[/math] defined by

[[math]] f(\theta) = 1 + \cos \theta, \;\;\; 0 \leq \theta \leq \pi, [[/math]]

is both continuous and nonnegative. It follows from (7.1) that

[[math]] \begin{eqnarray*} area(R) &=& 2 \left[ \frac{1}{2} \int_0^\pi (1 + \cos \theta)^2 d\theta \right]\\ &=& \int_0^\pi (1 + 2 \cos \theta + \cos^2 \theta) d\theta \\ &=& \int_0^\pi [ 1 + 2\cos \theta + \frac{1}{2}(1+\cos2 \theta)] d\theta \\ &=& \int_0^\pi (\frac{3}{2} + 2 \cos \theta + \frac{1}{2} \cos 2 \theta) d\theta\\ &=& (\frac{3}{2} \theta + 2 \sin \theta + \frac{1}{4} \sin 2\theta)|_0^\pi \\ &=& \frac{3}{2} \pi . \end{eqnarray*} [[/math]]

If [math]f[/math] is negative on the interval [math][a, b][/math], the integral [math]\frac{1}{2}\int_a^b f(\theta)^2 d\theta[/math] is also equal to an area. Specifically, let us assume that [math]f[/math] is continuous on [math][a, b][/math], that [math]b - a \leq 2\pi[/math], and that [math]f(\theta) \leq 0[/math] for every [math]\theta[/math] in [math][a, b][/math]. Let [math]R[/math] be the set of all points which have polar coordinates [math](r, \theta)[/math] such that [math]a \leq \theta \leq b[/math] and [math]f(\theta) \leq r \leq 0[/math] (see Figure 33). Then the following formula is still valid:

Theorem

Let [math]g[/math] be the function defined by [math]g(\theta) = -f(\theta)[/math], and let [math]S[/math] be the set of all points with polar coordinates [math](r, \theta)[/math] such that [math]a \leq \theta \leq b[/math] and [math]0 \leq r \leq g(\theta)[/math]. The set [math]S[/math] is symmetric about the origin to the set [math]R[/math], and we therefore conclude that

[[math]] area(R) = area(S). [[/math]]

But, by (7.1),

[[math]] \begin{eqnarray*} area(S) &=& \frac{1}{2} \int_a^b g(\theta)^2 d\theta = \frac{1}{2} \int_a^b [-f(\theta)]^2 d\theta \\ &=& \frac{1}{2} \int_a^b f(\theta)^2 d\theta, \end{eqnarray*} [[/math]]

which completes the proof.

Show Proof

{{{4}}}

■

If the function [math]f[/math] can take on both positive and negative values in the interval [math][a, b][/math] or if [math]b - a \gt 2\pi[/math] (or both), then the integral [math]\frac{1}{2} \int_a^b f(\theta)^2 d\theta[/math] will in general give the sum of the areas of nondisjoint (i.e., overlapping) regions. It is frequently necessary to subdivide the interval [math][a, b][/math] into subintervals and to compute the integrals of [math]\frac{f^2}{2}[/math] over these subintervals separately to find a desired area.

File:Guide c5467 scanfig10 34.png

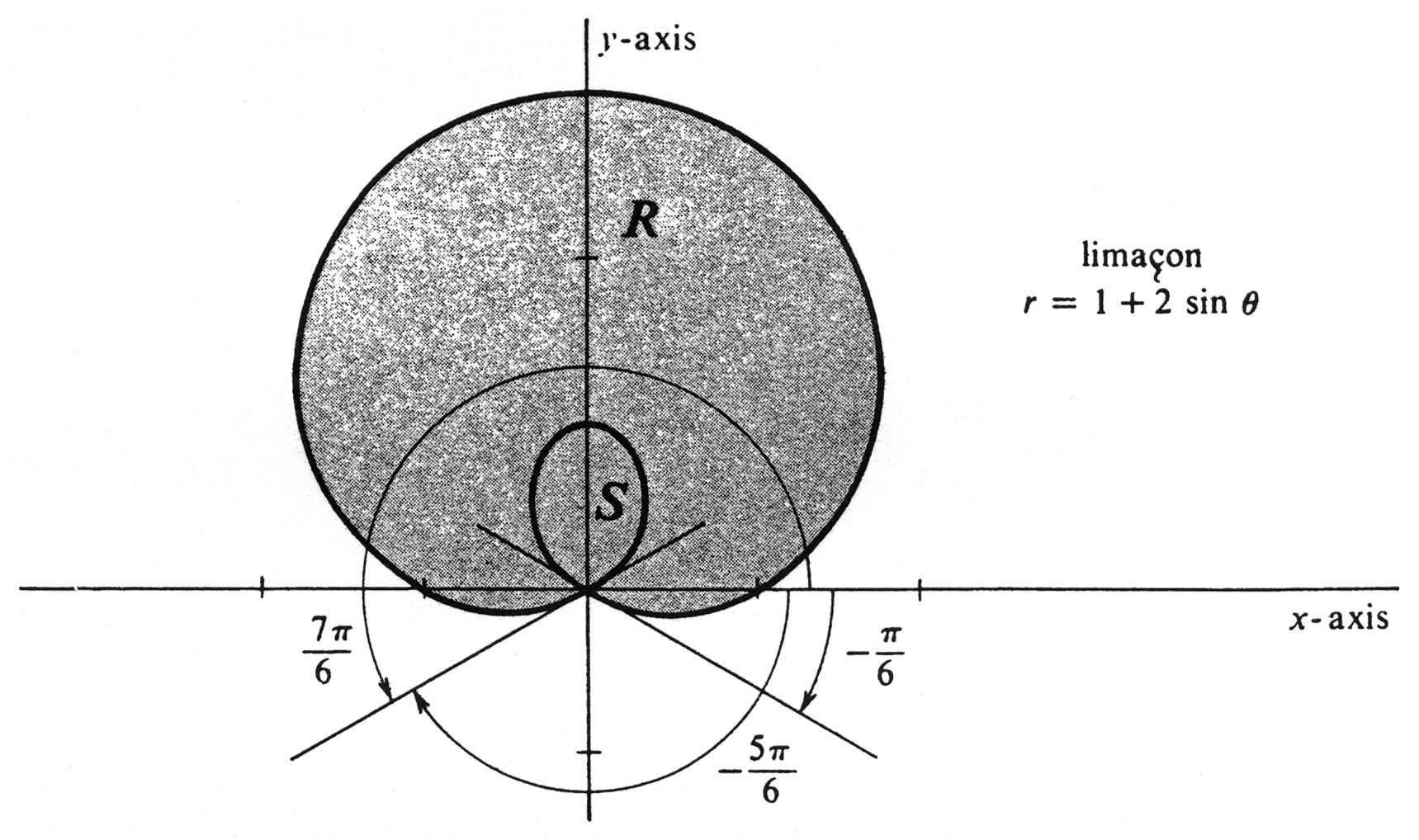
Example The polar graph of the equation [math]r = 1 + 2 \sin \theta[/math] is the limaçon shown in Figure. The function [math]f[/math] defined by [math]f(\theta) = 1 + 2 \sin \theta[/math] satisfies the inequalities

[[math]] \begin{array}{ll} f(\theta) \geq 0 \;\;\;&\mbox{if} \;\;\; -\frac{\pi}{6} \leq \theta \leq \pi + \frac{\pi}{6}, \\ f(\theta) \leq 0 \;\;\;&\mbox{if} \;\;\; \frac{\pi}{6} - \pi \leq \theta \leq - \frac{\pi}{6} . \end{array} [[/math]]

Let [math]R[/math] and [math]S[/math] be, respectively, the regions bounded by the outer and inner loops of the curve, as shown in the figure. Then

[[math]] \begin{equation} area(R) = 2\int_{-\pi/6}^{7\pi/6} (1 + 2 \sin \theta) d\theta, \label{eq10.7.7} \end{equation} [[/math]]

[[math]] \begin{equation} area(S) = 2\int_{-5\pi/6}^{-\pi/6} (1 + 2 \sin \theta) d\theta. \label{eq10.7.8} \end{equation} [[/math]]

If we integrate [math]\frac{1}{2}f(\theta)^2[/math] from 0 to [math]2\pi[/math], the result will be equal to the area of [math]R[/math] plus the area of [math]S[/math]. That is, we will pick up the area of [math]S[/math] twice and get

[[math]] \begin{equation} area(R) + area(S) = \frac{1}{2} \int_0^{2\pi} (1 + 2 \sin \theta)^2 d\theta. \label{eq10.7.9} \end{equation} [[/math]]

The consistency of [[#eq10.7.7 |equations,]], and can be checked as follows: [[#eq10.7.7 |From,]], and the additivity of the definite integral, we get

[[math]] \begin{eqnarray*} area(S) + area(R) &=& \left[ \frac{1}{2} \int_{-5\pi/6}^{-\pi/6} \int (1 + 2 \sin \theta)^2 d\theta + \int_{-\pi/6}^{7\pi/6} (1 + 2 \sin \theta)^2 d\theta \right] \\ &=& \frac{1}{2} \int_{-5\pi/6}^{7\pi/6} (1 + 2 \sin \theta)^2 d\theta. \end{eqnarray*} [[/math]]

Since the function [math](1 + 2 \sin \theta)^2[/math] has period [math]2\pi[/math], its definite integral over every interval of length [math]2\pi[/math] will be the same. In particular,

[[math]] \begin{eqnarray*} area(S) + area(R) &=& \frac{1}{2} \int_{-5\pi/6}^{7\pi/6} (1 + 2 \sin \theta)^2 d\theta \\ &=& \frac{1}{2} \int_{0}^{2\pi} (1 + 2 \sin \theta)^2 d\theta, \end{eqnarray*} [[/math]]

in agreement with. Evaluation of the integrals is left to the reader. The results are

[[math]] \begin{eqnarray*} area(R) &=& \frac{1}{2} \int_{-\pi/6}^{7\pi/6} (1 + 2 \sin \theta)^2 d\theta = 2\pi + \frac{3}{2} \sqrt 3, \\ area(S) &=& \frac{1}{2} \int_{-5\pi/6}^{-\pi/6} (1 + 2 \sin \theta)^2 d\theta = \pi - \frac{3}{2} \sqrt 3. \end{eqnarray*} [[/math]]

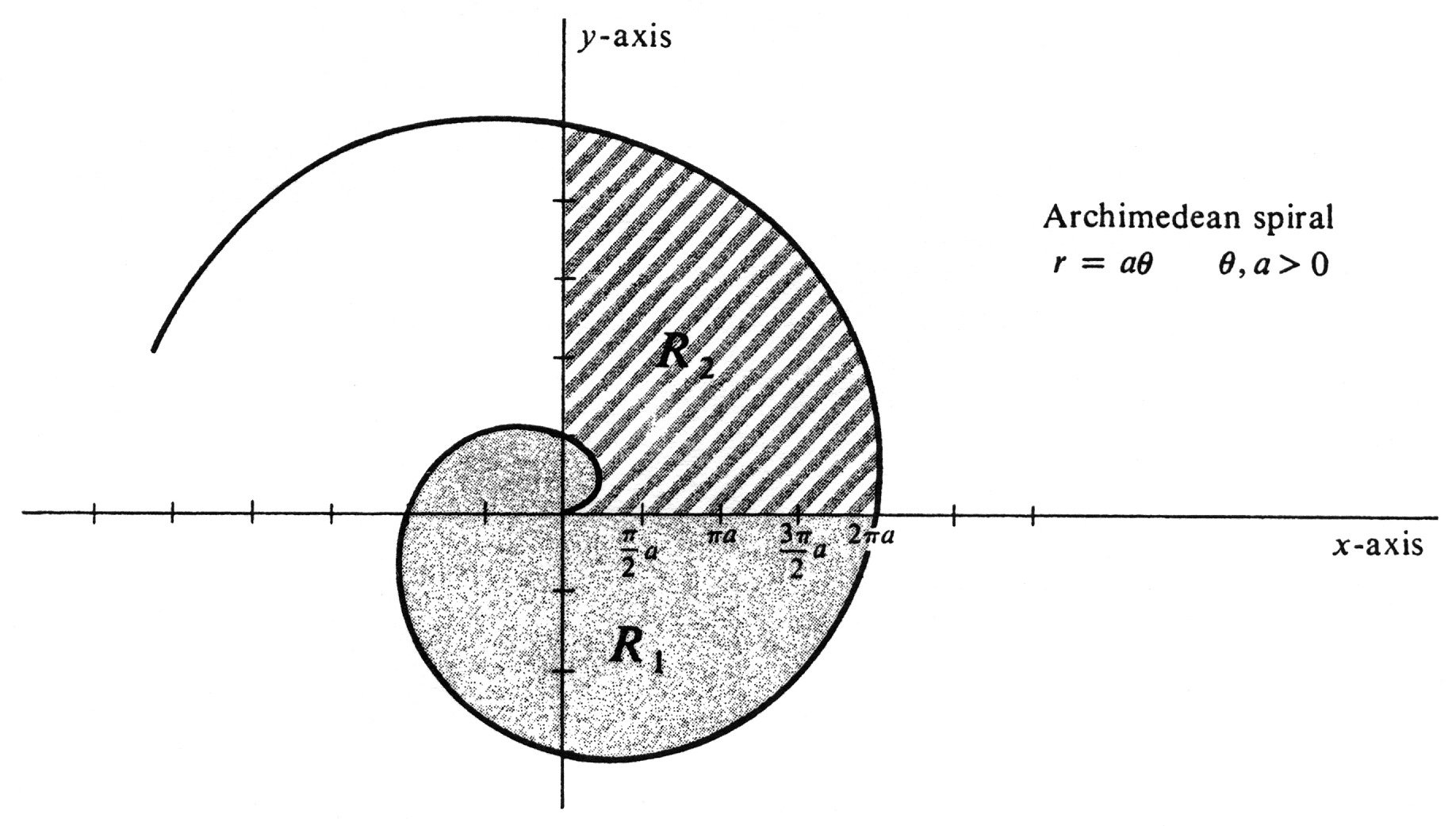
It follows that the area of the region between the two loops of the limaçon is equal to the difference, [math]\pi + 3 \sqrt 3[/math]. Example Find the area [math]A[/math] of the region bounded by the positive [math]y[/math]-axis and the Archimedean spiral [math]r = a\theta (a \gt 0)[/math], where [math]0 \leq \theta \leq \frac{5\pi}{2}[/math]. The region, shown in Figure 35, is the union of two subsets [math]R_1[/math] and [math]R_2[/math]. The set [math]R_1[/math] consists of all points with polar coordinates [math](r, \theta)[/math] which satisfy the inequalities [math]0 \leq \theta \leq 2\pi[/math] and [math]0 \leq r \leq a\theta[/math]; i.e., it is the region bounded by the positive [math]x[/math]-axis and that part of the spiral for which [math]0 \leq \theta \leq 2\pi[/math]. We find

[[math]] \begin{eqnarray*} area(R_1) &=& \frac{1}{2} \int_0^{2\pi} r^2 d\theta = \frac{1}{2} \int_0^{2\pi} a^2 \theta^2 d \theta \\ &=& \frac{a^2}{2} \frac{\theta^3}{3} \Big|_0^{2\pi} = \frac{4a^2 {\pi}^3}{3}. \end{eqnarray*} [[/math]]

File:Guide c5467 scanfig10 35.png

The set [math]R_2[/math] consists of all points with polar coordinates [math](r, \theta)[/math] which satisfy the inequalities [math]2\pi \leq \theta \leq \frac{5\pi}{2}[/math] and [math]a(\theta - 2\pi) \leq r \leq a\theta[/math] (see Figure 35). This region can be equivalently described as that bounded by the lines [math]\theta = 0[/math] and [math]\theta = \frac{\pi}{2}[/math] and the two polar curves:

[[math]] \left \{ \begin{array}{ll} r_1 = a\theta, &\\ r_2 = a(\theta + 2\pi), \;\;\; & 0 \leq \theta \leq \frac{\pi}{2} . \end{array} \right . [[/math]]

Since [math]0 \leq r_1(\theta) \leq r_2(\theta)[/math] for every [math]\theta[/math] on the interval [math]\Big[0, \frac{\pi}{2}\Big][/math], the area of [math]R_2[/math] is obviously given by the formula

[[math]] \begin{eqnarray*} area(R_2) &=& \frac{1}{2} \int_0^{\pi/2} (r_2^2 - r_1^2) d\theta \\ &=& \frac{1}{2} \int_0^{\pi/2} [a^2 (\theta + 2\pi)^2 - a^2 \theta^2] d\theta \\ &=& \frac{a^2}{2} \int_0^{\pi/2} (4 \pi \theta + 4\pi^2) d\theta \\ &=& 2\pi a^2 \Big(\frac{\theta^2}{2} + \pi \theta\Big) \Big|_0^{\pi/2} = 2\pi a^2 \Big(\frac{\pi^2}{8} + \frac{\pi^2}{2}\Big) \\ &=& \frac{5a^2 \pi^3}{4} . \end{eqnarray*} [[/math]]

We conclude that

[[math]] \begin{eqnarray*} A &=& aren(R_1) + area(R_2)\\ &=& \frac{4a^2 \pi^3}{3} + \frac{5a^2 \pi^3}{4} = \frac{31a^2 \pi^3}{12} . \end{eqnarray*} [[/math]]

An alternative way of finding the answer is to realize that the integral

[[math]] \frac{1}{2} \int_0^{5\pi/2} r^2 d\theta = \frac{1}{2} \int_0^{5\pi/2} a^2 \theta^2 d\theta [[/math]]

is equal to the area [math]A[/math] except for the fact that it counts twice the area bounded by the lines [math]\theta = 0[/math] and [math]\theta = \frac{\pi}{2}[/math] and the curve [math]r = a\theta[/math] for [math]0 \leq \theta \leq \frac{\pi}{2}[/math]. Hence we also obtain

[[math]] \begin{eqnarray*} A &=& \frac{1}{2} \int_0^{5\pi/2} a^2 \theta^2 d\theta - \frac{1}{2} \int_0^{\pi/2} a^2 \theta^2 d\theta \\ &=& \frac{31a^2 \pi^3}{12} . \end{eqnarray*} [[/math]]

The second topic of this section is the computation of the arc length of a curve defined by an equation in polar coordinates. No new methods are needed, since the problem is simply a special case of the more general one of finding the arc length of a parametrized curve. As noted in the second paragraph of this section, if [math]f[/math] is a continuous function containing the interval [math][a, b][/math] in its domain, then the polar graph of the equation

[[math]] r = f(\theta), \;\;\;\mbox{with}\; a \leq \theta \leq b, [[/math]]

is a parametrized curve [see equations (2)]. Specifically, the curve is the range of the parametrization [math]P: [a, b] \rightarrow R^2[/math] defined by

[[math]] P(\theta) = (x(\theta), y(\theta)) = (f(\theta) \cos \theta, f(\theta) \sin \theta), [[/math]]

for every [math]\theta[/math] in [math][a, b][/math]. We shall make the assumption that the derivative [math]f'[/math] is a continuous function on [math][a, b][/math], and this implies that the derivatives [math]x'[/math] and [math]y'[/math] are also continuous. It then follows directly from Theorem (2.2), page 553, that the arc length of the curve from [math]P(a)[/math] to [math]P(b)[/math] is given by

[[math]] L_a^b = \int_a^b \sqrt{x'(\theta)^2 + y'(\theta)^2} \;d\theta. [[/math]]

Since

[[math]] \begin{eqnarray*} x'(\theta) = f'(\theta) \cos \theta - f(\theta) \sin \theta,\\ y'(\theta) = f'(\theta) \sin \theta + f(\theta) \cos \theta, \end{eqnarray*} [[/math]]

we find that

[[math]] \begin{eqnarray*} x'(\theta)^2 + y'(\theta)^2 &=& f'(\theta)^2 \cos^2 \theta - 2f'(\theta)f(\theta) \sin \theta \cos \theta + f(\theta)^2 \sin^2 \theta\\ &&+ f'(\theta)^2 \sin^2 \theta + 2f'(\theta)f (\theta) \sin \theta \cos \theta + f(\theta)^2 \cos^2 \theta\\ &=& f'(\theta)^2 + f(\theta)^2. \end{eqnarray*} [[/math]]

Thus we obtain the following integral formula for the arc length [math]L_a^b[/math] of the polar graph of the equation [math]r = f(\theta)[/math], in which [math]a \leq \theta \leq b[/math]:

Theorem

(7.3)

[[math]] L_a^b = \int_a^b \sqrt{f'(\theta)^2 + f(\theta)^2} \;d\theta. [[/math]]

Alternatively, if we set [math]r = f(\theta)[/math] in the formula and write [math]f'(\theta) = \frac{dr}{d\theta}[/math], we have

Theorem

(7.3')

[[math]] L_a^b = \int_a^b \sqrt{ \Big(\frac{dr}{d\theta} \Big)^2 + r^2} \;d\theta . [[/math]]

Example

Find the arc length of the cardioid defined in polar coordinates by the equation [math]r = 1 + \cos \theta[/math]. This curve is shown in Figure 32, and the area of the region which it bounds is computed in Example 1. We have

[[math]] \begin{eqnarray*} \frac{dr}{d\theta} &=& - \sin \theta,\\ r^2 &=& (1 + \cos \theta)^2 = 1 + 2 \cos \theta + \cos^2 \theta. \end{eqnarray*} [[/math]]

Hence

[[math]] \begin{eqnarray*} r^2 + \Big( \frac{dr}{d \theta} \Big)^2 &=& 1 + 2 \cos \theta + \cos^2 \theta + \sin^2 \theta \\ &=& 2(1 + \cos \theta). \end{eqnarray*} [[/math]]

The trigonometric identity

[[math]] \cos^2 \frac{\theta}{2} = \frac{1}{2} (1 + \cos \theta) [[/math]]

implies that

[[math]] r^2 + \Big( \frac{dr}{d \theta} \Big)^2 = 4 \cos^2 \frac{\theta}{2} , [[/math]]

and it follows from the integral formula (7.3') that the arc length [math]L[/math] of the cardioid is given by

[[math]] L = \int_0^{2\pi} \sqrt{4\cos^2 \frac{\theta}{2}} \;d\theta = 2\int_0^{2\pi} \Big| \cos \frac{\theta}{2} \Big| \;d\theta. [[/math]]

However, because the cardioid is symmetric about the [math]x[/math]-axis, we conclude that

[[math]] L= 2 \int_0^\pi \sqrt{4\cos^2 \frac{\theta}{2}} \;d\theta = 4 \int_0^\pi \Big|\cos \frac{\theta}{2} \Big| \;d\theta. [[/math]]

lf [math]0 \leq \theta \leq \pi[/math], then [math]\cos \frac{\theta}{2} \geq 0[/math] and so [math]\Big|\cos \frac{\theta}{2}\Big| = \cos \frac{\theta}{2}[/math]. Hence the arc length [math]L[/math] is equal to

[[math]] L = 4\int_0^\pi \cos \frac{\theta}{2} d\theta = 8 \sin \frac{\theta}{2} \Big|_0^\pi = 8. [[/math]]

\end{exercise}

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.