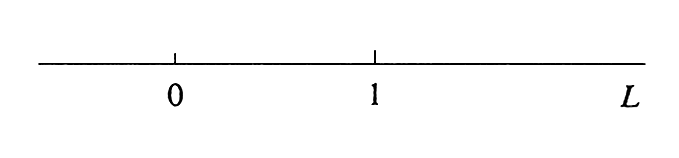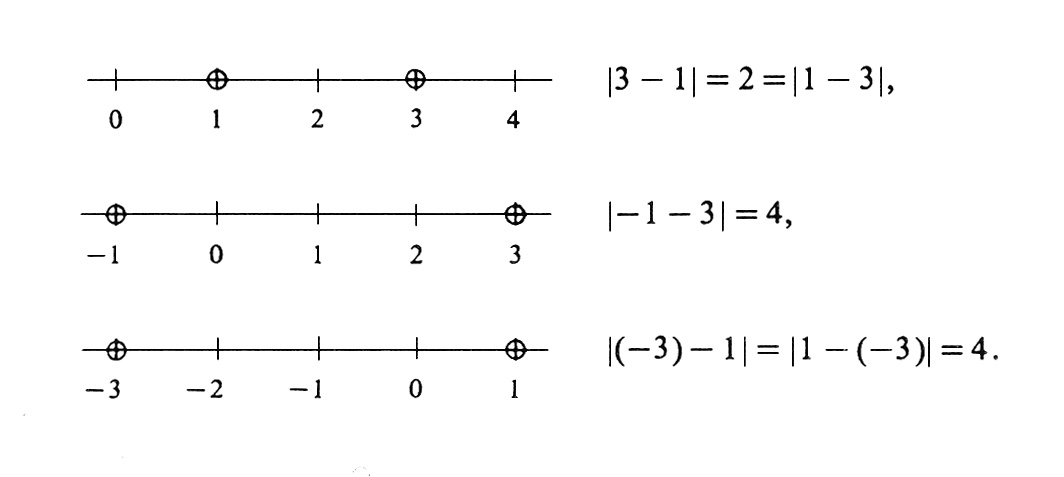guide:A5dd35d44b: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 33: | Line 33: | ||
</math></div> | </math></div> | ||
<span id="sec 1.1"> | |||
Calculus deals with numerical-valued quantities and, | Calculus deals with numerical-valued quantities and, | ||
| Line 74: | Line 74: | ||
</math> | </math> | ||
Another subset is the set <math>\Q</math> of all rational numbers. | Another subset is the set <math>\Q</math> of all rational numbers. | ||
A real number <math>r</math> is | A real number <math>r</math> is '''rational''' | ||
if it can be expressed as the ratio of two integers, | if it can be expressed as the ratio of two integers, | ||
more precisely, | more precisely, | ||
| Line 81: | Line 81: | ||
Since every integer <math>m</math> can be written <math>\frac{m}{1}</math>, | Since every integer <math>m</math> can be written <math>\frac{m}{1}</math>, | ||
it follows that every integer is also a rational number. | it follows that every integer is also a rational number. | ||
A scheme, analogous | A scheme, analogous to \ref{eq1.1.1}, | ||
which lists all the positive rational | which lists all the positive rational | ||
numbers is the following: | numbers is the following: | ||
| Line 105: | Line 105: | ||
For example, | For example, | ||
a very simple and beautiful argument shows that <math>\sqrt 2</math> is not rational. | a very simple and beautiful argument shows that <math>\sqrt 2</math> is not rational. | ||
(See | (See [[exercise:8162304386 |Exercise]].) | ||
It is not hard to prove that a real number is rational | It is not hard to prove that a real number is rational | ||
if and only if its decimal expansion beyond some digit | if and only if its decimal expansion beyond some digit | ||
| Line 132: | Line 132: | ||
are defined so that the following six facts are true: | are defined so that the following six facts are true: | ||
{{proofcard|Associate Laws|axiom.i| | |||
<math display="block"> | <math display="block"> | ||
a + (b + c) = (a + b) + c, | a + (b + c) = (a + b) + c, | ||
| Line 141: | Line 139: | ||
<math display="block"> | <math display="block"> | ||
a(bc) = (ab)c. | a(bc) = (ab)c. | ||
</math> | </math>|}} | ||
{{proofcard|Commutative Laws|axiom.ii| | |||
<math display="block"> | <math display="block"> | ||
| Line 152: | Line 149: | ||
<math display="block"> | <math display="block"> | ||
ab= ba. | ab= ba. | ||
</math> | </math>| | ||
}} | |||
{{proofcard|Distributive Law|axiom.iii| | |||
<math display="block"> | <math display="block"> | ||
(a + b) c = ac + bc. | (a + b) c = ac + bc. | ||
</math> | </math>|}} | ||
{{proofcard|Existence of Identities|axiom.iv| | |||
<math>\R</math> contains two distinct elements <math>0</math> and <math>1</math> | <math>\R</math> contains two distinct elements <math>0</math> and <math>1</math> | ||
with the properties that <math>0 + a = a</math> and <math>1 \cdot a = a</math> | with the properties that <math>0 + a = a</math> and <math>1 \cdot a = a</math> | ||
for every <math>a</math> in <math>\R</math>. | for every <math>a</math> in <math>\R</math>.|}} | ||
{{proofcard|Existence of Subtraction|axiom.v| | |||
For every <math>a</math> in <math>\R</math>, | For every <math>a</math> in <math>\R</math>, | ||
there is an element in <math>\R</math> denoted by <math>-a</math> | there is an element in <math>\R</math> denoted by <math>-a</math> | ||
such that <math>a + (-a) = 0</math>. | such that <math>a + (-a) = 0</math>. | ||
{{alert-info|<math>a - b</math> is an abbreviation of <math>a + (-b)</math>.}}|}} | |||
<math>a - b</math> is an abbreviation of <math>a + (-b)</math>. | |||
{{proofcard|Existence of Division|axiom.vi| | |||
For every <math>a \neq 0</math> in <math>\R</math>, | For every <math>a \neq 0</math> in <math>\R</math>, | ||
there is an element in <math>\R</math> denoted by <math>a^{-1}</math> or <math>\frac{1}{a}</math> | there is an element in <math>\R</math> denoted by <math>a^{-1}</math> or <math>\frac{1}{a}</math> | ||
such that <math>aa^{-1} = 1</math>. | such that <math>aa^{-1} = 1</math>. | ||
{{alert-info|<math>\frac{a}{b}</math> is an abbreviation of <math>ab^{-1}</math>.}}|}} | |||
<math>\frac{a}{b}</math> is an abbreviation of <math>ab^{-1}</math>. | |||
Addition and multiplication are here introduced as binary operations. | Addition and multiplication are here introduced as binary operations. | ||
However, as a result of the associative law of addition, | However, as a result of the associative law of addition, | ||
| Line 210: | Line 197: | ||
which we choose to denote by <math> < </math>. | which we choose to denote by <math> < </math>. | ||
{{proofcard|Transitive Law|axiom.vii|If <math>a < b</math> and <math>b < c</math>, then <math>a < c</math>.|}} | |||
If <math>a < b</math> and <math>b < c</math>, then <math>a < c</math>. | |||
Note that each of the above Axioms [[#axiom.vi | | {{proofcard|Law of Trichotomy|axiom.viii|For every real number <math>a</math>,one and only one of the following alternatives holds:<math>a = 0</math>, or <math>a < 0</math>, or <math>0 < a</math>.|}} | ||
remains true when restricted to the set <math>\Z</math> of integers. | |||
{{proofcard|Axiom|axiom.ix|If <math>a < b</math>, then <math>a + c < b + c</math>.|}} | |||
{{proofcard|Axiom|axiom.x|If <math>a < b</math> and <math>0 < c</math>, then <math>ac < bc</math>.|}} | |||
Note that each of the above Axioms except [[#axiom.vi |Axiom]] remains true when restricted to the set <math>\Z</math> of integers. | |||
Moreover, | Moreover, | ||
all the axioms are true for the set <math>\Q</math> of rational numbers. | all the axioms are true for the set <math>\Q</math> of rational numbers. | ||
| Line 244: | Line 219: | ||
and abbreviate the statement that <math>a</math> is greater than <math>b</math> | and abbreviate the statement that <math>a</math> is greater than <math>b</math> | ||
by writing <math>a > b</math>. | by writing <math>a > b</math>. | ||
Clearly <math>a > b</math> if and only if <math>b < a</math>. | Clearly <math>a > b</math> if and only if <math>b < a</math>. [[#axiom.x |Axiom]], when translated into English, | ||
[[#axiom.x |Axiom]], | |||
when translated into English, | |||
says that the direction of an inequality is preserved | says that the direction of an inequality is preserved | ||
if both sides are multiplied by the same positive number. | if both sides are multiplied by the same positive number. | ||
| Line 252: | Line 225: | ||
The inequality is reversed. | The inequality is reversed. | ||
That is, | That is, | ||
{{proofcard|Proposition|thm_1.1.1|If <math>a < b</math> and <math>c < 0</math>, then <math>ac > bc</math>. | |||
|Since <math>c < 0</math>, [[#axiom.iv [[#axiom.v | | {{proofcard|Proposition|thm_1.1.1|If <math>a < b</math> and <math>c < 0</math>, then <math>ac > bc</math>.|Since <math>c < 0</math>, [[#axiom.iv|Axiom]], [[#axiom.v |Axiom]], and [[#axiom.ix |Axiom]] imply | ||
[[#axiom.ix | | |||
imply | |||
<math display="block"> | <math display="block"> | ||
| Line 271: | Line 242: | ||
Hence <math>bc < ac</math>, | Hence <math>bc < ac</math>, | ||
and this is equivalent to <math>ac > bc</math>.}} | and this is equivalent to <math>ac > bc</math>.}} | ||
Two more abbreviations complete the mathematician's array of symbols | Two more abbreviations complete the mathematician's array of symbols | ||
for writing inequalities: | for writing inequalities: | ||
| Line 342: | Line 314: | ||
<math display="block"> | <math display="block"> | ||
\begin{array}{r} | \begin{array}{r} | ||
-\infty < x < a \;\;\; \mbox{is equivalent to $x < a$}, \\ | -\infty < x < a \;\;\; \mbox{is equivalent to $x < a$}, \\ | ||
a \leq x < \infty \;\;\;\mbox{is equivalent to | a \leq x < \infty \;\;\;\mbox{is equivalent to $a \leq x$}, | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Line 367: | Line 339: | ||
'''Example''' | '''Example''' | ||
Draw the intervals | Draw the intervals | ||
<math>[0, 1]</math>, <math>[-1, 4)</math>, <math>(2, \infty</math>), <math>(-\infty, -1]</math>, <math>(-1, 3)</math>, | <math>[0, 1]</math>, <math>[-1, 4)</math>, <math>(2, \infty</math>), <math>(-\infty, -1]</math>, <math>(-1, 3)</math>, | ||
| Line 382: | Line 353: | ||
|a| = \left \{ \begin{array}{rl} | |a| = \left \{ \begin{array}{rl} | ||
a & \mbox{if $a \geq 0$}, \\ | a & \mbox{if $a \geq 0$}, \\ | ||
-a & \mbox{if | -a & \mbox{if $a < 0 $}. | ||
\end{array} | \end{array} | ||
\right. | \right. | ||
| Line 399: | Line 370: | ||
is to look at a few illustrations (see [[#fig 1.4|Figure]]). | is to look at a few illustrations (see [[#fig 1.4|Figure]]). | ||
<div id="fig 1.4" class="d-flex justify-content-center"> | <div id="fig 1.4" class="d-flex justify-content-center"> | ||
[[File:guide_c5467_scanfig1_4.png | 400px | thumb | [[File:guide_c5467_scanfig1_4.png | 400px | thumb ]] | ||
</div> | </div> | ||
<span id="exam 1.1.2"/> | <span id="exam 1.1.2"/> | ||
'''Example''' | '''Example''' | ||
Describe the set <math>I</math> of all real numbers <math>x</math> | Describe the set <math>I</math> of all real numbers <math>x</math> | ||
such that <math>|x - 5| < 3</math>. | such that <math>|x - 5| < 3</math>. | ||
For any number <math>x</math>, | For any number <math>x</math>, the number <math>|x - 5|</math> is the distance between <math>x</math> and <math>5</math> on a real number line (see [[#fig 1.5|Figure]]). | ||
the number <math>|x - 5|</math> is the distance between <math>x</math> and <math>5</math> | |||
on a real number line (see [[#fig 1.5|Figure]]). | <div id="fig_1.5" class="d-flex justify-content-center"> | ||
<div id=" | [[File:guide_c5467_scanfig1_5.png | 400px | thumb ]] | ||
[[File:guide_c5467_scanfig1_5.png | 400px | thumb | </div> | ||
That distance will be less than <math>3</math> | That distance will be less than <math>3</math> | ||
if and only if <math>x</math> satisfies the inequalities <math>2 < x < 8</math>. | if and only if <math>x</math> satisfies the inequalities <math>2 < x < 8</math>. | ||
| Line 450: | Line 421: | ||
|x| = \sqrt a | |x| = \sqrt a | ||
</math> | </math> | ||
are equivalent. | |||
Having made these remarks, we observe that | are equivalent. Having made these remarks, we observe that | ||
\ | |||
</ | {{proofcard|Proposition|thm 1.1.2|<math display = "block"> | ||
and since the positive square root of a product of two positive numbers | |a| = \sqrt {a^2} . | ||
</math>|}} | |||
The [[#thm_1.1.2|formulation]] is a handy one for establishing two of the basic properties of absolute value. | |||
They are | |||
{{Proofcard|Proposition|thm_1.1.3|<math display="block">|ab| = |a| |b|.</math>|Since <math>(ab)^2 = {a^2}{b^2}</math> and since the positive square root of a product of two positive numbers | |||
is the product of their positive square roots, | is the product of their positive square roots, | ||
we get | we get | ||
<math display="block"> | <math display="block"> | ||
|ab| = \sqrt {(ab)^2} = \sqrt {{a^2}{b^2}} = \sqrt{a^2} \sqrt{b^2} = |a| |b|. | |ab| = \sqrt {(ab)^2} = \sqrt {{a^2}{b^2}} = \sqrt{a^2} \sqrt{b^2} = |a| |b|. | ||
</math> | </math>}} | ||
{{proofcard|Proposition|thm_1.1.4|<math display="block"> | |||
|a + b| \leq |a| + |b|. | |||
</math>|We observe, first of all, that <math>ab \leq |ab|</math>. | |||
Hence | Hence | ||
| Line 473: | Line 451: | ||
|a + b|^{2} = (a + b)^{2} \leq (|a| + |b|)^{2}. | |a + b|^{2} = (a + b)^{2} \leq (|a| + |b|)^{2}. | ||
</math> | </math> | ||
Now take the positive square root of each side of the inequality (see [[exercise:C24f7adcb0 |Exercise]]).}} | |||
(see | |||
As remarked above, [[#axiom.i |Axiom]] through [[#axiom.x |Axiom]] about the set <math>\R</math> of real numbers is incomplete. | |||
As remarked above, | |||
about the set <math>\R</math> of real numbers is incomplete. | |||
One important property of real numbers | One important property of real numbers | ||
that together with the others gives a complete characterization | that together with the others gives a complete characterization | ||
is the following: | is the following: | ||
{{proofcard|Least Upper Bound Property |axiom.xi|Every nonempty subset of <math>\R</math> which has an upper bound has a least upper bound.|}} | |||
Every nonempty subset of <math>\R</math> which has an upper bound | |||
has a least upper bound. | |||
Suppose <math>S</math> is a nonempty subset of <math>\R</math> which has an upper bound. | Suppose <math>S</math> is a nonempty subset of <math>\R</math> which has an upper bound. | ||
What [[#axiom.xi |Axiom]] says | What [[#axiom.xi |Axiom]] says is that there is some number <math>b</math> which | ||
is that there is some number <math>b</math> which | |||
(1) is an upper bound, i.e., <math>s \leq b</math> for every <math>s</math> in <math>S</math>, and | (1) is an upper bound, i.e., <math>s \leq b</math> for every <math>s</math> in <math>S</math>, and | ||
(2) if <math>c</math> is any other upper bound of <math>S</math>, then <math>b \leq c</math>. | (2) if <math>c</math> is any other upper bound of <math>S</math>, then <math>b \leq c</math>. | ||
| Line 503: | Line 475: | ||
there will always exist a smaller one. | there will always exist a smaller one. | ||
Hence there is no rational least upper bound. | Hence there is no rational least upper bound. | ||
==General references== | ==General references== | ||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | {{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | ||
Latest revision as of 21:22, 3 November 2024
Calculus deals with numerical-valued quantities and, in the beginning, with quantities whose values are real numbers. Some understanding of the basic set [math]\R[/math] of all real numbers is therefore essential. A real number is one that can be written as a decimal: positive or negative or zero, terminating or nonterminating. Examples are
The most familiar subset of [math]R[/math] is the set [math]\Z[/math] of integers. These are the numbers
Another subset is the set [math]\Q[/math] of all rational numbers. A real number [math]r[/math] is rational if it can be expressed as the ratio of two integers, more precisely, if [math]r = \frac{m}{n}[/math], where [math]m[/math] and [math]n[/math] are integers and [math]n \neq 0[/math]. Since every integer [math]m[/math] can be written [math]\frac{m}{1}[/math], it follows that every integer is also a rational number. A scheme, analogous to \ref{eq1.1.1}, which lists all the positive rational numbers is the following:
Of course there are infinitely many repetitions in this presentation since, for example, [math]\frac{2}{1} = \frac{4}{2} = \frac{6}{3} = \ldots.[/math] An unsophisticated guess would be that all real numbers are rational. There are, however, many famous proofs that this is not so. For example, a very simple and beautiful argument shows that [math]\sqrt 2[/math] is not rational. (See Exercise.) It is not hard to prove that a real number is rational if and only if its decimal expansion beyond some digit consists of a finite sequence of digits repeated forever. Thus the numbers
are rational, but
is not. The fundamental algebraic operations on real numbers are addition and multiplication: For any two elements [math]a[/math] and [math]b[/math] in [math]\R[/math], two elements [math]a + b[/math] and [math]ab[/math] in [math]\R[/math] are uniquely determined. These elements, called the sum and product of [math]a[/math] and [math]b[/math], respectively, are defined so that the following six facts are true:
[math]\R[/math] contains two distinct elements [math]0[/math] and [math]1[/math]
with the properties that [math]0 + a = a[/math] and [math]1 \cdot a = a[/math]
for every [math]a[/math] in [math]\R[/math].
For every [math]a[/math] in [math]\R[/math],
there is an element in [math]\R[/math] denoted by [math]-a[/math]
such that [math]a + (-a) = 0[/math].
For every [math]a \neq 0[/math] in [math]\R[/math],
there is an element in [math]\R[/math] denoted by [math]a^{-1}[/math] or [math]\frac{1}{a}[/math]
such that [math]aa^{-1} = 1[/math].
Addition and multiplication are here introduced as binary operations. However, as a result of the associative law of addition, [math]a + b + c[/math] is defined to be the common value of [math](a + b) + c[/math] and [math]a + (b + c)[/math]. In a like manner we may define the triple product [math]abc[/math] and, more generally, [math]a_{1} + \ldots + a_{n}[/math] and [math]a_{1} \ldots a_{n}[/math]. Many theorems of algebra are consequences of the above six facts, and we shall assume them without proof. They are, in fact, frequently taken as part of a set of axioms for [math]\R[/math]. Another essential property of the real numbers is that of order. We write [math]a \lt b[/math] as an abbreviation of the statement that [math]a[/math] is less than [math]b[/math]. Presumably the reader, given two decimals, knows how to tell which one is the smaller. The following four facts simply recall the basic properties governing inequalities. On the other hand, they may also be taken as axioms for an abstractly defined relation between elements of [math]\R[/math], which we choose to denote by [math] \lt [/math].
If [math]a \lt b[/math] and [math]b \lt c[/math], then [math]a \lt c[/math].
For every real number [math]a[/math],one and only one of the following alternatives holds:[math]a = 0[/math], or [math]a \lt 0[/math], or [math]0 \lt a[/math].
If [math]a \lt b[/math], then [math]a + c \lt b + c[/math].
If [math]a \lt b[/math] and [math]0 \lt c[/math], then [math]ac \lt bc[/math].
Note that each of the above Axioms except Axiom remains true when restricted to the set [math]\Z[/math] of integers. Moreover, all the axioms are true for the set [math]\Q[/math] of rational numbers. Hence as a set of axioms for [math]\R[/math], they fail to distinguish between two very different sets: [math]\R[/math] and its subset [math]\Q[/math]. Later in this section we shall add one more item to the list, which will complete the algebraic description of [math]\R[/math]. A real number [math]a[/math] is if positive [math]0 \lt a[/math] and negative if [math]a \lt 0[/math]. Since the relation “greater than” is just as useful as “less than,” we adopt a symbol for it, too, and abbreviate the statement that [math]a[/math] is greater than [math]b[/math] by writing [math]a \gt b[/math]. Clearly [math]a \gt b[/math] if and only if [math]b \lt a[/math]. Axiom, when translated into English, says that the direction of an inequality is preserved if both sides are multiplied by the same positive number. Just the opposite happens if the number is negative: The inequality is reversed. That is,
If [math]a \lt b[/math] and [math]c \lt 0[/math], then [math]ac \gt bc[/math].
Show ProofSince [math]c \lt 0[/math], Axiom, Axiom, and Axiom imply
Two more abbreviations complete the mathematician's array of symbols for writing inequalities: [math]a \leq b[/math] means [math]a \lt b[/math] or [math]a=b[/math], [math]a \geq b[/math] means [math]a \gt b[/math] or [math]a=b[/math]. The geometric interpretation of the set [math]\R[/math] of all real numbers as a straight line is familiar to anyone who has ever used a ruler, and it is essential to an understanding of calculus. To describe the assignment of points to numbers, consider an arbitrary straight line [math]L[/math], and choose on it two distinct points, one of which we assign to, or identify with, the number [math]0[/math], and the other to the number [math]1[/math]. (See Figure.)
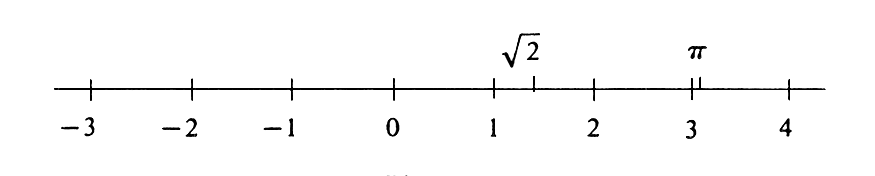
The rest is automatic. The scale on [math]L[/math] is chosen so that the unit of distance is the length of the line segment between the points [math]0[/math] and [math]1[/math]. Every positive number [math]a[/math] is assigned the point on the side of [math]0[/math] containing [math]1[/math] which is [math]a[/math] units of distance from [math]0[/math]. Every negative number [math]a[/math] is assigned the point on the side of [math]0[/math] not containing [math]1[/math] which is [math]-a[/math] units of distance from [math]0[/math]. Note that if [math]L[/math] is oriented so that [math]1[/math] lies to the right of [math]0[/math], then for any two numbers [math]a[/math] and [math]b[/math] (positive, negative, or zero), [math]a \lt b[/math] if and only if [math]a[/math] lies to the left of [math]b[/math]. A line which has been identified with [math]\R[/math] under a correspondence such as the one just described is called a real number line. (See Figure.)
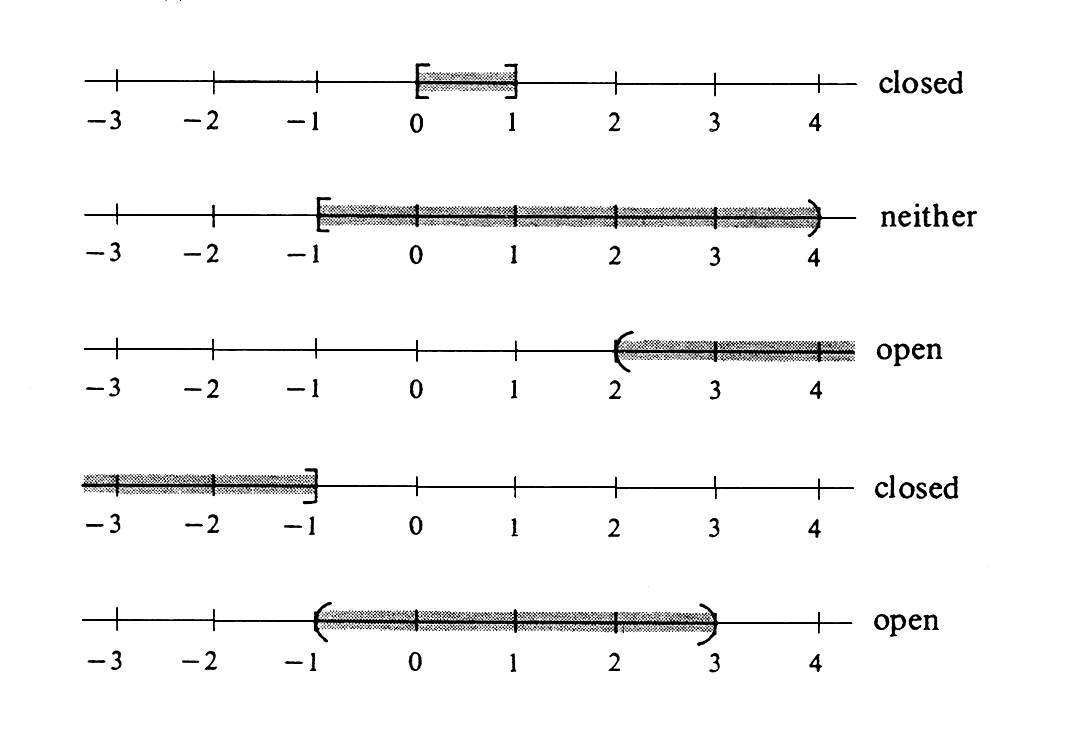
An interval is a subset [math]I[/math] of [math]\R[/math] with the property that whenever [math]a[/math] and [math]c[/math] belong to [math]I[/math] and [math]a \leq b \leq c[/math], then [math]b[/math] also belongs to [math]I[/math]. Geometrically an interval is a connected piece of a real number line. A number d is called a lower bound of a set [math]S[/math] of real numbers if [math]d \leq s[/math] for every [math]s[/math] in [math]S[/math]. It is an upper bound of [math]S[/math] if [math]s \leq d[/math] for every [math]s[/math] in [math]S[/math]. A given subset of [math]\R[/math], and in particular an interval, is called bounded if it has both an upper and lower bound. There are four different kinds of bounded intervals: [math](a, b)[/math], the set of all numbers [math]x[/math] such that [math]a \lt x \lt b[/math]; [math][a, b][/math], the set of all numbers [math]x[/math] such that [math]a \leq x \leq b[/math]; [math][a, b)[/math], the set of all numbers [math]x[/math] such that [math]a \leq x \lt b[/math]; [math](a, b][/math], the set of all numbers [math]x[/math] such that [math]a \lt x \leq b[/math]. In each case the numbers [math]a[/math] and [math]b[/math] are called the endpoints of the interval. The set [math][a, b][/math] contains both its endpoints, whereas [math](a, b)[/math] contains neither one. Clearly [math][a, b)[/math] contains its left endpoint but not its right one, and an analogous remark holds for [math](a, b][/math]. It is important to realize that there is no element [math]\infty[/math] (infinity) in the set [math]\R[/math]. Nevertheless, the symbols [math]\infty[/math] and [math]-\infty[/math] are commonly used in denoting unbounded intervals. Thus [math](a, \infty)[/math] is the set of all numbers [math]x[/math] such that [math]a \lt x[/math]; [math][a, \infty)[/math] is the set of all numbers [math]x[/math] such that [math]a \leq x[/math]; [math](-\infty, a)[/math] is the set of all numbers [math]x[/math] such that [math]x \lt a[/math]; [math](-\infty, a][/math] is the set of all numbers [math]x[/math] such that [math]x \leq a[/math]; [math](-\infty, \infty)[/math] is the entire set [math]\R[/math]. The symbols [math]\infty[/math] and [math]-\infty[/math] also appear frequently in inequalities although they are really unnecessary, because, for example,
etc. Since [math]\infty[/math] is not an element of [math]\R[/math], we shall never use the notations [math][a, \infty], x \leq \infty[/math], etc. An unbounded interval has either one endpoint or none; in each of the above cases it is the number [math]a[/math]. We call an interval open if it contains none of its endpoints, and closed if it contains them all. Thus, for example, [math](a, b)[/math] and [math](-\infty, a)[/math] are open, but [math][a, b][/math] and [math][a, \infty)[/math] are closed. The intervals [math][a, b)[/math] and [math](a, b][/math] are neither open nor closed, although they are sometimes called half-open or half-closed. Since [math](-\infty, \infty)[/math] has no endpoints, it vacuously both does and does not contain them. Hence [math](-\infty, \infty)[/math] has the dubious distinction of being both open and closed.
Example
Draw the intervals [math][0, 1][/math], [math][-1, 4)[/math], [math](2, \infty[/math]), [math](-\infty, -1][/math], [math](-1, 3)[/math], and identify them as open, closed, neither, or both (see Figure).
It is frequently necessary to talk about the size of a real number without regard to its sign, not caring whether it is positive or negative. This happens often enough to warrant a definition and special notation: The absolute value of a real number [math]a[/math] is denoted by [math]|a|[/math] and defined by
Thus [math]|3| = 3[/math], [math]|0| = 0[/math], [math]|- 3| = 3[/math]. Obviously, the absolute value of a real number cannot be negative. Geometrically, [math]|a|[/math] is the distance between the points [math]0[/math] and [math]a[/math] on the real number line. A generalization that is of extreme importance is the fact that [math]|a - b|[/math] is the distance between the points [math]a[/math] and [math]b[/math] on the real number line for any two numbers [math]a[/math] and [math]b[/math] whatsoever. Probably the best way to convince oneself that this is true is to look at a few illustrations (see Figure).
Example
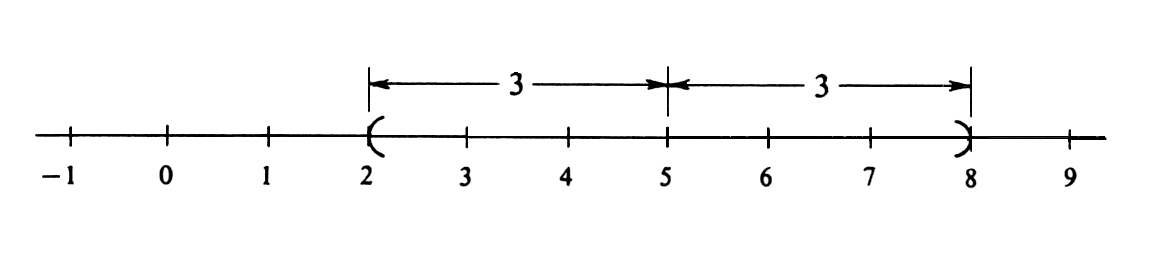
Describe the set [math]I[/math] of all real numbers [math]x[/math] such that [math]|x - 5| \lt 3[/math]. For any number [math]x[/math], the number [math]|x - 5|[/math] is the distance between [math]x[/math] and [math]5[/math] on a real number line (see Figure).
That distance will be less than [math]3[/math] if and only if [math]x[/math] satisfies the inequalities [math]2 \lt x \lt 8[/math]. We conclude that [math]I[/math] is the open interval [math](2, 8)[/math].
There is an alternative way of writing the definition of the absolute value of a number [math]a[/math] which requires only one equation: We do not have to give separate definitions for positive and negative [math]a[/math]. This definition uses a square root, and before proceeding to it, we call attention to the following mathematical custom: Although every positive real number a has two square roots, in this book the expression [math]\sqrt a[/math] always denotes the positive root. Thus the two solutions of the equation [math]x^2 = 5[/math] are [math]\sqrt 5[/math] and [math]-\sqrt 5[/math]. Note that the two equations
and
are not equivalent. The second implies the first, but not conversely. On the other hand,
and
are equivalent. Having made these remarks, we observe that
The formulation is a handy one for establishing two of the basic properties of absolute value. They are
Since [math](ab)^2 = {a^2}{b^2}[/math] and since the positive square root of a product of two positive numbers is the product of their positive square roots, we get
We observe, first of all, that [math]ab \leq |ab|[/math]. Hence
As remarked above, Axiom through Axiom about the set [math]\R[/math] of real numbers is incomplete. One important property of real numbers that together with the others gives a complete characterization is the following:
Every nonempty subset of [math]\R[/math] which has an upper bound has a least upper bound.
Suppose [math]S[/math] is a nonempty subset of [math]\R[/math] which has an upper bound. What Axiom says is that there is some number [math]b[/math] which (1) is an upper bound, i.e., [math]s \leq b[/math] for every [math]s[/math] in [math]S[/math], and (2) if [math]c[/math] is any other upper bound of [math]S[/math], then [math]b \leq c[/math]. It is hard to see at first how such a statement can be so significant. Intuitively it says nothing more than this: If you cannot go on forever, you have to stop somewhere. Note, however, that the rational numbers do not have this property. The set of all rational numbers less than the irrational number [math]\sqrt2[/math] certainly has an upper bound. In fact, each of the numbers [math]2[/math], [math]1.5[/math], [math]1.42[/math], [math]1.415[/math], [math]1.4143[/math], and [math]1.41422[/math] is an upper bound. However, for every rational upper bound, there will always exist a smaller one. Hence there is no rational least upper bound.
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.