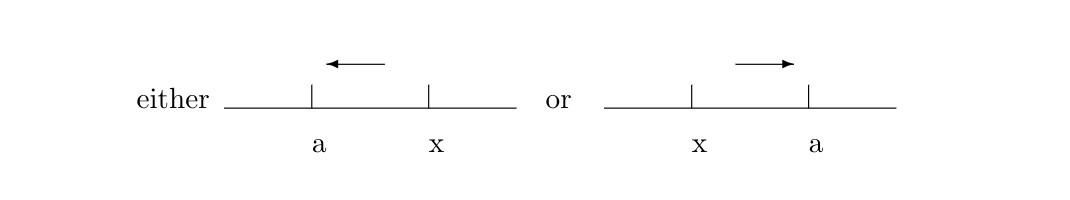guide:Ffb82a6ded: Difference between revisions
No edit summary |
mNo edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
\newcommand{\dilemma}[2] { | |||
\left\{ | |||
\begin{array}{ll} | |||
#1 \\ | |||
#2 | |||
\end{array} | |||
\right. | |||
} | |||
\newcommand{\trilemma}[3] { | |||
\left\{ | |||
\begin{array}{ll} | |||
#1 \\ | |||
#2 \\ | |||
#3 | |||
\end{array} | |||
\right. | |||
} | |||
</math></div> | |||
Consider the function <math>f</math> defined by | |||
<math display="block"> | |||
f(x) = \frac{x^{2} - 3x + 2}{x - 2}, | |||
\prov{x \neq 2}. | |||
</math> | |||
The domain of <math>f</math> is the set of all real numbers | |||
with the exception of the number <math>2</math>, | |||
which has been excluded because substitution of <math>x = 2</math> | |||
in the expression for <math>f(x)</math> | |||
yields the undefined term <math>\frac{0}{0}</math>. | |||
On the other hand, | |||
<math>x^{2} - 3x + 2 = (x - 1)(x - 2)</math> | |||
and | |||
<span id{{=}}"eq1.4.1"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\frac{(x - 1)(x - 2)}{x - 2} = x - 1, | |||
\provx{provided $x \neq 2$}. | |||
\label{eq1.4.1} | |||
\end{equation} | |||
</math> | |||
The proviso is essential. | |||
Without it, (1) is false because, | |||
if <math>x = 2</math>, | |||
the left side is undefined | |||
and the right side is equal to 1. | |||
We therefore obtain | |||
<math display="block"> | |||
f(x) = x - 1, | |||
\prov{x \neq 2}. | |||
</math> | |||
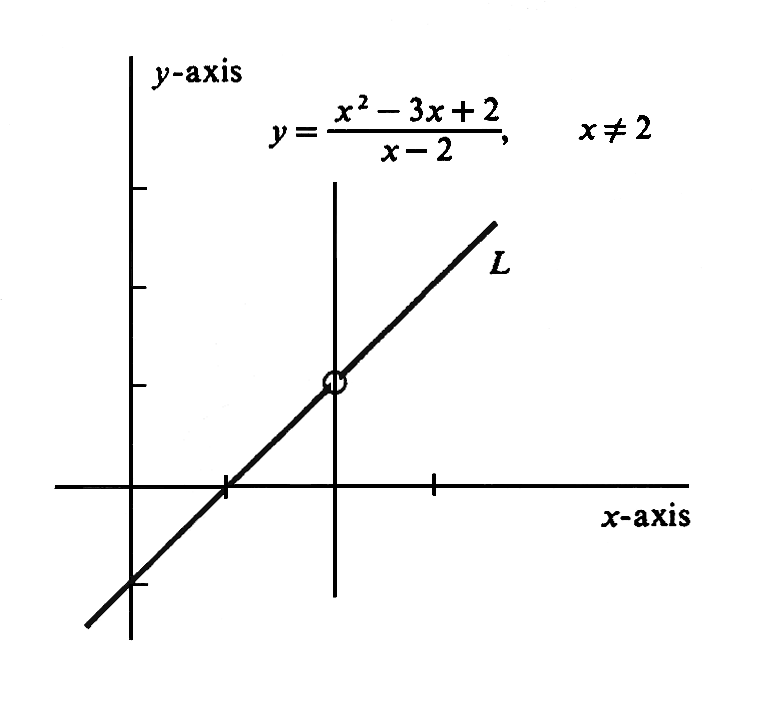
The graph of the function <math>x - 1</math> is a straight line <math>L</math>; | |||
so the graph of <math>f</math> is the punctured line | |||
obtained from <math>L</math> | |||
by omitting the one point <math>(2,1)</math> | |||
(see [[#fig 1.22|Figure]]). | |||
<div id="fig 1.22" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_22.png | 400px | thumb | ]] | |||
</div> | |||
Although the function <math>f</math> is not defined at <math>x = 2</math>, | |||
we know its behavior for values of <math>x</math> near <math>2</math>. | |||
The graph makes it clear that if <math>x</math> is close to <math>2</math>, | |||
then <math>f(x)</math> is close to <math>1</math>. | |||
In fact, the values <math>f(x)</math> can be brought arbitrarily close to <math>1</math> | |||
by taking <math>x</math> sufficiently close to <math>2</math>. | |||
We express this fact by writing | |||
<math display="block"> | |||
\lim_{x \goesto 2} {\frac{x^2 - 3x + 2}{x -2}} = 1, | |||
</math> | |||
which is translated: | |||
''The limit of <math>\frac{x^2 - 3x +2''{x - 2}</math> | |||
is <math>1</math> as <math>x</math> approaches <math>2</math>.} | |||
<span id="exam 1.4.1"/> | |||
'''Example''' | |||
Evaluate | |||
<math>\lim_{x \goesto 3} {\frac{\sqrt{x} - \sqrt{3}}{x - 3}}</math>. | |||
The function | |||
<math>\frac{\sqrt{x} - \sqrt{3}}{x - 3}</math> | |||
is not defined at <math>x = 3</math>. | |||
The following algebraic manipulation | |||
puts the function in a form | |||
in which its behavior close to <math>3</math> can be read off easily: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\frac{\sqrt{x} - \sqrt{3}}{x - 3} | |||
&=& \frac{\sqrt{x} - \sqrt{3}}{x - 3} | |||
\frac{\sqrt{x} + \sqrt{3}}{\sqrt{x} + \sqrt{3}} \\ | |||
&=& \frac{x - 3}{x - 3} \frac{1}{\sqrt{x} + \sqrt{3}} \\ | |||
&=& \frac{1}{\sqrt{x} + \sqrt{3}}, \provx{if $x \neq 3$}. | |||
\end{eqnarray*} | |||
</math> | |||
Again note the proviso <math>x \neq 3</math>: | |||
When <math>x = 3</math>, | |||
the last quantity in the preceding equations | |||
is equal to <math>\frac{1}{\sqrt{3} + \sqrt{3}}</math>, | |||
but the first quantity is not defined. | |||
However, by taking values of <math>x</math> close to 3, | |||
it is clear that the corresponding values of | |||
<math>\frac{1}{\sqrt{x} + \sqrt{3}}</math> | |||
can be brought as close as we please to | |||
<math>\frac{1}{2 \sqrt{3}}</math>. | |||
We conclude that | |||
<math display="block"> | |||
\lim_{x \goesto 3} | |||
{\frac {\sqrt{x} - \sqrt{3}}{x - 3}} | |||
= | |||
\frac{1}{2{\sqrt{3}}}. | |||
</math> | |||
In words: | |||
The limit of | |||
<math>\frac {\sqrt{x} - \sqrt{3}}{x - 3}</math>, | |||
as <math>x</math> approaches <math>3</math>, | |||
is <math>\frac{1}{2{\sqrt{3}}}</math>. | |||
<span id="exam 1.4.2"/> | |||
'''Example''' | |||
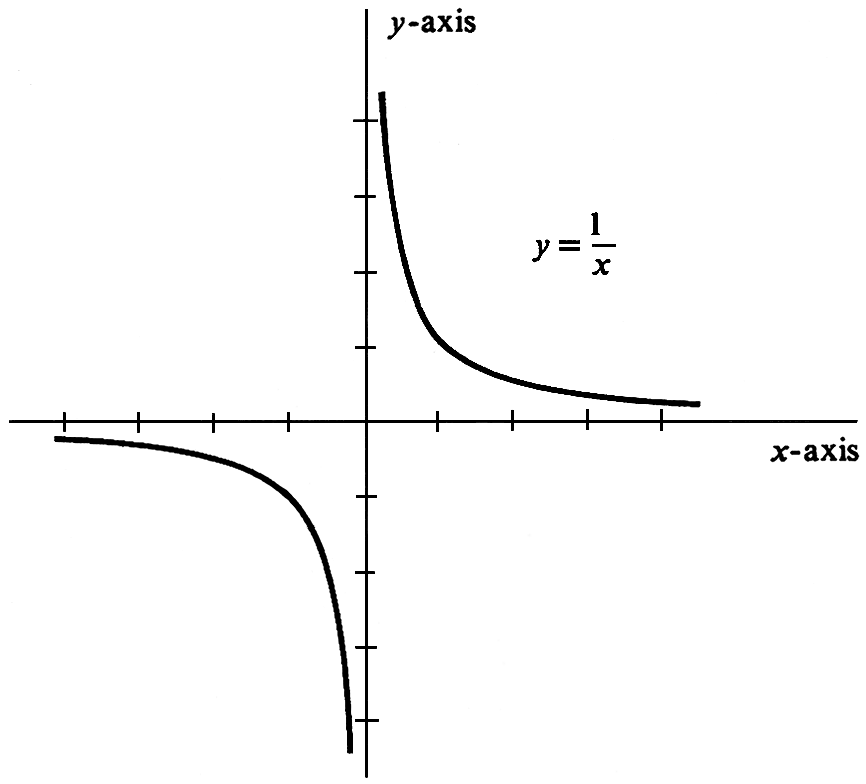
If <math>f(x) = \frac{1}{x}</math>, | |||
evaluate | |||
<math>\lim_{x \goesto 0} f(x)</math>. | |||
The function <math>f</math> is not defined at <math>0</math> | |||
(i.e., the number 0 is not in the domain of <math>f</math>). | |||
From the graph of <math>f</math> and the list of ordered pairs <math>(x, f(x))</math> | |||
shown in [[#fig 1.23|Figure]], | |||
<div id="fig 1.23" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_23.png | 400px | thumb | ]] | |||
</div> | |||
it is clear that there are values of <math>x</math> | |||
arbitrarily close to 0 for which the | |||
corresponding values of <math>f(x)</math> | |||
are arbitrarily large in absolute value | |||
(see [[#table 1.5 |Table]]). | |||
We conclude that | |||
<math>\lim_{x \goesto 0}{\frac{1}{x}}</math> does not exist. | |||
<span id="table 1.5"/> | |||
{|class="table" | |||
|- | |||
|<math>x</math> || <math>f(x) = \frac{1}{x}</math> | |||
|- | |||
|1 || 1 | |||
|- | |||
|0.1 || 10 | |||
|- | |||
|0.01 || 100 | |||
|- | |||
|0.001 || 1000 | |||
|- | |||
|0.0001 || 10000 | |||
|- | |||
|<math>\cdots</math> || <math>\cdots</math> | |||
|- | |||
|-1 || -1 | |||
|- | |||
|-0.1 || -10 | |||
|- | |||
|-0.01 || -100 | |||
|- | |||
|-0.001 || -1000 | |||
|- | |||
|-0.0001 || -10000 | |||
|- | |||
|<math>\cdots</math> || <math>\cdots</math> | |||
|} | |||
Thus far our examples have been confined to | |||
the problem of finding the limit of a function | |||
at a number which happens to lie outside | |||
the domain of the function. | |||
If it happens that the number <math>a</math> | |||
is in the domain of <math>f</math>, | |||
then it is frequently possible to determine | |||
<math>\lim_{x \goesto a}f(x)</math> at a glance. | |||
Consider, for example, | |||
the function | |||
<math>f(x) = 2x^2 - x - 2</math>. | |||
As <math>x</math> takes on values closer and closer to 3, | |||
the corresponding value of | |||
<math>2x^{2}</math> approaches <math>18</math>, | |||
the value of <math>-x</math> approaches <math>-3</math>, | |||
and the constant <math>-2</math> does not change. | |||
We conclude that | |||
<math display="block"> | |||
\lim_{x \goesto 3} {(2x^2 - x - 2)} = 13, | |||
</math> | |||
or that, for this particular function, <math>\lim_{x \goesto 3}f(x) = f(3)</math>. | |||
<span id="exam 1.4.3"/> | |||
'''Example''' | |||
It would be incorrect to suppose that | |||
if <math>a</math> is in the domain of <math>f</math>, | |||
then it always happens that | |||
<math>\lim_{x \goesto a}f(x) = f(a)</math>. | |||
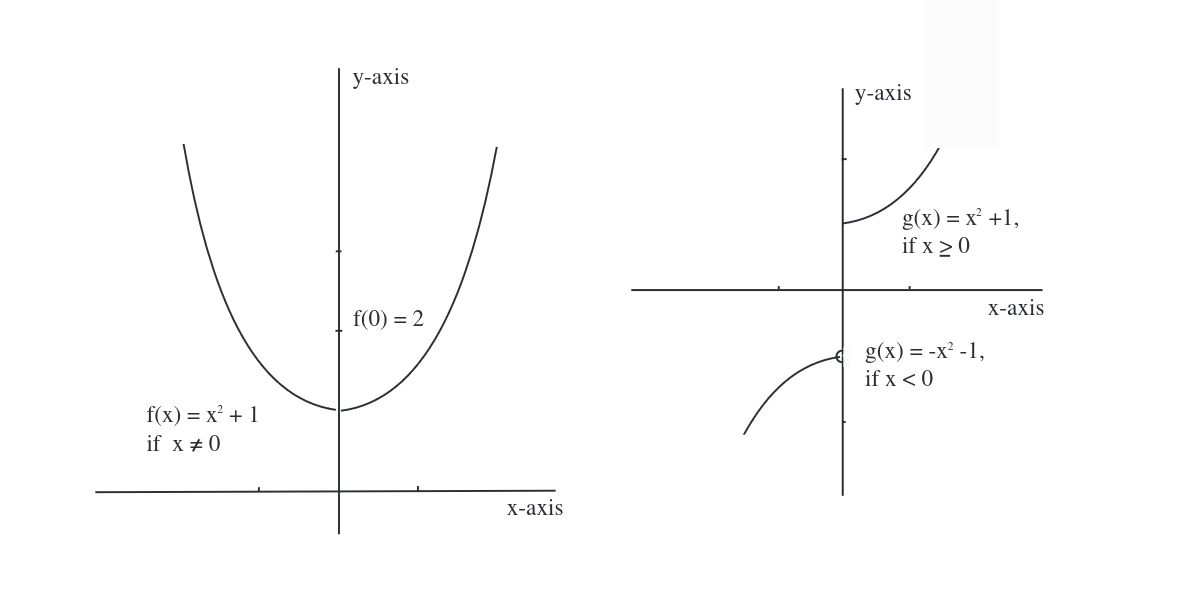
Consider the two functions <math>f</math> and <math>g</math> defined by | |||
<math display="block"> | |||
f(x) = | |||
\dilemma | |||
{x^2+1 & \mbox{if $|x| > 0$}} | |||
{2 & \mbox{if $x = 0$}} | |||
</math> | |||
<math display="block"> | |||
g(x) = | |||
\dilemma | |||
{x^2 + 1 & \mbox{if $x \geq 0$},} | |||
{-x^2 -1 & \mbox{if $x < 0$}.} | |||
</math> | |||
Both these functions are defined on the whole real line; | |||
i.e., domain <math>f</math> = domain <math>g = \R</math> | |||
(see [[#fig 1.24|Figure]]). | |||
<div id="fig 1.24" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_24.png | 400px | thumb | ]] | |||
</div> | |||
Furthermore, | |||
<math display="block"> | |||
f(0) = 2 | |||
\intext{and} | |||
g(0) = 1. | |||
</math> | |||
As <math>x</math> approaches 0, however, | |||
it is clear that <math>x^2 + 1</math> approaches 1 and not 2. | |||
Hence | |||
<math display="block"> | |||
\lim_{x \goesto 0}f(x) = 1 \neq f(0). | |||
</math> | |||
[Note that in computing <math>\lim_{x \goesto a}f(x)</math>, | |||
we consider values of <math>f(x)</math> | |||
for all <math>x</math> arbitrarily close to <math>a</math> | |||
''but not equal to'' <math>a</math>. | |||
This point will be made explicit | |||
when we give the formal definition.] | |||
Turning to <math>g</math>, | |||
we see that the value of <math>g(x)</math> near 0 | |||
depends on whether <math>x</math> is positive or negative. | |||
For any small positive number <math>x</math>, | |||
the corresponding number <math>g(x)</math> is close to 1, | |||
but if <math>x</math> is small in absolute value and negative, | |||
then <math>g(x)</math> is close to <math>-1</math>. | |||
Since there is no reason to prefer numbers of one sign to those of the other, | |||
we conclude that there is no limit. | |||
Thus | |||
<math display="block"> | |||
\lim_{x \goesto 0} g(x) \; \mbox{ does not exist}. | |||
</math> | |||
The reader may feel that [[#exam 1.4.3 |Example]] | |||
loses force because the functions used to make the point | |||
were in some sense artificial. | |||
There is some truth in the objection. | |||
Recall, however, | |||
that one of our major objectives | |||
is to reduce the class of all functions | |||
to those we wish to study in this course. | |||
After defining | |||
<math>\lim_{x \goesto a}f(x)</math> precisely, | |||
we shall turn our point of view around | |||
and use this definition as the major tool | |||
in the problem of deciding what does constitute a well-behaved function. | |||
The conceptual problems | |||
in trying to give an exact meaning | |||
to the expression | |||
<math>\lim_{x \goesto a}f(x) = b</math> | |||
revolve around phrases such as | |||
“arbitrarily close,” | |||
“sufficiently near,” | |||
and “arbitrarily small.” | |||
After all, | |||
there is no such thing in any absolute sense | |||
as a ''small'' positive real number. | |||
The number <math>0.000001</math> | |||
is small in most contexts, | |||
but in comparison with <math>0.000000000001</math> | |||
it is huge. | |||
However, we can assert that one number is | |||
''smaller than'' another. | |||
Moreover, | |||
the actual closeness of one number <math>x</math> | |||
to another number <math>a</math> | |||
is just the distance between them: | |||
It is <math>|x - a|</math>. | |||
One way to say that a function <math>f</math> takes on values | |||
arbitrarily close to a number <math>b</math> | |||
is to state that, | |||
for any positive real number <math>\epsilon</math>, | |||
there are numbers <math>x</math> such that <math>|f(x) - b| < \epsilon</math>. | |||
We are stating that | |||
no matter what positive number <math>\epsilon</math> is selected, | |||
<math>10^{17}</math>, or <math>10^{-17}</math>, or <math>10^{-127}</math>, | |||
there are numbers <math>x</math> so that the distance between <math>f(x)</math> and <math>b</math> | |||
is smaller than <math>\epsilon</math>. | |||
Thus the difficulty inherent in the phrase “arbitrarily close” | |||
has been circumvented by the prefix “for any.” | |||
To finish the definition, | |||
we want to be able to say that | |||
<math>f(x)</math> is arbitrarily close to <math>b</math> | |||
whenever <math>x</math> is sufficiently close, | |||
but not equal, to <math>a</math>. | |||
What does “sufficiently close” mean? | |||
The answer is this: | |||
If an arbitrary <math>\epsilon > 0</math> is chosen | |||
with which to measure the distance between <math>f(x)</math> and <math>b</math>, | |||
then it must be the case that | |||
there is a number <math>\delta > 0</math> | |||
such that whenever <math>x</math> is in the domain of <math>f</math> | |||
and within a distance <math>\delta</math> of <math>a</math>, | |||
but not equal to <math>a</math>, | |||
then the distance between <math>f(x)</math> and <math>b</math> | |||
is less than <math>\epsilon</math>. | |||
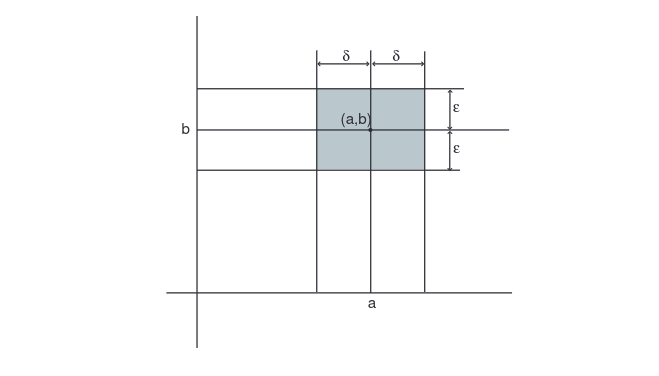
The situation is pictured in [[#fig 1.25|Figure]]. | |||
<div id="fig 1.25" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_25.png | 400px | thumb | ]] | |||
</div> | |||
First <math>\epsilon > 0</math> is chosen arbitrarily. | |||
There must then exist a number <math>\delta > 0</math> | |||
such that whenever | |||
<math>x</math> lies in the interval <math>(a - \delta, a + \delta)</math>, | |||
and <math>x \neq a</math> then | |||
the point <math>(x, f(x))</math> lies in the shaded rectangle. | |||
We summarize by giving the definition: | |||
Let <math>f</math> be a real-valued function of a real variable. | |||
Then '''the limit as <math>x</math> approaches <math>a</math> of <math>f(x)</math> is <math>b</math>''', | |||
written | |||
<math display="block"> | |||
\lim_{x \goesto a} {f(x)} = b, | |||
</math> | |||
if, for any <math>\epsilon > 0</math>, | |||
there exists <math>\delta > 0</math> | |||
such that whenever <math>x</math> is in the domain of <math>f</math> | |||
and <math>0 < |x - a| < \delta</math>, | |||
then <math>|f(x) - b| < \epsilon</math>. | |||
(There is a strong tradition for using | |||
the Greek letters <math>\epsilon</math> and <math>\delta</math> | |||
in the definition of limit. | |||
In fact, the part of calculus | |||
that deals with rigorous proofs of the various properties of limits | |||
is sometimes referred to as “epsilonics.”) | |||
<span id="exam 1.4.4"/> | |||
'''Example''' | |||
The idea behind a formal definition | |||
can sometimes be grasped most easily | |||
by looking at an example | |||
where the condition is not satisfied. | |||
Consider the function <math>g</math> | |||
defined in [[#exam 1.4.3 |Example]] | |||
whose graph is drawn in [[#fig 1.24|Figure]](b). | |||
We shall prove that | |||
<math>\lim_{x \goesto 0} {g(x)} \neq 1</math>. | |||
To do this, | |||
we must establish the negation of the limit condition: | |||
There is an <math>\epsilon > 0</math> | |||
such that, | |||
for any <math>\delta > 0</math>, | |||
there is a number <math>x</math> in the domain of <math>g</math> such that | |||
<math>0 < |x| < \delta</math> and <math>|g(x) - 1| \geq \epsilon</math>. | |||
There are many possible choices for <math>\epsilon</math>. | |||
To be specific, | |||
take <math>\epsilon = \frac{1}{2}</math>. | |||
We must now show that for every positive number <math>\delta</math>, | |||
there is a nonzero number <math>x</math> in the open interval | |||
<math>(-\delta, \delta)</math> | |||
such that the distance between <math>g(x)</math> and <math>1</math> | |||
is greater than or equal to <math>\frac{1}{2}</math> | |||
([[#fig 1.26|Figure]]). | |||
<div id="fig 1.26" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_26.png | 400px | thumb | ]] | |||
</div> | |||
Take <math>x = -\frac{\delta}{2}</math>. | |||
This number is non-zero, | |||
lies in <math>(-\delta, \delta)</math>, | |||
and furthermore | |||
<math display="block"> | |||
g(x) = g \Bigl( -\frac{\delta}{2} \Bigr) = -\frac{\delta^2}{4} - 1 < -1 . | |||
</math> | |||
Hence <math>|g(x) - 1| > 2 \geq \frac{1}{2}</math>. | |||
The basic limit theorem is the following: | |||
{{proofcard|Proposition|thm_1.4.1|If <math>\lim_{x \goesto a} f(x) = b_1</math> and <math>\lim_{x \goesto a} g(x) = b_2</math>, then | |||
<ul style{{=}}"list-style-type:lower-roman"> | |||
<li> | |||
<math>\lim_{x \goesto a} [ f(x) + g(x) ] = b_1 + b_2.</math> | |||
</li> | |||
<li> | |||
<math>\lim_{x \goesto a} cf(x) = cb_1.</math> | |||
</li> | |||
<li> | |||
<math>\lim_{x \goesto a} f(x)g(x) = b_1b_2.</math> | |||
</li> | |||
<li> | |||
<math>\lim_{x \goesto a} \frac{f(x)}{g(x)} = \frac{b_1}{b_2} | |||
\provx{provided $b_2 \neq 0$}</math></li></ul>|}} | |||
The proofs are given in Appendix A. | |||
They are not difficult, | |||
and (i) and (ii) especially follow directly from | |||
the definition of limit and the properties of the absolute value. | |||
Some ingenuity in algebraic manipulation is required for (iii) and (iv). | |||
Note that we have already assumed that this theorem is true. | |||
For example, | |||
the assertion that <math>\lim_{x \goesto 3} (2x^2 - x - 2) = 13</math> | |||
is a corollary of (i), (ii), and (iii). | |||
If a function <math>f</math> is defined for every <math>x</math> in <math>\R</math> | |||
and if its graph contains no breaks, | |||
then it is apparent from looking at the graph that | |||
<math>\lim_{x \goesto a}f(x) = f(a)</math>. | |||
Logically, however, this intuitive point of view is backward. | |||
So far, we have constructed the graph of a function <math>f</math> | |||
by plotting a few isolated points | |||
and then joining them with a smooth curve. | |||
In so doing we are assuming that if | |||
<math>x</math> is close to <math>a</math>, | |||
then <math>f(x)</math> is close to <math>f(a)</math>. | |||
That is, we are assuming that | |||
<math>\lim_{x \goesto a} {f(x)} = f(a)</math>. | |||
Now that we have given a formal definition of limit, | |||
we shall reverse ourselves | |||
and use it to say precisely what is meant by | |||
a function whose graph has no breaks. | |||
Sueh a function is ealled continuous. | |||
The definitions are as follows: | |||
A real-valued function <math>f</math> of a real variable is | |||
'''continuous at <math>a</math>''' | |||
if <math>a</math> is in the domain of <math>f</math> | |||
and <math>\lim_{x \goesto a}f(x) = f(a)</math>. | |||
The function <math>f</math> is simply said to be '''continuous''' | |||
if it is continuous at every number in its domain. | |||
A continuous function whose domain is an interval | |||
is one whose graph has no breaks, | |||
but the graph need not be a smooth curve. | |||
For example, the function with the sawtooth graph | |||
shown in [[#fig 1.27|Figure]] is continuous. | |||
<div id="fig 1.27" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_27.png | 400px | thumb | ]] | |||
</div> | |||
Many functions that are not continuous | |||
fail to be so at only a few isolated places. | |||
Thus the function <math>f</math> in [[#exam 1.4.3 |Example]], | |||
whose graph is drawn in [[#fig 1.24|Figure]](a), | |||
has its only discontinuity at 0. | |||
It is continuous everywhere else. | |||
Finally, we emphasize the fact that | |||
there are two conditions in the definition of continuity. | |||
Even though | |||
<math>\lim_{x \goesto 1} {\frac{x^{3} - 1}{x - 1}} = 3</math>, | |||
the function | |||
<math>\frac{x^{3} - 1}{x - 1}</math> | |||
is not continuous at <math>x = 1</math> | |||
simply because it is not defined there. | |||
If two functions <math>f</math> and <math>g</math> are continuous at <math>a</math>, | |||
then it is not difficult to prove that | |||
the sum <math>f + g</math> is also continuous at <math>a</math>. | |||
To begin with, | |||
<math>a</math> is in the domain of <math>f + g</math> | |||
since we have <math>(f + g)(a) = f(a) + g(a)</math>. | |||
Furthermore, we know that | |||
<math>\lim_{x \goesto a}f(x) = f(a)</math> | |||
and that | |||
<math>\lim_{x \goesto a} g(x) = g(a)</math>. | |||
It follows by [[#thm blt |Theorem]](i) | |||
that | |||
<math display="block"> | |||
\lim_{x \goesto a} {[f(x) + g(x)]} = f(a) + g(a). | |||
</math> | |||
Since <math>f(x) + g(x) = (f + g)(x)</math>, we get | |||
<math display="block"> | |||
\lim_{x \goesto a} {(f + g)(x)} = (f + g)(a), | |||
</math> | |||
which proves the continuity of <math>f + g</math> at <math>a</math>. | |||
The other parts of the basic limit [[#thm blt |theorem]] | |||
imply similar results about the products and quotients | |||
of continuous functions. | |||
We summarize these in | |||
{{proofcard|Proposition|thm_1.4.2|If two functions <math>f</math> and <math>g</math> are continuous at <math>a</math>, then so are | |||
#<math>f + g</math>. | |||
#<math>c f, \provx{for any constant $c$}</math>. | |||
# <math>f g</math>. | |||
# <math>\frac{f}{g}, \provx{provided $g(a) \neq 0$}</math>.|}} | |||
A real-valued function <math>f</math> of one real variable is called a '''polynomial''' | |||
if there exist a nonnegative integer <math>n</math> and real numbers | |||
<math>a_{0}, a_{1}, \ldots, a_{n}</math> | |||
such that, for every real number <math>x</math>, | |||
<math display="block"> | |||
f(x) = a_{0} + a_{1}x + ... + a_{n}x^{n} . | |||
</math> | |||
The following functions are all examples of polynomials: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
f(x) &=& 2 - 4x + 3x^2, \\ | |||
f(y) &=& 117y^{239} + {\frac{3}{2}}y + \pi, \\ | |||
f(x) &=& x, \\ | |||
f(x) &=& 5, \\ | |||
g(s) &=& (s^2 + 2)(s^5 - 1) = s^7 + 2s^5 - s^2 - 2 . | |||
\end{eqnarray*} | |||
</math> | |||
It is equally important to be able to recognize that a given function is not a polynomial. Examples of functions which are not polynomials are | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
f(x) &=& |x|, \\ | |||
f(x) &=& \frac{1}{x}, \\ | |||
f(x) &=& x^2 + x + 3x^{-2}, \\ | |||
f(x) &=& \sqrt{x}, \\ | |||
F(y) &=& (y^2 - 1)^{3/2} . | |||
\end{eqnarray*} | |||
</math> | |||
Algebraically the set of all polynomials is much like the set of integers: | |||
The sum, difference, and product of any two polynomials | |||
is again a polynomial, | |||
but, in general, | |||
the quotient of two polynomials is not a polynomial. | |||
Moreover, the algebraic [[guide:A5dd35d44b#axiom.i |axioms]] [[guide:A5dd35d44b#axiom.v |through]] | |||
listed in Section \secref{1.1} | |||
also hold. | |||
Just as a rational number is one | |||
which can be expressed as the ratio of two integers, | |||
a '''rational function''' | |||
is one which can be expressed as the ratio of two polynomials. | |||
Examples are the functions | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
f(x) &=& \frac{x^3 + 2x + 2}{x^4 + 1}, \\ | |||
g(x) &=& x^{-3} = \frac{1}{x^3}, \\ | |||
f(x) &=& x^2 + 2x + 1 = \frac{x^2 + 2x + 1}{1}, \\ | |||
g(x) &=& \pi. | |||
\end{eqnarray*} | |||
</math> | |||
The domain of every polynomial | |||
is the entire set <math>\R</math> of real numbers. | |||
Similarly, the domain of a given rational function | |||
<math>\frac{p(x)}{q(x)}</math>, | |||
where <math>p(x)</math> and <math>q(x)</math> are polynomials, | |||
is the whole set <math>\R</math> | |||
with the exception of those numbers <math>x</math> | |||
for which <math>q(x) = 0</math>. | |||
Furthermore, we have | |||
{{proofcard|Proposition|thm_1.4.3|Every polynomial is a continuous function, and every rational function | |||
<math>\frac{p(x)}{q(x)}</math> is continuous except at those values of <math>x</math> | |||
for which <math>q(x) = 0</math>. | |||
|The identity function <math>x</math> | |||
is clearly continuous, | |||
and so is every constant function. | |||
Since every polynomial can be constructed from | |||
the identity function <math>x</math> | |||
and from constants | |||
using only the sums and products of these and the resulting functions, | |||
it follows from [[#thm 1.4.2 |Theorem]] | |||
that every polynomial is continuous. | |||
The assertion about the continuity of rational functions then | |||
follows from part (iv) of [[#thm 1.4.2 |Theorem]].}} | |||
It is occasionally useful | |||
to modify the definition of | |||
<math>\lim_{x \goesto a}f(x)</math> | |||
to allow <math>x</math> to approach <math>a</math> from only one side: | |||
<div id="fig 1.27" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_picture1.png | 400px | thumb | ]] | |||
</div> | |||
When this is done, we speak of either the limit from the right or the limit from the left and write either | |||
<math display="block"> | |||
\lim_{x \goesto a+}f(x) \;\;\; \mbox{or}\;\;\; \lim_{x \goesto a-}f(x), | |||
</math> | |||
according as the additional condition is <math>x > a</math> or <math>x < a</math>. | |||
Thus for the function | |||
<math display="block"> | |||
f(x) = \left\{ \begin{array}{ll} | |||
x - 1, & x \geq 2, \\ | |||
x^{2} - 1, & x < 2 , | |||
\end{array} | |||
\right. | |||
</math> | |||
whose graph is shown in [[#fig 1.28|Figure]], | |||
<div id="fig 1.28" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_28.png | 400px | thumb | ]] | |||
</div> | |||
the limit of <math>f(x)</math> as <math>x</math> approaches 2 does not exist. | |||
Nevertheless, we obtain | |||
<math display="block"> | |||
\lim_{x \goesto 2+} {f(x)} = 1,\;\;\; \lim_{x \goesto 2-} {f(x)} = 3. | |||
</math> | |||
Similarly, for the function <math>g</math> in [[#fig 1.24|Figure]](b), | |||
we have | |||
<math>\lim_{x \goesto 0+}g(x) = 1</math>, <math>\lim_{x \goesto 0-}g(x) = -1</math>. | |||
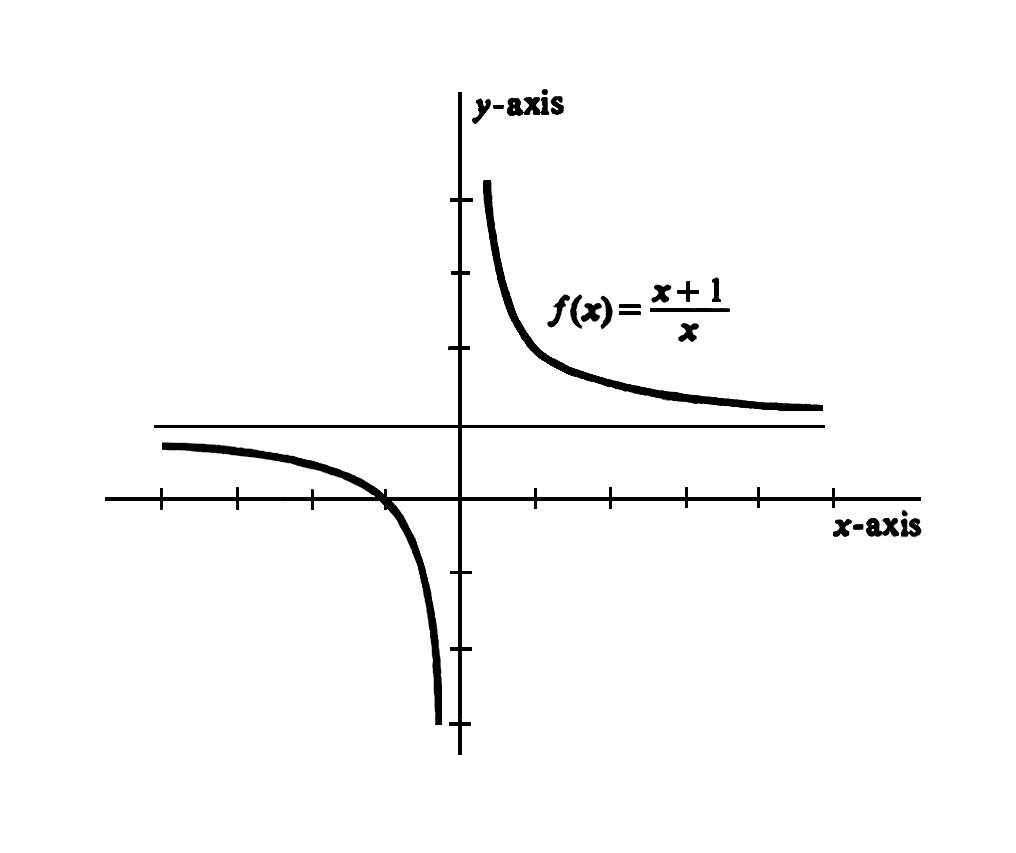
The graph of the rational function | |||
<math display="block"> | |||
f(x) = \frac{x + 1}{x} = 1 + \frac{1}{x}, \;\;\; x \neq 0, | |||
</math> | |||
together with a list of some of the ordered pairs <math>(x,f(x))</math> | |||
that comprise <math>f</math> is shown in [[#fig 1.29|Figure]]. | |||
<div id="fig 1.29" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_29.png | 400px | thumb | ]] | |||
</div> | |||
From both [[#fig 1.29|Figure]] and [[#table 1.6 |Table]] | |||
it is clear that as <math>x</math> increases without bound, | |||
<math>f(x)</math> becomes arbitrarily close to 1. | |||
We express this fact by writing | |||
<math display="block"> | |||
\lim_{x \goesto +\infty} {\frac{x + 1}{x}} = 1. | |||
</math> | |||
<span id="table 1.6"/> | |||
{|class="table" | |||
|- | |||
|<math>x</math> || <math>f(x)</math> | |||
|- | |||
|1 || 2 | |||
|- | |||
|10 || 1.1 | |||
|- | |||
|100 || 1.01 | |||
|- | |||
|1,000 || 1.001 | |||
|- | |||
|1,000,000 || 1.000001 | |||
|- | |||
|<math>\vdots </math> || | |||
|} | |||
Since <math>f(x)</math> also becomes arbitrarily close to 1 | |||
as <math>x</math> decreases without bound, | |||
i.e., as <math>-x</math> increases without bound, | |||
we write | |||
<math display="block"> | |||
\lim_{x \goesto {-\infty}} {\frac{x + 1}{x}} = 1. | |||
</math> | |||
The definition is as follows: | |||
Let <math>f</math> be a real-valued function of a real variable. | |||
Then '''the limit of <math>f(x)</math> is <math>b</math> as <math>x</math> increases without bound''', | |||
written | |||
<math display="block"> | |||
\lim_{x \goesto {+\infty}} {f(x)} = b, | |||
</math> | |||
if, for any <math>\epsilon > 0</math>, | |||
there exists <math>\delta > 0</math> such that | |||
whenever <math>x</math> is in the domain of <math>f</math> | |||
and <math>\delta < x</math>, | |||
then <math>|f(x) - b| < \epsilon</math>. | |||
The analogous definition for | |||
<math>\lim_{x \goesto -\infty}f(x) = b</math> is obvious. | |||
The symbols <math>+\infty</math> and <math>-\infty</math> | |||
can also be used to refer to | |||
the behavior of the values of the function | |||
as well as the independent variable. | |||
If, as <math>x</math> approaches <math>a</math>, | |||
the corresponding value <math>f(x)</math> of the function increases without bound, | |||
we may express the fact by writing | |||
<math display="block"> | |||
\lim_{x \goesto \infty} f(x) = + \infty. | |||
</math> | |||
The reader should be able to attach the correct meanings | |||
to the various other possibilities: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\lim_{x \goesto a} f(x) &=& - \infty, \\ | |||
\lim_{x \goesto -\infty} f(x) &=& + \infty, \\ | |||
\lim_{x \goesto a+} f(x) &=& - \infty, \; \mbox{etc.} | |||
\end{eqnarray*} | |||
</math> | |||
It is essential to keep in mind that | |||
''<math>+\infty</math> and <math>-\infty</math> are not numbers''. | |||
They are not elements of <math>\R</math>. | |||
They are used simply as convenient abbreviations | |||
for describing the unbounded characteristics of certain functions. | |||
The symbol <math>+\infty</math> (or simply <math>\infty</math>) | |||
in an expression for a bound | |||
will always mean that the quantity referred to increases without limit | |||
in the positive direction. | |||
Similarly, <math>-\infty</math> always indicates the negative direction. | |||
Thus we shall not say | |||
<math>\lim_{x \goesto 0}\frac{1}{x} = \infty</math>. | |||
But we do say | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\lim_{x \goesto 0+} \frac{1}{x} &=& \infty, \\ | |||
\lim_{x \goesto 0-} \frac{1}{x} &=& -\infty, \\ | |||
\lim_{x \goesto 0} \Big|\frac{1}{x} \Big| &=& \infty. | |||
\end{eqnarray*} | |||
</math> | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Latest revision as of 00:30, 4 November 2024
Consider the function [math]f[/math] defined by
The domain of [math]f[/math] is the set of all real numbers with the exception of the number [math]2[/math], which has been excluded because substitution of [math]x = 2[/math] in the expression for [math]f(x)[/math] yields the undefined term [math]\frac{0}{0}[/math]. On the other hand, [math]x^{2} - 3x + 2 = (x - 1)(x - 2)[/math] and
The proviso is essential. Without it, (1) is false because, if [math]x = 2[/math], the left side is undefined and the right side is equal to 1. We therefore obtain
The graph of the function [math]x - 1[/math] is a straight line [math]L[/math]; so the graph of [math]f[/math] is the punctured line obtained from [math]L[/math] by omitting the one point [math](2,1)[/math] (see Figure).
Although the function [math]f[/math] is not defined at [math]x = 2[/math], we know its behavior for values of [math]x[/math] near [math]2[/math]. The graph makes it clear that if [math]x[/math] is close to [math]2[/math], then [math]f(x)[/math] is close to [math]1[/math]. In fact, the values [math]f(x)[/math] can be brought arbitrarily close to [math]1[/math] by taking [math]x[/math] sufficiently close to [math]2[/math]. We express this fact by writing
which is translated: The limit of [math]\frac{x^2 - 3x +2''{x - 2}[/math] is [math]1[/math] as [math]x[/math] approaches [math]2[/math].}
Example
Evaluate [math]\lim_{x \goesto 3} {\frac{\sqrt{x} - \sqrt{3}}{x - 3}}[/math]. The function [math]\frac{\sqrt{x} - \sqrt{3}}{x - 3}[/math] is not defined at [math]x = 3[/math]. The following algebraic manipulation puts the function in a form in which its behavior close to [math]3[/math] can be read off easily:
Again note the proviso [math]x \neq 3[/math]: When [math]x = 3[/math], the last quantity in the preceding equations is equal to [math]\frac{1}{\sqrt{3} + \sqrt{3}}[/math], but the first quantity is not defined. However, by taking values of [math]x[/math] close to 3, it is clear that the corresponding values of [math]\frac{1}{\sqrt{x} + \sqrt{3}}[/math] can be brought as close as we please to [math]\frac{1}{2 \sqrt{3}}[/math]. We conclude that
In words: The limit of [math]\frac {\sqrt{x} - \sqrt{3}}{x - 3}[/math], as [math]x[/math] approaches [math]3[/math], is [math]\frac{1}{2{\sqrt{3}}}[/math].
Example
If [math]f(x) = \frac{1}{x}[/math], evaluate [math]\lim_{x \goesto 0} f(x)[/math]. The function [math]f[/math] is not defined at [math]0[/math] (i.e., the number 0 is not in the domain of [math]f[/math]). From the graph of [math]f[/math] and the list of ordered pairs [math](x, f(x))[/math] shown in Figure,
it is clear that there are values of [math]x[/math] arbitrarily close to 0 for which the corresponding values of [math]f(x)[/math] are arbitrarily large in absolute value (see Table). We conclude that [math]\lim_{x \goesto 0}{\frac{1}{x}}[/math] does not exist.
| [math]x[/math] | [math]f(x) = \frac{1}{x}[/math] |
| 1 | 1 |
| 0.1 | 10 |
| 0.01 | 100 |
| 0.001 | 1000 |
| 0.0001 | 10000 |
| [math]\cdots[/math] | [math]\cdots[/math] |
| [math]\cdots[/math] | [math]\cdots[/math] |
Thus far our examples have been confined to the problem of finding the limit of a function at a number which happens to lie outside the domain of the function. If it happens that the number [math]a[/math] is in the domain of [math]f[/math], then it is frequently possible to determine [math]\lim_{x \goesto a}f(x)[/math] at a glance. Consider, for example, the function [math]f(x) = 2x^2 - x - 2[/math]. As [math]x[/math] takes on values closer and closer to 3, the corresponding value of [math]2x^{2}[/math] approaches [math]18[/math], the value of [math]-x[/math] approaches [math]-3[/math], and the constant [math]-2[/math] does not change. We conclude that
or that, for this particular function, [math]\lim_{x \goesto 3}f(x) = f(3)[/math].
Example
It would be incorrect to suppose that if [math]a[/math] is in the domain of [math]f[/math], then it always happens that [math]\lim_{x \goesto a}f(x) = f(a)[/math]. Consider the two functions [math]f[/math] and [math]g[/math] defined by
Both these functions are defined on the whole real line; i.e., domain [math]f[/math] = domain [math]g = \R[/math] (see Figure).
Furthermore,
As [math]x[/math] approaches 0, however, it is clear that [math]x^2 + 1[/math] approaches 1 and not 2. Hence
[Note that in computing [math]\lim_{x \goesto a}f(x)[/math], we consider values of [math]f(x)[/math] for all [math]x[/math] arbitrarily close to [math]a[/math] but not equal to [math]a[/math]. This point will be made explicit when we give the formal definition.] Turning to [math]g[/math], we see that the value of [math]g(x)[/math] near 0 depends on whether [math]x[/math] is positive or negative. For any small positive number [math]x[/math], the corresponding number [math]g(x)[/math] is close to 1, but if [math]x[/math] is small in absolute value and negative, then [math]g(x)[/math] is close to [math]-1[/math]. Since there is no reason to prefer numbers of one sign to those of the other, we conclude that there is no limit. Thus
The reader may feel that Example loses force because the functions used to make the point were in some sense artificial. There is some truth in the objection. Recall, however, that one of our major objectives is to reduce the class of all functions to those we wish to study in this course. After defining [math]\lim_{x \goesto a}f(x)[/math] precisely, we shall turn our point of view around and use this definition as the major tool in the problem of deciding what does constitute a well-behaved function. The conceptual problems in trying to give an exact meaning to the expression [math]\lim_{x \goesto a}f(x) = b[/math] revolve around phrases such as “arbitrarily close,” “sufficiently near,” and “arbitrarily small.” After all, there is no such thing in any absolute sense as a small positive real number. The number [math]0.000001[/math] is small in most contexts, but in comparison with [math]0.000000000001[/math] it is huge. However, we can assert that one number is smaller than another. Moreover, the actual closeness of one number [math]x[/math] to another number [math]a[/math] is just the distance between them: It is [math]|x - a|[/math]. One way to say that a function [math]f[/math] takes on values arbitrarily close to a number [math]b[/math] is to state that, for any positive real number [math]\epsilon[/math], there are numbers [math]x[/math] such that [math]|f(x) - b| \lt \epsilon[/math]. We are stating that no matter what positive number [math]\epsilon[/math] is selected, [math]10^{17}[/math], or [math]10^{-17}[/math], or [math]10^{-127}[/math], there are numbers [math]x[/math] so that the distance between [math]f(x)[/math] and [math]b[/math] is smaller than [math]\epsilon[/math]. Thus the difficulty inherent in the phrase “arbitrarily close” has been circumvented by the prefix “for any.” To finish the definition, we want to be able to say that [math]f(x)[/math] is arbitrarily close to [math]b[/math] whenever [math]x[/math] is sufficiently close, but not equal, to [math]a[/math]. What does “sufficiently close” mean? The answer is this: If an arbitrary [math]\epsilon \gt 0[/math] is chosen with which to measure the distance between [math]f(x)[/math] and [math]b[/math], then it must be the case that there is a number [math]\delta \gt 0[/math] such that whenever [math]x[/math] is in the domain of [math]f[/math] and within a distance [math]\delta[/math] of [math]a[/math], but not equal to [math]a[/math], then the distance between [math]f(x)[/math] and [math]b[/math] is less than [math]\epsilon[/math]. The situation is pictured in Figure.
First [math]\epsilon \gt 0[/math] is chosen arbitrarily. There must then exist a number [math]\delta \gt 0[/math] such that whenever [math]x[/math] lies in the interval [math](a - \delta, a + \delta)[/math], and [math]x \neq a[/math] then the point [math](x, f(x))[/math] lies in the shaded rectangle. We summarize by giving the definition: Let [math]f[/math] be a real-valued function of a real variable. Then the limit as [math]x[/math] approaches [math]a[/math] of [math]f(x)[/math] is [math]b[/math], written
if, for any [math]\epsilon \gt 0[/math], there exists [math]\delta \gt 0[/math] such that whenever [math]x[/math] is in the domain of [math]f[/math] and [math]0 \lt |x - a| \lt \delta[/math], then [math]|f(x) - b| \lt \epsilon[/math]. (There is a strong tradition for using the Greek letters [math]\epsilon[/math] and [math]\delta[/math] in the definition of limit. In fact, the part of calculus that deals with rigorous proofs of the various properties of limits is sometimes referred to as “epsilonics.”)
Example
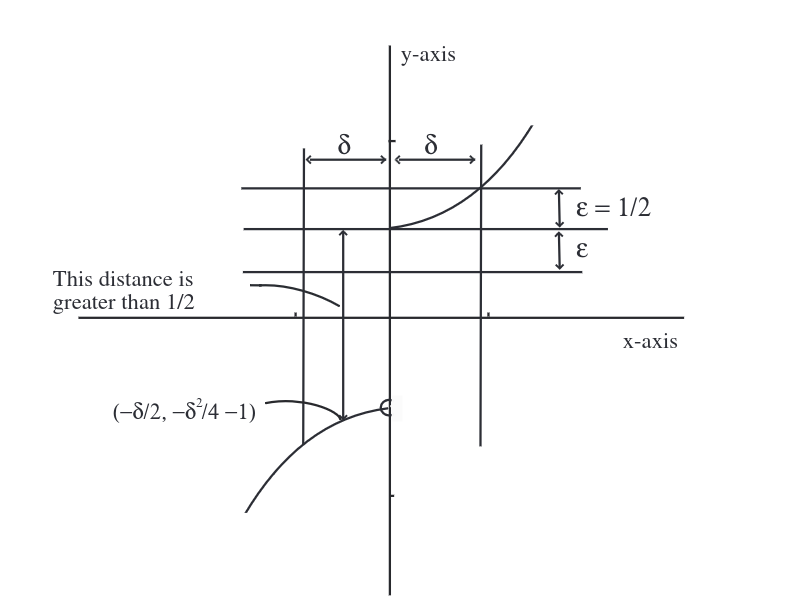
The idea behind a formal definition can sometimes be grasped most easily by looking at an example where the condition is not satisfied. Consider the function [math]g[/math] defined in Example whose graph is drawn in Figure(b). We shall prove that [math]\lim_{x \goesto 0} {g(x)} \neq 1[/math]. To do this, we must establish the negation of the limit condition: There is an [math]\epsilon \gt 0[/math] such that, for any [math]\delta \gt 0[/math], there is a number [math]x[/math] in the domain of [math]g[/math] such that [math]0 \lt |x| \lt \delta[/math] and [math]|g(x) - 1| \geq \epsilon[/math]. There are many possible choices for [math]\epsilon[/math]. To be specific, take [math]\epsilon = \frac{1}{2}[/math]. We must now show that for every positive number [math]\delta[/math], there is a nonzero number [math]x[/math] in the open interval [math](-\delta, \delta)[/math] such that the distance between [math]g(x)[/math] and [math]1[/math] is greater than or equal to [math]\frac{1}{2}[/math] (Figure).
Take [math]x = -\frac{\delta}{2}[/math]. This number is non-zero, lies in [math](-\delta, \delta)[/math], and furthermore
Hence [math]|g(x) - 1| \gt 2 \geq \frac{1}{2}[/math].
The basic limit theorem is the following:
If [math]\lim_{x \goesto a} f(x) = b_1[/math] and [math]\lim_{x \goesto a} g(x) = b_2[/math], then
- [math]\lim_{x \goesto a} [ f(x) + g(x) ] = b_1 + b_2.[/math]
- [math]\lim_{x \goesto a} cf(x) = cb_1.[/math]
- [math]\lim_{x \goesto a} f(x)g(x) = b_1b_2.[/math]
- [math]\lim_{x \goesto a} \frac{f(x)}{g(x)} = \frac{b_1}{b_2} \provx{provided $b_2 \neq 0$}[/math]
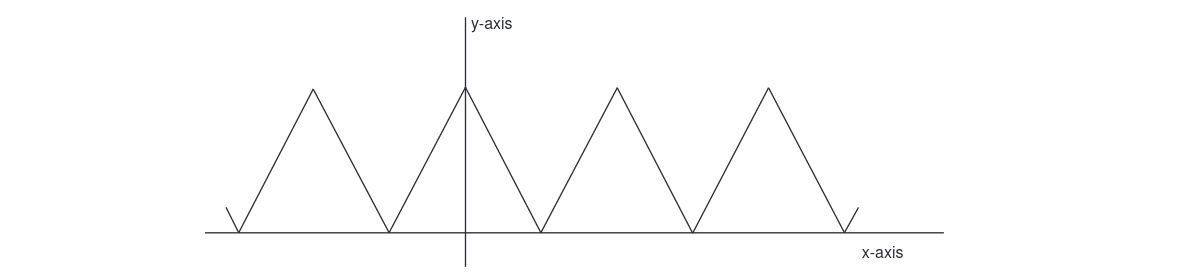
The proofs are given in Appendix A. They are not difficult, and (i) and (ii) especially follow directly from the definition of limit and the properties of the absolute value. Some ingenuity in algebraic manipulation is required for (iii) and (iv). Note that we have already assumed that this theorem is true. For example, the assertion that [math]\lim_{x \goesto 3} (2x^2 - x - 2) = 13[/math] is a corollary of (i), (ii), and (iii). If a function [math]f[/math] is defined for every [math]x[/math] in [math]\R[/math] and if its graph contains no breaks, then it is apparent from looking at the graph that [math]\lim_{x \goesto a}f(x) = f(a)[/math]. Logically, however, this intuitive point of view is backward. So far, we have constructed the graph of a function [math]f[/math] by plotting a few isolated points and then joining them with a smooth curve. In so doing we are assuming that if [math]x[/math] is close to [math]a[/math], then [math]f(x)[/math] is close to [math]f(a)[/math]. That is, we are assuming that [math]\lim_{x \goesto a} {f(x)} = f(a)[/math]. Now that we have given a formal definition of limit, we shall reverse ourselves and use it to say precisely what is meant by a function whose graph has no breaks. Sueh a function is ealled continuous. The definitions are as follows: A real-valued function [math]f[/math] of a real variable is continuous at [math]a[/math] if [math]a[/math] is in the domain of [math]f[/math] and [math]\lim_{x \goesto a}f(x) = f(a)[/math]. The function [math]f[/math] is simply said to be continuous if it is continuous at every number in its domain. A continuous function whose domain is an interval is one whose graph has no breaks, but the graph need not be a smooth curve. For example, the function with the sawtooth graph shown in Figure is continuous.
Many functions that are not continuous fail to be so at only a few isolated places. Thus the function [math]f[/math] in Example, whose graph is drawn in Figure(a), has its only discontinuity at 0. It is continuous everywhere else. Finally, we emphasize the fact that there are two conditions in the definition of continuity. Even though [math]\lim_{x \goesto 1} {\frac{x^{3} - 1}{x - 1}} = 3[/math], the function [math]\frac{x^{3} - 1}{x - 1}[/math] is not continuous at [math]x = 1[/math] simply because it is not defined there. If two functions [math]f[/math] and [math]g[/math] are continuous at [math]a[/math], then it is not difficult to prove that the sum [math]f + g[/math] is also continuous at [math]a[/math]. To begin with, [math]a[/math] is in the domain of [math]f + g[/math] since we have [math](f + g)(a) = f(a) + g(a)[/math]. Furthermore, we know that [math]\lim_{x \goesto a}f(x) = f(a)[/math] and that [math]\lim_{x \goesto a} g(x) = g(a)[/math]. It follows by Theorem(i) that
Since [math]f(x) + g(x) = (f + g)(x)[/math], we get
which proves the continuity of [math]f + g[/math] at [math]a[/math]. The other parts of the basic limit theorem imply similar results about the products and quotients of continuous functions. We summarize these in
If two functions [math]f[/math] and [math]g[/math] are continuous at [math]a[/math], then so are
- [math]f + g[/math].
- [math]c f, \provx{for any constant $c$}[/math].
- [math]f g[/math].
- [math]\frac{f}{g}, \provx{provided $g(a) \neq 0$}[/math].
A real-valued function [math]f[/math] of one real variable is called a polynomial if there exist a nonnegative integer [math]n[/math] and real numbers [math]a_{0}, a_{1}, \ldots, a_{n}[/math] such that, for every real number [math]x[/math],
The following functions are all examples of polynomials:
It is equally important to be able to recognize that a given function is not a polynomial. Examples of functions which are not polynomials are
Algebraically the set of all polynomials is much like the set of integers: The sum, difference, and product of any two polynomials is again a polynomial, but, in general, the quotient of two polynomials is not a polynomial. Moreover, the algebraic axioms through listed in Section \secref{1.1} also hold. Just as a rational number is one which can be expressed as the ratio of two integers, a rational function is one which can be expressed as the ratio of two polynomials. Examples are the functions
The domain of every polynomial is the entire set [math]\R[/math] of real numbers. Similarly, the domain of a given rational function [math]\frac{p(x)}{q(x)}[/math], where [math]p(x)[/math] and [math]q(x)[/math] are polynomials, is the whole set [math]\R[/math] with the exception of those numbers [math]x[/math] for which [math]q(x) = 0[/math]. Furthermore, we have
Every polynomial is a continuous function, and every rational function [math]\frac{p(x)}{q(x)}[/math] is continuous except at those values of [math]x[/math] for which [math]q(x) = 0[/math].
The identity function [math]x[/math] is clearly continuous, and so is every constant function. Since every polynomial can be constructed from the identity function [math]x[/math] and from constants using only the sums and products of these and the resulting functions, it follows from Theorem that every polynomial is continuous. The assertion about the continuity of rational functions then follows from part (iv) of Theorem.
It is occasionally useful to modify the definition of [math]\lim_{x \goesto a}f(x)[/math] to allow [math]x[/math] to approach [math]a[/math] from only one side:
When this is done, we speak of either the limit from the right or the limit from the left and write either
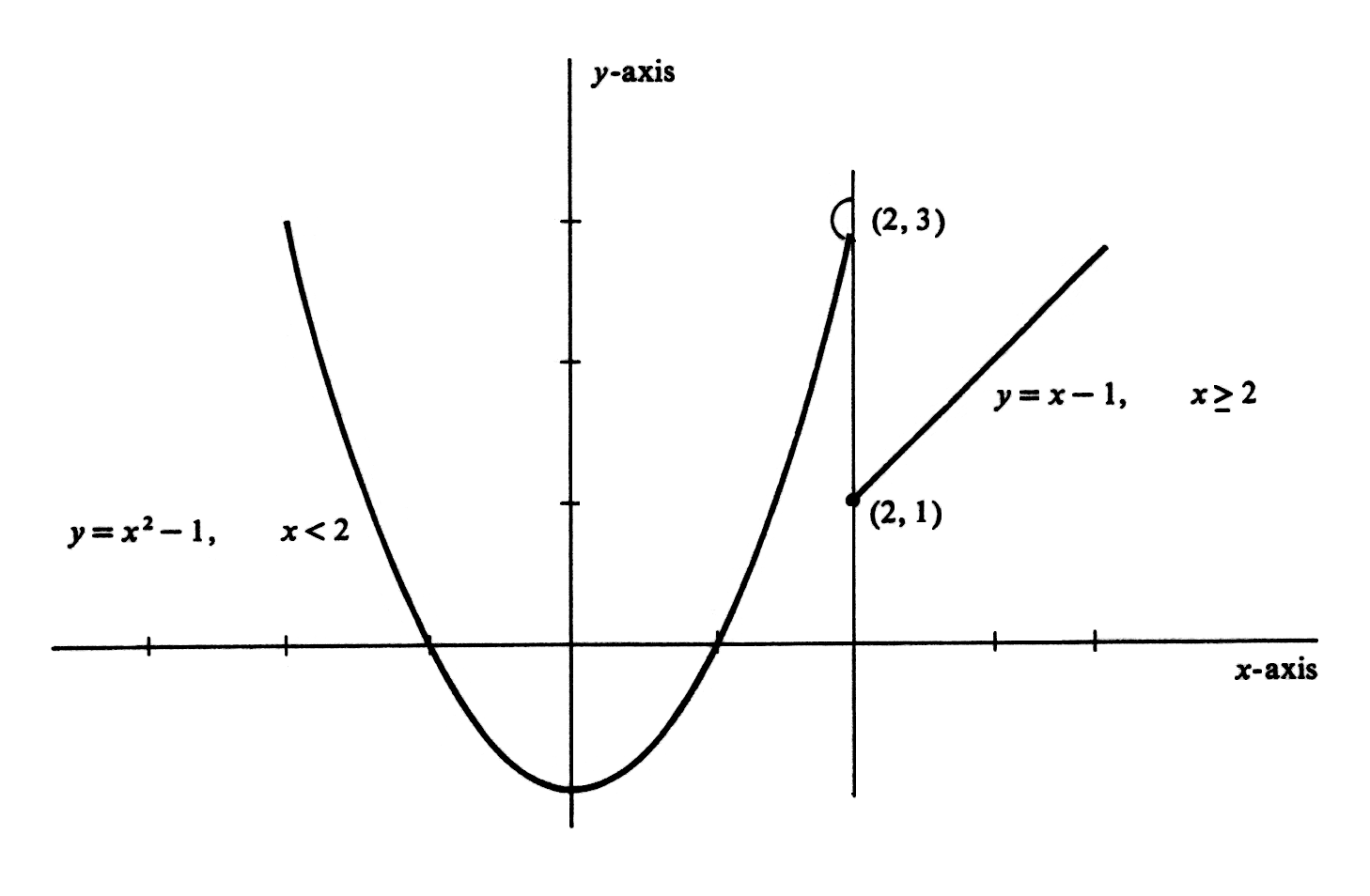
according as the additional condition is [math]x \gt a[/math] or [math]x \lt a[/math]. Thus for the function
whose graph is shown in Figure,
the limit of [math]f(x)[/math] as [math]x[/math] approaches 2 does not exist. Nevertheless, we obtain
Similarly, for the function [math]g[/math] in Figure(b), we have [math]\lim_{x \goesto 0+}g(x) = 1[/math], [math]\lim_{x \goesto 0-}g(x) = -1[/math]. The graph of the rational function
together with a list of some of the ordered pairs [math](x,f(x))[/math] that comprise [math]f[/math] is shown in Figure.
From both Figure and Table it is clear that as [math]x[/math] increases without bound, [math]f(x)[/math] becomes arbitrarily close to 1. We express this fact by writing
| [math]x[/math] | [math]f(x)[/math] |
| 1 | 2 |
| 10 | 1.1 |
| 100 | 1.01 |
| 1,000 | 1.001 |
| 1,000,000 | 1.000001 |
| [math]\vdots [/math] |
Since [math]f(x)[/math] also becomes arbitrarily close to 1 as [math]x[/math] decreases without bound, i.e., as [math]-x[/math] increases without bound, we write
It is essential to keep in mind that
[math]+\infty[/math] and [math]-\infty[/math] are not numbers.
They are not elements of [math]\R[/math].
They are used simply as convenient abbreviations
for describing the unbounded characteristics of certain functions.
The symbol [math]+\infty[/math] (or simply [math]\infty[/math])
in an expression for a bound
will always mean that the quantity referred to increases without limit
in the positive direction.
Similarly, [math]-\infty[/math] always indicates the negative direction.
Thus we shall not say
[math]\lim_{x \goesto 0}\frac{1}{x} = \infty[/math].
But we do say
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.