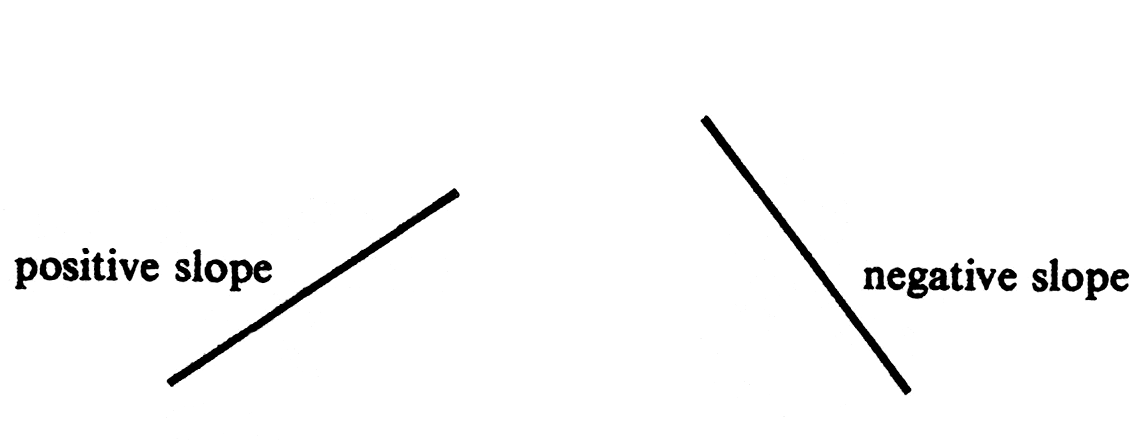guide:0d227dcd1c: Difference between revisions
No edit summary |
mNo edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
We shall define a '''straight line''' in <math>\R^2</math> to be any subset <math>L</math> | |||
consisting of all ordered pairs <math>(x, y)</math> | |||
such that | |||
<span id{{=}}"eq1.5.0"/> | |||
<math display="block"> | |||
\begin{equation} | |||
ax + by + c = 0, \;\;\; \mbox{where} \;\;\; a^2 + b^2 > 0. | |||
\label{eq1.5.0} | |||
\end{equation} | |||
</math> | |||
The inequality <math>a^2 + b^2 > 0</math> | |||
simply says that the constants <math>a</math> and <math>b</math> are not both equal to zero. | |||
Of course two different equations can define the same line. | |||
For example, the set of all ordered pairs <math>(x, y)</math> | |||
such that <math>4x - 3y + 5 = 0</math> is the same line as the set of pairs for which <math>28x = 21y - 35</math>. | |||
For this reason, | |||
we speak of ''an'' equation of a straight line | |||
and not ''the'' equation. | |||
{{proofcard|Proposition|thm_1.5.1|Suppose that straight lines <math>L_1</math> and <math>L_2</math> are defined, respectioely, by | |||
<math display="block"> | |||
\begin{array}{ll} | |||
a_{1}x + b_{1}y + c_1 = 0, & {a_1}^2 + {b_1}^2 > 0,\\ | |||
a_{2}x + b_{2}y + c_2 = 0, & {a_2}^2 + {b_2}^2 > 0. | |||
\end{array} | |||
</math> | |||
Then <math>L_{1} = L_{2}</math> if and only if there is a nonzero constant <math>k</math> | |||
such that | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
a_2 &=& ka_{1}, \\ | |||
b_2 &=& kb_{1}, \\ | |||
c_2 &=& kc_{1}. | |||
\end{eqnarray*} | |||
</math> | |||
|If such a <math>k</math> exists, | |||
then the two equations are equivalent, and so <math>L_1 = L_2</math>. | |||
Conversely, suppose that <math>L_1 = L_2</math>. | |||
We may assume without loss of generality that <math>b_{1} \neq 0</math>. | |||
Then the point <math>\Bigl(0, -\frac{c_1}{b_1} \Bigr)</math> lies on <math>L_1</math> since it satisfies the first equation; i.e., | |||
<math display="block"> | |||
a_{1} \cdot 0 + b_{1} \Bigl(- \frac{c_1}{b_1} \Bigr) + c_{1} = 0. | |||
</math> | |||
Because the two lines are equal, the point also lies on <math>L_2</math>, and so | |||
<math display="block"> | |||
a_2 \cdot 0 + b_2 \Bigl( - \frac{c_1}{b_1} \Bigr) + c_2 = 0. | |||
</math> | |||
Hence | |||
<math display="block"> | |||
c_2 = \Bigl( \frac{b_2}{b_1} \Bigr) c_1. | |||
</math> | |||
In addition, the point <math>\Bigl(1, - \frac{a_1 + c_1}{b_1} \Bigr)</math> | |||
lies on <math>L_1</math> because | |||
<math display="block"> | |||
a_1 + b_{1} \Bigl( \frac{- a_1 - c_1}{ b_1} \Bigr) + c_1 = 0. | |||
</math> | |||
This point then also lies on <math>L_2</math>, and this fact means that | |||
<math display="block"> | |||
a_2 + b_{2} \Bigl(\frac{- a_1 - c_1}{b_1} \Bigr) + c_2 = 0. | |||
</math> | |||
Hence | |||
<math display="block"> | |||
a_2 = {\frac{b_2}{b_1}} a_{1} + {\frac{b_2}{b_1}} c_1 - c_2 | |||
= \Bigl( \frac{b_2}{b_1} \Bigr) a_{1}. | |||
</math> | |||
Since <math>b_2 = \Bigl( \frac{b_2}{b_1} \Bigr) b_1</math> trivially, | |||
we obtain the desired conclusion by setting <math>k = \frac{b_2}{b_1}</math>. | |||
Note that <math>k \neq 0</math>, for if it were zero, | |||
we would get <math>a_2 = b_2 = 0</math>, | |||
contrary to assumption.}} | |||
One consequence of [[#thm 1.5.1 |Theorem]] | |||
is that it enables us to recognize at a glance whether or not different equations define the same straight line. | |||
Another corollary arises in connection with the following definitions: A line <math>L</math> defined by an equation <math>ax + by + c = 0</math> with <math>a^2 + b^2 > 0</math> will be called '''vertical''' if <math>b = 0</math> and '''horizontal''' if <math>a = 0</math>. | |||
It follows from the theorem that <math>b</math> must equal zero for every such equation which defines a vertical line and that <math>a</math> must equal zero for every such equation which defines a horizontal line. | |||
Thus the definitions are not dependent on the particular equation which defines <math>L</math>. | |||
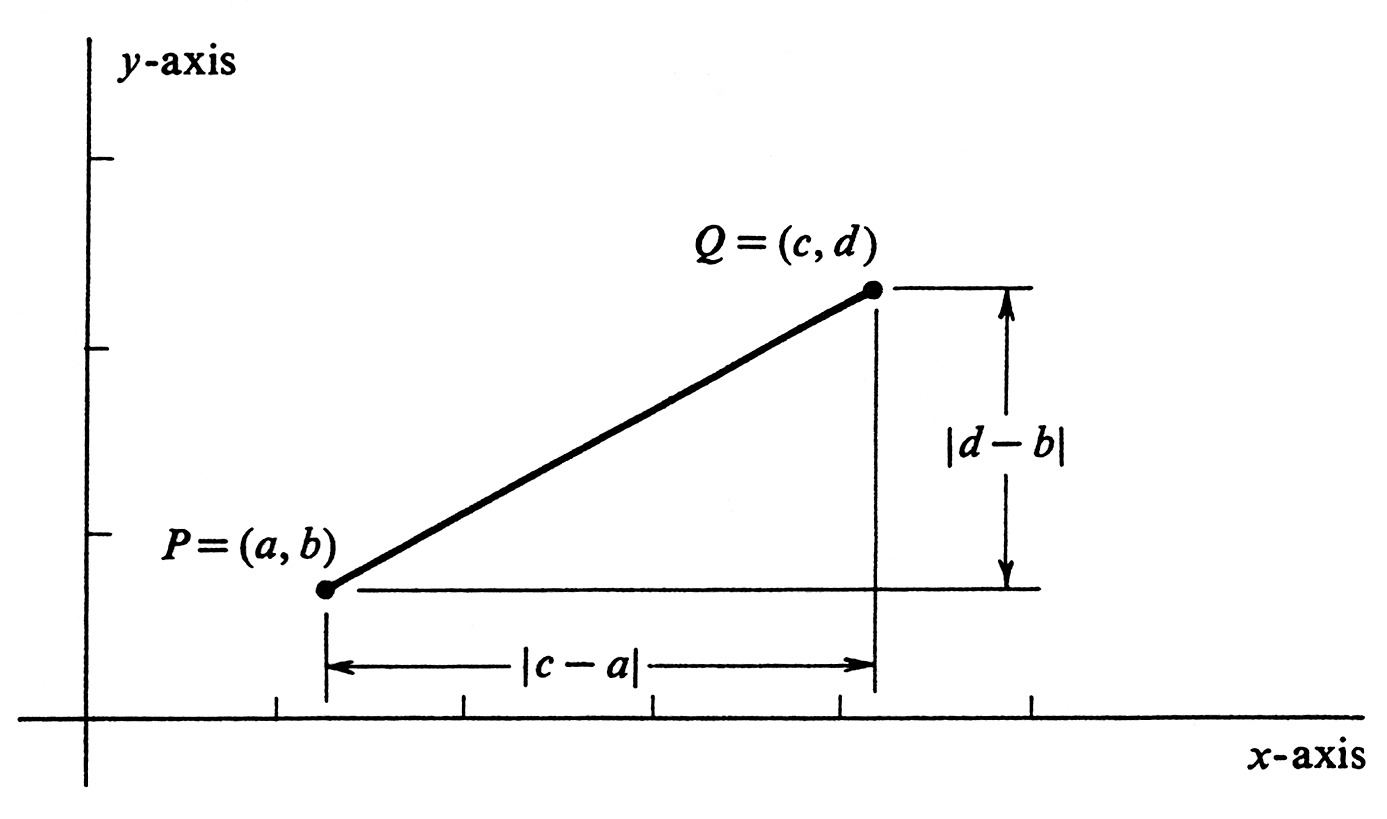
If <math>P = (a, b)</math> and <math>Q = (c, d)</math> are two points in <math>\R^2</math> and <math>a \neq c</math>, the '''slope of the line segment''' joining <math>P</math> to <math>Q</math> is, by definition, | |||
<math display="block"> | |||
m(P, Q) = \frac{d - b}{c - a} . | |||
</math> | |||
Note that | |||
<math display="block"> | |||
m(P, Q) = \frac{d - b}{c - a} = \frac{b - d}{a - c} = m(Q, P) . | |||
</math> | |||
The absolute value of <math>m(P, Q)</math> is the ratio of the vertical to horizontal distance between <math>P</math> and <math>Q</math> (see [[#fig 1.30|Figure]]). | |||
It is simply a measure of steepness. | |||
A segment with positive slope goes up as it goes to the right; one with negative slope goes down as it goes to the right ([[#fig 1.31|Figure]]). | |||
If <math>a = c</math>, the segment is vertical, and the slope is not defined. | |||
<div id="fig 1.30" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_30.png | 400px | thumb | ]] | |||
</div> | |||
{{proofcard|Proposition|thm_1.5.2|Let <math>L</math> be the straight line defined by the equation <math>ax + by + c = 0</math>, where <math>b \neq 0</math>. | |||
If <math>P</math> and <math>Q</math> are any two distinct points on the line, then <math>m(P, Q) = -\frac{a}{b}</math>. | |||
|Let <math>P = (x_1, y_1)</math> and <math>Q = (x_2, y_2)</math>. | |||
An equation equivalent to the original one is | |||
<span id{{=}}"eq1.5.1"/> | |||
<math display="block"> | |||
\begin{equation} | |||
y = - \Bigl( \frac{a}{b} \Bigr) x - \frac{c}{b} . | |||
\label{eq1.5.1} | |||
\end{equation} | |||
</math> | |||
It follows that <math>x_1 \neq x_2</math>, since, otherwise, substitution in this equation would yield <math>y_1 = y_2</math>, which would then imply <math>P = Q</math>. | |||
We obtain | |||
<math display="block"> | |||
m(P, Q) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ | |||
- \frac{a}{b} x_2 | |||
- \frac{c}{b} | |||
+ \frac{a}{b} x_1 | |||
+ \frac{c}{b}} | |||
{x_2 - x_1} = -\frac{a}{b} , | |||
</math> | |||
and this completes the proof.}} | |||
<div id="fig 1.31" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_31.png | 400px | thumb | ]] | |||
</div> | |||
As a result of [[#thm 1.5.1 |Theorem]] and [[#thm 1.5.2 |Theorem]], | |||
we can unambiguously define the '''slope of a nonvertical line <math>L</math>''', | |||
which we shall denote by <math>m_{L}</math>, | |||
as follows: | |||
For any pair of distinct points <math>P</math> and <math>Q</math> on <math>L</math>, we define | |||
<math display="block"> | |||
m_{L} = m(P, Q). | |||
</math> | |||
It follows at once that <math>m_{L}</math> depends only on the line <math>L</math>. | |||
For if <math>P'</math> and <math>Q'</math> are any other two distinct points on the line, then | |||
<math display="block"> | |||
m(P, Q) = - \frac{a}{b} = m(P', Q'). | |||
</math> | |||
(Since <math>L</math> is not vertical, <math>b \neq 0</math>.) Furthermore, any other equation defining <math>L</math> can be written <math>kax + kby + kc = 0</math> with <math>k \neq 0</math>, and, of course, <math>-\frac{ka}{kb} = -\frac{a}{b}</math>. | |||
We note that the slope of a vertical line is not defined. | |||
<span id="exam 1.5.1"/> | |||
'''Example''' | |||
Find an equation of the straight line <math>L</math> through the point <math>(a, b)</math> and with slope <math>m</math>. | |||
If <math>(x, y)</math> is any other point on the line, then | |||
<math display="block"> | |||
m = \frac{y - b}{x - a}, | |||
</math> | |||
which implies | |||
<span id{{=}}"eq1.5.2"/> | |||
<math display="block"> | |||
\begin{equation} | |||
y - b = m(x - a). | |||
\label{eq1.5.2} | |||
\end{equation} | |||
</math> | |||
This is an equation of the line. | |||
For suppose <math>L</math> were defined by some equation <math>a_{1}x + b_{1}y + c_1 = 0</math>. | |||
An equivalent equation is | |||
<math display="block"> | |||
y = -\Bigl( \frac {a_1}{b_1} \Bigr) x -\frac{c_1}{b_1}, | |||
</math> | |||
or, since <math>m = -\frac{a_1}{b_1}</math>, | |||
<span id{{=}}"eq1.5.3"/> | |||
<math display="block"> | |||
\begin{equation} | |||
y = mx - \frac{c_1}{b_1}. | |||
\label{eq1.5.3} | |||
\end{equation} | |||
</math> | |||
Since we are given that <math>(a, b)</math> lies on <math>L</math>, we get <math>b = ma - \frac{c_1}{b_1}</math>, or | |||
<math display="block"> | |||
\frac{c_1}{b_1} = ma - b. | |||
</math> | |||
Substitution [[#eq1.5.3 |in]] yields <math>y = mx - ma + b</math>, | |||
which is equivalent [[#eq1.5.2 |to]]. | |||
Suppose that <math>S</math> is an arbitrary subset of <math>\R^2</math> with the following three properties: | |||
#<math>S</math> contains a point <math>(a, b)</math>; i.e., <math>S</math> is a nonempty set. | |||
# The slope <math>m(P, Q)</math> is defined and is equal to the same fixed number <math>m</math>, for every pair of distinct points <math>P</math> and <math>Q</math> in <math>S</math>. | |||
#<math>S</math> contains every point <math>(x, y)</math> in <math>\R^2</math> which is connected to <math>(a, b)</math> by a line segment of slope <math>m</math>. | |||
These are certainly the geometric properties of a nonvertical straight line. | |||
It follows from (i) and (ii) that the coordinates of every point <math>(x, y)</math> in <math>S</math> satisfy the equation | |||
<span id{{=}}"eq1.5.4"/> | |||
<math display="block"> | |||
\begin{equation} | |||
y - b = m(x - a). | |||
\label{eq1.5.4} | |||
\end{equation} | |||
</math> | |||
Conversely, it follows from (iii) that, for every pair of real numbers <math>x</math> and <math>y</math> which satisfy (4), the point <math>(x, y)</math> must lie in <math>S</math>. | |||
Thus the set <math>S</math> is the graph of (4), and, as such, it is a straight line. | |||
Since nonvertical straight lines, as we have defined them, have the above three properties, we conclude that our definition coincides with the natural geometric one. | |||
We define two lines <math>L_1</math> and <math>L_2</math> to be '''parallel''' if they are both vertical or if they have the same slope. | |||
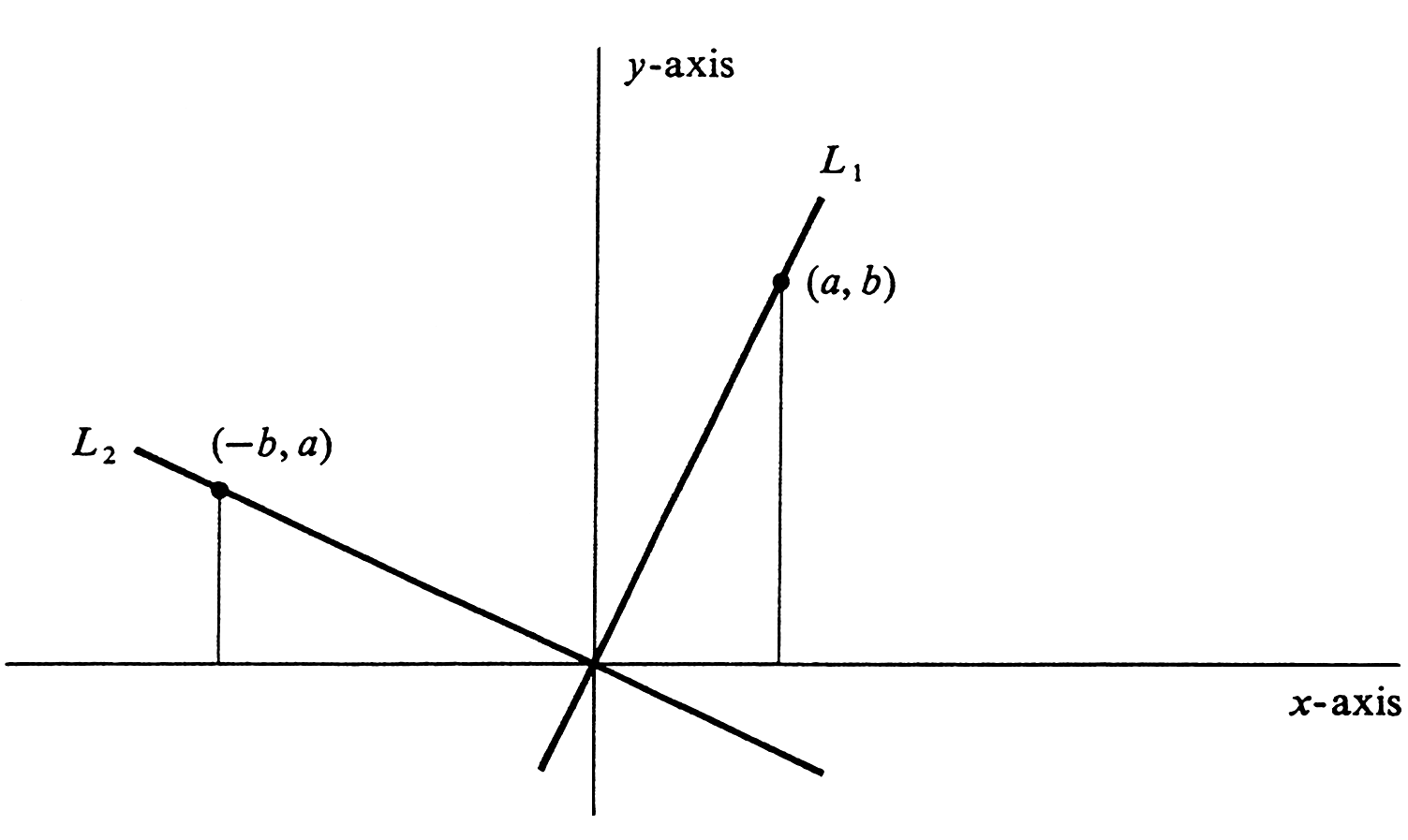
The following fact, which we shall prove later using trigonometry, can also be deduced from [[#fig 1.32|Figure]] by the methods of plane geometry. | |||
<div id="fig 1.32" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_32.png | 400px | thumb | ]] | |||
</div> | |||
{{proofcard|Proposition|thm_1.5.3|Two nonvertical lines <math>L_1</math> and <math>L_2</math> with slopes <math>m_1</math> and <math>m_2</math>, respectively, are perpendicular if and only if <math>m_{1}m_{2} = -1</math>.|}} | |||
<span id="exam 1.5.2"/> | |||
'''Example''' | |||
(a) Write an equation of the straight line <math>L_1</math> that passes through <math>(-2, 4)</math> and (3, 7). | |||
(b) Write an equation of the line <math>L_2</math> passing through <math>(5, -2)</math> and parallel to <math>L_1</math>. | |||
(c) Write an equation defining the line <math>L_3</math> that passes through <math>(-1, -3)</math> and is perpendicular to <math>L_1</math>. | |||
The slope of the segment joining <math>(-2, 4)</math> and (3, 7) is <math>\frac{7 - 4}{3 + 2} = \frac{3}{5}</math>. | |||
An arbitrary point <math>(x, y)</math> other than (3, 7) belongs to <math>L_1</math> if and only if | |||
<math display="block"> | |||
\frac{y - 7}{x - 3} = \frac{3}{5}. | |||
</math> | |||
Hence an equation defining <math>L_1</math> is <math>5(y - 7) = 3(x - 3)</math>, or, equivalently, | |||
<math display="block"> | |||
3x - 5y + 26 = 0. | |||
</math> | |||
The line <math>L_2</math> also has slope 5. Since it passes through <math>(5, -2)</math>, it is defined by | |||
<math display="block"> | |||
\frac{y + 2}{x - 5} = \frac{3}{5} \;\;\; \mbox{if} \;\;\; x \neq 5, | |||
</math> | |||
or, more generally, by <math>5(y + 2) = 3(x - 5)</math>, which is equivalent to | |||
<math display="block"> | |||
3x - 5y - 25 = 0. | |||
</math> | |||
The slope of the perpendicular is <math>-\frac{5}{3}</math>. | |||
Hence we obtain the equation | |||
<math display="block"> | |||
\frac{y + 3}{x + 1} = - \frac{5}{3}, \;\;\; x \neq -1, | |||
</math> | |||
or <math>3y + 9 = -5x - 5</math>, as an equation of <math>L_3</math>. | |||
What functions have graphs that are straight lines? The answer is an easy one. | |||
If <math>f</math> is defined by | |||
<math display="block"> | |||
f(x) = ax + b, \;\;\; - \infty < x < \infty, | |||
</math> | |||
then its graph, which is the set of all ordered pairs <math>(x, y)</math> | |||
such that <math>y = ax + b</math>, is certainly a straight line. | |||
Conversely, if the graph of an arbitrary function <math>f</math> is a straight line, then the equation <math>y = f(x)</math> is equivalent to one of the form | |||
<span id{{=}}"eq1.5.5"/> | |||
<math display="block"> | |||
\begin{equation} | |||
a_{1}x + b_{1}y + c_1 = 0, \;\;\; {a_1}^2 + {b_1}^2 > 0. | |||
\label{eq1.5.5} | |||
\end{equation} | |||
</math> | |||
If <math>b_1</math> were zero, both points <math>\Bigl( - \frac{c_1}{b_1}, 0 \Bigr)</math> and <math>\Bigl( -\frac{ c_1}{b_1}, 1 \Bigr)</math> would satisfy (5), but the definition of function makes this impossible for the equation <math>y = f(x)</math>. | |||
We conclude that <math>b_1 \neq 0</math> and that (5) is therefore equivalent to | |||
<math display="block"> | |||
y = - \Bigl(\frac{a_1}{b_1} \Bigr) x - \frac{c_1}{b_1}. | |||
</math> | |||
It follows [see [[guide:E8d7c0f552#thm 1.2.4 |Theorem]]] | |||
that the functions <math>f(x)</math> and | |||
<math>-\Bigl( \frac{a_1}{b_1} \Bigr) x -\frac{c_1}{b_1}</math> are equal. | |||
Thus the functions whose graphs are straight lines | |||
are precisely those of the form <math>ax + b</math>. | |||
These are the polynomials of degree less than 2, | |||
the '''linear functions'''. | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Latest revision as of 00:40, 4 November 2024
We shall define a straight line in [math]\R^2[/math] to be any subset [math]L[/math] consisting of all ordered pairs [math](x, y)[/math] such that
The inequality [math]a^2 + b^2 \gt 0[/math] simply says that the constants [math]a[/math] and [math]b[/math] are not both equal to zero. Of course two different equations can define the same line. For example, the set of all ordered pairs [math](x, y)[/math] such that [math]4x - 3y + 5 = 0[/math] is the same line as the set of pairs for which [math]28x = 21y - 35[/math]. For this reason, we speak of an equation of a straight line and not the equation.
Suppose that straight lines [math]L_1[/math] and [math]L_2[/math] are defined, respectioely, by
If such a [math]k[/math] exists, then the two equations are equivalent, and so [math]L_1 = L_2[/math]. Conversely, suppose that [math]L_1 = L_2[/math]. We may assume without loss of generality that [math]b_{1} \neq 0[/math]. Then the point [math]\Bigl(0, -\frac{c_1}{b_1} \Bigr)[/math] lies on [math]L_1[/math] since it satisfies the first equation; i.e.,
One consequence of Theorem is that it enables us to recognize at a glance whether or not different equations define the same straight line. Another corollary arises in connection with the following definitions: A line [math]L[/math] defined by an equation [math]ax + by + c = 0[/math] with [math]a^2 + b^2 \gt 0[/math] will be called vertical if [math]b = 0[/math] and horizontal if [math]a = 0[/math]. It follows from the theorem that [math]b[/math] must equal zero for every such equation which defines a vertical line and that [math]a[/math] must equal zero for every such equation which defines a horizontal line. Thus the definitions are not dependent on the particular equation which defines [math]L[/math]. If [math]P = (a, b)[/math] and [math]Q = (c, d)[/math] are two points in [math]\R^2[/math] and [math]a \neq c[/math], the slope of the line segment joining [math]P[/math] to [math]Q[/math] is, by definition,
Note that
The absolute value of [math]m(P, Q)[/math] is the ratio of the vertical to horizontal distance between [math]P[/math] and [math]Q[/math] (see Figure). It is simply a measure of steepness. A segment with positive slope goes up as it goes to the right; one with negative slope goes down as it goes to the right (Figure). If [math]a = c[/math], the segment is vertical, and the slope is not defined.
Let [math]L[/math] be the straight line defined by the equation [math]ax + by + c = 0[/math], where [math]b \neq 0[/math]. If [math]P[/math] and [math]Q[/math] are any two distinct points on the line, then [math]m(P, Q) = -\frac{a}{b}[/math].
Let [math]P = (x_1, y_1)[/math] and [math]Q = (x_2, y_2)[/math]. An equation equivalent to the original one is
As a result of Theorem and Theorem, we can unambiguously define the slope of a nonvertical line [math]L[/math], which we shall denote by [math]m_{L}[/math], as follows: For any pair of distinct points [math]P[/math] and [math]Q[/math] on [math]L[/math], we define
It follows at once that [math]m_{L}[/math] depends only on the line [math]L[/math]. For if [math]P'[/math] and [math]Q'[/math] are any other two distinct points on the line, then
(Since [math]L[/math] is not vertical, [math]b \neq 0[/math].) Furthermore, any other equation defining [math]L[/math] can be written [math]kax + kby + kc = 0[/math] with [math]k \neq 0[/math], and, of course, [math]-\frac{ka}{kb} = -\frac{a}{b}[/math]. We note that the slope of a vertical line is not defined.
Example
Find an equation of the straight line [math]L[/math] through the point [math](a, b)[/math] and with slope [math]m[/math].
If [math](x, y)[/math] is any other point on the line, then
Suppose that [math]S[/math] is an arbitrary subset of [math]\R^2[/math] with the following three properties:
- [math]S[/math] contains a point [math](a, b)[/math]; i.e., [math]S[/math] is a nonempty set.
- The slope [math]m(P, Q)[/math] is defined and is equal to the same fixed number [math]m[/math], for every pair of distinct points [math]P[/math] and [math]Q[/math] in [math]S[/math].
- [math]S[/math] contains every point [math](x, y)[/math] in [math]\R^2[/math] which is connected to [math](a, b)[/math] by a line segment of slope [math]m[/math].
These are certainly the geometric properties of a nonvertical straight line. It follows from (i) and (ii) that the coordinates of every point [math](x, y)[/math] in [math]S[/math] satisfy the equation
Two nonvertical lines [math]L_1[/math] and [math]L_2[/math] with slopes [math]m_1[/math] and [math]m_2[/math], respectively, are perpendicular if and only if [math]m_{1}m_{2} = -1[/math].
Example
(a) Write an equation of the straight line [math]L_1[/math] that passes through [math](-2, 4)[/math] and (3, 7).
(b) Write an equation of the line [math]L_2[/math] passing through [math](5, -2)[/math] and parallel to [math]L_1[/math].
(c) Write an equation defining the line [math]L_3[/math] that passes through [math](-1, -3)[/math] and is perpendicular to [math]L_1[/math].
The slope of the segment joining [math](-2, 4)[/math] and (3, 7) is [math]\frac{7 - 4}{3 + 2} = \frac{3}{5}[/math].
An arbitrary point [math](x, y)[/math] other than (3, 7) belongs to [math]L_1[/math] if and only if
Hence an equation defining [math]L_1[/math] is [math]5(y - 7) = 3(x - 3)[/math], or, equivalently,
The line [math]L_2[/math] also has slope 5. Since it passes through [math](5, -2)[/math], it is defined by
or, more generally, by [math]5(y + 2) = 3(x - 5)[/math], which is equivalent to
What functions have graphs that are straight lines? The answer is an easy one. If [math]f[/math] is defined by
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.