guide:75821cb7c5

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

According to the definition in Chapter 1, page 13, a function [math]f[/math] is a set of ordered pairs with the property that the first member [math]x[/math] of any pair [math](x, y)[/math] in the set determines the second member [math]y[/math], which we call [math]f(x)[/math]. For example, the set [math]\{(1, 3), (2, 5), (4, 3))\}[/math] is a function. Suppose, for a given functionf, we consider the set of all pairs [math](y, x)[/math] such that [math](x, y)[/math] is in [math]f[/math]. This set may or may not be a function. In our example it is the set [math]\{(3, 1), (5, 2), (3, 4)\}[/math], which is not a function because it contains both (3, 1) and (3, 4). Hence the first member does not determine the second uniquely. However, if the new set is a function, it is called the inverse function of [math]f[/math] and is denoted by [math]f^{-1}[/math]. If [math]f[/math] is the function defined by [math]f(x) = 7x[/math], for every real number [math]x[/math], then the inverse function [math]f^{-1}[/math] exists and is defined by [math]f^{-1}(x) = \frac{1}{7}x[/math]. On the other hand, the function [math]f[/math] defined by

[[math]] f(x) = x^2, \;\;\; -\infty \lt x \lt \infty, [[/math]]

does not have an inverse. The reason is that if [math]f(x) = x^2 = 4[/math], for example, we have no way of knowing whether [math]x = 2[/math] or [math]x = - 2[/math]. If we restrict the domain of [math]f[/math] to the set of nonnegative real numbers, i.e.,

[[math]] f(x) = x^2, \;\;\; 0 \leq x, [[/math]]

then [math]f^{-1}[/math] exists and is the function defined by

[[math]] f^{-1}(x) = \sqrt x, \;\;\; 0 \leq x. [[/math]]

The following three elementary properties of functions and their inverses should be noted:

Theorem

[[math]] (f^{-1})^{-1} = f. [[/math]]

Theorem

[[math]] y = f (x) \;\mbox{if and only if}\; x = f^{-1}(y). [[/math]]

Theorem

Two functions [math]f[/math] and [math]g[/math] are inverses of each other if and only if

[[math]] \begin{array}{ll} f(g(x)) = x, &\;\;\; \mbox{for every}\; x \;\mbox{in the domain of}\; g,\\ g(f(x)) = x, &\;\;\; \mbox{for every}\; x \;\mbox{in the domain of}\; f. \end{array} [[/math]]

The first of these, [math](f^{-1})^{-1} = f[/math], follows at once from the definition of [math]f^{-1}[/math]. To prove (2.2), suppose first that [math]y = f (x)[/math]. This means that the ordered pair [math](x, y)[/math] belongs to the set [math]f[/math]. Hence the pair [math](y, x)[/math] belongs to [math]f^{-1}[/math]. But this says that [math]x = f^{-1}(y)[/math]. To prove the converse, suppose that [math]x = f^{-1}(y)[/math]. Hence, by what we have just proved, we know that [math]y = (f^{-1})^{-1}(x)[/math]. Since [math](f^{-1})^{-1} = f[/math], we obtain [math]y = f (x)[/math]. The importance of (2.3) is that it provides a simple criterion for deciding when two functions are inverses of each other. For example, if [math]f(x) = 3x + 5[/math] and [math]g(x) = \frac{x - 5}{3}[/math], then

[[math]] \begin{eqnarray*} f(g(x)) &=& f \Bigl( \frac{x - 5}{3} \Bigr) = 3 \Bigl(\frac{x - 5}{3} \Bigr) + 5 = x, \\ g(f(x)) &=& g(3x + 5) = \frac{(3x + 5) - 5}{3} = x, \end{eqnarray*} [[/math]]

and we may therefore conclude that [math]g = f^{-1}[/math] and that [math]g^{-1} = f[/math]. The proof is completely straightforward (and rather tedious), and we omit it. The only way a function [math]f[/math] can fail to have an inverse is if there exist at least two elements [math]a[/math] and [math]b[/math] in its domain for which [math]a \neq b[/math] and [math]f(a) = f(b)[/math]. Suppose that [math]f[/math] is a strictly increasing function and that [math]a[/math] and [math]b[/math] are two distinct numbers in its domain. Then either [math]a \lt b[/math] or [math]b \lt a[/math]. If [math]a \lt b[/math], then [math]f(a) \lt f(b)[/math]; and if [math]b \lt a[/math], then [math]f(b) \lt f(a)[/math]. Thus it is impossible that [math]f(a) = f(b)[/math], and we conclude that [math]f^{-1}[/math] exists. A similar argument applies to any function that is strictly decreasing, and so

Theorem

If [math]f[/math] is strictly increasing or strictly decreasing, then [math]f[/math] has an inverse.

The natural logarithm has been shown to be a strictly increasing function, and hence must have an inverse. Let us call this function [math]\exp (x)[/math] and justify the name after we have looked at its properties. Thus, by (2.2),

[[math]] y = \exp (x) \;\;\; \mbox{if and only if}\; x = \ln\; y. [[/math]]

Since [math]\ln y[/math] is defined only for positive [math]y[/math], we see immediately that [math]\exp(x)[/math] is always positive. Furthermore, for any real number [math]x[/math], there exists a number y such that [math]x = \ln y[/math] because the graph of the equation [math]x = \ln y[/math] crosses every vertical line. Hence [math]\exp (x)[/math] is defined for every real number [math]x[/math]. Finally, since [math]0 = \ln 1[/math], we obtain [math]1 = \exp(0)[/math]. Summarizing, we have

Theorem

[[math]] \left \{ \begin{array}{ll} \exp(x) \gt 0, &\;\;\; -\infty \lt x \lt \infty, \\ \exp(0) = 1. & \end{array} \right. [[/math]]

To develop the algebraic properties of the function [math]\exp[/math], let [math]p = \exp (a)[/math] and [math]q = \exp (b)[/math]. Then [math]a = \ln p[/math] and [math]b = \ln q[/math]. Hence

[[math]] a + b = \ln p + \ln q = \ln pq, [[/math]]

and therefore [math]pq = \exp(a + b)[/math]. Replacing [math]p[/math] and [math]q[/math] in this last equation, we obtain the important fact that

Theorem

[[math]] \exp(a) \cdot \exp(b) = \exp(a + b). [[/math]]

Similarly, [math]-a = -\ln p = \ln {\frac{1}{p}}[/math], and therefore [math]\frac{1}{p} = \exp (-a)[/math]. Replacing [math]p[/math] in this equation, we find that

Theorem

[[math]] \frac{1}{\exp (a)} = \exp (-a). [[/math]]

If we apply (2.6) to the sum of the two numbers [math]a[/math] and [math]-b[/math], we get

[[math]] \exp (a - b) = \exp [a + (-b)] = \exp(a) \cdot \exp(-b). [[/math]]

Since

[[math]] \exp(-b) = \frac{1}{\exp(b)}, [[/math]]

it follows that

Theorem

[[math]] \frac{\exp(a)}{\exp(b)} = \exp(a - b). [[/math]]

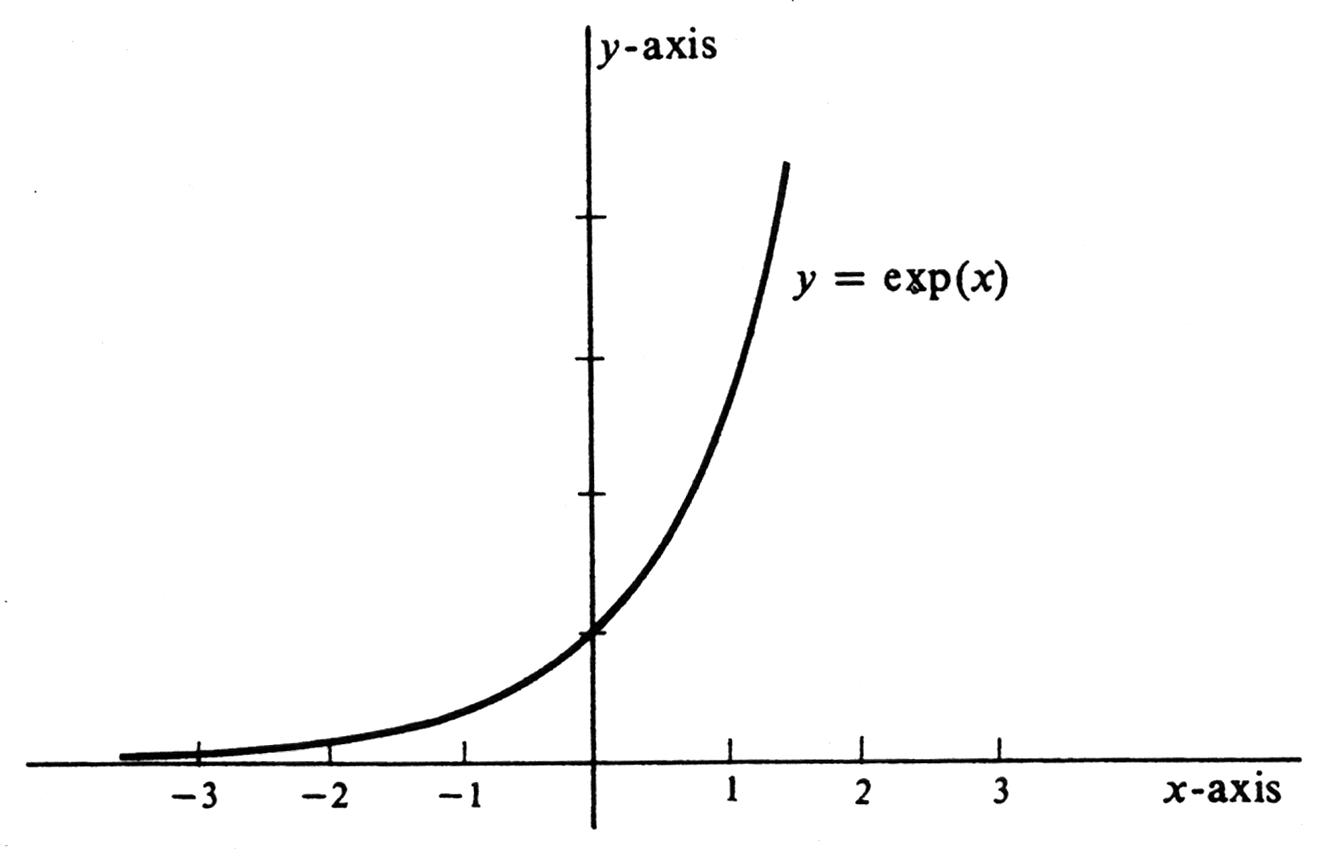
If a function [math]f[/math] has an inverse, then the ordered pairs which comprise it become the ordered pairs of [math]f^{-1}[/math]when we interchange the order of each pair. Hence the graph of [math]f^{-1}[/math] may be obtained from the graph of [math]f[/math] by interchanging [math]x[/math] and [math]y[/math]. This is equivalent to a reflection across the line [math]y = x[/math]. The graph of [math]y = \exp(x)[/math] is thus the reflection of the graph of [math]y = \ln\; x[/math] across this line, and it is shown in Figure. The curve passes through (0, 1) and gets closer and closer to the [math]x[/math]-axis as [math]x[/math] decreases without bound. As [math]x[/math] increases without bound, so also does [math]\exp(x)[/math].

File:Guide c5467 scanfig5 4.png

The graph of [math]y = \exp(x)[/math] is a smooth curve, and it is obvious geometrically that there is a tangent line at every point. We conclude that [math]\exp[/math] is a differentiable function. [For an analytic proof of this fact, see Theorem (3.4) in the next section.] We may compute the derivative by implicit differentiation. Consider the equation [math]y = \exp(x)[/math] and its equivalent equation [math]\ln y = x[/math]. The latter implicitly defines [math]\exp(x)[/math] since [math]\ln [\exp (x)] = x[/math]. Hence from [math]\ln y = x[/math] we obtain

[[math]] \begin{eqnarray*} \frac{d}{dx} \ln y &=& \frac{d}{dx} x,\\ \frac{1}{y} \frac{dy}{dx} &=& 1,\\ \frac{dy}{dx} &=& y. \end{eqnarray*} [[/math]]

Replacing [math]y[/math] by [math]\exp (x)[/math], we get

Theorem

[[math]] \frac{d}{dx} \exp (x) = \exp (x). [[/math]]

Alternatively we may write: If [math]f(x) = \exp (x)[/math], then [math]f'(x) = \exp(x)[/math] for every real number [math]x[/math]. Thus [math]\exp (x)[/math] is a most remarkable function, one which is equal to its own derivative. It is quite easy to show that this function and constant multiples of it are the only functions with this property. [See Problem 8 at the end of this section.] Another property of [math]\exp[/math] arises as a consequence of the logarithmic equation, [math]\ln p^r = r \ln p[/math], for positive [math]p[/math] and rational [math]r[/math]. If we again let [math]a = \ln p[/math], then [math]p = \exp (a)[/math] and [math]ar= r \ln p = \ln p^r[/math]. Equivalent to [math]ar = \ln p^r[/math] is [math]p^r = \exp (ar)[/math]. Since [math]p[/math] stood for [math]\exp (a)[/math], we conclude that

Theorem

[[math]] [\exp(a)]^{r} = \exp(ar), \;\;\; \mbox{for all $a$ and rational $r$}. [[/math]]

We know that [math]\exp(0) = 1[/math] and may wonder what [math]\exp(1)[/math] is. If we set [math]y = \exp (1)[/math], then [math]1 = \ln y[/math]. But [math]e[/math] is the only number with a natural logarithm equal to 1. Hence, [math]\exp(1) = e[/math]. As an application of (2.10), we see that if [math]x[/math] is a rational number, then

[[math]] e^{x} = [\exp (1)]^{x} = \exp (1 \cdot x) = \exp(x). [[/math]]

What about [math]e^{x}[/math] if [math]x[/math] is real but not rational? Note that if [math]a[/math] is any positive number, we have previously encountered a raised only to rational powers. For example, at this point we have no idea what [math]3^{\sqrt 2}[/math] even means. For the number [math]e[/math], however, there is a very natural way to define [math]e^{x}[/math] for all real numbers [math]x[/math]. We have just shown that if [math]x[/math] is rational, then [math]e^{x} = \exp (x)[/math]. Since the function [math]\exp[/math] has every real number in its domain, we shall define [math]e^{x}[/math] to be [math]\exp (x)[/math] if [math]x[/math] is not rational. Hence

[[math]] e^{x} = \exp(x), \;\;\;\mbox{for every real number}\; x. [[/math]]

We shall define [math]a^{x}[/math], for an arbitrary positive number [math]a[/math] and real [math]x[/math], in Section 4, and then [math]3^{\sqrt 2}[/math] will make sense. The reason for the term “exp,” which is an abbreviation for “exponential,” should now be clear. The function agrees with our previous idea of an exponential for rational values, and it has the following properties translated from those derived earlier in this section:

[[math]] \begin{equation} \left \{ \begin{array}{c} e^{0} = 1,\\ \\ e^{a} \cdot e^{b} = e^{a + b},\\ \\ e^{-a} = \frac{1}{e^a},\\ \\ \frac{e^a}{e^b} = e^{a-b}. \end{array} \right. \label{eq5.2.1} \end{equation} [[/math]]

Thus [math]e^{x}[/math] obeys the familiar laws of exponents. In addition,

[[math]] \begin{equation} \frac{d}{dx} e^{x} = e^{x}. \label{eq5.2.2} \end{equation} [[/math]]

If [math]u[/math] is a differentiable function of [math]x[/math], then the Chain Rule implies that [math]\frac{d}{dx} e^u = \Bigl( \frac{d}{du} e^{u} \Bigr) \frac{du}{dx}[/math]. Since[math] \frac{d}{du} e^u = e^u[/math], we have

[[math]] \begin{equation} \frac{d}{dx} e^u = e^u \frac{du}{dx}. \label{eq5.2.3} \end{equation} [[/math]]

Example

Find the derivative of each of the composite functions

[[math]] (a)\; e^{2x+7}, \;\;\; (b)\; e^{x^2}, \;\;\; (c)\; \frac{1}{e^{2x^3}}. [[/math]]

For the first, we have [math]\frac{d}{dx} e^{2x+7} = e^{2x + 7} \frac{d}{dx} (2x + 7) = 2e^{2x+7}[/math]. For (b), [math]\frac{d}{dx} e^{x^2} = e^{x^2} \frac{d}{dx} x^2 = 2xe^{x^2}[/math]. For (c), we writ [math]\frac{1}{e^{2x^3}}[/math] as [math]e^{-2x^3}[/math] and differentiate to get [math]e^{-2x^3} (-6x^2)[/math] or [math]-\frac{6x^2}{ e^{2x^3}}[/math]. \medskip Since [math]e^{x}[/math] is its own derivative, it is also its own indefinite integral. Hence

Theorem

[[math]] \int e^{x} dx = e^{x} + c. [[/math]]

More generally, from (3) [or, equivalently, from (6.5), page 213] we obtain the integral formula

Theorem

[[math]] \int e^{u} \frac{du}{dt} dx = e^u + c. [[/math]]

Example

Compute the following integrals:

[[math]] (a) \int e^{5x} dx, \;\;\; (b) \int x^{2} e^{x^{3} +7} dx,\;\;\; (c) \int \frac{e^{x} dx}{4e^{x} - 3}. [[/math]]

To solve (a), we let [math]u = 5x[/math]. Then [math]\frac{du}{dx} = 5[/math], and multiplying by [math]\frac{5}{5}[/math], we have

[[math]] \begin{eqnarray*} \int e^{5x} dx &=& \frac{1}{5} \int e^{u} 5 dx = \frac{1}{5} \int e^{u} \frac{du}{dx} dx\\ &=& \frac{1}{5} e^{u} + c = \frac{1}{5}e^{5x} + c. \end{eqnarray*} [[/math]]

In the same manner we solve (b) by letting [math]u = x^3 + 7[/math]. Then [math]\frac{du}{dx} = 3x^2[/math]. Omitting the explicit substitution of the variable [math]u[/math], we write

[[math]] \int x^{2} e^{x^{3} +7} dx = \frac{1}{3} \int e^{x^{3}+7} 3x^{2} dx = \frac{1}{3} e^{x^{3}+7} + c. [[/math]]

Part (c) combines logarithms and exponentials. Since [math]e^{x}[/math] lacks only a factor of 4 to be the derivative of [math]4e^{x} - 3[/math], we can supply the 4, and the integral is then of the form [math]\int \frac{1}{u} \frac{du}{dx} dx[/math], which is equal to [math]\ln |u| + c[/math]. Hence

[[math]] \int \frac{e^{x} dx}{4e^{x} - 3} = \frac{1}{4} \int \frac{1}{4e^{x} -3} 4e^{x} dx = \frac{1}{4} \ln |4e^{x}-3| + c. [[/math]]

Each of these answers can be checked by differentiating to see if we get back the original integrand. For example, in (b) we get

[[math]] \begin{eqnarray*} \frac{d}{dx} (\frac{1}{3}e^{x^{3}+7} + c) &=& \frac{1}{3}e^{x^{3} + 7} \frac{d}{dx} (x^3 + 7)\\ &=& \frac{1}{3}e^{x^{3} +7} 3x^2 = x^{2} e^{x^{3}+7}. \end{eqnarray*} [[/math]]

In (c),

[[math]] \begin{eqnarray*} \frac{d}{dx} (\frac{1}{4} \ln |4e^{x} - 3| + c) &=& \frac{1}{4} \frac{1}{4e^{x} - 3} \frac{d}{dx} (4e^{x} - 3)\\ &=& \frac{e^{x}}{4e^{x} - 3}. \end{eqnarray*} [[/math]]

Since the natural logarithm and the exponential functions are inverses of each other, an application of (2.3) gives the two useful formulas

[[math]] \begin{eqnarray*} \ln e^x &=& x, \;\;\; -\infty \lt x \lt \infty,\\ e^{\ln x} &=& x, \;\;\; 0 \lt x \lt \infty. \end{eqnarray*} [[/math]]

Example

Simplify (a) [math]e^{2 \ln x}[/math] and (b) [math]e^{3 + 5 \ln x}[/math]. For the first, since [math]2 \ln x = \ln x^2[/math], we have

[[math]] e^{2 \ln x} = e^{\ln x^2} = x^2. [[/math]]

For part (b),

[[math]] e^{3+ 5 \ln x} = e^{3} e^{5 \ln x} = e^{3} e^{\ln x^5} = e^{3}x^{5}. [[/math]]

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.