guide:17598b3b3c: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 32: | Line 32: | ||
\newcommand{\mathds}{\mathbb} | \newcommand{\mathds}{\mathbb} | ||
</math></div> | </math></div> | ||
The formulas for the derivative and integral of the functions <math>\sin</math> | The formulas for the derivative and integral of the functions <math>\sin</math> | ||
and <math>\cos</math> follow in a straightforward way from one fundamental limit theorem. It is | and <math>\cos</math> follow in a straightforward way from one fundamental limit theorem. It is | ||
{{proofcard|Theorem|theorem-1| | {{proofcard|Theorem|theorem-1| | ||
<math display="block"> | <math display="block"> | ||
\lim_{t \rightarrow 0} \frac{\sin t}{t} = 1. | \lim_{t \rightarrow 0} \frac{\sin t}{t} = 1. | ||
</math> | </math> | ||
<div id="fig 6.6" class="d-flex justify-content-center"> | <div id{{=}}"fig 6.6" class{{=}}"d-flex justify-content-center"> | ||
[[File:guide_c5467_scanfig6_6.png | 400px | thumb | ]] | [[File:guide_c5467_scanfig6_6.png | 400px | thumb | ]] | ||
</div> | </div> | ||
| Line 113: | Line 114: | ||
It is interesting to compare actual numerical values of <math>t</math> and <math>\sin t</math>. | It is interesting to compare actual numerical values of <math>t</math> and <math>\sin t</math>. | ||
Table 1 illustrates the limit theorem (2.1) quite effectively. | Table 1 illustrates the limit theorem (2.1) quite effectively. | ||
<span id="table 6.1"/> | <span id="table 6.1"/> | ||
{|class="table" | {|class="table" | ||
|- | |- | ||
| | | <math>t</math> || <math>\sin t</math> | ||
|- | |- | ||
|0.50 || 0.4794 | |0.50 || 0.4794 | ||
| Line 137: | Line 138: | ||
|0.02 || 0.0200 | |0.02 || 0.0200 | ||
|} | |} | ||
A useful corollary of (2.1) is | A useful corollary of (2.1) is | ||
{{proofcard|Theorem|theorem-2| | {{proofcard|Theorem|theorem-2| | ||
| Line 333: | Line 334: | ||
The graphs of the functions <math>\sin</math> and <math>\cos</math> are extremely interesting and important curves. | The graphs of the functions <math>\sin</math> and <math>\cos</math> are extremely interesting and important curves. | ||
To begin with, let us consider the graph of <math>\sin x</math> only for <math>0 \leq x \leq \frac{\pi}{2}</math>. A few isolated points can be plotted immediately (see Table 2). | To begin with, let us consider the graph of <math>\sin x</math> only for <math>0 \leq x \leq \frac{\pi}{2}</math>. A few isolated points can be plotted immediately (see Table 2). | ||
<span id="table 6.2"/> | <span id="table 6.2"/> | ||
{|class="table" | {|class="table" | ||
| Line 349: | Line 350: | ||
|<math>\frac{\pi}{2}</math> || 1 | |<math>\frac{\pi}{2}</math> || 1 | ||
|} | |} | ||
The slope of the graph is given by the derivative, <math>\frac{d}{dx} \sin x = \cos x</math>. | The slope of the graph is given by the derivative, <math>\frac{d}{dx} \sin x = \cos x</math>. | ||
At the origin it is <math>\cos 0 = 1</math>, and, where <math>x = \frac{\pi}{2}</math> the slope is <math>\cos \frac{\pi}{2} = 0</math>. | At the origin it is <math>\cos 0 = 1</math>, and, where <math>x = \frac{\pi}{2}</math> the slope is <math>\cos \frac{\pi}{2} = 0</math>. | ||
| Line 397: | Line 398: | ||
</div> | </div> | ||
==General references== | ==General references== | ||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | {{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | ||
Latest revision as of 19:51, 19 November 2024
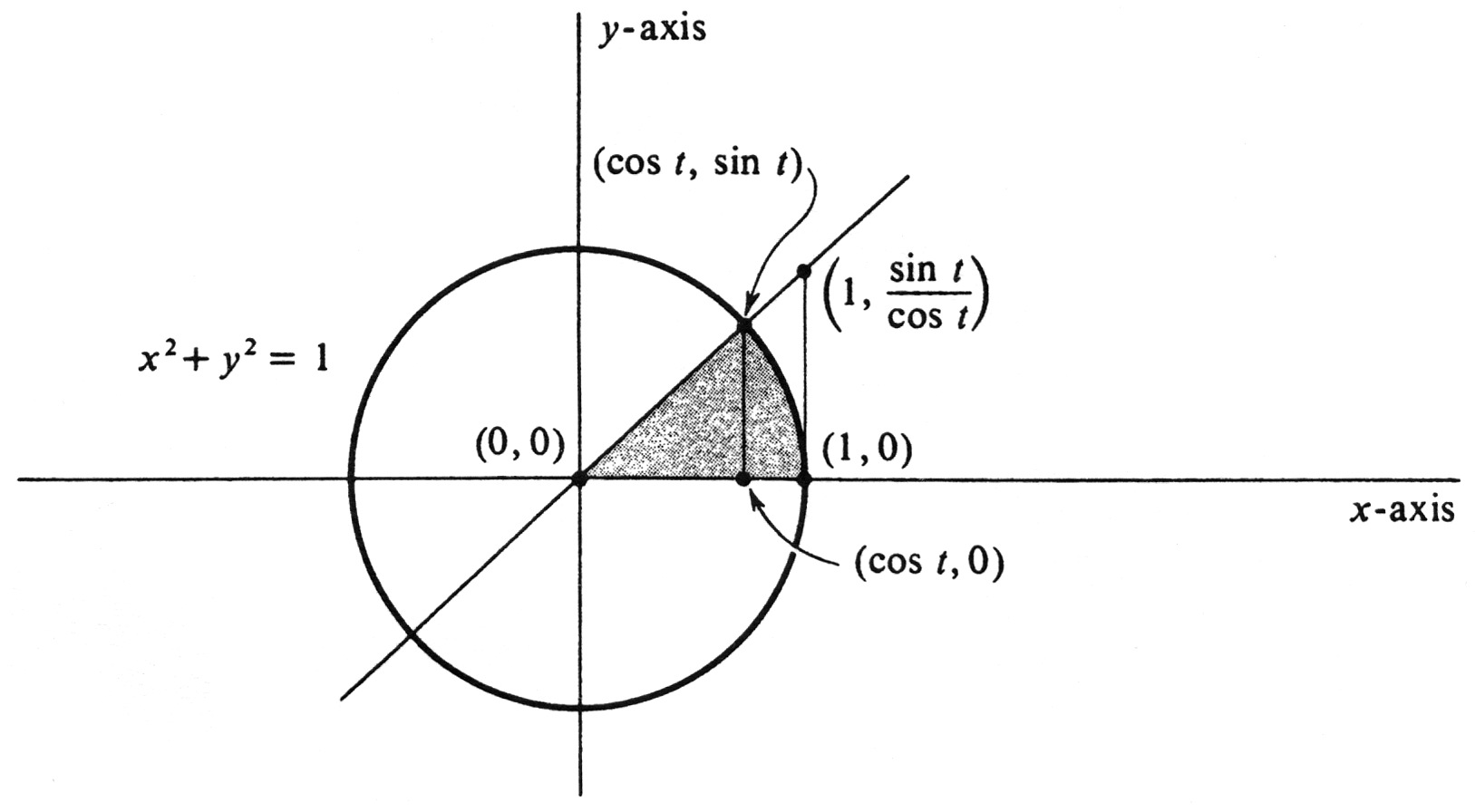
The formulas for the derivative and integral of the functions [math]\sin[/math] and [math]\cos[/math] follow in a straightforward way from one fundamental limit theorem. It is
It is convenient first to impose the restriction that [math]t \gt 0[/math] and prove that the limit from the right equals 1; i.e.,
It is now a simple matter to remove the restriction [math]t \gt 0[/math]. Since [math]\frac{\sin t}{t} = \frac{- \sin t}{-t} = \frac{\sin(-t)}{-t}[/math], we know that
It is interesting to compare actual numerical values of [math]t[/math] and [math]\sin t[/math]. Table 1 illustrates the limit theorem (2.1) quite effectively.
| [math]t[/math] | [math]\sin t[/math] |
| 0.50 | 0.4794 |
| 0.40 | 0.3894 |
| 0.30 | 0.2955 |
| 0.20 | 0.1987 |
| 0.10 | 0.0998 |
| 0.08 | 0.0799 |
| 0.06 | 0.0600 |
| 0.04 | 0.0400 |
| 0.02 | 0.0200 |
A useful corollary of (2.1) is
Using trigonometric identities, we write [math]\frac{1 - \cos t}{t}[/math] in such a form that (2.1) is applicable.
In writing values of the functions [math]\sin[/math] and [math]\cos[/math], we have thus far avoided the letter [math]x[/math] and have not written [math]\sin x[/math] and [math]\cos x[/math] simply because the point on the circle [math]x^{2} + y^{2} = 1[/math] whose coordinates define the value of [math]\cos[/math] and [math]\sin[/math] has nothing to do with, and generally does not lie on, the [math]x[/math]-axis. However, when we study [math]\sin[/math] and [math]\cos[/math] as two real-valued functions of a real variable, it is natural to use [math]x[/math] as the independent variable. We shall not hesitate to do so from now on.
Example Evaluate the limits
We evaluate the first two limits by writing the quotients in such a form that the fundamental trigonometric limit theorem, [math]\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1[/math], is applicable. For (a),
As [math]x[/math] approaches zero, so does [math]3x[/math] and so does [math]7x[/math]. Hence [math]\frac{\sin 3x}{3x}[/math] approaches 1, and [math]\frac{7x}{\sin 7x} = \Bigl(\frac{\sin 7x}{7x} \Bigr)^{-1}[/math] approaches [math]1^{-1} = 1[/math]. We conclude that
To do (b), we use the identity [math]\cos^{2} x + \sin^{2} x = 1[/math]. Thus
As [math]x[/math] approaches zero, [math]\sin x[/math] approaches [math]\sin 0 = 0[/math], and [math]\frac{\sin x}{x}[/math] approaches 1. Hence
For (c), no limit exists. The numerator approaches 1, and the denominator approaches zero. Note that we cannot even write the limit as [math]+\infty[/math] or [math]-\infty[/math] because [math]\sin x[/math] may be either positive or negative. As a result, [math]\frac{\cos x}{\sin x}[/math] takes on both arbitrarily large positive values and arbitrarily large negative values as [math]x[/math] approaches zero.
We are now ready to find [math]\frac{d}{dx} \sin x[/math]. The value of the derivative at an arbitrary number [math]a[/math] is by definition
As always, the game is to manipulate the quotient into a form in which we can see what the limit is. Since [math]\sin(a + t) = \sin a \cos t + \cos a \sin t[/math], we have
As [math]t[/math] approaches 0, the quantities [math]\cos a[/math] and [math]\sin a[/math] stay fixed. Moreover, [math]\frac{\sin t}{t}[/math] approaches 1, and [math]\frac{1 - \cos t}{t}[/math] approaches 0. Hence, the right side of the above equation approaches [math](\cos a) \cdot 1 - (\sin a) \cdot 0 = \cos a[/math]. We conclude that
Writing this result as an equality between functions, we get the simpler form
The derivative of the cosine may be found from the derivative of the sine using the Chain Rule and the twin identities [math]\cos x = \sin \Bigl(\frac{\pi}{2} - x \Bigr)[/math] and [math]\sin x = \cos \Bigl(\frac{\pi}{2} - x \Bigr)[/math] [see (1 6), page 286].
Writing this result in a single equation, we have
Example
Find the following derivatives.
These are routine exercises which combine the basic derivatives with the Chain Rule. For (a) we have
The solution to (b) is
For (c),
and for (d),
Every derivative formula has its corresponding integral formula. For the trigonometric
functions [math]\sin[/math] and [math]\cos[/math], they are
The proofs consist of simply verifying that the derivative of the proposed integral is the integrand. For example,
Example Find the following integrals.
The solutions use only the basic integral formulas and the fact that if [math]F' = f[/math], then [math]\int f(u) \frac{du}{dx} = F(u) + c[/math]. Integral (a) is simple enough to write down at a glance:
To do (b), let [math]u = x^2[/math]. Then [math]\frac{du}{dx} = 2x[/math], and
For (c), we let [math]u = \cos x[/math]. Then [math]\frac{du}{dx} = -\sin x[/math]. Hence
The graphs of the functions [math]\sin[/math] and [math]\cos[/math] are extremely interesting and important curves.
To begin with, let us consider the graph of [math]\sin x[/math] only for [math]0 \leq x \leq \frac{\pi}{2}[/math]. A few isolated points can be plotted immediately (see Table 2).
| [math]x[/math] | [math]y = \sin x[/math] |
| 0 | 0 |
| [math]\frac{\pi}{6}[/math] | [math]\frac{1}{2}[/math] |
| [math]\frac{\pi}{4}[/math] | [math]\frac{1}{2} \sqrt 2[/math] = 0.71 (approximately) |
| [math]\frac{\pi}{3}[/math] | [math]\frac{1}{2} \sqrt 3[/math] = 0.87 (approximately) |
| [math]\frac{\pi}{2}[/math] | 1 |
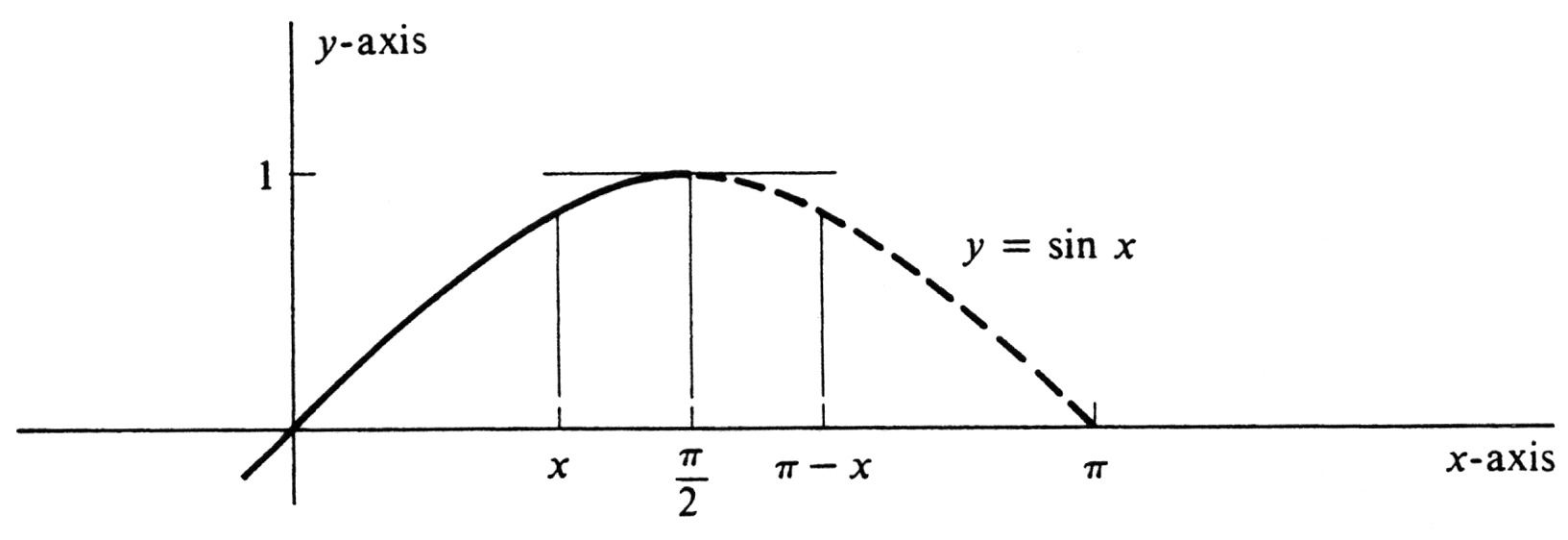
The slope of the graph is given by the derivative, [math]\frac{d}{dx} \sin x = \cos x[/math]. At the origin it is [math]\cos 0 = 1[/math], and, where [math]x = \frac{\pi}{2}[/math] the slope is [math]\cos \frac{\pi}{2} = 0[/math]. Since
we know that [math]\sin x[/math] is a strictly increasing function on the open interval [math]\Bigl(0, \frac{\pi}{2} \Bigr)[/math]. In addition, there are no points of inflection on the open interval and the curve is concave downward there because
On the other hand, the second derivative changes sign at [math]x = 0[/math], and so there is a point of inflection at the origin. With all these facts we can draw quite an accurate graph. It is shown in Figure 7.
It is now a simple matter to fill in as much of the rest of the graph of [math]\sin x[/math] as we like. For every real number [math]x[/math], the points [math]x[/math] and [math]\pi - x[/math] on the real number line are symmetrically located about the point [math]\frac{\pi}{2}[/math]. The midpoint between [math]x[/math] and [math]\pi - x[/math] is given by [math]\frac{x + (\pi - x)}{2} = \frac{\pi}{2}[/math]. As [math]x[/math] increases from 0 to [math]\frac{\pi}{2}[/math] the number [math]\pi - x[/math] decreases from [math]\pi[/math] to [math]\frac{\pi}{2}[/math]. Moreover,
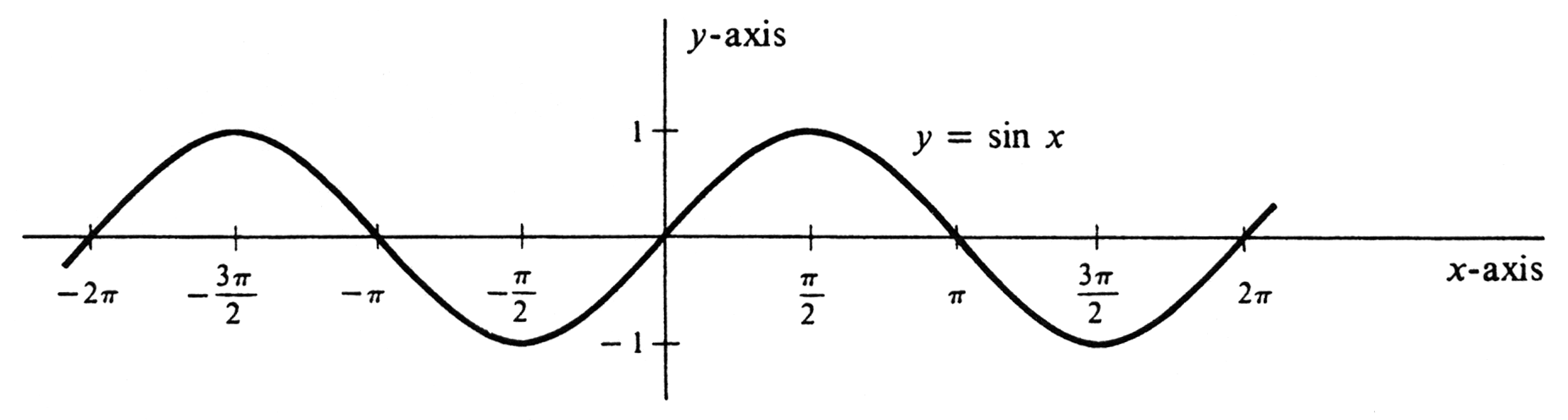
It follows that the graph of [math]\sin x[/math] on the interval [math]\Bigl[\frac{\pi}{2}, \pi \Bigr][/math] is the mirror image of the graph on [math]\Bigl[0, \frac{\pi}{2} \Bigr][/math] reflected across the line [math]x = \frac{\pi}{2}[/math] . This is the dashed curve in Figure 7. Now, because [math]\sin x[/math] is an odd function, its graph for [math]x \leq 0[/math] is obtained by reflecting the graph for [math]x \geq 0[/math] about the origin (i.e., reflecting first about one coordinate axis and then the other). This gives us the graph for [math]-\pi \leq x \leq \pi[/math]. Finally, since [math]\sin x[/math] is a periodic function with period [math]2\pi[/math], its values repeat after intervals of length [math]2\pi[/math]. It follows that the entire graph of [math]\sin x[/math] is the infinite wave, part of which is shown in Figure 8.
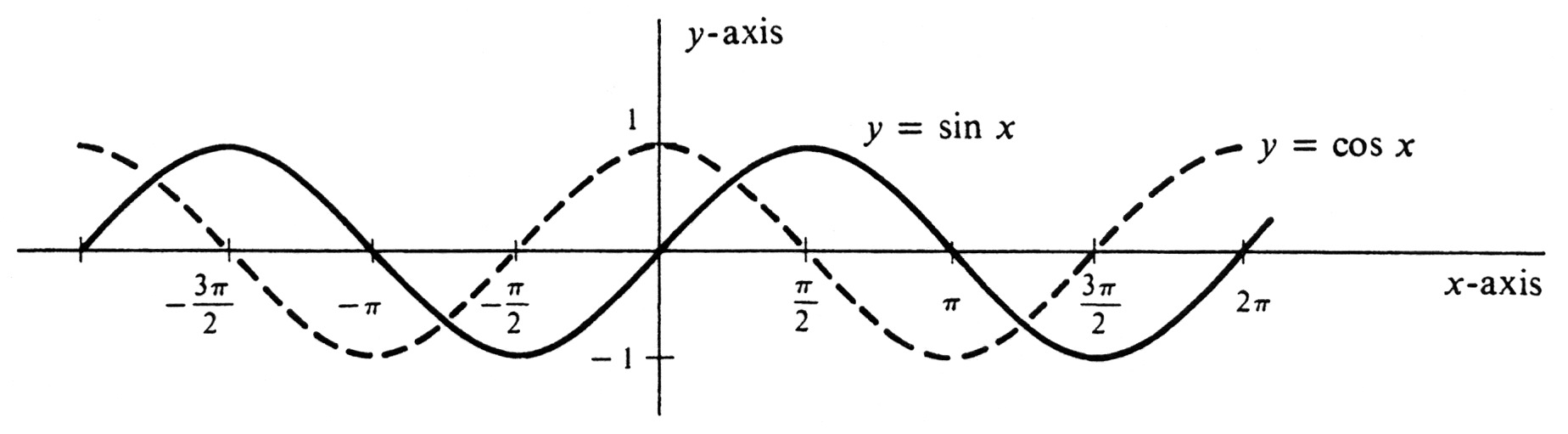
The graph of [math]\cos x[/math] is obtained by translating (sliding) the graph of [math]\sin x[/math] to the left a distance [math]\frac{\pi}{2}[/math]. This geometric assertion is equivalent to the algebraic equation [math]\cos x = \sin \Bigl(x + \frac{\pi}{2} \Bigr).[/math] But this follows from the trigonometric identity
The graphs of [math]\cos x[/math] and [math]\sin x[/math] are shown together in Figure 9.
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.