guide:D1cdd1f26e

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

The theory of convergence of infinite series is in many respects simpler for those series which do not contain both positive and negative terms. A series which contains no negative terms is called nonnegative. Thus [math]\sum_{i=m}^\infty a_i[/math] is nonnegative if and only if [math]a_i \geq 0[/math] for every integer [math]i \geq m[/math]. In this section we shall study two convergence criteria for such series: The Integral Test and the Comparison Test. Let [math]\sum_{i=m}^\infty a_i[/math] be an arbitrary infinite series (not necessarily nonnegative), and let [math]\{ s_n \}[/math] be the corresponding sequence of partial sums. We recall that [math]s_n = \sum_{i=m}^n a_i[/math], for every integer [math]n \geq m[/math], and that, if [math]\{ s_n \}[/math] converges, then [math]\sum_{i=m}^\infty a_i = \lim_{n \rightarrow \infty} s_n[/math]. We shall extend the convention regarding the symbol [math]\infty[/math] and write

[[math]] \sum_{i=m}^{\infty} a_i = \infty \;\;\;(\mbox{or}\; -\infty) [[/math]]

if and only if [math]\lim_{n \rightarrow \infty} s_n = \infty \; (\mbox{or}\; - \infty)[/math]. It may very well happen that a series neither converges nor satisfies [math]\sum_{i=m}^{\infty} a_i = \pm \infty[/math]. For example, the divergent series

[[math]] \sum_{i=0}^{\infty} (-1)^i = 1 - 1 + 1 - 1 + 1 - \cdots [[/math]]

has for its sequence of partial sums the oscillating sequence 1, 0, 1, 0, 1, .... However, for nonnegative series, there are only two alternatives:

Theorem

Every nonnegative series [math]\sum_{i=m}^{\infty} a_i[/math] either convefges or satisfies [math]\sum_{i=m}^{\infty} a_i = \infty[/math] .

The proof of this fact follows directly from the following two lemmas:

Theorem

If [math]\sum_{i=m}^{\infty} a_i[/math] is a nonnegative series, then the corresponding sequence [math]\{s\}[/math] of partial sums is an increasing sequence.

Show Proof

For every integer [math]n \geq m[/math], we have [math]s_{n+1} = s_n + a_{n+1}[/math]. Since the series is nonnegative, it follows that [math]s_{n+1} - s_n = a_{n+1} \geq 0[/math]. Hence

[[math]] s_{n+1} \geq s_n, \;\;\;\mbox{for every integer}\; n \geq m, [[/math]]

which is the definition of an increasing sequence.

■

Theorem

If [math]\{ s_n \}[/math] is an increasing infinite sequence of real numbers, then either it is bounded above and therefore converges or else [math]\lim_{n \rightarrow \infty} s_n = \infty[/math].

Show Proof

If the sequence is bounded above, then it is proved in Theorem ( 1.4), page 479, that it must converge. Suppose it is not so bounded. Then, for every real number [math]B[/math], there exists an integer [math]N[/math] such that [math]s_N \gt B[/math]. Since the sequence is increasing, it follows that [math]s_n \geq s_N[/math] for every [math]n \gt N[/math]. Hence [math]s_n \gt B[/math], for every integer [math]n \gt N[/math], and this is precisely the definition of the expression [math]\lim_{n \rightarrow \infty} s_n = \infty[/math].

■

We come now to the first of the tests for convergence of nonnegative infinite series. It is a generalization of the method used in Section 2 to prove the divergence of the harmonic series.

Theorem

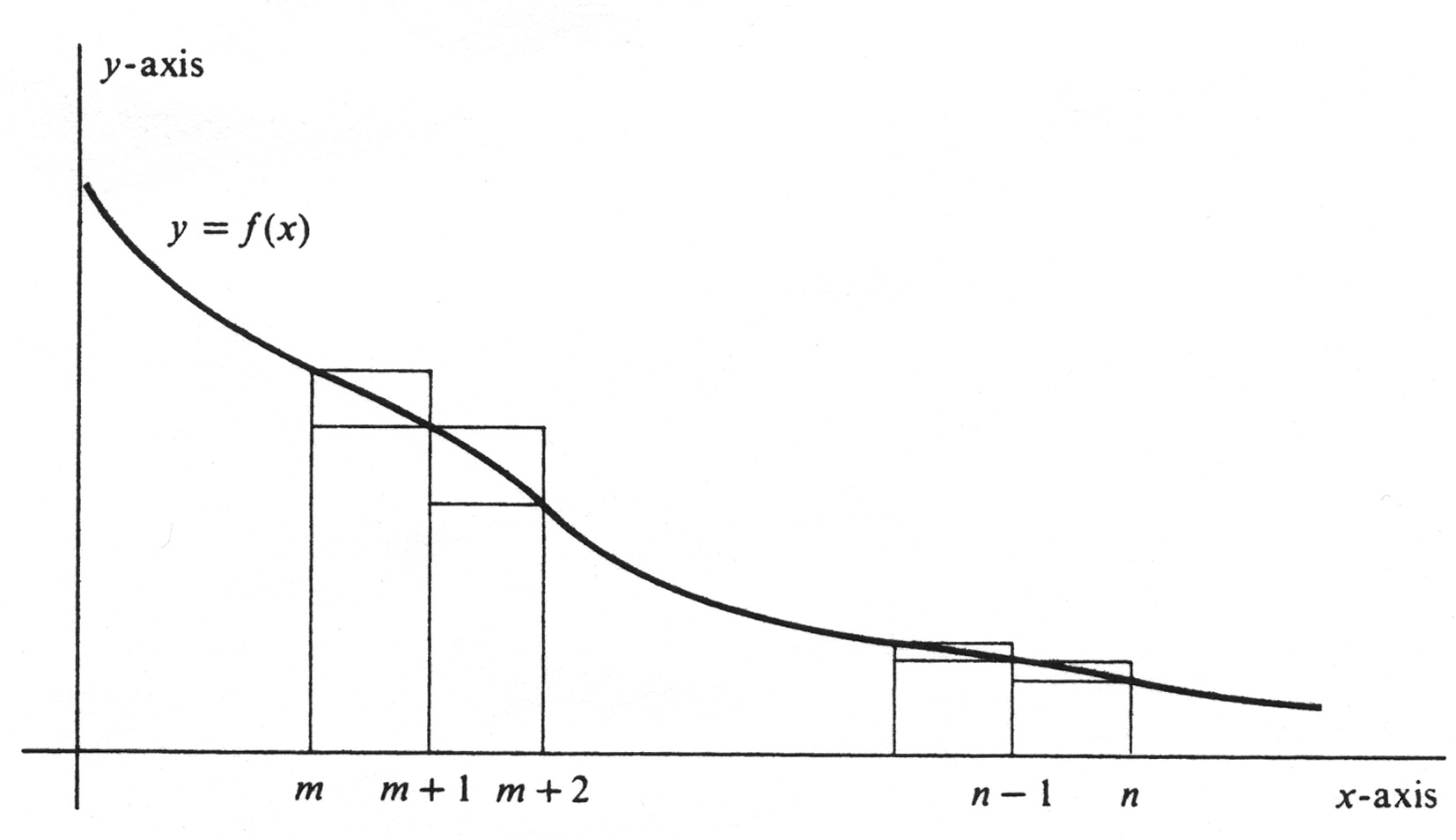
INTEGRAL TEST. Let [math]f[/math] be a function which is nonnegative and decreasing on the interval [math][m, \infty)[/math]. Then the infinite series [math]\sum_{i=m}^{\infty} a_i[/math] defined by

[[math]] a_i = f(i), \;\;\;\mbox{for every integer}\; i \geq m, [[/math]]

is convergent if and only if the improper integral [math]\int_m^\infty f(x) dx[/math] is convergent.

File:Guide c5467 scanfig9 4.png

Show Proof

The series [math]\sum_{i=m}^\infty a_i[/math] is nonnegative, and its corresponding sequence [math]\{ s_n \}[/math] of partial sums is therefore increasing. Figure 4 illustrates the graph of the function [math]f[/math] over an interval [math][m, n][/math], where [math]n[/math] is an arbitrary integer greater than [math]m[/math]. Since [math]f[/math] is decreasing, its maximum value on each subinterval of the partition [math]\sigma = \{ m, m + 1, . . ., n \}[/math], occurs at the left endpoint. Moreover, each subinterval has length 1. Hence the upper sum [math]U_\sigma[/math], which is equal to the sum of the areas of the rectangles Iying above the graph in the figure, is given by

[[math]] U_\sigma = \sum_{i=m}^{n-1} f(i) = \sum_{i=m}^{n-1} a_i = s_{n-1}. [[/math]]

Similarly, the lower sum [math]L_\sigma[/math] is equal to

[[math]] L_\sigma = \sum_{i=m+1}^n f(i) = \sum_{i=m+1}^n a_i = s_n - a_m. [[/math]]

As always, we have

[[math]] L_\sigma \leq \int_m^n f(x) dx \leq U_\sigma, [[/math]]

and it follows that

[[math]] \begin{equation} s_n - a_m \leq \int_m^n f(x) dx \leq s_{n-1}. \label{eq9.3.1} \end{equation} [[/math]]

The crux of the proof of the Integral Test is in the inequalities (1). In completing the argument, we consider the “if” and “only if” parts of the theorem separately. “If.” Let [math]\int_m^\infty f(x) dx[/math] be a convergent improper integral. That is, [math]\lim_{b \rightarrow \infty} \int_m^b f(x) dx[/math] exists. Since [math]f[/math] is nonnegative on [math][m, \infty)[/math], the integral [math]\int_m^b f(x) dx[/math] is an increasing function of [math]b[/math]. Hence

[[math]] \int_m^n f(x)dx \leq \int_m^\infty f(x) dx, \;\;\;\mbox{for every integer}\; n \geq m, [[/math]]

[see (1.3'), page 479]. From (1) it follows that

[[math]] s_n \leq a_m + \int_m^n f(x) dx \leq a_m + \int_m^\infty f(x) dx, [[/math]]

for every integer [math]n \gt m[/math]. Hence the increasing sequence [math]\{ s_n \}[/math] is bounded above and therefore converges. The convergence of the sequence of partial sums is equivalent to the convergence of the corresponding infinite series, so we conclude that [math]\sum_{i=m}^\infty a_i[/math] converges. “Only if.” Suppose that [math]\sum_{i=m}^\infty a_i[/math] converges. Then

[[math]] s_{n-1} \leq s_n \leq \sum_{i=m}^\infty a_i , [[/math]]

for every integer [math]n \gt m[/math] [see (1.3), page 478]. For any real number [math]b[/math] in [math][m, \infty)[/math], choose an integer [math]n \gt b[/math]. Since [math]\int_m^b f(x) dx[/math] is an increasing function of [math]b[/math], we obtain from (1)

[[math]] \int_m^b f(x) dx \leq \int_m^n f(x) dx \leq s_{n-1}. [[/math]]

Hence

[[math]] \int_m^b f(x) dx \leq \sum_{i=m}^\infty a_i. [[/math]]

The integral is therefore bounded above, and it follows that [math]\lim_{b \rightarrow \infty} \int_m^b f(x) dx[/math] exists [see (1.4'), page 480]. Hence [math]\int_m^\infty f(x) dx[/math] is a convergent improper integral, and the proof of the Integral Test is complete.

■

The convergence or divergence of many infinite series can be determined easily by the Integral Test. Important among these are series of the form

[[math]] \sum_{i=1}^\infty \frac{1}{i^p} = 1 + \frac{1}{2^p} + \frac{1}{3^p} + \cdots , [[/math]]

where [math]p[/math] is a positive real number. Such a series is called a [math]p[/math]-series. An example is the divergent harmonic series, for which [math]p = 1[/math]. The basic convergence theorem is

Theorem

The [math]p[/math]-series [math]\sum_{i=1}^\infty \frac{1}{i^p}[/math] converges if and only if [math]p \gt 1[/math].

Show Proof

The function [math]f[/math] defined by [math]f(x) = \frac{1}{x^p}[/math] is nonnegative on the interval [math][1, \infty)[/math], and is also decreasing on that interval since we have made the assumption that [math]p \gt 0[/math]. Moreover, it is obvious that [math]f(i) = \frac{1}{i^p}[/math] for every positive integer [math]i[/math]. If [math]p \neq 1[/math], then

[[math]] \int \frac{1}{x^p} dx = \frac{1}{1-p}x^{1-p} + c. [[/math]]

Hence we have the three computations:

[[math]] \begin{eqnarray*} 0 \lt &p& \lt 1: \int_1^\infty \frac{1}{x^p} dx = \frac{1}{1 - p} \lim_{b \rightarrow \infty} (b^{1-p} - 1) = \infty, \\ &p& = 1: \int_1^\infty \frac{1}{x^p} dx = \int_1^\infty \frac{1}{x} dx = \lim_{b \rightarrow \infty} \ln b = \infty, \\ &p& \gt 1: \int_1^\infty \frac{1}{x^p} dx = \frac{1}{1-p} \lim_{b \rightarrow \infty} (\frac{1}{b^{p-1}} - 1) = \frac{1}{p-1}. \end{eqnarray*} [[/math]]

It follows that [math]\int_1^\infty \frac{1}{x^p}dx[/math] is convergent if and only if [math]p \gt 1[/math], and the Integral Test therefore completes the proof.

■

Thus the first of the following three p-series diverges, and the last two converge:

[[math]] \begin{eqnarray*} \sum_{i=1}^\infty \frac{1}{\sqrt i} &=& 1+ \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots , \\ \sum_{i=1}^\infty \frac{1}{k ^{3/2}} &=& 1 + \frac{1}{2 \sqrt 2} + \frac{1}{3 \sqrt 3} + \cdots ,\\ \sum_{i=1}^\infty \frac{1}{j^2} &=& 1 + \frac{1}{2^2} + \frac{1}{3^2} + \cdots . \end{eqnarray*} [[/math]]

Example

Determine whether the series [math]\sum_{i=1}^\infty \frac{1}{2k^2 + 1}[/math] converges or diverges. The function [math]f[/math] defined by [math]f(x) = \frac{1}{2x^2 + 1}[/math] is nonnegative and decreasing on the interval [math][1, \infty)[/math], and obviously [math]f(k) = \frac{1}{2k^2 + 1}[/math]. Since

[[math]] \int \frac{1}{2x^2 + 1} dx = \frac{1}{\sqrt 2} \arctan \sqrt 2 x + c, [[/math]]

we have

[[math]] \begin{eqnarray*} \int_1^\infty \frac{1}{2x^2 + 1} dx &=& \frac{1}{\sqrt 2} (\arctan \sqrt{2} b - \arctan \sqrt 2)\\ &=& \frac{1}{\sqrt 2} (\frac{\pi}{2} - \arctan \sqrt 2) . \end{eqnarray*} [[/math]]

Hence the integral is convergent, and therefore so is the series.

We come now to the second of our convergence tests.

Theorem

COMPARISON TEST. [math]\sum_{i=m}^\infty a_i[/math] is a nonnegative series and if [math]\sum_{i=m}^\infty b_i[/math] is a convergent series with [math]a_i \leq b_i[/math] for every [math]i \geq m[/math], then [math]\sum_{i=m}^\infty a_i[/math] converges and [math]\sum_{i=m}^\infty a_i \leq \sum_{i=m}^\infty b_i[/math] .

Show Proof

Let [math]\{s_n\}[/math] and [math]\{t_n\}[/math] be the sequences of partial sums for [math]\sum_{i=m}^\infty a_i[/math] and [math]\sum_{i=m}^\infty b_i[/math], respectively. The hypotheses [math]0 \leq a_i \leq b_i[/math] imply that

[[math]] \begin{equation} s_n \leq t_n, \;\;\;\mbox{for every integer}\; n \geq m, \label{eq9.3.2} \end{equation} [[/math]]

and also that both series are nonnegative. Hence both [math]\{s_n\}[/math] and [math]\{t_n\}[/math] are increasing sequences. The convergence of [math]\sum_{t=m}^\infty b_i[/math] means that [math]\{t_n\}[/math] converges and that [math]\lim_{n \rightarrow \infty} t_n = \sum_{i=m}^\infty b_i[/math]. It follows that

[[math]] t_n \leq \sum_{i=m}^\infty b_i, \;\;\;\mbox{for every integer}\; n \geq m [[/math]]

[see (1.3), page 478]. Hence, by (2),

[[math]] s_n \leq \sum_{i=m}^\infty b_i, \;\;\;\mbox{for every integer}\; n \geq m. [[/math]]

Thus [math]\{s_n\}[/math] is increasing and bounded above by [math]\sum_{i=m}^\infty b_i[/math]. The sequence therefore converges and

[[math]] \lim_{n \rightarrow \infty} s_n \leq \sum_{i=m}^\infty b_i [[/math]]

[see (1.4), page 479]. The convergence of [math]s_n[/math] implies the convergence of [math]\sum_{i=m}^\infty a_i[/math] and that the value of the series is [math]\lim_{n \rightarrow \infty} s_n[/math]. Hence

[[math]] \sum_{i=m}^\infty a_i \leq \sum_{i=m}^\infty b_i, [[/math]]

and the proof is complete.

■

Example

Use the Comparison Test to prove that the series [math]\sum_{i=0}^\infty \frac{1}{2i^2 - 7}[/math] converges. We first observe that the first two terms of the series are negative. However, [math]2i^2 - 7 \gt 0[/math] provided [math]i \geq 2[/math], and so the series [math]\sum_{i=2}^\infty \frac{1}{2i^2 - 7}[/math] is nonnegative. It is sufficient to prove the latter series convergent because of the important fact that the convergence of an infinite series is unaffected by any finite number of terms at the beginning. As our test series we take the convergent [math]p[/math]-series [math]\sum_{i=1}^\infty \frac{1}{i^2}[/math]. To use the Comparison Test, we wish to show that

[[math]] \begin{equation} \frac{1}{2i^2 - 7} \leq \frac{1}{i^2}, \;\;\;\mbox{for every integer}\; i \geq 2. \label{eq9.3.3} \end{equation} [[/math]]

This inequality is equivalent to [math]i^2 \leq 2i^2 - 7[/math], which in turn is equivalent to [math]i^2 \geq 7[/math]. The last is clearly true provided [math]i \geq 3[/math]. Thus we have proved

[[math]] \begin{equation} \frac{1}{2i^2 - 7} \leq \frac{1}{i^2}, \;\;\;\mbox{for every integer}\; i \geq 3, \label{eq9.3.4} \end{equation} [[/math]]

which is slightly weaker than (3). However, (4) is certainly sufficient. We know that the series [math]\sum_{i=3}^\infty \frac{1}{i^2}[/math] , converges. It follows from (4) by the Comparison Test that [math]\sum_{i=3}^\infty \frac{1}{2i^2 - 7}[/math] converges and, as a result, the original series [math]\sum_{i=0}^\infty \frac{1}{2i^2 - 7}[/math] does also.

Example 2 illustrates a useful extension of the Comparison Test: The series [math]\sum_{i=m}^\infty a_i[/math] converges if there exists a convergent series [math]\sum_{i=m}^\infty b_i[/math] such that [math]0 \leq a_i \leq b_i[/math] eventually. The assertion that [math]0 \leq a_i \leq b_i[/math] eventually means simply that there exists an integer [math]N[/math] such that [math]0 \leq a_i \leq b_i[/math] for every integer [math]i \geq N[/math]. The just)fication for this extension is Theorem (2.3), page 486. A similar observation should be made about the Integral Test. It may be necessary to drop a finite number of terms from the beginning of the series under consideration before a convenient function [math]f[/math] can be found which satisfies the conditions of the test.

The Comparison Test is as useful for proving divergence as convergence. It is an immediate corollary that if the nonnegative series [math]\sum_{i=m}^\infty a_i[/math] diverges and if [math]a_i \leq b_i[/math] for every [math]i \geq m[/math], then [math]\sum_{i=m}^\infty b_i[/math] also diverges. For if [math]\sum_{i=m}^\infty b_i[/math] converges, the Comparison Test implies that [math]\sum_{i=m}^\infty a_i[/math] converges, which is contrary to assumption.

Example

Determine whether the series [math]\sum_{k=1}^\infty \frac{1}{(k^2 + 5)^{1/3}}[/math] converges or diverges. If we use the Comparison Test, we must decide whether to look for a convergent test series with larger terms to prove convergence, or a divergent test series with smaller terms to prove divergence. To decide which, observe that for large values of [math]k[/math], the number [math]k^2 + 5[/math] is not very different from [math]k^2[/math], and therefore [math]\frac{1}{(k^2 + 5)^{1/3}}[/math] is approximately equal to [math]\frac{1}{k^{2/3}}[/math]. Stated more formally, we have

[[math]] \begin{eqnarray*} \lim_{k \rightarrow \infty} \frac{(k^2 + 5)^{1/3}}{k^{2/3}} &=& \lim_{k \rightarrow \infty} (\frac{k^2 + 5}{k^2})^{1/3} \\ &=& \lim_{k \rightarrow \infty}(1 + \frac{5}{k^2})^{1/3} = 1. \end{eqnarray*} [[/math]]

This comparison, together with the divergence of the [math]p[/math]-series [math]\sum_{k=1}^\infty \frac{1}{k^{2/3}}[/math], leads us to believe that the series [math]\sum_{k=1}^\infty \frac{1}{(k^2 + 5)^{1/3}}[/math] diverges. Hence we shall try a divergent test series. The most obvious candidate, [math]\sum_{k=1}^\infty \frac{1}{k^{2/3}}[/math], fails to be useful, since the necessary inequality,

[[math]] \frac{1}{k^{2/3}} \leq \frac{1}{(k^2 + 5)^{1/3}}, [[/math]]

is clearly false for every value of [math]k[/math]. However, the series [math]\sum_{k=1}^\infty \frac{1}{2k^{2/3}}[/math] is also divergent, and we may ask whether or not it is true that

[[math]] \begin{equation} \frac{1}{2k^{2/3}} \leq \frac{1}{(k^2 + 5)^{1/3}} \label{eq9.3.5} \end{equation} [[/math]]

This inequality is equivalent to [math]8k^2 \geq k^2 + 5[/math], and hence to [math]7k^2 \geq 5[/math], which is certainly true for every positive integer [math]k[/math]. Hence (5) holds for every integer [math]k \geq 1[/math], and it therefore follows by the Comparison Test that the series [math]\sum_{k=1}^\infty \frac{1}{(k^2 + 5)^{1/3}}[/math] diverges.

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.