guide:B4edc7c00c: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 32: | Line 32: | ||
\newcommand{\mathds}{\mathbb} | \newcommand{\mathds}{\mathbb} | ||
</math></div> | </math></div> | ||
In this section we shall consider the motion of a particle in the plane during an interval of time. We shall assume that the particle moves without jumping. As a result, if <math>P</math> is the function which associates to every instant of time in the interval the corresponding position of the particle in the plane, then <math>P</math> is continuous; i.e., it is a parametrization. The points <math>P(t)</math> trace out the parametrized curve over which the particle moves. | In this section we shall consider the motion of a particle in the plane during an interval of time. We shall assume that the particle moves without jumping. As a result, if <math>P</math> is the function which associates to every instant of time in the interval the corresponding position of the particle in the plane, then <math>P</math> is continuous; i.e., it is a parametrization. The points <math>P(t)</math> trace out the parametrized curve over which the particle moves. | ||
Velocity is a vector concept which combines two ingredients: the number which measures how fast the particle is moving, and the direction of the motion. If the position of a particle during an interval of time <math>I</math> is described by a differentiable parametrization <math>P: I \rightarrow R^2</math>, then the '''velocity''' of the particle at any time t during the interval will be denoted by <math>v(t)</math> and defined to be the derived vector of <math>P</math> at <math>t</math>. Thus | Velocity is a vector concept which combines two ingredients: the number which measures how fast the particle is moving, and the direction of the motion. If the position of a particle during an interval of time <math>I</math> is described by a differentiable parametrization <math>P: I \rightarrow R^2</math>, then the '''velocity''' of the particle at any time t during the interval will be denoted by <math>v(t)</math> and defined to be the derived vector of <math>P</math> at <math>t</math>. Thus | ||
| Line 75: | Line 75: | ||
\item[(c)] How does the speed of the particle depend on time during the entire interval of motion? | \item[(c)] How does the speed of the particle depend on time during the entire interval of motion? | ||
The parametrized curve over which the particle moves is the set of all points <math>(x, y)</math> such that | The parametrized curve over which the particle moves is the set of all points <math>(x, y)</math> such that | ||
| Line 111: | Line 110: | ||
\end{eqnarray*} | \end{eqnarray*} | ||
</math> | </math> | ||
<div id="fig 10.17" class="d-flex justify-content-center"> | <div id="fig 10.17" class="d-flex justify-content-center"> | ||
[[File:guide_c5467_scanfig10_17.png | 400px | thumb | ]] | [[File:guide_c5467_scanfig10_17.png | 400px | thumb | ]] | ||
| Line 269: | Line 268: | ||
</math> | </math> | ||
Thus, acceleration, like velocity, is a vector. | Thus, acceleration, like velocity, is a vector. | ||
We can derive a simple formula for acceleration in terms of the coordinate functions of <math>P</math>. Let <math>P(t) = (x(t), y(t))</math>, as usual. Then | We can derive a simple formula for acceleration in terms of the coordinate functions of <math>P</math>. Let <math>P(t) = (x(t), y(t))</math>, as usual. Then | ||
| Line 411: | Line 410: | ||
==General references== | ==General references== | ||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | {{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | ||
Revision as of 01:46, 21 November 2024
In this section we shall consider the motion of a particle in the plane during an interval of time. We shall assume that the particle moves without jumping. As a result, if [math]P[/math] is the function which associates to every instant of time in the interval the corresponding position of the particle in the plane, then [math]P[/math] is continuous; i.e., it is a parametrization. The points [math]P(t)[/math] trace out the parametrized curve over which the particle moves. Velocity is a vector concept which combines two ingredients: the number which measures how fast the particle is moving, and the direction of the motion. If the position of a particle during an interval of time [math]I[/math] is described by a differentiable parametrization [math]P: I \rightarrow R^2[/math], then the velocity of the particle at any time t during the interval will be denoted by [math]v(t)[/math] and defined to be the derived vector of [math]P[/math] at [math]t[/math]. Thus
Since the derived vector is a tangent vector, the velocity is also one. Specifically, [math]\mbox'''{v'''}(t)[/math] is a tangent vector at [math]t[/math] to the parametrized curve defined by [math]P[/math]. If we write [math]P(t) = (x(t), y(t))[/math], then it follows from the formula for the derived vector [see (4.1), page 571] that the velocity vector is given by
The speed of the particle at time [math]t[/math] is defined to be the length [math]|\mbox'''{v'''}(t)|[/math] of the velocity vector. The equation for the length of a vector in terms of its coordinates [see (3.1), page 561] implies that the speed is equal to
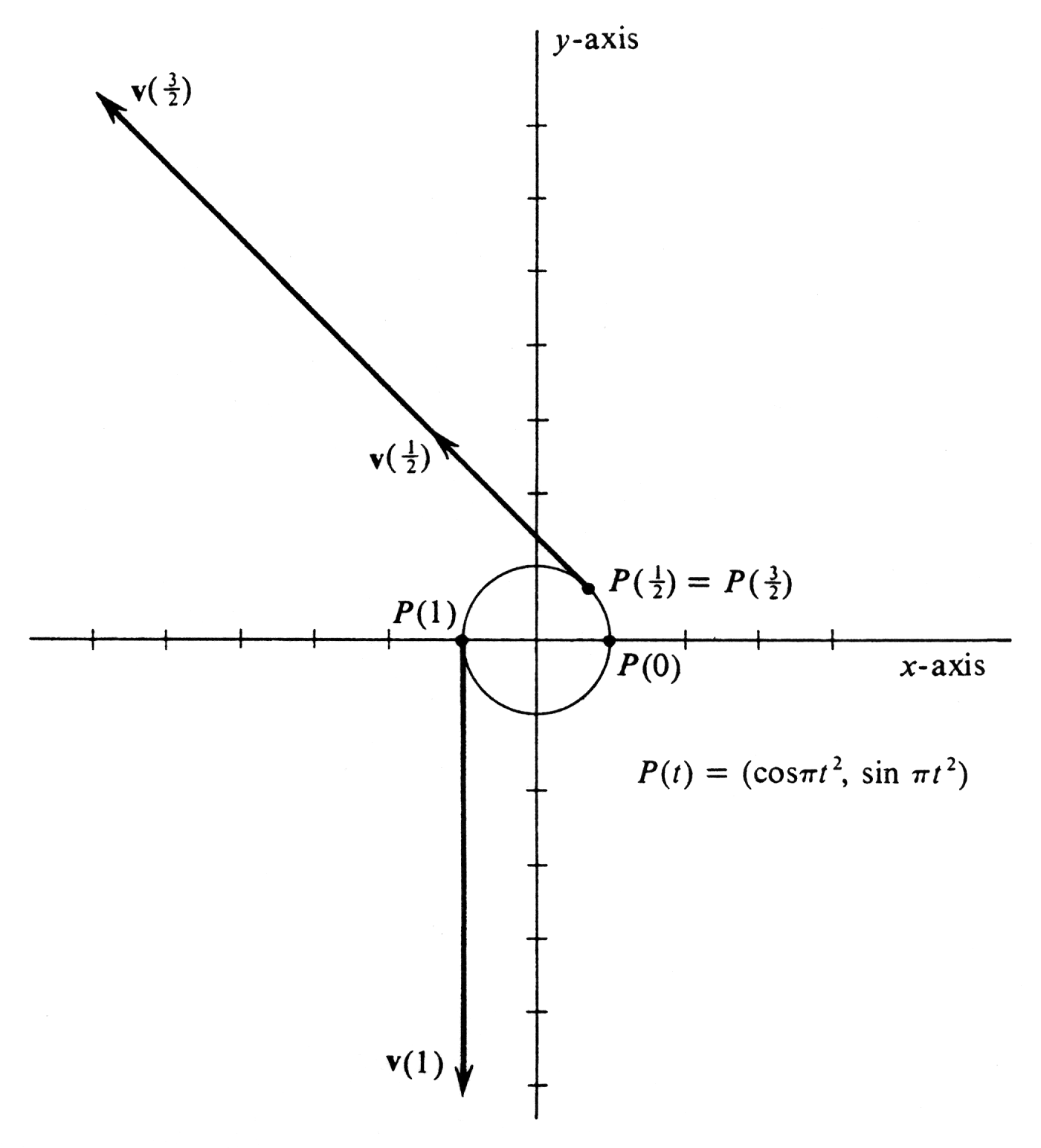
\item[a]] Identify and draw the curve traced out by the particle, and describe its motion during the interval [math][0, 2][/math]. \item[(b)] Compute the position, velocity, and speed of the particle at [math]t = 0[/math], [math]t = \frac{1}{2}[/math], [math]t = 1[/math], and [math]t = \frac{3}{2}[/math]. Show these four positions, and draw the corresponding velocity vectors in the figure in (a). \item[(c)] How does the speed of the particle depend on time during the entire interval of motion?
The parametrized curve over which the particle moves is the set of all points [math](x, y)[/math] such that
Hence the coordinates of every point [math](x, y)[/math] on the curve satisfy
Hence
Thus the four speeds are
The motion of a particle along a straight line was studied in Section 3 of Chapter 2 and again in Section 8 of Chapter 4. When the motion is restricted to a straight line, which for convenience we may take to be the [math]x[/math]-axis, then the velocity vector has only one nonzero coordinate, [math]x'(t)[/math]. In this case velocity may be identified with [math]x'(t)[/math], and it is not necessary to consider it as a vector. In our earlier treatments [math]x'(t)[/math] was defined to be the velocity and it was denoted by [math]v(t)[/math]. The distance on the line which the particle moves during the time interval [math][a, b][/math] was defined by the formula
Formula (5.1) is the generalization of the distance formula (5) from rectilinear to curvilinear motion.
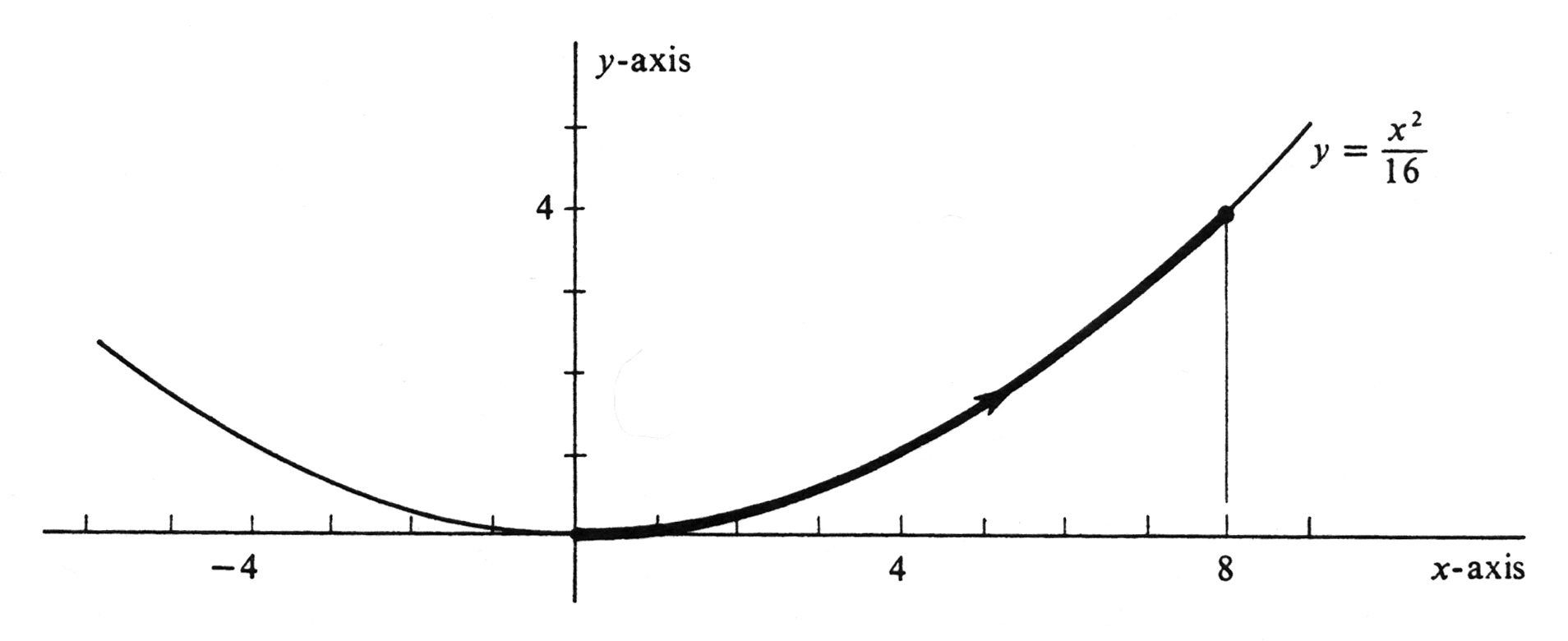
Example A steel ball is rolling on a plane during an interval from [math]t = 0[/math] to [math]t = 4[/math] seconds. It has an [math]x[/math]-coordinate of velocity which is constant and equal to 2 feet per second. Its [math]y[/math]-coordinate of velocity is [math]\frac{1}{2}t[/math] feet per second, for every [math]t[/math] in the interval. (a) Write a definite integral equal to the distance (in feet) which the ball rolls during the interval from [math]t = 0[/math] to [math]t = 4[/math] seconds. (b) Identify and draw the curve on which the ball rolls. The coordinates of the velocity vector [math]\mbox'''{v'''}(t)[/math] are [math]x'(t)[/math] and [math]y'(t)[/math]. Hence
Hence the distance the ball rolls is half this quantity, approximately 9.2 feet.
A parametrization which defines the position of the ball may be found by integrating the functions [math]x'[/math] and [math]y'[/math]. From equations (6), we get
Nothing in the statement of the problem specifies the position of the ball at [math]t = 0[/math], so, for simplicity, we shall choose it to be the origin. This choice is equivalent to setting [math]c_1 = c_2 = 0[/math]. It follows that the parametrized curve in which the ball rolls is the set of all points [math](x, y)[/math] such that
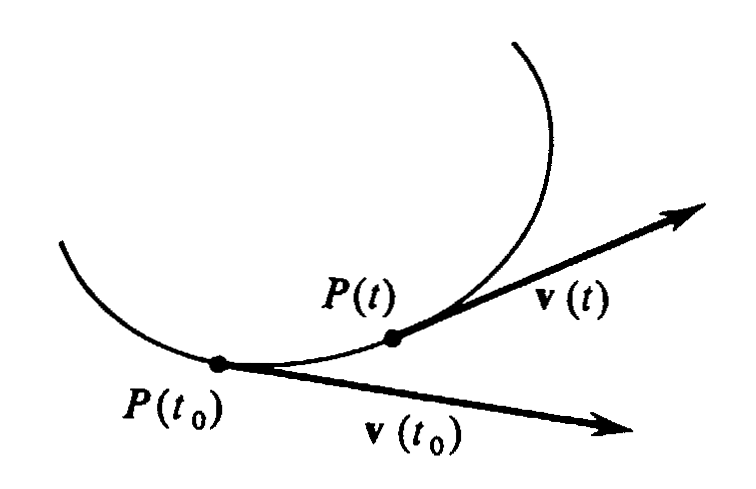
We next consider what is meant by the acceleration of a moving particle. The intuitive idea is that acceleration is the rate of change of the velocity vector. To be more precise: Let the position of the particle during an interval of time [math]I[/math] be given by a differentiable parametrization [math]P: I \rightarrow R[/math], and let [math]t_0[/math] be in [math]I[/math]. If [math]t[/math] is a number in [math]I[/math] distinct from [math]t_0[/math], then the velocity vectors [math]\mbox'''{v'''}(t_0)[/math] and [math]\mbox'''{v'''}(t)[/math] are tangent vectors with initial points [math]P(t_0)[/math] and [math]P(t)[/math], respectively, as illustrated in Figure 19. In defining the acceleration at [math]t_0[/math], we should like to form the scalar product of [math]\frac{1}{t - t_0}[/math] and the difference [math]\mbox'''{v'''}(t) - \mbox'''{v'''}(t_0)[/math], and to take the limit of this product as [math]t[/math] approaches [math]t_0[/math]. The difficulty is that, since the points [math]P(t)[/math] and [math]P(t_0)[/math] are usually distinct, the difference [math]\mbox'''{v'''}(t) - \mbox'''{v'''}(t_0)[/math] is generally not defined. (Recall that two vectors can be added or subtracted if and only if they have the same initial point.) It is for this reason that, before defining acceleration, we introduce the notion of parallel translation of vectors in [math]R^2[/math].
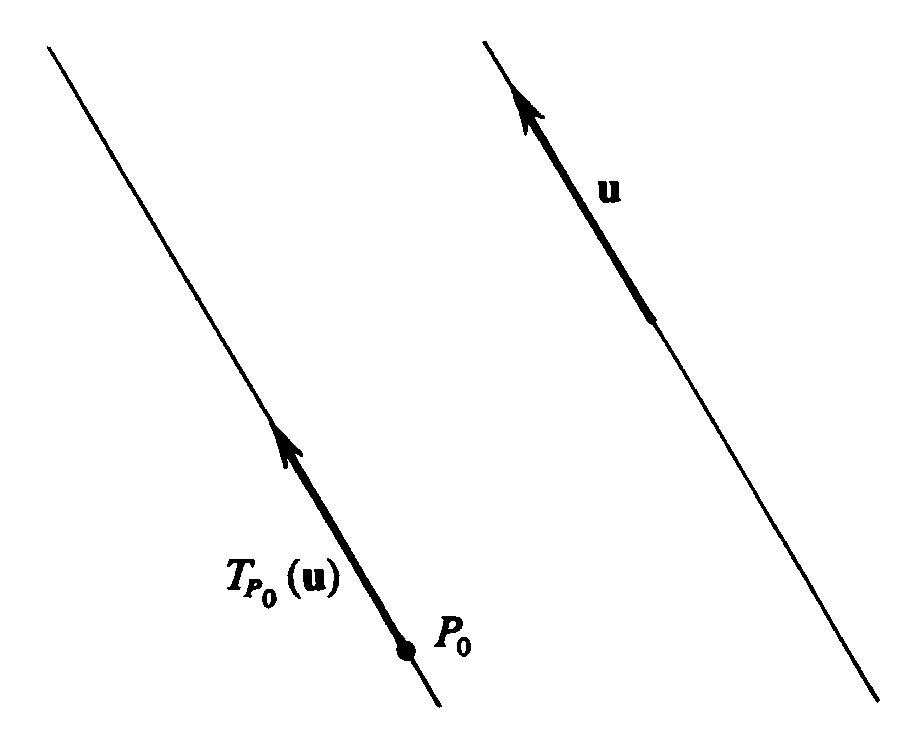
Let [math]P_0[/math] be an arbitrary point in [math]R^2[/math]. We shall define a function [math]T_{P_0}[/math] whose domain is the set [math]\mathcal{V}[/math] of all vectors in [math]R^2[/math] and whose range is the vector space [math]\mathcal{V}_{P_0}[/math] of all vectors with initial point [math]P_0[/math]. The definition is as follows: For every vector [math]\mbox'''{u'''}[/math] in [math]\mathcal{V}[/math], the value [math]T_{P_0}(\mbox'''{u'''})[/math] is the vector with the same coordinates as [math]\mbox'''{u'''}[/math], but with initial point [math]P_0[/math]. Thus
We can now define the acceleration of a moving particle. As before, let the position be defined by the differentiable parametrization [math]P: I \rightarrow R^2[/math]. We consider [math]t_0[/math] in [math]I[/math], and set [math]P(t_0) = P_0[/math]. Then the acceleration of the particle at [math]t_0[/math] is the vector [math]\mbox'''{a'''}(t_0)[/math] defined by
We can derive a simple formula for acceleration in terms of the coordinate functions of [math]P[/math]. Let [math]P(t) = (x(t), y(t))[/math], as usual. Then
If [math]P(t) = (x(t), y(t))[/math], then the acceleration vector [math]\mbox'''{a'''}(t_0)[/math] exists if and only if the second derivatives [math]X,'(t_0)[/math] and [math]y',(t_0)[/math] exist. lf they do exist, then
Example
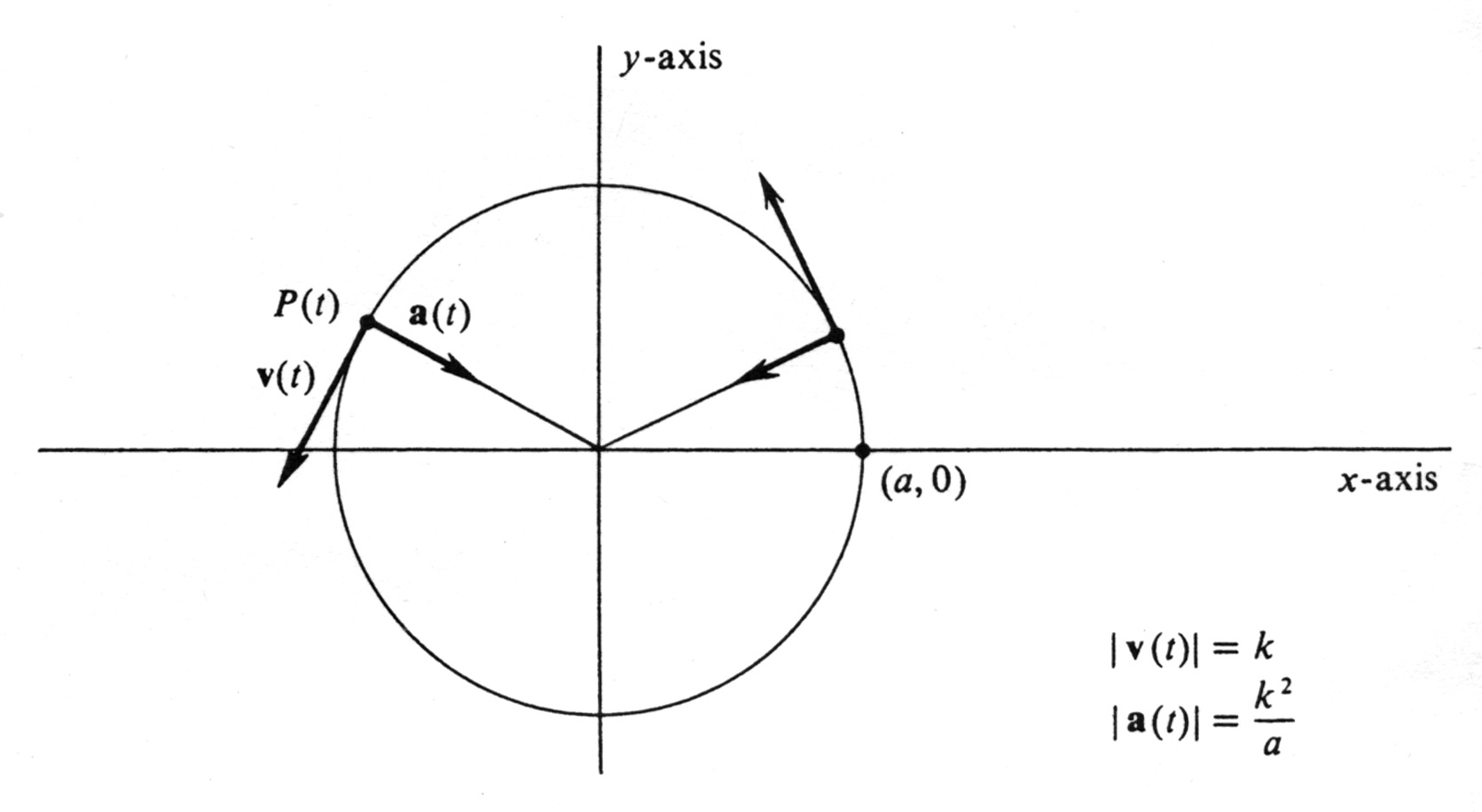
A particle is moving with constant speed [math]k[/math] in a fixed circle of radius [math]a[/math]. Show that, at any time [math]t[/math] during the interval of motion, the acceleration vector [math]\mbox'''{a'''}(t)[/math] has constant length equal to [math]\frac{k^2}{a}[/math] and always points directly toward the center of the circle (see Figure 21).
We shall take the center of the circle to be the origin in the [math]xy[/math]-plane. The position of the particle can then be defined by a parametrization [math]P(t) = (x(t), y(t)) = (x, y)[/math] for which
Hence
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.