excans:62e7609d87: Difference between revisions
From Stochiki
(Created page with "'''Solution: C''' Define X and Y to be loss amounts covered by the policies having deductibles of 1 and 2, respectively. The shaded portion of the graph below shows the regio...") |
mNo edit summary |
||
| Line 2: | Line 2: | ||
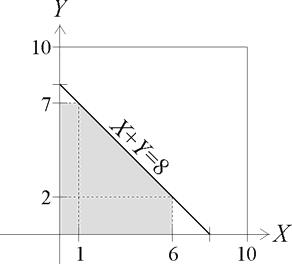
Define X and Y to be loss amounts covered by the policies having deductibles of 1 and 2, respectively. The shaded portion of the graph below shows the region over which the total benefit paid to the family does not exceed 5: | Define X and Y to be loss amounts covered by the policies having deductibles of 1 and 2, respectively. The shaded portion of the graph below shows the region over which the total benefit paid to the family does not exceed 5: | ||
<div class="d-flex justify-content-center"> | |||
[[File:examp202393.jpg | 300px ]] | |||
</div> | |||
We can also infer from the graph that the uniform random variables <math>X</math> and <math>Y</math> have joint density function | We can also infer from the graph that the uniform random variables <math>X</math> and <math>Y</math> have joint density function | ||
Latest revision as of 00:02, 29 June 2023
Solution: C
Define X and Y to be loss amounts covered by the policies having deductibles of 1 and 2, respectively. The shaded portion of the graph below shows the region over which the total benefit paid to the family does not exceed 5:
We can also infer from the graph that the uniform random variables [math]X[/math] and [math]Y[/math] have joint density function
[[math]]
f(x,y) = \frac{1}{100}, \, 0 \lt x \lt 10, \, 0 \lt y \lt 10
[[/math]]
We could integrate f over the shaded region in order to determine the desired probability. However, since X and Y are uniform random variables, it is simpler to determine the portion of the 10 x 10 square that is shaded in the graph above. That is, [math]\operatorname{P} ( \textrm{Total Benefit Paid Does not Exceed 5})[/math]
[[math]]
\begin{align*}
&= \operatorname{P}(0 \lt X \lt 6, 0 \lt Y \lt 2) + \operatorname{P}(0 \lt X \lt1, 2 \lt Y \lt 7) + \operatorname{P}( 1 \lt X \lt 6, 2 \lt Y \lt 8-X ) \\
&= \frac{(6)(2)}{100} + \frac{(1)(5)}{100} + \frac{(1/2)(5)(5)}{100} \\
&= \frac{12}{100} + \frac{5}{100} + \frac{12.5}{100} \\
&= 0.295.
\end{align*}
[[/math]]