guide:18616d319a: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 62: | Line 62: | ||
The interest rate is the change, expressed as a percentage, in the amount of money during one compounding period. A compounding period is the length of time that must transpire before interest is credited, or added to the total.<ref name=Broverman/> For example, interest that is compounded annually is credited once a year, and the compounding period is one year. Interest that is compounded quarterly is credited four times a year, and the compounding period is three months. A compounding period can be any length of time, but some common periods are annually, semiannually, quarterly, monthly, daily, and even continuously. | The interest rate is the change, expressed as a percentage, in the amount of money during one compounding period. A compounding period is the length of time that must transpire before interest is credited, or added to the total.<ref name=Broverman/> For example, interest that is compounded annually is credited once a year, and the compounding period is one year. Interest that is compounded quarterly is credited four times a year, and the compounding period is three months. A compounding period can be any length of time, but some common periods are annually, semiannually, quarterly, monthly, daily, and even continuously. | ||
There are several types and terms associated with | There are several types and terms associated with interest rates: | ||
{| class="table" | |||
|- | |||
! Interest rate !! Description | |||
|- | |||
|[[#Compound_Interest | Compound interest]] || interest that increases exponentially over subsequent periods | |||
|- | |||
|[[#Simple_Interest|Simple interest]] || additive interest that does not increase | |||
|- | |||
|[[#Effective_Interest_Rate|Effective interest rate]] || the effective equivalent compared to multiple compound interest periods | |||
|- | |||
|[[wikipedia:Nominal_Interest_Rate|Nominal annual interest]] || the simple annual interest rate of multiple interest periods | |||
|- | |||
|[[wikipedia:Discount window|Discount rate]] || an inverse interest rate when performing calculations in reverse | |||
|- | |||
|[[#Continuous_compounding | Continuously compounded interest]] || [[wikipedia:mathematical limit|mathematical limit]] of an interest rate with a period of zero time | |||
|- | |||
|[[wikipedia:Real interest rate|Real interest rate]] || which accounts for inflation | |||
|} | |||
==Compound Interest== | ==Compound Interest== | ||
Revision as of 11:26, 23 November 2023
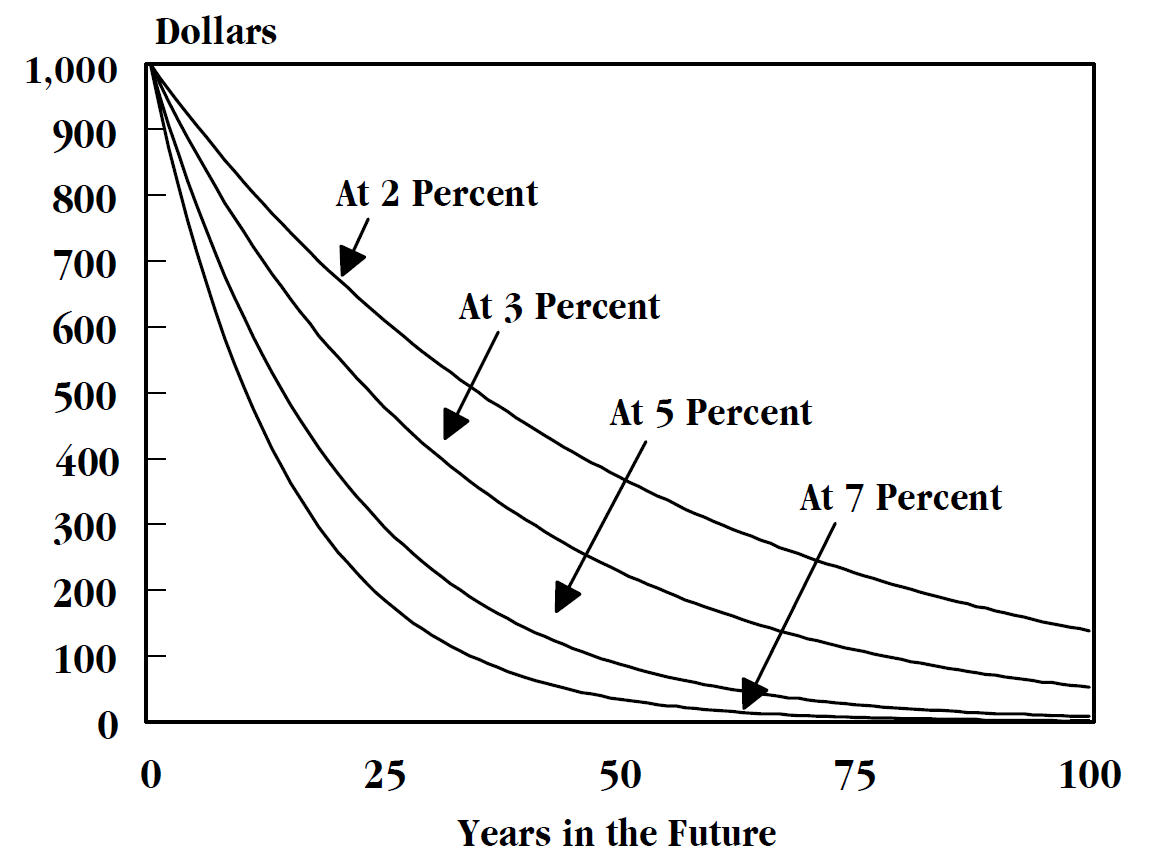
The time value of money is the widely accepted conjecture that there is greater benefit to receiving a sum of money now rather than an identical sum later. It may be seen as an implication of the later-developed concept of time preference.
The time value of money is among the factors considered when weighing the opportunity costs of spending rather than saving or investing money. As such, it is among the reasons why interest is paid or earned: interest, whether it is on a bank deposit or debt, compensates the depositor or lender for the loss of their use of their money. Investors are willing to forgo spending their money now only if they expect a favorable net n on their investment in the future, such that the increased value to be available later is sufficiently high to offset both the preference to spending money now and inflation (if present); see required rate of return.
Calculations
Time value of money problems involve the net value of cash flows at different points in time.
In a typical case, the variables might be: a balance (the real or nominal value of a debt or a financial asset in terms of monetary units), a periodic rate of interest, the number of periods, and a series of cash flows. (In the case of a debt, cash flows are payments against principal and interest; in the case of a financial asset, these are contributions to or withdrawals from the balance.) More generally, the cash flows may not be periodic but may be specified individually. Any of these variables may be the independent variable (the sought-for answer) in a given problem. For example, one may know that: the interest is 0.5% per period (per month, say); the number of periods is 60 (months); the initial balance (of the debt, in this case) is 25,000 units; and the final balance is 0 units. The unknown variable may be the monthly payment that the borrower must pay.
For example, £100 invested for one year, earning 5% interest, will be worth £105 after one year; therefore, £100 paid now and £105 paid exactly one year later both have the same value to a recipient who expects 5% interest assuming that inflation would be zero percent. That is, £100 invested for one year at 5% interest has a future value of £105 under the assumption that inflation would be zero percent.[1]
This principle allows for the valuation of a likely stream of income in the future, in such a way that annual incomes are g and then added together, thus providing a lump-sum "present value" of the entire income stream; all of the standard calculations for time value of money derive from the most basic algebraic expression for the present value of a future sum, "discounted" to the present by an amount equal to the time value of money. For example, the future value sum [math]FV[/math] to be received in one year is discounted at the rate of interest [math]r[/math] to give the present value sum [math]PV[/math]:
Some standard calculations based on the time value of money are:
- Present value: The current worth of a future sum of money or stream of cash flows, given a specified rate of return. Future cash flows are "discounted" at the discount rate; the higher the discount rate, the lower the present value of the future cash flows. Determining the appropriate discount rate is the key to valuing future cash flows properly, whether they be earnings or obligations.[2]
- Present value of an annuity: An annuity is a series of equal payments or receipts that occur at evenly spaced intervals. Leases and rental payments are examples. The payments or receipts occur at the end of each period for an ordinary annuity while they occur at the beginning of each period for an annuity due.[3]
- Present value of a perpetuity is an infinite and constant stream of identical cash flows.[4]
- Future value: The value of an asset or cash at a specified date in the future, based on the value of that asset in the present.[5]
- Future value of an annuity (FVA): The future value of a stream of payments (annuity), assuming the payments are invested at a given rate of interest.
There are several basic equations that represent the equalities listed above. The solutions may be found using (in most cases) the formulas, a financial calculator or a spreadsheet. The formulas are programmed into most financial calculators and several spreadsheet functions (such as PV, FV, RATE, NPER, and PMT).[6]
For any of the equations below, the formula may also be rearranged to determine one of the other unknowns. In the case of the standard annuity formula, there is no closed-form algebraic solution for the interest rate (although financial calculators and spreadsheet programs can readily determine solutions through rapid trial and error algorithms).
These equations are frequently combined for particular uses. For example, bonds can be readily priced using these equations. A typical coupon bond is composed of two types of payments: a stream of coupon payments similar to an annuity, and a lump-sum return of capital at the end of the bond's maturity—that is, a future payment. The two formulas can be combined to determine the present value of the bond.
An important note is that the interest rate i is the interest rate for the relevant period. For an annuity that makes one payment per year, i will be the annual interest rate. For an income or payment stream with a different payment schedule, the interest rate must be converted into the relevant periodic interest rate. For example, a monthly rate for a mortgage with monthly payments requires that the interest rate be divided by 12 (see the example below). See compound interest for details on converting between different periodic interest rates.
The rate of return in the calculations can be either the variable solved for, or a predefined variable that measures a discount rate, interest, inflation, rate of return, cost of equity, cost of debt or any number of other analogous concepts. The choice of the appropriate rate is critical to the exercise, and the use of an incorrect discount rate will make the results meaningless.
For calculations involving annuities, it must be decided whether the payments are made at the end of each period (known as an ordinary annuity), or at the beginning of each period (known as an annuity due). When using a financial calculator or a spreadsheet, it can usually be set for either calculation. The following formulas are for an ordinary annuity. For the answer for the present value of an annuity due, the PV of an ordinary annuity can be multiplied by (1 + i).
Present Value
In economics and finance, present value (PV), also known as present discounted value, is the value of an expected income stream determined as of the date of valuation. The present value is usually less than the future value because money has interest-earning potential, a characteristic referred to as the time value of money, except during times of negative interest rates, when the present value will be equal or more than the future value.[7]
Time value can be described with the simplified phrase, "A dollar today is worth more than a dollar tomorrow". Here, 'worth more' means that its value is greater than tomorrow. A dollar today is worth more than a dollar tomorrow because the dollar can be invested and earn a day's worth of interest, making the total accumulate to a value more than a dollar by tomorrow. Interest can be compared to g.[8] Just as rent is paid to a landlord by a tenant without the ownership of the asset being transferred, interest is paid to a lender by a borrower who gains access to the money for a time before paying it back. By letting the borrower have access to the money, the lender has sacrificed the exchange value of this money, and is compensated for it in the form of interest. The initial amount of borrowed funds (the present value) is less than the total amount of money paid to the lender.
Present value calculations, and similarly future value calculations, are used to value loans, mortgages, annuities, sinking funds, perpetuities, bonds, and more. These calculations are used to make comparisons between cash flows that don’t occur at simultaneous times,[7] since time and dates must be consistent in order to make comparisons between values. When deciding between projects in which to invest, the choice can be made by comparing respective present values of such projects by means of discounting the expected income streams at the corresponding project interest rate, or rate of return. The project with the highest present value, i.e. that is most valuable today, should be chosen.
Background
If offered a choice between $100 today or $100 in one year, and there is a positive real interest rate throughout the year, a rational person will choose $100 today. This is described by economists as time preference. Time preference can be measured by auctioning off a risk free security—like a US Treasury bill. If a $100 note with a zero coupon, payable in one year, sells for $80 now, then $80 is the present value of the note that will be worth $100 a year from now. This is because money can be put in a bank account or any other (safe) investment that will return interest in the future.
An investor who has some money has two options: to spend it right now or to save it. But the financial compensation for saving it (and not spending it) is that the money value will accrue through the compound interest that he or she will receive from a borrower (the bank account in which he has the money deposited).
Therefore, to evaluate the real value of an amount of money today after a given period of time, economic agents compound the amount of money at a given (interest) rate. Most e calculations use the wikipedia:risk-free interest rate which corresponds to the minimum guaranteed rate provided by a bank's saving account for example, assuming no risk of default by the bank to return the money to the account holder on time. To compare the change in purchasing power, the real interest rate (nominal interest rate minus inflation rate) should be used.
The operation of evaluating a present value into the future value is called a capitalization (how much will $100 today be worth in 5 years?). The reverse operation—evaluating the present value of a future amount of money—is called a discounting (how much will $100 received in 5 years—at a lottery for example—be worth today?).
It follows that if one has to choose between receiving $100 today and $100 in one year, the rational decision is to choose the $100 today. If the money is to be received in one year and assuming the savings account interest rate is 5%, the person has to be offered at least $105 in one year so that the two options are equivalent (either receiving $100 today or receiving $105 in one year). This is because if $100 is deposited in a savings account, the value will be $105 after one year, again assuming no risk of losing the initial amount through bank default.
Interest rates
Interest is the additional amount of money gained between the beginning and the end of a time period. Interest represents the time value of money, and can be thought of as rent that is required of a borrower in order to use money from a lender.[8][9] For example, when an individual takes out a bank loan, the individual is charged interest. Alternatively, when an individual deposits money into a bank, the money earns interest. In this case, the bank is the borrower of the funds and is responsible for crediting interest to the account holder. Similarly, when an individual invests in a company (through corporate bonds, or through stock), the company is borrowing funds, and must pay interest to the individual (in the form of coupon payments, dividends, or stock price appreciation).[7] The interest rate is the change, expressed as a percentage, in the amount of money during one compounding period. A compounding period is the length of time that must transpire before interest is credited, or added to the total.[8] For example, interest that is compounded annually is credited once a year, and the compounding period is one year. Interest that is compounded quarterly is credited four times a year, and the compounding period is three months. A compounding period can be any length of time, but some common periods are annually, semiannually, quarterly, monthly, daily, and even continuously.
There are several types and terms associated with interest rates:
| Interest rate | Description |
|---|---|
| Compound interest | interest that increases exponentially over subsequent periods |
| Simple interest | additive interest that does not increase |
| Effective interest rate | the effective equivalent compared to multiple compound interest periods |
| Nominal annual interest | the simple annual interest rate of multiple interest periods |
| Discount rate | an inverse interest rate when performing calculations in reverse |
| Continuously compounded interest | mathematical limit of an interest rate with a period of zero time |
| Real interest rate | which accounts for inflation |
Compound Interest
Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on principal plus interest. It is the result of reinvesting interest, or adding it to the loaned capital rather than paying it out, or requiring payment from borrower, so that interest in the next period is then earned on the principal sum plus previously accumulated interest. Compound interest is standard in finance and economics.
Compound interest is contrasted with simple interest, where previously accumulated interest is not added to the principal amount of the current period, so there is no compounding. The simple annual interest rate is the interest amount per period, multiplied by the number of periods per year. The simple annual interest rate is also known as the nominal interest rate (not to be confused with the interest rate not adjusted for inflation, which goes by the same name).
Compounding frequency
The compounding frequency is the number of times per year (or rarely, another unit of time) the accumulated interest is paid out, or capitalized (credited to the account), on a regular basis. The frequency could be yearly, half-yearly, quarterly, monthly, weekly, daily, or g (or not at all, until maturity).
For example, monthly capitalization with interest expressed as an annual rate means that the compounding frequency is 12, with time periods measured in months.
The effect of compounding depends on:
- The nominal interest rate which is applied and
- The frequency interest is compounded.
Annual equivalent rate
The nominal rate cannot be directly compared between loans with different compounding frequencies. Both the nominal interest rate and the compounding frequency are required in order to compare interest-bearing financial instruments.
To help consumers compare retail financial products more fairly and easily, many countries require financial institutions to disclose the annual compound interest rate on deposits or advances on a comparable basis. The interest rate on an annual equivalent basis may be referred to variously in different markets as effective annual percentage rate (EAPR), annual equivalent rate (AER), effective interest rate, effective annual rate, annual percentage yield and other terms. The effective annual rate is the total accumulated interest that would be payable up to the end of one year, divided by the principal sum.
There are usually two aspects to the rules defining these rates:
- The rate is the annualised compound interest rate, and
- There may be charges other than interest. The effect of fees or taxes which the customer is charged, and which are directly related to the product, may be included. Exactly which fees and taxes are included or excluded varies by country, may or may not be comparable between different jurisdictions, because the use of such terms may be inconsistent, and vary according to local practice.
Examples
- 1,000 Brazilian real (BRL) is deposited into a Brazilian savings account paying 20% per annum, compounded annually. At the end of one year, 1,000 × 20% = 200 BRL interest is credited to the account. The account then earns 1,200 × 20% = 240 BRL in the second year.
- A rate of 1% per month is equivalent to a simple annual interest rate (nominal rate) of 12%, but allowing for the effect of compounding, the annual equivalent compound rate is 12.68% per annum (1.0112 − 1).
- The interest on corporate bonds and government bonds is usually payable twice yearly. The amount of interest paid (every six months) is the disclosed interest rate divided by two and multiplied by the principal. The yearly compounded rate is higher than the disclosed rate.
- Canadian mortgage loans are generally compounded semi-annually with monthly (or more frequent) payments.[10]
- U.S. mortgages use an amortizing loan, not compound interest. With these loans, an amortization schedule is used to determine how to apply payments toward principal and interest. Interest generated on these loans is not added to the principal, but rather is paid off monthly as the payments are applied.
Periodic compounding
The total accumulated value, including the principal sum [math]P[/math] plus compounded interest [math]I[/math], is given by the formula:[11][12]
where:
- A is the final amount
- P is the original principal sum
- r is the nominal annual interest rate
- n is the compounding frequency
- t is the overall length of time the interest is applied (expressed using the same time units as r, usually years).
The total compound interest generated is the final value minus the initial principal:[13]
Example 1
Suppose a principal amount of $1,500 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly.
Then the balance after 6 years is found by using the formula above, with P = 1500, r = 0.043, n = 4, and t = 6:
So the amount A after 6 years is approximately $1,938.84.
Subtracting the original principal from this amount gives the amount of interest received:
Example 2
Suppose the same amount of $1,500 is compounded biennially (every 2 years). (This is very unusual in practice.) Then the balance after 6 years is found by using the formula above, with P = 1500, r = 0.043 (4.3%), n = 1/2 (the interest is compounded every two years), and t = 6 :
So, the balance after 6 years is approximately $1,921.24.
The amount of interest received can be calculated by subtracting the principal from this amount.
The interest is less compared with the previous case, as a result of the lower compounding frequency.
Accumulation function
Since the principal P is simply a coefficient, it is often dropped for simplicity, and the resulting accumulation function is used instead. The accumulation function shows what $1 grows to after any length of time.
Accumulation functions for simple and compound interest are
If [math]n t = 1[/math], then these two functions are the same.
Continuous compounding
As n, the number of compounding periods per year, increases without limit, the case is known as continuous compounding, in which case the effective annual rate approaches an upper limit of er − 1, where e is a mathematical constant that is the base of the natural logarithm.
Continuous compounding can be thought of as making the compounding period infinitesimally small, achieved by taking the limit as n goes to infinity. See definitions of the exponential function for the mathematical proof of this limit. The amount after t periods of continuous compounding can be expressed in terms of the initial amount P0 as
Force of interest
As the number of compounding periods [math]n[/math] tends to infinity in continuous compounding, the continuous compound interest rate is referred to as the force of interest [math]\delta[/math].
In mathematics, the accumulation functions are often expressed in terms of e, the base of the natural logarithm. This facilitates the use of calculus to manipulate interest formulae.
For any continuously differentiable accumulation function a(t), the force of interest, or more generally the logarithmic or continuously compounded return is a function of time defined as follows:
This is the logarithmic derivative of the accumulation function.
Conversely:
(since [math]a(0) = 1[/math]; this can be viewed as a particular case of a product integral.)
When the above formula is written in differential equation format, then the force of interest is simply the coefficient of amount of change:
For compound interest with a constant annual interest rate r, the force of interest is a constant, and the accumulation function of compounding interest in terms of force of interest is a simple power of e:
or
The force of interest is less than the annual effective interest rate, but more than the annual effective discount rate. It is the reciprocal of the e-folding time. See also notation of interest rates.
A way of modeling the force of inflation is with Stoodley's formula: [math]\delta_t = p + {s \over {1+rse^{st}}}[/math] where p, r and s are estimated.
Compounding basis
To convert an interest rate from one compounding basis to another compounding basis, so that
use
where r1 is the interest rate with compounding frequency n1, and r2 is the interest rate with compounding frequency n2.
When interest is continuously compounded, use
where [math]\delta[/math] is the interest rate on a continuous compounding basis, and r is the stated interest rate with a compounding frequency n.
Simple Interest
Simple interest is calculated only on the principal amount, or on that portion of the principal amount that remains. It excludes the effect of t. Simple interest can be applied over a time period other than a year, for example, every month.
Simple interest is calculated according to the following formula:
where
r is the simple annual interest rate, B is the initial balance, m is the number of time periods elapsed and n is the frequency of applying interest.
For example, imagine that a credit card holder has an outstanding balance of $2500 and that the simple annual interest rate is 12.99% per annum, applied monthly, so the frequency of applying interest is 12 per year. Over one month,
interest is due (rounded to the nearest cent).
Simple interest applied over 3 months would be
If the card holder pays off only interest at the end of each of the 3 months, the total amount of interest paid would be
which is the simple interest applied over 3 months, as calculated above.
Effective Interest Rate
The effective interest rate (EIR), effective annual interest rate, annual equivalent rate (AER) or simply effective rate is the percentage of e on a loan or financial product if compound interest accumulates over a year during which no payments are made. It is the compound interest payable annually in arrears, based on the nominal interest rate. It is used to compare the interest rates between loans with different compounding periods, such as weekly, monthly, half-yearly or yearly.
Depending on the jurisdictional definition, the effective interest rate may be higher than the annual percentage rate (APR), since the APR method does not take compounding into account.[14] By contrast, the EIR annualizes the periodic rate with compounding. EIR is the standard in the European Union and many other countries, while APR is often used in the United States.
The EIR is more relevant for borrowers who are short of income, because it computes the effects of compounding assuming no periodic payment of interest, so that future interest accrues on both the principal and the current interest. However, the APR reflects the annual total interest charge assuming periodic interest is paid as soon as it accrues. For example, if one borrows a principal debt of $1000 at an interest of 2% every month, and makes no monthly payments, the compounded debt at the end of the year is $1000 × (1.02)12 = $1268.24, or $268.24 of interest, making EIR 26.8%. By contrast, if the interest of $1000 × 0.02 = $20 is paid each month, but none of the principal, the annual interest is $20 × 12 = $240, making APR 24%.
The term nominal EIR or nominal APR can refer (subject to regulation) to an annualized rate that does not take into account front-fees and other costs.
Annual percentage yield or effective annual yield is the analogous concept for savings or investments, such as a certificate of deposit. Since a loan by a borrower is an investment for the lender, both terms can apply to the same transaction, depending on the point of view.
Effective annual interest or yield may be calculated or applied differently depending on circumstances, and the definition should be studied carefully. For example, a bank may compute effective yield on a portfolio of loans after subtracting expected losses and adding income from fees, meaning that the interest paid by each borrower may differ substantially from the bank's effective yield.
Calculation
The effective interest rate is calculated as if compounded annually. The effective rate is calculated in the following way, where r is the effective annual rate, i the nominal rate, and n the number of compounding periods per year (for example, 12 for monthly compounding):
For example, a nominal interest rate of 6% compounded monthly is equivalent to an effective interest rate of 6.17%. 6% compounded monthly is credited as 6%/12 = 0.005 every month. After one year, the initial capital is increased by the factor (1 + 0.005)12 ≈ 1.0617. Note that the yield increases with the frequency of compounding.
When the frequency of compounding is increased up to infinity (as for many processes in nature) the calculation simplifies to:
where [math]e\approx 2.72[/math] is Euler's mathematical constant.
| Nominal annual rate |
Frequency of compounding | ||||
|---|---|---|---|---|---|
| Semi-annual | Quarterly | Monthly | Daily | Continuous | |
| 1% | 1.003% | 1.004% | 1.005% | 1.005% | 1.005% |
| 5% | 5.063% | 5.095% | 5.116% | 5.127% | 5.127% |
| 10% | 10.250% | 10.381% | 10.471% | 10.516% | 10.517% |
| 15% | 15.563% | 15.865% | 16.075% | 16.180% | 16.183% |
| 20% | 21.000% | 21.551% | 21.939% | 22.134% | 22.140% |
| 30% | 32.250% | 33.547% | 34.489% | 34.969% | 34.986% |
| 40% | 44.000% | 46.410% | 48.213% | 49.150% | 49.182% |
| 50% | 56.250% | 60.181% | 63.209% | 64.816% | 64.872% |
The effective interest rate is a special case of the internal rate of return.
The annual percentage rate (APR) is calculated in the following way, where i is the interest rate for the period and n is the number of periods.
Nominal Interest Rate
The nominal interest rate or nominal rate of interest is the rate of interest stated on a loan or investment, without any adjustments or fees.
Examples of adjustments or fees
- An adjustment for inflation (in contrast with the real interest rate).
- Compound interest (also referred to as the nominal annual rate).
Nominal versus real interest rate
The concept of real interest rate is useful to account for the impact of inflation. In the case of a loan, it is this real interest that the lender effectively receives. For example, if the lender is receiving 8 percent from a loan and the inflation rate is also 8 percent, then the (effective) real rate of interest is zero: despite the increased nominal amount of currency received, the lender would have no monetary value benefit from such a loan because each unit of currency would be n due to inflation by the same factor as the nominal amount gets increased.
The relationship between the real interest value [math]r[/math], the nominal interest rate value [math]R[/math], and the inflation rate value [math]i[/math] is given by[15]
or
When the inflation rate [math]i[/math] is low, the real interest rate is approximately given by the nominal interest rate minus the inflation rate, i.e.,
In this analysis, the nominal rate is the stated rate, and the real interest rate is the interest after the expected losses due to inflation. Since the future inflation rate can only be estimated, the ex ante and ex post (before and after the fact) real interest rates may be different; the premium paid to actual inflation (higher or lower).
Nominal versus effective interest rate
The nominal interest rate, also known as an e or APR, is the periodic interest rate multiplied by the number of periods per year. For example, a nominal annual interest rate of 12% based on monthly t means a 1% interest rate per month (compounded).[16] A nominal interest rate for compounding periods less than a year is always lower than the equivalent rate with annual compounding (this immediately follows from elementary algebraic manipulations of the formula for compound interest). Note that a nominal rate without the compounding frequency is not fully defined: for any interest rate, the effective interest rate cannot be specified without knowing the compounding frequency and the rate. Although some conventions are used where the compounding frequency is understood, consumers in particular may fail to understand the importance of knowing the effective rate.
Nominal interest rates are not comparable unless their compounding periods are the same; effective interest rates correct for this by "converting" nominal rates into annual compound interest. In many cases, depending on local regulations, interest rates as quoted by lenders and in advertisements are based on nominal, not effective interest rates, and hence may understate the interest rate compared to the equivalent effective annual rate.
Confusingly, in the context of inflation, 'nominal' has a different meaning. A nominal rate can mean a rate before adjusting for inflation, and a real rate is a constant-prices rate. The Fisher equation is used to convert between real and nominal rates. To avoid confusion about the term nominal which has these different meanings, some finance textbooks use the term 'Annualised Percentage Rate' or APR rather than 'nominal rate' when they are discussing the difference between effective rates and APR's.
The term should not be confused with simple interest (as opposed to compound interest) which is not compounded.
The effective interest rate is always calculated as if compounded annually. The effective rate is calculated in the following way, where r is the effective rate, i the nominal rate (as a decimal, e.g. 12% = 0.12), and n the number of compounding periods per year (for example, 12 for monthly compounding):
Examples
Monthly compounding
Example 1: A nominal interest rate of 6% compounded monthly is equivalent to an effective interest rate of 6.17%.
Example 2: 6% annually is credited as 6%/12 = 0.5% every month. After one year, the initial capital is increased by the factor (1+0.005)12 ≈ 1.0617.
Daily compounding
A loan with daily compounding has a substantially higher rate in effective annual terms. For a loan with a 10% nominal annual rate and daily compounding, the effective annual rate is 10.516%. For a loan of $10,000 (paid at the end of the year in a single lump sum), the borrower would pay $51.56 more than one who was charged 10% interest, compounded annually.
Wikipedia References
- Wikipedia contributors. "Time value of money". Wikipedia. Wikipedia. Retrieved 5 November 2023.
- Wikipedia contributors. "Present value". Wikipedia. Wikipedia. Retrieved 5 November 2023.
- Wikipedia contributors. "Compound interest". Wikipedia. Wikipedia. Retrieved 5 November 2023.
- Wikipedia contributors. "Interest". Wikipedia. Wikipedia. Retrieved 5 November 2023.
- Wikipedia contributors. "Effective interest rate". Wikipedia. Wikipedia. Retrieved 5 November 2023.
References
- Carther, Shauna (3 December 2003). "Understanding the Time Value of Money".
- Staff, Investopedia (25 November 2003). "Present Value - PV".
- "Present Value of an Annuity".
- Staff, Investopedia (24 November 2003). "Perpetuity".
- Staff, Investopedia (23 November 2003). "Future Value - FV".
- Hovey, M. (2005). Spreadsheet Modelling for Finance. Frenchs Forest, N.S.W.: Pearson Education Australia.
- 7.0 7.1 7.2 Moyer, Charles; William Kretlow; James McGuigan (2011). Contemporary Financial Management (12 ed.). Winsted: South-Western Publishing Co. pp. 147–498. ISBN 9780538479172.
- 8.0 8.1 8.2 Broverman, Samuel (2010). Mathematics of Investment and Credit. Winsted: ACTEX Publishers. pp. 4–229. ISBN 9781566987677.
- Ross, Stephen; Randolph W. Westerfield; Bradford D. Jordan (2010). Fundamentals of Corporate Finance (9 ed.). New York: McGraw-Hill. pp. 145–287. ISBN 9780077246129.
- http://laws.justice.gc.ca/en/showdoc/cs/I-15/bo-ga:s_6//en#anchorbo-ga:s_6Template:Dead link Interest Act (Canada), Department of Justice. The Interest Act specifies that interest is not recoverable unless the mortgage loan contains a statement showing the rate of interest chargeable, "calculated yearly or half-yearly, not in advance." In practice, banks use the half-yearly rate.
- "Compound Interest Formula". qrc.depaul.edu. Retrieved 2018-12-05.
- Investopedia Staff (2003-11-19). "Continuous Compounding". Investopedia (in English). Retrieved 2018-12-05.
- "Compound Interest Formula - Explained". www.thecalculatorsite.com. Retrieved 2018-12-05.
- "Microfinance TRAPS - The Microfinance Transparent Pricing Supervision Handbook" (PDF). MFTransparency. June 2013.
- Richard A. Brealey and Steward C. Meyer. Principles of Corporate Finance, Sixth Edition. Irwin McGraw-Hill, London, 2000. p. 49.
- Charles Moyer, James R. McGuigan, William J. Kretlow. Contemporary Financial Management, Tenth Edition. Thomson-South-Western, Mason, Ohio, 2006 pg. 163.