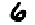guide:090050c501

[math] \newcommand{\DS}{\displaystyle} \newcommand{\intbeta}{\lfloor \beta \rfloor} \newcommand{\cA}{\mathcal{A}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cD}{\mathcal{D}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cG}{\mathcal{G}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cO}{\mathcal{O}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cQ}{\mathcal{Q}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cU}{\mathcal{U}} \newcommand{\cV}{\mathcal{V}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cZ}{\mathcal{Z}} \newcommand{\sg}{\mathsf{subG}} \newcommand{\subE}{\mathsf{subE}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bO}{\mathbf{O}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\bflambda}{\boldsymbol{\lambda}} \newcommand{\bftheta}{\boldsymbol{\theta}} \newcommand{\bfg}{\boldsymbol{g}} \newcommand{\bfy}{\boldsymbol{y}} \def\thetaphat{\hat{\bftheta}_\bp} \def\bflam{\boldsymbol{\lambda}} \def\Lam{\Lambda} \def\lam{\lambda} \def\bfpi{\boldsymbol{\pi}} \def\bfz{\boldsymbol{z}} \def\bfw{\boldsymbol{w}} \def\bfeta{\boldsymbol{\eta}} \newcommand{\R}{\mathrm{ I}\kern-0.18em\mathrm{ R}} \newcommand{\h}{\mathrm{ I}\kern-0.18em\mathrm{ H}} \newcommand{\K}{\mathrm{ I}\kern-0.18em\mathrm{ K}} \newcommand{\p}{\mathrm{ I}\kern-0.18em\mathrm{ P}} \newcommand{\E}{\mathrm{ I}\kern-0.18em\mathrm{ E}} %\newcommand{\Z}{\mathrm{ Z}\kern-0.26em\mathrm{ Z}} \newcommand{\1}{\mathrm{ 1}\kern-0.24em\mathrm{ I}} \newcommand{\N}{\mathrm{ I}\kern-0.18em\mathrm{ N}} \newcommand{\field}[1]{\mathbb{#1}} \newcommand{\q}{\field{Q}} \newcommand{\Z}{\field{Z}} \newcommand{\X}{\field{X}} \newcommand{\Y}{\field{Y}} \newcommand{\bbS}{\field{S}} \newcommand{\n}{\mathcal{N}} \newcommand{\x}{\mathcal{X}} \newcommand{\pp}{{\sf p}} \newcommand{\hh}{{\sf h}} \newcommand{\ff}{{\sf f}} \newcommand{\Bern}{\mathsf{Ber}} \newcommand{\Bin}{\mathsf{Bin}} \newcommand{\Lap}{\mathsf{Lap}} \newcommand{\tr}{\mathsf{Tr}} \newcommand{\phin}{\varphi_n} \newcommand{\phinb}{\overline \varphi_n(t)} \newcommand{\pn}{\p_{\kern-0.25em n}} \newcommand{\pnm}{\p_{\kern-0.25em n,m}} \newcommand{\psubm}{\p_{\kern-0.25em m}} \newcommand{\psubp}{\p_{\kern-0.25em p}} \newcommand{\cfi}{\cF_{\kern-0.25em \infty}} \newcommand{\e}{\mathrm{e}} \newcommand{\ic}{\mathrm{i}} \newcommand{\Leb}{\mathrm{Leb}_d} \newcommand{\Var}{\mathrm{Var}} \newcommand{\ddelta}{d_{\symdiffsmall}} \newcommand{\dsubh}{d_H} \newcommand{\indep}{\perp\kern-0.95em{\perp}} \newcommand{\supp}{\mathop{\mathrm{supp}}} \newcommand{\rank}{\mathop{\mathrm{rank}}} \newcommand{\vol}{\mathop{\mathrm{vol}}} \newcommand{\conv}{\mathop{\mathrm{conv}}} \newcommand{\card}{\mathop{\mathrm{card}}} \newcommand{\argmin}{\mathop{\mathrm{argmin}}} \newcommand{\argmax}{\mathop{\mathrm{argmax}}} \newcommand{\ud}{\mathrm{d}} \newcommand{\var}{\mathrm{var}} \newcommand{\re}{\mathrm{Re}} \newcommand{\MSE}{\mathsf{MSE}} \newcommand{\im}{\mathrm{Im}} \newcommand{\epr}{\hfill\hbox{\hskip 4pt\vrule width 5pt height 6pt depth 1.5pt}\vspace{0.5cm}\par} \newcommand{\bi}[1]{^{(#1)}} \newcommand{\eps}{\varepsilon} \newcommand{\Deq}{\stackrel{\mathcal{D}}{=}} \newcommand{\ubar}{\underbar} \newcommand{\Kbeta}{K_{\hspace{-0.3mm} \beta}} \newcommand{\crzero}[1]{\overset{r_0}{\underset{#1}{\longleftrightarrow}}} \newcommand{\hint}[1]{\texttt{[Hint:#1]}} \newcommand{\vp}{\vspace{.25cm}} \newcommand{\vm}{\vspace{.5cm}} \newcommand{\vg}{\vspace{1cm}} \newcommand{\vgneg}{\vspace{-1cm}} \newcommand{\vneg}{\vspace{-.5cm}} \newcommand{\vpneg}{\vspace{-.25cm}} \newcommand{\tp}{\ptsize{10}} \newcommand{\douzp}{\ptsize{12}} \newcommand{\np}{\ptsize{9}} \newcommand{\hp}{\ptsize{8}} \newcommand{\red}{\color{red}} \newcommand{\ndpr}[1]{{\textsf{\red[#1]}}} \newcommand\iid{i.i.d\@ifnextchar.{}{.\@\xspace} } \newcommand\MoveEqLeft[1][2]{\kern #1em & \kern -#1em} \newcommand{\leadeq}[2][4]{\MoveEqLeft[#1] #2 \nonumber} \newcommand{\leadeqnum}[2][4]{\MoveEqLeft[#1] #2} \newcommand\independent{\protect\mathpalette{\protect\independenT}{\perp}} \def\independenT#1#2{\mathrel{\rlap{$#1#2$}\mkern2mu{#1#2}}} \newcommand{\MIT}[1]{{\color{MITred} #1}} \newcommand{\dHyp}{\{-1,1\}^d} \newcommand{\thetahard}{\hat \theta^{hrd}} \newcommand{\thetasoft}{\hat \theta^{sft}} \newcommand{\thetabic}{\hat \theta^{bic}} \newcommand{\thetalasso}{\hat \theta^{\cL}} \newcommand{\thetaslope}{\hat \theta^{\cS}} \newcommand{\thetahard}{\hat \theta^{hrd}} \newcommand{\thetasoft}{\hat \theta^{sft}} \newcommand{\thetabic}{\hat \theta^{bic}} \newcommand{\thetalasso}{\hat \theta^{\cL}} \newcommand{\thetaslope}{\hat \theta^{\cS}} \newcommand{\thetals}{\hat \theta^{ls}} \newcommand{\thetalsm}{\tilde \theta^{ls_X}} \newcommand{\thetaridge}{\hat\theta^{\mathrm{ridge}}_\tau} \newcommand{\thetalsK}{\hat \theta^{ls}_K} \newcommand{\muls}{\hat \mu^{ls}} [/math]

\label{chap:GSM}

\newcommand{\thetahard}{\hat \theta^{\textsc{hrd}}} \newcommand{\thetasoft}{\hat \theta^{\textsc{sft}}} \newcommand{\thetabic}{\hat \theta^{\textsc{bic}}} \newcommand{\thetalasso}{\hat \theta^{\cL}} \newcommand{\thetaslope}{\hat \theta^{\cS}} \newcommand{\thetals}{\hat \theta^{\textsc{ls}}} \newcommand{\thetalsm}{\tilde \theta^{\textsc{ls}}_X} \newcommand{\thetaridge}{\hat\theta^{\mathrm{ridge}}_\tau} \newcommand{\thetalsK}{\hat \theta^{\textsc{ls}}_K} \newcommand{\muls}{\hat \mu^{\textsc{ls}}}

In this chapter, we consider the following regression model:

[[math]] \begin{equation} \label{EQ:regmod} Y_i=f(X_i)+\eps_i,\quad i=1, \ldots, n\,, \end{equation} [[/math]]

where [math]\eps=(\eps_1, \ldots, \eps_n)^\top [/math] is sub-Gaussian with variance proxy [math]\sigma^2[/math] and such that [math]\E[\eps]=0[/math]. Our goal is to estimate the function [math]f[/math] under a linear assumption. Namely, we assume that [math]x \in \R^d[/math] and [math]f(x)=x^\top\theta^*[/math] for some unknown [math]\theta^* \in \R^d[/math].

Fixed design linear regression

Depending on the nature of the design points [math]X_1, \ldots, X_n[/math], we will favor a different measure of risk. In particular, we will focus either on fixed or random design.

Random design

The case of random design corresponds to the statistical learning setup. Let [math](X_1,Y_1), \ldots, (X_{n+1}, Y_{n+1})[/math] be [math]n+1[/math] \iid random couples. Given the pairs [math](X_1,Y_1), \ldots, (X_{n}, Y_{n})[/math], the goal is construct a function [math]\hat f_n[/math] such that [math]\hat f_n(X_{n+1})[/math] is a good predictor of [math]Y_{n+1}[/math]. Note that when [math]\hat f_n[/math] is constructed, [math]X_{n+1}[/math] is still unknown and we have to account for what value it is likely to take. Consider the following example from~. The response variable [math]Y[/math] is the log-volume of a cancerous tumor, and the goal is to predict it based on [math]X \in \R^6[/math], a collection of variables that are easier to measure (age of patient, log-weight of prostate, \ldots). Here the goal is clearly to construct [math]f[/math] for prediction purposes. Indeed, we want to find an automatic mechanism that outputs a good prediction of the log-weight of the tumor given certain inputs for a new (unseen) patient.

A natural measure of performance here is the [math]L_2[/math]-risk employed in the introduction:

[[math]] R(\hat f_n)=\E[Y_{n+1}-\hat f_n(X_{n+1})]^2=\E[Y_{n+1}-f(X_{n+1})]^2+\|\hat f_n -f\|^2_{L^2(P_X)}\,, [[/math]]

where [math]P_X[/math] denotes the marginal distribution of [math]X_{n+1}[/math]. It measures how good the prediction of [math]Y_{n+1}[/math] is in average over realizations of [math]X_{n+1}[/math]. In particular, it does not put much emphasis on values of [math]X_{n+1}[/math] that are not very likely to occur. Note that if the [math]\eps_i[/math] are random variables with variance [math]\sigma^2[/math], then one simply has [math]R(\hat f_n)=\sigma^2+\|\hat f_n -f\|^2_{L^2(P_X)}[/math]. Therefore, for random design, we will focus on the squared [math]L_2[/math] norm [math]\|\hat f_n -f\|^2_{L^2(P_X)}[/math] as a measure of accuracy. It measures how close [math]\hat f_n[/math] is to the unknown [math]f[/math] in average over realizations of [math]X_{n+1}[/math].

Fixed design

In fixed design, the points (or vectors) [math]X_1, \ldots, X_n[/math] are deterministic. To emphasize this fact, we use lowercase letters [math]x_1, \ldots, x_n[/math] to denote fixed design. Of course, we can always think of them as realizations of a random variable but the distinction between fixed and random design is deeper and significantly affects our measure of performance. Indeed, recall that for random design, we look at the performance in average over realizations of [math]X_{n+1}[/math]. Here, there is no such thing as a marginal distribution of [math]X_{n+1}[/math]. Rather, since the design points [math]x_1, \ldots, x_n[/math] are considered deterministic, our goal is to estimate [math]f[/math] only at these points. This problem is sometimes called denoising since our goal is to recover [math]f(x_1), \ldots, f(x_n)[/math] given noisy observations of these values. In many instances, fixed designs exhibit particular structures. A typical example is the regular design on [math][0,1][/math], given by [math]x_i=i/n[/math], [math]i=1, \ldots, n[/math]. Interpolation between these points is possible under smoothness assumptions. Note that in fixed design, we observe [math]\mu^*+\eps[/math], where [math]\mu^*=\big(f(x_1), \ldots, f(x_n)\big)^\top \in \R^n[/math] and [math]\eps=(\eps_1, \ldots, \eps_n)^\top \in \R^n[/math] is sub-Gaussian with variance proxy [math]\sigma^2[/math]. Instead of a functional estimation problem, it is often simpler to view this problem as a vector problem in [math]\R^n[/math]. This point of view will allow us to leverage the Euclidean geometry of [math]\R^n[/math]. In the case of fixed design, we will focus on the Mean Squared Error (MSE) as a measure of performance. It is defined by

[[math]] \MSE(\hat f_n)=\frac{1}{n}\sum_{i=1}^n \big(\hat f_n(x_i)-f(x_i)\big)^2\,. [[/math]]

Equivalently, if we view our problem as a vector problem, it is defined by

[[math]] \MSE(\hat \mu)=\frac{1}{n}\sum_{i=1}^n \big(\hat \mu_i -\mu^*_i\big)^2=\frac{1}{n} |\hat \mu -\mu^*|_2^2\,. [[/math]]

Often, the design vectors [math]x_1, \ldots, x_n \in \R^d[/math] are stored in an [math]n\times d[/math] design matrix [math]\X[/math], whose [math]j[/math]th row is given by [math]x_j^\top[/math]. With this notation, the linear regression model can be written as

[[math]] \begin{equation} \label{EQ:regmod_matrix} Y = \X \theta^* +\eps\,, \end{equation} [[/math]]

where [math]Y=(Y_1, \ldots, Y_n)^\top[/math] and [math]\eps=(\eps_1, \ldots, \eps_n)^\top[/math]. Moreover,

[[math]] \begin{equation} \label{EQ:mse_matrix} \MSE(\X\hat \theta)=\frac{1}{n} |\X(\hat \theta -\theta^*)|_2^2=(\hat \theta -\theta^*)^\top \frac{\X^\top \X}{n} (\hat \theta -\theta^*)\,. \end{equation} [[/math]]

A natural example of fixed design regression is image denoising. Assume that [math]\mu^*_i, i \in 1, \ldots, n[/math] is the grayscale value of pixel [math]i[/math] of an image. We do not get to observe the image [math]\mu^*[/math] but rather a noisy version of it [math]Y=\mu^*+\eps[/math]. Given a library of [math]d[/math] images [math]\{x_1, \ldots, x_d\}, x_j \in \R^{n}[/math], our goal is to recover the original image [math]\mu^*[/math] using linear combinations of the images [math]x_1, \ldots, x_d[/math]. This can be done fairly accurately (see Figure~Linear Regression Model).

[[File:|400px]]

File:Guide e2965 spa 10.png

Reconstruction of the digit ‘`6": Original (left), Noisy (middle) and Reconstruction (right). Here [math]n=16\times 16=256[/math] pixels. Source~.

As we will see in Remark~Linear Regression Model, properly choosing the design also ensures that if [math]\MSE(\hat f)[/math] is small for some linear estimator [math]\hat f(x)=x^\top \hat \theta[/math], then [math]|\hat \theta -\theta^*|_2^2[/math] is also small. \begin{center} \MIT{\framebox{In this chapter we only consider the fixed design case.}} \end{center}

Least squares estimators

Throughout this section, we consider the regression model~\eqref{EQ:regmod_matrix} with fixed design.

Unconstrained least squares estimator

Define the (unconstrained) ’'least squares estimator [math]\thetals[/math] to be any vector such that

[[math]] \thetals \in \argmin_{\theta \in \R^d}|Y-\X\theta|_2^2\,. [[/math]]

Note that we are interested in estimating [math]\X\theta^*[/math] and not [math]\theta^*[/math] itself, so by extension, we also call [math]\muls=\X\thetals[/math] least squares estimator. Observe that [math]\muls[/math] is the projection of [math]Y[/math] onto the column span of [math]\X[/math].

It is not hard to see that least squares estimators of [math]\theta^*[/math] and [math]\mu^*=\X\theta^*[/math] are maximum likelihood estimators when [math]\eps \sim \cN(0,\sigma^2I_n)[/math].

Proposition

The least squares estimator [math]\muls=\X\thetals \in \R^n[/math] satisfies

[[math]] \X^\top \muls=\X^\top Y\,. [[/math]]

Moreover, [math]\thetals[/math] can be chosen to be

[[math]] \thetals = (\X^\top \X)^\dagger\X^\top Y\,, [[/math]]

where [math](\X^\top \X)^\dagger[/math] denotes the Moore-Penrose pseudoinverse of [math]\X^\top \X[/math].

Show Proof

The function [math]\theta \mapsto |Y-\X\theta|_2^2[/math] is convex so any of its minima satisfies

[[math]] \nabla_\theta |Y-\X\theta|_2^2=0, [[/math]]

where [math]\nabla_\theta[/math] is the gradient operator. Using matrix calculus, we find

[[math]] \nabla_\theta |Y-\X\theta|_2^2=\nabla_\theta\big\{|Y|_2^2 -2Y^\top \X \theta + \theta^\top \X^\top \X\theta\big\}=-2(Y^\top\X-\theta^\top \X^\top \X)^\top\,. [[/math]]

Therefore, solving [math]\nabla_\theta |Y-\X\theta|_2^2=0[/math] yields

[[math]] \X^\top\X \theta=\X^\top Y\,. [[/math]]

It concludes the proof of the first statement. The second statement follows from the definition of the Moore-Penrose pseudoinverse.

■

We are now going to prove our first result on the finite sample performance of the least squares estimator for fixed design.

Theorem

Assume that the linear model~\eqref{EQ:regmod_matrix} holds where [math]\eps\sim \sg_n(\sigma^2)[/math]. Then the least squares estimator [math]\thetals[/math] satisfies

[[math]] \E\big[\MSE(\X\thetals)\big]=\frac{1}{n}\E|\X\thetals - \X\theta^*|_2^2 \lesssim \sigma^2 \frac{r}{n}\,, [[/math]]

where [math]r=\rank(\X^\top \X)[/math]. Moreover, for any [math]\delta \gt 0[/math], with probability at least [math]1-\delta[/math], it holds

[[math]] \MSE(\X\thetals)\lesssim \sigma^2 \frac{r+\log(1/\delta)}{n}\,. [[/math]]

Show Proof

Note that by definition

[[math]] \begin{equation} \label{EQ:fund_ineq_ls} |Y-\X\thetals|_2^2 \le |Y-\X\theta^*|_2^2=|\eps|^2_2\,. \end{equation} [[/math]]

Moreover,

[[math]] |Y-\X\thetals|_2^2 =|\X\theta^*+\eps-\X\thetals|_2^2= |\X\thetals-\X\theta^*|_2^2-2\eps^\top\X(\thetals -\theta^*) + |\eps|_2^2\,. [[/math]]

Therefore, we get

[[math]] \begin{equation} \label{EQ:bound_ls_1} |\X\thetals-\X\theta^*|_2^2\le 2\eps^\top\X(\thetals - \theta^*)=2|\X\thetals-\X\theta^*|_2\frac{\eps^\top\X(\thetals - \theta^*)}{|\X(\thetals - \theta^*)|_2} \end{equation} [[/math]]

Note that it is difficult to control

[[math]] \frac{\eps^\top\X(\thetals - \theta^*)}{|\X(\thetals - \theta^*)|_2} [[/math]]

as [math]\thetals[/math] depends on [math]\eps[/math] and the dependence structure of this term may be complicated. To remove this dependency, a traditional technique is to ‘`sup-out" [math]\thetals[/math]. This is typically where maximal inequalities are needed. Here we have to be a bit careful. Let [math]\Phi=[\phi_1, \ldots, \phi_r] \in \R^{n \times r}[/math] be an orthonormal basis of the column span of [math]\X[/math]. In particular, there exists [math]\nu \in \R^r[/math] such that [math]\X(\thetals - \theta^*)=\Phi \nu[/math]. It yields

[[math]] \frac{\eps^\top\X(\thetals - \theta^*)}{|\X(\thetals - \theta^*)|_2}=\frac{\eps^\top \Phi \nu}{|\Phi\nu|_2} =\frac{\eps^\top \Phi \nu}{|\nu|_2}= \tilde \eps^\top \frac{\nu}{|\nu|_2}\le \sup_{u \in \cB_2}\tilde \eps^\top u\,, [[/math]]

where [math]\cB_2[/math] is the unit ball of [math]\R^r[/math] and [math]\tilde \eps=\Phi^\top\eps[/math]. Thus

[[math]] |\X\thetals-\X\theta^*|_2^2 \le 4\sup_{u \in \cB_2}(\tilde \eps^\top u)^2\,, [[/math]]

Next, let [math] u \in \cS^{r-1} [/math] and note that [math]|\Phi u|_2^2=u^\top \Phi^\top \Phi u=u^\top u=1[/math], so that for any [math]s \in \R[/math], we have

[[math]] \E[e^{s \tilde \eps^\top u}]=\E[e^{s \eps^\top \Phi u}]\le \e^{\frac{s^2\sigma^2}{2}}\,. [[/math]]

Therefore, [math]\tilde \eps\sim \sg_r(\sigma^2)[/math]. To conclude the bound in expectation, observe that Lemma~Sub-Gaussian Random Variables yields

[[math]] 4\E\big[\sup_{u \in \cB_2}(\tilde \eps^\top u )^2\big]=4\sum_{i=1}^r \E[\tilde \eps_i^2]\le 16\sigma^2r\,. [[/math]]

Moreover, with probability [math]1-\delta[/math], it follows from the last step in the proof of Theorem~Sub-Gaussian Random Variables that

[[math]] \sup_{u \in \cB_2}(\tilde \eps^\top u)^2 \le 8\log(6)\sigma^2 r + 8\sigma^2\log(1/\delta)\,. [[/math]]

■

\label{rem:lam_min} If [math]d \le n[/math] and [math]B:=\frac{\X^\top \X}{n}[/math] has rank [math]d[/math], then we have

[[math]] |\thetals -\theta^*|_2^2 \le \frac{\MSE(\X\thetals)}{\lambda_{\mathrm{min}} (B)}\,, [[/math]]

and we can use Theorem~Linear Regression Model to bound [math]|\thetals -\theta^*|_2^2[/math] directly. By contrast, in the high-dimensional case, we will need more structural assumptions to come to a similar conclusion.

Constrained least squares estimator

Let [math]K\subset \R^d[/math] be a symmetric convex set. If we know ’'a priori that [math]\theta^* \in K[/math], we may prefer a constrained least squares estimator [math]\thetalsK[/math] defined by

[[math]] \thetalsK \in \argmin_{\theta \in K} |Y-\X\theta|_2^2\,. [[/math]]

The fundamental inequality~\eqref{EQ:fund_ineq_ls} would still hold and the bounds on the MSE may be smaller. Indeed, ~\eqref{EQ:bound_ls_1} can be replaced by

[[math]] |\X\thetalsK-\X\theta^*|_2^2\le 2\eps^\top\X(\thetalsK - \theta^*)\le 2\sup_{\theta \in K-K}(\eps^\top\X\theta)\,, [[/math]]

where [math]K-K=\{x-y\,:\, x, y \in K\}[/math]. It is easy to see that if [math]K[/math] is symmetric ([math]x \in K \Leftrightarrow -x \in K[/math]) and convex, then [math]K-K=2K[/math] so that

[[math]] 2\sup_{\theta \in K-K}(\eps^\top\X\theta)=4\sup_{v \in \X K}(\eps^\top v) [[/math]]

where [math]\X K=\{\X\theta\,:\, \theta \in K\} \subset \R^n[/math]. This is a measure of the size (width) of [math]\X K[/math]. If [math]\eps\sim \cN(0,I_d)[/math], the expected value of the above supremum is actually called Gaussian width of [math]\X K[/math]. While [math]\eps[/math] is not Gaussian but sub-Gaussian here, similar properties will still hold.

[math]\ell_1[/math] constrained least squares

Assume here that [math]K=\cB_1[/math] is the unit [math]\ell_1[/math] ball of [math]\R^d[/math]. Recall that it is defined by

[[math]] \cB_1=\Big\{x \in \R^d\,:\, \sum_{i=1}^d|x_i|\le 1\big\}\,, [[/math]]

and it has exactly [math]2d[/math] vertices [math]\cV=\{e_1, -e_1, \ldots, e_d, -e_d\}[/math], where [math]e_j[/math] is the [math]j[/math]-th vector of the canonical basis of [math]\R^d[/math] and is defined by

[[math]] e_j=(0, \ldots, 0,\underbrace{1}_{j\text{th position}},0, \ldots, 0)^\top\,. [[/math]]

It implies that the set [math]\X K=\{\X\theta, \theta \in K\} \subset \R^n[/math] is also a polytope with at most [math]2d[/math] vertices that are in the set [math]\X\cV=\{\X_1, -\X_1, \ldots, \X_d, -\X_d\}[/math] where [math]\X_j[/math] is the [math]j[/math]-th column of [math]\X[/math]. Indeed, [math]\X K[/math] is obtained by rescaling and embedding (resp. projecting) the polytope [math]K[/math] when [math]d \le n[/math] (resp., [math]d \ge n[/math]). Note that some columns of [math]\X[/math] might not be vertices of [math]\X K[/math] so that [math]\X \cV[/math] might be a strict superset of the set of vertices of [math]\X K[/math].

Theorem

Let [math]K=\cB_1[/math] be the unit [math]\ell_1[/math] ball of [math]\R^d, d\ge 2[/math] and assume that [math]\theta^* \in \cB_1[/math]. Moreover, assume the conditions of Theorem~Linear Regression Model and that the columns of [math]\X[/math] are normalized in such a way that [math]\max_j|\X_j|_2\le \sqrt{n}[/math]. Then the constrained least squares estimator [math]\thetals_{\cB_1}[/math] satisfies

[[math]] \E\big[\MSE(\X\thetals_{\cB_1})\big]=\frac{1}{n}\E|\X\thetals_{\cB_1} - \X\theta^*|_2^2 \lesssim \sigma\sqrt{ \frac{\log d}{n}}\,, [[/math]]

Moreover, for any [math]\delta \gt 0[/math], with probability [math]1-\delta[/math], it holds

[[math]] \MSE(\X\thetals_{\cB_1})\lesssim \sigma \sqrt{\frac{\log (d/\delta)}{n}}\,. [[/math]]

Show Proof

From the considerations preceding the theorem, we get that

[[math]] |\X\thetals_{\cB_1}-\X\theta^*|_2^2\le4\sup_{v \in \X K}(\eps^\top v). [[/math]]

Observe now that since [math]\eps\sim \sg_n(\sigma^2)[/math], for any column [math]\X_j[/math] such that [math]|\X_j|_2\le \sqrt{n}[/math], the random variable [math]\eps^\top \X_j\sim \sg(n\sigma^2)[/math]. Therefore, applying Theorem~Sub-Gaussian Random Variables, we get the bound on [math]\E\big[\MSE(\X\thetalsK)\big][/math] and for any [math]t\ge 0[/math],

[[math]] \p\big[\MSE(\X\thetalsK) \gt t \big]\le \p\big[\sup_{v \in \X K}(\eps^\top v) \gt nt/4 \big]\le 2de^{-\frac{nt^2}{32\sigma^2}} [[/math]]

To conclude the proof, we find [math]t[/math] such that

[[math]] 2de^{-\frac{nt^2}{32\sigma^2}}\le \delta \ \Leftrightarrow \ t^2 \ge 32\sigma^2 \frac{ \log(2d)}{n} + 32 \sigma^2 \frac{ \log(1/\delta)}{n}\,. [[/math]]

■

Note that the proof of Theorem~Linear Regression Model also applies to [math]\thetals_{\cB_1}[/math] (exercise!) so that [math]\X \thetals_{\cB_1}[/math] benefits from the best of both rates,

[[math]] \E\big[\MSE(\X\thetals_{\cB_1})\big]\lesssim \min\Big(\sigma^2\frac{r}{n}, \sigma\sqrt{\frac{\log d}{n}}\Big)\,. [[/math]]

This is called an elbow effect. The elbow takes place around [math]r\simeq\sqrt{n}[/math] (up to logarithmic terms).

[math]\ell_0[/math] constrained least squares

By an abuse of notation, we call the number of non-zero coefficients of a vector [math] \theta \in \R^d [/math] its [math]\ell_0[/math] norm (it is not actually a norm). It is denoted by

[[math]] |\theta|_0=\sum_{j=1}^d \1(\theta_j \neq 0)\,. [[/math]]

We call a vector [math]\theta[/math] with ‘`small" [math]\ell_0[/math] norm a ’'sparse vector. More precisely, if [math]|\theta|_0\le k[/math], we say that [math]\theta[/math] is a [math]k[/math]-sparse vector. We also call support of [math]\theta[/math] the set

[[math]] \supp(\theta)=\big\{j \in \{1, \ldots, d\}\,:\, \theta_j \neq 0\big\} [[/math]]

so that [math]|\theta|_0=\card(\supp(\theta))=:|\supp(\theta)|[/math]\,.

The [math]\ell_0[/math] terminology and notation comes from the fact that

[[math]] \lim_{q \to 0^{\tiny +}}\sum_{j=1}^d|\theta_j|^q=|\theta|_0 [[/math]]

Therefore it is really [math]\lim_{q \to 0^{\tiny +}}|\theta|_q^q[/math] but the notation [math]|\theta|_0^0[/math] suggests too much that it is always equal to 1.

By extension, denote by [math]\cB_0(k)[/math] the [math]\ell_0[/math] ball of [math]\R^d[/math], i.e., the set of [math]k[/math]-sparse vectors, defined by

[[math]] \cB_0(k)=\{\theta \in \R^d\,:\, |\theta|_0 \le k\}\,. [[/math]]

In this section, our goal is to control the [math]\MSE[/math] of [math]\thetalsK[/math] when [math]K=\cB_0(k)[/math]. Note that computing [math]\thetals_{\cB_0(k)}[/math] essentially requires computing [math]\binom{d}{k}[/math] least squares estimators, which is an exponential number in [math]k[/math]. In practice this will be hard (or even impossible) but it is interesting to understand the statistical properties of this estimator and to use them as a benchmark.

Theorem

Fix a positive integer [math]k \le d/2[/math]. Let [math]K=\cB_0(k)[/math] be set of [math]k[/math]-sparse vectors of [math]\R^d[/math] and assume that [math]\theta^*\in \cB_0(k)[/math]. Moreover, assume the conditions of Theorem~Linear Regression Model. Then, for any [math]\delta \gt 0[/math], with probability [math]1-\delta[/math], it holds

[[math]] \MSE(\X\thetals_{\cB_0(k)})\lesssim \frac{\sigma^2}{n}\log\binom{d}{2k} + \frac{\sigma^2k}{n} +\frac{\sigma^2}{n}\log(1/\delta)\,. [[/math]]

Show Proof

We begin as in the proof of Theorem~Linear Regression Model to get~\eqref{EQ:bound_ls_1}:

[[math]] |\X\thetalsK-\X\theta^*|_2^2\le 2\eps^\top\X(\thetalsK - \theta^*)=2|\X\thetalsK-\X\theta^*|_2\frac{\eps^\top\X(\thetalsK - \theta^*)}{|\X(\thetalsK - \theta^*)|_2}\,. [[/math]]

We know that both [math]\thetalsK[/math] and [math]\theta^*[/math] are in [math]\cB_0(k)[/math] so that [math]\thetalsK-\theta^* \in \cB_0(2k)[/math]. For any [math]S \subset \{1, \ldots, d\}[/math], let [math]\X_S[/math] denote the [math]n\times |S|[/math] submatrix of [math]\X[/math] that is obtained from the columns of [math]\X_j, j \in S[/math] of [math]\X[/math]. Denote by [math]r_S \le |S|[/math] the rank of [math]\X_S[/math] and let [math]\Phi_S=[\phi_1, \ldots, \phi_{r_S}] \in \R^{n\times r_S}[/math] be an orthonormal basis of the column span of [math]\X_S[/math]. Moreover, for any [math]\theta \in \R^d[/math], define [math]\theta(S) \in \R^{|S|}[/math] to be the vector with coordinates [math]\theta_j, j \in S[/math]. If we denote by [math]\hat S=\supp(\thetalsK - \theta^*)[/math], we have [math]|\hat S|\le 2k[/math] and there exists [math]\nu \in \R^{r_{\hat S}}[/math] such that

[[math]] \X(\thetalsK - \theta^*)=\X_{\hat S}(\thetalsK(\hat S) - \theta^*(\hat S))=\Phi_{\hat S} \nu\,. [[/math]]

Therefore,

[[math]] \frac{\eps^\top\X(\thetalsK - \theta^*)}{|\X(\thetalsK - \theta^*)|_2} =\frac{\eps^\top \Phi_{\hat S} \nu}{|\nu|_2}\le \max_{|S|= 2k}\sup_{u \in \cB_2^{r_{S}}}[\eps^\top \Phi_S] u [[/math]]

where [math]\cB_2^{r_{S}}[/math] is the unit ball of [math]\R^{r_S}[/math]. It yields

[[math]] |\X\thetalsK-\X\theta^*|_2^2 \le 4 \max_{|S|= 2k}\sup_{u \in \cB_2^{r_{S}}}(\tilde \eps_S^\top u)^2\,, [[/math]]

with [math]\tilde \eps_S=\Phi_S^\top\eps \sim \sg_{r_S}(\sigma^2)[/math]. Using a union bound, we get for any [math]t \gt 0[/math],

[[math]] \p\big(\max_{|S|= 2k}\sup_{u \in \cB_2^{r_S}}(\tilde \eps^\top u)^2 \gt t\big) \le \sum_{|S|= 2k} \p\big( \sup_{u \in \cB_2^{r_S}}(\tilde \eps^\top u)^2 \gt t\big) [[/math]]

It follows from the proof of Theorem~Sub-Gaussian Random Variables that for any [math]|S| \le 2k[/math],

[[math]] \p\big( \sup_{u \in \cB_2^{r_S}}(\tilde \eps^\top u)^2 \gt t\big)\le 6^{|S|}e^{-\frac{t}{8\sigma^2}} \le 6^{2k}e^{-\frac{t}{8\sigma^2}}\,. [[/math]]

Together, the above three displays yield

[[math]] \begin{equation} \label{EQ:prMSEl0HP} \p(|\X\thetalsK-\X\theta^*|_2^2 \gt 4t) \le \binom{d}{2k} 6^{2k} e^{-\frac{t}{8\sigma^2}}\,. \end{equation} [[/math]]

To ensure that the right-hand side of the above inequality is bounded by [math]\delta[/math], we need

[[math]] t\ge C\sigma^2\Big\{\log \binom{d}{2k} + k\log(6) + \log(1/\delta)\Big\}\,. [[/math]]

■

How large is [math]\log\binom{d}{2k}[/math]? It turns out that it is not much larger than [math]k[/math].

Lemma

For any integers [math]1\le k \le n[/math], it holds

[[math]] \binom{n}{k} \le \Big(\frac{en}{k}\Big)^k. [[/math]]

Show Proof

Observe first that if [math]k=1[/math], since [math]n \ge 1[/math], it holds,

[[math]] \binom{n}{1}=n\le en=\Big(\frac{en}{1}\Big)^1 [[/math]]

Next, we proceed by induction and assume that it holds for some [math]k \le n-1[/math] that

[[math]] \binom{n}{k} \le \Big(\frac{en}{k}\Big)^k. [[/math]]

Observe that

[[math]] \binom{n}{k+1}=\binom{n}{k}\frac{n-k}{k+1}\le \Big(\frac{en}{k}\Big)^k\frac{n-k}{k+1} \leq \frac{e^k n^{k+1}}{(k+1)^{k+1}}\Big(1+\frac1k\Big)^k \,, [[/math]]

where we used the induction hypothesis in the first inequality. To conclude, it suffices to observe that

[[math]] \begin{equation*} \left(1+\frac1k\right)^k\le e. \qedhere \end{equation*} [[/math]]

■

It immediately leads to the following corollary:

Corollary

Under the assumptions of Theorem~Linear Regression Model, for any [math]\delta \gt 0[/math], with probability at least [math]1-\delta[/math], it holds

[[math]] \MSE(\X\thetals_{\cB_0(k)})\lesssim \frac{\sigma^2k}{n}\log \Big(\frac{ed}{2k}\Big) + \frac{\sigma^2k}{n}\log(6) + \frac{\sigma^2}{n}\log(1/\delta)\,. [[/math]]

Note that for any fixed [math]\delta[/math], there exits a constant [math]C_\delta \gt 0[/math] such that for any [math]n \ge 2k[/math], with high probability,

[[math]] \MSE(\X\thetals_{\cB_0(k)})\le C_\delta\frac{\sigma^2k}{n}\log \Big(\frac{ed}{2k}\Big)\,. [[/math]]

Comparing this result with Theorem~Linear Regression Model with [math]r=k[/math], we see that the price to pay for not knowing the support of [math]\theta^*[/math] but only its size, is a logarithmic factor in the dimension [math]d[/math]. This result immediately leads to the following bound in expectation.

Corollary

Under the assumptions of Theorem~Linear Regression Model,

[[math]] \E\big[\MSE(\X\thetals_{\cB_0(k)})\big]\lesssim\frac{\sigma^2k}{n}\log \Big(\frac{ed}{k}\Big)\,. [[/math]]

Show Proof

It follows from~\eqref{EQ:prMSEl0HP} that for any [math]H\ge 0[/math],

[[math]] \begin{align*} \E\big[\MSE(\X\thetals_{\cB_0(k)})\big]&=\int_0^\infty\p(|\X\thetalsK-\X\theta^*|_2^2 \gt nu) \ud u\\ &\le H+\int_0^\infty\p(|\X\thetalsK-\X\theta^*|_2^2 \gt n(u+H)) \ud u\\ &\le H+\sum_{j=1}^{2k}\binom{d}{j} 6^{2k} \int_0^\infty e^{-\frac{n(u+H)}{32\sigma^2}} \ud u\\ &=H+\sum_{j=1}^{2k}\binom{d}{j} 6^{2k}e^{-\frac{nH}{32\sigma^2}} \frac{32\sigma^2}{n}\,. \end{align*} [[/math]]

Next, take [math]H[/math] to be such that

[[math]] \sum_{j=1}^{2k}\binom{d}{j} 6^{2k}e^{-\frac{nH}{32\sigma^2}}=1\,. [[/math]]

This yields

[[math]] H \lesssim \frac{\sigma^2k}{n}\log \Big(\frac{ed}{k}\Big)\,, [[/math]]

which completes the proof.

■

The Gaussian Sequence Model

The Gaussian Sequence Model is a toy model that has received a lot of attention, mostly in the eighties. The main reason for its popularity is that it carries already most of the insight of nonparametric estimation. While the model looks very simple it allows to carry deep ideas that extend beyond its framework and in particular to the linear regression model that we are interested in. Unfortunately, we will only cover a small part of these ideas and the interested reader should definitely look at the excellent books by A. Tsybakov~ and I. Johnstone~. The model is as follows:

[[math]] \begin{equation} \label{EQ:gsm} Y_i=\theta^*_i +\eps_i\,,\qquad i=1, \ldots, d\,, \end{equation} [[/math]]

where [math]\eps_1, \ldots, \eps_d[/math] are \iid [math]\cN(0,\sigma^2)[/math] random variables. Note that often, [math]d[/math] is taken equal to [math]\infty[/math] in this sequence model and we will also discuss this case. Its links to nonparametric estimation will become clearer in Chapter~Misspecified Linear Models. The goal here is to estimate the unknown vector [math]\theta^*[/math].

The sub-Gaussian Sequence Model

Note first that the model~\eqref{EQ:gsm} is a special case of the linear model with fixed design~\eqref{EQ:regmod} with [math]n=d[/math] and [math]f(x_i)=x_i^\top \theta^*[/math], where [math]x_1, \ldots, x_n[/math] form the canonical basis [math] e_1, \dots, e_n [/math] of [math]\R^n[/math] and [math]\eps[/math] has a Gaussian distribution. Therefore, [math]n=d[/math] is both the dimension of the parameter [math]\theta[/math] and the number of observations and it looks like we have chosen to index this problem by [math]d[/math] rather than [math]n[/math] somewhat arbitrarily. We can bring [math]n[/math] back into the picture, by observing that this model encompasses slightly more general choices for the design matrix [math]\X[/math] as long as it satisfies the following assumption. \begin{assumption}{\textsf{ORT}} The design matrix satisfies

[[math]] \frac{\X^\top \X}{n}=I_d\,, [[/math]]

where [math]I_d[/math] denotes the identity matrix of [math]\R^d[/math]. \end{assumption} Assumption~\textsf{ORT} allows for cases where [math]d\le n[/math] but not [math]d \gt n[/math] (high dimensional case) because of obvious rank constraints. In particular, it means that the [math]d[/math] columns of [math]\X[/math] are orthogonal in [math]\R^n[/math] and all have norm [math]\sqrt{n}[/math]. Under this assumption, it follows from the linear regression model~\eqref{EQ:regmod_matrix} that

[[math]] \begin{align*} y:=\frac{1}{n}\X^\top Y&=\frac{\X^\top \X}{n}\theta^*+ \frac{1}{n}\X^\top\eps\\ &=\theta^*+\xi\,, \end{align*} [[/math]]

where [math]\xi=(\xi_1, \ldots, \xi_d)\sim \sg_d(\sigma^2/n)[/math] (If [math]\eps[/math] is Gaussian, we even have [math]\xi \sim \cN_d(0, \sigma^2/n)[/math]). As a result, under the assumption~\textsf{ORT}, when [math]\xi[/math] is Gaussian, the linear regression model~\eqref{EQ:regmod_matrix} is equivalent to the Gaussian Sequence Model~\eqref{EQ:gsm} up to a transformation of the data [math]Y[/math] and a rescaling of the variance. Moreover, for any estimator [math]\hat \theta \in \R^d[/math], under \textsf{ORT}, it follows from~\eqref{EQ:mse_matrix} that

[[math]] \MSE(\X\hat \theta)=(\hat \theta -\theta^*)^\top \frac{\X^\top \X}{n}(\hat \theta -\theta^*)=|\hat \theta - \theta^*|_2^2\,. [[/math]]

Furthermore, for any [math]\theta \in \R^d[/math], the assumption~\textsf{ORT} yields,

[[math]] \begin{align} |y-\theta|_2^2&=|\frac{1}{n}\X^\top Y-\theta|_2^2 \nonumber\\ &= |\theta|_2^2 - \frac{2}{n} \theta^\top \X^\top Y + \frac{1}{n^2} Y^\top \X \X^\top Y\nonumber \\ &= \frac{1}{n} |\X \theta|_2^2 - \frac{2}{n} ( \X\theta)^\top Y + \frac{1}{n} |Y|_2^2 +Q \nonumber \\ &= \frac{1}{n} |Y - \X \theta|_2^2 +Q\label{EQ:ERM_sGSM}\,, \end{align} [[/math]]

where [math]Q[/math] is a constant that does not depend on [math]\theta[/math] and is defined by

[[math]] Q=\frac{1}{n^2} Y^\top \X \X^\top Y- \frac{1}{n} |Y|_2^2 [[/math]]

This implies in particular that the least squares estimator [math]\thetals[/math] is equal to [math]y[/math]. \bigskip We introduce a sightly more general model called sub-Gaussian sequence model:

[[math]] \begin{equation} \label{EQ:sGSM} y=\theta^* +\xi \in \R^d\,, \end{equation} [[/math]]

where [math]\xi\sim \sg_d(\sigma^2/n)[/math]. In this section, we can actually completely ‘`forget" about our original model~\eqref{EQ:regmod_matrix}. In particular we can define this model independently of Assumption \textsf{ORT} and thus for any values of [math]n[/math] and [math]d[/math]. The sub-Gaussian sequence model and the Gaussian sequence model are called ’'direct (observation) problems as opposed to inverse problems where the goal is to estimate the parameter [math]\theta^*[/math] only from noisy observations of its image through an operator. The linear regression model is one such inverse problem where the matrix [math]\X[/math] plays the role of a linear operator. However, in these notes, we never try to invert the operator. See for an interesting survey on the statistical theory of inverse problems.

Sparsity adaptive thresholding estimators

If we knew a priori that [math]\theta[/math] was [math]k[/math]-sparse, we could directly employ Corollary~Linear Regression Model to obtain that with probability at least [math]1-\delta[/math], we have

[[math]] \MSE(\X\thetals_{\cB_0(k)})\le C_\delta\frac{\sigma^2k}{n}\log\Big(\frac{ed}{2k}\Big)\,. [[/math]]

As we will see, the assumption~\textsf{ORT} gives us the luxury to not know [math]k[/math] and yet adapt to its value. Adaptation means that we can construct an estimator that does not require the knowledge of [math]k[/math] (the smallest such that [math]|\theta^*|_0\le k[/math]) and yet perform as well as [math]\thetals_{\cB_0(k)}[/math], up to a multiplicative constant. Let us begin with some heuristic considerations to gain some intuition. Assume the sub-Gaussian sequence model~\eqref{EQ:sGSM}. If nothing is known about [math]\theta^*[/math] it is natural to estimate it using the least squares estimator [math]\thetals=y[/math]. In this case,

[[math]] \MSE(\X\thetals)=|y-\theta^*|_2^2=|\xi|_2^2 \le C_\delta\frac{\sigma^2d}{n}\,, [[/math]]

where the last inequality holds with probability at least [math]1-\delta[/math]. This is actually what we are looking for if [math]k=Cd[/math] for some positive constant [math]C\le 1[/math]. The problem with this approach is that it does not use the fact that [math]k[/math] may be much smaller than [math]d[/math], which happens when [math]\theta^*[/math] has many zero coordinates. If [math]\theta^*_j=0[/math], then, [math]y_j=\xi_j[/math], which is a sub-Gaussian random variable with variance proxy [math]\sigma^2/n[/math]. In particular, we know from Lemma~Sub-Gaussian Random Variables that with probability at least [math]1-\delta[/math],

[[math]] \begin{equation} \label{EQ:tau1} |\xi_j|\le \sigma\sqrt{\frac{2\log (2/\delta)}{n}}=\tau\,. \end{equation} [[/math]]

The consequences of this inequality are interesting. One the one hand, if we observe [math]|y_j|\gg \tau[/math] , then it must correspond to [math]\theta_j^*\neq 0[/math]. On the other hand, if [math]|y_j| \le \tau[/math] is smaller, then, [math]\theta_j^*[/math] cannot be very large. In particular, by the triangle inequality, [math]|\theta^*_j| \le |y_j|+|\xi_j| \le 2\tau[/math]. Therefore, we loose at most [math]2\tau[/math] by choosing [math]\hat \theta_j=0[/math]. It leads us to consider the following estimator.

Definition

The hard thresholding estimator with threshold [math]2\tau \gt 0[/math] is denoted by [math]\thetahard[/math] and has coordinates

[[math]] \thetahard_j=\left\{ \begin{array}{ll} y_j& \text{if} \ |y_j| \gt 2\tau\,,\\ 0& \text{if} \ |y_j|\le2\tau\,, \end{array} \right. [[/math]]

for [math]j=1, \ldots, d[/math]. In short, we can write [math]\thetahard_j=y_j\1(|y_j| \gt 2\tau)[/math].

From our above consideration, we are tempted to choose [math]\tau[/math] as in~\eqref{EQ:tau1}. Yet, this threshold is not large enough. Indeed, we need to choose [math]\tau[/math] such that [math]|\xi_j|\le \tau[/math] simultaneously for all [math]j[/math]. This can be done using a maximal inequality. Namely, Theorem~Sub-Gaussian Random Variables ensures that with probability at least [math]1-\delta[/math],

[[math]] \max_{1\le j\le d}|\xi_j|\le\sigma\sqrt{\frac{2\log (2d/\delta)}{n}}. [[/math]]

It yields the following theorem.

Theorem

Consider the linear regression model~\eqref{EQ:regmod_matrix} under the assumption~\textsf{ORT} or, equivalenty, the sub-Gaussian sequence model~\eqref{EQ:sGSM}. Then the hard thresholding estimator [math]\thetahard[/math] with threshold

[[math]] \begin{equation} \label{EQ:tau} 2\tau=2\sigma\sqrt{\frac{2\log (2d/\delta)}{n}} \end{equation} [[/math]]

enjoys the following two properties on the same event [math]\cA[/math] such that [math]\p(\cA)\ge 1-\delta[/math]:

• If [math]|\theta^*|_0=k[/math],
  [[math]] \MSE(\X\thetahard)=|\thetahard-\theta^*|_2^2\lesssim \sigma^2\frac{k\log (2d/\delta)}{n}\,. [[/math]]
• if [math]\min_{j \in \supp(\theta^*)}|\theta^*_j| \gt 3\tau[/math], then
  [[math]] \supp(\thetahard)=\supp(\theta^*)\,. [[/math]]

Show Proof

Define the event

[[math]] \cA=\Big\{\max_j|\xi_j|\le \tau\big\}\,, [[/math]]

and recall that Theorem~Sub-Gaussian Random Variables yields [math]\p(\cA)\ge 1-\delta[/math]. On the event [math]\cA[/math], the following holds for any [math]j=1, \ldots, d[/math]. First, observe that

[[math]] \begin{equation} \label{EQ:prthhard1} |y_j| \gt 2\tau \quad \Rightarrow \quad |\theta^*_j|\ge |y_j|-|\xi_j| \gt \tau \end{equation} [[/math]]

and

[[math]] \begin{equation} \label{EQ:prthhard2} |y_j|\le 2\tau \quad \Rightarrow \quad |\theta^*_j|\le |y_j| + |\xi_j|\le 3\tau. \end{equation} [[/math]]

It yields

[[math]] \begin{align*} |\thetahard_j-\theta^*_j|&=|y_j-\theta^*_j|\1(|y_j| \gt 2\tau)+ |\theta^*_j|\1(|y_j|\le2\tau)&\\ &\le \tau\1(|y_j| \gt 2\tau)+|\theta^*_j|\1(|y_j|\le2\tau)& \\\ &\le \tau\1(|\theta^*_j| \gt \tau)+|\theta^*_j|\1(|\theta^*_j|\le 3\tau)& \text{by}~\eqref{EQ:prthhard1} \text{ and}~\eqref{EQ:prthhard2}\\ &\le 4\min(|\theta^*_j|,\tau) \end{align*} [[/math]]

It yields

[[math]] \begin{align*} |\thetahard-\theta^*|_2^2=\sum_{j=1}^d|\thetahard_j-\theta^*_j|^2\le 16\sum_{j=1}^d\min(|\theta^*_j|^2,\tau^2)\le 16|\theta^*|_0\tau^2\,. \end{align*} [[/math]]

This completes the proof of (i). To prove (ii), note that if [math]\theta^*_j\neq 0[/math], then [math]|\theta^*_j| \gt 3\tau[/math] so that

[[math]] |y_j|=|\theta^*_j+\xi_j| \gt 3\tau-\tau=2\tau\,. [[/math]]

Therefore, [math]\thetahard_j\neq 0[/math] so that [math]\supp(\theta^*)\subset \supp(\thetahard)[/math]. Next, if [math]\thetahard_j\neq 0[/math], then [math]|\thetahard_j|=|y_j| \gt 2\tau[/math]. It yields

[[math]] |\theta^*_j|\ge |y_j|-\tau \gt \tau. [[/math]]

Therefore, [math]|\theta^*_j|\neq 0[/math] and [math]\supp(\thetahard)\subset \supp(\theta^*)[/math].

■

Similar results can be obtained for the soft thresholding estimator [math]\thetasoft[/math] defined by

[[math]] \thetasoft_j=\left\{ \begin{array}{ll} y_j-2\tau& \text{if} \ y_j \gt 2\tau\,,\\ y_j+2\tau& \text{if} \ y_j \lt -2\tau\,,\\ 0& \text{if} \ |y_j|\le2\tau\,, \end{array} \right. [[/math]]

In short, we can write

[[math]] \thetasoft_j=\Big(1-\frac{2\tau}{|y_j|}\Big)_+y_j [[/math]]

\begin{center}

[[File: | 400px | thumb | Transformation applied to [math]y_j[/math] with [math]2\tau=1[/math] to obtain the hard (left) and soft (right) thresholding estimators}\label{FIG:threshold ]]

\end{center}

High-dimensional linear regression

The BIC and Lasso estimators

It can be shown (see Problem~Linear Regression Model) that the hard and soft thresholding estimators are solutions of the following penalized empirical risk minimization problems:

[[math]] \begin{align*} \thetahard&=\argmin_{\theta \in \R^d} \Big\{|y-\theta|_2^2 + 4\tau^2|\theta|_0\Big\}\\ \thetasoft&=\argmin_{\theta \in \R^d} \Big\{|y-\theta|_2^2 + 4\tau|\theta|_1\Big\} \end{align*} [[/math]]

In view of~\eqref{EQ:ERM_sGSM}, under the assumption~\textsf{ORT}, the above variational definitions can be written as

[[math]] \begin{align*} \thetahard&=\argmin_{\theta \in \R^d} \Big\{\frac1n|Y-\X\theta|_2^2 + 4\tau^2|\theta|_0\Big\}\\ \thetasoft&=\argmin_{\theta \in \R^d} \Big\{\frac1n|Y-\X\theta|_2^2 + 4\tau|\theta|_1\Big\}\\ \end{align*} [[/math]]

When the assumption~\textsf{ORT} is not satisfied, they no longer correspond to thresholding estimators but can still be defined as above. We change the constant in the threshold parameters for future convenience.

Definition (id=)

Fix [math]\tau \gt 0[/math] and assume the linear regression model~\eqref{EQ:regmod_matrix}. The BIC estimator of [math]\theta^*[/math] is defined by any [math]\thetabic[/math] such that

[[math]] \thetabic \in \argmin_{\theta \in \R^d} \Big\{\frac1n|Y-\X\theta|_2^2 + \tau^2|\theta|_0\Big\}.\\ [[/math]]

Moreover, the Lasso estimator of [math]\theta^*[/math] is defined by any [math]\thetalasso[/math] such that

[[math]] \thetalasso \in \argmin_{\theta \in \R^d} \Big\{\frac1n|Y-\X\theta|_2^2 + 2\tau|\theta|_1\Big\}.\\ [[/math]]

[Numerical considerations] Computing the BIC estimator can be proved to be NP-hard in the worst case. In particular, no computational method is known to be significantly faster than the brute force search among all [math]2^d[/math] sparsity patterns. Indeed, we can rewrite:

[[math]] \min_{\theta \in \R^d} \Big\{\frac1n|Y-\X\theta|_2^2 + \tau^2|\theta|_0\Big\}=\min_{0\le k \le d} \Big\{\min_{\theta\,:\, |\theta|_0=k}\frac1n|Y-\X\theta|_2^2 + \tau^2k\Big\} [[/math]]

To compute [math]\min_{\theta\,:\, |\theta|_0=k}\frac1n|Y-\X\theta|_2^2[/math], we need to compute [math]\binom{d}{k}[/math] least squares estimators on a space of size [math]k[/math]. Each costs [math]O(k^3)[/math] (matrix inversion). Therefore the total cost of the brute force search is

[[math]] C\sum_{k=0}^d \binom{d}{k}k^3=Cd^32^d\,. [[/math]]

By contrast, computing the Lasso estimator is a convex problem and there exist many efficient algorithms to solve it. We will not describe this optimization problem in detail but only highlight a few of the best known algorithms:

• Probably the most popular method among statisticians relies on coordinate gradient descent. It is implemented in the \textsf{glmnet} package in \textsf{R} ,
• An interesting method called LARS computes the entire regularization path, i.e., the solution of the convex problem for all values of [math]\tau[/math]. It relies on the fact that, as a function of [math]\tau[/math], the solution [math]\thetalasso[/math] is a piecewise linear function (with values in [math]\R^d[/math]). Yet this method proved to be too slow for very large problems and has been replaced by glmnet which computes solutions for values of [math]\tau[/math] on a grid much faster.
• The optimization community has made interesting contributions to this field by using proximal methods to solve this problem. These methods exploit the structure of the objective function which is of the form smooth (sum of squares) + simple ([math]\ell_1[/math] norm). A good entry point to this literature is perhaps the FISTA algorithm .
• Recently there has been a lot of interest around this objective for very large [math]d[/math] and very large [math]n[/math]. In this case, even computing [math]|Y-\X\theta|_2^2 [/math] may be computationally expensive and solutions based on stochastic gradient descent are flourishing.

Note that by Lagrange duality, computing [math]\thetalasso[/math] is equivalent to solving an [math]\ell_1[/math] constrained least squares. Nevertheless, the radius of the [math]\ell_1[/math] constraint is unknown. In general, it is hard to relate Lagrange multipliers to the size constraints. The name ‘`Lasso" was originally given to the constrained version this estimator in the original paper of Robert Tibshirani .

Analysis of the BIC estimator

While computationally hard to implement, the BIC estimator gives us a good benchmark for sparse estimation. Its performance is similar to that of [math]\thetahard[/math] but without requiring the assumption \textsf{ORT}.

Theorem

Assume that the linear model~\eqref{EQ:regmod_matrix} holds, where [math]\eps \sim \sg_n(\sigma^2)[/math] and that [math]|\theta^*|_0\ge 1[/math]. Then, the BIC estimator [math]\thetabic[/math] with regularization parameter

[[math]] \begin{equation} \label{EQ:taubic} \tau^2=16\log(6)\frac{\sigma^2}{n} + 32\frac{\sigma^2 \log (ed)}{n}\,. \end{equation} [[/math]]

satisfies

[[math]] \begin{equation} \MSE(\X\thetabic)=\frac{1}{n}|\X\thetabic-\X\theta^*|_2^2\lesssim |\theta^*|_0 \sigma^2\frac{ \log(ed/\delta)}{n} \end{equation} [[/math]]

with probability at least [math]1-\delta[/math].

Show Proof

We begin as usual by noting that

[[math]] \frac1n|Y-\X\thetabic|_2^2 + \tau^2|\thetabic|_0 \le \frac1n|Y-\X\theta^*|_2^2 + \tau^2|\theta^*|_0\,. [[/math]]

It implies

[[math]] |\X\thetabic-\X\theta^*|_2^2 \le n\tau^2|\theta^*|_0 + 2\eps^\top\X(\thetabic-\theta^*)- n\tau^2|\thetabic|_0\,. [[/math]]

First, note that

[[math]] \begin{align*} 2\eps^\top\X(\thetabic-\theta^*)&=2\eps^\top\Big(\frac{\X\thetabic-\X\theta^*}{|\X\thetabic-\X\theta^*|_2}\Big)|\X\thetabic-\X\theta^*|_2\\ &\le 2\Big[\eps^\top\Big(\frac{\X\thetabic-\X\theta^*}{|\X\thetabic-\X\theta^*|_2}\Big)\Big]^2 + \frac12 |\X\thetabic-\X\theta^*|_2^2\,, \end{align*} [[/math]]

where we use the inequality [math]2ab\le 2a^2+\frac12b^2[/math]. Together with the previous display, it yields

[[math]] \begin{equation} \label{EQ:pr_bic_1} |\X\thetabic-\X\theta^*|_2^2 \le 2n\tau^2|\theta^*|_0 + 4\big[\eps^\top\cU(\thetabic-\theta^*)\big]^2- 2n\tau^2|\thetabic|_0\, \end{equation} [[/math]]

where

[[math]] \cU(z)=\frac{z}{|z|_2} [[/math]]

Next, we need to ``sup out" [math]\thetabic[/math]. To that end, we decompose the sup into a max over cardinalities as follows:

[[math]] \sup_{\theta \in \R^d}=\max_{1\le k \le d} \max_{|S|=k}\sup_{\supp(\theta)=S}\,. [[/math]]

Applied to the above inequality, it yields

[[math]] \begin{align*} 4\big[\eps^\top&\cU(\thetabic-\theta^*)\big]^2- 2n\tau^2|\thetabic|_0\\ & \le \max_{1\le k \le d}\big\{\max_{|S|=k} \sup_{\supp(\theta)=S}4\big[\eps^\top\cU(\theta-\theta^*)\big]^2- 2n\tau^2k\big\}\\ &\le \max_{1\le k \le d}\big\{\max_{|S|=k} \sup_{u\in \cB_2^{r_{S,*}}}4\big[\eps^\top\Phi_{S,*}u\big]^2- 2n\tau^2k\big\}\,, \end{align*} [[/math]]

where [math]\Phi_{S,*}=[\phi_1, \ldots, \phi_{r_{S,*}}][/math] is an orthonormal basis of the set [math]\{\X_j, j \in S \cup \supp(\theta^*)\}[/math] of columns of [math]\X[/math] and [math]r_{S,*} \le |S|+|\theta^*|_0[/math] is the dimension of this column span. Using union bounds, we get for any [math]t \gt 0[/math],

[[math]] \begin{align*} \p&\Big( \max_{1\le k \le d}\big\{\max_{|S|=k} \sup_{u\in \cB_2^{r_{S,*}}}4\big[\eps^\top\Phi_{S,*}u\big]^2- 2n\tau^2k\big\}\ge t\Big)\\ &\le \sum_{k=1}^d\sum_{|S|=k}\p\Big( \sup_{u\in \cB_2^{r_{S,*}}}\big[\eps^\top\Phi_{S,*}u\big]^2\ge \frac{t}4+ \frac12n\tau^2k\Big) \end{align*} [[/math]]

Moreover, using the [math]\eps[/math]-net argument from Theorem~Sub-Gaussian Random Variables, we get for [math]|S|=k[/math],

[[math]] \begin{align*} \p\Big( \sup_{u\in \cB_2^{r_{S,*}}}&\big[\eps^\top\Phi_{S,*}u\big]^2\ge \frac{t}4+ \frac12n\tau^2k\Big)\le 2\cdot 6^{r_{S,*}}\exp\Big(-\frac{\frac{t}4+ \frac12n\tau^2k}{8\sigma^2}\Big)\\ &\le 2 \exp\Big(-\frac{t}{32\sigma^2}- \frac{n\tau^2k}{16\sigma^2}+(k+|\theta^*|_0)\log(6)\Big) \\ &\le \exp\Big(-\frac{t}{32\sigma^2}- 2k\log(ed)+|\theta^*|_0\log(12)\Big) \end{align*} [[/math]]

where, in the last inequality, we used the definition~\eqref{EQ:taubic} of [math]\tau[/math]. Putting everything together, we get

[[math]] \begin{align*} \p&\Big(|\X\thetabic-\X\theta^*|_2^2 \ge 2n\tau^2|\theta^*|_0+t\Big) \le\\ & \sum_{k=1}^d\sum_{|S|=k} \exp\Big(-\frac{t}{32\sigma^2}- 2k\log(ed)+|\theta^*|_0\log(12)\Big)\\ &= \sum_{k=1}^d \binom{d}{k} \exp\Big(-\frac{t}{32\sigma^2}- 2k\log(ed)+|\theta^*|_0\log(12)\Big)\\ &\le \sum_{k=1}^d \exp\Big(-\frac{t}{32\sigma^2}-k\log(ed)+|\theta^*|_0\log(12)\Big)& \text{by Lemma~[[#lem:nchoosek |Linear Regression Model]]}\\ &= \sum_{k=1}^d(ed)^{-k} \exp\Big(-\frac{t}{32\sigma^2} + |\theta^*|_0\log(12)\Big)\\ &\le \exp\Big(-\frac{t}{32\sigma^2} + |\theta^*|_0\log(12)\Big)\,. \end{align*} [[/math]]

To conclude the proof, choose [math]t=32\sigma^2 |\theta^*|_0\log(12) + 32\sigma^2\log(1/\delta)[/math] and observe that combined with~\eqref{EQ:pr_bic_1}, it yields with probability [math]1-\delta[/math],

[[math]] \begin{align*} |\X\thetabic-\X\theta^*|_2^2 & \le 2n\tau^2|\theta^*|_0 + t \\ &= 64\sigma^2 \log(ed) |\theta^*|_0 +64\log(12)\sigma^2|\theta^*|_0 + 32\sigma^2\log(1/\delta)\\ &\le 224|\theta^*|_0 \sigma^2 \log(ed)+ 32\sigma^2\log(1/\delta)\,. \end{align*} [[/math]]

■

It follows from Theorem~Linear Regression Model that [math]\thetabic[/math] ’'adapts to the unknown sparsity of [math]\theta^*[/math], just like [math]\thetahard[/math]. Moreover, this holds under no assumption on the design matrix [math]\X[/math].

Analysis of the Lasso estimator

Slow rate for the Lasso estimator

The properties of the BIC estimator are quite impressive. It shows that under no assumption on [math]\X[/math], one can mimic two oracles: (i) the oracle that knows the support of [math]\theta^*[/math] (and computes least squares on this support), up to a [math]\log(ed)[/math] term and (ii) the oracle that knows the sparsity [math]|\theta^*|_0[/math] of [math]\theta^*[/math], up to a smaller logarithmic term [math]\log(ed/|\theta^*|_0)[/math], which is subsumed by [math]\log(ed)[/math]. Actually, the [math] \log(ed) [/math] can even be improved to [math] \log(ed/|\theta^\ast|_0) [/math] by using a modified BIC estimator (see Problem~Linear Regression Model). The Lasso estimator is a bit more difficult to analyze because, by construction, it should more naturally adapt to the unknown [math]\ell_1[/math]-norm of [math]\theta^*[/math]. This can be easily shown as in the next theorem, analogous to Theorem~Linear Regression Model.

Theorem

Assume that the linear model~\eqref{EQ:regmod_matrix} holds where [math]\eps\sim\sg_n(\sigma^2)[/math]. Moreover, assume that the columns of [math]\X[/math] are normalized in such a way that [math]\max_j|\X_j|_2\le \sqrt{n}[/math]. Then, the Lasso estimator [math]\thetalasso[/math] with regularization parameter

[[math]] \begin{equation} \label{EQ:taulasso} 2\tau=2\sigma\sqrt{\frac{2\log(2d)}{n}}+2\sigma\sqrt{\frac{2\log(1/\delta)}{n}} \end{equation} [[/math]]

satisfies

[[math]] \MSE(\X\thetalasso)=\frac{1}{n}|\X\thetalasso-\X\theta^*|_2^2\le 4|\theta^*|_1\sigma\sqrt{\frac{2\log(2d)}{n}}+4|\theta^*|_1\sigma\sqrt{\frac{2\log(1/\delta)}{n}} [[/math]]

with probability at least [math]1-\delta[/math].

Show Proof

From the definition of [math]\thetalasso[/math], it holds

[[math]] \frac1n|Y-\X\thetalasso|_2^2 + 2\tau|\thetalasso|_1 \le \frac1n|Y-\X\theta^*|_2^2 + 2\tau|\theta^*|_1\,. [[/math]]

Using H\"older's inequality, it implies

[[math]] \begin{align*} |\X\thetalasso-\X\theta^*|_2^2 &\le 2\eps^\top\X(\thetalasso-\theta^*)+ 2n\tau\big(|\theta^*|_1-|\thetalasso|_1\big) \\ &\le 2|\X^\top\eps|_\infty|\thetalasso|_1-2n\tau|\thetalasso|_1 + 2|\X^\top\eps|_\infty|\theta^*|_1+2n\tau|\theta^*|_1\\ &= 2(|\X^\top\eps|_\infty-n\tau)|\thetalasso|_1 + 2(|\X^\top\eps|_\infty+n\tau)|\theta^*|_1 \end{align*} [[/math]]

Observe now that for any [math]t \gt 0[/math],

[[math]] \p(|\X^\top\eps|_\infty\ge t)=\p(\max_{1\le j \le d}|\X_j^\top \eps| \gt t) \le 2de^{-\frac{t^2}{2n\sigma^2}} [[/math]]

Therefore, taking [math]t=\sigma\sqrt{2n\log(2d)}+\sigma\sqrt{2n\log(1/\delta)}=n\tau[/math], we get that with probability at least [math]1-\delta[/math],

[[math]] \begin{equation*} |\X\thetalasso-\X\theta^*|_2^2\le 4n\tau|\theta^*|_1\,. \qedhere \end{equation*} [[/math]]

■

Notice that the regularization parameter~\eqref{EQ:taulasso} depends on the confidence level [math]\delta[/math]. This is not the case for the BIC estimator (see~\eqref{EQ:taubic}). \medskip The rate in Theorem~Linear Regression Model is of order [math]\sqrt{(\log d)/n}[/math] (slow rate), which is much slower than the rate of order [math](\log d)/n[/math] (fast rate) for the BIC estimator. Hereafter, we show that fast rates can also be achieved by the computationally efficient Lasso estimator, but at the cost of a much stronger condition on the design matrix [math]\X[/math].

Incoherence

\begin{assumption}{[math]\mathsf{INC}(k)[/math]} We say that the design matrix [math]\X[/math] has incoherence [math]k[/math] for some integer [math]k \gt 0[/math] if

[[math]] \big|\frac{\X^\top \X}{n}-I_d\big|_\infty\le \frac{1}{32k} [[/math]]

where the [math]|A|_\infty[/math] denotes the largest element of [math]A[/math] in absolute value. Equivalently,

• For all [math]j=1, \ldots, d[/math],
  [[math]] \left|\frac{|\X_j|_2^2}{n}-1\right|\le \frac{1}{32k}\,. [[/math]]
• For all [math]1\le i,j\le d[/math], [math]i\neq j[/math], we have
  [[math]] \frac{|\X_i^\top \X_j|}{n} \le \frac{1}{32k}\,. [[/math]]

\end{assumption} Note that Assumption~\textsf{ORT} arises as the limiting case of [math]\mathsf{INC}(k)[/math] as [math]k \to \infty[/math]. However, while Assumption~\textsf{ORT} requires [math]d \le n[/math], here we may have [math]d \gg n[/math] as illustrated in Proposition~Linear Regression Model below. To that end, we simply have to show that there exists a matrix that satisfies [math]\mathsf{INC}(k)[/math] even for [math]d \gt n[/math]. We resort to the probabilistic method . The idea of this method is that if we can find a probability measure that assigns positive probability to objects that satisfy a certain property, then there must exist objects that satisfy said property. In our case, we consider the following probability distribution on random matrices with entries in [math]\{\pm 1\}[/math]. Let the design matrix [math]\X[/math] have entries that are \iid Rademacher [math](\pm 1)[/math] random variables. We are going to show that most realizations of this random matrix satisfy Assumption~[math]\mathsf{INC}(k)[/math] for large enough [math]n[/math].

Proposition

Let [math]\X \in \R^{n\times d}[/math] be a random matrix with entries [math]X_{ij}, i=1,\ldots, n, j=1, \ldots, d[/math], that are \iid Rademacher [math](\pm 1)[/math] random variables. Then, [math]\X[/math] has incoherence [math]k[/math] with probability [math]1-\delta[/math] as soon as

[[math]] n\ge 2^{11}k^2\log(1/\delta)+2^{13}k^2\log(d)\,. [[/math]]

It implies that there exist matrices that satisfy Assumption~[math]\mathsf{INC}(k)[/math] for

[[math]] n \geq C k^2\log(d)\,, [[/math]]

for some numerical constant [math]C[/math].

Show Proof

Let [math]\eps_{ij} \in \{-1,1\}[/math] denote the Rademacher random variable that is on the [math]i[/math]th row and [math]j[/math]th column of [math]\X[/math]. Note first that the [math]j[/math]th diagonal entries of [math]\X^\top\X/n[/math] are given by

[[math]] \frac{1}{n}\sum_{i=1}^n \eps_{i,j}^2=1. [[/math]]

Moreover, for [math]j\neq k[/math], the [math](j,k)[/math]th entry of the [math]d\times d[/math] matrix [math]\X^\top\X/n[/math] is given by

[[math]] \frac{1}{n}\sum_{i=1}^n \eps_{i,j}\eps_{i,k}=\frac{1}{n}\sum_{i=1}^n \xi_{i}^{(j,k)}\,, [[/math]]

where for each pair [math](j,k)[/math], [math]\xi_i^{(j,k)}=\eps_{i,j}\eps_{i,k}[/math], so that [math]\xi_1^{(j,k)}, \ldots, \xi_n^{(j,k)}[/math] are \iid Rademacher random variables. Therefore, we get that for any [math]t \gt 0[/math],

[[math]] \begin{align*} \p\left(\left|\frac{\X^\top \X}{n}-I_d\right|_\infty \gt t\right) &=\p\Big(\max_{j\neq k}\Big|\frac{1}{n}\sum_{i=1}^n \xi_{i}^{(j,k)}\Big| \gt t\Big)&\\ &\le \sum_{j\neq k}\p\Big(\Big|\frac{1}{n}\sum_{i=1}^n \xi_{i}^{(j,k)}\Big| \gt t\Big)&\text{(Union bound)}\\ &\le \sum_{j\neq k}2e^{-\frac{nt^2}{2}}&\text{(Hoeffding: Theorem~[[guide:0251dfcdad#TH:hoeffding |Sub-Gaussian Random Variables]])}\\ &\le 2 d^2e^{-\frac{nt^2}{2}}. \end{align*} [[/math]]

Taking now [math]t=1/(32k)[/math] yields

[[math]] \p\big(\big|\frac{\X^\top \X}{n}-I_d\big|_\infty \gt \frac{1}{32k}\big)\le 2 d^2e^{-\frac{n}{2^{11}k^2}} \le \delta [[/math]]

for

[[math]] \begin{equation*} n\ge 2^{11}k^2\log(1/\delta)+2^{13}k^2\log(d)\,. \qedhere \end{equation*} [[/math]]

■

\medskip For any [math]\theta \in \R^d[/math], [math]S\subset\{1, \ldots, d\}[/math], define [math]\theta_S[/math] to be the vector with coordinates

[[math]] \theta_{S,j}=\left\{\begin{array}{ll} \theta_{j} & \text{if} \ j \in S\,,\\ 0&\text{otherwise}\,. \end{array}\right. [[/math]]

In particular [math]|\theta|_1=|\theta_S|_1+|\theta_{S^c}|_1[/math]. The following lemma holds

Lemma

Fix a positive integer [math]k \le d[/math] and assume that [math]\X[/math] satisfies assumption [math]\mathsf{INC}(k)[/math]. Then, for any [math]S \in \{1, \ldots, d\}[/math] such that [math]|S|\le k[/math] and any [math]\theta \in \R^d[/math] that satisfies the cone condition

[[math]] \begin{equation} \label{EQ:conecond} |\theta_{S^c}|_1 \le 3|\theta_S|_1\,, \end{equation} [[/math]]

it holds

[[math]] |\theta|^2_2 \le 2\frac{|\X\theta|_2^2}n. [[/math]]

Show Proof

We have

[[math]] \frac{|\X\theta|_2^2}n = \frac{|\X\theta_S|_2^2}{n} +\frac{|\X\theta_{S^c}|_2^2}{n}+2\theta_S^\top \frac{\X^\top\X}{n}\theta_{S^c}. [[/math]]

We bound each of the three terms separately.

• First, if follows from the incoherence condition that
  [[math]] \frac{|\X\theta_S|_2^2}{n}=\theta_S^\top \frac{\X^\top\X}{n}\theta_S =|\theta_S|_2^2+\theta_S^\top \left(\frac{\X^\top\X}{n} - I_d\right)\theta_S \ge |\theta_S|_2^2-\frac{|\theta_S|_1^2}{32k}\,, [[/math]]
• Similarly,
  [[math]] \frac{|\X\theta_{S^c}|_2^2}{n} \ge |\theta_{S^c}|_2^2-\frac{|\theta_{S^c}|_1^2}{32k}\ge |\theta_{S^c}|_2^2-\frac{9|\theta_{S}|_1^2}{32k}\,, [[/math]]
  where, in the last inequality, we used the cone condition~\eqref{EQ:conecond}.
• Finally,
  [[math]] 2\Big|\theta_S^\top \frac{ \X^\top\X}{n}\theta_{S^c}\Big|\le \frac{2}{32k}|\theta_S|_1|\theta_{S^c}|_1\le \frac{6}{32k}|\theta_S|_1^2. [[/math]]
  where, in the last inequality, we used the cone condition~\eqref{EQ:conecond}.\

Observe now that it follows from the Cauchy-Schwarz inequality that

[[math]] |\theta_S|_1^2 \le |S||\theta_S|_2^2. [[/math]]

Thus for [math]|S|\le k[/math],

[[math]] \begin{equation*} \frac{|\X\theta|_2^2}{n} \ge |\theta_S|_2^2 +|\theta_{S^c}|_2^2- \frac{16|S|}{32k}|\theta_S|_2^2 \ge \frac12|\theta|_2^2. \qedhere \end{equation*} [[/math]]

■

Fast rate for the Lasso

Theorem

Fix [math]n \ge 2[/math]. Assume that the linear model~\eqref{EQ:regmod_matrix} holds where [math]\eps\sim \sg_n(\sigma^2)[/math]. Moreover, assume that [math]|\theta^*|_0\le k[/math] and that [math]\X[/math] satisfies assumption \textsf{INC$(k)$}. Then the Lasso estimator [math]\thetalasso[/math] with regularization parameter defined by

[[math]] 2\tau=8\sigma\sqrt{\frac{\log(2d)}{n}}+8\sigma\sqrt{\frac{\log(1/\delta)}{n}} [[/math]]

satisfies

[[math]] \begin{equation} \label{EQ:fastMSELasso} \MSE(\X\thetalasso)=\frac{1}{n}|\X\thetalasso-\X\theta^*|_2^2\lesssim k\sigma^2\frac{\log(2d/\delta)}{n} \end{equation} [[/math]]

and

[[math]] \begin{equation} \label{EQ:bornel2lasso} |\thetalasso-\theta^*|_2^2\lesssim k\sigma^2\frac{\log(2d/\delta)}{n}\,.\end{equation} [[/math]]

with probability at least [math]1-\delta[/math].

Show Proof

From the definition of [math]\thetalasso[/math], it holds

[[math]] \frac1n|Y-\X\thetalasso|_2^2 \le \frac1n|Y-\X\theta^*|_2^2 + 2\tau|\theta^*|_1- 2\tau|\thetalasso|_1 \,. [[/math]]

Adding [math]\tau|\thetalasso-\theta^*|_1[/math] on each side and multiplying by [math]n[/math], we get

[[math]] |\X\thetalasso-\X\theta^*|_2^2+n\tau|\thetalasso-\theta^*|_1 \le2\eps^\top\X(\thetalasso-\theta^*) +n\tau|\thetalasso-\theta^*|_1+ 2n\tau|\theta^*|_1- 2n\tau|\thetalasso|_1 \,. [[/math]]

Applying H\"older's inequality and using the same steps as in the proof of Theorem~Linear Regression Model, we get that with probability [math]1-\delta[/math], we get

[[math]] \begin{align*} \eps^\top\X(\thetalasso-\theta^*)&\le|\eps^\top\X|_\infty|\thetalasso-\theta^*|_1\\ &\le \frac{n\tau}2|\thetalasso-\theta^*|_1\,, \end{align*} [[/math]]

where we used the fact that [math]|\X_j|_2^2 \le n + 1/(32k) \le 2n[/math]. Therefore, taking [math]S=\supp(\theta^*)[/math] to be the support of [math]\theta^*[/math], we get

[[math]] \begin{align} |\X\thetalasso-\X\theta^*|_2^2 +n\tau|\thetalasso-\theta^*|_1 &\le 2n\tau|\thetalasso-\theta^*|_1+2n\tau|\theta^*|_1- 2n\tau|\thetalasso|_1\nonumber \\ &= 2n\tau|\thetalasso_S-\theta^*|_1+2n\tau|\theta^*|_1- 2n\tau|\thetalasso_S|_1\nonumber\\ &\le 4n\tau|\thetalasso_S-\theta^*|_1. \label{EQ:pr:lassofast1} \end{align} [[/math]]

In particular, it implies that

[[math]] \begin{equation} \label{EQ:conefordelta} |\thetalasso_{S^c}-\theta_{S^c}^*|_1\le 3 |\thetalasso_{S}-\theta_{S}^*|_1\,. \end{equation} [[/math]]

so that [math]\theta=\thetalasso-\theta^*[/math] satisfies the cone condition~\eqref{EQ:conecond}. Using now the Cauchy-Schwarz inequality and Lemma~Linear Regression Model respectively, we get, since [math]|S|\le k[/math],

[[math]] |\thetalasso_S-\theta^*|_1 \le \sqrt{|S|}|\thetalasso_S-\theta^*|_2 \le \sqrt{|S|}|\thetalasso-\theta^*|_2 \le\sqrt{\frac{2k}{n}}|\X\thetalasso-\X\theta^*|_2\,. [[/math]]

Combining this result with~\eqref{EQ:pr:lassofast1}, we find

[[math]] |\X\thetalasso-\X\theta^*|_2^2 \le 32nk\tau^2\,. [[/math]]

This concludes the proof of the bound on the MSE. To prove~\eqref{EQ:bornel2lasso}, we use Lemma~Linear Regression Model once again to get

[[math]] \begin{equation*} |\thetalasso -\theta^*|_2^2\le 2\MSE(\X\thetalasso)\le 64k\tau^2. \qedhere \end{equation*} [[/math]]

■

Note that all we required for the proof was not really incoherence but the conclusion of Lemma~Linear Regression Model:

[[math]] \begin{equation} \label{EQ:REcond} \inf_{|S|\le k}\inf_{\theta \in \cC_S}\frac{|\X\theta|_2^2}{n|\theta|^2_2}\ge \kappa, \end{equation} [[/math]]

where [math]\kappa=1/2[/math] and [math]\cC_S[/math] is the cone defined by

[[math]] \cC_S=\big\{ |\theta_{S^c}|_1 \le 3|\theta_S|_1 \big\}\,. [[/math]]

Condition~\eqref{EQ:REcond} is sometimes called restricted eigenvalue (RE) condition. Its name comes from the following observation. Note that all [math]k[/math]-sparse vectors [math]\theta[/math] are in a cone [math]\cC_{S}[/math] with [math]|S|\le k[/math] so that the RE condition implies that the smallest eigenvalue of [math]\X_S[/math] satisfies [math]\lambda_\textrm{min}(\X_S)\ge n\kappa[/math] for all [math]S[/math] such that [math]|S|\le k[/math]. Clearly, the RE condition is weaker than incoherence and it can actually be shown that a design matrix [math]\X[/math] of \iid Rademacher random variables satisfies the RE conditions as soon as [math]n\ge Ck\log(d)[/math] with positive probability.

The Slope estimator

We noticed that the BIC estimator can actually obtain a rate of [math] k\log(ed/k) [/math], where [math] k = |\theta^\ast|_0 [/math], while the LASSO only achieves [math] k \log(ed) [/math]. This begs the question whether the same rate can be achieved by an efficiently computable estimator. The answer is yes, and the estimator achieving this is a slight modification of the LASSO, where the entries in the [math] \ell_1 [/math]-norm are weighted differently according to their size in order to get rid of a slight inefficiency in our bounds.

Definition (Slope estimatorid=)

Let [math] \lambda = (\lambda_1, \dots, \lambda_d) [/math] be a non-increasing sequence of positive real numbers, [math] \lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_d \gt 0 [/math]. For [math] \theta = (\theta_1, \dots, \theta_d) \in \R^d [/math], let [math] (\theta^\ast_1, \dots, \theta^\ast_d) [/math] be a non-increasing rearrangement of the modulus of the entries, [math] |\theta_1|, \dots, |\theta_d| [/math]. We define the sorted [math] \ell_1 [/math] norm of [math] \theta [/math] as

[[math]] \begin{equation} |\theta|_\ast = \sum_{j=1}^{d} \lambda_j \theta^\ast_j, \end{equation} [[/math]]

or equivalently as

[[math]] \begin{equation} |\theta|_\ast = \max_{\phi \in S_d} \sum_{j=1}^{d} \lambda_j | \theta_{\phi(j)} |. \end{equation} [[/math]]

The Slope estimator is then given by

[[math]] \begin{equation} \label{eq:ad} \thetaslope \in \argmin_{\theta \in \R^d} \{ \frac{1}{n} | Y - \X \theta|_2^2 + 2 \tau | \theta |_\ast \} \end{equation} [[/math]]

for a choice of tuning parameters [math] \lambda [/math] and [math] \tau \gt 0 [/math].

Slope stands for Sorted L-One Penalized Estimation and was introduced in , motivated by the quest for a penalized estimation procedure that could offer a control of false discovery rate for the hypotheses [math] H_{0,j}: \theta^\ast_j = 0 [/math]. We can check that [math] |\,.\,|_\ast [/math] is indeed a norm and that [math] \thetaslope [/math] can be computed efficiently, for example by proximal gradient algorithms, see . In the following, we will consider

[[math]] \begin{equation} \label{eq:ab} \lambda_j = \sqrt{\log (2d/j)}, \quad j = 1, \dots, d. \end{equation} [[/math]]

With this choice, we will exhibit a scaling in [math] \tau [/math] that leads to the desired high probability bounds, following the proofs in . We begin with refined bounds on the suprema of Gaussians.

Lemma

Let [math] g_1, \dots, g_d [/math] be zero-mean Gaussian variables with variance at most [math] \sigma^2 [/math]. Then, for any [math]k\le d[/math],

[[math]] \begin{equation} \label{eq:j} \p\left(\frac{1}{k \sigma^2} \sum_{j = 1}^{k} (g_j^\ast)^2 \gt t \log \left( \frac{2d}{k} \right) \right) \leq \left( \frac{2d}{k} \right)^{1-3t/8}. \end{equation} [[/math]]

Show Proof

We consider the moment generating function to apply a Chernoff bound.

Use Jensen's inequality on the sum to get

[[math]] \begin{align*} \label{eq:j} \E \exp \left( \frac{3}{8 k \sigma^2} \sum_{j=1}^{k} (g^\ast_j)^2 \right) \leq {} & \frac{1}{k} \sum_{j=1}^{k} \E \exp \left( \frac{3 (g_j^\ast)^2}{8 \sigma^2} \right)\\ \leq {} & \frac{1}{k} \sum_{j=1}^{d} \E \exp \left( \frac{3 g_j^2}{8 \sigma^2} \right)\\ \leq {} & \frac{2d}{k}, \end{align*} [[/math]]

where we used the bound on the moment generating function of the [math] \chi^2 [/math] distribution from Problem Sub-Gaussian Random Variables to get that [math] \E[\exp(3g^2/8)] = 2 [/math] for [math] g \sim \cN(0,1) [/math]. The rest follows from a Chernoff bound.

■

Lemma

Define [math][d]:=\{1, \ldots, d\}[/math]. Under the same assumptions as in Lemma Linear Regression Model,

[[math]] \begin{equation} \sup_{k \in [d]} \frac{(g^\ast_k)}{\sigma \lambda_k} \leq 4 \sqrt{\log(1/\delta)}, \end{equation} [[/math]]

with probability at least [math] 1 - \delta [/math], for [math] \delta \lt \frac{1}{2} [/math].

Show Proof

We can estimate [math] (g^\ast_k)^2 [/math] by the average of all larger variables,

[[math]] \begin{equation} \label{eq:m} (g^\ast_k)^2 \leq \frac{1}{k} \sum_{j=1}^{k} (g^\ast_j)^2. \end{equation} [[/math]]

Applying Lemma Linear Regression Model yields

[[math]] \begin{equation} \label{eq:n} \p\left(\frac{(g^\ast_k)^2}{\sigma^2 \lambda_k^2} \gt t\right) \leq \left( \frac{2d}{k} \right)^{1-3t/8} \end{equation} [[/math]]

For [math] t \gt 8 [/math],

[[math]] \begin{align} \label{eq:o} \p \left( \sup_{k \in [d]} \frac{(g^\ast_k)^2}{\sigma^2 \lambda_k^2} \gt t \right) \leq {} & \sum_{j=1}^{d} \left( \frac{2d}{j} \right)^{1-3t/8}\\ \leq {} & (2d)^{1-3t/8} \sum_{j=1}^{d} \frac{1}{j^2}\\ \leq {} & 4 \cdot 2^{-3t/8}. \end{align} [[/math]]

In turn, this means that

[[math]] \begin{equation} \label{eq:p} \sup_{k \in [d]} \frac{(g^\ast_k)}{\sigma \lambda_k} \leq 4 \sqrt{\log(1/\delta)}, \end{equation} [[/math]]

for [math] \delta \leq 1/2 [/math].

■

Theorem

Fix [math]n \ge 2[/math]. Assume that the linear model~\eqref{EQ:regmod_matrix} holds where [math]\eps\sim \cN_n(0,\sigma^2 I_n)[/math]. Moreover, assume that [math]|\theta^*|_0\le k[/math] and that [math]\X[/math] satisfies assumption \textsf{INC$(k')$} with [math] k' \geq 4k \log(2de/k) [/math]. Then the Slope estimator [math]\thetaslope[/math] with regularization parameter defined by

[[math]] \begin{equation} \tau = 8 \sqrt{2} \sigma \sqrt{\frac{\log(1/\delta)}{n}} \end{equation} [[/math]]

satisfies

[[math]] \begin{equation} \label{EQ:fastMSESlope} \MSE(\X\thetaslope)=\frac{1}{n}|\X\thetaslope-\X\theta^*|_2^2 \lesssim \sigma^2\frac{k\log(2d/k) \log(1/\delta)}{n} \end{equation} [[/math]]

and

[[math]] \begin{equation} \label{EQ:fastL2slope} |\thetaslope-\theta^*|_2^2\lesssim \sigma^2\frac{k\log(2d/k) \log(1/\delta)}{n}\,.\end{equation} [[/math]]

with probability at least [math]1-\delta[/math].

The multplicative depedence on [math] \log(1/\delta) [/math] in \eqref{EQ:fastMSESlope} is an artifact of the simplified proof we give here and can be improved to an additive one similar to the lasso case, \eqref{EQ:fastMSELasso}, by appealing to stronger and more general concentration inequalities. For more details, see .

Show Proof

By minimality of [math] \thetaslope [/math] in \eqref{eq:ad}, adding [math] n \tau |\thetaslope - \theta^\ast|_\ast [/math] on both sides,

[[math]] \begin{equation} \label{eq:r} |\X\thetaslope-\X\theta^*|_2^2+n \tau |\thetaslope-\theta^*|_\ast \leq 2\eps^\top\X(\thetaslope-\theta^*) +n \tau |\thetaslope-\theta^*|_\ast+ 2 \tau n|\theta^*|_\ast- 2 \tau n|\thetaslope|_\ast \,. \end{equation} [[/math]]

Set

[[math]] \begin{equation} \label{eq:l} u := \thetaslope - \theta^\ast, \quad g_j = (\X^\top \varepsilon)_j, \end{equation} [[/math]]

By Lemma Linear Regression Model, we can estimate

[[math]] \begin{align} \label{eq:k} \varepsilon^\top \X u = {} & \sum_{j = 1}^{d} (\X^\top \varepsilon)_j u_j \leq \sum_{j = 1}^{d} g^\ast_j u^\ast_j\\ = {} & \sum_{j=1}^{d} \frac{g^\ast_j}{\lambda_j} (\lambda_j u^\ast_j)\\ \leq {} & \sup_{j} \left\{ \frac{g^\ast_j}{\lambda_j} \right\} | u |_\ast\\ \leq {} & 4 \sqrt{2} \sigma \sqrt{n \log(1/\delta)} | u |_\ast = \frac{n \tau}{2} |u|_\ast, \end{align} [[/math]]

where we used that [math] |\X_j|_2^2 \leq 2n [/math]. Pick a permutation [math] \phi [/math] such that [math] | \theta^\ast |_\ast = \sum_{j = 1}^{k} \lambda_j | \theta_{\phi(j)} | [/math] and [math] | u_{\phi(k+1)} | \geq \dots \geq | u_{\phi(d)}| [/math]. Then, noting that [math] \lambda_j [/math] is monotonically decreasing,

[[math]] \begin{align} \label{eq:q} | \theta^\ast |_\ast - | \thetaslope |_\ast = {} & \sum_{j=1}^{k} \lambda_j | \theta^\ast_{\phi(j)}| - \sum_{j = 1}^{d} \lambda_j (\thetaslope)^\ast_j\\ \leq {} & \sum_{j=1}^{k} \lambda_j ( | \theta^\ast_{\phi(j)} | - | \thetaslope_{\phi(j)} |) - \sum_{j=k+1}^{d} \lambda_j | \thetaslope_{\phi(j)} |\\ \leq {} & \sum_{j=1}^{k} \lambda_j | u_{\phi(j)} | - \sum_{j=k+1}^{d} \lambda_j u^\ast_j \\ \leq {} & \sum_{j=1}^{k} \lambda_j u^\ast_{j} - \sum_{j=k+1}^{d} \lambda_j u^\ast_j. \end{align} [[/math]]

Combined with [math] \tau = 8 \sqrt{2} \sigma \sqrt{\log(1/\delta)/n} [/math] and the basic inequality \eqref{eq:r}, we have that

[[math]] \begin{align} \label{eq:s} |\X\thetaslope-\X\theta^*|_2^2+n \tau |u|_\ast \leq {} & 2n \tau |u|_\ast + 2 \tau n |\theta^*|_\ast- 2 \tau n|\thetaslope|_\ast\\ \leq {} & 4 n \tau \sum_{j=1}^{k} \lambda_j u^\ast_j, \label{eq:w} \end{align} [[/math]]

whence

[[math]] \begin{equation} \label{eq:t} \sum_{j=k+1}^{d} \lambda_j u^\ast_j \leq 3 \sum_{j=1}^{k} \lambda_j u^\ast_j. \end{equation} [[/math]]

We can now repeat the incoherence arguments from Lemma Linear Regression Model, with [math] S [/math] being the [math] k [/math] largest entries of [math] |u| [/math], to get the same conclusion under the restriction [math] \textsf{INC}(k') [/math]. First, by exactly the same argument as in Lemma Linear Regression Model, we have

[[math]] \begin{equation} \label{eq:ah} \frac{|\X u_{S}|_2^2}{n} \ge | u_S |_2^2 - \frac{| u_{S} |_1^2}{32 k'} \ge | u_S |_2^2 - \frac{k}{32 k'} | u_S |_2^2. \end{equation} [[/math]]

Next, for the cross terms, we have

[[math]] \begin{align} \label{eq:u} 2\Big|u_S^\top \frac{ \X^\top\X}{n}u_{S^c}\Big| \leq {} & \frac{2}{32k'} \sum_{i=1}^{k} u^\ast_i \sum_{j=k+1}^{d} u^\ast_j\\ = {} & \frac{2}{32k'} \sum_{i=1}^{k} u^\ast_i \sum_{j=k+1}^{d} \frac{\lambda_j}{\lambda_j} u^\ast_j\\ \leq {} & \frac{2}{32k' \lambda_d} \sum_{i=1}^{k} u^\ast_i \sum_{j=k+1}^{d} \lambda_j u^\ast_j\\ \leq {} & \frac{6}{32k' \lambda_d} \sum_{i=1}^{k} u^\ast_i \sum_{j=1}^{k} \lambda_j u^\ast_j\\ \leq {} & \frac{6 \sqrt{k}}{32k' \lambda_d} \left(\sum_{i=1}^{k} \lambda_j^2\right)^{1/2} \sum_{i=1}^{k} (u^\ast_i)^2\\ \leq {} & \frac{6 k}{32k' \lambda_d} \sqrt{\log (2de/k)} | u_S |_2^2. \end{align} [[/math]]

where we estimated the sum by

[[math]] \begin{align} \sum_{j=1}^{k} \log \left( \frac{2d}{j} \right) = {} & k \log(2d) - \log(k!) \leq k \log(2d) - k \log(k/e)\\ = {} & k \log(2de/k), \end{align} [[/math]]

using Stirling's inequality, [math] k! \geq (k/e)^k [/math]. Finally, from a similar calculation, using the cone condition twice,

[[math]] \begin{equation} \label{eq:v} \frac{|\X u_{S^c}|_2^2}{n} \ge |u_{S^c}|_2^2-\frac{9k}{32k' \lambda_d^2} \log(2de/k) |u_S|_2^2. \end{equation} [[/math]]

Concluding, if [math] \textsf{INC}( k') [/math] holds with [math] k' \geq 4k \log(2de/k) [/math], taking into account that [math] \lambda_d \ge 1/2 [/math], we have

[[math]] \begin{equation} \label{eq:ak} \frac{| \X u |_2^2}{n} \ge | u_S |_2^2 + | u_{S^c} |_2^2 - \frac{36 + 12 + 1}{128} | u_S |_2^2 \ge \frac{1}{2} | u |_2^2. \end{equation} [[/math]]

Hence, from \eqref{eq:w},

[[math]] \begin{align} \label{eq:x} |\X u|_2^2+n \tau |u|_\ast \leq {} & 4 n \tau \left( \sum_{j=1}^{k} \lambda_j^2 \right)^{1/2} \left( \sum_{j=1}^{k} (u^\ast_j)^2 \right)^{1/2}\\ \leq {} & 4 \sqrt{2} \tau \sqrt{n k \log (2de/k)} | \X u |_2\\ = {} & 2^6 \sigma \sqrt{\log(1/\delta)} \sqrt{k \log(2de/k)} | \X u |_2, \end{align} [[/math]]

which combined yields

[[math]] \begin{equation} \label{eq:y} \frac{1}{n} | \X u |_2^2 \leq 2^{12} \sigma^2 \frac{k}{n} \log(2de/k) \log(1/\delta), \end{equation} [[/math]]

and

[[math]] \begin{equation} \label{eq:z} |u|_2^2 \leq 2^{13} \frac{k}{n} \sigma^2 \log(2de/k) \log(1/\delta). \qedhere \end{equation} [[/math]]

■

General references

Rigollet, Philippe; Hütter, Jan-Christian (2023). "High-Dimensional Statistics". arXiv:2310.19244 [math.ST].