guide:C64b6be05f: Difference between revisions
No edit summary |
mNo edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | <div class="d-none"><math> | ||
\newcommand{\smallfrac}[2]{\frac{#1}{#2}} | |||
\newcommand{\medfrac}[2]{\frac{#1}{#2}} | |||
\newcommand{\textfrac}[2]{\frac{#1}{#2}} | |||
\newcommand{\smallfrac}[2] | |||
\newcommand{\medfrac}[2] | |||
\newcommand{\textfrac}[2] | |||
\newcommand{\tr}{\operatorname{tr}} | \newcommand{\tr}{\operatorname{tr}} | ||
\newcommand{\e}{\operatorname{e}} | \newcommand{\e}{\operatorname{e}} | ||
\newcommand{\B}{\operatorname{B}} | \newcommand{\B}{\operatorname{B}} | ||
\newcommand{\Bbar}{\ | \newcommand{\Bbar}{\overline{\operatorname{B}}} | ||
\newcommand{\pr}{\operatorname{pr}} | \newcommand{\pr}{\operatorname{pr}} | ||
\newcommand{\dd}{\operatorname{d | \newcommand{\dd}{\operatorname{d}} | ||
\newcommand{\E}{\operatorname{E}} | \newcommand{\E}{\operatorname{E}} | ||
\newcommand{\V}{\operatorname{V}} | \newcommand{\V}{\operatorname{V}} | ||
\newcommand{\Cov}{\operatorname{Cov}} | \newcommand{\Cov}{\operatorname{Cov}} | ||
\newcommand{\Bigsum}[2] | \newcommand{\Bigsum}[2]{\mathop{\textstyle\sum}_{#1}^{#2}} | ||
\newcommand{\ran}{\operatorname{ran}} | \newcommand{\ran}{\operatorname{ran}} | ||
\newcommand{\ | \newcommand{\Conv}{\ast} | ||
\ | \renewcommand{\P}{\operatorname{P}} | ||
\renewcommand{\L}{\operatorname{L}} | |||
\newcommand{\mathds}{\mathbb}</math></div> | |||
We now turn to points that are chosen at random from the whole space according to a Gaussian distribution with mean zero and unit variance. Our first result is the so-called ''Gaussian Annulus Theorem'' which states that a point chosen at random will, with high probability, be located in a small annulus around the sphere with radius <math>\sqrt{d}</math>. On a first sight that might seem surprising as the density function has its largest values around zero and decays if we move away from zero. The results of Chapter [[guide:D9c33cd067|Concentration of measure]] however show that close to the origin there is located only little volume and since for the probability to be in a Borel set <math>A\subseteq\mathbb{R}^d</math> we ought to integrate the density function over <math>A</math>, the lack of volume around the origin makes this integral small if <math>A</math> is located in the vicinity of zero. At a certain radius then the concentration of volume compensates the smaller values of the density function. Going beyond this radius, the small values of the density function determine the value of the integral and make it small again. | |||
Before we can start, we need to fill in several facts about Gaussian random vectors, namely that | Before we can start, we need to fill in several facts about Gaussian random vectors, namely that | ||
<ul style="list-style-type:lower-alpha"><li> spherical Gaussian random vectors are precisely those which are independently coordinate-wise Gaussian [[#PROP-9-1 |(Proposition]]), | <ul style="list-style-type:lower-alpha"><li> spherical Gaussian random vectors are precisely those which are independently coordinate-wise Gaussian [[#PROP-9-1 |(Proposition]]), | ||
| Line 53: | Line 30: | ||
The reader familiar with the above can skip the proofs and jump directly to [[#LEM-10-1 |Lemma]] which will be the final preparation for the Gaussian Annulus Theorem. | The reader familiar with the above can skip the proofs and jump directly to [[#LEM-10-1 |Lemma]] which will be the final preparation for the Gaussian Annulus Theorem. | ||
{{proofcard|Proposition|PROP-9-1|Let <math>(\Omega,\Sigma,\P)</math> be a probability space and <math>X\colon\Omega\rightarrow\mathbb{R}^d</math> be a random vector with coordinate functions <math>X_1,\dots,X_d</math>. Then <math>X</math> is spherically Gaussian distributed with mean zero and variance <math>\sigma > 0</math> if and only if its coordinates are independent and | {{proofcard|Proposition|PROP-9-1|Let <math>(\Omega,\Sigma,\P)</math> be a probability space and <math>X\colon\Omega\rightarrow\mathbb{R}^d</math> be a random vector with coordinate functions <math>X_1,\dots,X_d</math>. Then <math>X</math> is spherically Gaussian distributed with mean zero and variance <math>\sigma > 0</math> if and only if its coordinates are independent and | ||
| Line 72: | Line 49: | ||
</math> | </math> | ||
where the first equality is true if <math>X\sim\mathcal{N}(0,1)</math> holds and the last if <math>X_i\sim\mathcal{N}(0,1)</math> for each <math>i=1,\dots,d</math>. This computation now shows both implications. | where the first equality is true if <math>X\sim\mathcal{N}(0,1)</math> holds and the last if <math>X_i\sim\mathcal{N}(0,1)</math> for each <math>i=1,\dots,d</math>. This computation now shows both implications. | ||
“<math>\Rightarrow</math>” Let <math>B\subseteq\mathbb{R}</math> be Borel and let <math>1\leqslant i\leqslant d</math> be fixed. Then we have <math>\P[X_i\in B] = \P[X\in\mathbb{R}^{i-1}\times{}B\times\mathbb{R}^{d-i}]</math> and reading the computation above from the beginning until line four shows | |||
<math display="block"> | <math display="block"> | ||
| Line 79: | Line 56: | ||
</math> | </math> | ||
as all the other integrals are equal to one. | as all the other integrals are equal to one. | ||
“<math>\Leftarrow</math>” Let <math>A=A_1\times\cdots\times A_d\subseteq\mathbb{R}^d</math> with bounded and open intervals <math>A_i\subseteq\mathbb{R}</math> be an open cuboid. Since the <math>X_i</math>'s are independent, we get <math>\P[X\in A] = \P[X_1\in A_1]\cdots\P[X_d\in A_d]</math>. Reading now our initial computation backwards until the very first equality, we get | |||
<math display="block"> | <math display="block"> | ||
| Line 103: | Line 80: | ||
where we used the independence of <math>X</math> and <math>Y</math> in the second equality and Tonelli's Theorem in the last. Since the rectangles generate the Borel <math>\sigma</math>-algebra, we get | where we used the independence of <math>X</math> and <math>Y</math> in the second equality and Tonelli's Theorem in the last. Since the rectangles generate the Borel <math>\sigma</math>-algebra, we get | ||
<span id="EQ-7-0"/> | <span id{{=}}"EQ-7-0"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EQ-7-0} | \begin{equation}\label{EQ-7-0} | ||
| Line 111: | Line 88: | ||
for every Borel set <math>A</math> which establishes the claim. Now we compute for <math>a < b</math> | for every Borel set <math>A</math> which establishes the claim. Now we compute for <math>a < b</math> | ||
<span id="EQ-7-1"/> | <span id{{=}}"EQ-7-1"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EQ-7-1} | \begin{equation}\label{EQ-7-1} | ||
| Line 121: | Line 98: | ||
</math> | </math> | ||
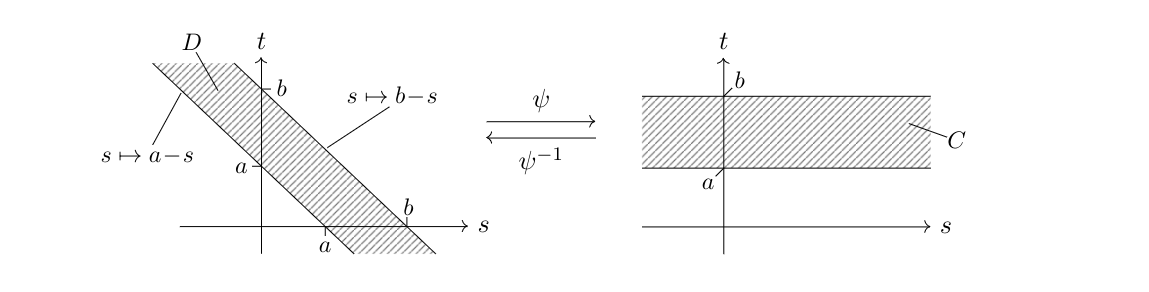
where <math>D = \{(s,t)\in\mathbb{R}^2\:;\:a < s+t < b\}</math> is a diagonal strip in the plane as illustrated on the left of following picture and \eqref{EQ-7-0} was used in the last equality. We put <math>C:=\mathbb{R}\times(a,b)</math> as shown on the right of the following picture and see that <math>\psi\colon C\rightarrow D</math>, <math>\psi(s,t)=(s,t-s)</math> is a diffeomorphism between open sets and <math>\det(\operatorname{J}_{\psi}(s,t))=1</math> holds for all <math>(s,t)\in C</math>. | where <math>D = \{(s,t)\in\mathbb{R}^2\:;\:a < s+t < b\}</math> is a diagonal strip in the plane as illustrated on the left of following picture and \eqref{EQ-7-0} was used in the last equality. We put <math>C:=\mathbb{R}\times(a,b)</math> as shown on the right of the following picture and see that <math>\psi\colon C\rightarrow D</math>, <math>\psi(s,t)=(s,t-s)</math> is a diffeomorphism between open sets and <math>\det(\operatorname{J}_{\psi}(s,t))=1</math> holds for all <math>(s,t)\in C</math>. | ||
<div class{{=}}"d-flex justify-content-center"> | |||
[[File:tikzbbc59b1b.png | 600px ]] | |||
</div> | |||
[[File: | |||
</div> | |||
We can thus apply the change of variables formula and compute | We can thus apply the change of variables formula and compute | ||
<span id="EQ-7-2"/> | <span id{{=}}"EQ-7-2"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EQ-7-2} | \begin{equation}\label{EQ-7-2} | ||
| Line 153: | Line 122: | ||
</math> | </math> | ||
holds for every Borel set as desired.}} | holds for every Borel set as desired.}} | ||
In order to extend the above to more than two summands, we need to establish first that the convolution of density functions is commutative and associative. | In order to extend the above to more than two summands, we need to establish first that the convolution of density functions is commutative and associative. | ||
| Line 162: | Line 132: | ||
</math> | </math> | ||
holds for every <math>s\in\mathbb{R}</math>. | holds for every <math>s\in\mathbb{R}</math>. | ||
The proof of [[#SUM-GAUSS-LEM-0 |Lemma]] shows as a byproduct that the convolution of any two density functions is again a density function and in particular integrable. We thus get | The proof of [[#SUM-GAUSS-LEM-0 |Lemma]] shows as a byproduct that the convolution of any two density functions is again a density function and in particular integrable. We thus get | ||
| Line 187: | Line 157: | ||
where the second equality holds as the <math>X_i</math> are independent. We now denote by <math>\rho = (2\pi)^{-1/2}\exp(-x/2)</math> the Gaussian density with mean zero and variance one. Then we need to show that | where the second equality holds as the <math>X_i</math> are independent. We now denote by <math>\rho = (2\pi)^{-1/2}\exp(-x/2)</math> the Gaussian density with mean zero and variance one. Then we need to show that | ||
<span id="EQ-GAUSS"/> | <span id{{=}}"EQ-GAUSS"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EQ-GAUSS} | \begin{equation}\label{EQ-GAUSS} | ||
| Line 195: | Line 165: | ||
holds where on the left hand side <math>d</math>--many <math>\rho</math>'s appear. We will now show \eqref{EQ-GAUSS} for <math>d=2</math>. The extension to general <math>d</math> is then immediate by iteration. We compute for arbitrary <math>s\in\mathbb{R}</math> | holds where on the left hand side <math>d</math>--many <math>\rho</math>'s appear. We will now show \eqref{EQ-GAUSS} for <math>d=2</math>. The extension to general <math>d</math> is then immediate by iteration. We compute for arbitrary <math>s\in\mathbb{R}</math> | ||
<span id="CONV-COMP"/> | <span id{{=}}"CONV-COMP"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{CONV-COMP} | \begin{equation}\label{CONV-COMP} | ||
| Line 251: | Line 221: | ||
where the integral can be seen to be one by the substitution <math>u:=t-(bs)/c</math>. Iteration of this completes the proof.}} | where the integral can be seen to be one by the substitution <math>u:=t-(bs)/c</math>. Iteration of this completes the proof.}} | ||
We mention that [[#LK-GAUSS-LEM |Proposition]] extends further to the case of a linear combination of arbitrary Gaussian random variables which not necessarily have mean zero or unit variance. The proof then becomes again one step more complicated than the above, as the means <math>\mu_i</math> appear inside the exponential functions. Since for our purposes below the result as stated above will be sufficient, we leave this last generalization to the reader as [[ | We mention that [[#LK-GAUSS-LEM |Proposition]] extends further to the case of a linear combination of arbitrary Gaussian random variables which not necessarily have mean zero or unit variance. The proof then becomes again one step more complicated than the above, as the means <math>\mu_i</math> appear inside the exponential functions. Since for our purposes below the result as stated above will be sufficient, we leave this last generalization to the reader as [[exercise:Ef47114a42 |Problem]]. | ||
Our final preparation is the following formula for the integral of the Gaussian function against a polynomial which we will need, in order to estimate moments in the next proof. | Our final preparation is the following formula for the integral of the Gaussian function against a polynomial which we will need, in order to estimate moments in the next proof. | ||
| Line 312: | Line 282: | ||
|Let a random vector <math>X\sim\mathcal{N}(0,1)</math> be given and let <math>X_1,\dots,X_d</math> denote its coordinate functions. By [[#PROP-9-1 |Proposition]] we have <math>X_i\sim\mathcal{N}(0,1)</math> for every <math>i=1,\dots,d</math>. We define <math>Y_i:=(X_i^2-1)/2</math> and see that | |Let a random vector <math>X\sim\mathcal{N}(0,1)</math> be given and let <math>X_1,\dots,X_d</math> denote its coordinate functions. By [[#PROP-9-1 |Proposition]] we have <math>X_i\sim\mathcal{N}(0,1)</math> for every <math>i=1,\dots,d</math>. We define <math>Y_i:=(X_i^2-1)/2</math> and see that | ||
<span id="EQ-10-1"/> | <span id{{=}}"EQ-10-1"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EQ-10-1} | \begin{equation}\label{EQ-10-1} | ||
| Line 365: | Line 335: | ||
</math> | </math> | ||
Finally, we recall that the constant in [[guide:B846f441d7#MTB-THM |Theorem]] was <math>C=1/4</math> and thus the exponent equals <math>-c\epsilon^2</math> with <math>c=1/16</math>.}} | Finally, we recall that the constant in [[guide:B846f441d7#MTB-THM |Theorem]] was <math>C=1/4</math> and thus the exponent equals <math>-c\epsilon^2</math> with <math>c=1/16</math>.}} | ||
In Chapter | |||
In Chapter [[guide:4ed4d3330a|The curse of high dimensions]] we propagated the intuition that a point chosen at random will have norm close to <math>\sqrt{d}</math> with ‘a high probability.’ More precisely, [[#FIG-1|Figure]] suggested that the deviation from <math>\sqrt{d}</math> to be expected will not increase with <math>d</math>. [[#GA-THM |Theorem]] allows to quantify this intuition as follows. If we pick, e.g., <math>\epsilon=10</math> then a random point's norm will satisfy <math>\sqrt{d}-10\leqslant \|x\|\leqslant \sqrt{d}+10</math> with probability greater or equal to <math>0.99</math> whenever we are in a space with dimension <math>d\geqslant100</math>. | |||
We note the following byproduct the proof of [[#GA-THM |Theorem]] which gives a similar estimate but of the square of the norm. Notice that one of our first results in Chapter | |||
We note the following byproduct the proof of [[#GA-THM |Theorem]] which gives a similar estimate but of the square of the norm. Notice that one of our first results in Chapter [[guide:4ed4d3330a|The curse of high dimensions]] was the equality <math>\E(\|X\|^2)=d</math> for any fixed <math>d</math>---and that we on the other hand proved a statement without the squares, namely <math>\E(\|X\|)\approx\sqrt{d}</math>, asymptotically. | |||
{{proofcard|Proposition|GA-COR|Let <math>x\in\mathbb{R}^d</math> be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then | {{proofcard|Proposition|GA-COR|Let <math>x\in\mathbb{R}^d</math> be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then | ||
| Line 382: | Line 353: | ||
which leads to the claimed inequality taking <math>C=1/4</math> into account.}} | which leads to the claimed inequality taking <math>C=1/4</math> into account.}} | ||
In the next two theorems we divide by <math>\|x\|</math> and <math>\|y\|</math> where <math>x</math> and <math>y</math> are picked at random. Notice however that <math>x=0</math> or <math>y=0</math> occurs only with probability zero. To be completely precise, we could use the conditional probability <math>\P[|\langle{}x/\|x\|,y/\|y\|\rangle{}|\leqslant\epsilon\,|\,x\not=0\text{ and }y\not=0]</math>. We will instead tacitly assume this. Observe that the bound below is non-trivial if <math>\epsilon > 2/(\sqrt{d}-7)</math>. In this result it thus possible to think of <math>\epsilon\rightarrow0</math>, ''but only if simultaneously <math>d\rightarrow\infty</math> suitably fast''. | In the next two theorems we divide by <math>\|x\|</math> and <math>\|y\|</math> where <math>x</math> and <math>y</math> are picked at random. Notice however that <math>x=0</math> or <math>y=0</math> occurs only with probability zero. To be completely precise, we could use the conditional probability <math>\P[|\langle{}x/\|x\|,y/\|y\|\rangle{}|\leqslant\epsilon\,|\,x\not=0\text{ and }y\not=0]</math>. We will instead tacitly assume this. Observe that the bound below is non-trivial if <math>\epsilon > 2/(\sqrt{d}-7)</math>. In this result it thus possible to think of <math>\epsilon\rightarrow0</math>, ''but only if simultaneously <math>d\rightarrow\infty</math> suitably fast''. | ||
{{proofcard|Theorem|GO-THM|Let <math>x,y\in\mathbb{R}^d</math> be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then for every <math>\epsilon > 0</math> and for all <math>d\geqslant1</math> the estimate | {{proofcard|Theorem|GO-THM|Let <math>x,y\in\mathbb{R}^d</math> be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then for every <math>\epsilon > 0</math> and for all <math>d\geqslant1</math> the estimate | ||
| Line 444: | Line 415: | ||
[[#GO-THM |Theorem]] now also quantifies our intuition that two points chosen at random will have scalar product close to zero and thus will be ‘almost orthogonal’ with ‘a high probability.’ If we pick for instance <math>\epsilon = 0.1</math> and <math>d\geqslant 100\,000</math>, then by [[#GO-THM |Theorem]] we get that two points drawn at random will, with probability greater or equal to <math>0.9</math>, have (normalized) scalar product less or equal to <math>0.1</math>. This corresponds to an angle of <math>90^{\circ}\pm 6^{\circ}</math>. | [[#GO-THM |Theorem]] now also quantifies our intuition that two points chosen at random will have scalar product close to zero and thus will be ‘almost orthogonal’ with ‘a high probability.’ If we pick for instance <math>\epsilon = 0.1</math> and <math>d\geqslant 100\,000</math>, then by [[#GO-THM |Theorem]] we get that two points drawn at random will, with probability greater or equal to <math>0.9</math>, have (normalized) scalar product less or equal to <math>0.1</math>. This corresponds to an angle of <math>90^{\circ}\pm 6^{\circ}</math>. | ||
The proof of the previous result shows also the following. | The proof of the previous result shows also the following. | ||
{{proofcard|Corollary|COR-ANGLE-ESTIM|Let <math>X\sim\mathcal{N}(0,1,\mathbb{R}^d)</math> and <math>0\not=\xi\in\mathbb{R}^d</math> be fixed. Then we have | {{proofcard|Corollary|COR-ANGLE-ESTIM|Let <math>X\sim\mathcal{N}(0,1,\mathbb{R}^d)</math> and <math>0\not=\xi\in\mathbb{R}^d</math> be fixed. Then we have | ||
| Line 461: | Line 432: | ||
which establishes the result.}} | which establishes the result.}} | ||
Since the probability that two random points are ''exactly'' orthogonal is obviously zero, we have on the other hand to expect that the probability of being ''very'' close to zero is again small. The estimate below is non-trivial if <math>\epsilon < 1</math> and <math>d > 16\ln(\frac{2}{1-\epsilon})</math>. In particular we can now let <math>\epsilon</math> tend to zero ''for a fixed <math>d</math>'' if we wish so. However, the threshold on the left hand side tends to zero for <math>d\rightarrow\infty</math> even if we fix <math>0 < \epsilon < 1</math> since we divide by <math>\sqrt{d}</math> inside the square bracket. | Since the probability that two random points are ''exactly'' orthogonal is obviously zero, we have on the other hand to expect that the probability of being ''very'' close to zero is again small. The estimate below is non-trivial if <math>\epsilon < 1</math> and <math>d > 16\ln(\frac{2}{1-\epsilon})</math>. In particular we can now let <math>\epsilon</math> tend to zero ''for a fixed <math>d</math>'' if we wish so. However, the threshold on the left hand side tends to zero for <math>d\rightarrow\infty</math> even if we fix <math>0 < \epsilon < 1</math> since we divide by <math>\sqrt{d}</math> inside the square bracket. | ||
| Line 487: | Line 458: | ||
where we used [[#GA-THM |Theorem]] and the formula for <math>\P\bigl[|U_Y(X)|\leqslant \delta\bigr]</math> that we established in the proof of [[#GO-THM |Theorem]].}} | where we used [[#GA-THM |Theorem]] and the formula for <math>\P\bigl[|U_Y(X)|\leqslant \delta\bigr]</math> that we established in the proof of [[#GO-THM |Theorem]].}} | ||
If we now fix the dimension such that the exponential term is already quite small (e.g., <math>d=100</math>, then <math>2\exp(-cd) < 0.01</math>) and pick, e.g., <math>\epsilon=0.1</math>, then the result shows that the (normalized) scalar product of two random points is less than <math>0.005</math> only with a probability less than <math>0.11</math>. | If we now fix the dimension such that the exponential term is already quite small (e.g., <math>d=100</math>, then <math>2\exp(-cd) < 0.01</math>) and pick, e.g., <math>\epsilon=0.1</math>, then the result shows that the (normalized) scalar product of two random points is less than <math>0.005</math> only with a probability less than <math>0.11</math>. | ||
Combining the last two results we can think of the scalar products for a fixed high dimension <math>d</math>, with high probability, to be small numbers which are however bounded away from zero. | Combining the last two results we can think of the scalar products for a fixed high dimension <math>d</math>, with high probability, to be small numbers which are however bounded away from zero. | ||
Our last result in this section quantifies our finding from Chapter | Our last result in this section quantifies our finding from Chapter [[guide:4ed4d3330a|The curse of high dimensions]] that for two points <math>x</math> and <math>y</math> drawn at random from a unit Gaussian we have <math>\|x-y\|\approx\sqrt{2d}</math>. Using <math>\epsilon=18</math> in (ii) below shows that the values possible for the dimension are <math>d > 324</math>. In this case the estimate is however still trivial. Interesting cases appear only if <math>\epsilon > 18</math> and <math>d</math> so large that the sum on the right hand side of (ii) stays below one. | ||
{{proofcard|Theorem|THM-distance-of-two-points-sqrt-2d|Let <math>x</math>, <math>y\in\mathbb{R}^d</math> be drawn at random with respect to a spherical Gaussian distribution with zero mean and unit variance. Then we have the following. | {{proofcard|Theorem|THM-distance-of-two-points-sqrt-2d|Let <math>x</math>, <math>y\in\mathbb{R}^d</math> be drawn at random with respect to a spherical Gaussian distribution with zero mean and unit variance. Then we have the following. | ||
<ul style="list-style-type:lower-roman"><li> <math>\forall\:\epsilon > 18\;\exists\:d_0\in\mathbb{N}\;\forall\:d\geqslant d_0\colon \P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon}.</math> | <ul style{{=}}"list-style-type:lower-roman"><li> <math>\forall\:\epsilon > 18\;\exists\:d_0\in\mathbb{N}\;\forall\:d\geqslant d_0\colon \P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon}.</math> | ||
</li> | </li> | ||
<li> <math>\forall\:\epsilon > 18,\,d\geqslant\epsilon^2\colon\P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon} +\medfrac{8}{\sqrt{d}}.</math> | <li> <math>\forall\:\epsilon > 18,\,d\geqslant\epsilon^2\colon\P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon} +\medfrac{8}{\sqrt{d}}.</math> | ||
| Line 520: | Line 491: | ||
where we used <math>\sqrt{d}\geqslant\epsilon</math> for the second estimate. This leads to | where we used <math>\sqrt{d}\geqslant\epsilon</math> for the second estimate. This leads to | ||
<span id="EST-1"/> | <span id{{=}}"EST-1"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EST-1} | \begin{equation}\label{EST-1} | ||
| Line 540: | Line 511: | ||
where we used [[#GA-COR |Proposition]] with <math>\epsilon=d</math> to treat the second factor in the last estimate. Bringing the squared factor in the last expression on the other side and recalling <math>\delta:=\epsilon/(6\sqrt{2d})</math> leads to | where we used [[#GA-COR |Proposition]] with <math>\epsilon=d</math> to treat the second factor in the last estimate. Bringing the squared factor in the last expression on the other side and recalling <math>\delta:=\epsilon/(6\sqrt{2d})</math> leads to | ||
<span id="EST-2"/> | <span id{{=}}"EST-2"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation}\label{EST-2} | \begin{equation}\label{EST-2} | ||
| Line 574: | Line 545: | ||
as desired.}} | as desired.}} | ||
Since we do need this later, let us formulate the following probability estimate that we established in the proof above. | Since we do need this later, let us formulate the following probability estimate that we established in the proof above. | ||
{{proofcard|Corollary|COR-distance-of-two-points-sqrt-2d|Let <math>x</math>, <math>y\in\mathbb{R}^d</math> be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then | {{proofcard|Corollary|COR-distance-of-two-points-sqrt-2d|Let <math>x</math>, <math>y\in\mathbb{R}^d</math> be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then | ||
| Line 579: | Line 551: | ||
\forall\:\epsilon > 18,\,d\geqslant\epsilon^2\colon \P\bigl[\bigl|\|x-y\|^2-2d\bigr|\geqslant\epsilon\sqrt{2d}\bigr]\leqslant \medfrac{18}{\epsilon}+\medfrac{8}{\sqrt{d}} | \forall\:\epsilon > 18,\,d\geqslant\epsilon^2\colon \P\bigl[\bigl|\|x-y\|^2-2d\bigr|\geqslant\epsilon\sqrt{2d}\bigr]\leqslant \medfrac{18}{\epsilon}+\medfrac{8}{\sqrt{d}} | ||
</math> | </math> | ||
holds. | holds.|}} | ||
==General references== | |||
{{cite arXiv|last1=Wegner|first1=Sven-Ake|year=2024|title=Lecture Notes on High-Dimensional Data|eprint=2101.05841|class=math.FA}} | {{cite arXiv|last1=Wegner|first1=Sven-Ake|year=2024|title=Lecture Notes on High-Dimensional Data|eprint=2101.05841|class=math.FA}} | ||
Latest revision as of 23:48, 1 June 2024
We now turn to points that are chosen at random from the whole space according to a Gaussian distribution with mean zero and unit variance. Our first result is the so-called Gaussian Annulus Theorem which states that a point chosen at random will, with high probability, be located in a small annulus around the sphere with radius [math]\sqrt{d}[/math]. On a first sight that might seem surprising as the density function has its largest values around zero and decays if we move away from zero. The results of Chapter Concentration of measure however show that close to the origin there is located only little volume and since for the probability to be in a Borel set [math]A\subseteq\mathbb{R}^d[/math] we ought to integrate the density function over [math]A[/math], the lack of volume around the origin makes this integral small if [math]A[/math] is located in the vicinity of zero. At a certain radius then the concentration of volume compensates the smaller values of the density function. Going beyond this radius, the small values of the density function determine the value of the integral and make it small again.
Before we can start, we need to fill in several facts about Gaussian random vectors, namely that
- spherical Gaussian random vectors are precisely those which are independently coordinate-wise Gaussian (Proposition),
- a linear combination of normal random variables is Gaussian with mean zero and variance given by the sum of the squares of the coefficients (Proposition).
The reader familiar with the above can skip the proofs and jump directly to Lemma which will be the final preparation for the Gaussian Annulus Theorem.
Let [math](\Omega,\Sigma,\P)[/math] be a probability space and [math]X\colon\Omega\rightarrow\mathbb{R}^d[/math] be a random vector with coordinate functions [math]X_1,\dots,X_d[/math]. Then [math]X[/math] is spherically Gaussian distributed with mean zero and variance [math]\sigma \gt 0[/math] if and only if its coordinates are independent and
Let [math]A=A_1\times\cdots\times A_d\subseteq\mathbb{R}^d[/math] be given with Borel sets [math]A_i\subseteq\mathbb{R}[/math]. By Fubini's Theorem we compute
“[math]\Rightarrow[/math]” Let [math]B\subseteq\mathbb{R}[/math] be Borel and let [math]1\leqslant i\leqslant d[/math] be fixed. Then we have [math]\P[X_i\in B] = \P[X\in\mathbb{R}^{i-1}\times{}B\times\mathbb{R}^{d-i}][/math] and reading the computation above from the beginning until line four shows
“[math]\Leftarrow[/math]” Let [math]A=A_1\times\cdots\times A_d\subseteq\mathbb{R}^d[/math] with bounded and open intervals [math]A_i\subseteq\mathbb{R}[/math] be an open cuboid. Since the [math]X_i[/math]'s are independent, we get [math]\P[X\in A] = \P[X_1\in A_1]\cdots\P[X_d\in A_d][/math]. Reading now our initial computation backwards until the very first equality, we get
As mentioned we need also to show that the distribution of the sum of Gaussian random variables is again Gaussian. We start with the case of two summands.
Let [math]X,\,Y\colon\Omega\rightarrow\mathbb{R}[/math] be independent real random variables with probability density functions [math]\rho[/math] and [math]\sigma[/math]. Then the random variable [math]X+Y[/math] has a probability density function which is given by the convolution [math]\rho\Conv\sigma\colon\mathbb{R}\rightarrow\mathbb{R}[/math], [math](\rho\Conv\sigma)(s)=\int_{\mathbb{R}}\rho(s-t)\sigma(t)\dd\lambda(t)[/math].
We first show that [math]\varphi\colon\mathbb{R}^2\rightarrow\mathbb{R}[/math], [math]\varphi(x,y):=\rho(x)\sigma(y)[/math] is a probability density function for the random vector [math][\begin{smallmatrix}X\\Y\end{smallmatrix}]\colon\Omega\rightarrow\mathbb{R}^2[/math]. Indeed, for a rectangle [math][a,b]\times[c,d]\subseteq\mathbb{R}^2[/math] with [math]a \lt b[/math] and [math]c \lt d[/math] we compute
We can thus apply the change of variables formula and compute
In order to extend the above to more than two summands, we need to establish first that the convolution of density functions is commutative and associative.
Let [math]\rho,\,\sigma,\,\tau\colon\mathbb{R}\rightarrow\mathbb{R}[/math] be integrable. Then we have [math]\rho\Conv\sigma=\sigma\Conv\rho[/math] and [math](\rho\Conv\sigma)\Conv\tau=\rho\Conv(\sigma\Conv\tau)[/math].
By substituting [math]u:=s-t[/math] we see that
The proof of Lemma shows as a byproduct that the convolution of any two density functions is again a density function and in particular integrable. We thus get
In view of Lemma we can drop parentheses and simply write [math]\rho_1\Conv\cdots\Conv\rho_n[/math] for the convolution of [math]n[/math] density functions. Employing this, we can now extend Lemma to the sum of more than two random variables.
For [math]i=1,\dots,d[/math] let [math]X_i\colon\Omega\rightarrow\mathbb{R}[/math] be independent Gaussian random variables with zero mean and unit variance. Then [math]X:=X_1+\cdots+X_d[/math] is a Gaussian random variable with mean zero and variance [math]d[/math].
Since the sum of measurable functions is measurable, [math]X=X_1+\cdots+X_d[/math] is a random variable. We compute
Let us now show what we later really need, namely the case of a linear combination of Gaussian random variables with zero mean and unit variance.
For [math]i=1,\dots,d[/math] let [math]X_i\sim\mathcal{N}(0,1)[/math] be independent Gaussian random variables and let [math]\lambda_i\not=0[/math] be real number. Then [math]X:=\lambda_1X_1+\cdots+\lambda_dX_d\sim\mathcal{N}(0,\sigma^2)[/math] with [math]\sigma^2:=\lambda_1^2+\cdots+\lambda_d^2\not=0[/math].
We observe that for [math]\lambda\not=0[/math], [math]X\sim\mathcal{N}(0,1)[/math] and a Borel set [math]A[/math] the following holds
We mention that Proposition extends further to the case of a linear combination of arbitrary Gaussian random variables which not necessarily have mean zero or unit variance. The proof then becomes again one step more complicated than the above, as the means [math]\mu_i[/math] appear inside the exponential functions. Since for our purposes below the result as stated above will be sufficient, we leave this last generalization to the reader as Problem.
Our final preparation is the following formula for the integral of the Gaussian function against a polynomial which we will need, in order to estimate moments in the next proof.
For [math]k\in\mathbb{N}[/math] the equality
We first use Lebesgue's Theorem to see that
Now we can prove the first main result of this chapter. Notice that the inequality is only non-trivial, i.e., the right hand side strictly less than one, if [math]\epsilon \gt 4\ln2\,(\approx2.8)[/math] holds. This means, although we are using the variable [math]\epsilon[/math] here, the typical intuition that we can let [math]\epsilon\rightarrow0[/math] does not apply.
(Gaussian Annulus Theorem) Let [math]x\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then
Let a random vector [math]X\sim\mathcal{N}(0,1)[/math] be given and let [math]X_1,\dots,X_d[/math] denote its coordinate functions. By Proposition we have [math]X_i\sim\mathcal{N}(0,1)[/math] for every [math]i=1,\dots,d[/math]. We define [math]Y_i:=(X_i^2-1)/2[/math] and see that
In Chapter The curse of high dimensions we propagated the intuition that a point chosen at random will have norm close to [math]\sqrt{d}[/math] with ‘a high probability.’ More precisely, Figure suggested that the deviation from [math]\sqrt{d}[/math] to be expected will not increase with [math]d[/math]. Theorem allows to quantify this intuition as follows. If we pick, e.g., [math]\epsilon=10[/math] then a random point's norm will satisfy [math]\sqrt{d}-10\leqslant \|x\|\leqslant \sqrt{d}+10[/math] with probability greater or equal to [math]0.99[/math] whenever we are in a space with dimension [math]d\geqslant100[/math].
We note the following byproduct the proof of Theorem which gives a similar estimate but of the square of the norm. Notice that one of our first results in Chapter The curse of high dimensions was the equality [math]\E(\|X\|^2)=d[/math] for any fixed [math]d[/math]---and that we on the other hand proved a statement without the squares, namely [math]\E(\|X\|)\approx\sqrt{d}[/math], asymptotically.
Let [math]x\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then
We define the random variables [math]Y_i[/math] as in the proof of Theorem and then proceed using the Bernstein inequality as in the last part of the previous proof. This way we obtain
In the next two theorems we divide by [math]\|x\|[/math] and [math]\|y\|[/math] where [math]x[/math] and [math]y[/math] are picked at random. Notice however that [math]x=0[/math] or [math]y=0[/math] occurs only with probability zero. To be completely precise, we could use the conditional probability [math]\P[|\langle{}x/\|x\|,y/\|y\|\rangle{}|\leqslant\epsilon\,|\,x\not=0\text{ and }y\not=0][/math]. We will instead tacitly assume this. Observe that the bound below is non-trivial if [math]\epsilon \gt 2/(\sqrt{d}-7)[/math]. In this result it thus possible to think of [math]\epsilon\rightarrow0[/math], but only if simultaneously [math]d\rightarrow\infty[/math] suitably fast.
Let [math]x,y\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then for every [math]\epsilon \gt 0[/math] and for all [math]d\geqslant1[/math] the estimate
Let [math]y\in\mathbb{R}^d\backslash\{0\}[/math] be fixed and let [math]X\colon\Omega\rightarrow\mathbb{R}^d[/math] be a random vector with [math]X\sim\mathcal{N}(0,1)[/math] whose coordinate functions we denote by [math]X_i[/math] for [math]i=1,\dots d[/math]. We define
Theorem now also quantifies our intuition that two points chosen at random will have scalar product close to zero and thus will be ‘almost orthogonal’ with ‘a high probability.’ If we pick for instance [math]\epsilon = 0.1[/math] and [math]d\geqslant 100\,000[/math], then by Theorem we get that two points drawn at random will, with probability greater or equal to [math]0.9[/math], have (normalized) scalar product less or equal to [math]0.1[/math]. This corresponds to an angle of [math]90^{\circ}\pm 6^{\circ}[/math].
The proof of the previous result shows also the following.
Let [math]X\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math] and [math]0\not=\xi\in\mathbb{R}^d[/math] be fixed. Then we have
In the notation of the proof of Theorem we calculate
Since the probability that two random points are exactly orthogonal is obviously zero, we have on the other hand to expect that the probability of being very close to zero is again small. The estimate below is non-trivial if [math]\epsilon \lt 1[/math] and [math]d \gt 16\ln(\frac{2}{1-\epsilon})[/math]. In particular we can now let [math]\epsilon[/math] tend to zero for a fixed [math]d[/math] if we wish so. However, the threshold on the left hand side tends to zero for [math]d\rightarrow\infty[/math] even if we fix [math]0 \lt \epsilon \lt 1[/math] since we divide by [math]\sqrt{d}[/math] inside the square bracket.
Let [math]x[/math], [math]y\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then for [math]\epsilon \gt 0[/math] and [math]d\geqslant1[/math] we have
Let [math]X,Y\colon\Omega\rightarrow\mathbb{R}^d[/math] be random vectors with normal distribution. Let [math]U_Y(X)[/math] be defined as in the proof of Theorem. We compute
If we now fix the dimension such that the exponential term is already quite small (e.g., [math]d=100[/math], then [math]2\exp(-cd) \lt 0.01[/math]) and pick, e.g., [math]\epsilon=0.1[/math], then the result shows that the (normalized) scalar product of two random points is less than [math]0.005[/math] only with a probability less than [math]0.11[/math].
Combining the last two results we can think of the scalar products for a fixed high dimension [math]d[/math], with high probability, to be small numbers which are however bounded away from zero.
Our last result in this section quantifies our finding from Chapter The curse of high dimensions that for two points [math]x[/math] and [math]y[/math] drawn at random from a unit Gaussian we have [math]\|x-y\|\approx\sqrt{2d}[/math]. Using [math]\epsilon=18[/math] in (ii) below shows that the values possible for the dimension are [math]d \gt 324[/math]. In this case the estimate is however still trivial. Interesting cases appear only if [math]\epsilon \gt 18[/math] and [math]d[/math] so large that the sum on the right hand side of (ii) stays below one.
Let [math]x[/math], [math]y\in\mathbb{R}^d[/math] be drawn at random with respect to a spherical Gaussian distribution with zero mean and unit variance. Then we have the following.
- [math]\forall\:\epsilon \gt 18\;\exists\:d_0\in\mathbb{N}\;\forall\:d\geqslant d_0\colon \P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon}.[/math]
- [math]\forall\:\epsilon \gt 18,\,d\geqslant\epsilon^2\colon\P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon} +\medfrac{8}{\sqrt{d}}.[/math]
We use the same trick as in the beginning of the proof of the Gaussian Annulus Theorem (Theorem) and then use the cosine law to get
Since we do need this later, let us formulate the following probability estimate that we established in the proof above.
Let [math]x[/math], [math]y\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then
General references
Wegner, Sven-Ake (2024). "Lecture Notes on High-Dimensional Data". arXiv:2101.05841 [math.FA].