guide:69043688f2: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
\newcommand{\mathds}{\mathbb}</math></div> | \newcommand{\mathds}{\mathbb}</math></div> | ||
We are now in a position to prove our first fundamental theorem of probability. | We are now in a position to prove our first fundamental theorem of probability. | ||
We have seen that an intuitive way to view the probability of a certain outcome is as the | We have seen that an intuitive way to view the probability of a certain outcome is as the | ||
| Line 15: | Line 15: | ||
with the frequency interpretation of probability. This theorem is sometimes called the ''law | with the frequency interpretation of probability. This theorem is sometimes called the ''law | ||
of averages.'' To find out what would happen if this law were not true, see the article by | of averages.'' To find out what would happen if this law were not true, see the article by | ||
Robert M. Coates.<ref group="Notes" >R. | Robert M. Coates.<ref group="Notes" >R.M.Coates, “The Law,” ''The World of | ||
Mathematics,'' ed. James R. Newman (New York: Simon and Schuster, 1956.</ref> | Mathematics,'' ed. James R. Newman (New York: Simon and Schuster, 1956.</ref> | ||
| Line 27: | Line 27: | ||
<math display="block"> | <math display="block"> | ||
P(|X - \mu| \geq \epsilon) \leq \frac {V(X)}{\epsilon^2}\ . | P(|X - \mu| \geq \epsilon) \leq \frac {V(X)}{\epsilon^2}\ . | ||
</math> | </math>|Let <math>m(x)</math> denote the distribution function of <math>X</math>. Then the probability that <math>X</math> | ||
differs from <math>\mu</math> by at least <math>\epsilon</math> is given by | differs from <math>\mu</math> by at least <math>\epsilon</math> is given by | ||
| Line 60: | Line 60: | ||
Note that <math>X</math> in the above theorem can be any discrete random variable, and | Note that <math>X</math> in the above theorem can be any discrete random variable, and | ||
<math>\epsilon</math> any positive number. | <math>\epsilon</math> any positive number. | ||
'''Example''' | '''Example''' | ||
Let <math>X</math> by any random variable with <math>E(X) = \mu</math> and <math>V(X) = \sigma^2</math>. Then, | Let <math>X</math> by any random variable with <math>E(X) = \mu</math> and <math>V(X) = \sigma^2</math>. Then, | ||
| Line 91: | Line 92: | ||
===Law of Large Numbers=== | ===Law of Large Numbers=== | ||
{{proofcard|Theorem|theorem-2|''' (Law of Large Numbers)''' | {{proofcard|Theorem|theorem-2|''' (Law of Large Numbers)''' | ||
Let <math>X_1 | Let <math>X_1,X_2, \ldots, X_n</math> be an independent trials process, with | ||
finite expected value <math>\mu = E(X_j)</math> and finite variance <math>\sigma^2 = | finite expected value <math>\mu = E(X_j)</math> and finite variance <math>\sigma^2 = | ||
V(X_j)</math>. Let <math>S_n = X_1 + X_2 +\cdots+ X_n</math>. Then for | V(X_j)</math>. Let <math>S_n = X_1 + X_2 +\cdots+ X_n</math>. Then for | ||
| Line 106: | Line 107: | ||
P\left( \left| \frac {S_n}n - \mu \right| < \epsilon \right) \to 1 | P\left( \left| \frac {S_n}n - \mu \right| < \epsilon \right) \to 1 | ||
</math> | </math> | ||
as <math>n \rightarrow \infty</math>. | as <math>n \rightarrow \infty</math>.|Since <math>X_1,X_2, \ldots,X_n</math> are independent and have the same distributions, | ||
we can apply [[guide:C631488f9a#thm 6.9 |Theorem]]. We obtain | we can apply [[guide:C631488f9a#thm 6.9 |Theorem]]. We obtain | ||
| Line 147: | Line 148: | ||
predicted with a high degree of certainty. The Law of Large Numbers, as we | predicted with a high degree of certainty. The Law of Large Numbers, as we | ||
have stated it, is often called the “Weak Law of Large Numbers” to | have stated it, is often called the “Weak Law of Large Numbers” to | ||
distinguish it from the “Strong Law of Large Numbers” described in | distinguish it from the “Strong Law of Large Numbers” described in [[exercise:1d6f182f87 |Exercise]]. | ||
Consider the important special case of Bernoulli trials with probability <math>p</math> | Consider the important special case of Bernoulli trials with probability <math>p</math> | ||
for success. Let <math>X_j = 1</math> if the <math>j</math>th outcome is a success and 0 if it is a | for success. Let <math>X_j = 1</math> if the <math>j</math>th outcome is a success and 0 if it is a | ||
| Line 169: | Line 169: | ||
of Large Numbers predicts that the outcomes for this random variable will, for | of Large Numbers predicts that the outcomes for this random variable will, for | ||
large <math>n</math>, be near 1/2. | large <math>n</math>, be near 1/2. | ||
In | |||
In [[#fig 8.1|Figure]], we have plotted the distribution for this example for increasing values of | |||
<math>n</math>. We have marked the outcomes between .45 and .55 by dots at the top of the | <math>n</math>. We have marked the outcomes between .45 and .55 by dots at the top of the | ||
spikes. We see that as | spikes. We see that as <math>n</math> increases the distribution gets more and more concentrated around .5 and a larger | ||
<math>n</math> increases the distribution gets more and more concentrated around .5 and a larger | |||
and larger percentage of the total area is contained within the interval | and larger percentage of the total area is contained within the interval | ||
<math>(.45,.55)</math>, as predicted by the Law of Large Numbers. | <math>(.45,.55)</math>, as predicted by the Law of Large Numbers. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig8-1. | <div id="fig 8.1" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig8-1.png | 600px | thumb | Bernoulli trials distributions. ]] | |||
</div> | </div> | ||
===Die Rolling=== | |||
'''Example''' | '''Example''' | ||
Consider <math>n</math> rolls of a die. Let <math>X_j</math> be the outcome of the <math>j</math>th roll. Then | Consider <math>n</math> rolls of a die. Let <math>X_j</math> be the outcome of the <math>j</math>th roll. Then | ||
| Line 207: | Line 208: | ||
In the following example, we compare the estimates given by Chebyshev's Inequality with the | In the following example, we compare the estimates given by Chebyshev's Inequality with the | ||
actual values. | actual values. | ||
'''Example''' | '''Example''' | ||
Let <math>X_1 | Let <math>X_1, X_2, \ldots, X_n</math> be a Bernoulli trials process with | ||
probability .3 for success and .7 for failure. Let <math>X_j = 1</math> if the <math>j</math>th | probability .3 for success and .7 for failure. Let <math>X_j = 1</math> if the <math>j</math>th | ||
outcome is a success and 0 otherwise. Then, <math>E(X_j) = .3</math> and <math>V(X_j) = | outcome is a success and 0 otherwise. Then, <math>E(X_j) = .3</math> and <math>V(X_j) = | ||
| Line 263: | Line 265: | ||
more difficult than the proof we have presented using Chebyshev's inequality. | more difficult than the proof we have presented using Chebyshev's inequality. | ||
Chebyshev developed his inequality to prove a general form of the Law of Large | Chebyshev developed his inequality to prove a general form of the Law of Large | ||
Numbers (see | Numbers (see [[exercise:C07205adb1 |Exercise]]). The inequality itself appeared | ||
much earlier in a work by Bienaymé, and in discussing its history | much earlier in a work by Bienaymé, and in discussing its history | ||
Maistrov remarks that it was referred to as the Bienaymé-Chebyshev | Maistrov remarks that it was referred to as the Bienaymé-Chebyshev | ||
Inequality for a long time.<ref group="Notes" >L. E. Maistrov, ''Probability Theory: A Historical | Inequality for a long time.<ref group="Notes" >L. E. Maistrov, ''Probability Theory: A Historical | ||
Approach,'' trans. | Approach,'' trans. and ed. Samual Kotz, (New York: Academic Press, 1974), | ||
p. 202</ref> | p. 202</ref> | ||
In ''Ars Conjectandi'' Bernoulli provides his reader with a long discussion | In ''Ars Conjectandi'' Bernoulli provides his reader with a long discussion | ||
| Line 291: | Line 293: | ||
nature ''per se'' and by no previous instruction (this is truly amazing)--- | nature ''per se'' and by no previous instruction (this is truly amazing)--- | ||
knows for sure that the more observations of this sort that are taken, the less | knows for sure that the more observations of this sort that are taken, the less | ||
the danger will be of straying from the mark.<ref group="Notes" >Bernoulli, op. | the danger will be of straying from the mark.<ref group="Notes" >Bernoulli, op. cit., p. 38.</ref> | ||
</blockquote> | </blockquote> | ||
But he goes on to say that he must contemplate another possibility. | But he goes on to say that he must contemplate another possibility. | ||
| Line 326: | Line 328: | ||
past.<ref group="Notes" >ibid., pp. 65--66.</ref> | past.<ref group="Notes" >ibid., pp. 65--66.</ref> | ||
</blockquote> | </blockquote> | ||
==General references== | |||
{{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | {{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | ||
==Notes== | ==Notes== | ||
{{Reflist|group=Notes}} | {{Reflist|group=Notes}} | ||
Revision as of 02:29, 11 June 2024
We are now in a position to prove our first fundamental theorem of probability. We have seen that an intuitive way to view the probability of a certain outcome is as the frequency with which that outcome occurs in the long run, when the experiment is repeated a large number of times. We have also defined probability mathematically as a value of a distribution function for the random variable representing the experiment. The Law of Large Numbers, which is a theorem proved about the mathematical model of probability, shows that this model is consistent with the frequency interpretation of probability. This theorem is sometimes called the law of averages. To find out what would happen if this law were not true, see the article by Robert M. Coates.[Notes 1]
Chebyshev Inequality
To discuss the Law of Large Numbers, we first need an important inequality called the Chebyshev Inequality.
(Chebyshev Inequality) Let [math]X[/math] be a discrete random variable with expected value [math]\mu = E(X)[/math], and let [math]\epsilon \gt 0[/math] be any positive real number. Then
Let [math]m(x)[/math] denote the distribution function of [math]X[/math]. Then the probability that [math]X[/math] differs from [math]\mu[/math] by at least [math]\epsilon[/math] is given by
Note that [math]X[/math] in the above theorem can be any discrete random variable, and [math]\epsilon[/math] any positive number.
Example Let [math]X[/math] by any random variable with [math]E(X) = \mu[/math] and [math]V(X) = \sigma^2[/math]. Then, if [math]\epsilon = k\sigma[/math], Chebyshev's Inequality states that
Thus, for any random variable, the probability of a deviation from the mean of more than [math]k[/math] standard deviations is [math]{} \leq 1/k^2[/math]. If, for example, [math]k = 5[/math], [math]1/k^2 = .04[/math].
Chebyshev's Inequality is the best possible inequality in the sense that, for any [math]\epsilon \gt 0[/math], it is possible to give an example of a random variable for which Chebyshev's Inequality is in fact an equality. To see this, given [math]\epsilon \gt 0[/math], choose [math]X[/math] with distribution
Then [math]E(X) = 0[/math], [math]V(X) = \epsilon^2[/math], and
We are now prepared to state and prove the Law of Large Numbers.
Law of Large Numbers
(Law of Large Numbers) Let [math]X_1,X_2, \ldots, X_n[/math] be an independent trials process, with finite expected value [math]\mu = E(X_j)[/math] and finite variance [math]\sigma^2 = V(X_j)[/math]. Let [math]S_n = X_1 + X_2 +\cdots+ X_n[/math]. Then for any [math]\epsilon \gt 0[/math],
Since [math]X_1,X_2, \ldots,X_n[/math] are independent and have the same distributions, we can apply Theorem. We obtain
Law of Averages
Note that [math]S_n/n[/math] is an average of the individual outcomes, and one often calls the Law of Large Numbers the “law of averages.” It is a striking fact that we can start with a random experiment about which little can be predicted and, by taking averages, obtain an experiment in which the outcome can be predicted with a high degree of certainty. The Law of Large Numbers, as we have stated it, is often called the “Weak Law of Large Numbers” to distinguish it from the “Strong Law of Large Numbers” described in Exercise. Consider the important special case of Bernoulli trials with probability [math]p[/math] for success. Let [math]X_j = 1[/math] if the [math]j[/math]th outcome is a success and 0 if it is a failure. Then [math]S_n = X_1 + X_2 +\cdots+ X_n[/math] is the number of successes in [math]n[/math] trials and [math]\mu = E(X_1) = p[/math]. The Law of Large Numbers states that for any [math]\epsilon \gt 0[/math]
as [math]n \rightarrow \infty[/math]. The above statement says that, in a large number of repetitions of a Bernoulli experiment, we can expect the proportion of times the event will occur to be near [math]p[/math]. This shows that our mathematical model of probability agrees with our frequency interpretation of probability.
Coin Tossing
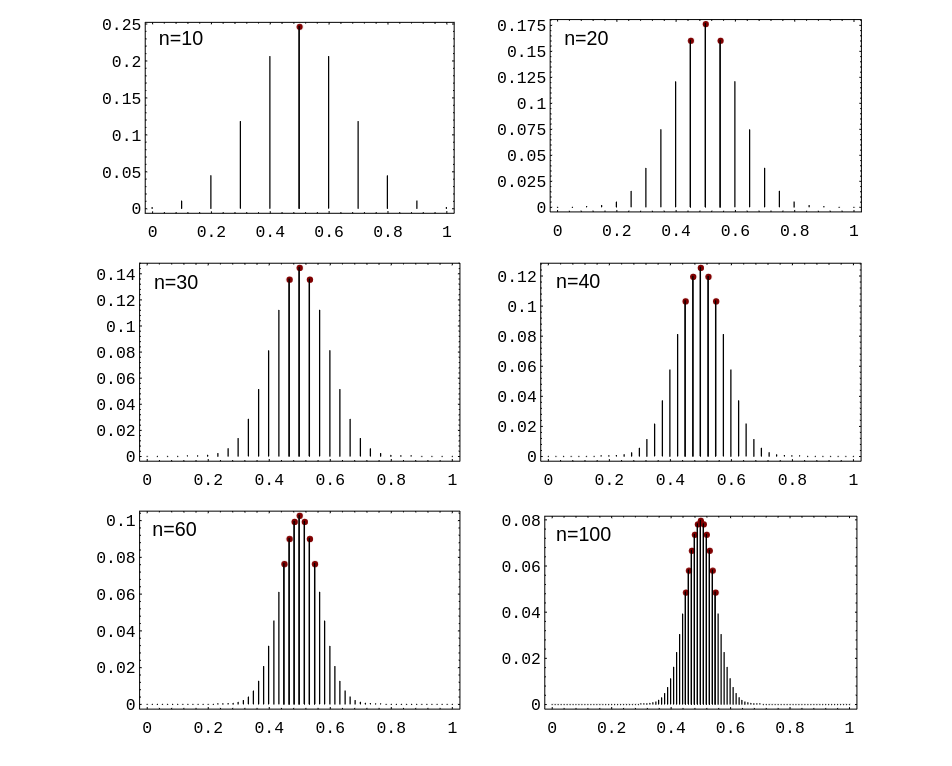
Let us consider the special case of tossing a coin [math]n[/math] times with [math]S_n[/math] the number of heads that turn up. Then the random variable [math]S_n/n[/math] represents the fraction of times heads turns up and will have values between 0 and 1. The Law of Large Numbers predicts that the outcomes for this random variable will, for large [math]n[/math], be near 1/2.
In Figure, we have plotted the distribution for this example for increasing values of [math]n[/math]. We have marked the outcomes between .45 and .55 by dots at the top of the spikes. We see that as [math]n[/math] increases the distribution gets more and more concentrated around .5 and a larger and larger percentage of the total area is contained within the interval [math](.45,.55)[/math], as predicted by the Law of Large Numbers.
Die Rolling
Example Consider [math]n[/math] rolls of a die. Let [math]X_j[/math] be the outcome of the [math]j[/math]th roll. Then [math]S_n = X_1 + X_2 +\cdots+ X_n[/math] is the sum of the first [math]n[/math] rolls. This is an independent trials process with [math]E(X_j) = 7/2[/math]. Thus, by the Law of Large Numbers, for any [math]\epsilon \gt 0[/math]
as [math]n \rightarrow \infty[/math]. An equivalent way to state this is that, for any [math]\epsilon \gt 0[/math],
as [math]n \rightarrow \infty[/math].
Numerical Comparisons
It should be emphasized that, although Chebyshev's Inequality proves the Law of Large Numbers, it is actually a very crude inequality for the probabilities involved. However, its strength lies in the fact that it is true for any random variable at all, and it allows us to prove a very powerful theorem.
In the following example, we compare the estimates given by Chebyshev's Inequality with the
actual values.
Example Let [math]X_1, X_2, \ldots, X_n[/math] be a Bernoulli trials process with probability .3 for success and .7 for failure. Let [math]X_j = 1[/math] if the [math]j[/math]th outcome is a success and 0 otherwise. Then, [math]E(X_j) = .3[/math] and [math]V(X_j) = (.3)(.7) = .21[/math]. If
is the average of the [math]X_i[/math], then [math]E(A_n) = .3[/math] and [math]V(A_n) = V(S_n)/n^2 = .21/n[/math]. Chebyshev's Inequality states that if, for example, [math]\epsilon = .1[/math],
Thus, if [math]n = 100[/math],
or if [math]n = 1000[/math],
These can be rewritten as
These values should be compared with the actual values, which are (to six decimal places)
The program Law can be used to carry out the above calculations in a systematic way.
Historical Remarks
The Law of Large Numbers was first proved by the Swiss mathematician James Bernoulli in the fourth part of his work Ars Conjectandi published posthumously in 1713.[Notes 2] As often happens with a first proof, Bernoulli's proof was much more difficult than the proof we have presented using Chebyshev's inequality. Chebyshev developed his inequality to prove a general form of the Law of Large Numbers (see Exercise). The inequality itself appeared much earlier in a work by Bienaymé, and in discussing its history Maistrov remarks that it was referred to as the Bienaymé-Chebyshev Inequality for a long time.[Notes 3] In Ars Conjectandi Bernoulli provides his reader with a long discussion of the meaning of his theorem with lots of examples. In modern notation he has an event that occurs with probability [math]p[/math] but he does not know [math]p[/math]. He wants to estimate [math]p[/math] by the fraction [math]\bar{p}[/math] of the times the event occurs when the experiment is repeated a number of times. He discusses in detail the problem of estimating, by this method, the proportion of white balls in an urn that contains an unknown number of white and black balls. He would do this by drawing a sequence of balls from the urn, replacing the ball drawn after each draw, and estimating the unknown proportion of white balls in the urn by the proportion of the balls drawn that are white. He shows that, by choosing [math]n[/math] large enough he can obtain any desired accuracy and reliability for the estimate. He also provides a lively discussion of the applicability of his theorem to estimating the probability of dying of a particular disease, of different kinds of weather occurring, and so forth. In speaking of the number of trials necessary for making a judgement, Bernoulli observes that the “man on the street” believes the “law of averages.”
Further, it cannot escape anyone that for judging in this way about any event at all, it is not enough to use one or two trials, but rather a great number of trials is required. And sometimes the stupidest man---by some instinct of nature per se and by no previous instruction (this is truly amazing)--- knows for sure that the more observations of this sort that are taken, the less the danger will be of straying from the mark.[Notes 4]
But he goes on to say that he must contemplate another possibility.
Something futher must be contemplated here which perhaps no one has thought about till now. It certainly remains to be inquired whether after the number of observations has been increased, the probability is increased of attaining the true ratio between the number of cases in which some event can happen and in which it cannot happen, so that this probability finally exceeds any given degree of certainty; or whether the problem has, so to speak, its own asymptote---that is, whether some degree of certainty is given which one can never exceed.[Notes 5]
Bernoulli recognized the importance of this theorem, writing:
Therefore, this is the problem which I now set forth and make known after I have already pondered over it for twenty years. Both its novelty and its very great usefullness, coupled with its just as great difficulty, can exceed in weight and value all the remaining chapters of this thesis.[Notes 6]
Bernoulli concludes his long proof with the remark:
Whence, finally, this one thing seems to follow: that if observations of all events were to be continued throughout all eternity, (and hence the ultimate probability would tend toward perfect certainty), everything in the world would be perceived to happen in fixed ratios and according to a constant law of alternation, so that even in the most accidental and fortuitous occurrences we would be bound to recognize, as it were, a certain necessity and, so to speak, a certain fate. I do now know whether Plato wished to aim at this in his doctrine of the universal return of things, according to which he predicted that all things will return to their original state after countless ages have past.[Notes 7]
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- R.M.Coates, “The Law,” The World of Mathematics, ed. James R. Newman (New York: Simon and Schuster, 1956.
- J. Bernoulli, The Art of Conjecturing IV, trans. Bing Sung, Technical Report No. 2, Dept.\ of Statistics, Harvard Univ., 1966
- L. E. Maistrov, Probability Theory: A Historical Approach, trans. and ed. Samual Kotz, (New York: Academic Press, 1974), p. 202
- Bernoulli, op. cit., p. 38.
- ibid., p. 39.
- ibid., p. 42.
- ibid., pp. 65--66.