guide:4add108640: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
\newcommand{\mathds}{\mathbb}</math></div> | \newcommand{\mathds}{\mathbb}</math></div> | ||
We have illustrated the Central Limit Theorem in the case of Bernoulli trials, but | We have illustrated the Central Limit Theorem in the case of Bernoulli trials, but this theorem applies to a much more general class of chance processes. In particular, it applies to any independent trials process such that the individual trials have finite variance. For such a process, both the normal approximation for individual terms and the Central Limit Theorem are valid. | ||
this theorem applies to a much more general class of chance processes. In | |||
particular, it applies to any independent trials process such that the individual trials have | |||
finite variance. For such a process, both the normal approximation for individual terms and the | |||
Central Limit Theorem are valid. | |||
Let <math>S_n = X_1 + X_2 +\cdots+ X_n</math> be the sum of <math>n</math> independent discrete random | Let <math>S_n = X_1 + X_2 +\cdots+ X_n</math> be the sum of <math>n</math> independent discrete random | ||
variables of an independent trials process with common distribution function <math>m(x)</math> defined on | variables of an independent trials process with common distribution function <math>m(x)</math> defined on | ||
the integers, with mean <math>\mu</math> and variance <math>\sigma^2</math>. | the integers, with mean <math>\mu</math> and variance <math>\sigma^2</math>. Just as we have seen | ||
for the sums of Bernoulli trials the distribution | for the sums of Bernoulli trials the distribution for more general independent sums have shapes resembling the normal curve, but the largest | ||
for more general independent sums have shapes resembling the normal curve, but the largest | values drift to the right and flatten out. We have seen in [[guide:Ec62e49ef0|Sums of Continuous Random Variables]] that the distributions for such independent sums have shapes | ||
values drift to the right and flatten out. | resembling the normal curve, but the largest values drift to the right and the curves flatten out (see [[#fig 7.9|Figure]]). We can prevent this just as we did for Bernoulli trials. | ||
resembling the normal curve, but the largest values drift to the right and the | |||
curves flatten out (see | |||
this just as we did for Bernoulli trials. | |||
===Standardized Sums=== | ===Standardized Sums=== | ||
| Line 27: | Line 20: | ||
<math display="block"> | <math display="block"> | ||
S_n^* = \frac {S_n - n\mu}{\sqrt{n\sigma^2}} | S_n^* = \frac {S_n - n\mu}{\sqrt{n\sigma^2}} . | ||
</math> | </math> | ||
| Line 36: | Line 29: | ||
x_j = \frac {j - n\mu}{\sqrt{n\sigma^2}}\ . | x_j = \frac {j - n\mu}{\sqrt{n\sigma^2}}\ . | ||
</math> | </math> | ||
We can construct a spike graph just as we did for Bernoulli trials. Each spike is | We can construct a spike graph just as we did for Bernoulli trials. Each spike is centered at some <math>x_j</math>. The distance between successive spikes is | ||
centered at some <math>x_j</math>. The distance between successive spikes is | |||
<math display="block"> | <math display="block"> | ||
| Line 61: | Line 53: | ||
</math> | </math> | ||
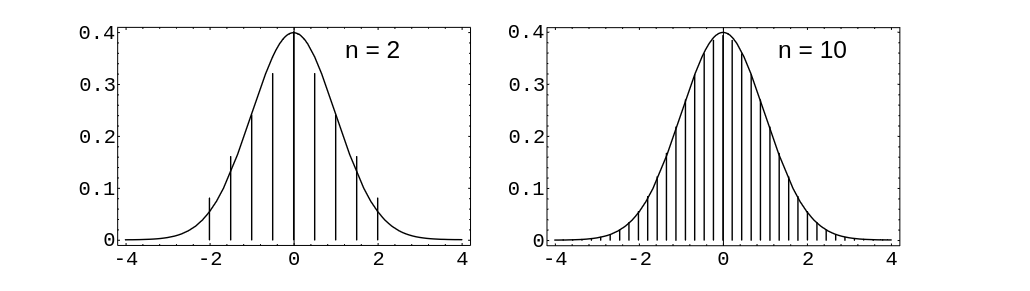
In | In [[#fig 9.5|Figure]] we show the standardized sums for this distribution for the cases | ||
<math>n = 2</math> and <math>n = 10</math>. Even for <math>n = 2</math> the approximation is surprisingly good. | <math>n = 2</math> and <math>n = 10</math>. Even for <math>n = 2</math> the approximation is surprisingly good. | ||
<div id=" | <div id="fig 9.5" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig9-5. | [[File:guide_e6d15_PSfig9-5.png | 600px | thumb | Distribution of standardized sums. ]] | ||
</div> | </div> | ||
For our second discrete distribution, we choose | For our second discrete distribution, we choose | ||
| Line 78: | Line 69: | ||
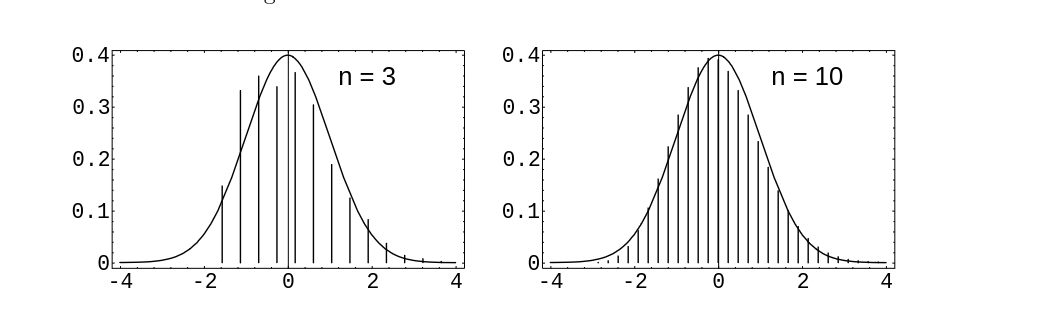
This distribution is quite asymmetric and the approximation is not very good for <math>n | This distribution is quite asymmetric and the approximation is not very good for <math>n | ||
= 3</math>, but by <math>n = 10</math> we again have an excellent approximation (see | = 3</math>, but by <math>n = 10</math> we again have an excellent approximation (see [[#fig 9.5.5|Figure]]). | ||
[[#fig 9.5|Figure]] and [[#fig 9.5.5|Figure]] were produced by the program ''' CLTIndTrialsPlot'''. | |||
<div id=" | <div id="fig 9.5.5" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig9-5-5. | [[File:guide_e6d15_PSfig9-5-5.png | 600px | thumb | Distribution of standardized sums. ]] | ||
</div> | </div> | ||
| Line 88: | Line 79: | ||
As in the case of Bernoulli trials, these graphs suggest the following | As in the case of Bernoulli trials, these graphs suggest the following | ||
approximation theorem for the individual probabilities. | approximation theorem for the individual probabilities. | ||
{{proofcard|Theorem|thm_9.3.5|Let <math>X_1 | {{proofcard|Theorem|thm_9.3.5|Let <math>X_1, X_2, \dots, X_n</math> be an independent trials process and let <math>S_n = | ||
X_1 + X_2 +\cdots+ X_n</math>. Assume that the greatest common divisor of the | X_1 + X_2 +\cdots+ X_n</math>. Assume that the greatest common divisor of the | ||
differences of all the values that the <math>X_j</math> can take on is 1. Let <math>E(X_j) = | differences of all the values that the <math>X_j</math> can take on is 1. Let <math>E(X_j) = | ||
| Line 106: | Line 97: | ||
===Central Limit Theorem for a Discrete Independent Trials Process=== | ===Central Limit Theorem for a Discrete Independent Trials Process=== | ||
The Central Limit Theorem for a discrete independent trials process is as follows. | The Central Limit Theorem for a discrete independent trials process is as follows. | ||
{{proofcard|Theorem|theorem-1|''' (Central Limit Theorem)''' | {{proofcard|Theorem|theorem-1|''' (Central Limit Theorem)''' | ||
Let <math>S_n = X_1 + X_2 +\cdots+ X_n</math> be the sum of <math>n</math> | Let <math>S_n = X_1 + X_2 +\cdots+ X_n</math> be the sum of <math>n</math> | ||
discrete independent random variables with common distribution having expected value <math>\mu</math> and | discrete independent random variables with common distribution having expected value <math>\mu</math> and | ||
| Line 116: | Line 107: | ||
</math>|}} | </math>|}} | ||
<ref group="Notes" >The proofs of [[#thm 9.3.5 |Theorem]] and [[#thm 9.3.6 |Theorem]] are given in Section 10.3 of the complete Grinstead-Snell book.</ref> We will give the proofs of [[#thm 9.3.5 |Theorem]] and [[#thm 9.3.6 |Theorem]] in [[guide:31815919f9|Generating Functions for Continuous Densities]]. Here we consider several examples. | |||
9.3.6 | |||
of [[#thm 9.3.5 | | |||
consider several examples. | |||
===Examples=== | ===Examples=== | ||
| Line 194: | Line 181: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
This means that there is only a 17.7 | This means that there is only a 17.7% chance that a given student's grade point average is | ||
accurate to within .05. (Thus, for example, if two candidates for valedictorian have recorded | accurate to within .05. (Thus, for example, if two candidates for valedictorian have recorded | ||
averages of 97.1 and 97.2, there is an appreciable probability that their correct averages are | averages of 97.1 and 97.2, there is an appreciable probability that their correct averages are | ||
in the reverse order.) For a further discussion of this example, see the article by R. M. | in the reverse order.) For a further discussion of this example, see the article by R. M. | ||
Kozelka.<ref group="Notes" >R. M. Kozelka, “Grade-Point Averages and the Central Limit | Kozelka.<ref group="Notes" >R. M. Kozelka, “Grade-Point Averages and the Central Limit | ||
Theorem,” ''American Math. | Theorem,” ''American Math. Monthly,'' vol. 86 (Nov 1979), pp. 773-777.</ref> | ||
===A More General Central Limit Theorem=== | ===A More General Central Limit Theorem=== | ||
| Line 211: | Line 197: | ||
well, in the sense that if the condition does not hold, then the sum <math>S_n</math> is not asymptotically | well, in the sense that if the condition does not hold, then the sum <math>S_n</math> is not asymptotically | ||
normally distributed. For a precise statement of Lindeberg's Theorem, we refer the reader to | normally distributed. For a precise statement of Lindeberg's Theorem, we refer the reader to | ||
Feller.<ref group="Notes" >W. Feller, ''Introduction to Probability Theory and its | Feller.<ref group="Notes" >W. Feller, ''Introduction to Probability Theory and its Applications,'' vol. 1, 3rd ed. (New York: John Wiley & Sons, 1968), p. 254.</ref> A sufficient condition that is stronger (but easier to state) than Lindeberg's condition, and is weaker than | ||
Applications,'' vol. 1, 3rd ed. (New York: John Wiley | |||
condition that is stronger (but easier to state) than Lindeberg's condition, and is weaker than | |||
the condition in [[#thm 9.3.6 |Theorem]], is given in the following theorem. | the condition in [[#thm 9.3.6 |Theorem]], is given in the following theorem. | ||
{{proofcard|Theorem|theorem-2|''' (Central Limit Theorem)''' | {{proofcard|Theorem|theorem-2|''' (Central Limit Theorem)''' | ||
Let <math>X_1,\ X_2,\ \ldots,\ X_n\ ,\ \ldots</math> be a sequence of independent discrete random variables, | Let <math>X_1,\ X_2,\ \ldots,\ X_n\ ,\ \ldots</math> be a sequence of independent discrete random variables, | ||
and let <math>S_n = X_1 + X_2 +\cdots+ X_n</math>. For each <math>n</math>, denote the mean and variance of <math>X_n</math> by | and let <math>S_n = X_1 + X_2 +\cdots+ X_n</math>. For each <math>n</math>, denote the mean and variance of <math>X_n</math> by | ||
| Line 228: | Line 212: | ||
</math>|}} | </math>|}} | ||
The condition that <math>|X_n| \le A</math> for all <math>n</math> is sometimes described by saying that the sequence | The condition that <math>|X_n| \le A</math> for all <math>n</math> is sometimes described by saying that the sequence | ||
<math>\{X_n\}</math> is uniformly bounded. The condition that <math>s_n \rightarrow \infty</math> is necessary (see | <math>\{X_n\}</math> is uniformly bounded. The condition that <math>s_n \rightarrow \infty</math> is necessary (see [[exercise:C71a3f441f |Exercise]]). | ||
| Line 238: | Line 221: | ||
and compare it with the normal density. The program ''' CLTGeneral''' | and compare it with the normal density. The program ''' CLTGeneral''' | ||
carries out this procedure. | carries out this procedure. | ||
<div id=" | <div id="fig 9.6" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig9-6. | [[File:guide_e6d15_PSfig9-6.png | 600px | thumb |Sums of randomly chosen random variables.]] | ||
</div> | </div> | ||
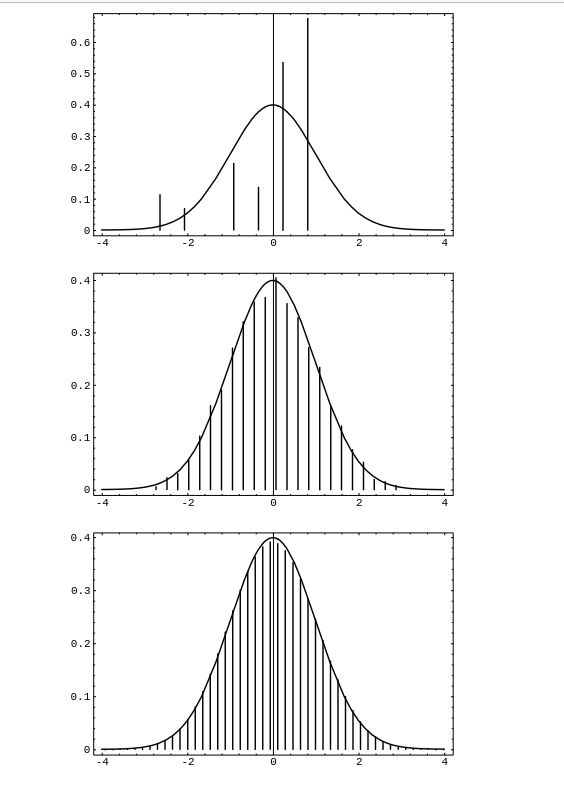
In | In [[#fig 9.6|Figure]] we show the result of running this | ||
program for <math>[a, b] = [-2, 4]</math>, and <math>n = 1,\ 4,</math> and 10. We see that our first random | program for <math>[a, b] = [-2, 4]</math>, and <math>n = 1,\ 4,</math> and 10. We see that our first random | ||
distribution is quite asymmetric. By the time we choose the sum of ten such | distribution is quite asymmetric. By the time we choose the sum of ten such | ||
| Line 255: | Line 238: | ||
When one looks at the distribution of heights of adults of one sex | When one looks at the distribution of heights of adults of one sex | ||
in a given population, one cannot help but notice that this distribution looks like the normal | in a given population, one cannot help but notice that this distribution looks like the normal | ||
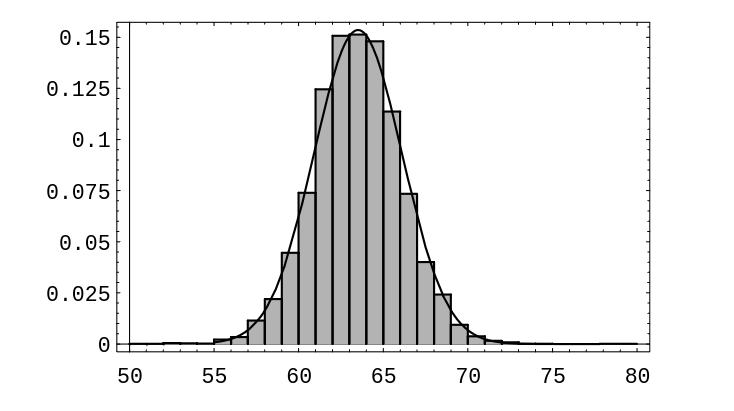
distribution. An example of this is shown in | distribution. An example of this is shown in [[#fig 9.61|Figure]]. This figure shows the | ||
distribution of heights of 9593 women between the ages of 21 and 74. These | distribution of heights of 9593 women between the ages of 21 and 74. These | ||
data come from the Health and Nutrition Examination Survey I (HANES I). | data come from the Health and Nutrition Examination Survey I (HANES I). | ||
| Line 268: | Line 251: | ||
invented by Galton in his attempts to understand these genetic effects. | invented by Galton in his attempts to understand these genetic effects. | ||
<div id=" | <div id="fig 9.61" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig9-61. | [[File:guide_e6d15_PSfig9-61.png | 400px | thumb | Distribution of heights of adult women. ]] | ||
</div> | </div> | ||
| Line 305: | Line 288: | ||
problem. | problem. | ||
We will now consider the modern explanation of why certain traits, such as heights, are approximately normally distributed. In order to do so, we need to introduce some terminology from the field of genetics. The cells in a living organism that are | |||
We will now consider the modern explanation of why certain traits, such as heights, are | |||
approximately normally distributed. In order to do so, we need to introduce some terminology | |||
from the field of genetics. The cells in a living organism that are | |||
not directly involved in the transmission of genetic material to offspring are called somatic | not directly involved in the transmission of genetic material to offspring are called somatic | ||
cells, and the remaining cells are called germ cells. Organisms of a given species have | cells, and the remaining cells are called germ cells. Organisms of a given species have | ||
| Line 362: | Line 342: | ||
assume that the <math>X_i</math>'s have a significantly larger cumulative effect than <math>W</math> does, then <math>H</math> is | assume that the <math>X_i</math>'s have a significantly larger cumulative effect than <math>W</math> does, then <math>H</math> is | ||
approximately normally distributed. | approximately normally distributed. | ||
Another observed feature of the distribution of heights of adults of one sex in a population is | Another observed feature of the distribution of heights of adults of one sex in a population is | ||
| Line 385: | Line 364: | ||
if the number of individuals in the parent population is large, then whether or not we allow this | if the number of individuals in the parent population is large, then whether or not we allow this | ||
event does not affect the probabilities very much.) | event does not affect the probabilities very much.) | ||
For <math>1 \le i \le k</math>, we let <math>p_i</math> denote the proportion of alleles in the parent population that | For <math>1 \le i \le k</math>, we let <math>p_i</math> denote the proportion of alleles in the parent population that | ||
| Line 393: | Line 371: | ||
equally likely to be chosen for any particular offspring, the distribution of alleles in the | equally likely to be chosen for any particular offspring, the distribution of alleles in the | ||
offspring is the same as in the parents. | offspring is the same as in the parents. | ||
We next consider the distribution of genotypes in the two generations. We will prove the | We next consider the distribution of genotypes in the two generations. We will prove the | ||
| Line 469: | Line 446: | ||
quincunx to explain how inheritance affects the distribution of a trait among offspring. | quincunx to explain how inheritance affects the distribution of a trait among offspring. | ||
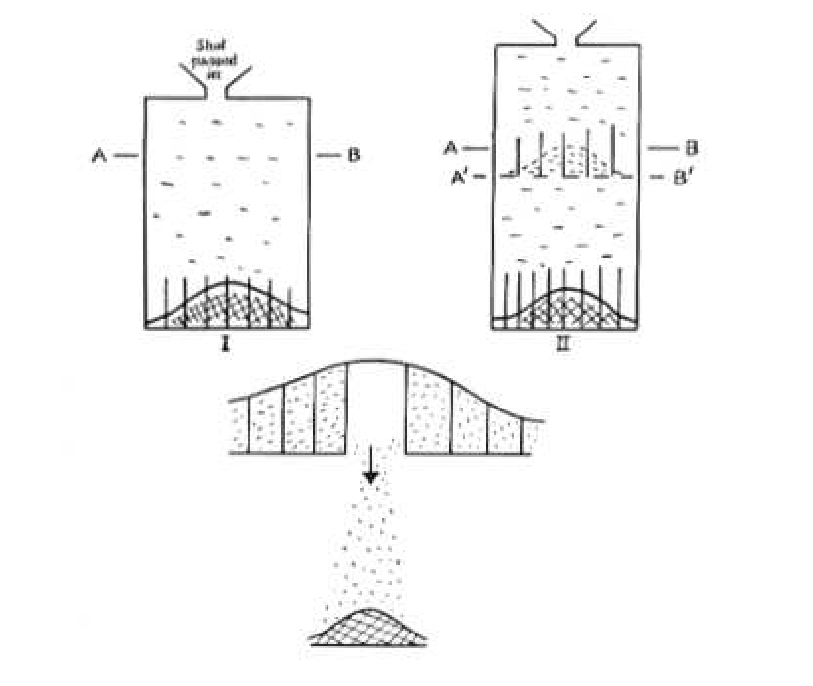
We consider, as Galton did, what happens if we interrupt, at some intermediate height, the progress of the shot that is falling in the quincunx. The reader is referred to [[#fig 9.62|Figure]]. | |||
<div id="fig 9.62" class="d-flex justify-content-center"> | |||
[[File:guide_e6d15_PSfigBC.png | 400px | thumb | Two-stage version of the quincunx.]] | |||
<div id=" | |||
[[File:guide_e6d15_PSfigBC. | |||
</div> | </div> | ||
This figure is a drawing of Karl Pearson,<ref group="Notes" >Karl Pearson, ''The Life, | |||
Letters and Labours of Francis Galton,'' vol. IIIB, (Cambridge at the University Press 1930.) p. 466. | This figure is a drawing of Karl Pearson,<ref group="Notes" >Karl Pearson, ''The Life, Letters and Labours of Francis Galton,'' vol. IIIB, (Cambridge at the University Press 1930.) p. 466. | ||
Reprinted with permission.</ref> | Reprinted with permission.</ref> | ||
based upon Galton's notes. In this figure, the shot is being temporarily segregated into compartments | based upon Galton's notes. In this figure, the shot is being temporarily segregated into compartments | ||
at the line AB. (The line A<math>^{\prime}</math>B<math>^{\prime}</math> forms a platform on which the shot can | at the line AB. (The line A<math>^{\prime}</math>B<math>^{\prime}</math> forms a platform on which the shot can | ||
| Line 505: | Line 481: | ||
normal distributions. | normal distributions. | ||
He now was faced with a problem. We have shown in [[guide:4c79910a98|Sums of Independent Random Variables]], and Galton knew, that the | |||
He now was faced with a problem. We have shown in [[guide: | |||
convolution of two normal distributions produces a normal distribution with a larger variance | convolution of two normal distributions produces a normal distribution with a larger variance | ||
than either of the original distributions. But his data on the sweet pea seeds showed that the | than either of the original distributions. But his data on the sweet pea seeds showed that the | ||
| Line 522: | Line 497: | ||
</blockquote> | </blockquote> | ||
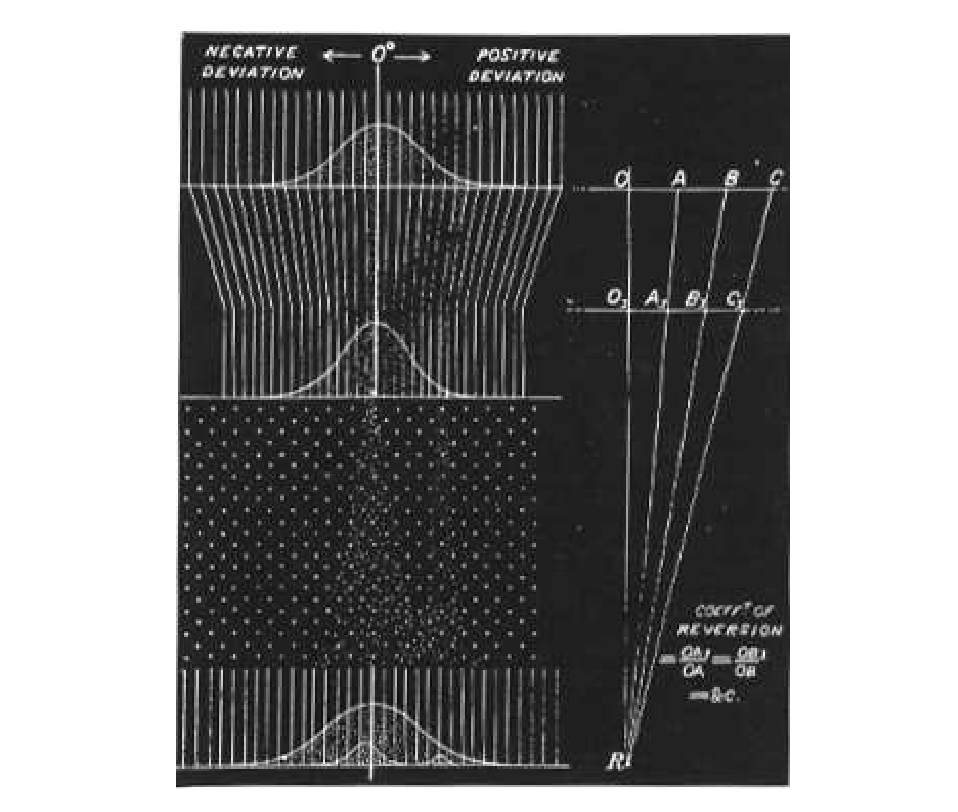
Galton illustrated reversion with the illustration shown in [[#fig 9.63|Figure]].<ref group="Notes" >Karl | |||
Galton illustrated reversion with the illustration shown in | |||
Pearson, ''The Life, Letters and Labours of Francis Galton,'' vol. IIIA, (Cambridge at the University | Pearson, ''The Life, Letters and Labours of Francis Galton,'' vol. IIIA, (Cambridge at the University | ||
Press 1930.) p. 9. Reprinted with permission.</ref> The parent population is shown at the top of the | Press 1930.) p. 9. Reprinted with permission.</ref> The parent population is shown at the top of the | ||
figure, and the slanted lines are meant to correspond to the reversion effect. The offspring | figure, and the slanted lines are meant to correspond to the reversion effect. The offspring | ||
population is shown at the bottom of the figure. | population is shown at the bottom of the figure. | ||
<div id=" | <div id="fig 9.63" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfigblack. | [[File:guide_e6d15_PSfigblack.png | 600px | thumb | Galton's explanation of reversion. ]] | ||
</div> | </div> | ||
==General references== | |||
{{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | {{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | ||
==Notes== | ==Notes== | ||
{{Reflist|group=Notes}} | {{Reflist|group=Notes}} | ||
Revision as of 15:00, 11 June 2024
We have illustrated the Central Limit Theorem in the case of Bernoulli trials, but this theorem applies to a much more general class of chance processes. In particular, it applies to any independent trials process such that the individual trials have finite variance. For such a process, both the normal approximation for individual terms and the Central Limit Theorem are valid.
Let [math]S_n = X_1 + X_2 +\cdots+ X_n[/math] be the sum of [math]n[/math] independent discrete random variables of an independent trials process with common distribution function [math]m(x)[/math] defined on the integers, with mean [math]\mu[/math] and variance [math]\sigma^2[/math]. Just as we have seen for the sums of Bernoulli trials the distribution for more general independent sums have shapes resembling the normal curve, but the largest values drift to the right and flatten out. We have seen in Sums of Continuous Random Variables that the distributions for such independent sums have shapes resembling the normal curve, but the largest values drift to the right and the curves flatten out (see Figure). We can prevent this just as we did for Bernoulli trials.
Standardized Sums
Consider the standardized random variable
This standardizes [math]S_n[/math] to have expected value 0 and variance 1. If [math]S_n = j[/math], then [math]S_n^*[/math] has the value [math]x_j[/math] with
We can construct a spike graph just as we did for Bernoulli trials. Each spike is centered at some [math]x_j[/math]. The distance between successive spikes is
and the height of the spike is
The case of Bernoulli trials is the special case for which [math]X_j = 1[/math] if the [math]j[/math]th outcome is a success and 0 otherwise; then [math]\mu = p[/math] and [math]\sigma^2 = \sqrt {pq}[/math].
We now illustrate this process for two different discrete distributions. The first is the
distribution [math]m[/math], given by
In Figure we show the standardized sums for this distribution for the cases [math]n = 2[/math] and [math]n = 10[/math]. Even for [math]n = 2[/math] the approximation is surprisingly good.
For our second discrete distribution, we choose
This distribution is quite asymmetric and the approximation is not very good for [math]n
= 3[/math], but by [math]n = 10[/math] we again have an excellent approximation (see Figure).
Figure and Figure were produced by the program CLTIndTrialsPlot.
Approximation Theorem
As in the case of Bernoulli trials, these graphs suggest the following approximation theorem for the individual probabilities.
Let [math]X_1, X_2, \dots, X_n[/math] be an independent trials process and let [math]S_n = X_1 + X_2 +\cdots+ X_n[/math]. Assume that the greatest common divisor of the differences of all the values that the [math]X_j[/math] can take on is 1. Let [math]E(X_j) = \mu[/math] and [math]V(X_j) = \sigma^2[/math]. Then for [math]n[/math] large,
The program CLTIndTrialsLocal implements this approximation. When we run this program for 6 rolls of a die, and ask for the probability that the sum of the rolls equals 21, we obtain an actual value of .09285, and a normal approximation value of .09537. If we run this program for 24 rolls of a die, and ask for the probability that the sum of the rolls is 72, we obtain an actual value of .01724 and a normal approximation value of .01705. These results show that the normal approximations are quite good.
Central Limit Theorem for a Discrete Independent Trials Process
The Central Limit Theorem for a discrete independent trials process is as follows.
(Central Limit Theorem) Let [math]S_n = X_1 + X_2 +\cdots+ X_n[/math] be the sum of [math]n[/math] discrete independent random variables with common distribution having expected value [math]\mu[/math] and variance [math]\sigma^2[/math]. Then, for [math]a \lt b[/math],
[Notes 1] We will give the proofs of Theorem and Theorem in Generating Functions for Continuous Densities. Here we consider several examples.
Examples
Example A die is rolled 420 times. What is the probability that the sum of the rolls lies between 1400 and 1550? The sum is a random variable
where each [math]X_j[/math] has distribution
We have seen that [math]\mu = E(X) = 7/2[/math] and [math]\sigma^2 = V(X) = 35/12[/math]. Thus, [math]E(S_{420}) = 420 \cdot 7/2 = 1470[/math], [math]\sigma^2(S_{420}) = 420 \cdot 35/12 = 1225[/math], and [math]\sigma(S_{420}) = 35[/math]. Therefore,
We note that the program CLTIndTrialsGlobal could be used to calculate these probabilities.
Example A student's grade point average is the average of his grades in 30 courses. The grades are based on 100 possible points and are recorded as integers. Assume that, in each course, the instructor makes an error in grading of [math]k[/math] with probability [math]|p/k|[/math], where [math]k = \pm1[/math], [math]\pm2[/math], [math]\pm3[/math], [math]\pm4[/math], [math]\pm5[/math]. The probability of no error is then [math]1 - (137/30)p[/math]. (The parameter [math]p[/math] represents the inaccuracy of the instructor's grading.) Thus, in each course, there are two grades for the student, namely the “correct” grade and the recorded grade. So there are two average grades for the student, namely the average of the correct grades and the average of the recorded grades.
We wish to estimate the probability that these two average grades differ by less than .05 for a given
student. We now assume that [math]p = 1/20[/math]. We also assume that the total error
is the sum [math]S_{30}[/math] of 30 independent random variables each with distribution
One can easily calculate that [math]E(X) = 0[/math] and [math]\sigma^2(X) = 1.5[/math]. Then we have
This means that there is only a 17.7% chance that a given student's grade point average is accurate to within .05. (Thus, for example, if two candidates for valedictorian have recorded averages of 97.1 and 97.2, there is an appreciable probability that their correct averages are in the reverse order.) For a further discussion of this example, see the article by R. M. Kozelka.[Notes 2]
A More General Central Limit Theorem
In Theorem, the discrete random variables that were being summed were assumed to be independent and identically distributed. It turns out that the assumption of identical distributions can be substantially weakened. Much work has been done in this area, with an important contribution being made by J. W. Lindeberg. Lindeberg found a condition on the sequence [math]\{X_n\}[/math] which guarantees that the distribution of the sum [math]S_n[/math] is asymptotically normally distributed. Feller showed that Lindeberg's condition is necessary as well, in the sense that if the condition does not hold, then the sum [math]S_n[/math] is not asymptotically normally distributed. For a precise statement of Lindeberg's Theorem, we refer the reader to Feller.[Notes 3] A sufficient condition that is stronger (but easier to state) than Lindeberg's condition, and is weaker than the condition in Theorem, is given in the following theorem.
(Central Limit Theorem) Let [math]X_1,\ X_2,\ \ldots,\ X_n\ ,\ \ldots[/math] be a sequence of independent discrete random variables, and let [math]S_n = X_1 + X_2 +\cdots+ X_n[/math]. For each [math]n[/math], denote the mean and variance of [math]X_n[/math] by [math]\mu_n[/math] and [math]\sigma^2_n[/math], respectively. Define the mean and variance of [math]S_n[/math] to be [math]m_n[/math] and [math]s_n^2[/math], respectively, and assume that [math]s_n \rightarrow \infty[/math]. If there exists a constant [math]A[/math], such that [math]|X_n| \le A[/math] for all [math]n[/math], then for [math]a \lt b[/math],
The condition that [math]|X_n| \le A[/math] for all [math]n[/math] is sometimes described by saying that the sequence [math]\{X_n\}[/math] is uniformly bounded. The condition that [math]s_n \rightarrow \infty[/math] is necessary (see Exercise).
We illustrate this theorem by generating a sequence of [math]n[/math] random distributions on
the interval [math][a, b][/math]. We then convolute these distributions to find the distribution of
the sum of [math]n[/math] independent experiments governed by these distributions. Finally, we
standardize the distribution for the sum to have mean 0 and standard deviation 1
and compare it with the normal density. The program CLTGeneral
carries out this procedure.
In Figure we show the result of running this program for [math][a, b] = [-2, 4][/math], and [math]n = 1,\ 4,[/math] and 10. We see that our first random distribution is quite asymmetric. By the time we choose the sum of ten such experiments we have a very good fit to the normal curve.
The above theorem essentially says that anything that can be thought of as being made up as the
sum of many small independent pieces is approximately normally distributed. This brings us to
one of the most important questions that was asked about genetics in the 1800's.
The Normal Distribution and Genetics
When one looks at the distribution of heights of adults of one sex in a given population, one cannot help but notice that this distribution looks like the normal distribution. An example of this is shown in Figure. This figure shows the distribution of heights of 9593 women between the ages of 21 and 74. These data come from the Health and Nutrition Examination Survey I (HANES I). For this survey, a sample of the U.S.\ civilian population was chosen. The survey was carried out between 1971 and 1974.
A natural question to ask is “How does this come about?”. Francis Galton, an English scientist in the 19th century, studied this question, and other related
questions, and constructed probability models that were of great importance in explaining
the genetic effects on such attributes as height. In fact, one of the most important ideas
in statistics, the idea of regression to the mean, was
invented by Galton in his attempts to understand these genetic effects.
Galton was faced with an apparent contradiction. On the one hand, he knew that the normal
distribution arises in situations in which many small independent effects are being summed. On
the other hand, he also knew that many quantitative attributes, such as height, are strongly
influenced by genetic factors: tall parents tend to have tall offspring. Thus in this case,
there seem to be two large effects, namely the parents. Galton was certainly aware of the fact
that non-genetic factors played a role in determining the height of an individual. Nevertheless,
unless these non-genetic factors overwhelm the genetic ones, thereby refuting the hypothesis that
heredity is important in determining height, it did not seem possible for sets of parents of
given heights to have offspring whose heights were normally distributed.
One can express the above problem symbolically as follows. Suppose that we choose two specific
positive real numbers [math]x[/math] and [math]y[/math], and then find all pairs of parents one of whom is [math]x[/math] units tall
and the other of whom is [math]y[/math] units tall. We then look at all of the offspring of these pairs of
parents. One can postulate the existence of a function [math]f(x, y)[/math] which denotes
the genetic effect of the parents' heights on the heights of the offspring. One can then let [math]W[/math]
denote the effects of the non-genetic factors on the heights of the offspring. Then, for a given
set of heights [math]\{x, y\}[/math], the random variable which represents the heights of the offspring is
given by
where [math]f[/math] is a deterministic function, i.e., it gives one output for a pair of inputs [math]\{x, y\}[/math]. If we assume that the effect of [math]f[/math] is large in comparison with the effect of [math]W[/math], then the variance of [math]W[/math] is small. But since f is deterministic, the variance of [math]H[/math] equals the variance of [math]W[/math], so the variance of [math]H[/math] is small. However, Galton observed from his data that the variance of the heights of the offspring of a given pair of parent heights is not small. This would seem to imply that inheritance plays a small role in the determination of the height of an individual. Later in this section, we will describe the way in which Galton got around this problem.
We will now consider the modern explanation of why certain traits, such as heights, are approximately normally distributed. In order to do so, we need to introduce some terminology from the field of genetics. The cells in a living organism that are not directly involved in the transmission of genetic material to offspring are called somatic cells, and the remaining cells are called germ cells. Organisms of a given species have their genetic information encoded in sets of physical entities, called chromosomes. The chromosomes are paired in each somatic cell. For example, human beings have 23 pairs of chromosomes in each somatic cell. The sex cells contain one chromosome from each pair. In sexual reproduction, two sex cells, one from each parent, contribute their chromosomes to create the set of chromosomes for the offspring.
Chromosomes contain many subunits, called genes. Genes consist of molecules of
DNA, and one gene has, encoded in its DNA, information that leads to the regulation of
proteins. In the present context, we will consider those genes containing information that
has an effect on some physical trait, such as height, of the organism. The pairing of the
chromosomes gives rise to a pairing of the genes on the chromosomes.
In a given species, each gene can be any one of several forms. These various forms are called
alleles. One should think of the different alleles as potentially producing
different effects on the physical trait in question. Of the two alleles that are found in a
given gene pair in an organism, one of the alleles came from one parent and the other allele came
from the other parent. The possible types of pairs of alleles (without regard to order) are
called genotypes.
If we assume that the height of a human being is largely controlled by a specific gene,
then we are faced with the same difficulty that Galton was. We are assuming that each parent
has a pair of alleles which largely controls their heights. Since each parent contributes one
allele of this gene pair to each of its offspring, there are four possible allele pairs for the
offspring at this gene location. The assumption is that these pairs of alleles largely
control the height of the offspring, and we are also assuming that genetic factors outweigh
non-genetic factors. It follows that among the offspring we should see several modes in the
height distribution of the offspring, one mode corresponding to each possible pair of alleles.
This distribution does not correspond to the observed distribution of heights.
An alternative hypothesis, which does explain the observation of normally distributed heights in
offspring of a given sex, is the multiple-gene hypothesis.
Under this hypothesis, we assume that there are many genes that affect the height of an
individual. These genes may differ in the amount of their effects. Thus, we can represent each
gene pair by a random variable [math]X_i[/math], where the value of the random variable is the allele pair's
effect on the height of the individual. Thus, for example, if each parent has two different
alleles in the gene pair under consideration, then the offspring has one of four possible pairs
of alleles at this gene location. Now the height of the offspring is a random variable, which
can be expressed as
if there are [math]n[/math] genes that affect height. (Here, as before, the random variable [math]W[/math] denotes non-genetic effects.) Although [math]n[/math] is fixed, if it is fairly large, then Theorem implies that the sum [math]X_1 + X_2 + \cdots + X_n[/math] is approximately normally distributed. Now, if we assume that the [math]X_i[/math]'s have a significantly larger cumulative effect than [math]W[/math] does, then [math]H[/math] is approximately normally distributed.
Another observed feature of the distribution of heights of adults of one sex in a population is that the variance does not seem to increase or decrease from one generation to the next. This was known at the time of Galton, and his attempts to explain this led him to the idea of regression to the mean. This idea will be discussed further in the historical remarks at the end of the section. (The reason that we only consider one sex is that human heights are clearly sex-linked, and in general, if we have two populations that are each normally distributed, then their union need not be normally distributed.)
Using the multiple-gene hypothesis, it is easy to explain why the variance should be constant
from generation to generation. We begin by assuming that for a specific gene location, there are
[math]k[/math] alleles, which we will denote by [math]A_1,\ A_2,\ \ldots,\ A_k[/math]. We assume that the offspring are
produced by random mating. By this we mean that given any offspring, it is equally likely that it
came from any pair of parents in the preceding generation. There is another way to look at random
mating that makes the calculations easier. We consider the set [math]S[/math] of all of the alleles (at the
given gene location) in all of the germ cells of all of the individuals in the parent generation.
In terms of the set [math]S[/math], by random mating we mean that each pair of alleles in [math]S[/math] is equally
likely to reside in any particular offspring. (The reader might object to this way of thinking
about random mating, as it allows two alleles from the same parent to end up in an offspring; but
if the number of individuals in the parent population is large, then whether or not we allow this
event does not affect the probabilities very much.)
For [math]1 \le i \le k[/math], we let [math]p_i[/math] denote the proportion of alleles in the parent population that are of type [math]A_i[/math]. It is clear that this is the same as the proportion of alleles in the germ cells of the parent population, assuming that each parent produces roughly the same number of germs cells. Consider the distribution of alleles in the offspring. Since each germ cell is equally likely to be chosen for any particular offspring, the distribution of alleles in the offspring is the same as in the parents.
We next consider the distribution of genotypes in the two generations. We will prove the following fact: the distribution of genotypes in the offspring generation depends only upon the distribution of alleles in the parent generation (in particular, it does not depend upon the distribution of genotypes in the parent generation). Consider the possible genotypes; there are [math]k(k+1)/2[/math] of them. Under our assumptions, the genotype [math]A_iA_i[/math] will occur with frequency [math]p_i^2[/math], and the genotype [math]A_iA_j[/math], with [math]i \ne j[/math], will occur with frequency [math]2p_ip_j[/math]. Thus, the frequencies of the genotypes depend only upon the allele frequencies in the parent generation, as claimed.
This means that if we start with a certain generation, and a certain distribution of alleles, then
in all generations after the one we started with, both the allele distribution and the genotype
distribution will be fixed. This last statement is known as the
Hardy-Weinberg Law.
We can describe the consequences of this law for the
distribution of heights among adults of one sex in a population. We recall that the height of an
offspring was given by a random variable [math]H[/math], where
with the [math]X_i[/math]'s corresponding to the genes that affect height, and the random variable [math]W[/math] denoting non-genetic effects. The Hardy-Weinberg Law states that for each [math]X_i[/math], the distribution in the offspring generation is the same as the distribution in the parent generation. Thus, if we assume that the distribution of [math]W[/math] is roughly the same from generation to generation (or if we assume that its effects are small), then the distribution of [math]H[/math] is the same from generation to generation. (In fact, dietary effects are part of [math]W[/math], and it is clear that in many human populations, diets have changed quite a bit from one generation to the next in recent times. This change is thought to be one of the reasons that humans, on the average, are getting taller. It is also the case that the effects of [math]W[/math] are thought to be small relative to the genetic effects of the parents.)
Discussion
Generally speaking, the Central Limit Theorem contains more information than the Law of Large Numbers, because it gives us detailed information about the shape of the distribution of [math]S_n^*[/math]; for large [math]n[/math] the shape is approximately the same as the shape of the standard normal density. More specifically, the Central Limit Theorem says that if we standardize and height-correct the distribution of [math]S_n[/math], then the normal density function is a very good approximation to this distribution when [math]n[/math] is large. Thus, we have a computable approximation for the distribution for [math]S_n[/math], which provides us with a powerful technique for generating answers for all sorts of questions about sums of independent random variables, even if the individual random variables have different distributions.
Historical Remarks
In the mid-1800's, the Belgian mathematician Quetelet[Notes 4] had shown empirically that the normal distribution occurred in real data, and had also given a method for fitting the normal curve to a given data set. Laplace[Notes 5] had shown much earlier that the sum of many independent identically distributed random variables is approximately normal. Galton knew that certain physical traits in a population appeared to be approximately normally distributed, but he did not consider Laplace's result to be a good explanation of how this distribution comes about. We give a quote from Galton that appears in the fascinating book by S. Stigler[Notes 6] on the history of statistics:
First, let me point out a fact which Quetelet and all writers who have followed in his paths have unaccountably overlooked, and which has an intimate bearing on our work to-night. It is that, although characteristics of plants and animals conform to the law, the reason of their doing so is as yet totally unexplained. The essence of the law is that differences should be wholly due to the collective actions of a host of independent petty influences in various combinations...Now the processes of heredity...are not petty influences, but very important ones...The conclusion is...that the processes of heredity must work harmoniously with the law of deviation, and be themselves in some sense conformable to it.
Galton invented a device known as a quincunx (now commonly called a Galton
board), which we used in Example to show how to physically
obtain a binomial distribution. Of course, the Central Limit Theorem says that for large values
of the parameter [math]n[/math], the binomial distribution is approximately normal. Galton used the
quincunx to explain how inheritance affects the distribution of a trait among offspring.
We consider, as Galton did, what happens if we interrupt, at some intermediate height, the progress of the shot that is falling in the quincunx. The reader is referred to Figure.
This figure is a drawing of Karl Pearson,[Notes 7]
based upon Galton's notes. In this figure, the shot is being temporarily segregated into compartments at the line AB. (The line A[math]^{\prime}[/math]B[math]^{\prime}[/math] forms a platform on which the shot can rest.) If the line AB is not too close to the top of the quincunx, then the shot will be approximately normally distributed at this line. Now suppose that one compartment is opened, as shown in the figure. The shot from that compartment will fall, forming a normal distribution at the bottom of the quincunx. If now all of the compartments are opened, all of the shot will fall, producing the same distribution as would occur if the shot were not temporarily stopped at the line AB. But the action of stopping the shot at the line AB, and then releasing the compartments one at a time, is just the same as convoluting two normal distributions. The normal distributions at the bottom, corresponding to each compartment at the line AB, are being mixed, with their weights being the number of shot in each compartment. On the other hand, it is already known that if the shot are unimpeded, the final distribution is approximately normal. Thus, this device shows that the convolution of two normal distributions is again normal.
Galton also considered the quincunx from another perspective. He segregated into seven groups, by
weight, a set of 490 sweet pea seeds. He gave 10 seeds from each of the seven group to each of
seven friends, who grew the plants from the seeds. Galton found that each group
produced seeds whose weights were normally distributed. (The sweet pea reproduces by
self-pollination, so he did not need to consider the possibility of interaction between different
groups.) In addition, he found that the variances of the weights of the offspring were the same
for each group. This segregation into groups corresponds to the compartments at the line AB in the
quincunx. Thus, the sweet peas were acting as though they were being governed by a convolution of
normal distributions.
He now was faced with a problem. We have shown in Sums of Independent Random Variables, and Galton knew, that the convolution of two normal distributions produces a normal distribution with a larger variance than either of the original distributions. But his data on the sweet pea seeds showed that the variance of the offspring population was the same as the variance of the parent population. His answer to this problem was to postulate a mechanism that he called reversion, and is now called regression to the mean. As Stigler puts it:[Notes 8]
The seven groups of progeny were normally distributed, but not about their parents' weight. Rather they were in every case distributed about a value that was closer to the average population weight than was that of the parent. Furthermore, this reversion followed “the simplest possible law,” that is, it was linear. The average deviation of the progeny from the population average was in the same direction as that of the parent, but only a third as great. The mean progeny reverted to type, and the increased variation was just sufficient to maintain the population variability.
Galton illustrated reversion with the illustration shown in Figure.[Notes 9] The parent population is shown at the top of the figure, and the slanted lines are meant to correspond to the reversion effect. The offspring population is shown at the bottom of the figure.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- The proofs of Theorem and Theorem are given in Section 10.3 of the complete Grinstead-Snell book.
- R. M. Kozelka, “Grade-Point Averages and the Central Limit Theorem,” American Math. Monthly, vol. 86 (Nov 1979), pp. 773-777.
- W. Feller, Introduction to Probability Theory and its Applications, vol. 1, 3rd ed. (New York: John Wiley & Sons, 1968), p. 254.
- S. Stigler, The History of Statistics, (Cambridge: Harvard University Press, 1986), p. 203.
- ibid., p. 136
- ibid., p. 281.
- Karl Pearson, The Life, Letters and Labours of Francis Galton, vol. IIIB, (Cambridge at the University Press 1930.) p. 466. Reprinted with permission.
- ibid., p. 282.
- Karl Pearson, The Life, Letters and Labours of Francis Galton, vol. IIIA, (Cambridge at the University Press 1930.) p. 9. Reprinted with permission.