guide:Ff217e6881

[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

In the last several chapters, we have studied sums of random variables with the goal being to describe the distribution and density functions of the sum. In this chapter, we shall look at sums of discrete random variables from a different perspective. We shall be concerned with properties which can be associated with the sequence of partial sums, such as the number of sign changes of this sequence, the number of terms in the sequence which equal 0, and the expected size of the maximum term in the sequence.

We begin with the following definition.

Definition

Let [math]\{X_k\}_{k = 1}^\infty[/math] be a sequence of independent, identically distributed discrete random variables. For each positive integer [math]n[/math], we let [math]S_n[/math] denote the sum [math]X_1 + X_2 + \cdots + X_n[/math]. The sequence [math]\{S_n\}_{n = 1}^\infty[/math] is called a random walk. If the common range of the [math]X_k[/math]'s is [math]{\mathbf R}^m[/math], then we say that [math]\{S_n\}[/math] is a random walk in [math]{\mathbf R}^m[/math].

We view the sequence of [math]X_k[/math]'s as being the outcomes of independent experiments. Since the [math]X_k[/math]'s are independent, the probability of any particular (finite) sequence of outcomes can be obtained by multiplying the probabilities that each [math]X_k[/math] takes on the specified value in the sequence. Of course, these individual probabilities are given by the common distribution of the [math]X_k[/math]'s. We will typically be interested in finding probabilities for events involving the related sequence of [math]S_n[/math]'s. Such events can be described in terms of the [math]X_k[/math]'s, so their probabilities can be calculated using the above idea.

There are several ways to visualize a random walk. One can imagine that a particle is placed at the origin in [math]{\mathbf R}^m[/math] at time [math]n = 0[/math]. The sum [math]S_n[/math] represents the position of the particle at the end of [math]n[/math] seconds. Thus, in the time interval [math][n-1, n][/math], the particle moves (or jumps) from position [math]S_{n-1}[/math] to [math]S_{n}[/math]. The vector representing this motion is just [math]S_n - S_{n-1}[/math], which equals [math]X_n[/math]. This means that in a random walk, the jumps are independent and identically distributed. If [math]m = 1[/math], for example, then one can imagine a particle on the real line that starts at the origin, and at the end of each second, jumps one unit to the right or the left, with probabilities given by the distribution of the [math]X_k[/math]'s. If [math]m = 2[/math], one can visualize the process as taking place in a city in which the streets form square city blocks. A person starts at one corner (i.e., at an intersection of two streets) and goes in one of the four possible directions according to the distribution of the [math]X_k[/math]'s. If [math]m = 3[/math], one might imagine being in a jungle gym, where one is free to move in any one of six directions (left, right, forward, backward, up, and down). Once again, the probabilities of these movements are given by the distribution of the [math]X_k[/math]'s.

Another model of a random walk (used mostly in the case where the range is [math]{\mathbf R}^1[/math]) is a game, involving two people, which consists of a sequence of independent, identically distributed moves. The sum [math]S_n[/math] represents the score of the first person, say, after [math]n[/math] moves, with the assumption that the score of the second person is [math]-S_n[/math]. For example, two people might be flipping coins, with a match or non-match representing [math]+1[/math] or [math]-1[/math], respectively, for the first player. Or, perhaps one coin is being flipped, with a head or tail representing [math]+1[/math] or [math]-1[/math], respectively, for the first player.

Random Walks on the Real Line

We shall first consider the simplest non-trivial case of a random walk in [math]{\mathbf R}^1[/math], namely the case where the common distribution function of the random variables [math]X_n[/math] is given by

[[math]] f_X(x) = \left \{ \begin{array}{ll} 1/2, & \mbox{if $x = \pm 1,$} \\ 0, & \mbox{otherwise.} \end{array} \right. [[/math]]

This situation corresponds to a fair coin being flipped, with [math]S_n[/math] representing the number of heads minus the number of tails which occur in the first [math]n[/math] flips. We note that in this situation, all paths of length [math]n[/math] have the same probability, namely [math]2^{-n}[/math].

It is sometimes instructive to represent a random walk as a polygonal line, or path, in the plane, where the horizontal axis represents time and the vertical axis represents the value of [math]S_n[/math]. Given a sequence [math]\{S_n\}[/math] of partial sums, we first plot the points [math](n, S_n)[/math], and then for each [math]k \lt n[/math], we connect [math](k, S_k)[/math] and [math](k+1, S_{k+1})[/math] with a straight line segment. 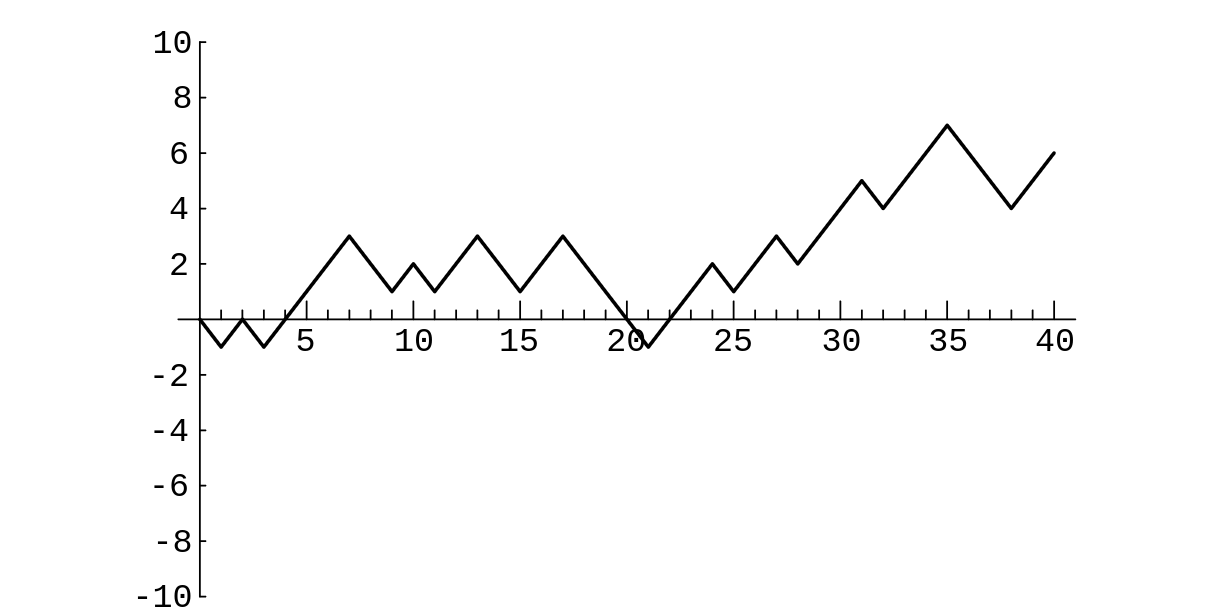The length of a path is just the difference in the time values of the beginning and ending points on the path. The reader is referred to Figure. This figure, and the process it illustrates, are identical with the example, given in Chapter 1, of two people playing heads or tails.

A random walk of length 40.

Returns and First Returns

We say that an equalization has occurred, or there is a return to the origin at time [math]n[/math], if [math]S_n = 0[/math]. We note that this can only occur if [math]n[/math] is an even integer. To calculate the probability of an equalization at time [math]2m[/math], we need only count the number of paths of length [math]2m[/math] which begin and end at the origin. The number of such paths is clearly

[[math]] {2m \choose m}\ . [[/math]]

Since each path has probability [math]2^{-2m}[/math], we have the following theorem.

Theorem

The probability of a return to the origin at time [math]2m[/math] is given by

[[math]] u_{2m} = {2m \choose m}2^{-2m}\ . [[/math]]

The probability of a return to the origin at an odd time is 0.

A random walk is said to have a first return to the origin at time

[math]2m[/math] if [math]m \gt 0[/math], and [math]S_{2k} \ne 0[/math] for all [math]k \lt m[/math]. In Figure, the first return occurs at time 2. We define [math]f_{2m}[/math] to be the probability of this event. (We also define [math]f_0 = 0[/math].) One can think of the expression [math]f_{2m}2^{2m}[/math] as the number of paths of length [math]2m[/math] between the points [math](0, 0)[/math] and [math](2m, 0)[/math] that do not touch the horizontal axis except at the endpoints. Using this idea, it is easy to prove the following theorem.

Theorem

For [math]n \ge 1[/math], the probabilities [math]\{u_{2k}\}[/math] and [math]\{f_{2k}\}[/math] are related by the equation

[[math]] u_{2n} = f_0 u_{2n} + f_2 u_{2n-2} + \cdots + f_{2n}u_0\ . [[/math]]

Show Proof

There are [math]u_{2n}2^{2n}[/math] paths of length [math]2n[/math] which have endpoints [math](0, 0)[/math] and [math](2n, 0)[/math]. The collection of such paths can be partitioned into [math]n[/math] sets, depending upon the time of the first return to the origin. A path in this collection which has a first return to the origin at time [math]2k[/math] consists of an initial segment from [math](0, 0)[/math] to [math](2k, 0)[/math], in which no interior points are on the horizontal axis, and a terminal segment from [math](2k, 0)[/math] to [math](2n, 0)[/math], with no further restrictions on this segment. Thus, the number of paths in the collection which have a first return to the origin at time [math]2k[/math] is given by

[[math]] f_{2k}2^{2k}u_{2n-2k}2^{2n-2k} = f_{2k}u_{2n-2k}2^{2n}\ . [[/math]]

If we sum over [math]k[/math], we obtain the equation

[[math]] u_{2n}2^{2n} = f_0u_{2n} 2^{2n} + f_2u_{2n-2}2^{2n} + \cdots + f_{2n}u_0 2^{2n}\ . [[/math]]

Dividing both sides of this equation by [math]2^{2n}[/math] completes the proof.

■

The expression in the right-hand side of the above theorem should remind the reader of a sum that appeared in Definition of the convolution of two distributions. The convolution of two sequences is defined in a similar manner. The above theorem says that the sequence [math]\{u_{2n}\}[/math] is the convolution of itself and the sequence [math]\{f_{2n}\}[/math]. Thus, if we represent each of these sequences by an ordinary generating function, then we can use the above relationship to determine the value [math]f_{2n}[/math].

Theorem

For [math]m \ge 1[/math], the probability of a first return to the origin at time [math]2m[/math] is given by

[[math]] f_{2m} = {{u_{2m}}\over{2m-1}} = {{2m \choose m}\over{(2m-1)2^{2m}}}\ . [[/math]]

Show Proof

We begin by defining the generating functions

[[math]] U(x) = \sum_{m = 0}^\infty u_{2m}x^m [[/math]]

and

[[math]] F(x) = \sum_{m = 0}^\infty f_{2m}x^m\ . [[/math]]

Theorem says that

[[math]] \begin{equation} U(x) = 1 + U(x)F(x)\ . \label{eq 12.1.1} \end{equation} [[/math]]

(The presence of the 1 on the right-hand side is due to the fact that [math]u_0[/math] is defined to be 1, but Theorem only holds for [math]m \ge 1[/math].) We note that both generating functions certainly converge on the interval [math](-1, 1)[/math], since all of the coefficients are at most 1 in absolute value. Thus, we can solve the above equation for [math]F(x)[/math], obtaining

[[math]] F(x) = {{U(x) - 1}\over{U(x)}}\ . [[/math]]

Now, if we can find a closed-form expression for the function [math]U(x)[/math], we will also have a closed-form expression for [math]F(x)[/math]. From Theorem, we have

[[math]] U(x) = \sum_{m = 0}^\infty {2m \choose m}2^{-2m}x^m\ . [[/math]]

In Wilf, we find that

[[math]] {1\over{\sqrt {1 - 4x}}} = \sum_{m = 0}^\infty {2m \choose m} x^m\ . [[/math]]

The reader is asked to prove this statement in Exercise. If we replace [math]x[/math] by [math]x/4[/math] in the last equation, we see that

[[math]] U(x) = {1\over{\sqrt {1-x}}}\ . [[/math]]

Therefore, we have

[[math]] \begin{eqnarray*} F(x) &=& {{U(x) - 1}\over{U(x)}}\\ &=& {{(1-x)^{-1/2} - 1}\over{(1-x)^{-1/2}}}\\ &=& 1 - (1-x)^{1/2}\ . \end{eqnarray*} [[/math]]

Although it is possible to compute the value of [math]f_{2m}[/math] using the Binomial Theorem, it is easier to note that [math]F'(x) = U(x)/2[/math], so that the coefficients [math]f_{2m}[/math] can be found by integrating the series for [math]U(x)[/math]. We obtain, for [math]m \ge 1[/math],

[[math]] \begin{eqnarray*} f_{2m} &=& {u_{2m-2}\over{2m}}\\ &=& {2m-2 \choose m-1}\over{m2^{2m-1}}\\ &=& {2m \choose m}\over{(2m-1)2^{2m}}\\ &=& {u_{2m}\over{2m-1}}\ , \end{eqnarray*} [[/math]]

since

[[math]] {2m-2 \choose m-1} = {m\over{2(2m-1)}}{2m\choose m}\ . [[/math]]

This completes the proof of the theorem.

■

Probability of Eventual Return

In the symmetric random walk process in [math]{\mathbf R}^m[/math], what is the probability that the particle eventually returns to the origin? We first examine this question in the case that [math]m = 1[/math], and then we consider the general case. The results in the next two examples are due to Pòlya.

Example One has to approach the idea of eventual return with some care, since the sample space seems to be the set of all walks of infinite length, and this set is non-denumerable. To avoid difficulties, we will define [math]w_n[/math] to be the probability that a first return has occurred no later than time [math]n[/math]. Thus, [math]w_n[/math] concerns the sample space of all walks of length [math]n[/math], which is a finite set. In terms of the [math]w_n[/math]'s, it is reasonable to define the probability that the particle eventually returns to the origin to be

[[math]] w_* = \lim_{n \rightarrow \infty} w_n\ . [[/math]]

This limit clearly exists and is at most one, since the sequence [math]\{w_n\}_{n = 1}^\infty[/math] is an increasing sequence, and all of its terms are at most one.

In terms of the [math]f_n[/math] probabilities, we see that

[[math]] w_{2n} = \sum_{i = 1}^n f_{2i}\ . [[/math]]

Thus,

[[math]] w_* = \sum_{i = 1}^\infty f_{2i}\ . [[/math]]

In the proof of Theorem, the generating function

[[math]] F(x) = \sum_{m = 0}^\infty f_{2m}x^m [[/math]]

was introduced. There it was noted that this series converges for [math]x \in (-1, 1)[/math]. In fact, it is possible to show that this series also converges for [math]x = \pm 1[/math] by using Exercise, together with the fact that

[[math]] f_{2m} = {{u_{2m}}\over{2m-1}}\ . [[/math]]

(This fact was proved in the proof of Theorem.) Since we also know that

[[math]] F(x) = 1 - (1-x)^{1/2}\ , [[/math]]

we see that

[[math]] w_* = F(1) = 1\ . [[/math]]

Thus, with probability one, the particle returns to the origin.

An alternative proof of the fact that [math]w_* = 1[/math] can be obtained by using the results in Exercise.

Example We now turn our attention to the case that the random walk takes place in more than one dimension. We define [math]f^{(m)}_{2n}[/math] to be the probability that the first return to the origin in [math]{\mathbf R}^m[/math] occurs at time [math]2n[/math]. The quantity [math]u^{(m)}_{2n}[/math] is defined in a similar manner. Thus, [math]f^{(1)}_{2n}[/math] and [math]u^{(1)}_{2n}[/math] equal [math]f_{2n}[/math] and [math]u_{2n}[/math], which were defined earlier. If, in addition, we define [math]u^{(m)}_0 = 1[/math] and [math]f^{(m)}_0 = 0[/math], then one can mimic the proof of Theorem, and show that for all [math]m \ge 1[/math],

[[math]] \begin{equation} u^{(m)}_{2n} = f^{(m)}_0 u^{(m)}_{2n} + f^{(m)}_2 u^{(m)}_{2n-2} + \cdots + f^{(m)}_{2n}u^{(m)}_0\ . \label{eq 12.1.1.5} \end{equation} [[/math]]

We continue to generalize previous work by defining

[[math]] U^{(m)}(x) = \sum_{n = 0}^\infty u^{(m)}_{2n} x^n [[/math]]

and

[[math]] F^{(m)}(x) = \sum_{n = 0}^\infty f^{(m)}_{2n} x^n\ . [[/math]]

Then, by using Equation, we see that

[[math]] U^{(m)}(x) = 1 + U^{(m)}(x) F^{(m)}(x)\ , [[/math]]

as before. These functions will always converge in the interval [math](-1, 1)[/math], since all of their coefficients are at most one in magnitude. In fact, since

[[math]] w^{(m)}_* = \sum_{n = 0}^\infty f^{(m)}_{2n} \le 1 [[/math]]

for all [math]m[/math], the series for [math]F^{(m)}(x)[/math] converges at [math]x = 1[/math] as well, and [math]F^{(m)}(x)[/math] is left-continuous at [math]x = 1[/math], i.e.,

[[math]] \lim_{x \uparrow 1} F^{(m)}(x) = F^{(m)}(1)\ . [[/math]]

Thus, we have

[[math]] \begin{equation} w^{(m)}_* = \lim_{x \uparrow 1} F^{(m)}(x) = \lim_{x \uparrow 1} \frac{U^{(m)}(x) - 1}{U^{(m)}(x)}\ , \label{eq 12.1.1.6} \end{equation} [[/math]]

so to determine [math]w^{(m)}_*[/math], it suffices to determine

[[math]] \lim_{x \uparrow 1} U^{(m)}(x)\ . [[/math]]

We let [math]u^{(m)}[/math] denote this limit.

We claim that

[[math]] u^{(m)} = \sum_{n = 0}^\infty u^{(m)}_{2n}\ . [[/math]]

(This claim is reasonable; it says that to find out what happens to the function [math]U^{(m)}(x)[/math] at [math]x = 1[/math], just let [math]x = 1[/math] in the power series for [math]U^{(m)}(x)[/math].) To prove the claim, we note that the coefficients [math]u^{(m)}_{2n}[/math] are non-negative, so [math]U^{(m)}(x)[/math] increases monotonically on the interval [math][0, 1)[/math]. Thus, for each [math]K[/math], we have

[[math]] \sum_{n = 0}^K u^{(m)}_{2n} \le \lim_{x \uparrow 1} U^{(m)}(x) = u^{(m)} \le \sum_{n = 0}^\infty u^{(m)}_{2n}\ . [[/math]]

By letting [math]K \rightarrow \infty[/math], we see that

[[math]] u^{(m)} = \sum_{2n}^\infty u^{(m)}_{2n}\ . [[/math]]

This establishes the claim.

From Equation, we see that if [math]u^{(m)} \lt \infty[/math], then the probability of an eventual return is

[[math]] \frac {u^{(m)} - 1}{u^{(m)}}\ , [[/math]]

while if [math]u^{(m)} = \infty[/math], then the probability of eventual return is 1.

To complete the example, we must estimate the sum

[[math]] \sum_{n = 0}^\infty u^{(m)}_{2n}\ . [[/math]]

In Exercise, the reader is asked to show that

[[math]] u^{(2)}_{2n} = \frac 1 {4^{2n}} {{2n}\choose n}^2\ . [[/math]]

Using Stirling's Formula, it is easy to show that (see Exercise)

[[math]] {{2n}\choose n} \sim \frac {2^{2n}}{\sqrt {\pi n}}\ , [[/math]]

so

[[math]] u^{(2)}_{2n} \sim \frac 1{\pi n}\ . [[/math]]

From this it follows easily that

[[math]] \sum_{n = 0}^\infty u^{(2)}_{2n} [[/math]]

diverges, so [math]w^{(2)}_* = 1[/math], i.e., in [math]{\mathbf R}^2[/math], the probability of an eventual return is 1.

When [math]m = 3[/math], Exercise shows that

[[math]] u^{(3)}_{2n} = \frac 1{2^{2n}}{{2n}\choose n} \sum_{j,k} \biggl(\frac 1{3^n}\frac{n!}{j!k!(n-j-k)!}\biggr)^2\ . [[/math]]

Let [math]M[/math] denote the largest value of

[[math]] \frac 1{3^n}\frac {n!}{j!k!(n - j - k)!}\ , [[/math]]

over all non-negative values of [math]j[/math] and [math]k[/math] with [math]j + k \le n[/math]. It is easy, using Stirling's Formula, to show that

[[math]] M \sim \frac cn\ , [[/math]]

for some constant [math]c[/math]. Thus, we have

[[math]] u^{(3)}_{2n} \le \frac 1{2^{2n}}{{2n}\choose n} \sum_{j,k} \biggl(\frac M{3^n}\frac{n!}{j!k!(n-j-k)!}\biggr)\ . [[/math]]

Using Exercise, one can show that the right-hand expression is at most

[[math]] \frac {c'}{n^{3/2}}\ , [[/math]]

where [math]c'[/math] is a constant. Thus,

[[math]] \sum_{n = 0}^\infty u^{(3)}_{2n} [[/math]]

converges, so [math]w^{(3)}_*[/math] is strictly less than one. This means that in [math]{\mathbf R}^3[/math], the probability of an eventual return to the origin is strictly less than one (in fact, it is approximately .34).

One may summarize these results by stating that one should not get drunk in more than two dimensions.

Expected Number of Equalizations

We now give another example of the use of generating functions to find a general formula for terms in a sequence, where the sequence is related by recursion relations to other sequences. Exercise gives still another example.

Example In this example, we will derive a formula for the expected number of equalizations in a random walk of length [math]2m[/math]. As in the proof of Theorem, the method has four main parts. First, a recursion is found which relates the [math]m[/math]th term in the unknown sequence to earlier terms in the same sequence and to terms in other (known) sequences. An example of such a recursion is given in Theorem. Second, the recursion is used to derive a functional equation involving the generating functions of the unknown sequence and one or more known sequences. Equation \ref{eq 12.1.1} is an example of such a functional equation. Third, the functional equation is solved for the unknown generating function. Last, using a device such as the Binomial Theorem, integration, or differentiation, a formula for the [math]m[/math]th coefficient of the unknown generating function is found.

We begin by defining [math]g_{2m}[/math] to be the number of equalizations among all of the random walks of length [math]2m[/math]. (For each random walk, we disregard the equalization at time 0.) We define [math]g_0 = 0[/math]. Since the number of walks of length [math]2m[/math] equals [math]2^{2m}[/math], the expected number of equalizations among all such random walks is [math]g_{2m}/2^{2m}[/math]. Next, we define the generating function [math]G(x)[/math]:

[[math]] G(x) = \sum_{k = 0}^\infty g_{2k}x^k\ . [[/math]]

Now we need to find a recursion which relates the sequence [math]\{g_{2k}\}[/math] to one or both of the known sequences [math]\{f_{2k}\}[/math] and [math]\{u_{2k}\}[/math]. We consider [math]m[/math] to be a fixed positive integer, and consider the set of all paths of length [math]2m[/math] as the disjoint union

[[math]] E_2 \cup E_4 \cup \cdots \cup E_{2m} \cup H\ , [[/math]]

where [math]E_{2k}[/math] is the set of all paths of length [math]2m[/math] with first equalization at time [math]2k[/math], and [math]H[/math] is the set of all paths of length [math]2m[/math] with no equalization. It is easy to show (see Exercise) that

[[math]] |E_{2k}| = f_{2k} 2^{2m}\ . [[/math]]

We claim that the number of equalizations among all paths belonging to the set [math]E_{2k}[/math] is equal to

[[math]] \begin{equation} |E_{2k}| + 2^{2k} f_{2k} g_{2m - 2k}\ . \label{eq 12.1.2} \end{equation} [[/math]]

Each path in [math]E_{2k}[/math] has one equalization at time [math]2k[/math], so the total number of such equalizations is just [math]|E_{2k}|[/math]. This is the first summand in expression Equation \ref{eq 12.1.2}. There are [math]2^{2k} f_{2k}[/math] different initial segments of length [math]2k[/math] among the paths in [math]E_{2k}[/math]. Each of these initial segments can be augmented to a path of length [math]2m[/math] in [math]2^{2m-2k}[/math] ways, by adjoining all possible paths of length [math]2m - 2k[/math]. The number of equalizations obtained by adjoining all of these paths to any one initial segment is [math]g_{2m - 2k}[/math], by definition. This gives the second summand in Equation \ref{eq 12.1.2}. Since [math]k[/math] can range from 1 to [math]m[/math], we obtain the recursion

[[math]] \begin{equation} g_{2m} = \sum_{k = 1}^m \Bigl(|E_{2k}| + 2^{2k}f_{2k}g_{2m - 2k}\Bigr)\ . \label{eq 12.1.3} \end{equation} [[/math]]

The second summand in the typical term above should remind the reader of a convolution. In fact, if we multiply the generating function [math]G(x)[/math] by the generating function

[[math]] F(4x) = \sum_{k = 0}^\infty 2^{2k}f_{2k} x^k\ , [[/math]]

the coefficient of [math]x^m[/math] equals

[[math]] \sum_{k = 0}^m 2^{2k}f_{2k}g_{2m-2k}\ . [[/math]]

Thus, the product [math]G(x)F(4x)[/math] is part of the functional equation that we are seeking. The first summand in the typical term in Equation \ref{eq 12.1.3} gives rise to the sum

[[math]] 2^{2m}\sum_{k = 1}^m f_{2k}\ . [[/math]]

From Exercise, we see that this sum is just [math](1 - u_{2m})2^{2m}[/math]. Thus, we need to create a generating function whose [math]m[/math]th coefficient is this term; this generating function is

[[math]] \sum_{m = 0}^\infty (1- u_{2m})2^{2m} x^m\ , [[/math]]

or

[[math]] \sum_{m = 0}^\infty 2^{2m} x^m - \sum_{m = 0}^\infty u_{2m}2^{2m} x^m\ . [[/math]]

The first sum is just [math](1-4x)^{-1}[/math], and the second sum is [math]U(4x)[/math]. So, the functional equation which we have been seeking is

[[math]] G(x) = F(4x)G(x) + {1\over{1-4x}} - U(4x)\ . [[/math]]

If we solve this recursion for [math]G(x)[/math], and simplify, we obtain

[[math]] \begin{equation} G(x) = {1\over{(1-4x)^{3/2}}} - {1\over{(1-4x)}}\ . \label{eq 12.1.4} \end{equation} [[/math]]

We now need to find a formula for the coefficient of [math]x^m[/math]. The first summand in Equation \ref{eq 12.1.4} is [math](1/2)U'(4x)[/math], so the coefficient of [math]x^m[/math] in this function is

[[math]] u_{2m+2} 2^{2m+1}(m+1)\ . [[/math]]

The second summand in Equation \ref{eq 12.1.4} is the sum of a geometric series with common ratio [math]4x[/math], so the coefficient of [math]x^m[/math] is [math]2^{2m}[/math]. Thus, we obtain

[[math]] \begin{eqnarray*} g_{2m} &=& u_{2m+2}2^{2m+1}(m+1) - 2^{2m}\\ &=& {1\over 2}{{2m+2} \choose {m+1}} (m+1) - 2^{2m}\ . \end{eqnarray*} [[/math]]

We recall that the quotient [math]g_{2m}/2^{2m}[/math] is the expected number of equalizations among all paths of length [math]2m[/math]. Using Exercise, it is easy to show that

[[math]] {{g_{2m}}\over{2^{2m}}} \sim \sqrt{2\over \pi}\sqrt {2m}\ . [[/math]]

In particular, this means that the average number of equalizations among all paths of length [math]4m[/math] is not twice the average number of equalizations among all paths of length [math]2m[/math]. In order for the average number of equalizations to double, one must quadruple the lengths of the random walks. It is interesting to note that if we define

[[math]] M_n = \max_{0 \le k \le n} S_k\ , [[/math]]

then we have

[[math]] E(M_n) \sim \sqrt{2\over \pi}\sqrt n\ . [[/math]]

This means that the expected number of equalizations and the expected maximum value for random walks of length [math]n[/math] are asymptotically equal as [math]n \rightarrow \infty[/math]. (In fact, it can be shown that the two expected values differ by at most [math]1/2[/math] for all positive integers [math]n[/math]. See (Exercise.)

General references

Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.