guide:356ab09fff: Difference between revisions
From Stochiki
No edit summary |
mNo edit summary |
||
| Line 1: | Line 1: | ||
==Cumulative from minus infinity to Z== | |||
[[File:Z cumulative from minus infinity.svg|thumb|right|The values correspond to the shaded area for given {{mvar|Z}}]] | |||
This table gives a probability that a statistic is between minus infinity and {{mvar|Z}}. | |||
<math display = "block"> f(z) = \Phi(z)</math> | |||
The values are calculated using the cumulative distribution function of a standard normal distribution with mean of zero and standard deviation of one, usually denoted with the capital Greek letter <math>\Phi</math>, is the integral | |||
<math display = "block">\Phi(z) = \frac 1 {\sqrt{2\pi}} \int_{-\infty}^z e^{-t^2/2} \, dt</math> | |||
<math>\Phi</math>(z) is related to the error function, or {{math|erf(''z'')}}. | |||
<math display ="block"> \Phi(z) = \frac12\left[1 + \operatorname{erf}\left( \frac z {\sqrt 2} \right) \right]</math> | |||
==Cumulative (less than Z)== | |||
This table gives a probability that a statistic is less than {{mvar|Z}} (i.e. between negative infinity and {{mvar|Z}}). | |||
{| class="table" | |||
! ''z'' !! −0.00!! −0.01!! −0.02!! −0.03!! −0.04!! −0.05!! −0.06!! −0.07!! −0.08!! −0.09 | |||
|- | |||
! -4.0 | |||
|0.00003||0.00003||0.00003||0.00003||0.00003||0.00003||0.00002||0.00002||0.00002||0.00002 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! -3.9 | |||
|0.00005||0.00005||0.00004||0.00004||0.00004||0.00004||0.00004||0.00004||0.00003||0.00003 | |||
|- | |||
! -3.8 | |||
|0.00007||0.00007||0.00007||0.00006||0.00006||0.00006||0.00006||0.00005||0.00005||0.00005 | |||
|- | |||
! -3.7 | |||
|0.00011||0.00010||0.00010||0.00010||0.00009||0.00009||0.00008||0.00008||0.00008||0.00008 | |||
|- | |||
! -3.6 | |||
|0.00016||0.00015||0.00015||0.00014||0.00014||0.00013||0.00013||0.00012||0.00012||0.00011 | |||
|- | |||
! -3.5 | |||
|0.00023||0.00022||0.00022||0.00021||0.00020||0.00019||0.00019||0.00018||0.00017||0.00017 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −3.4 | |||
|0.00034||0.00032||0.00031||0.00030||0.00029||0.00028||0.00027||0.00026||0.00025||0.00024 | |||
|- | |||
! −3.3 | |||
|0.00048||0.00047||0.00045||0.00043||0.00042||0.00040||0.00039||0.00038||0.00036||0.00035 | |||
|- | |||
! −3.2 | |||
|0.00069||0.00066||0.00064||0.00062||0.00060||0.00058||0.00056||0.00054||0.00052||0.00050 | |||
|- | |||
! −3.1 | |||
|0.00097||0.00094||0.00090||0.00087||0.00084||0.00082||0.00079||0.00076||0.00074||0.00071 | |||
|- | |||
! −3.0 | |||
|0.00135||0.00131||0.00126||0.00122||0.00118||0.00114||0.00111||0.00107||0.00104||0.00100 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −2.9 | |||
|0.00187||0.00181||0.00175||0.00169||0.00164||0.00159||0.00154||0.00149||0.00144||0.00139 | |||
|- | |||
! −2.8 | |||
|0.00256||0.00248||0.00240||0.00233||0.00226||0.00219||0.00212||0.00205||0.00199||0.00193 | |||
|- | |||
! −2.7 | |||
|0.00347||0.00336||0.00326||0.00317||0.00307||0.00298||0.00289||0.00280||0.00272||0.00264 | |||
|- | |||
! −2.6 | |||
|0.00466||0.00453||0.00440||0.00427||0.00415||0.00402||0.00391||0.00379||0.00368||0.00357 | |||
|- | |||
! −2.5 | |||
|0.00621||0.00604||0.00587||0.00570||0.00554||0.00539||0.00523||0.00508||0.00494||0.00480 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −2.4 | |||
|0.00820||0.00798||0.00776||0.00755||0.00734||0.00714||0.00695||0.00676||0.00657||0.00639 | |||
|- | |||
! −2.3 | |||
|0.01072||0.01044||0.01017||0.00990||0.00964||0.00939||0.00914||0.00889||0.00866||0.00842 | |||
|- | |||
! −2.2 | |||
|0.01390||0.01355||0.01321||0.01287||0.01255||0.01222||0.01191||0.01160||0.01130||0.01101 | |||
|- | |||
! −2.1 | |||
|0.01786||0.01743||0.01700||0.01659||0.01618||0.01578||0.01539||0.01500||0.01463||0.01426 | |||
|- | |||
! −2.0 | |||
|0.02275||0.02222||0.02169||0.02118||0.02068||0.02018||0.01970||0.01923||0.01876||0.01831 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −1.9 | |||
|0.02872||0.02807||0.02743||0.02680||0.02619||0.02559||0.02500||0.02442||0.02385||0.02330 | |||
|- | |||
! −1.8 | |||
|0.03593||0.03515||0.03438||0.03362||0.03288||0.03216||0.03144||0.03074||0.03005||0.02938 | |||
|- | |||
! −1.7 | |||
|0.04457||0.04363||0.04272||0.04182||0.04093||0.04006||0.03920||0.03836||0.03754||0.03673 | |||
|- | |||
! −1.6 | |||
|0.05480||0.05370||0.05262||0.05155||0.05050||0.04947||0.04846||0.04746||0.04648||0.04551 | |||
|- | |||
! −1.5 | |||
|0.06681||0.06552||0.06426||0.06301||0.06178||0.06057||0.05938||0.05821||0.05705||0.05592 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −1.4 | |||
|0.08076||0.07927||0.07780||0.07636||0.07493||0.07353||0.07215||0.07078||0.06944||0.06811 | |||
|- | |||
! −1.3 | |||
|0.09680||0.09510||0.09342||0.09176||0.09012||0.08851||0.08692||0.08534||0.08379||0.08226 | |||
|- | |||
! −1.2 | |||
|0.11507||0.11314||0.11123||0.10935||0.10749||0.10565||0.10383||0.10204||0.10027||0.09853 | |||
|- | |||
! −1.1 | |||
|0.13567||0.13350||0.13136||0.12924||0.12714||0.12507||0.12302||0.12100||0.11900||0.11702 | |||
|- | |||
! −1.0 | |||
|0.15866||0.15625||0.15386||0.15151||0.14917||0.14686||0.14457||0.14231||0.14007||0.13786 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −0.9 | |||
|0.18406||0.18141||0.17879||0.17619||0.17361||0.17106||0.16853||0.16602||0.16354||0.16109 | |||
|- | |||
! −0.8 | |||
|0.21186||0.20897||0.20611||0.20327||0.20045||0.19766||0.19489||0.19215||0.18943||0.18673 | |||
|- | |||
! −0.7 | |||
|0.24196||0.23885||0.23576||0.23270||0.22965||0.22663||0.22363||0.22065||0.21770||0.21476 | |||
|- | |||
! −0.6 | |||
|0.27425||0.27093||0.26763||0.26435||0.26109||0.25785||0.25463||0.25143||0.24825||0.24510 | |||
|- | |||
! −0.5 | |||
|0.30854||0.30503||0.30153||0.29806||0.29460||0.29116||0.28774||0.28434||0.28096||0.27760 | |||
|- | |||
| colspan="11" style="padding:0;"| | |||
|- | |||
! −0.4 | |||
|0.34458||0.34090||0.33724||0.33360||0.32997||0.32636||0.32276||0.31918||0.31561||0.31207 | |||
|- | |||
! −0.3 | |||
|0.38209||0.37828||0.37448||0.37070||0.36693||0.36317||0.35942||0.35569||0.35197||0.34827 | |||
|- | |||
! −0.2 | |||
|0.42074||0.41683||0.41294||0.40905||0.40517||0.40129||0.39743||0.39358||0.38974||0.38591 | |||
|- | |||
! −0.1 | |||
|0.46017||0.45620||0.45224||0.44828||0.44433||0.44038||0.43644||0.43251||0.42858||0.42465 | |||
|- | |||
! −0.0 | |||
|0.50000||0.49601||0.49202||0.48803||0.48405||0.48006||0.47608||0.47210||0.46812||0.46414 | |||
|- | |||
! ''z'' !! −0.00!! −0.01!! −0.02!! −0.03!! −0.04!! −0.05!! −0.06!! −0.07!! −0.08!! −0.09 | |||
|} | |||
{| class="table" | |||
! ''z'' !! + 0.00!! + 0.01!! + 0.02!! + 0.03!! + 0.04!! + 0.05!! + 0.06!! + 0.07!! + 0.08!! + 0.09 | |||
|- | |||
! 0.0 | |||
|0.50000||0.50399||0.50798||0.51197||0.51595||0.51994||0.52392||0.52790||0.53188||0.53586 | |||
|- | |||
! 0.1 | |||
|0.53983||0.54380||0.54776||0.55172||0.55567||0.55962||0.56360||0.56749||0.57142||0.57535 | |||
|- | |||
! 0.2 | |||
|0.57926||0.58317||0.58706||0.59095||0.59483||0.59871||0.60257||0.60642||0.61026||0.61409 | |||
|- | |||
! 0.3 | |||
|0.61791||0.62172||0.62552||0.62930||0.63307||0.63683||0.64058||0.64431||0.64803||0.65173 | |||
|- | |||
! 0.4 | |||
|0.65542||0.65910||0.66276||0.66640||0.67003||0.67364||0.67724||0.68082||0.68439||0.68793 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 0.5 | |||
|0.69146||0.69497||0.69847||0.70194||0.70540||0.70884||0.71226||0.71566||0.71904||0.72240 | |||
|- | |||
! 0.6 | |||
|0.72575||0.72907||0.73237||0.73565||0.73891||0.74215||0.74537||0.74857||0.75175||0.75490 | |||
|- | |||
! 0.7 | |||
|0.75804||0.76115||0.76424||0.76730||0.77035||0.77337||0.77637||0.77935||0.78230||0.78524 | |||
|- | |||
! 0.8 | |||
|0.78814||0.79103||0.79389||0.79673||0.79955||0.80234||0.80511||0.80785||0.81057||0.81327 | |||
|- | |||
! 0.9 | |||
|0.81594||0.81859||0.82121||0.82381||0.82639||0.82894||0.83147||0.83398||0.83646||0.83891 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 1.0 | |||
|0.84134||0.84375||0.84614||0.84849||0.85083||0.85314||0.85543||0.85769||0.85993||0.86214 | |||
|- | |||
! 1.1 | |||
|0.86433||0.86650||0.86864||0.87076||0.87286||0.87493||0.87698||0.87900||0.88100||0.88298 | |||
|- | |||
! 1.2 | |||
|0.88493||0.88686||0.88877||0.89065||0.89251||0.89435||0.89617||0.89796||0.89973||0.90147 | |||
|- | |||
! 1.3 | |||
|0.90320||0.90490||0.90658||0.90824||0.90988||0.91149||0.91308||0.91466||0.91621||0.91774 | |||
|- | |||
! 1.4 | |||
|0.91924||0.92073||0.92220||0.92364||0.92507||0.92647||0.92785||0.92922||0.93056||0.93189 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 1.5 | |||
|0.93319||0.93448||0.93574||0.93699||0.93822||0.93943||0.94062||0.94179||0.94295||0.94408 | |||
|- | |||
! 1.6 | |||
|0.94520||0.94630||0.94738||0.94845||0.94950||0.95053||0.95154||0.95254||0.95352||0.95449 | |||
|- | |||
! 1.7 | |||
|0.95543||0.95637||0.95728||0.95818||0.95907||0.95994||0.96080||0.96164||0.96246||0.96327 | |||
|- | |||
! 1.8 | |||
|0.96407||0.96485||0.96562||0.96638||0.96712||0.96784||0.96856||0.96926||0.96995||0.97062 | |||
|- | |||
! 1.9 | |||
|0.97128||0.97193||0.97257||0.97320||0.97381||0.97441||0.97500||0.97558||0.97615||0.97670 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 2.0 | |||
|0.97725||0.97778||0.97831||0.97882||0.97932||0.97982||0.98030||0.98077||0.98124||0.98169 | |||
|- | |||
! 2.1 | |||
|0.98214||0.98257||0.98300||0.98341||0.98382||0.98422||0.98461||0.98500||0.98537||0.98574 | |||
|- | |||
! 2.2 | |||
|0.98610||0.98645||0.98679||0.98713||0.98745||0.98778||0.98809||0.98840||0.98870||0.98899 | |||
|- | |||
! 2.3 | |||
|0.98928||0.98956||0.98983||0.99010||0.99036||0.99061||0.99086||0.99111||0.99134||0.99158 | |||
|- | |||
! 2.4 | |||
|0.99180||0.99202||0.99224||0.99245||0.99266||0.99286||0.99305||0.99324||0.99343||0.99361 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 2.5 | |||
|0.99379||0.99396||0.99413||0.99430||0.99446||0.99461||0.99477||0.99492||0.99506||0.99520 | |||
|- | |||
! 2.6 | |||
|0.99534||0.99547||0.99560||0.99573||0.99585||0.99598||0.99609||0.99621||0.99632||0.99643 | |||
|- | |||
! 2.7 | |||
|0.99653||0.99664||0.99674||0.99683||0.99693||0.99702||0.99711||0.99720||0.99728||0.99736 | |||
|- | |||
! 2.8 | |||
|0.99744||0.99752||0.99760||0.99767||0.99774||0.99781||0.99788||0.99795||0.99801||0.99807 | |||
|- | |||
! 2.9 | |||
|0.99813||0.99819||0.99825||0.99831||0.99836||0.99841||0.99846||0.99851||0.99856||0.99861 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 3.0 | |||
|0.99865||0.99869||0.99874||0.99878||0.99882||0.99886||0.99889||0.99893||0.99896||0.99900 | |||
|- | |||
! 3.1 | |||
|0.99903||0.99906||0.99910||0.99913||0.99916||0.99918||0.99921||0.99924||0.99926||0.99929 | |||
|- | |||
! 3.2 | |||
|0.99931||0.99934||0.99936||0.99938||0.99940||0.99942||0.99944||0.99946||0.99948||0.99950 | |||
|- | |||
! 3.3 | |||
|0.99952||0.99953||0.99955||0.99957||0.99958||0.99960||0.99961||0.99962||0.99964||0.99965 | |||
|- | |||
! 3.4 | |||
|0.99966||0.99968||0.99969||0.99970||0.99971||0.99972||0.99973||0.99974||0.99975||0.99976 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 3.5 | |||
|0.99977||0.99978||0.99978||0.99979||0.99980||0.99981||0.99981||0.99982||0.99983||0.99983 | |||
|- | |||
! 3.6 | |||
|0.99984||0.99985||0.99985||0.99986||0.99986||0.99987||0.99987||0.99988||0.99988||0.99989 | |||
|- | |||
! 3.7 | |||
|0.99989||0.99990||0.99990||0.99990||0.99991||0.99991||0.99992||0.99992||0.99992||0.99992 | |||
|- | |||
! 3.8 | |||
|0.99993||0.99993||0.99993||0.99994||0.99994||0.99994||0.99994||0.99995||0.99995||0.99995 | |||
|- | |||
! 3.9 | |||
|0.99995||0.99995||0.99996||0.99996||0.99996||0.99996||0.99996||0.99996||0.99997||0.99997 | |||
|- | |||
| colspan="1" style="padding:0;"| | |||
|- | |||
! 4.0 | |||
|0.99997||0.99997||0.99997||0.99997||0.99997||0.99997||0.99998||0.99998||0.99998||0.99998 | |||
|- | |||
! ''z'' !! +0.00!! +0.01!! +0.02!! +0.03!! +0.04!! +0.05!! +0.06!! +0.07!! +0.08!! +0.09 | |||
|} | |||
<ref>0.5 + each value in ''Cumulative from mean'' table</ref> | |||
==Notes== | |||
Latest revision as of 19:18, 12 June 2024
Cumulative from minus infinity to Z
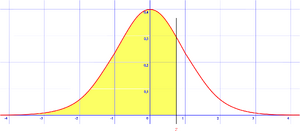
This table gives a probability that a statistic is between minus infinity and Z.
[[math]] f(z) = \Phi(z)[[/math]]
The values are calculated using the cumulative distribution function of a standard normal distribution with mean of zero and standard deviation of one, usually denoted with the capital Greek letter [math]\Phi[/math], is the integral
[[math]]\Phi(z) = \frac 1 {\sqrt{2\pi}} \int_{-\infty}^z e^{-t^2/2} \, dt[[/math]]
[math]\Phi[/math](z) is related to the error function, or erf(z).
[[math]] \Phi(z) = \frac12\left[1 + \operatorname{erf}\left( \frac z {\sqrt 2} \right) \right][[/math]]
Cumulative (less than Z)
This table gives a probability that a statistic is less than Z (i.e. between negative infinity and Z).
| z | −0.00 | −0.01 | −0.02 | −0.03 | −0.04 | −0.05 | −0.06 | −0.07 | −0.08 | −0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| -4.0 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00002 | 0.00002 | 0.00002 | 0.00002 |
| -3.9 | 0.00005 | 0.00005 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00003 | 0.00003 |
| -3.8 | 0.00007 | 0.00007 | 0.00007 | 0.00006 | 0.00006 | 0.00006 | 0.00006 | 0.00005 | 0.00005 | 0.00005 |
| -3.7 | 0.00011 | 0.00010 | 0.00010 | 0.00010 | 0.00009 | 0.00009 | 0.00008 | 0.00008 | 0.00008 | 0.00008 |
| -3.6 | 0.00016 | 0.00015 | 0.00015 | 0.00014 | 0.00014 | 0.00013 | 0.00013 | 0.00012 | 0.00012 | 0.00011 |
| -3.5 | 0.00023 | 0.00022 | 0.00022 | 0.00021 | 0.00020 | 0.00019 | 0.00019 | 0.00018 | 0.00017 | 0.00017 |
| −3.4 | 0.00034 | 0.00032 | 0.00031 | 0.00030 | 0.00029 | 0.00028 | 0.00027 | 0.00026 | 0.00025 | 0.00024 |
| −3.3 | 0.00048 | 0.00047 | 0.00045 | 0.00043 | 0.00042 | 0.00040 | 0.00039 | 0.00038 | 0.00036 | 0.00035 |
| −3.2 | 0.00069 | 0.00066 | 0.00064 | 0.00062 | 0.00060 | 0.00058 | 0.00056 | 0.00054 | 0.00052 | 0.00050 |
| −3.1 | 0.00097 | 0.00094 | 0.00090 | 0.00087 | 0.00084 | 0.00082 | 0.00079 | 0.00076 | 0.00074 | 0.00071 |
| −3.0 | 0.00135 | 0.00131 | 0.00126 | 0.00122 | 0.00118 | 0.00114 | 0.00111 | 0.00107 | 0.00104 | 0.00100 |
| −2.9 | 0.00187 | 0.00181 | 0.00175 | 0.00169 | 0.00164 | 0.00159 | 0.00154 | 0.00149 | 0.00144 | 0.00139 |
| −2.8 | 0.00256 | 0.00248 | 0.00240 | 0.00233 | 0.00226 | 0.00219 | 0.00212 | 0.00205 | 0.00199 | 0.00193 |
| −2.7 | 0.00347 | 0.00336 | 0.00326 | 0.00317 | 0.00307 | 0.00298 | 0.00289 | 0.00280 | 0.00272 | 0.00264 |
| −2.6 | 0.00466 | 0.00453 | 0.00440 | 0.00427 | 0.00415 | 0.00402 | 0.00391 | 0.00379 | 0.00368 | 0.00357 |
| −2.5 | 0.00621 | 0.00604 | 0.00587 | 0.00570 | 0.00554 | 0.00539 | 0.00523 | 0.00508 | 0.00494 | 0.00480 |
| −2.4 | 0.00820 | 0.00798 | 0.00776 | 0.00755 | 0.00734 | 0.00714 | 0.00695 | 0.00676 | 0.00657 | 0.00639 |
| −2.3 | 0.01072 | 0.01044 | 0.01017 | 0.00990 | 0.00964 | 0.00939 | 0.00914 | 0.00889 | 0.00866 | 0.00842 |
| −2.2 | 0.01390 | 0.01355 | 0.01321 | 0.01287 | 0.01255 | 0.01222 | 0.01191 | 0.01160 | 0.01130 | 0.01101 |
| −2.1 | 0.01786 | 0.01743 | 0.01700 | 0.01659 | 0.01618 | 0.01578 | 0.01539 | 0.01500 | 0.01463 | 0.01426 |
| −2.0 | 0.02275 | 0.02222 | 0.02169 | 0.02118 | 0.02068 | 0.02018 | 0.01970 | 0.01923 | 0.01876 | 0.01831 |
| −1.9 | 0.02872 | 0.02807 | 0.02743 | 0.02680 | 0.02619 | 0.02559 | 0.02500 | 0.02442 | 0.02385 | 0.02330 |
| −1.8 | 0.03593 | 0.03515 | 0.03438 | 0.03362 | 0.03288 | 0.03216 | 0.03144 | 0.03074 | 0.03005 | 0.02938 |
| −1.7 | 0.04457 | 0.04363 | 0.04272 | 0.04182 | 0.04093 | 0.04006 | 0.03920 | 0.03836 | 0.03754 | 0.03673 |
| −1.6 | 0.05480 | 0.05370 | 0.05262 | 0.05155 | 0.05050 | 0.04947 | 0.04846 | 0.04746 | 0.04648 | 0.04551 |
| −1.5 | 0.06681 | 0.06552 | 0.06426 | 0.06301 | 0.06178 | 0.06057 | 0.05938 | 0.05821 | 0.05705 | 0.05592 |
| −1.4 | 0.08076 | 0.07927 | 0.07780 | 0.07636 | 0.07493 | 0.07353 | 0.07215 | 0.07078 | 0.06944 | 0.06811 |
| −1.3 | 0.09680 | 0.09510 | 0.09342 | 0.09176 | 0.09012 | 0.08851 | 0.08692 | 0.08534 | 0.08379 | 0.08226 |
| −1.2 | 0.11507 | 0.11314 | 0.11123 | 0.10935 | 0.10749 | 0.10565 | 0.10383 | 0.10204 | 0.10027 | 0.09853 |
| −1.1 | 0.13567 | 0.13350 | 0.13136 | 0.12924 | 0.12714 | 0.12507 | 0.12302 | 0.12100 | 0.11900 | 0.11702 |
| −1.0 | 0.15866 | 0.15625 | 0.15386 | 0.15151 | 0.14917 | 0.14686 | 0.14457 | 0.14231 | 0.14007 | 0.13786 |
| −0.9 | 0.18406 | 0.18141 | 0.17879 | 0.17619 | 0.17361 | 0.17106 | 0.16853 | 0.16602 | 0.16354 | 0.16109 |
| −0.8 | 0.21186 | 0.20897 | 0.20611 | 0.20327 | 0.20045 | 0.19766 | 0.19489 | 0.19215 | 0.18943 | 0.18673 |
| −0.7 | 0.24196 | 0.23885 | 0.23576 | 0.23270 | 0.22965 | 0.22663 | 0.22363 | 0.22065 | 0.21770 | 0.21476 |
| −0.6 | 0.27425 | 0.27093 | 0.26763 | 0.26435 | 0.26109 | 0.25785 | 0.25463 | 0.25143 | 0.24825 | 0.24510 |
| −0.5 | 0.30854 | 0.30503 | 0.30153 | 0.29806 | 0.29460 | 0.29116 | 0.28774 | 0.28434 | 0.28096 | 0.27760 |
| −0.4 | 0.34458 | 0.34090 | 0.33724 | 0.33360 | 0.32997 | 0.32636 | 0.32276 | 0.31918 | 0.31561 | 0.31207 |
| −0.3 | 0.38209 | 0.37828 | 0.37448 | 0.37070 | 0.36693 | 0.36317 | 0.35942 | 0.35569 | 0.35197 | 0.34827 |
| −0.2 | 0.42074 | 0.41683 | 0.41294 | 0.40905 | 0.40517 | 0.40129 | 0.39743 | 0.39358 | 0.38974 | 0.38591 |
| −0.1 | 0.46017 | 0.45620 | 0.45224 | 0.44828 | 0.44433 | 0.44038 | 0.43644 | 0.43251 | 0.42858 | 0.42465 |
| −0.0 | 0.50000 | 0.49601 | 0.49202 | 0.48803 | 0.48405 | 0.48006 | 0.47608 | 0.47210 | 0.46812 | 0.46414 |
| z | −0.00 | −0.01 | −0.02 | −0.03 | −0.04 | −0.05 | −0.06 | −0.07 | −0.08 | −0.09 |
| z | + 0.00 | + 0.01 | + 0.02 | + 0.03 | + 0.04 | + 0.05 | + 0.06 | + 0.07 | + 0.08 | + 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.50000 | 0.50399 | 0.50798 | 0.51197 | 0.51595 | 0.51994 | 0.52392 | 0.52790 | 0.53188 | 0.53586 |
| 0.1 | 0.53983 | 0.54380 | 0.54776 | 0.55172 | 0.55567 | 0.55962 | 0.56360 | 0.56749 | 0.57142 | 0.57535 |
| 0.2 | 0.57926 | 0.58317 | 0.58706 | 0.59095 | 0.59483 | 0.59871 | 0.60257 | 0.60642 | 0.61026 | 0.61409 |
| 0.3 | 0.61791 | 0.62172 | 0.62552 | 0.62930 | 0.63307 | 0.63683 | 0.64058 | 0.64431 | 0.64803 | 0.65173 |
| 0.4 | 0.65542 | 0.65910 | 0.66276 | 0.66640 | 0.67003 | 0.67364 | 0.67724 | 0.68082 | 0.68439 | 0.68793 |
| 0.5 | 0.69146 | 0.69497 | 0.69847 | 0.70194 | 0.70540 | 0.70884 | 0.71226 | 0.71566 | 0.71904 | 0.72240 |
| 0.6 | 0.72575 | 0.72907 | 0.73237 | 0.73565 | 0.73891 | 0.74215 | 0.74537 | 0.74857 | 0.75175 | 0.75490 |
| 0.7 | 0.75804 | 0.76115 | 0.76424 | 0.76730 | 0.77035 | 0.77337 | 0.77637 | 0.77935 | 0.78230 | 0.78524 |
| 0.8 | 0.78814 | 0.79103 | 0.79389 | 0.79673 | 0.79955 | 0.80234 | 0.80511 | 0.80785 | 0.81057 | 0.81327 |
| 0.9 | 0.81594 | 0.81859 | 0.82121 | 0.82381 | 0.82639 | 0.82894 | 0.83147 | 0.83398 | 0.83646 | 0.83891 |
| 1.0 | 0.84134 | 0.84375 | 0.84614 | 0.84849 | 0.85083 | 0.85314 | 0.85543 | 0.85769 | 0.85993 | 0.86214 |
| 1.1 | 0.86433 | 0.86650 | 0.86864 | 0.87076 | 0.87286 | 0.87493 | 0.87698 | 0.87900 | 0.88100 | 0.88298 |
| 1.2 | 0.88493 | 0.88686 | 0.88877 | 0.89065 | 0.89251 | 0.89435 | 0.89617 | 0.89796 | 0.89973 | 0.90147 |
| 1.3 | 0.90320 | 0.90490 | 0.90658 | 0.90824 | 0.90988 | 0.91149 | 0.91308 | 0.91466 | 0.91621 | 0.91774 |
| 1.4 | 0.91924 | 0.92073 | 0.92220 | 0.92364 | 0.92507 | 0.92647 | 0.92785 | 0.92922 | 0.93056 | 0.93189 |
| 1.5 | 0.93319 | 0.93448 | 0.93574 | 0.93699 | 0.93822 | 0.93943 | 0.94062 | 0.94179 | 0.94295 | 0.94408 |
| 1.6 | 0.94520 | 0.94630 | 0.94738 | 0.94845 | 0.94950 | 0.95053 | 0.95154 | 0.95254 | 0.95352 | 0.95449 |
| 1.7 | 0.95543 | 0.95637 | 0.95728 | 0.95818 | 0.95907 | 0.95994 | 0.96080 | 0.96164 | 0.96246 | 0.96327 |
| 1.8 | 0.96407 | 0.96485 | 0.96562 | 0.96638 | 0.96712 | 0.96784 | 0.96856 | 0.96926 | 0.96995 | 0.97062 |
| 1.9 | 0.97128 | 0.97193 | 0.97257 | 0.97320 | 0.97381 | 0.97441 | 0.97500 | 0.97558 | 0.97615 | 0.97670 |
| 2.0 | 0.97725 | 0.97778 | 0.97831 | 0.97882 | 0.97932 | 0.97982 | 0.98030 | 0.98077 | 0.98124 | 0.98169 |
| 2.1 | 0.98214 | 0.98257 | 0.98300 | 0.98341 | 0.98382 | 0.98422 | 0.98461 | 0.98500 | 0.98537 | 0.98574 |
| 2.2 | 0.98610 | 0.98645 | 0.98679 | 0.98713 | 0.98745 | 0.98778 | 0.98809 | 0.98840 | 0.98870 | 0.98899 |
| 2.3 | 0.98928 | 0.98956 | 0.98983 | 0.99010 | 0.99036 | 0.99061 | 0.99086 | 0.99111 | 0.99134 | 0.99158 |
| 2.4 | 0.99180 | 0.99202 | 0.99224 | 0.99245 | 0.99266 | 0.99286 | 0.99305 | 0.99324 | 0.99343 | 0.99361 |
| 2.5 | 0.99379 | 0.99396 | 0.99413 | 0.99430 | 0.99446 | 0.99461 | 0.99477 | 0.99492 | 0.99506 | 0.99520 |
| 2.6 | 0.99534 | 0.99547 | 0.99560 | 0.99573 | 0.99585 | 0.99598 | 0.99609 | 0.99621 | 0.99632 | 0.99643 |
| 2.7 | 0.99653 | 0.99664 | 0.99674 | 0.99683 | 0.99693 | 0.99702 | 0.99711 | 0.99720 | 0.99728 | 0.99736 |
| 2.8 | 0.99744 | 0.99752 | 0.99760 | 0.99767 | 0.99774 | 0.99781 | 0.99788 | 0.99795 | 0.99801 | 0.99807 |
| 2.9 | 0.99813 | 0.99819 | 0.99825 | 0.99831 | 0.99836 | 0.99841 | 0.99846 | 0.99851 | 0.99856 | 0.99861 |
| 3.0 | 0.99865 | 0.99869 | 0.99874 | 0.99878 | 0.99882 | 0.99886 | 0.99889 | 0.99893 | 0.99896 | 0.99900 |
| 3.1 | 0.99903 | 0.99906 | 0.99910 | 0.99913 | 0.99916 | 0.99918 | 0.99921 | 0.99924 | 0.99926 | 0.99929 |
| 3.2 | 0.99931 | 0.99934 | 0.99936 | 0.99938 | 0.99940 | 0.99942 | 0.99944 | 0.99946 | 0.99948 | 0.99950 |
| 3.3 | 0.99952 | 0.99953 | 0.99955 | 0.99957 | 0.99958 | 0.99960 | 0.99961 | 0.99962 | 0.99964 | 0.99965 |
| 3.4 | 0.99966 | 0.99968 | 0.99969 | 0.99970 | 0.99971 | 0.99972 | 0.99973 | 0.99974 | 0.99975 | 0.99976 |
| 3.5 | 0.99977 | 0.99978 | 0.99978 | 0.99979 | 0.99980 | 0.99981 | 0.99981 | 0.99982 | 0.99983 | 0.99983 |
| 3.6 | 0.99984 | 0.99985 | 0.99985 | 0.99986 | 0.99986 | 0.99987 | 0.99987 | 0.99988 | 0.99988 | 0.99989 |
| 3.7 | 0.99989 | 0.99990 | 0.99990 | 0.99990 | 0.99991 | 0.99991 | 0.99992 | 0.99992 | 0.99992 | 0.99992 |
| 3.8 | 0.99993 | 0.99993 | 0.99993 | 0.99994 | 0.99994 | 0.99994 | 0.99994 | 0.99995 | 0.99995 | 0.99995 |
| 3.9 | 0.99995 | 0.99995 | 0.99996 | 0.99996 | 0.99996 | 0.99996 | 0.99996 | 0.99996 | 0.99997 | 0.99997 |
| 4.0 | 0.99997 | 0.99997 | 0.99997 | 0.99997 | 0.99997 | 0.99997 | 0.99998 | 0.99998 | 0.99998 | 0.99998 |
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 |