guide:4c4e15c536: Difference between revisions
No edit summary |
mNo edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
The function <math>\sin</math> does not have an inverse function. The reason is that it is perfectly possible to have <math>a \neq b</math> and <math>\sin a = \sin b</math>. Another way to reach the same conclusion is to consider the equation <math>x = \sin y</math>. Its graph is the curve in Figure 14. It does not define a function of <math>x</math> because it does not satisfy the condition in the definition of function (see page 14) which asserts that every vertical line intersects the graph of a function in at most one point. | |||
<div id="fig 6.14" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig6_14.png | 400px | thumb | ]] | |||
</div> | |||
However, on the interval <math>\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr]</math> the function <math>\sin</math> is a strictly increasing function. Hence, although <math>\sin</math> does not have an inverse, it follows by Theorem (2.4), page 250, | |||
that the function <math>\sin</math> ''with domain restricted to'' <math>\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr]</math> does have an inverse. This inverse function is denoted by either <math>\sin^{-1}</math> or <math>\arcsin</math>, and in this book we shall use the latter notation. Thus | |||
<math display="block"> | |||
\begin{array}{c} | |||
y = \arcsin x \;\;\;\mbox{if and only if}\;\;\; x = \sin y \\ | |||
\mbox{and}\;\;\; -\frac{\pi}{2} \leq y \leq \frac{\pi}{2}. | |||
\end{array} | |||
</math> | |||
The graph of the function <math>\arcsin</math> is shown in Figure 15(b). It is that part of the graph of the | |||
equation <math>x = \sin y</math> for which <math>y</math> satisfies the inequality <math>-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}</math>. Note that the graph of <math>\arcsin</math> is obtained from the graph of the restricted function <math>\sin</math> by reflection across the diagonal line <math>y = x</math>. It follows both from the definition of <math>\arcsin</math> and also from the illustration that ''the domain of <math>\arcsin</math> is the closed interval <math>[ -1, 1]</math> and the range is the closed interval <math>\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr]</math>.'' | |||
<div id="fig 6.15" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig6_15.png | 400px | thumb | ]] | |||
</div> | |||
It is a consequence of Theorem (3.4), page 261, that the function <math>\arcsin</math> is differentiable at every point of its domain except at -1 and +1. [In applying (3.4), let <math>f</math> be the function <math>\sin</math> restricted to <math>\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr]</math> and then <math>f^{-1} = \arcsin</math>.] We may compute the formula for the derivative either directly from (3.4) or by implicit differentiation. Choosing the latter method, we begin with <math>y = \arcsin x</math> and seek to find <math>\frac{dy}{dx}</math>. If <math>y = \arcsin x</math>, then <math>x = \sin y</math>, and so | |||
<math display="block"> | |||
\frac{d}{dx} x = \frac{d}{dx} \sin y, \;\;\; \mbox{or}\;\;\; 1 = \cos y \frac{dy}{dx} | |||
</math> | |||
Hence | |||
<math display="block"> | |||
\frac{dy}{dx} = \frac{1}{\cos y}. | |||
</math> | |||
To express <math>\cos y</math> in terms of <math>x</math>, we use the identity <math>\cos^{2} y + \sin^{2} y = 1</math> | |||
and the fact that <math>x = \sin y</math>. Hence <math>\cos^{2} y + x^{2} = 1</math>, and therefore | |||
<math display="block"> | |||
\cos y = \pm \sqrt {1 - x^2} . | |||
</math> | |||
However, <math>y</math> is restricted by the inequality <math>-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}</math> and in this interval <math>\cos y</math> is never negative. Hence the positive square root is the correct one, and we conclude that <math>\frac{dy}{dx} = \frac{1}{\sqrt{1 - x^2}}</math>. Thus | |||
{{proofcard|Theorem|theorem-1| | |||
<math display="block"> | |||
\frac{d}{dx} \arcsin x = \frac{1}{\sqrt{1 - x^2}}. | |||
</math>|}} | |||
'''Example''' | |||
Find the domain, range, and derivative of each of the composite functions | |||
<math display="block"> | |||
\mbox{(a)}\;\;\; \arcsin \frac{1}{1 + x^2}, \;\;\; \mbox{(b)}\;\;\; \arcsin(\ln x). | |||
</math> | |||
The quantity <math>\frac{1}{1 + x^2}</math> is defined for every real number <math>x</math> and also satisfies the inequalities <math>0 < \frac{1}{1 + x^{2}} \leq 1</math>. Hence, <math>\arcsin \frac{1}{1 + x^{2}}</math> is defined for every <math>x</math>; i.e., its domain is the set of all real numbers. The range of the function <math>\frac{1}{1 + x^{2}}</math>, however, is the half-open interval (0, 1]. It can be seen from Figure 15(b) that the function <math>\arcsin</math> maps the interval (0, 1] on the <math>x</math>-axis onto the interval <math>\Bigl(0, \frac{\pi}{2}\Bigr]</math> on the <math>y</math>-axis. It follows that the range of the composition <math>\arcsin \frac{1}{1 + x^{2}}</math> is the half-open interval <math>\Bigl(0, \frac{\pi}{2}\Bigr]</math>. The derivative is found using (4.1) and the Chain Rule: | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\frac{d}{dx} \arcsin \frac{1}{1 + x^{2}} | |||
&=& \frac{1}{\sqrt{1 - \Bigl(\frac{1}{1 + x^2}\Bigr)^2}} \frac{d}{dx} \Bigl(\frac{1}{1 + x^2}\Bigr) \\ | |||
&=& \frac{1}{\sqrt { \frac{(1 + x^2)^2 - 1}{(1 + x^2)^2} } } \frac{-2x}{(1 + x^2)^2} \\ | |||
&=& \frac{-2x}{(1 + x^2) \sqrt {2x^{2} + x^{4}}}= \frac{-2x}{(1 + x^2) |x| \sqrt {2 + x^2}}. | |||
\end{eqnarray*} | |||
</math> | |||
For any particular value of <math>x</math>, the quantity <math>\arcsin(\ln x)</math> is defined if and only if <math>\ln x</math> is defined and also lies in the domain of the function <math>\arcsin</math>, which is the interval [ - 1, 1]. Thus <math>x</math> must be positive, and <math>\ln x</math> must satisfy the inequalities <math>-1 \leq \ln x \leq 1</math>. Hence <math>x</math> must satisfy <math>\frac{1}{e} \leq x \leq e</math>. The domain of <math>\arcsin (\ln x)</math> is therefore the interval <math>\Bigl[\frac{1}{e}, e\Bigr]</math>, and the range is the same as that of <math>\arcsin</math>, i.e., the interval <math>\Bigl[ -\frac{\pi}{2}, \frac{\pi}{2} \Bigr]</math>. The derivative is given by | |||
<math display="block"> | |||
\frac{d}{dx} \arcsin(\ln x) = \frac{1}{\sqrt {1 - (\ln x)^2}} \frac{d}{dx} \ln x | |||
= \frac{1}{x \sqrt{1 - (\ln x)^2}} . | |||
</math> | |||
The integral formula corresponding to (4.1) is | |||
{{proofcard|Theorem|theorem-2| | |||
<math display="block"> | |||
\int \frac{dx}{\sqrt {1 - x^2}} = \arcsin x + c. | |||
</math>|}} | |||
'''Example''' | |||
Find <math>\int \frac{x dx}{\sqrt 4 - x^4}</math>. The first thing we do is to write the denominator, as closely as possible, in the form <math>\sqrt {1 - u^2}</math>. | |||
<math display="block"> | |||
\frac{1}{\sqrt{4 - x^4}} = \frac{1}{\sqrt{4 \Bigl(1 - \frac{x^4}{4}\Bigr)}} = \frac{1}{2 \sqrt {1 - \Bigl(\frac{x^2}{2}\Bigr)^2}} | |||
</math> | |||
Hence, letting <math>u = \frac{x^2}{2}</math>, we have <math>\frac{du}{dx} = x</math> and | |||
<math display="block"> | |||
\int \frac{x dx}{\sqrt{4 - x^4}} | |||
= \frac{1}{2} \int \frac{x dx}{\sqrt {1 - \Bigl(\frac{x^2}{2}\Bigr)^2} } | |||
= \frac{1}{2} \int \frac{1}{\sqrt{1 - u^2}} \frac {du}{dx} dx . | |||
</math> | |||
By (4.2), | |||
<math display="block"> | |||
\frac{1}{2} \int \frac{1}{\sqrt {1 - u^2}} \frac{du}{dx} dx = \frac{1}{2} \arcsin u + c. | |||
</math> | |||
Finally, substituting <math>\frac{x^2}{2}</math> for <math>u</math>, we obtain | |||
<math display="block"> | |||
\int \frac{xdx}{\sqrt {4 - x^4}} = \frac{1}{2} \arcsin \frac{x^2}{2} + c. | |||
</math> | |||
<div id="fig 6.16" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig6_16.png | 400px | thumb | ]] | |||
</div> | |||
The function <math>\cos</math> does not have an inverse for the same reason that <math>\sin</math> does not. However, a partial inverse can be obtained, just as before, by restricting the domain to an interval on which <math>\cos</math> is either increasing or decreasing. Any such interval can be chosen. With the function <math>\sin</math> it was natural to choose the largest possible interval containing the number 0---the closed interval <math>\Bigl[ -\frac{\pi}{2}, \frac{\pi}{2}\Bigr]</math>. With <math>\cos</math> the choice is less obvious. However, we shall select the interval <math>[0, \pi]</math>, on which <math>\cos</math> is strictly decreasing [see Figure 16(a)]. The function <math>\cos</math> with domain restricted to <math>[0, \pi]</math> then has an inverse, which is denoted <math>\cos^{-1}</math> or <math>\arccos</math>. As before, we shall use the second notation. Thus | |||
<math display="block"> | |||
\begin{array}{c} | |||
y = \arccos x \;\;\; \mbox{if and only if}\;\;\; x = \cos y \\ | |||
\mbox{and}\;\;\; 0 \leq y \leq \pi. | |||
\end{array} | |||
</math> | |||
The graph of <math>\arccos</math> is shown in Figure 16(b). | |||
It should come as no surprise that the two functions <math>\arcsin</math> and <math>\arccos</math> are closely related. In fact, | |||
{{proofcard|Theorem|theorem-3| | |||
<math display="block"> | |||
\arcsin x = \frac{\pi}{2} - \arccos x. | |||
</math> | |||
|Let <math>y = \frac{\pi}{2} - \arccos x</math>. Then <math>\arccos x = \frac{\pi}{2} - y</math>, and so | |||
<math>x = \cos \Bigl(\frac{\pi}{2} - y \Bigr)</math>. | |||
Hence | |||
<math display="block"> | |||
x = \cos \Bigl(\frac{\pi}{2} - y \Bigr) = \cos \frac{\pi}{2} \cos y + \sin \frac{\pi}{2} \sin y = \sin y. | |||
</math> | |||
Since <math>0 \leq \arccos x \leq \pi</math>, it follows that <math>-\pi \leq - \arccos x \leq 0</math> and hence | |||
<math>- \frac{\pi}{2} \leq \frac{\pi}{2} -\arccos x \leq \frac{\pi}{2}</math> or, equivalently, <math>- \frac{\pi}{2} \leq y \leq \frac{\pi}{2}</math> . This, together with <math>x = \sin y</math>, implies that <math>y = \arcsin x</math>, and the proof is complete.}} | |||
Note that the validity of (4.3) depends on our having chosen <math>\arccos</math> so that its range is the interval <math>[0, \pi]</math>. | |||
It follows from (4.3) that the derivative of <math>\arccos</math> is the negative of the derivative of <math>\arcsin</math>. Thus | |||
{{proofcard|Theorem|theorem-4| | |||
<math display="block"> | |||
\frac{d}{dx} \arccos x = -\frac{1}{\sqrt{1 - x^2}}. | |||
</math>|}} | |||
From (4.4) we see that another indefinite integral of <math>\frac{1}{\sqrt{1 - x^2}}</math> is <math>-\arccos x</math>. | |||
Obviously, not one of the six trigonometric functions with unrestricted domain has an inverse. | |||
The function <math>\tan</math> with its domain restricted to the open interval <math>\Bigl( -\frac{\pi}{2}, \frac{\pi}{2} \Bigr)</math> is strictly increasing and so has an inverse function, which we denote <math>\tan^{-1}</math> or <math>\arctan</math>. | |||
<math display="block"> | |||
\begin{array}{c} | |||
y = \arctan x \;\;\; \mbox{if and only if} \;\;\; x = \tan y \\ | |||
\mbox{and}\;\;\; -\frac{\pi}{2} < y < \frac{\pi}{2}. | |||
\end{array} | |||
</math> | |||
The graph of <math>\arctan</math> is obtained by reflecting the graph of <math>\tan</math> with domain restricted to | |||
<math>\Bigl( -\frac{\pi}{2}, \frac{\pi}{2}\Bigr)</math> across the diagonal line <math>y = x</math>. It is shown in Figure 17(b). | |||
As can be seen from Figure 17(a), the function <math>\tan</math> maps the open interval <math>\Bigl( -\frac{\pi}{2}, \frac{\pi}{2}\Bigr )</math> onto the entire set of real numbers. That is, for every real number <math>y</math>, | |||
there exists a real number <math>x</math> in <math>\Bigl( -\frac{\pi}{2}, \frac{\pi}{2} \Bigr)</math> such that <math>y = \tan x</math>. Hence the domain of arctun is the whole real line <math>( -\infty, \infty)</math>. The range is the interval | |||
<math>\Bigl( -\frac{\pi}{2}, \frac{\pi}{2}\Bigr)</math>.'' | |||
<div id="fig 6.17" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig6_17.png | 400px | thumb | ]] | |||
</div> | |||
It is a corollary of Theorem (3.4), page 261, that <math>\arctan</math> is a differentiable function. | |||
We compute the derivative by implicit differentiation. Let <math>y = \arctan x</math>. Then <math>x = \tan y</math>, and | |||
<math display="block"> | |||
\frac{d}{dx} x = \frac{d}{dx} \tan y \;\;\;\mbox{or}\;\;\; 1 = \sec^{2}y \frac{dy}{dx}. | |||
</math> | |||
Hence | |||
<math display="block"> | |||
\frac{dy}{dx} = \frac{1}{\sec^{2} y}. | |||
</math> | |||
From the identity <math>\sec^{2} y = 1 + \tan^{2} y</math>, we get <math>\sec^{2} y = 1 + x^{2}</math>. | |||
It follows that <math>\frac{d}{dx} = \frac{1}{1 + x^2}</math>. Thus | |||
{{proofcard|Theorem|theorem-5| | |||
<math display="block"> | |||
\frac{d}{dx} \arctan x = \frac{1}{1 + x^{2}}. | |||
</math>|}} | |||
The corresponding integral formula is | |||
{{proofcard|Theorem|theorem-6| | |||
<math display="block"> | |||
\int \frac{dx}{1 + x^2} = \arctan x + c . | |||
</math>|}} | |||
'''Example''' | |||
Compute the definite integral <math>\int_{0}^{1} \frac{dx}{1 + x^2}</math>. We get immediately | |||
<math display="block"> | |||
\int_{0}^{1} \frac{dx}{1 + x^2} = \arctan x \big |_{0}^{1} = \arctan 1 - \arctan 0. | |||
</math> | |||
Since <math>\tan 0 = 0</math> and <math>\tan \frac{\pi}{4} = 1</math>, we know that <math>0 = \arctan 0</math> | |||
and <math>\frac{\pi}{4} = \arctan 1</math>. Hence | |||
<math display="block"> | |||
\int_{0}^{1} \frac{dx}{1 + x^2} = \frac{\pi}{4}. | |||
</math> | |||
This is a fascinating result: The number <math>\pi</math> is equal to four times the area bounded by the curve <math>y = \frac{1}{1 + x^2}</math>, the <math>x</math>-axis, and the lines <math>x= 0</math> and <math>x = 1</math>. | |||
The function <math>\cot</math> is strictly decreasing on the open interval <math>(0, \pi)</math>. With its domain restricted to this interval, <math>\cot</math> therefore has an inverse function, which we denote <math>\cot^{-1}</math> or <math>\mathrm{arccot}</math>. | |||
The relation between the two functions <math>\mathrm{arccot}</math> and <math>\arctan</math> is the same as that between <math>\arccos</math> and <math>\arcsin</math>, | |||
{{proofcard|Theorem|theorem-7| | |||
<math display="block"> | |||
\mbox{arccot} x = \frac{\pi}{2} - \arctan x. | |||
</math>|}} | |||
The proof is analogous to the proof of (4.3) and is left to the reader as an exercise. It is a corollary that the derivative of <math>\mathrm{arccot}</math> is the negative of the derivative of <math>\arctan</math>. Hence | |||
{{proofcard|Theorem|theorem-8| | |||
<math display="block"> | |||
\frac{d}{dx} \mathrm{arccot}\; x = - \frac{1}{1 + x^{2}}. | |||
</math>|}} | |||
Here again, we see another indefinite integral of <math>\frac{1}{1 + x^2}</math>, the function <math>-\mathrm{arccot}\; x</math>. | |||
The union of the two half-open intervals <math>\Bigl[0, \frac{\pi}{2}\Bigr)</math> and <math>(\frac{\pi}{2}, \pi]</math> consists | |||
of all real numbers <math>x</math> such that <math>0 \leq x \leq \pi</math> and <math>x \neq \frac{\pi}{2}</math>. It can be seen from | |||
the graph of the equation <math>y = \sec x</math> in Figure 13, page 308, that if <math>a</math> and <math>b</math> are two numbers | |||
in the union <math>[0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi]</math> and if <math>a \neq b</math>, then | |||
<math>\sec a \neq \sec b</math>. We omit <math>\frac{\pi}{2}</math> because the secant of that number is not defined. | |||
It follows that the function <math>\sec</math> with domain restricted to <math>\Bigl[0, \frac{\pi}{2}\Bigr) \cup \Bigl(\frac{\pi}{2}, \pi\Bigr]</math> has an inverse, which is denoted <math>\sec^{-1}</math> or <math>\mathrm{arcsec}</math>. Thus | |||
<math display="block"> | |||
\begin{array}{c} | |||
y = \mathrm{arcsec}\; x \;\;\; \mbox{if and only if} \;\;\; x = \sec y \\ | |||
\mbox{and $y$ is in}\; [0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi]. | |||
\end{array} | |||
</math> | |||
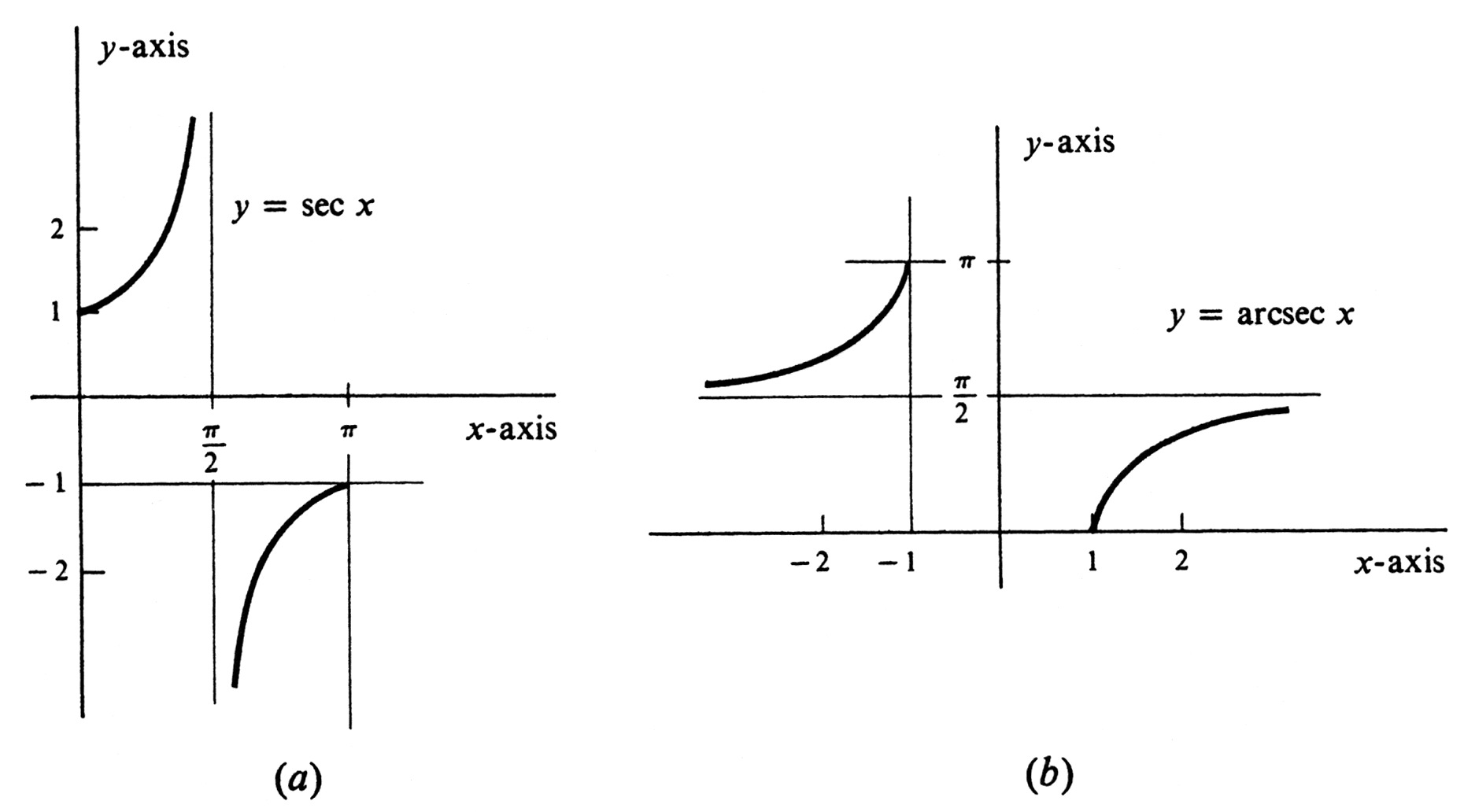
The graph of the function <math>\mathrm{arcsec}</math> is shown in Figure 18(b). ''Its range is the union'' <math>\Bigl[0,\frac{\pi}{2}\Bigr) \cup \Bigl(\frac{\pi}{2}, \pi \Bigr]</math>. As can be seen from Figure 18(a), the function sec maps the set <math>\Bigl[0, \frac{\pi}{2}\Bigr) \cup \Bigl(\frac{\pi}{2}, \pi \Bigr]</math> onto the set of all real numbers with absolute value greater than or equal to 1. Hence ''the domain of $\mathrm{arcsec}$ is the set of all real numbers $x$ such that $|x| \geq 1$.'' | |||
<div id="fig 6.18" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig6_18.png | 400px | thumb | ]] | |||
</div> | |||
The derivative can again be found by implicit differentiation. Let <math>y = \mathrm{arcsec}\; x</math>. Then <math>x = \sec y</math> and | |||
<math display="block"> | |||
\frac{d}{dx} x = \frac{d}{dx} \sec y, \;\;\;\mbox{which implies}\;\;\; 1 = \sec y \tan y \frac{dy}{dx}. | |||
</math> | |||
Thus | |||
<math display="block"> | |||
\frac{dy}{dx} = \frac{ 1} {\sec y \tan y}. | |||
</math> | |||
Using the identity <math>\sec^{2} y = 1 + \tan^{2} y</math> and the equation <math>x = \sec y</math>, we obtain | |||
<math display="block"> | |||
\sec y \tan y = \pm x \sqrt{x^{2} - 1}. | |||
</math> | |||
If <math>x \geq 1</math>, then <math>0 \leq y < \frac{\pi}{2}</math>, and so <math>\sec y \tan y</math> is nonnegative. Hence | |||
<math display="block"> | |||
\sec y \tan y = x \sqrt{x^{2} - 1} \;\;\;\mbox{if}\; x \geq 1. | |||
</math> | |||
On the other hand, if <math>x \leq -1</math>, then <math>\frac{\pi}{2} < y \leq \pi</math>, and in this case both <math>\sec y</math> and <math>\tan y</math> are nonpositive. Their product is therefore again nonnegative; i.e., | |||
<math display="block"> | |||
\sec y \tan y = -x \sqrt{x^{2} - 1}\;\;\; \mbox{if}\; x \leq -1. | |||
</math> | |||
It follows that both cases are covered by the single equation <math>\sec y \tan y = |x| \sqrt{x^{2} -1}</math>. Hence <math>\frac{dy}{dx} = \frac{1}{|x| \sqrt{x^2 - 1}}</math>, and we have derived the formula | |||
{{proofcard|Theorem|theorem-9| | |||
<math display="block"> | |||
\frac{d}{dx} \mathrm{arcsec}\; x = \frac{1}{|x| \sqrt{x^{2} - 1}}. | |||
</math>|}} | |||
The final inverse trigonometric function is the inverse of the cosecant with domain restricted to the union <math>\Bigl[ -\frac{\pi}{2}, 0\Bigr) \cup \Bigl(0, \frac{\pi}{2}\Bigr]</math>. This function, denoted <math>\csc^{-1}</math> or <math>\mathrm{arccsc}</math>, has range equal to <math>\Bigl[ - \frac{\pi}{2}, 0\Bigr) \cup \Bigl(0, \frac{\pi}{2}\Bigr]</math> and domain equal to the set of all real numbers <math>x</math> such that <math>|x| \geq 1</math>. The analogue of (4.3) and (4.7) is valid. That is, | |||
{{proofcard|Theorem|theorem-10| | |||
<math display="block"> | |||
\mathrm{arcsec}\; x = \frac{\pi}{2} - \mathrm{arccsc}\; x. | |||
</math> | |||
|The proof mimics that of (4.3). Let <math>y = -\frac{\pi}{2} - \mathrm{arccsc}\; x</math>. | |||
Then <math>\mathrm{arccsc}\; x = \frac{\pi}{2} - y</math>, and so <math>x = \csc \Bigl(\frac{\pi}{2} - y \Bigr)</math>. Thus | |||
<math display="block"> | |||
x = \csc \Bigl(\frac{\pi}{2} - y \Bigr) = \frac{1}{\sin \Bigl(\frac{\pi}{2} - y \Bigr)} = \frac{1}{\cos y} = \sec y. | |||
</math> | |||
Since <math>-\frac{\pi}{2} \leq \mathrm{arccsc}\; x \leq \frac{\pi}{2}</math> it follows that <math>0 \leq \frac{\pi}{2} - \mathrm{arccsc}\; x \leq \pi</math>, or, equivalently, that <math>0 \leq y \leq \pi</math>. This, together with <math>x = \sec y</math>, implies that <math>y = \mathrm{arcsec}\; x</math>, and the proof is complete.}} | |||
From this it follows at once that | |||
{{proofcard|Theorem|theorem-11| | |||
<math display="block"> | |||
\frac{d}{dx} \mathrm{arccsc}\; x | |||
= -\frac{1}{|x| \sqrt{x^{2} - 1}} . | |||
</math>|}} | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Latest revision as of 20:33, 19 November 2024
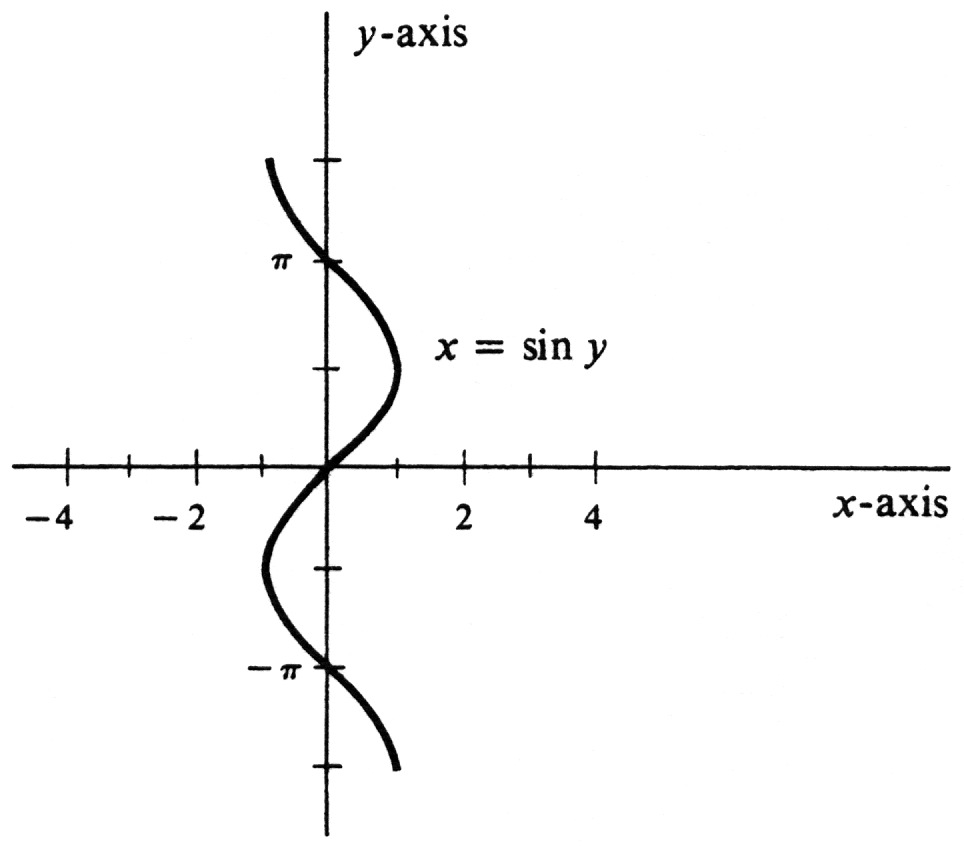
The function [math]\sin[/math] does not have an inverse function. The reason is that it is perfectly possible to have [math]a \neq b[/math] and [math]\sin a = \sin b[/math]. Another way to reach the same conclusion is to consider the equation [math]x = \sin y[/math]. Its graph is the curve in Figure 14. It does not define a function of [math]x[/math] because it does not satisfy the condition in the definition of function (see page 14) which asserts that every vertical line intersects the graph of a function in at most one point.
However, on the interval [math]\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr][/math] the function [math]\sin[/math] is a strictly increasing function. Hence, although [math]\sin[/math] does not have an inverse, it follows by Theorem (2.4), page 250, that the function [math]\sin[/math] with domain restricted to [math]\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr][/math] does have an inverse. This inverse function is denoted by either [math]\sin^{-1}[/math] or [math]\arcsin[/math], and in this book we shall use the latter notation. Thus
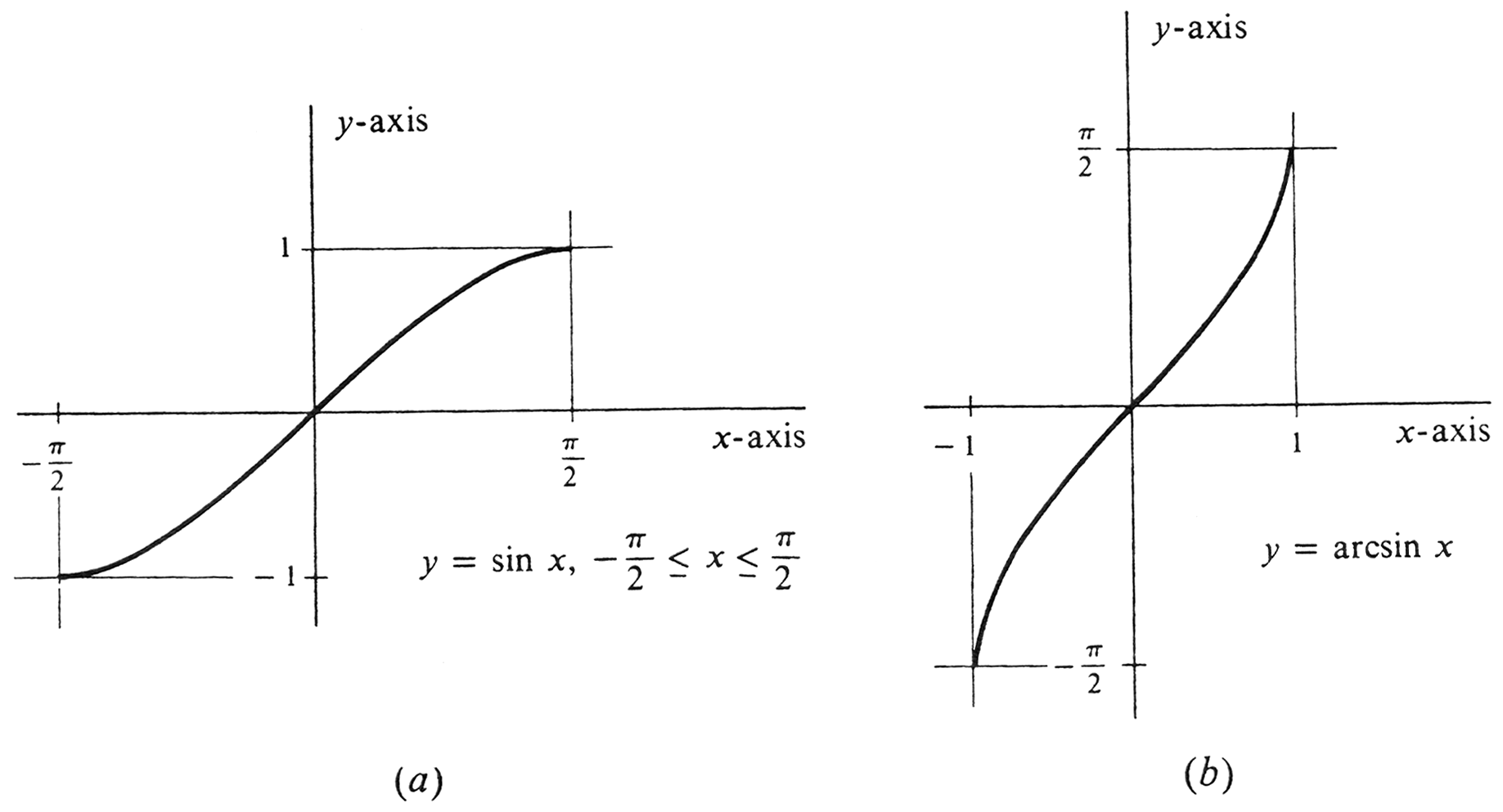
The graph of the function [math]\arcsin[/math] is shown in Figure 15(b). It is that part of the graph of the equation [math]x = \sin y[/math] for which [math]y[/math] satisfies the inequality [math]-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}[/math]. Note that the graph of [math]\arcsin[/math] is obtained from the graph of the restricted function [math]\sin[/math] by reflection across the diagonal line [math]y = x[/math]. It follows both from the definition of [math]\arcsin[/math] and also from the illustration that the domain of [math]\arcsin[/math] is the closed interval [math][ -1, 1][/math] and the range is the closed interval [math]\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr][/math].
It is a consequence of Theorem (3.4), page 261, that the function [math]\arcsin[/math] is differentiable at every point of its domain except at -1 and +1. [In applying (3.4), let [math]f[/math] be the function [math]\sin[/math] restricted to [math]\Bigl[-\frac{\pi}{2}, \frac{\pi}{2}\Bigr][/math] and then [math]f^{-1} = \arcsin[/math].] We may compute the formula for the derivative either directly from (3.4) or by implicit differentiation. Choosing the latter method, we begin with [math]y = \arcsin x[/math] and seek to find [math]\frac{dy}{dx}[/math]. If [math]y = \arcsin x[/math], then [math]x = \sin y[/math], and so
Hence
To express [math]\cos y[/math] in terms of [math]x[/math], we use the identity [math]\cos^{2} y + \sin^{2} y = 1[/math] and the fact that [math]x = \sin y[/math]. Hence [math]\cos^{2} y + x^{2} = 1[/math], and therefore
However, [math]y[/math] is restricted by the inequality [math]-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}[/math] and in this interval [math]\cos y[/math] is never negative. Hence the positive square root is the correct one, and we conclude that [math]\frac{dy}{dx} = \frac{1}{\sqrt{1 - x^2}}[/math]. Thus
Example
Find the domain, range, and derivative of each of the composite functions
The quantity [math]\frac{1}{1 + x^2}[/math] is defined for every real number [math]x[/math] and also satisfies the inequalities [math]0 \lt \frac{1}{1 + x^{2}} \leq 1[/math]. Hence, [math]\arcsin \frac{1}{1 + x^{2}}[/math] is defined for every [math]x[/math]; i.e., its domain is the set of all real numbers. The range of the function [math]\frac{1}{1 + x^{2}}[/math], however, is the half-open interval (0, 1]. It can be seen from Figure 15(b) that the function [math]\arcsin[/math] maps the interval (0, 1] on the [math]x[/math]-axis onto the interval [math]\Bigl(0, \frac{\pi}{2}\Bigr][/math] on the [math]y[/math]-axis. It follows that the range of the composition [math]\arcsin \frac{1}{1 + x^{2}}[/math] is the half-open interval [math]\Bigl(0, \frac{\pi}{2}\Bigr][/math]. The derivative is found using (4.1) and the Chain Rule:
For any particular value of [math]x[/math], the quantity [math]\arcsin(\ln x)[/math] is defined if and only if [math]\ln x[/math] is defined and also lies in the domain of the function [math]\arcsin[/math], which is the interval [ - 1, 1]. Thus [math]x[/math] must be positive, and [math]\ln x[/math] must satisfy the inequalities [math]-1 \leq \ln x \leq 1[/math]. Hence [math]x[/math] must satisfy [math]\frac{1}{e} \leq x \leq e[/math]. The domain of [math]\arcsin (\ln x)[/math] is therefore the interval [math]\Bigl[\frac{1}{e}, e\Bigr][/math], and the range is the same as that of [math]\arcsin[/math], i.e., the interval [math]\Bigl[ -\frac{\pi}{2}, \frac{\pi}{2} \Bigr][/math]. The derivative is given by
The integral formula corresponding to (4.1) is
Example
Find [math]\int \frac{x dx}{\sqrt 4 - x^4}[/math]. The first thing we do is to write the denominator, as closely as possible, in the form [math]\sqrt {1 - u^2}[/math].
Hence, letting [math]u = \frac{x^2}{2}[/math], we have [math]\frac{du}{dx} = x[/math] and
By (4.2),
Finally, substituting [math]\frac{x^2}{2}[/math] for [math]u[/math], we obtain
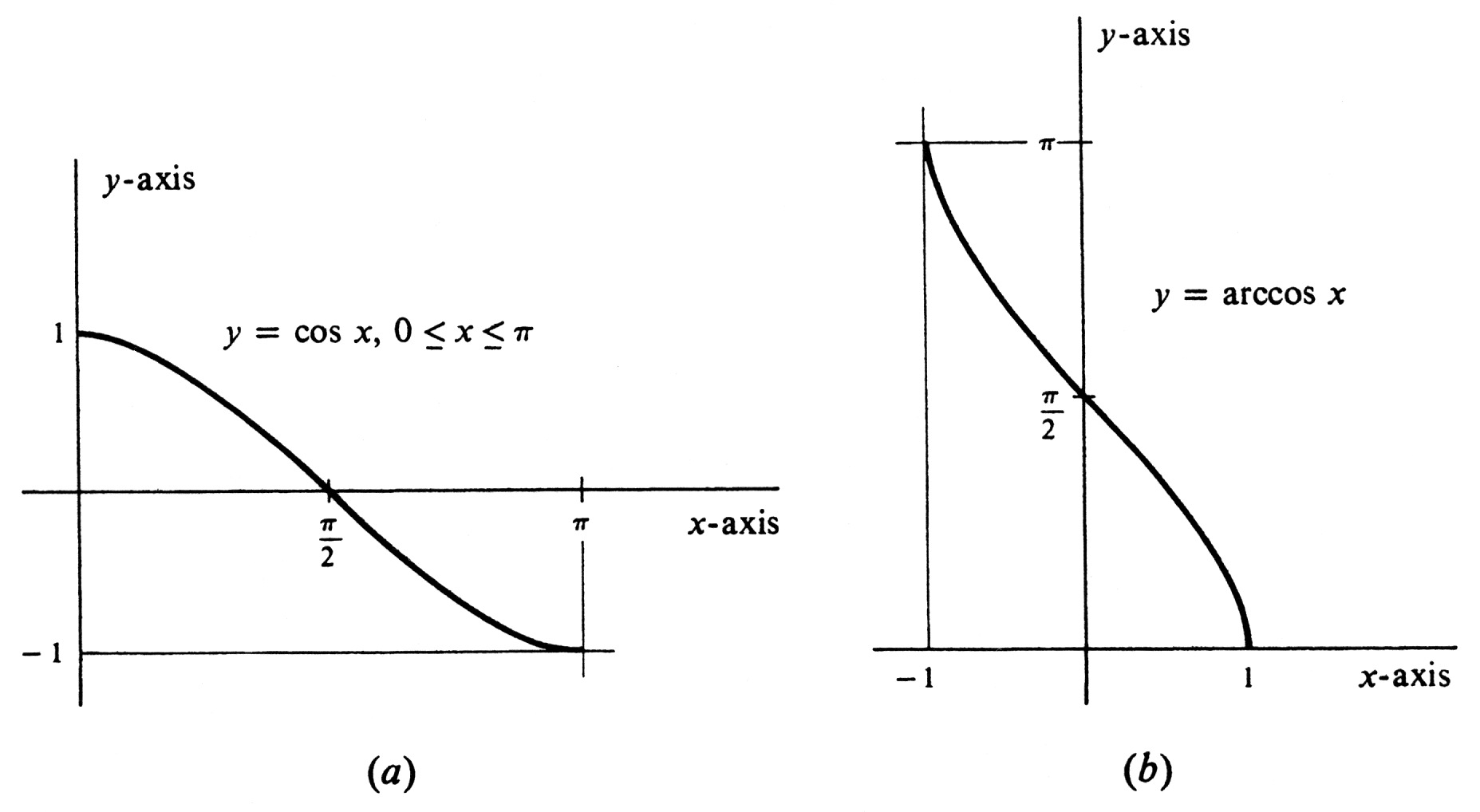
The function [math]\cos[/math] does not have an inverse for the same reason that [math]\sin[/math] does not. However, a partial inverse can be obtained, just as before, by restricting the domain to an interval on which [math]\cos[/math] is either increasing or decreasing. Any such interval can be chosen. With the function [math]\sin[/math] it was natural to choose the largest possible interval containing the number 0---the closed interval [math]\Bigl[ -\frac{\pi}{2}, \frac{\pi}{2}\Bigr][/math]. With [math]\cos[/math] the choice is less obvious. However, we shall select the interval [math][0, \pi][/math], on which [math]\cos[/math] is strictly decreasing [see Figure 16(a)]. The function [math]\cos[/math] with domain restricted to [math][0, \pi][/math] then has an inverse, which is denoted [math]\cos^{-1}[/math] or [math]\arccos[/math]. As before, we shall use the second notation. Thus
The graph of [math]\arccos[/math] is shown in Figure 16(b). It should come as no surprise that the two functions [math]\arcsin[/math] and [math]\arccos[/math] are closely related. In fact,
Let [math]y = \frac{\pi}{2} - \arccos x[/math]. Then [math]\arccos x = \frac{\pi}{2} - y[/math], and so [math]x = \cos \Bigl(\frac{\pi}{2} - y \Bigr)[/math]. Hence
Note that the validity of (4.3) depends on our having chosen [math]\arccos[/math] so that its range is the interval [math][0, \pi][/math]. It follows from (4.3) that the derivative of [math]\arccos[/math] is the negative of the derivative of [math]\arcsin[/math]. Thus
From (4.4) we see that another indefinite integral of [math]\frac{1}{\sqrt{1 - x^2}}[/math] is [math]-\arccos x[/math]. Obviously, not one of the six trigonometric functions with unrestricted domain has an inverse. The function [math]\tan[/math] with its domain restricted to the open interval [math]\Bigl( -\frac{\pi}{2}, \frac{\pi}{2} \Bigr)[/math] is strictly increasing and so has an inverse function, which we denote [math]\tan^{-1}[/math] or [math]\arctan[/math].
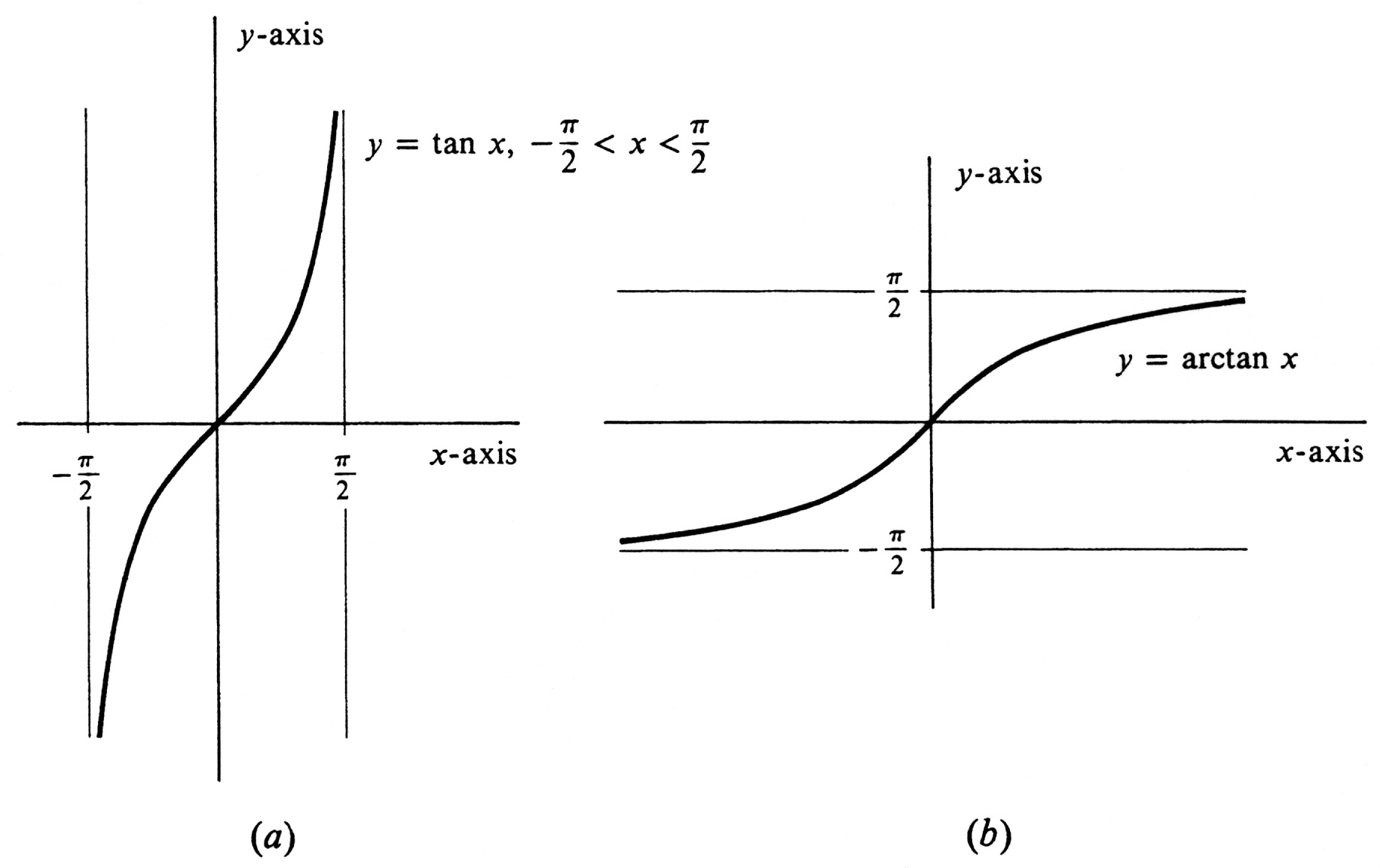
The graph of [math]\arctan[/math] is obtained by reflecting the graph of [math]\tan[/math] with domain restricted to [math]\Bigl( -\frac{\pi}{2}, \frac{\pi}{2}\Bigr)[/math] across the diagonal line [math]y = x[/math]. It is shown in Figure 17(b). As can be seen from Figure 17(a), the function [math]\tan[/math] maps the open interval [math]\Bigl( -\frac{\pi}{2}, \frac{\pi}{2}\Bigr )[/math] onto the entire set of real numbers. That is, for every real number [math]y[/math], there exists a real number [math]x[/math] in [math]\Bigl( -\frac{\pi}{2}, \frac{\pi}{2} \Bigr)[/math] such that [math]y = \tan x[/math]. Hence the domain of arctun is the whole real line [math]( -\infty, \infty)[/math]. The range is the interval
[math]\Bigl( -\frac{\pi}{2}, \frac{\pi}{2}\Bigr)[/math].
It is a corollary of Theorem (3.4), page 261, that [math]\arctan[/math] is a differentiable function. We compute the derivative by implicit differentiation. Let [math]y = \arctan x[/math]. Then [math]x = \tan y[/math], and
Hence
From the identity [math]\sec^{2} y = 1 + \tan^{2} y[/math], we get [math]\sec^{2} y = 1 + x^{2}[/math]. It follows that [math]\frac{d}{dx} = \frac{1}{1 + x^2}[/math]. Thus
The corresponding integral formula is
Example
Compute the definite integral [math]\int_{0}^{1} \frac{dx}{1 + x^2}[/math]. We get immediately
Since [math]\tan 0 = 0[/math] and [math]\tan \frac{\pi}{4} = 1[/math], we know that [math]0 = \arctan 0[/math] and [math]\frac{\pi}{4} = \arctan 1[/math]. Hence
This is a fascinating result: The number [math]\pi[/math] is equal to four times the area bounded by the curve [math]y = \frac{1}{1 + x^2}[/math], the [math]x[/math]-axis, and the lines [math]x= 0[/math] and [math]x = 1[/math].
The function [math]\cot[/math] is strictly decreasing on the open interval [math](0, \pi)[/math]. With its domain restricted to this interval, [math]\cot[/math] therefore has an inverse function, which we denote [math]\cot^{-1}[/math] or [math]\mathrm{arccot}[/math]. The relation between the two functions [math]\mathrm{arccot}[/math] and [math]\arctan[/math] is the same as that between [math]\arccos[/math] and [math]\arcsin[/math],
The proof is analogous to the proof of (4.3) and is left to the reader as an exercise. It is a corollary that the derivative of [math]\mathrm{arccot}[/math] is the negative of the derivative of [math]\arctan[/math]. Hence
Here again, we see another indefinite integral of [math]\frac{1}{1 + x^2}[/math], the function [math]-\mathrm{arccot}\; x[/math]. The union of the two half-open intervals [math]\Bigl[0, \frac{\pi}{2}\Bigr)[/math] and [math](\frac{\pi}{2}, \pi][/math] consists of all real numbers [math]x[/math] such that [math]0 \leq x \leq \pi[/math] and [math]x \neq \frac{\pi}{2}[/math]. It can be seen from the graph of the equation [math]y = \sec x[/math] in Figure 13, page 308, that if [math]a[/math] and [math]b[/math] are two numbers in the union [math][0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi][/math] and if [math]a \neq b[/math], then [math]\sec a \neq \sec b[/math]. We omit [math]\frac{\pi}{2}[/math] because the secant of that number is not defined. It follows that the function [math]\sec[/math] with domain restricted to [math]\Bigl[0, \frac{\pi}{2}\Bigr) \cup \Bigl(\frac{\pi}{2}, \pi\Bigr][/math] has an inverse, which is denoted [math]\sec^{-1}[/math] or [math]\mathrm{arcsec}[/math]. Thus
The graph of the function [math]\mathrm{arcsec}[/math] is shown in Figure 18(b). Its range is the union [math]\Bigl[0,\frac{\pi}{2}\Bigr) \cup \Bigl(\frac{\pi}{2}, \pi \Bigr][/math]. As can be seen from Figure 18(a), the function sec maps the set [math]\Bigl[0, \frac{\pi}{2}\Bigr) \cup \Bigl(\frac{\pi}{2}, \pi \Bigr][/math] onto the set of all real numbers with absolute value greater than or equal to 1. Hence the domain of $\mathrm{arcsec}$ is the set of all real numbers $x$ such that $|x| \geq 1$.
The derivative can again be found by implicit differentiation. Let [math]y = \mathrm{arcsec}\; x[/math]. Then [math]x = \sec y[/math] and
Thus
Using the identity [math]\sec^{2} y = 1 + \tan^{2} y[/math] and the equation [math]x = \sec y[/math], we obtain
If [math]x \geq 1[/math], then [math]0 \leq y \lt \frac{\pi}{2}[/math], and so [math]\sec y \tan y[/math] is nonnegative. Hence
On the other hand, if [math]x \leq -1[/math], then [math]\frac{\pi}{2} \lt y \leq \pi[/math], and in this case both [math]\sec y[/math] and [math]\tan y[/math] are nonpositive. Their product is therefore again nonnegative; i.e.,
It follows that both cases are covered by the single equation [math]\sec y \tan y = |x| \sqrt{x^{2} -1}[/math]. Hence [math]\frac{dy}{dx} = \frac{1}{|x| \sqrt{x^2 - 1}}[/math], and we have derived the formula
The final inverse trigonometric function is the inverse of the cosecant with domain restricted to the union [math]\Bigl[ -\frac{\pi}{2}, 0\Bigr) \cup \Bigl(0, \frac{\pi}{2}\Bigr][/math]. This function, denoted [math]\csc^{-1}[/math] or [math]\mathrm{arccsc}[/math], has range equal to [math]\Bigl[ - \frac{\pi}{2}, 0\Bigr) \cup \Bigl(0, \frac{\pi}{2}\Bigr][/math] and domain equal to the set of all real numbers [math]x[/math] such that [math]|x| \geq 1[/math]. The analogue of (4.3) and (4.7) is valid. That is,
The proof mimics that of (4.3). Let [math]y = -\frac{\pi}{2} - \mathrm{arccsc}\; x[/math]. Then [math]\mathrm{arccsc}\; x = \frac{\pi}{2} - y[/math], and so [math]x = \csc \Bigl(\frac{\pi}{2} - y \Bigr)[/math]. Thus
From this it follows at once that
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.