guide:4347f93d74: Difference between revisions
No edit summary |
mNo edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
This section is divided into two parts. The first is devoted to an alternative approach to the definite integral, which is useful for many purposes. The second is an application of the first part to the problem of computing definite integrals by numerical approximations. We begin by reviewing briefly the definitions in Section 1 of Chapter 4. If the function <math>f</math> is bounded on the closed interval <math>[a, b]</math>, then, for every partition <math>\sigma</math> of <math>[a, b]</math>, there are defined an upper sum <math>U_\sigma</math> and a lower sum <math>L_\sigma</math>, which approximate the definite integral from above and below, respectively. The function <math>f</math> is defined to be integrable over <math>[a, b]</math> if there exists one and only one number, denoted by <math>\int_a^b f</math>, with the property that | |||
<math display="block"> | |||
L_\sigma \leq \int_a^b f \leq U_\tau, | |||
</math> | |||
for every pair of partitions <math>\sigma</math> and <math>\tau</math> of <math>[a, b]</math>. | |||
In the alternative description of the integral, the details are similar, but not the same. As above, let <math>\sigma = \{ x_0, . . ., x_n \}</math> be a partition of <math>[a, b]</math>, which satisfies the inequalities | |||
<math display="block"> | |||
a = x_0 \leq x_1 \leq ... \leq x_n = b. | |||
</math> | |||
In each subinterval <math>[x_{i-1}, x_i]</math> we select an arbitrary number, which we shall denote by <math>x_i^{*}</math>. Then the sum | |||
<math display="block"> | |||
R_\sigma = \sum_{i = 1}^{n} f(x_i^{*})(x_i - x_{i-1}) | |||
</math> | |||
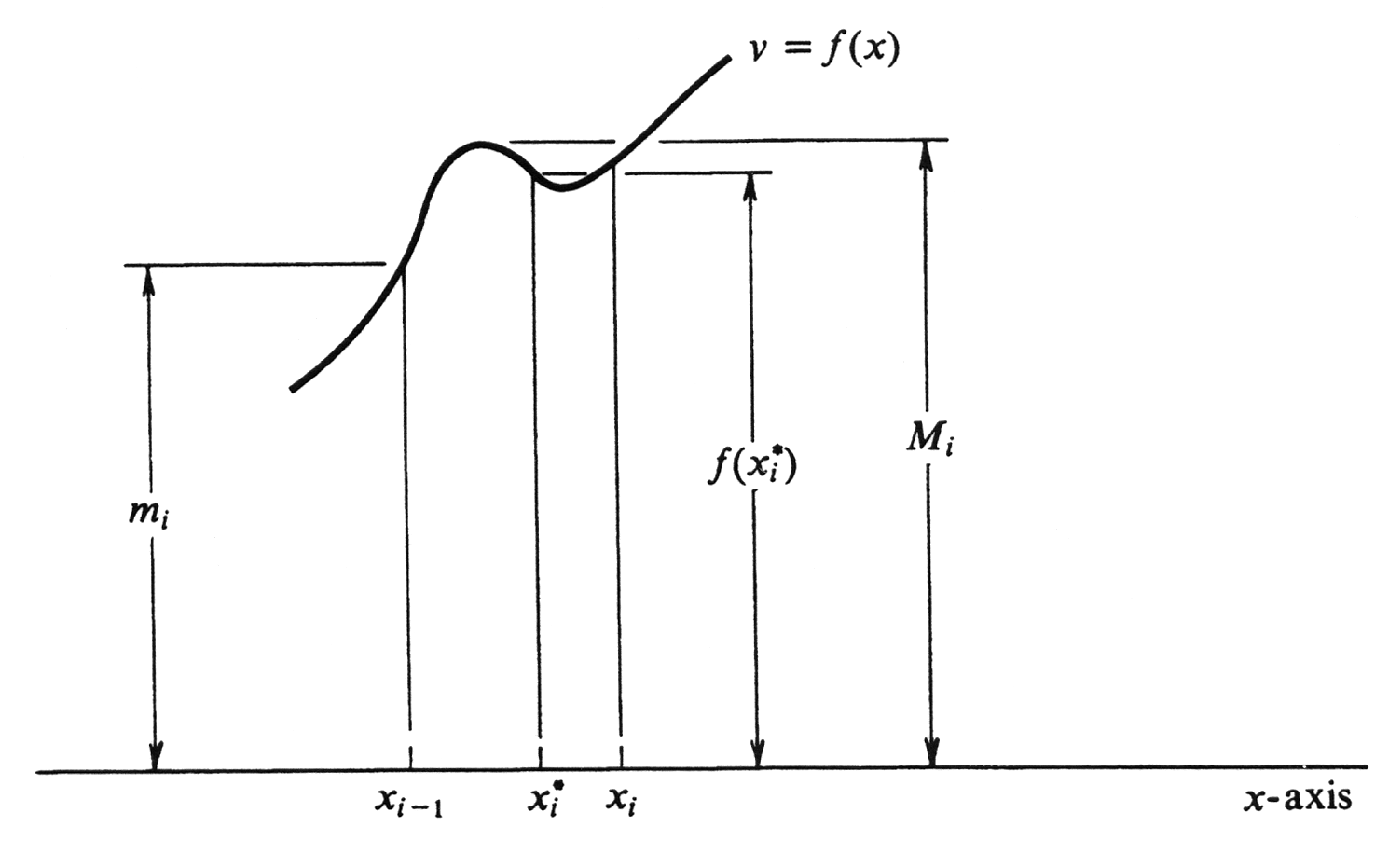
is called a '''Riemann sum''' for <math>f</math> relative to the partition <math>\sigma</math>. (The name commemorates the great mathematician Bernhard Riemann, 1826-1866.) It is important to realize that since <math>x_i^{*}</math> may be any number which satisfies <math>x_{i-1} \leq x_i^{*} \leq x_i</math>, there are in general infinitely many Riemann sums <math>R_\sigma</math> for a given <math>f</math> and partition <math>\sigma</math>. However, every <math>R_\sigma</math> lies between the corresponding upper and lower sums <math>U_\sigma</math> and <math>L_\sigma</math>. For, if the least upper bound of the values of <math>f</math> on <math>[x_{i-1}, x_i]</math> is denoted by <math>M_i</math> and the greatest lower bound by <math>m_i</math>, then <math>f(x_i^{*})</math> is an intermediate value and | |||
<math display="block"> | |||
m_i \leq f(x_i^{*}) \leq M_i, | |||
</math> | |||
as shown in Figure 4. It follows that | |||
<math display="block"> | |||
\sum_{i=1}^n m_{i}(x_i - x_{i - 1}) \leq \sum_{i=1}^n f(x_i^{*})(x_i - x_{i - 1}) \leq \sum_{i=1}^n M_i(x_i - x_{i-1}), | |||
</math> | |||
which states that | |||
<math display="block"> | |||
L_\sigma \leq R_\sigma \leq U_\sigma, | |||
</math> | |||
for every Riemann sum <math>R_\sigma</math> for <math>f</math> relative to <math>\sigma</math>. | |||
<div id="fig 8.4" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_4.png | 400px | thumb | ]] | |||
</div> | |||
Every Riemann sum is an approximation to the definite integral. By taking partitions which subdivide the interval of integration into smaller and smaller subintervals, we should expect to get better and better approximations to <math>\int_a^b f</math>. One number which measures the fineness of a given partition <math>\sigma</math> is the length of the largest subinterval into which <math>\sigma</math> subdivides <math>[a, b]</math>. This number is called the '''mesh''' of the partition and is denoted by <math>||\sigma ||</math>. Thus if <math>\sigma = \{ x_0, ..., x_n \}</math> is a partition of <math>[a, b]</math> with | |||
<math display="block"> | |||
a = x_0 \leq x_1 \leq \cdots \leq x_n = b, | |||
</math> | |||
then | |||
<math display="block"> | |||
||\sigma || = \mbox{maximum} \{ (x_i - x_{i-1}) \} . \;\;\; 1 \leq i \leq n | |||
</math> | |||
The following definition states precisely what we mean when we say that the Riemann sums approach a limit as the mesh tends to zero. Let the function <math>f</math> be bounded on the interval <math>[a, b]</math>. We shall write | |||
<math display="block"> | |||
\lim_{||\sigma || \rightarrow 0} R_\sigma = L, | |||
</math> | |||
where <math>L</math> is a real number, if the difference between the number <math>L</math> and any Riemann sum <math>R_\sigma</math> for <math>f</math> is arbitrarily small provided the mesh <math>||\sigma||</math> is sufficiently small. Stated formally, the limit exists if: For any positive real number <math>\epsilon</math>, there exists a positive real number <math>\delta</math> such that, if <math>R_\sigma</math> is any Riemann sum for <math>f</math> relative to a partition <math>\sigma</math> of <math>[a, b]</math> and if <math>|| \sigma || < \delta</math>, then <math> | R_\sigma - L | < \epsilon</math>. | |||
The fundamental fact that integrability is equivalent to the existence of the limit of Riemann sums is expressed in the following theorem. | |||
{{proofcard|Theorem|theorem-1|Let <math>f</math> be bounded on <math>[a, b]</math>. Then <math>f</math> is integrable over <math>[a, b]</math> if and only if <math>\lim_{|| \sigma || \rightarrow 0} R_\sigma</math> exists. If this limit exists, then it is equal to <math>\int_a^b f</math>.|}} | |||
The proof is given in Appendix C. | |||
'''Example''' | |||
Using the fact that the definite integral is the limit of Riemann sums, evaluate | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} \frac{\sqrt 1 + \sqrt 2 + ... + \sqrt n}{n^{3/2}}. | |||
</math> | |||
The numerator of this fraction suggests trying the function <math>f</math> defined by <math>f(x) = \sqrt x</math>. If <math> \sigma = \{ x_0, . . ., x_n \}</math> is the partition of the interval <math>[0, 1]</math> into subintervals of length <math>\frac{1}{n}</math>, then | |||
<math display="block"> | |||
\begin{array}{rl} | |||
x_0 = 0, \;\;\; x_1 = \frac{1}{n},\;\;\;& x_2 = \frac{2}{n}, ... , x_i = \frac{i}{n},\\ | |||
x_i - x_{i-1} = \frac{1}{n},\;\;\;& \;\;\;\mbox{for}\; i = 1, ... , n. | |||
\end{array} | |||
</math> | |||
In each subinterval <math>[x_{i-1}, x_i]</math> we take <math>x_{i}^{*} = x_i</math>. Then | |||
<math display="block"> | |||
f(x_i^{*}) = f(x_i) = \sqrt {\frac{i}{n}} = \frac{\sqrt i}{\sqrt n}, | |||
</math> | |||
and the resulting Riemann sum, denoted by <math>R_n</math>, is given by | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
R_n &=& \sum_{i = 1}^{n} f(x_{i}^{*})(x_i - x_{i-1}) = \sum_{i = 1}^{n} \frac{\sqrt i}{\sqrt n} \frac{1}{n} \\ | |||
&=& \frac{1}{n^{3/2}} \sum_{i = 1}^{n} \sqrt i \\ | |||
&=& \frac{\sqrt 1 + \sqrt 2 + ... + \sqrt n}{n^{3/2}} . | |||
\end{eqnarray*} | |||
</math> | |||
The function <math>\sqrt x</math> is continuous and hence integrable over the interval <math>[0, 1]</math>. Since <math>|| \sigma || \rightarrow 0</math> as <math>n \rightarrow \infty</math>, it follows from Theorem (2.1) that | |||
<math display="block"> | |||
\int_a^b f = \int_0^1 \sqrt x dx = \lim_{n \rightarrow \infty} R_n. | |||
</math> | |||
Hence | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\lim_{n \rightarrow \infty} \frac{\sqrt 1 + \sqrt 2 + ... + \sqrt n}{n^{3/2}} | |||
&=& \int_0^1 \sqrt x dx \\ | |||
&=& \frac{2}{3} x^{3/2} \Big|_0^1 = \frac{2}{3}, | |||
\end{eqnarray*} | |||
</math> | |||
and the problem is solved. | |||
Theorem (2.1) shows that it is immaterial whether we define the definite integral in terms of upper and lower sums (as is done in this book) or as the limit of Riemann sums. Hence there is no logical necessity for introducing the latter at all. However, a striking illustration of the practical use of Riemann sums arises in studying the problem of evaluating definite integrals by numerical methods. | |||
In spite of the variety of techniques which exist for finding antiderivatives and the existence of tables of indefinite integrals,there are still many functions for which we cannog find an antiderivative. More often than not, the only way of computing <math>\int_a^b f(x) dx</math> is by numerical approximation. However, the increasing availability of high-speed computers has placed these methods in an entirely new light. Evaluating <math>\int_a^b f (x) dx</math> by numerical approximation is no longer to be regarded as a last resort to be used only if all else fails. It is an interesting, instructive, and simple task to write a machine program to do the job, and the hundreds, thousands, or even millions of arithmetic operations which may be needed to obtain the answer to a desired accuracy can be performed by a machine in a matter of seconds or minutes. | |||
One of the simplest and best of the techniques of numerical integration is the Trapezoid Rule, which we now describe. Suppose that the function <math>f</math> is integrable over the interval <math>[a, b]</math>. For every positive integer <math>n</math>, let <math>\sigma_n</math> be the partition which subdivides <math>[a, b]</math> into <math>n</math> subintervals of equal length <math>h</math>. Thus <math>\sigma_n = \{ x_0, . . ., x_n \}</math> and | |||
<math display="block"> | |||
h = \frac{b - a}{n} = x_i - x_{i-1}, \;\;\; i = 1, ... , n. | |||
</math> | |||
It is convenient to set | |||
<math display="block"> | |||
y_i = f(x_i), \;\;\; i = 0, 1, ... , n. | |||
</math> | |||
Then the Riemann sum obtained by choosing <math>x_i^*</math> to be the left endpoint of each subinterval <math>[x_{i-1}, x_i]</math>, i.e., by choosing <math>x_{i}^{*} = x_{i-1}</math>, is given by | |||
<math display="block"> | |||
\sum_{i=1}^{n} f (x_{i}^{*})(x_i - x_{i-1}) = \sum_{i=1}^{n} f (x_{i-1})h = h \sum_{i=1}^{n} y_{i-1} . | |||
</math> | |||
Similarly, the Riemann sum obtained by choosing <math>x_{i}^{*}</math> to be the right endpoint, i.e., by taking <math>x_{i}^{*} = x_i</math>, is | |||
<math display="block"> | |||
\sum_{i=1}^{n} f(x_{i}^{*})(x_i - x_{i-1}) = \sum_{i=1}^{n} f(x_i) h = h \sum_{i=1}^{n} y_i . | |||
</math> | |||
The approximation to <math>\int_a^b f</math> prescribed by the Trapezoid Rule, which we denote by <math>T_n</math> is by definition the average of these two Riemann sums. Thus | |||
<span id{{=}}"eq8.2.1"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\begin{array}{ll} | |||
T_n &= \frac{h \sum_{i=1}^{n} y_{i-1} + h \sum_{i=1}^{n} y_i}{2} \\ | |||
&= \frac{h}{2} \Bigl( \sum_{i=1}^{n} y_{i - 1} + \sum_{i=1}^{n} y_i \Bigr) . | |||
\end{array} | |||
\label{eq8.2.1} | |||
\end{equation} | |||
</math> | |||
The last expression above can be simplified by observing that | |||
<math display="block"> | |||
\sum_{i=1}^{n} y_{i - 1} + \sum_{i=1}^{n} y_i = y_0 + 2\sum_{i=1}^{n-1} y_i + y_n . | |||
</math> | |||
Hence | |||
<span id{{=}}"eq8.2.2"/> | |||
<math display="block"> | |||
\begin{equation} | |||
T_n = h(\frac{1}{2} y_0 + \sum_{i=1}^{n-1} y_i + \frac{1}{2}y_n) . | |||
\label{eq8.2.2} | |||
\end{equation} | |||
</math> | |||
We shall express the fact that <math>T_n</math> is an approximation to the integral <math>\int_a^b f</math> by writing <math>\int_a^b f \approx T_n</math>. The '''Trapezoid Rule''' then appears as the formula | |||
{{proofcard|Theorem|theorem-2| | |||
<math display="block"> | |||
\int_a^b f \approx T_n = h (\frac{1}{2}y_0 + y_1 + \cdots + y_{n-1} + \frac{1}{2} y_n) . | |||
</math>|}} | |||
Why is this formula called the Trapezoid Rule? Suppose that <math>f(x) \geq 0</math> for every <math>x</math> in <math>[a, b]</math>, and observe that | |||
<math display="block"> | |||
\int_a^b f = \int_{x_0}^{x_1} f + \int_{x_1}^{x_2} f + \cdots + \int_{x_{n-1}}^{x_n} f. | |||
</math> | |||
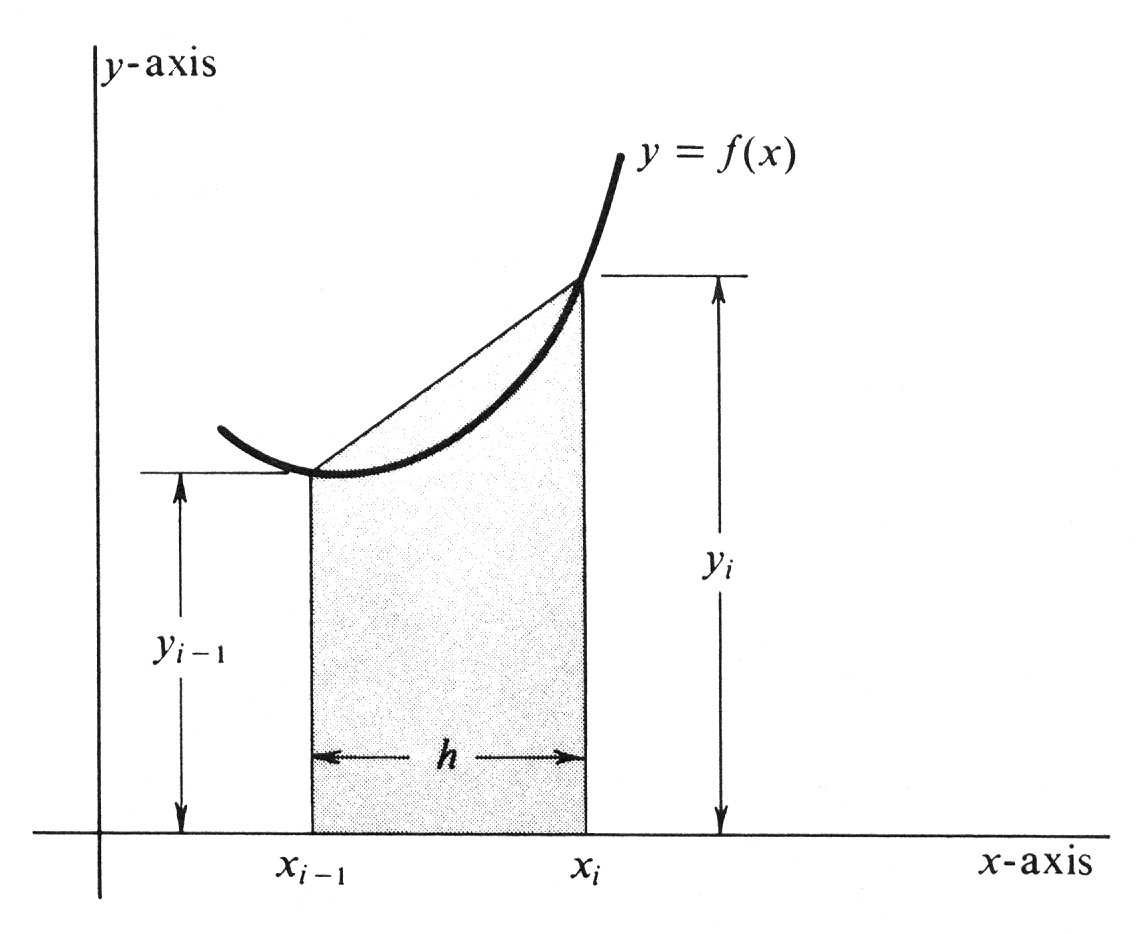
The area of the shaded trapezoid shown in Figure 5 is an approximation to <math>\int_{x_{i-1}}^{x_i} f</math>. This trapezoid has bases <math>y_{i-1} = f(x_{i-1})</math> and <math>y_i = f(x_i)</math> and altitude <math>h</math>. By a well-known formula, its area is therefore equal to <math>\frac{h}{2} (y_{i-1} + y_i)</math>. The integral <math>\int_a^b f</math> is therefore approximated by the sum of the areas of the trapezoids, which is equal to | |||
<math display="block"> | |||
\sum \frac{h}{2} (y_{i-1} + y_i) = \frac{h}{2} \Bigl( \sum_{i=1}^{n} y_{i -1} + \sum _{i=1}^{n} y_i \Bigr). | |||
</math> | |||
Equation (1) shows that this number is equal to <math>T_n</math>. | |||
<div id="fig 8.5" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_5.png | 400px | thumb | ]] | |||
</div> | |||
<span id="table 8.1"/> | |||
'''Example''' | |||
Using the Trapezoid Rule, find an approximate value for <math>\int_{-1}^1 (x^3 + x^2) dx</math>. We shall subdivide the interval <math>[-1, 1]</math> into <math>n = 8</math> subintervals each of length <math>h = \frac{1}{4}</math>. The relevant numbers are compiled in Table 1. | |||
<span id="table 8.1"/> | |||
{|class="table" | |||
|- | |||
|<math>i</math> || <math>x_i</math> ||<math>y_i = x_i^2 + x_i^3</math> | |||
|- | |||
|0 ||<math>-1</math> ||<math>1 - 1 = 0\;\;</math> | |||
|- | |||
|1 ||<math>-\frac{3}{4}</math>||<math>\frac{9}{16} - \frac{27}{64} = \frac{9}{64}</math> | |||
|- | |||
|2 ||<math>-\frac{2}{4}</math>||<math>\frac{4}{16} - \frac{8}{64} = \frac{8}{64}</math> | |||
|- | |||
|3 ||<math>-\frac{1}{4}</math>||<math>\frac{1}{16} - \frac{1}{64} = \frac{3}{64}</math> | |||
|- | |||
|4 || 0 ||<math>0 + 0 = 0\;\;</math> | |||
|- | |||
|5 ||<math>\frac{1}{4}</math> ||<math>\frac{1}{16} + \frac{1}{64} = \frac{5}{64}</math> | |||
|- | |||
|6 ||<math>\frac{2}{4}</math> ||<math>\frac{4}{16} + \frac{8}{64} = \frac{24}{64}</math> | |||
|- | |||
|7 ||<math>\frac{3}{4}</math> ||<math>\frac{9}{16} + \frac{27}{64} = \frac{63}{64}</math> | |||
|- | |||
|8 || 1 ||<math>1 + 1 = 2\;\;</math> | |||
|} | |||
Hence | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
T_8 | |||
&=& \frac{1}{4} (\frac{1}{2}y_0 + y_1 + \cdots + y_7 + \frac{1}{2}y_8)\\ &=& \frac{1}{4} \Bigl( 0 + \frac{9+8+3+0+5+24+63}{64} + 1 \Bigr)\\ | |||
&=& \frac{1}{4} \frac{176}{64} = \frac{11}{16}. | |||
\end{eqnarray*} | |||
</math> | |||
With the Fundamental Theorem of Calculus it is easy in this case to compute the integral exactly. We get | |||
<math display="block"> | |||
\int_{-1}^1 (x^3 + x^2)dx = \Bigl( \frac{x^4}{4} + \frac{x^3}{3} \Bigr) \Big|_{-1}^1 = \frac{2}{3}. | |||
</math> | |||
The error obtained using the Trapezoid Rule is, therefore, | |||
<math display="block"> | |||
\frac{11}{16} - \frac{2}{3} = \frac{33}{48} - \frac{22}{48} = \frac{1}{48}. | |||
</math> | |||
In Example 2, the error can be reduced by taking a larger value of <math>n</math>, or, equivalently, a smaller value of <math>h = \frac{b - a}{n}</math>. Indeed, it is easy to show that in any application of the Trapezoid Rule the error approaches zero as <math>h</math> increases without bound (or as <math>h</math> approaches zero). That is, we have the theorem | |||
{{proofcard|Theorem|theorem-3| | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} T_n = \int_a^b f(x) dx . | |||
</math> | |||
|It follows from equation (1) that | |||
<math display="block"> | |||
T_n = \frac{1}{2} \Bigl( h \sum_{i = 1}^{n} y_{i - 1} + h \sum_{i = 1}^{n} y_i \Bigr) | |||
</math> | |||
Both <math>h \sum_{i = 1}^{n} y_{i - 1}</math> and <math>h \sum_{i = 1}^{n} y_i</math> are Riemann sums for <math>f</math>. Hence, by Theorem (2.1), both approach the integral as <math>n \rightarrow \infty</math>. Thus | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\lim_{n \rightarrow \infty} h \sum_{i = 1}^{n} y_{i - 1} &=& \int_a^b f(x) dx,\\ | |||
\lim_{n \rightarrow \infty} h \sum_{i = 1}^{n} y_{i} &=& \int_a^b f(x) dx, | |||
\end{eqnarray*} | |||
</math> | |||
and so | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} T_n = \frac{1}{2} \Bigl[ \int_a^b f(x) dx + \int_a^b f(x) dx \Bigr] = \int_a^b f(x)dx, | |||
</math> | |||
and the proof is complete.}} | |||
As a practical aid to computation, Theorem (2.3) is actually of little value. What is needed instead is a method of estimating the error, which is equal to | |||
<math display="block"> | |||
\big| \int_a^b f - T_n \big|, | |||
</math> | |||
for a particular choice of <math>n</math> used in a particular application of the Trapezoid Rule. For this purpose the following theorem is useful. | |||
{{proofcard|Theorem|theorem-4|If the second derivative <math>f''</math> is continuous at every point of <math>[a, b]</math>, then there exists a number <math>c</math> such that <math>a < c < b</math> and | |||
<math display="block"> | |||
\int_a^b f = T_n -\frac{b -a}{12} f''(c)h^2. | |||
</math>|}} | |||
An outline of a proof of this theorem can be found in J. M. H. Olmsted, ''Advanced Calculus'', Appleton-Century-Crofts, 1961, pages 118 and 119. | |||
To see how this theorem can be used, consider Example 2, in which <math>f(x) = x^3 + x^2</math> and in which the interval of integration is <math>[-1, 1]</math>. In this case <math>f''(x) = 6x + 2</math>, from which it is easy to see that | |||
<math display="block"> | |||
f''(x) \leq 8, \;\;\;\mbox{for every} x\; \mbox{in}\; [-1, 1]. | |||
</math> | |||
Applying (2.4), we have | |||
<math display="block"> | |||
\int_{-1}^{1} (x^3 + x^2) dx - T_n = - \frac{1 - (-1)}{12} f''(c)h^2. | |||
</math> | |||
Hence the error satisfies | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\big| \int_{-1}^{1} (x^3 + x^2) dx - T_n \big| | |||
&=& \frac{1}{6} | f''(c) | h^2 \\ | |||
&\leq& \frac{1}{6} \cdot 8 \cdot h^2 = \frac{4}{3}h^2. | |||
\end{eqnarray*} | |||
</math> | |||
It follows that by halving <math>h</math>, we could have quartered the error. If we were to replace <math>h</math> by <math>\frac{h}{10}</math>, which would be no harder with a machine, we would divide the error by 100. | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Latest revision as of 23:15, 19 November 2024
This section is divided into two parts. The first is devoted to an alternative approach to the definite integral, which is useful for many purposes. The second is an application of the first part to the problem of computing definite integrals by numerical approximations. We begin by reviewing briefly the definitions in Section 1 of Chapter 4. If the function [math]f[/math] is bounded on the closed interval [math][a, b][/math], then, for every partition [math]\sigma[/math] of [math][a, b][/math], there are defined an upper sum [math]U_\sigma[/math] and a lower sum [math]L_\sigma[/math], which approximate the definite integral from above and below, respectively. The function [math]f[/math] is defined to be integrable over [math][a, b][/math] if there exists one and only one number, denoted by [math]\int_a^b f[/math], with the property that
for every pair of partitions [math]\sigma[/math] and [math]\tau[/math] of [math][a, b][/math]. In the alternative description of the integral, the details are similar, but not the same. As above, let [math]\sigma = \{ x_0, . . ., x_n \}[/math] be a partition of [math][a, b][/math], which satisfies the inequalities
In each subinterval [math][x_{i-1}, x_i][/math] we select an arbitrary number, which we shall denote by [math]x_i^{*}[/math]. Then the sum
is called a Riemann sum for [math]f[/math] relative to the partition [math]\sigma[/math]. (The name commemorates the great mathematician Bernhard Riemann, 1826-1866.) It is important to realize that since [math]x_i^{*}[/math] may be any number which satisfies [math]x_{i-1} \leq x_i^{*} \leq x_i[/math], there are in general infinitely many Riemann sums [math]R_\sigma[/math] for a given [math]f[/math] and partition [math]\sigma[/math]. However, every [math]R_\sigma[/math] lies between the corresponding upper and lower sums [math]U_\sigma[/math] and [math]L_\sigma[/math]. For, if the least upper bound of the values of [math]f[/math] on [math][x_{i-1}, x_i][/math] is denoted by [math]M_i[/math] and the greatest lower bound by [math]m_i[/math], then [math]f(x_i^{*})[/math] is an intermediate value and
as shown in Figure 4. It follows that
which states that
for every Riemann sum [math]R_\sigma[/math] for [math]f[/math] relative to [math]\sigma[/math].
Every Riemann sum is an approximation to the definite integral. By taking partitions which subdivide the interval of integration into smaller and smaller subintervals, we should expect to get better and better approximations to [math]\int_a^b f[/math]. One number which measures the fineness of a given partition [math]\sigma[/math] is the length of the largest subinterval into which [math]\sigma[/math] subdivides [math][a, b][/math]. This number is called the mesh of the partition and is denoted by [math]||\sigma ||[/math]. Thus if [math]\sigma = \{ x_0, ..., x_n \}[/math] is a partition of [math][a, b][/math] with
then
The following definition states precisely what we mean when we say that the Riemann sums approach a limit as the mesh tends to zero. Let the function [math]f[/math] be bounded on the interval [math][a, b][/math]. We shall write
where [math]L[/math] is a real number, if the difference between the number [math]L[/math] and any Riemann sum [math]R_\sigma[/math] for [math]f[/math] is arbitrarily small provided the mesh [math]||\sigma||[/math] is sufficiently small. Stated formally, the limit exists if: For any positive real number [math]\epsilon[/math], there exists a positive real number [math]\delta[/math] such that, if [math]R_\sigma[/math] is any Riemann sum for [math]f[/math] relative to a partition [math]\sigma[/math] of [math][a, b][/math] and if [math]|| \sigma || \lt \delta[/math], then [math] | R_\sigma - L | \lt \epsilon[/math]. The fundamental fact that integrability is equivalent to the existence of the limit of Riemann sums is expressed in the following theorem.
Let [math]f[/math] be bounded on [math][a, b][/math]. Then [math]f[/math] is integrable over [math][a, b][/math] if and only if [math]\lim_{|| \sigma || \rightarrow 0} R_\sigma[/math] exists. If this limit exists, then it is equal to [math]\int_a^b f[/math].
The proof is given in Appendix C.
Example Using the fact that the definite integral is the limit of Riemann sums, evaluate
The numerator of this fraction suggests trying the function [math]f[/math] defined by [math]f(x) = \sqrt x[/math]. If [math] \sigma = \{ x_0, . . ., x_n \}[/math] is the partition of the interval [math][0, 1][/math] into subintervals of length [math]\frac{1}{n}[/math], then
In each subinterval [math][x_{i-1}, x_i][/math] we take [math]x_{i}^{*} = x_i[/math]. Then
and the resulting Riemann sum, denoted by [math]R_n[/math], is given by
The function [math]\sqrt x[/math] is continuous and hence integrable over the interval [math][0, 1][/math]. Since [math]|| \sigma || \rightarrow 0[/math] as [math]n \rightarrow \infty[/math], it follows from Theorem (2.1) that
Hence
and the problem is solved.
Theorem (2.1) shows that it is immaterial whether we define the definite integral in terms of upper and lower sums (as is done in this book) or as the limit of Riemann sums. Hence there is no logical necessity for introducing the latter at all. However, a striking illustration of the practical use of Riemann sums arises in studying the problem of evaluating definite integrals by numerical methods. In spite of the variety of techniques which exist for finding antiderivatives and the existence of tables of indefinite integrals,there are still many functions for which we cannog find an antiderivative. More often than not, the only way of computing [math]\int_a^b f(x) dx[/math] is by numerical approximation. However, the increasing availability of high-speed computers has placed these methods in an entirely new light. Evaluating [math]\int_a^b f (x) dx[/math] by numerical approximation is no longer to be regarded as a last resort to be used only if all else fails. It is an interesting, instructive, and simple task to write a machine program to do the job, and the hundreds, thousands, or even millions of arithmetic operations which may be needed to obtain the answer to a desired accuracy can be performed by a machine in a matter of seconds or minutes. One of the simplest and best of the techniques of numerical integration is the Trapezoid Rule, which we now describe. Suppose that the function [math]f[/math] is integrable over the interval [math][a, b][/math]. For every positive integer [math]n[/math], let [math]\sigma_n[/math] be the partition which subdivides [math][a, b][/math] into [math]n[/math] subintervals of equal length [math]h[/math]. Thus [math]\sigma_n = \{ x_0, . . ., x_n \}[/math] and
It is convenient to set
Then the Riemann sum obtained by choosing [math]x_i^*[/math] to be the left endpoint of each subinterval [math][x_{i-1}, x_i][/math], i.e., by choosing [math]x_{i}^{*} = x_{i-1}[/math], is given by
Similarly, the Riemann sum obtained by choosing [math]x_{i}^{*}[/math] to be the right endpoint, i.e., by taking [math]x_{i}^{*} = x_i[/math], is
The approximation to [math]\int_a^b f[/math] prescribed by the Trapezoid Rule, which we denote by [math]T_n[/math] is by definition the average of these two Riemann sums. Thus
The last expression above can be simplified by observing that
Hence
We shall express the fact that [math]T_n[/math] is an approximation to the integral [math]\int_a^b f[/math] by writing [math]\int_a^b f \approx T_n[/math]. The Trapezoid Rule then appears as the formula
Why is this formula called the Trapezoid Rule? Suppose that [math]f(x) \geq 0[/math] for every [math]x[/math] in [math][a, b][/math], and observe that
The area of the shaded trapezoid shown in Figure 5 is an approximation to [math]\int_{x_{i-1}}^{x_i} f[/math]. This trapezoid has bases [math]y_{i-1} = f(x_{i-1})[/math] and [math]y_i = f(x_i)[/math] and altitude [math]h[/math]. By a well-known formula, its area is therefore equal to [math]\frac{h}{2} (y_{i-1} + y_i)[/math]. The integral [math]\int_a^b f[/math] is therefore approximated by the sum of the areas of the trapezoids, which is equal to
Equation (1) shows that this number is equal to [math]T_n[/math].
Example Using the Trapezoid Rule, find an approximate value for [math]\int_{-1}^1 (x^3 + x^2) dx[/math]. We shall subdivide the interval [math][-1, 1][/math] into [math]n = 8[/math] subintervals each of length [math]h = \frac{1}{4}[/math]. The relevant numbers are compiled in Table 1.
| [math]i[/math] | [math]x_i[/math] | [math]y_i = x_i^2 + x_i^3[/math] |
| 0 | [math]-1[/math] | [math]1 - 1 = 0\;\;[/math] |
| 1 | [math]-\frac{3}{4}[/math] | [math]\frac{9}{16} - \frac{27}{64} = \frac{9}{64}[/math] |
| 2 | [math]-\frac{2}{4}[/math] | [math]\frac{4}{16} - \frac{8}{64} = \frac{8}{64}[/math] |
| 3 | [math]-\frac{1}{4}[/math] | [math]\frac{1}{16} - \frac{1}{64} = \frac{3}{64}[/math] |
| 4 | 0 | [math]0 + 0 = 0\;\;[/math] |
| 5 | [math]\frac{1}{4}[/math] | [math]\frac{1}{16} + \frac{1}{64} = \frac{5}{64}[/math] |
| 6 | [math]\frac{2}{4}[/math] | [math]\frac{4}{16} + \frac{8}{64} = \frac{24}{64}[/math] |
| 7 | [math]\frac{3}{4}[/math] | [math]\frac{9}{16} + \frac{27}{64} = \frac{63}{64}[/math] |
| 8 | 1 | [math]1 + 1 = 2\;\;[/math] |
Hence
With the Fundamental Theorem of Calculus it is easy in this case to compute the integral exactly. We get
The error obtained using the Trapezoid Rule is, therefore,
In Example 2, the error can be reduced by taking a larger value of [math]n[/math], or, equivalently, a smaller value of [math]h = \frac{b - a}{n}[/math]. Indeed, it is easy to show that in any application of the Trapezoid Rule the error approaches zero as [math]h[/math] increases without bound (or as [math]h[/math] approaches zero). That is, we have the theorem
It follows from equation (1) that
As a practical aid to computation, Theorem (2.3) is actually of little value. What is needed instead is a method of estimating the error, which is equal to
for a particular choice of [math]n[/math] used in a particular application of the Trapezoid Rule. For this purpose the following theorem is useful.
If the second derivative [math]f''[/math] is continuous at every point of [math][a, b][/math], then there exists a number [math]c[/math] such that [math]a \lt c \lt b[/math] and
An outline of a proof of this theorem can be found in J. M. H. Olmsted, Advanced Calculus, Appleton-Century-Crofts, 1961, pages 118 and 119. To see how this theorem can be used, consider Example 2, in which [math]f(x) = x^3 + x^2[/math] and in which the interval of integration is [math][-1, 1][/math]. In this case [math]f''(x) = 6x + 2[/math], from which it is easy to see that
Applying (2.4), we have
Hence the error satisfies
It follows that by halving [math]h[/math], we could have quartered the error. If we were to replace [math]h[/math] by [math]\frac{h}{10}[/math], which would be no harder with a machine, we would divide the error by 100.
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.