[math]
\newcommand{\ex}[1]{\item }
\newcommand{\sx}{\item}
\newcommand{\x}{\sx}
\newcommand{\sxlab}[1]{}
\newcommand{\xlab}{\sxlab}
\newcommand{\prov}[1] {\quad #1}
\newcommand{\provx}[1] {\quad \mbox{#1}}
\newcommand{\intext}[1]{\quad \mbox{#1} \quad}
\newcommand{\R}{\mathrm{\bf R}}
\newcommand{\Q}{\mathrm{\bf Q}}
\newcommand{\Z}{\mathrm{\bf Z}}
\newcommand{\C}{\mathrm{\bf C}}
\newcommand{\dt}{\textbf}
\newcommand{\goesto}{\rightarrow}
\newcommand{\ddxof}[1]{\frac{d #1}{d x}}
\newcommand{\ddx}{\frac{d}{dx}}
\newcommand{\ddt}{\frac{d}{dt}}
\newcommand{\dydx}{\ddxof y}
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}}
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}}
\newcommand{\dist}{\mathrm{distance}}
\newcommand{\arccot}{\mathrm{arccot\:}}
\newcommand{\arccsc}{\mathrm{arccsc\:}}
\newcommand{\arcsec}{\mathrm{arcsec\:}}
\newcommand{\arctanh}{\mathrm{arctanh\:}}
\newcommand{\arcsinh}{\mathrm{arcsinh\:}}
\newcommand{\arccosh}{\mathrm{arccosh\:}}
\newcommand{\sech}{\mathrm{sech\:}}
\newcommand{\csch}{\mathrm{csch\:}}
\newcommand{\conj}[1]{\overline{#1}}
\newcommand{\mathds}{\mathbb}
[/math]
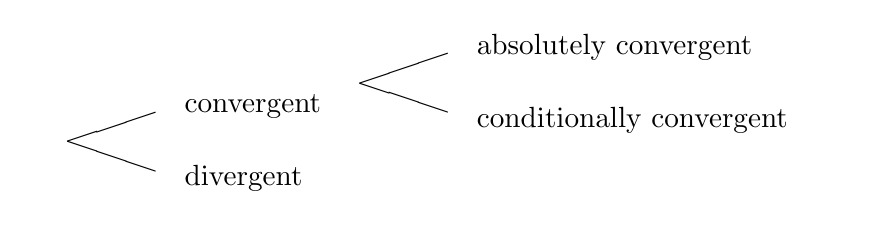
An infinite series [math]\sum_{i=m}^{\infty} a_i[/math] is said to be absolutely convergent if the corresponding series of absolute values [math]\sum_{i=m}^{\infty} |a_i|[/math] is convergent. If a series [math]\sum_{i=m}^{\infty} a_i[/math] converges, but [math]\sum_{i=m}^{\infty} |a_i|[/math] does not, then we say that [math]\sum_{i=m}^{\infty} a_i[/math] is conditionally convergent. An example of a conditionally convergent series is the alternating harmonic series: We have shown that
[[math]]
\sum_{i=1}^{\infty} a_i = \sum_{i=1}^{\infty} (- 1)^{i+1} \frac{1}{i} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots
[[/math]]
converges, but that
[[math]]
\sum_{i=1}^{\infty} |a_i| = \sum_{i=1}^{\infty} \frac{1}{i} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots
[[/math]]
diverges.
There are many examples of series for which both [math]\sum_{i=m}^{\infty} a_i[/math] and [math]\sum_{i=m}^{\infty} |a_i|[/math] converge, and also many where both diverge. (In particular, for nonnegative series, the two are the same.) There is the remaining possibility that [math]\sum_{i=m}^{\infty} |a_i|[/math] might converge, and [math]\sum_{i=m}^{\infty} |a_i|[/math] diverge. However, the following theorem shows that this cannot happen.
If the infinite series [math]\sum_{i=m}^{\infty} a_i[/math] is absolutely convergent, then it is convergent.
Show Proof
Since [math]|a_i| \geq -a_i[/math], we have [math]a_i + |a_i| \geq 0[/math], for every integer [math]i \geq m[/math]. Hence the series [math]\sum_{i=m}^{\infty} (a_i + |a_i|)[/math] is nonnegative. Since [math]a_i \leq |a_i|[/math], we also have
[[math]]
\begin{equation}
a_i + |a_i| \leq |a_i| + |a_i| = 2|a_i|,
\label{eq9.5.1}
\end{equation}
[[/math]]
for every integer
[math]i \geq m[/math]. The assumption that
[math]\sum_{i=m}^{\infty} a_i[/math] is absolutely convergent means that the series
[math]\sum_{i=m}^{\infty} |a_i|[/math] converges, and, hence, so does the series
[math]\sum_{i=m}^{\infty} 2|a_i|[/math]. It therefore follows from (1) by the Comparison Test that the nonnegative series
[math]\sum_{i=m}^{\infty} (a_i + |a_i|)[/math] is convergent. We conclude from Theorem (2.2), page 485, that
[[math]]
\sum_{i=m}^{\infty} a_i = \sum_{i=m}^{\infty} (a_i + |a_i |) - \sum_{i=m}^{\infty} |a_i|
[[/math]]
and that
[math]\sum_{i=m}^{\infty} a_i[/math] converges. This completes the proof.
■
Thus the only possibilities for a given series are those illustrated. by the following scheme:
Example
Classify each of the following infinite series as absolutely convergent, conditionally convergent, or divergent.
[[math]]
\mbox{(a)}\;\;\; \sum_{k=1}^\infty (-1)^k \frac{1}{\sqrt {k+1}} , \;\;\;
\mbox{(b)}\;\;\; \sum_{k=1}^\infty (-1)^k \frac{1}{2k^2 - 15} .
[[/math]]
If we let [math]a_k = (-1)^k \frac{1}{\sqrt {k+1}}[/math], the alternating series in (a) will converge if:
- [math]|a_{k+1}| \leq |a_k|, \mathrm{for every integer} k \geq 1, \;\mathrm{and}[/math]
- [math]\lim_{k \rightarrow \infty} |a_k| = 0.[/math]
[See Theorem (4.1), page 498.] We have
[[math]]
|a_k| = \frac{1}{\sqrt{k + 1}}\;\;\; \mbox{and}\;\;\; |a_{k+1}| = \frac{1}{\sqrt{k + 2}} .
[[/math]]
Hence condition (i) becomes
[[math]]
\frac{1}{\sqrt{k + 2}} \leq \frac{1}{\sqrt{k + 1}}, \;\;\;\mbox{for every integer}\; k \geq 1,
[[/math]]
which is certainly true. Condition (ii) is also satisfied, since
[[math]]
\lim_{k \rightarrow \infty} \frac{1}{\sqrt{k + 1}} = 0,
[[/math]]
and it follows that the series [math]\sum_{k=1}^\infty a_k[/math] converges. However, it is easy to show that [math]\sum_{k=1}^\infty |a_k|[/math] diverges by either the Comparison Test or the Integral Test. Using the latter, we consider the function [math]f[/math] defined by [math]f(x) = \frac{1}{\sqrt{x+1}}[/math], which is nonnegative and decreasing on the interval [math][1, \infty)[/math]. We have [math]f(k) = \frac{1}{\sqrt{k+1}} = |a_k|[/math] and
[[math]]
\begin{eqnarray*}
\int_1^\infty f(x) dx &=& \int_1^\infty \frac{1}{\sqrt{x + 1}} dx = \lim_{b \rightarrow \infty} [2 \sqrt{x + 1}|_1^b ] \\
&=& \lim_{b \rightarrow \infty} [2\sqrt{b + 1} - 2 \sqrt2] = \infty .
\end{eqnarray*}
[[/math]]
The divergence of the integral implies the divergence of the corresponding series [math]\sum_{k=1}^\infty |a_k|[/math], and we conclude that the series (a) is conditionally convergent.
For the series in (b), we might apply the same technique: Test first for convergence and then for absolute convergence. However, if we suspect that the series is absolutely convergent, we may save a step by first testing for absolute convergence. In this particular case, the corresponding series of absolute values is [math] \sum_{k = 1}^\infty \frac{1}{|2k^2 - 15|}[/math]. The latter can be shown to be convergent
by the CoMparison Test. For a test series we choose the convergent series [math]\sum_{k=1}^\infty \frac{2}{k^2}[/math]. The condition of the test is that the inequality
[[math]]
\frac{1}{|2k^2 - 15|} \leq \frac{2}{k^2}
[[/math]]
must be true eventually. We shall consider only integers [math]k \geq 3[/math], since, for these values, [math]2k^2 \geq18[/math] and hence [math]|2k^2 - 15| = 2k^2 - 15[/math]. For those integers for which [math]k \geq 3[/math], the inequality
[[math]]
\frac{1}{2k^2 - 15} \leq \frac{2}{k^2}
[[/math]]
is equivalent to [math]k^2 \leq 4k^2 - 30[/math], which in turn is equivalent to [math]k^2 \geq 10[/math]. The last is true for every integer [math]k \geq 4[/math]. Hence
[[math]]
\frac{1}{|2k^2 - 15|} \leq \frac{2}{k^2}, \;\;\;\mbox{for every integer}\; k \geq 4.
[[/math]]
lt follows that [math]\sum_{k=1}^\infty \frac{1}{|2k^2 - 15|}[/math] converges, and therefore that the series (b) is absolutely convergent.
Let [math]\sum_{i=m}^\infty a_i[/math] be an infinite series for which [math]\lim_{n \rightarrow \infty} \frac{|a_{n+1}|}{|a_n|} = q[/math] (or [math]\infty[/math]).
- If [math]q \lt 1[/math], then the series is absolutely convergent.
- If [math]q \gt 1[/math] (including [math]q = \infty[/math] ), then the series is divergent.
- If [math]q = 1[/math], then the series may either converge or diverge; i.e., the test fails.
Show Proof
Suppose, first of all, that [math]\lim_{n \rightarrow \infty} \frac{|a_{n+1}|}{|a_n|} = q \lt 1[/math]. This implies that the ratio [math]\frac{|a_{n+1}|}{|a_n|}[/math] is arbitrarily close to [math]q[/math] if [math]n[/math] is sufficiently large. Hence if we pick an arbitrary number [math]r[/math] such that [math]q \lt r \lt 1[/math], then there exists an integer [math]N \geq m[/math] such that
[[math]]
\begin{equation}
\frac{|a_{n+1}|}{|a_n|} \leq r, \;\;\;\mbox{for every integer}\; n \geq N.
\label{eq9.5.2}
\end{equation}
[[/math]]
We shall show by mathematical induction that (2) implies that
[[math]]
\begin{equation}
|a_{N+i}| \leq r^{i}|a_N|, \;\;\;\mbox{for every integer}\; i \geq 0. \label{eq9.5.3}
\end{equation}
[[/math]]
If
[math]i = 0[/math], then the inequality in (3) becomes
[math]|a_{N+0}| \leq r^{0}|a_N|[/math], which is true. In the second part of an inductive proof we need to show that, if the inequality
(3) is true for
[math]i = k[/math], then it is also true for
[math]i = k + 1[/math]. The assumption. then, is that
[[math]]
\begin{equation}
|a_{N+1}| \leq r^k |a_N|,
\label{eq9.5.4}
\end{equation}
[[/math]]
and we want to prove that
[[math]]
|a_{N+k+1}| \leq r^{k+1} |a_N| .
[[/math]]
If we multiply both sides of inequality (4) by the positive number
[math]r[/math], we get
[[math]]
\begin{equation}
r |a_{N+k}| \leq r^{k+1} |a_N| .
\label{eq9.5.5}
\end{equation}
[[/math]]
But, inequality (2) tells us that
[[math]]
\frac{|a_{N+k+1}|}{|a_{N+k}|} \leq r,
[[/math]]
and hence that
[[math]]
\begin{equation}
|a_{N+k+1}| \leq r|a_{N+k}|
\label{eq9.5.6}
\end{equation}
[[/math]]
Combining inequalities (5) and (6) we have
[[math]]
|a_{N+k+1}| \leq r^{k+1} |a_{N}|,
[[/math]]
completing the inductive proof. Since
[math]|r| \lt 1[/math], the geometric series
[math]\sum_{i=0}^\infty |a_N| r^i[/math] converges, and it follows from (3) by the Comparison Test that the series
[math]\sum_{i=0}^\infty |a_{N+i}|[/math] converges. However,
[[math]]
\sum_{i=0}^\infty |a_{N+i}| = \sum_{i=N}^\infty |a_i| ,
[[/math]]
and the convergence of
[math]\sum_{i=N}^{\infty} |a_i|[/math] implies the convergence of
[math]\sum_{i=m}^\infty |a_i|[/math]. Hence the series
[math]\sum_{i=m}^\infty a_i[/math] converges absolutely, and the proof of part (i) of the theorem is complete.
We next assume that
[math]\lim_{n \rightarrow \infty} |\frac{a_{n+1}}{a_n} |= q \gt 1[/math], and let
[math]r[/math] be an arbitrary number such that
[math]1 \lt r \lt q[/math]. Then there exists an integer
[math]N \geq m[/math] such that
[[math]]
\frac{|a_{n+1}|}{|a_n|} \geq r, \;\;\;\mbox{for every integer}\; n \geq N.
[[/math]]
In the same way in which we proved that (2) implies (3), it follows by induction from the preceding inequality that
[[math]]
|a_{N+i}| \geq r^i |a_N|, \;\;\;\mbox{for every integer}\; i \geq 0.
[[/math]]
Since
[math]r \gt 1[/math], we know that
[math]\lim_{i \rightarrow \infty} r^i = \infty[/math] (see Problem 5, page 481), and therefore also that
[[math]]
\lim_{n \rightarrow \infty} |a_n| = \lim_{n \rightarrow \infty} |a_{N+i} | = \infty .
[[/math]]
However, if the series [math]\sum_{i=m}^\infty a_i[/math] converges, then it necessarily follows that [math]\lim_{n \rightarrow \infty} |a_n| = \lim_{n \rightarrow \infty} a_n = 0[/math]. [See Theorem (2.1), page 483, and Problem 2, page 502.] Hence [math]\sum_{i=m}^\infty a_i[/math] diverges, and part (ii) is proved.
Part (iii) is proved by giving an example of an absolutely convergent series and one of a divergent series such that [math]q = 1[/math] for each of them. Consider the convergent [math]p[/math]-series [math]\sum_{i=1}^\infty \frac{1}{i^2}[/math], which, being nonnegative, is also absolutely convergent. Setting [math]a_n = \frac{1}{n^2}[/math], we obtain
[[math]]
a_{n+1} = \frac{1}{(n+ 1)^2} = \frac{1}{n^2 + 2n + 1}
[[/math]]
and
[[math]]
\frac{|a_{n+1}|}{|a_n|} = \frac{a_{n+1}}{a_n} = \frac{n^2}{n^2 + 2n + 1} = \frac{1}{1 + \frac{2}{n} + \frac{1}{n^2}} .
[[/math]]
Hence
[[math]]
\lim_{n \rightarrow \infty} \frac{|a_{n+1}|}{|a_n|} = \lim_{n \rightarrow \infty} \frac{1}{1 + \frac{2}{n} + \frac{1}{n^2}} = 1.
[[/math]]
For the second example, we take the divergent harmonic series [math]\sum_{i=1}^\infty \frac{1}{i}[/math]. If we let [math]a_n = \frac{1}{n}[/math], then [math]a_{n+1} = \frac{1}{n + 1}[/math] and
[[math]]
\frac{|a_{n+1}|}{|a_n|} = \frac{a_{n+1}}{a_n} = \frac{n}{n + 1} = \frac{1}{1 + \frac{1}{n}} .
[[/math]]
For this series we also get
[[math]]
\lim_{n \rightarrow \infty} \frac{|a_{n+1}|}{|a_n|} = \lim_{n \rightarrow \infty} \frac{1}{1 + \frac{1}{n}} = 1.
[[/math]]
The Ratio Test is therefore inconclusive if`
[math]q = 1[/math], and this completes the proof.
■
If [math]n[/math] is an arbitrary positive integer, the product [math]n(n - 1) \cdots 3 \cdot 2 \cdot 1[/math] is called [math]n[/math] factorial and is denoted by [math]n![/math] Thus [math]3! = 3 \cdot 2 \cdot 1 = 6[/math] and [math]5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120[/math]. Although it may seem strange, [math]0![/math] is also defined and has the value 1. A convenient recursive definition of the factorial is given by the formulas
[[math]]
\begin{eqnarray*}
0! &=& 1,\\
(n + 1)! &=& (n + 1)n!, \;\;\;\mbox{for every integer}\; n \geq 0.
\end{eqnarray*}
[[/math]]
Example
Prove that the following series converges:
[[math]]
\sum_{n=0}^\infty \frac{1}{n!} = 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \cdots .
[[/math]]
We write the series as [math]\sum_{i=0}^{\infty} a_n [/math] by defining [math]a_n = \frac{1}{n!}[/math] for every integer [math]n \geq 0[/math]. Then
[[math]]
\begin{eqnarray*}
\frac{|a_{n+1}|}{|a_n|}
&=& \frac{\frac{1}{(n+1)!} }{\frac{1}{n!}} = \frac{n!}{(n+1)!}\\
&=&\frac{n!}{(n+1)n!} = \frac{1}{n+1} .
\end{eqnarray*}
[[/math]]
Hence
[[math]]
q = \lim_{n \rightarrow \infty} \frac{|a_{n+1}|}{|a_n|} = \lim_{n \rightarrow \infty} \frac{1}{n + 1} = 0.
[[/math]]
Since [math]q \lt 1[/math], it follows from the Ratio Test that the series is absolutely convergent. But absolute convergence implies convergence [Theorem (5.1)], and we conclude that the series [math]\sum_{n=0}^{\infty} \frac{1}{n!}[/math] converges.
Example
Show that the infinite series
[[math]]
\sum_{i=1}^{\infty} ir^{i-1} = 1 + 2r + 3r^2 + 4r^3 + \cdots
[[/math]]
converges absolutely if [math]|r| \lt 1[/math] and diverges if [math]|r| \geq 1[/math]. This series is related to the geometric series [math]\sum_{i=0}^{\infty} r^i = 1 + r + r^2 + \cdots [/math], and in a later section we shall make use of the relationship. To settle the immediate question of convergence, however, we set [math]a_i = ir^{i-1}[/math] for every positive integer [math]i[/math], and write the series as [math]\sum_{i=1}^{\infty} a_i[/math]. Observe, first of all, that if [math]|r| \geq 1[/math], then [math]|a_n| = n|r|^{n-1}[/math] and
[[math]]
\lim_{n \rightarrow \infty} |a_n| = \lim_{n \rightarrow \infty} n|r|^{n-1} = \infty .
[[/math]]
Hence, if [math]|r| \geq 1[/math], the series must diverge, since convergence would imply [math]\lim_{n \rightarrow \infty} |a_n| = 0[/math]. This proves the second part of what is asked, and we now assume that [math]|r| \lt 1[/math]. lf [math]r = 0[/math], the series is absolutely convergent with value 1, so we further assume that [math]r \neq 0[/math]. Then
[[math]]
\frac{|a_{n+1}|}{|a_n|} = \frac{(n+1) |r|^n}{n |r|^{n-1}} = \frac{n+1}{n} |r| = (1 + \frac{1}{n}) |r|,
[[/math]]
and so
[[math]]
\lim_{n \rightarrow \infty} \frac{|a_{n+1}|}{|a_n|} = \lim_{n \rightarrow \infty} (1 + \frac{1}{n}) |r| = |r|.
[[/math]]
Thus [math]q = |r| \lt 1[/math], and the Ratio Test therefore implies that the series is absolutely convergent.
The next theorem, with which we conclude the section, establishes a ttseful inequality.
If the series [math]\sum_{i=m}^{\infty} a_i[/math] converges, then [math]|\sum_{i=m}^{\infty} a_i| \leq \sum_{i=m}^{\infty} |a_i|[/math].
The result is true even if [math]\sum_{i=m}^{\infty} a_i[/math] is not absolutely convergent, for in that case [math]\sum_{i=m}^{\infty} |a_i| = \infty[/math], and the inequality becomes [math]\sum_{i=m}^{\infty} |a_i| \leq \infty[/math].
Show Proof
In view of the preceding remark, we shall assume throughout the proof that [math]\sum_{i=m}^{\infty} |a_i|[/math] converges. Let [math]\{s_n\}[/math] be the sequence of partial sums corresponding to the series [math]\sum_{i=m}^{\infty} a_i[/math]. Then
[[math]]
s_n = \sum_{i=m}^{\infty} a_i, \;\;\;\mbox{for every integer}\; n \geq m,
[[/math]]
and the assumption that
[math]\sum_{i=m}^{\infty} a_i[/math] converges means that the sequence
[math]\{ s_n \}[/math] converges and that
[[math]]
\begin{equation}
\lim_{n \rightarrow \infty} s_n = \sum_{i=m}^{\infty} a_i .
\label{eq9.5.7}
\end{equation}
[[/math]]
The general fact that
[math]|a + b| \leq |a| + |b|[/math], for any two real numbers
[math]a[/math] and
[math]b[/math], can be extended to any finite number of summands, and we therefore have
[[math]]
|s_n| = |\sum_{i=m}^{n} a_i| \leq \sum_{i=m}^{n} |a_i| .
[[/math]]
Furthermore,
[[math]]
\sum_{i=m}^{n} |a_i| \leq \sum_{i=m}^{\infty} |a_i|
[[/math]]
[see (3.2), page 490, and (1.3)1 page 478). Hence
[[math]]
\begin{equation}
|s_n| \leq \sum_{i=m}^{\infty} |a_i|, \;\;\;\mbox{for every integer}\; n \geq m.
\label{eq9.5.8}
\end{equation}
[[/math]]
It follows from (8) that
[[math]]
\begin{equation}
|\lim_{n \rightarrow \infty} s_n | \leq \sum_{i=m}^{\infty} |a_i| .
\label{eq9.5.9}
\end{equation}
[[/math]]
[It is easy to see that (8) implies (9) if we regard the numbers
[math]s_n[/math] and
[math]\sum_{i=m}^{\infty} |a_i|[/math] as points on the line. The geometric statement of (8) is that all the points
[math]s_n[/math] lie in the closed interval whose endpoints are
[math]-\sum_{i=m}^{\infty} |a_i|[/math] and
[math]\sum_{i=m}^{\infty} |a_i|[/math]. If
(9) were false, it would mean that
[math]\lim_{n \rightarrow \infty} s_n[/math] lay outside this interval, a positive distance away from it. But this cannot happen, since Sn is arbitrarily close to
[math]\lim_{n \rightarrow \infty} s_n[/math] for
[math]n[/math] sufficiently large.] Combining (7) and (9), we obtain the in-equality which was to be proved.
■
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.