guide:86f63a466d

There are two main job roles for actuaries, namely

• pricing (calculating premiums: prices of insurance products) and
• valuation or reserving (calculating policy values or reserves, which are indeed the same thing)

The two main topics (premiums and reserves (or policy values)) discussed in this chapter are directly related to these two job roles.

Premiums

In previous chapter, we have studied insurances and whole life annuities, and their actuarial present values. Now, those ideas will be combined for calculating premiums here. Intuitively, it appears that we can simply set the actuarial present value of an insurance/life annuity as its price, which is required to be paid by the insured/annuitant at its issue. However, in practice, the products are purchased by installments, instead of just a single payment at issue (time 0) (if this is the case, we refer the premium to as net single premium made at time 0). To be more specific, we usually use life annuities of premium to purchase insurance products.

Now, to actually calculate the premium, we need to have some rules, or principles that defines the way of calculation. Otherwise, different people may have different opinions on how to calculate the premium. Of course, in reality, the premium of insurance products are not just calculated by a single principle. The calculation is much more complex than what we discuss here, since there are many factors that can affect the premium in practice, and also there are many opinions from different stakeholders to be considered. So, setting a "right" premium is not an easy task in practice. Hence, pricing actuaries are needed for calculating premiums.

Before stating the principle for calculating premiums, let us define a term that is the basis for calculating premiums, namely the insurer's loss.

Definition (Insurer's loss)

The insurer's loss at policy issue (time 0), denoted by [math]L_0[/math], is the present value random variable (p.v.r.v.) of benefits paid, subtracted by the p.v.r.v. of annuity of premiums received.

• Apart from the benefits and premiums, expenses should also be considered in the insurer's loss. However, we just ignore the expenses at the moment for simplicity. In later sections, we will address the effects from the expenses.

• If the premiums are calculated without considering expenses, then they are called net premiums. Otherwise, they are called gross premiums.

Symbolically, we can write

[[math]]L_0=Z-PY[[/math]]

where [math]Z[/math] is the p.v.r.v. of the benefits, and [math]PY[/math] is the p.v.r.v. of the annuity of premiums ([math]Y[/math] is the p.v.r.v. of the life annuity with unit payment, and [math]P[/math] is the amount of each premium paid in the life annuity). Then, based on [math]L_0[/math], we can introduce various principles for calculating premiums. Intuitively, the insurer should avoid having losses, and hence do not want [math]L_0[/math] to be positive. This is the main idea in the following principle.

Definition (Portfolio percentile principle)

Portfolio percentile principle suggests that the premium amount should be set such that the probability [math]\mathbb P(L_0\gt0)\le\alpha[/math], where [math]\alpha[/math] is the percentile.

In the portfolio percentile principle, even if the probability for having a positive loss is very small, the size of the loss is not considered. For example, having a probability 0.01 to have a loss of $1 trillion should be more problematic than having a probability of 0.5 to have a loss of $100, right? This suggests that apart from the probability of having positive losses, the size of the losses also matters. When both size and probability are involved, what do you think of?

Definition (Equivalence principle)

Equivalence principle suggests that the premium amount should be set such that [math]\mathbb E[L_0]=0[/math].

• In some sense, this definition is similar to the "fair price" of stocks and bonds where the price is set such that the sum of present value of all payments involved is zero.
• Under this principle, the actuarial present value of the premiums ([math]\mathbb E[PY][/math]) is the same as that of the benefits ([math]\mathbb E[Z][/math]), and hence the premiums (financial obligations for the policyholder) and benefits (financial obligations for the insurer) can be thought of as "equivalent". In other words, the insurer should be indifferent between accepting the risk (allowing the purchase) and not accepting the risk (not allowing the purchase).

Since under equivalence principle, the calculations of premiums are quite simple, it will be used for premium calculation in the following, unless otherwise specified.

As we have mentioned previously, the concepts related to insurances and life annuities are applied here for calculating premiums. As a result, there are not many "new" concepts involved in the calculation of premiums for purchasing insurances and life annuities.

Fully continuous premiums

Let us first consider the premiums for purchasing a whole life insurance with benefit of 1 payable at the moment of death, issued to a life aged [math] x[/math]. Unless otherwise specified, we will assume the premiums will be paid in the same payment pattern as in the insurance product. In this case, the payment pattern of the premiums is paying continuously, since the benefit for the insurance is paid continuously.

So, we have mentioned how should the payment pattern be determined. How about the length of the payments? Of course, the payments must cease when the insured/annuitant dies (it makes no sense for a dead person to continue paying premiums, right?). But, the payments may also cease before the insured/annuitant dies, if it is specified in the terms of the insurance product. For instance, for a whole life insurance, perhaps premiums are only payable for the first 10 years after the policy issue.

In this case, the insurer's loss is

[[math]]L_0=v^T-\bar P\bar a_{\overline T|},\quad T\gt0[[/math]]

where [math]\bar P[/math] is the continuous level annual premium. By equivalence principle, we then have

[[math]]\mathbb E[L_0]=0\implies \bar A_x-\bar P\bar a_x=0\implies \bar P=\frac{\bar A_x}{\bar a_x}.[[/math]]

In this case, the premium [math]\bar P[/math] can be denoted by [math]\bar P(\bar A_x)[/math] (the notation specifies that this premium corresponds to continuous whole life insurance).

Example

A whole life insurance with benefit of 10000 payable at the moment of death is issued to a life aged 30. Suppose the constant force of interest is 0.08, and the mortality of the life follows the de Moivre's law with [math]\omega=100[/math]. Level annual premiums of [math]\bar P[/math] are payable continuously for purchasing this insurance. Calculate [math]\bar P[/math].

Solution.

In this case, since calculating [math]\bar A_{30}[/math] is more convenient than calculating [math]\bar a_{30}[/math], we will just calculate [math]\bar A_{30}[/math], and then relate [math]\bar a_{30}[/math] to [math]\bar A_{30}[/math] for calculating [math]\bar P[/math].

Now, we have

[[math]]\bar A_x=\int_{0}^{70}e^{-0.08t}\cdot\frac{1}{100}\,dt=\frac{1}{100(-0.08)}\left[e^{-0.08 t}\right]_0^{70}\approx 0.1245.[[/math]]

Hence, by equivalence principle, we have

[[math]]\bar P=\frac{10000\bar A_x}{\bar a_x}=\frac{10000\delta\bar A_x}{1-\bar A_x}\approx\frac{800(0.1245)}{1-0.1245}\approx 113.803.[[/math]]

For other types of insurance products, the formulas for the annual premium [math]\bar P[/math] are similar. So, some of them are summarized in the following table.

Summary

Insurance product name	[math]Z[/math]	[math]Y[/math]	[math]L_0=Z-\bar PY[/math]	[math]\bar P=\frac{\mathbb E[Z]}{\mathbb E[Y]}[/math]
Whole life insurance	[math]v^T,\quad T\ge 0[/math]	[math]\bar a_{\overline T|},\quad T\ge 0[/math]	[math]v^T-\bar P\bar a_{\overline T|},\quad T\ge 0[/math]	[math]\bar P(\bar A_x)=\frac{\bar A_x}{\bar a_x}[/math].
[math]n[/math]-year term life insurance	[math]\begin{cases}v^T,& T\le n;\\ 0,&t \gt n\end{cases}[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le n;\\ \bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\begin{cases}v^T-\bar P\bar a_{\overline T|},& T\le n;\\ -\bar P\bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\bar P(\bar A^1_{x:\overline n|})=\frac{\bar A^1_{x:\overline n|}}{\bar a_{x:\overline n|}}[/math]
[math]n[/math]-year endowment insurance	[math]\begin{cases}v^T,& T\le n;\\ v^n,&t \gt n\end{cases}[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le n;\\ \bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\begin{cases}v^T-\bar P\bar a_{\overline T|},& T\le n;\\ v^n-\bar P\bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\bar P(\bar A_{x:\overline n|})=\frac{\bar A_{x:\overline n|}}{\bar a_{x:\overline n|}}[/math]
[math]n[/math]-year pure endowment	[math]\begin{cases}0,& T\le n;\\ v^n,& t \gt n\end{cases}[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le n;\\ \bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\begin{cases}-\bar P\bar a_{\overline T|},& T\le n;\\ v^n-\bar P\bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\bar P(A^{\;\;1}_{x:\overline n|})=\frac{A^{\;\;1}_{x:\overline n|}}{\bar a_{x:\overline n|}}[/math] or [math]\bar P({}_n E_x)=\frac{{}_n E_x}{\bar a_{x:\overline n|}}[/math]
[math] h[/math]-payment years whole life insurance	[math]v^T,\quad T\ge 0[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le h;\\ \bar a_{\overline h|},& T\gt h\end{cases}[/math]	[math]\begin{cases}v^T-\bar P\bar a_{\overline T|},& T\le h;\\ v^T-\bar P\bar a_{\overline h|},& T\gt h\end{cases}[/math]	[math]_h\bar P(\bar A_x)=\frac{\bar A_x}{\bar a_{x:\overline h|}}[/math]
[math] h[/math]-payment years [math]n[/math]-year term life insurance ([math] h \lt n[/math])	[math]\begin{cases}v^T,& T\le h;\\v^T,& h\lt T\le n;\\ 0,&t \gt n\end{cases}[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le h;\\ \bar a_{\overline h|},& h \lt T\le n;\\ \bar a_{\overline h|},& t \gt n\end{cases}[/math]	[math]\begin{cases}v^T-\bar P\bar a_{\overline T|},& T\le h;\\ v^T-\bar P\bar a_{\overline h|},& h \lt T\le n;\\ -\bar P\bar a_{\overline h|},& t \gt n\end{cases}[/math]	[math]_h\bar P(\bar A_{x:\overline n|})=\frac{\bar A^{1}_{x:\overline n|}}{\bar a_{x:\overline h|}}[/math]
[math] h[/math]-payment years [math]n[/math]-year endowment insurance ([math] h \lt n[/math])	[math]\begin{cases}v^T,& T\le h;\\v^T,& h\lt T\le n;\\ v^n,&t \gt n\end{cases}[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le h;\\ \bar a_{\overline h|},& h \lt T\le n;\\ \bar a_{\overline h|},& t \gt n\end{cases}[/math]	[math]\begin{cases}v^T-\bar P\bar a_{\overline T|},& T\le h;\\ v^T-\bar P\bar a_{\overline h|},& h \lt T\le n;\\ v^n-\bar P\bar a_{\overline h|},& t \gt n\end{cases}[/math]	[math]_h\bar P(\bar A_{x:\overline n|})=\frac{\bar A_{x:\overline n|}}{\bar a_{x:\overline h|}}[/math]
[math]n[/math]-year deferred whole life annuity	[math]\begin{cases}0,& T\le n;\\ \bar a_{\overline {T-n}|},& t \gt n\end{cases}[/math]	[math]\begin{cases}\bar a_{\overline T|},& T\le n;\\ \bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\begin{cases}-\bar P\bar a_{\overline T|},& T\le n;\\ \bar a_{\overline{T-n}|}-\bar P \bar a_{\overline n|},& t \gt n\end{cases}[/math]	[math]\bar P({}_{n|}\bar a_x)=\frac{{}_{n|}\bar a_x}{\bar a_{x:\overline n|}}=\frac{{}_n E_x\bar a_{x+n}}{\bar a_{x:\overline n|}}[/math]

• For the [math] h[/math]-payment years [math]n[/math]-year insurances, we have [math] h \lt n[/math] since the insurance company normally would only allow the insured to settle the premiums within the term of the insurances ([math]n[/math] years), and the insured normally cannot use more than [math]n[/math] years to settle the premiums.
• For the [math]n[/math]-year deferred whole life annuity, the payment of premiums should only last for a maximum of [math]n[/math] years (deferral period) (of course, the payments can similarly only last for, say [math] h \lt n[/math] years), since it does not quite make sense to receive the payments from the life annuity and make payments for premiums simultaneously.

Fully discrete premiums

Now, let us consider the discrete insurance products, where the premiums are also discretely, rather than continuously paid. However, a difference here is that the payment pattern of the premiums is not exactly the same as that for the insurance products. In particular, we assume that the premiums are always made at the beginning of each year unless otherwise specified. As a result, the premiums form a life annuity-due.

First, let us consider the case for a whole life insurance with benefit of 1 payable at the end of the year of death. Then, the insurer's loss is

[[math]]v^{K+1}-P\ddot a_{\overline {K+1}|}[[/math]]

where [math]P[/math] is the level annual premium. By equivalence principle, we then have

[[math]]\mathbb E[L_0]=0\implies A_x-P\ddot a_x=0\implies P=\frac{A_x}{\ddot a_x}.[[/math]]

In this case, we denote the premium [math]P[/math] by [math]P_x[/math], which is in the "same form" as the notation [math]A_x[/math]. For other types of insurance products, the formulas for premium are developed similarly. Some of them are summarized below.

Summary

Insurance product name	[math]Z[/math]	[math]Y[/math]	[math]L_0=Z-PY[/math]	[math]P=\frac{\mathbb E[Z]}{\mathbb E[Y]}[/math]
Whole life insurance	[math]v^{K+1},\quad K=0,1,\dotsc[/math]	[math]\ddot a_{\overline {K+1}|},\quad K=0,1,\dotsc[/math]	[math]v^{K+1}-P\ddot a_{\overline {K+1}|},\quad K=0,1,\dotsc[/math]	[math]P_x=\frac{A_x}{\ddot a_x}[/math].
[math]n[/math]-year term life insurance	[math]\begin{cases}v^{K+1},& K=0,1,\dotsc,n-1;\\ 0,&K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ \ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}v^{K+1}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ -P\ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]P^1_{x:\overline n|}=\frac{A^1_{x:\overline n|}}{\ddot a_{x:\overline n|}}[/math]
[math]n[/math]-year endowment insurance	[math]\begin{cases}v^{K+1},& K=0,1,\dotsc,n-1;\\ v^n,&K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ \ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}v^{K+1}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ v^n-P\ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]P_{x:\overline n|}=\frac{A_{x:\overline n|}}{\ddot a_{x:\overline n|}}[/math]
[math]n[/math]-year pure endowment	[math]\begin{cases}0,& K=0,1,\dotsc,n-1;\\ v^n,& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ \ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ v^n-P\ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]P^{\;\;1}_{x:\overline n|}=\frac{A^{\;\;1}_{x:\overline n|}}{\ddot a_{x:\overline n|}}[/math]
[math] h[/math]-payment years whole life insurance	[math]v^{K+1},\quad K=0,1,\dotsc[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,h-1;\\ \ddot a_{\overline h|},& K=h,h+1,\dotsc\end{cases}[/math]	[math]\begin{cases}v^{K+1}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,h-1;\\ v^{K+1}-P\ddot a_{\overline h|},& K=h,h+1,\dotsc\end{cases}[/math]	[math]_hP_x=\frac{A_x}{\ddot a_{x:\overline h|}}[/math]
[math] h[/math]-payment years [math]n[/math]-year term life insurance ([math] h \lt n[/math])	[math]\begin{cases}v^{K+1},& K=0,1,\dotsc,h-1;\\v^{K+1},& K=h,h+1,\dotsc,n-1;\\ 0,&K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,h-1;\\ \ddot a_{\overline h|},& K=h,h+1,\dotsc,n-1;\\ \ddot a_{\overline h|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}v^{K+1}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,h-1;\\ v^{K+1}-P\ddot a_{\overline h|},& K=h,h+1,\dotsc,n-1;\\ -P\ddot a_{\overline h|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]_hP_{x:\overline n|}=\frac{A^{1}_{x:\overline n|}}{\ddot a_{x:\overline h|}}[/math]
[math] h[/math]-payment years [math]n[/math]-year endowment insurance ([math] h \lt n[/math])	[math]\begin{cases}v^{K+1},& K=0,1,\dotsc,h-1;\\v^{K+1},& K=h,h+1,\dotsc,n-1;\\ v^n,&K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,h-1;\\ \ddot a_{\overline h|},& K=h,h+1,\dotsc,n-1;\\ \ddot a_{\overline h|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}v^{K+1}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,h-1;\\ v^{K+1}-P\ddot a_{\overline h|},& K=h,h+1,\dotsc,n-1;\\ v^n-P\ddot a_{\overline h|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]_hP(A_{x:\overline n|})=\frac{A_{x:\overline n|}}{\ddot a_{x:\overline h|}}[/math]
[math]n[/math]-year deferred whole life annuity	[math]\begin{cases}0,& K=0,1,\dotsc,n-1;\\ \ddot a_{\overline {K+1-n}|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ \ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]\begin{cases}-P\ddot a_{\overline {K+1}|},& K=0,1,\dotsc,n-1;\\ \ddot a_{\overline{K+1-n}|}-P \ddot a_{\overline n|},& K=n,n+1,\dotsc\end{cases}[/math]	[math]P({}_{n|}\ddot a_x)=\frac{{}_n E_x\ddot a_{x+n}}{\ddot a_{x:\overline n|}}[/math]

m-thly payment premiums

Of course, for the insurance products in the previous section, the premiums need not be payable annually. In general, they can be payable [math]m[/math] times for every policy year. We can similarly use equivalence principle to determine the amount of each premium in this case.

Let us first consider the case for whole life insurance with unit benefit payable at the end of year of death. Suppose the premiums are payable in [math]m[/math]-thly installments at the beginning of each [math]m[/math]-thly period . In this case, the insurer's loss is

[[math]]L_0=v^{K+1}-P^{(m)}\ddot a^{(m)}_{\overline{K+1}|}[[/math]]

where [math]P^{(m)}[/math] is the level annual premium payable [math]m[/math]-thly, that is, the actual amount of premium paid at the beginning of each [math]m[/math]-thly period is [math]P^{(m)}/m[/math]. (This is similar to the case for the interest rate where [math]i^{(m)}[/math] is the nominal annual interest rate, while the effective interest rate for each [math]m[/math]-thly period is [math]i^{(m)}/m[/math].) By equivalence principle, we can similarly get [math]P^{(m)}=\frac{A_x}{\ddot a_x^{(m)}}[/math]. In this case, we denote [math]P^{(m)}[/math] by [math]P_x^{(m)}[/math].

We can also apply this idea to insurances payable at the moment of death.For instance, when the above whole life insurance is instead the continuous one, then we have

[[math]]L_0=v^T-P^{(m)}\ddot a_{\overline{K+1}}^{(m)}.[[/math]]

Similarly, we have [math]P^{(m)}=\frac{\bar A_x}{\ddot a_x^{(m)}}[/math] by equivalence principle. In this case, we denote [math]P^{(m)}[/math] by [math]P^{(m)}(\bar A_x)[/math].

Of course, apart from the aforementioned insurance products, we can also apply the idea of equivalence principle for calculating the premiums for insurances where benefits are varying, other types of life annuities, etc. Also, the insurance products can be irregular, and the premium payments can be irregular as well. In those cases, there are no "formulas" for calculating the amount of premiums directly. But, we can always use the equivalence principle for the calculations.

Accumulation-type benefits

In practice, apart from the death benefits from the insurance products, some of the premiums paid may be refunded when death occurs. In particular, for [math]n[/math]-year deferred whole life annuity, the annuitant will get nothing from the life annuity itself if he dies during the deferral period. But when some of the premiums paid are refunded when death occurs in the deferral period, then the annuitant will at least get something if he dies during the deferral period. So, this may be better for the annuitant (but of course, in exchange for this, it is natural to expect that the premiums required will be higher).

For the refund of premiums, depending on the terms, the amount of the refund may or may not consider the interest effect. To be more specific, when the amount of premiums refunded is determined at some time [math] t[/math], we may use the accumulated value of the premiums paid at time [math] t[/math] with a certain interest rate (possibly different from the interest rate used for the calculation of actuarial present values), or simply zero interest rate.

In the following, we will discuss the development of formulas for these benefits when the premiums are payable annually (at the beginning of each year), and the refund will be made at the end of year of death. We can develop similar formulas when the premium are payable continuously or [math]m[/math]-thly, with the refund to be made at different time points.

Let us first develop a model of a special [math]n[/math]-year term insurance issued to a life aged [math] x[/math], where the benefit of [math]\ddot s_{\overline{k+1}|j}[/math] (evaluated at interest rate [math]j[/math]) is payable at the end of year [math]k \lt n[/math] (time [math]k+1[/math]) when death occurs in year [math]k[/math] (no benefit if death does not occur within [math]n[/math] years), and then apply this model for the refunds of premiums. Graphically, the situation looks like

"1": hypothetical "benefits" made at various time points (yet to be realized until death) (they may be interpreted as premiums paid in practice, and then they are not hypothetical in those cases)

Now, let us consider some simple cases first.

Case 1: interest rate [math]j=0[/math]. Then, the benefit is [math]\ddot s_{\overline{k+1}|j}=\underbrace{1+1+\dotsb+1}_{k+1\text{ times}}=k+1[/math].

Case 2: interest rate [math]j=i[/math] ([math]i[/math] is the interest rate used for calculating actuarial present value). Then, the benefit is [math]\ddot s_{\overline{k+1}|j}=\ddot s_{\overline{k+1}|i}[/math].

In case 1, the APV of the p.v.r.v. for this insurance is simply given by [math](IA)_x[/math] by considering the definition of [math](IA)_x[/math]. In case 2, the APV of the p.v.r.v. for this insurance is [math]\ddot a_{x:\overline n|i}-{}_n E_x\ddot s_{\overline n|i}[/math]. The formula for case 2 will be proven later in this section. For now, let us give an intuitive explanation to this formula in the following:

Indeed, when [math]j=i[/math], the special insurance is very similar to a [math]n[/math]-year life annuity-due (get a payment of 1 when the life still survives at the beginning of each of the first [math]n[/math] years), in the sense that in terms of value at time [math]k+1[/math], when death occurs in year [math]k+1[/math], the value of the benefit provided by the special insurance is [math]\ddot s_{\overline{k+1}|i}[/math].

On the other hand, for the [math]n[/math]-year life annuity-due (assume [math]k \lt n[/math]), the value of the benefits at time [math]k+1[/math] is also [math]\ddot s_{\overline{k+1}|i}[/math] (accumulate each of the [math]k+1[/math] survival benefits to time [math]k+1[/math]). So, the APV of the benefits of the special insurance and the life annuity-due are the same. However, we have made an important assumption in the process: [math]k \lt n[/math], i.e. death occurs before year [math]n[/math]. But this is not necessarily the case. The life can survive for at least [math]n[/math] years, right?

So we need to consider this situation also. In the situation where the life survives for at least [math]n[/math] years, the life annuity-due provides a benefit of [math]\ddot s_{\overline n|i}[/math] at time [math]n[/math], but the special insurance will not provide anything. Hence, we need to subtract [math]{}_n E_x\ddot s_{\overline n|i}[/math] (APV of that "extra" benefit, obtained by actuarially discounting the benefit to time 0) from the APV of the [math]n[/math]-year life annuity-due [math]\ddot a_{x:\overline n|i}[/math] to get the APV of the p.r.r.v. of this special insurance.

Now, let us formally define the present value random variable involved in the model of the special insurance:

[[math]]Z=\begin{cases}v_i^{K+1}\ddot s_{\overline{K+1}|j},& K=0,1,\dotsc,n-1;\\ 0,&K=n,n+1,\dotsc.\end{cases}[[/math]]

After that, we can derive a formula for the APV:

[[math]] \begin{align} \mathbb E[Z]&=\sum_{k=0}^{n-1}v_i^{k+1}\ddot s_{\overline{k+1}|j}{}_k p_x{}q_{x+k}\\ &=\sum_{k=0}^{n-1}\left((1+i)^{-(k+1)}\cdot\frac{(1+j)^{k+1}-1}{d_j}{}{}_k p_x{}q_{x+k}\right)\\ &=\frac{1}{d_j}\sum_{k=0}^{n-1}\left[\left(\frac{1+i}{1+j}\right)^{-(k+1)}{}{}_k p_x{}q_{x+k}-v_i^{k+1}{}_k p_x{}q_{x+k}\right]\\ &=\frac{1}{d_j}\Bigg[\sum_{k=0}^{n-1}\bigg(1+\underbrace{\frac{i-j}{1+j}}_{i_*}\bigg)^{-(k+1)}{}{}_k p_x{}q_{x+k}-\sum_{k=0}^{n-1}v_i^{k+1}{}{}_k p_x{}q_{x+k}\Bigg]\\ &=\frac{1}{d_j}\left[\sum_{k=0}^{n-1}v_*^{k+1}{}{}_k p_x{}q_{x+k}-A^{1}_{x:\overline n|i}\right]\\ &=\frac{1}{d_j}\left[A^1_{x:\overline n|i_*}-A^{1}_{x:\overline n|i}\right].\\ \end{align} [[/math]]

where [math]d_j[/math] is the discount rate equivalent to the interest rate [math]j[/math], i.e., [math]d_j=\frac{j}{1+j}[/math], [math]v_*=\frac{1}{1+i_*}[/math], and [math]v_i=\frac{1}{1+i}[/math] ([math]i_*[/math] and [math]i[/math] are added to the APV notations for insurances so that we can identify which interest rate we are using for evaluating the APV's), assuming [math]j\ne 0[/math].

• This formula fails when [math]j=0[/math], since [math]d_j=0[/math] when [math]j=0[/math], causing the value given by the formula to be undefined. However, as we have mentioned in case 1 above, the APV is actually [math](IA)_x[/math] when [math]j=0[/math], by considering the definition of [math](IA)_x[/math].

Through this formula, we can prove the formula in case 2 above:

Proposition

APV is

[[math]]\ddot a_{x:\overline n|}-{}_n E_x\ddot s_{\overline n|}[[/math]]

Show Proof

When [math]j=i[/math], we have [math]i_*=\frac{i-j}{1+j}=0[/math]. So the APV of the special insurance is (notice that [math]_k p_x {}q_{x+k}={}_{k|} q_x[/math])

[[math]]\frac{\sum_{k=0}^{n-1}{}_{k|}q_x -A_{x:\overline n|}^1}{d} =\frac{{}_n q_x-A_{x:\overline n|}^1}{d} =\frac{1{\color{blue}-{}_n p_x}-A_{x:\overline n|}{\color{blue}+v^n{}_n p_x}}{d} =\frac{1-A_{x:\overline n|}}{d}-{\color{blue}v^n{}_n p_x}\cdot\frac{{\color{blue}(1+i)^n-1}}{d} =\ddot a_{x:\overline n|}-{}_n E_x\ddot s_{\overline n|}.[[/math]]

■

Incorporating expenses

Previously, we have not considered expenses. Now, we will discuss the situation where expenses are incorporated to the premium calculations in this section. As we have mentioned, such premiums calculated are called gross premiums. To calculate gross premiums, we need to include expenses in the insurer's loss [math]L_0[/math]. Since the expenses are to be paid by the insurer, the p.v.r.v. of expenses are added to [math]L_0[/math], that is, we now have

[[math]]L_0=Z+\text{p.v.r.v. of expenses}-PY.[[/math]]

When we use the equivalence principle, we have

[[math]]P\mathbb E[Y]=\mathbb E[Z]+\mathbb E[\text{p.v.r.v. of expenses}].[[/math]]

The expenses may be incurred from the cost of claiming benefits, commissions, etc.

Reserves (or policy values)

In the section about premiums, we often use the equivalence principle to calculate premiums, which requires the expected value of the insurer's losses at policy issue (time 0) to be zero. But, after a period of time, say at time [math] t[/math], this expected value may not be zero anymore, since the "[math]Z[/math]" and "[math]Y[/math]" at this time [math] t[/math], are different from the "[math]Z[/math]" and "[math]Y[/math]" at time 0. Particularly, the "[math]Z[/math]" and "[math]Y[/math]" at time [math] t[/math] are considering the benefits/payments after time [math] t[/math], and the benefits/payments from time [math]0[/math] to time [math] t[/math] are not considered. Graphically, it looks like

For the "[math]Z[/math]" and "[math]Y[/math]" at time [math] t[/math] to be meaningful, the policyholder should still survive at time [math] t[/math]. Otherwise, the policy has already ended before time [math] t[/math], and it is meaningless to discuss the "[math]Z[/math]" and "[math]Y[/math]" at time [math] t[/math].

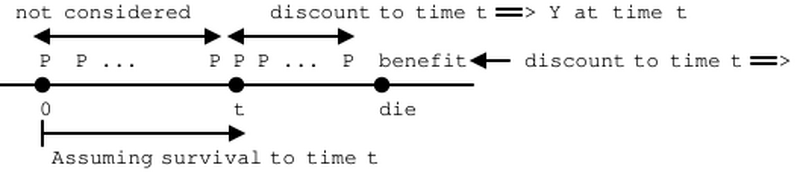
We may want the expected value to be still zero at time [math] t[/math], and in order for the insurer's loss at time [math] t[/math] to still have a zero expected value (so that there is still equivalence between the financial obligations for the policyholder and the insurer at this time point), a "balancing item" may be needed. To determine what the balancing item should be, let us consider the following two cases:

1. The expected value of the insurer's losses at time [math] t[/math] is positive. This means the insurer expects a prospective loss from the policy (since the future benefits paid are expected to be greater than the future premiums received). Then, the insurer should reserve an amount of money, so that the insurer can "encounter" the losses.
2. On the other hand, if the expected value of the insurer's losses at time [math] t[/math] is negative, then this means the insurer expects a prospective gain from the policy. So, the insurer can have a "negative reserve" (hypothetically) for that policy and still be able to encounter the losses.

• For the case 2, the "negative reserve" may be interpreted as a sum of money that can be "taken away" (hypothetically) from the policy for other usages.

From these, we can observe that in case 1, the insurer should spare an amount of money for the reserve for that policy (increase in financial obligation for the insurer), and in case 2, the insurer can hypothetically take away a sum of money from the policy (decrease in financial obligation for the insurer). Through these changes in the financial obligation for the insurer, there can still be an equivalence between the financial obligations for the policyholder and the insurer.

These lead us to the following definitions.

Definition (Prospective net loss)

The prospective net loss at time [math] t[/math], denoted by [math]L^n_t[/math], is the p.v.r.v. of future benefits less the p.v.r.v. of future net premiums, when the policyholder still survives at time [math] t[/math].

• To be more precise, "future" here means "after time [math] t[/math]". So, in general, the payment/benefit at time [math] t[/math] should not be included in prospective net loss. However, there are exceptions (see the following).

• In the discrete case, the payment/benefit exactly at time [math] t[/math] is sometimes regarded as "future", and also included in the prospective net loss.
• The convention for the decision is that we should consider which part of the time a payment/benefit is related to.
• For death benefit at time [math] t[/math], it is related to the death occurring in the year before time [math] t[/math] (time [math] t[/math] is the end of this year). So, it is not regarded as "future".
• For survival benefit at time [math] t[/math] (also applies to continuous case), it is related to the survival to, at least the moment after time [math] t[/math]. So, it is regarded as "future".
• For annuity payments at time [math] t[/math],

• if it is a payment from an annuity-due, then it is related to the year after time [math] t[/math] (time [math] t[/math] is the beginning of this year). So, it is regarded as "future".
• if it is a payment from an annuity-immediate, then it is related to the year before time [math] t[/math] (time [math] t[/math] is the end of this year). So, it is not regarded as "future".

• In particular, since premiums are in the form of annuity-due, premium at time [math] t[/math] is regarded as future premium.

• The prospective net loss at time [math] t[/math] is only defined when the policyholder still survives at time [math] t[/math], since if the life dies at or before time [math] t[/math], it means the policy has ended, and thus it is meaningless to consider the prospective net loss.
• When we add the p.v.r.v. of future expenses to [math]L^n_t[/math] and also change the net premiums to gross premiums, it becomes the prospective gross loss, denoted by [math]L^g_t[/math].

• We will mainly focus on [math]L^n_t[/math] for now. The results for [math]L^g_t[/math] can be obtained similarly and we will consider [math]L^g_t[/math] later.

• Notice that [math]L^n_0[/math] and [math]L^g_0[/math] are essentially the same as [math]L_0[/math] without considering expenses and [math]L_0[/math] with expenses considered respectively.
• For the discrete case, we commonly use [math]k[/math] in place of [math] t[/math], and the prospective net loss at time [math]k[/math] is only defined when [math]k[/math] is a nonnegative integer, corresponding to the support of [math]K_x[/math].

Definition (Reserve)

The net (gross) premium reserve at time [math] t[/math] is the conditional expectation of the prospective net (gross) loss at time [math] t[/math], given that the policyholder still survives at time [math] t[/math].

• Since prospective net (gross) loss is involved, such reserve is also called prospective reserve.
• Of course, this is just one definition of reserves by considering the equivalence principle, and there are many other alternative (and possibly more complicated) definitions.
• "net (gross) premium" indicates that the premiums involved (in the loss) are net (gross) premiums.
• Since we will focus on the net loss in the following, we may just use "reserve" to mean "net premium reserve".

Symbolically, if the policy is issued to a life aged [math] x[/math], then the net premium reserve is [math]\mathbb E[L^n_t|T \gt t][/math], and the gross premium reserve [math]\mathbb E[L^g_t|T \gt t][/math] (for gross loss), for the continuous case. (For discrete case, we use "[math]L^n_k[/math]" ([math]L^g_k[/math]) and "[math]K\ge k[/math]")

Actually, the "[math]|T \gt t[/math]" in the expectation is not necessary since prospective net loss is only defined when [math] t \gt t[/math], so its support is already [math]\{T \gt t\}[/math]. Hence, taking such condition will not change the value of expectation, i.e., [math]\mathbb E[L^n_t]=\mathbb E[L^n_t|T \gt t][/math]. But, we still include this in the expectation to show that we are considering the case where [math] t \gt t[/math] more explicitly, and it can be quite useful in some proofs (see the following).

By definition, to calculate the conditional expectation [math]\mathbb E[L^n_t|T \gt t][/math], we need to consider the conditional distribution of [math]L^n_t[/math] given [math] t \gt t[/math].

Proposition

The conditional distribution of [math] t_x-t[/math] ([math] t_x-t[/math] gives the prospective lifetime with respect to [math] t[/math], which should be involved in [math]L^n_t[/math]) given that [math] t_x \gt t[/math] is the same as the unconditional distribution of [math] t_{x+t}[/math]

Show Proof

Consider the survival functions of the two distributions. First, for the conditional distribution of [math] t_x-t[/math] given that [math] t_x \gt t[/math],

[[math]]\mathbb P(T_x-t \gt s|t_x \gt t)=\frac{\mathbb P(t_x \gt s+t)}{\mathbb P(t_x \gt t)}=\frac{\mathbb P(T_0 \gt x+s+t|T_0 \gt x)}{\mathbb P(T_0 \gt x+t|T_0 \gt x)}=\frac{\mathbb P(T_0 \gt x+s+t)/\mathbb P(T_0 \gt x)}{\mathbb P(T_0 \gt x+t)/\mathbb P(T_0 \gt x)}=\frac{\mathbb P(T_0 \gt x+s+t)}{\mathbb P(T_0 \gt x+t)}.[[/math]]

On the other hand, for the unconditional distribution of [math] t_{x+t}[/math],

[[math]]\mathbb P(T_{x+t} \gt s')=\mathbb P(T_0 \gt x+s'+t|T_0 \gt x+t)=\frac{\mathbb P(T_0 \gt x+s'+t)}{\mathbb P(T_0 \gt x+t)}.[[/math]]

These show the survival functions of the two distributions are the same (provided that all the conditional probabilities involved are defined). Hence, the two distributions are the same.

■

This result gives us an alternative and often more convenient method to calculate the conditional expectation [math]\mathbb E[L^n_t|t_x \gt t][/math]:

1. replace all "[math] t_x-t[/math]" by "[math] t_{x+t}[/math]" and remove the condition "[math] t_x \gt t[/math]"
2. calculate the unconditional expectation, which equals the value of conditional expectation since the distributions involved are the same

Notice that we can also apply this similarly to the discrete case where [math]K_x[/math] is involved, since [math]K_x[/math] is just defined as [math]\lfloor T_x\rfloor[/math], and we can have a similar alternative method for calculations.

Fully continuous reserves

First, let us consider the whole life insurance with unit benefit, the simplest case. In this case, we have

[[math]]L^n_t=v^{T-t}-\underbrace{\bar P(\bar A_x)}_{\text{notation}}\bar a_{\overline{T-t}|}.[[/math]]

To understand this, let us consider the following diagram.

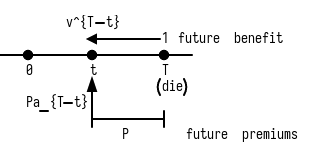
Then, the reserve, denoted by [math]_t \bar V(\bar A_x)[/math] ("[math]V[/math]" corresponds to the "v" in "policy value"), is by definition [math]\mathbb E[L^n_t|T \gt t][/math].

Example

Given constant force of mortality [math]\mu=0.06[/math] and constant force of interest [math]\delta=0.04[/math], calculate [math]_{10}\bar V(\bar A_{30})[/math].

Solution.

First, we have [math]\bar a_x=\frac{1}{0.06+0.04}=10[/math] and [math]\bar A_x=\frac{0.06}{0.06+0.04}=0.6[/math]. Hence,

[[math]]_{10}\bar V(\bar A_{30})=\bar A_{30+10}-\frac{\bar A_{30}}{\bar a_{30}}\cdot\bar a_{30+10}=0.6-\frac{0.6}{10}(10)=0.[[/math]]

Example

Suppose the mortality follows the de Moivre's law with [math]\omega=100[/math], and the constant force of interest is 4%. Calculate [math]_{20}\bar V(\bar A_{30})[/math].

Solution.

First, we have

• [math]\bar A_{30}=\frac{1}{70}\int_{0}^{70}e^{-0.04 t}\,dt=\frac{1}{70(-0.04)}[e^{-0.04t}]_0^{70}\approx 0.3354[/math].
• [math]\bar A_{50}=\frac{1}{50}\int_{0}^{50}e^{-0.04 t}\,dt=\frac{1}{50(-0.04)}[e^{-0.04t}]_0^{50}\approx 0.4323[/math].
• [math]\bar a_{30}=\frac{1-\bar A_{30}}{0.04}\approx 16.615[/math]
• [math]\bar a_{50}=\frac{1-\bar A_{50}}{0.04}\approx 14.193[/math]

So,

[[math]]_{20}\bar V(\bar A_{30})=\bar A_{50}-\frac{\bar A_{30}}{\bar a_{30}}\cdot\bar a_{50}\approx 0.1458.[[/math]]

Now, let us consider the [math]n[/math]-year term life insurance with unit benefit. In this case, the prospective net loss is different.

When [math] t \lt n[/math],

[[math]] L^n_t=\begin{cases}v^{T-t}-\bar P(\bar A^1_{x:\overline n|})\bar a_{\overline {T-t}|},& 0\lt T-t \lt n-t;\\ -\bar P(\bar A^1_{x:\overline n|})\bar a_{\overline {T-t}|},& T-t\ge n-t.\end{cases} [[/math]]

When [math] t=n[/math], there are no future premiums or benefits made, so [math]L^n_t=0[/math].

When [math] t \gt n[/math], the insurance has ended, so it is not meaningful to consider the reserve for it anymore. (Indeed, if we follow our definition, for other insurance products with finite term, the reserve at such time point must be zero since there will be no premiums or benefits after time [math] t[/math]. It is therefore meaningless to consider such reserves .)

Then, the reserve, denoted by [math]_t \bar V(\bar A^1_{x:\overline n|})[/math], is

[[math]]\mathbb E[L^n_t|T \gt t]= \begin{cases}\bar A_{x+t:\overline{n-t}|}^1-\bar P(\bar A_{x:\overline n|}^1)\bar a_{x+t:\overline{n-t}|},& t \lt n;\\ 0,& t=n.\end{cases} [[/math]]

(by considering the alternative method)

For the [math]n[/math]-year endowment insurance with unit benefits, the prospective net loss is different again.

When [math] t \lt n[/math],

[[math]] L^n_t=\begin{cases}v^{T-t}-\bar P(\bar A^1_{x:\overline n|})\bar a_{\overline {T-t}|},& 0\lt T-t \lt n-t;\\ {\color{darkgreen}v^{n-t}}-\bar P(\bar A^1_{x:\overline n|})\bar a_{\overline {T-t}|},& T-t\ge n-t.\end{cases} [[/math]]

When [math] t=n[/math], we have [math]L_t^n=1[/math] (there is only one benefit made at time [math]n[/math], namely the unit survival benefit made. So, the value is exactly one.). Then, the reserve, denoted by [math]_t\bar V(\bar A_{x:\overline n|})[/math], is

[[math]]\mathbb E[L^n_t|T \gt t]=\begin{cases}\bar A_{x+t:\overline{n-t}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+t:\overline{n-t}|},& t \lt n;\\ 1,&t=n.\end{cases}[[/math]]

(again by considering the alternative method)

To summarize, the reserves of the above policies and also some more other policies (with unit benefits) are tabulated below.

Summary

Insurance product name	net premium reserve at time [math] t[/math]
Whole life insurance	[math]_t \bar V(\bar A_x)=\bar A_{x+t}-\bar P(\bar A_x)\bar a_{x+t}[/math]
[math]n[/math]-year term life insurance	[math]_t\bar V(\bar A_{x:\overline n|}^1)=\begin{cases}\bar A_{x+t:\overline{n-t}|}^1-\bar P(\bar A_{x:\overline n|}^1)\bar a_{x+t:\overline{n-t}|},& t \lt n;\\ 0,& t=n.\end{cases}[/math]
[math]n[/math]-year endowment insurance	[math]_t\bar V(\bar A_{x:\overline n|})=\begin{cases}\bar A_{x+t:\overline{n-t}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+t:\overline{n-t}|},& t \lt n;\\ 1,&t=n.\end{cases}[/math]
[math] h[/math]-payment years whole life insurance	[math]^h_t\bar V(\bar A_x)=\begin{cases}\bar A_{x+t}-{}_h \bar P(\bar A_x)\bar a_{x+t:\overline{h-t}|},& T \lt h;\\ \bar A_{x+t},& t\ge h.\end{cases}[/math]
[math] h[/math]-payment years [math]n[/math]-year term life insurance ([math] h \lt n[/math])	[math]^h_t\bar V(\bar A_{x:\overline n|}^1)=\begin{cases}\bar A_{x+t:\overline{n-t}|}^{1}-{}_h\bar P(\bar A_{x:\overline n|}^1)\bar a_{x+t:\overline{h-t}|},& T \lt h;\\ \bar A_{x+t:\overline{n-t}|}^1, & h\le t \lt n;\\ 0,& t=n.\end{cases}[/math]
[math] h[/math]-payment years [math]n[/math]-year endowment insurance ([math] h \lt n[/math])	[math]^h_t\bar V(\bar A_{x:\overline n|})=\begin{cases}\bar A_{x+t:\overline{n-t}|}-{}_h\bar P(\bar A_{x:\overline n|})\bar a_{x+t:\overline{h-t}|},& T \lt h;\\ \bar A_{x+t:\overline{n-t}|}, & h\le t \lt n;\\ 1,& t=n.\end{cases}[/math]
[math]n[/math]-year pure endowment	[math]_t\bar V({}_n E_x)=\begin{cases}{}_{n-t}E_{x+t}-\bar P({}_n E_x)\bar a_{x+t:\overline{n-t}|},& t \lt n;\\ 1,&t=n.\end{cases}[/math]
[math]n[/math]-year deferred whole life annuity	[math]_t\bar V({}_{n|}\bar a_x)=\begin{cases}{}_{n-t|}\bar a_{x+t}-\bar P({}_{n|}\bar a_x)\bar a_{x+t:\overline{n-t}|},& t\le n;\\ \bar a_{x+t},& t \gt n.\end{cases}[/math]

Example

Amy, aged 30, purchases a 20-year (continuous) endowment insurance. It is given that

• [math]\bar A_{30:\overline{20}|}=0.2[/math]
• [math]\bar A_{30:\overline{5}|}^1=0.1[/math]
• [math]_5 E_{30}=0.3[/math]
• [math]\delta=0.02[/math]

Calculate the policy value of the insurance at time 5.

Solution.

Let us draw a diagram to understand the situation more clearly:

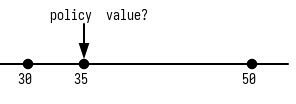
The policy value at time 5 is [math]\bar A_{35:\overline{15|}}-\bar P(\bar A_{30:\overline{20}|})\bar a_{35:\overline{15}|}[/math]. Let us calculate the terms involved one by one.

• [math]\bar P(\bar A_{30:\overline{20}|})=\frac{\bar A_{30:\overline{20}|}}{\bar a_{30:\overline{20}|}}=\frac{0.2}{(1-0.2)/0.02}= 0.005[/math].

By recursion relation, we have

[[math]]\bar A_{30:\overline{20}|}=\bar A_{30:\overline{5}|}^1+{}_5 E_{30}\bar A_{35:\overline{15}|}\implies 0.2=0.1+0.3(\bar A_{35:\overline{15}|})\implies \bar A_{35:\overline{15}|}\approx 0.333.[[/math]]

It follows that

[[math]]\bar a_{35:\overline{15}|}=\frac{1-0.333}{0.02}\approx 33.33.[[/math]]

Thus, the required policy value is approximately 0.166.

Example

Bob, aged 18, purchases a 50-year deferred whole life annuity payable continuous at an annual rate of 100000 for his retirement. Suppose the constant force of mortality is 0.05, and the constant force of interest is 5%. Calculate the reserve for this annuity at time 40.

Solution.

The reserve is [math]100000{}_{10|}\bar a_{58}-100000\bar P(_{50|}\bar a_{18})\bar a_{58:\overline{10}|}[/math]. Let us calculate the terms one by one.

• [math]_{10|}\bar a_{58}={}_{10}E_{58}\bar a_{68}=e^{-0.1(10)}\cdot\frac{1}{0.1}\approx 3.67879[/math]
• [math]\bar P({}_{50|}\bar a_{18})=\frac{{}_{50}E_{18}\bar a_{68}}{\bar a_{18:\overline{50}|}}=\frac{e^{-0.1(50)}\cdot\frac{1}{0.1}}{\int_{0}^{50}e^{-0.1t}\,dt}\approx\frac{0.067379}{(e^{-0.1(50)}-1)/(-0.1)}\approx 0.0067837[/math]
• [math]\bar a_{58:\overline{10}|}=\int_{0}^{10}e^{-0.1t}\,dt=\frac{e^{-0.1(10)}-1}{-0.1}\approx 6.3212[/math]

So, the reserve is [math]100000(3.67879-0.0067837(6.3212))\approx 363590.8876[/math].

Proposition (Premium-difference formula)

Show that [math]_t \bar V(\bar A_{x:\overline n|})=\big(\bar P(\bar A_{x+t:\overline{n-t}|})-\bar P(\bar A_{x:\overline n|})\big)\bar a_{x+t:\overline{n-t}|}[/math] where [math] t \lt n[/math]. ("[math]\bar P(\bar A_{x+t:\overline{n-t}|})-\bar P(\bar A_{x:\overline n|})[/math]" is a premium difference, and hence its name)

Show Proof

First, we have

[[math]]_t \bar V(\bar A_{x:\overline n|})=\bar A_{x+t:\overline{n-t}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+t:\overline{n-t}|}.[[/math]]

So, it suffices to show that [math]\bar A_{x+t:\overline{n-t}|}=\bar P(\bar A_{x+t:\overline{n-t}|})\bar a_{x+t:\overline{n-t}|}[/math], but this follows directly from the equivalence principle. Hence, we are done.

■

Proposition (Paid-up insurance formula)

Show that [math]_t \bar V(\bar A_{x:\overline n|})=\left(1-\frac{\bar P(\bar A_{x:\overline n|})}{\bar P(\bar A_{x+t:\overline{n-t}|})}\right)\bar A_{x+t:\overline{n-t}|}[/math] where [math] t \lt n[/math]. ("[math]\frac{\bar P(\bar A_{x:\overline n|})}{\bar P(\bar A_{x+t:\overline{n-t}|})}[/math]" is the amount of future benefit funded by just future benefit premiums . So, subtracting it from the benefit gives an insurance, called paid-up insurance, which is the "remaining part" of the insurance if the policyholder stops paying premiums at time [math] t[/math].)

Show Proof

First, we have

[[math]]_t \bar V(\bar A_{x:\overline n|})=\bar A_{x+t:\overline{n-t}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+t:\overline{n-t}|}.[[/math]]

So, it suffices to show that [math]\bar a_{x+t:\overline{n-t}|}=\frac{\bar A_{x+t:\overline{n-t}|}}{\bar P(\bar A_{x+t:\overline{n-t}|})}[/math]. But this follows directly from the equivalence principle.

■

The premium-difference and paid-up insurance formulas can also be developed similarly for other types of policies. However, we seldom use the formulas themselves for the actual calculation since these formulas can be derived in just a single step, and thus we are not necessary to use such formulas.

Recall that in financial mathematics, to determine the outstanding balance for a loan at a certain time point, we have prospective and retrospective methods. Indeed, the definition of reserves are prospective. Can we calculate the reserves using a retrospective way?

There are actually retrospective formulas for calculating premiums, as illustrated in the following exercise.

Proposition

By recursion relations, we have

[[math]] \begin{align} \bar A_{x+s:\overline{n-s}|}&=\bar A_{x+s:\overline t|}^1+{}_t E_{x+s}\;\bar A_{x+s+t:\overline{n-s-t}|},\text{ and }\\ \bar a_{x+s:\overline{n-s}|}&=\bar a_{x+s:\overline t|}+{}_t E_{x+s}\;\bar a_{x+s+t:\overline{n-s-t}|}.\\ \end{align} [[/math]]

([math]n-s-t\gt0[/math], and [math]n-s\gt0[/math])

(a) Show that [math]_s\bar V(\bar A_{x:\overline n|})+\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline t|}=\bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\;_{s+t}\bar V(\bar A_{x:\overline n|})[/math] (for every [math]n,s,t[/math] satisfying the above constraints).

An interpretation to the formula in (a) is that the LHS is the APV of the insurer's resources (initial reserves from the policy plus the future premiums), and the RHS is the APV of the insurer's obligations (future benefits plus the ending reserves for the policy). This is also a recursive relation for reserve.

(b) Using the formula in (a), or otherwise, prove the retrospective formula:

[[math]]_t\bar V(\bar A_{x:\overline n|})=\frac{1}{{}_t E_x}\big(\bar P(\bar A_{x:\overline n|})\bar a_{x:\overline t|}-\bar A_{x:\overline t|}^1\big).[[/math]]

(Hint: You may set the "initial reserves" in (a) to be zero using an appropriate value of [math] s[/math])

Show Proof

First, we have by definition

[[math]]_s\bar V(\bar A_{x:\overline n|})=\bar A_{x+s:\overline {n-s}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline {n-s}|}.[[/math]]

Applying the recursion relations, we then get

[[math]] \begin{align} && _s\bar V(\bar A_{x:\overline n|})&=\bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\;\bar A_{x+s+t:\overline{n-s-t}|} -\bar P(\bar A_{x:\overline n|})\left(\bar a_{x+s:\overline t|}+{}_t E_{x+s}\;\bar a_{x+s+t:\overline{n-s-t}|}\right)\\ &\Rightarrow& _s\bar V(\bar A_{x:\overline n|})+\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline t|}&= \bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\left(\bar A_{x+{\color{blue}s+t}:\overline{n-({\color{blue}s+t})}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+{\color{blue}s+t}:\overline{n-({\color{blue}s+t})}|}\right)\\ &\Rightarrow& _s\bar V(\bar A_{x:\overline n|})+\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline t|}&= \bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\;_{\color{blue}s+t}\bar V(\bar A_{x:\overline n|}), \end{align} [[/math]]

as desired.

■

Proposition

By recursion relations, we have

[[math]] \begin{align} \bar A_{x+s:\overline{n-s}|}&=\bar A_{x+s:\overline t|}^1+{}_t E_{x+s}\;\bar A_{x+s+t:\overline{n-s-t}|},\text{ and }\\ \bar a_{x+s:\overline{n-s}|}&=\bar a_{x+s:\overline t|}+{}_t E_{x+s}\;\bar a_{x+s+t:\overline{n-s-t}|}.\\ \end{align} [[/math]]

([math]n-s-t\gt0[/math], and [math]n-s\gt0[/math])

(a) Show that [math]_s\bar V(\bar A_{x:\overline n|})+\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline t|}=\bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\;_{s+t}\bar V(\bar A_{x:\overline n|})[/math] (for every [math]n,s,t[/math] satisfying the above constraints).

An interpretation to the formula in (a) is that the LHS is the APV of the insurer's resources (initial reserves from the policy plus the future premiums), and the RHS is the APV of the insurer's obligations (future benefits plus the ending reserves for the policy). This is also a recursive relation for reserve.

(b) Using the formula in (a), or otherwise, prove the retrospective formula:

[[math]]_t\bar V(\bar A_{x:\overline n|})=\frac{1}{{}_t E_x}\big(\bar P(\bar A_{x:\overline n|})\bar a_{x:\overline t|}-\bar A_{x:\overline t|}^1\big).[[/math]]

(Hint: You may set the "initial reserves" in (a) to be zero using an appropriate value of [math] s[/math])

It suggests that the (prospective) reserve at time [math] t[/math] is equal to the AAV of the past premiums received (unfulfilled obligations) minus the AAV of the past benefits paid (fulfilled obligations), which is called the retrospective reserve in this case. Actually, such equality applies to other types of policies also, and we will prove it later.

Show Proof

First, we have by definition

[[math]]_s\bar V(\bar A_{x:\overline n|})=\bar A_{x+s:\overline {n-s}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline {n-s}|}.[[/math]]

Applying the recursion relations, we then get

[[math]] \begin{align} && _s\bar V(\bar A_{x:\overline n|})&=\bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\;\bar A_{x+s+t:\overline{n-s-t}|} -\bar P(\bar A_{x:\overline n|})\left(\bar a_{x+s:\overline t|}+{}_t E_{x+s}\;\bar a_{x+s+t:\overline{n-s-t}|}\right)\\ &\Rightarrow& _s\bar V(\bar A_{x:\overline n|})+\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline t|}&= \bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\left(\bar A_{x+{\color{blue}s+t}:\overline{n-({\color{blue}s+t})}|}-\bar P(\bar A_{x:\overline n|})\bar a_{x+{\color{blue}s+t}:\overline{n-({\color{blue}s+t})}|}\right)\\ &\Rightarrow& _s\bar V(\bar A_{x:\overline n|})+\bar P(\bar A_{x:\overline n|})\bar a_{x+s:\overline t|}&= \bar A_{x+s:\overline t|}^{\;\;1}+{}_t E_{x+s}\;_{\color{blue}s+t}\bar V(\bar A_{x:\overline n|}), \end{align} [[/math]]

as desired.

■

• The expression [math]\frac{\bar A_{x:\overline t|}^1}{{}_t E_x}[/math] is called the accumulation cost of insurance, and is denoted by [math]{}_t \bar k_x[/math]. Using this notation, we can rewrite the retrospective formula as

[[math]]_t\bar V(\bar A_{x:\overline n|})=\frac{1}{{}_t E_x}\big(\bar P(\bar A_{x:\overline n|})\bar a_{x:\overline t|}\big)-{}_t \bar k_x[[/math]]

• Actually, since [math]\bar s_{x:\overline t|}=\frac{\bar a_{x:\overline t|}}{{}_t E_x}[/math], we can further rewrite the formula as

[[math]]_t\bar V(\bar A_{x:\overline n|})=\bar P(\bar A_{x:\overline n|})\bar s_{x:\overline t|}-{}_t \bar k_x.[[/math]]

• In discrete case, [math]\frac{A_{x:\overline t|}^1}{{}_t E_x}[/math] is also called the accumulation cost of insurance, and is denoted by [math]{}_t k_x[/math].

Indeed, the equality of prospective reserve and retrospective reserve under such conditions also applies to other types of policies.

Proposition (Equality of prospective and retrospective reserve)

Under the conditions

1. premiums are determined using equivalence principle
2. same basis (for interest, mortality, and expenses) is used for calculating prospective reserve, retrospective reserve, and premiums,

the prospective (gross premium) reserve and the retrospective (gross premium) reserve (AAV of premiums received minus AAV of benefits and expenses paid) at time [math] t[/math] are equal.

Show Proof

Let [math]L_{0,t}[/math] be the sum of p.v.r.v. of benefits and expenses from time 0 to [math] t[/math] less the p.v.r.v. of future premiums from time 0 to [math] t[/math]. Then, the retrospective reserve is symbolically

[[math]]\frac{-\mathbb E[L_{0,t}]}{{}_t E_x}.[[/math]]

Also, the insurer's loss at policy issue is

[[math]]L_0=L_{0,t}+v^t L_t^g\mathbf 1\{t_x \gt t\}.[[/math]]

The equality holds since the same basis is used for all three random variables (the basis for [math]L_0[/math] is the same as the basis for premiums because they are related by equivalence principle).

Then, by equivalence principle, we have

[[math]] \begin{align} && \mathbb E[L_0]&=0\\ &\Rightarrow& \mathbb E[L_{0,t}]+v^t\mathbb E[L_t^g\mathbf 1\{t_x \gt t\}]&=0\\ &\Rightarrow&\mathbb E[L_{0,t}]&=-v^t\mathbb E[L_t^g\mathbf 1\{t_x \gt t\}]\\ &\Rightarrow&\mathbb E[L_{0,t}]&=-v^t\mathbb P(t_x \gt t)\mathbb E[L_t^g|t_x \gt t]&(\text{result in probability})\\ &\Rightarrow&\mathbb E[L_{0,t}]&=-\underbrace{v^t{}_t p_x}_{{}_t E_x}\mathbb E[L_t^g|t_x \gt t]\\ &\Rightarrow &\underbrace{\frac{-\mathbb E[L_{0,t}]}{{}_t E_x}}_{\text{retrospective}}&=\underbrace{\mathbb E[L_t^g|t_x \gt t]}_{\text{prospective}}. \\ \end{align} [[/math]]

■

• In practice, the conditions are unlikely to be satisfied. For example, at time [math] t[/math], the insurance company may have some updated information about the policyholder, through possibly underwriting, and therefore update the mortality basis for the policyholder. In this case, it is wrong to write [math]L_0=L_{0,t}+v^t L_t^g\mathbf 1\{t_x \gt t\}[/math] since [math]L_0[/math] is determined from the basis at time 0, while [math]L_t^g[/math] is determined from the updated basis at time [math] t[/math].

• The interest basis and the expense basis may also vary from time to time.

• Also, even at the same time point, the basis used for premiums can be different from the basis used for the reserves due to regulations in practice.
• But, under our assumptions here, unless stated otherwise, the conditions are satisfied.
• Notice that this equality does not have requirement on the policy itself. Thus, it applies to both continuous and discrete cases.

Example

It is given that

• [math]_t \bar k_x=0.2[/math];
• [math]_t E_x=0.5[/math];
• [math]\bar A_{x+t}=0.6[/math];
• the force of interest is a constant, [math]\delta[/math].

Calculate [math]_t\bar V(\bar A_x)[/math] using (a) prospective method; (b) retrospective formula.

Solution.

(a) First, we have

[[math]] _t\bar V(\bar A_x)=\bar A_{x+t}-\bar P(\bar A_{x})\bar a_{x+t}=\bar A_{x+t}-\frac{\bar P(\bar A_{x})}{\delta}(1-\bar A_{x+t}). [[/math]]

Since [math]\bar A_{x+t}[/math] is given, it remains to calculate [math]\frac{\bar P(\bar A_x)}{\delta}[/math]:

[[math]] \frac{\bar P(\bar A_x)}{\delta} =\frac{\bar A_x}{\bar a_x\delta} =\frac{\bar A_x}{1-\bar A_x}. [[/math]]

Thus, it now remains to calculate [math]\bar A_x[/math]. Using [math]_t\bar k_x[/math], we have [math]\bar A_{x:\overline t|}^1={}_t E_x\;_t\bar k_x=0.5(0.2)=0.1[/math]. Then, by recursion relation,

[[math]]\bar A_x=\bar A_{x:\overline t|}^1+{}_t E_x\bar A_{x+t}=0.1+(0.5)(0.6)=0.4.[[/math]]

It follows that

[[math]]_t\bar V(\bar A_x)=0.6-\frac{0.4}{1-0.4}(1-0.6)\approx 0.333.[[/math]]

(b) Using the retrospective formula, we have

[[math]]_t\bar V(\bar A_x)=\frac{1}{{}_t E_x}(\bar P(\bar A_x)\bar a_{x:\overline t|})-{}_t\bar k_x =\frac{1}{{}_t E_x}\left(\bar P(\bar A_x)\cdot\frac{1-\bar A_{x:\overline t|}}{\delta}\right)-{}_t\bar k_x [[/math]]

From (a), we have

• [math]\bar A_x=0.4[/math]
• [math]\frac{\bar P(\bar A_x)}{\delta}=\frac{0.4}{1-0.4}[/math]

Also, [math]\bar A_{x:\overline t|}=\bar A_{x:\overline t|}^{\;\;1}+{}_t E_x=0.1+0.5=0.6[/math]. Thus, we have

[[math]] _t\bar V(\bar A_x) =\frac{1}{0.5}\left(\frac{0.4}{1-0.4}\cdot(1-0.6)\right)-0.2 \approx 0.333. [[/math]]

• Notice that the retrospective reserve (answer for (b)) is the same as the prospective reserve (answer for (a)). This is expected since the conditions for their equality are satisfied in this example.

Fully discrete reserves

Similar to the case for continuous reserves, we often use the "alternative method" to calculate the discrete reserves (i.e., [math]\mathbb E[L^n_k|K_x\ge k][/math]):

Proposition

The conditional distribution of [math]K_x-k[/math] given that [math]K_x\ge k[/math] is the same as the unconditional distribution of [math]K_{x+k}[/math] ([math]k[/math] is a nonnegative integer).

Show Proof

Consider the survival functions of the two distributions. First, for the conditional distribution of [math]K_x-k[/math] given that [math]K_x\ge k[/math],

[[math]]\mathbb P(K_x-k\ge m|K_x\ge k)=\frac{\mathbb P(K_x\ge k+m)}{\mathbb P(K_x\ge k)} =\frac{\mathbb P(T_x\ge \lfloor k+m\rfloor)}{\mathbb P(T_x\ge \lfloor k\rfloor)} =\frac{\mathbb P(T_x\ge k+m)}{\mathbb P(T_x\ge k)} .[[/math]]

([math]m[/math] and [math]k[/math] are integers) For the unconditional distribution of [math]K_{x+k}[/math],

[[math]]\mathbb P(K_{x+k}\ge m') =\mathbb P(T_{x+k}\ge\lfloor m'\rfloor) =\mathbb P(T_{x+k}\ge m') =\mathbb P(T_x\ge k+m'|T_x\ge k) =\frac{\mathbb P(T_x\ge k+m')}{\mathbb P(T_x\ge k)}. [[/math]]

([math]m'[/math] and [math]k[/math] are integers) These show that the two distributions are the same.

■

Similarly, this result gives us an alternative and often more convenient method to calculate the conditional expectation [math]\mathbb E[L^n_k|K_x\ge k][/math]:

1. replace all "[math]K_x-k[/math]" by "[math]K_{x+k}[/math]" and remove the condition "[math]K_x\ge k[/math]"
2. calculate the unconditional expectation, which equals the value of conditional expectation since the distributions involved are the same

Let us consider the whole life insurance first. We have

[[math]]L^n_k=v^{K-k+1}-P_x\ddot a_{\overline{K-k+1}|}.[[/math]]

Hence, the reserve, denoted by [math]_k V_x[/math], is

[[math]]\mathbb E[L^n_k|K_x\ge k] =\mathbb E[v^{{\color{blue}K_x-k}+1}-P_x\ddot a_{\overline{{\color{blue}K_x-k}+1}|}{\color{blue}|K_x\ge k}] =\mathbb E[v^{K_{x+k}+1}]-P_x\mathbb E[\ddot a_{\overline{K_{x+k}+1}|}] =A_{x+k}-P_x\ddot a_{x+k}. [[/math]]

Proposition

Show that

[[math]]\operatorname{Var}(L^n_k|K_x\ge k)=\left(1+\frac{P_x}{d}\right)^2\big({}^2 A_{x+k}-(A_{x+k})^2\big).[[/math]]

(Hint: notice that [math]^2 A_{x+k}-(A_{x+k})^2[/math] is the variance of the p.v.r.v. for the discrete whole life insurance with unit benefit, issued to [math](x+k)[/math])

Show Proof

First, we have

[[math]]L^n_k=v^{K-k+1}-P_x\ddot a_{\overline{K-k+1}|}=v^{K-k+1}-P_x\left(\frac{1-v^{K-k+1}}{d}\right)=\left(1+\frac{P_x}{d}\right)v^{K-k+1}-\frac{P_x}{d}.[[/math]]

Thus,

[[math]] \operatorname{Var}(L^n_k|K_x\ge k) =\left(1+\frac{P_x}{d}\right)^2\operatorname{Var}(v^{K_x-k+1}|K_x\ge k) =\left(1+\frac{P_x}{d}\right)^2\operatorname{Var}(v^{K_{x+k}+1}) =\left(1+\frac{P_x}{d}\right)^2\big({}^2 A_{x+k}-(A_{x+k})^2\big) [[/math]]

■

We can develop formulas for other types of policies, and a summary of the formulas for reserves is tabulated below.

Summary

Insurance product name	net premium reserve at time [math]k[/math]
Whole life insurance	[math]_k V_x=A_{x+k}-P_x\ddot a_{x+k}[/math]
[math]n[/math]-year term life insurance	[math]_k V_{x:\overline n|}^1=\begin{cases} A_{x+k:\overline{n-k}|}^1- P( A_{x:\overline n|}^1) \ddot a_{x+k:\overline{n-k}|},& k \lt n;\\ 0,& k=n.\end{cases}[/math]
[math]n[/math]-year endowment insurance	[math]_k V_{x:\overline n|}=\begin{cases} A_{x+k:\overline{n-k}|}- P( A_{x:\overline n|}) \ddot a_{x+k:\overline{n-k}|},& k \lt n;\\ 1,&k=n.\end{cases}[/math]
[math] h[/math]-payment years whole life insurance	[math]^h_k V_x=\begin{cases} A_{x+k}-{}_h P( A_x) \ddot a_{x+k:\overline{h-k}|},& k \lt h;\\ A_{x+k},& k\ge h.\end{cases}[/math]
[math] h[/math]-payment years [math]n[/math]-year term life insurance ([math] h \lt n[/math])	[math]^h_k V_{x:\overline n|}^1=\begin{cases} A_{x+k:\overline{n-k}|}^{1}-{}_h P( A_{x:\overline n|}^1) \ddot a_{x+k:\overline{h-k}|},& k \lt h;\\ A_{x+k:\overline{n-k}|}^1, & h\le k \lt n;\\ 0,& k=n.\end{cases}[/math]
[math] h[/math]-payment years [math]n[/math]-year endowment insurance ([math] h \lt n[/math])	[math]^h_k V_{x:\overline n|}=\begin{cases} A_{x+k:\overline{n-k}|}-{}_h P( A_{x:\overline n|}) \ddot a_{x+k:\overline{h-k}|},& k \lt h;\\ A_{x+k:\overline{n-k}|}, & h\le k \lt n;\\ 1,& k=n.\end{cases}[/math]
[math]n[/math]-year pure endowment	[math]_k V_{x:\overline n|}^{\;\;1}=\begin{cases}{}_{n-k}E_{x+k}- P({}_n E_x) \ddot a_{x+k:\overline{n-k}|},& k \lt n;\\ 1,&k=n.\end{cases}[/math]
[math]n[/math]-year deferred whole life annuity	[math]_k V({}_{n|} \ddot a_x)=\begin{cases}{}_{n-k|} \ddot a_{x+k}- P({}_{n|} \ddot a_x) \ddot a_{x+t:\overline{n-k}|},& k\le n;\\ \ddot a_{x+k},& k \gt n.\end{cases}[/math]

• For the [math]n[/math]-year term life insurance, the net premium reserve at time [math]n[/math] is 0 since there are no future premiums or benefits (the last premium is made at time [math]n-1[/math], and since the condition is that the life survives for [math]n[/math] years, no death benefits are made)
• For the [math]n[/math]-year endowment insurance, there is only survival benefit of 1 made at time [math]n[/math].

Example

For a discrete whole life insurance with unit benefit issued to a life aged 30, it is given that

• [math]i=0.06[/math]
• [math]A_{[30]}=0.07316[/math]
• [math]A_{[40]}=0.12296[/math]
• [math]A_{30}=0.07328[/math]
• [math]A_{40}=0.12313[/math]
• the select period is 2 years

Calculate the policy value of the insurance at time 10 with selection age 30, [math]_{10}V_{[30]}[/math].

Solution.

First, we have [math]d=\frac{i}{1+i}=\frac{0.06}{1.06}\approx 0.0566[/math]. Thus, the policy value is

[[math]]A_{[30]+10}-P_{[30]}\ddot a_{[30]+10} =A_{40}-\frac{A_{[30]}}{\ddot a_{[30]}}\cdot\ddot a_{40} =0.12313-\frac{0.07316}{(1-0.07316)/0.0566}\cdot\frac{1-0.12313}{0.0566} \approx 0.053914. [[/math]]

Example

Write down an expression for the (a) prospective; (b) retrospective net premium reserve at time 20 for a 35-year endowment insurance issued a life aged 30.

Solution.

(a) [math]A_{50:\overline{15}|}-P_{30:\overline {35}|}\ddot a_{50:\overline{15}|}[/math].

(b) [math]\frac{1}{{}_{20}E_{30}}(P_{30:\overline{35}|}\ddot a_{30:\overline{20}|})-{}_{20} k_{30}[/math].

• [math]_{20}k_{30}=\frac{A_{30:\overline{20}|}^{1}}{{}_{20}E_{30}}[/math] is the accumulation cost of insurance.
• The expression in (b) can also be [math]P_{30:\overline{35}|}\ddot s_{30:\overline{20}|}-{}_{20} k_{30}[/math], since [math]\ddot s_{30:\overline{20}|}=\frac{\ddot a_{30:\overline{20}|}}{{}_{20} E_{30}}[/math] .

We can develop a recursion relation for discrete insurances:

Proposition

Let [math]P_t[/math] be the premium payable at time [math] t[/math], [math]b_t[/math] be the death benefit paid at time [math] t[/math] if death occurs in the [math] t[/math] th year, and [math]_k V[/math] be the net premium policy value of a discrete insurance at time [math]k[/math]. Then, we have

[[math]]_k V=vp_{x+k}\;_{k+1}V+vq_{x+k}b_{k+1}-P_k.[[/math]]

• The recursion formula here is backward, i.e., it expresses [math]_k V[/math] in terms of [math]_{k+1}V[/math]. But sometimes, forward recursion is needed, and thus a forward recursion formula is more convenient. We can rewrite the above formula as a forward recursion formula:

[[math]]_{k+1}V=\frac{_k V+P_k-vq_{x+k}b_{k+1}}{vp_{x+k}}.[[/math]]

Show Proof

Split the prospective net loss at time [math]k[/math]: [math]L^n_k[/math], into two parts (i.e., [math]L^n_k[/math] is the sum of these two parts):

1. p.v.r.v. of benefits at time [math]k+1[/math] minus p.v.r.v. of premiums at time [math]k[/math] (denoted by [math]A[/math])
2. p.v.r.v. of benefits at time [math]k+2,k+3,\dotsc[/math] minus p.v.r.v. of premiums at time [math]k+1,k+2,\dotsc[/math] (denoted by [math]B[/math])

Thus, we have

[[math]]L^n_k=A+B.[[/math]]

Taking expectation, we have

[[math]]_k V=\mathbb E[A]+\mathbb E[B].[[/math]]

First, [math]\mathbb E[A]=vq_{x+k}b_{k+1}-P_k[/math]. Second, to be more explicit about the condition incorporated in [math]L^n_k[/math], we can write [math]\mathbb E[B|K_x\ge k][/math] in place of [math]\mathbb E[B][/math]:

[[math]] \begin{align} \mathbb E[B|K_x\ge k]&=\frac{\mathbb E[B\mathbf 1\{K_x\ge k\}]}{\mathbb P(K_x\ge k)}\\ &=\frac{\mathbb E[B\mathbf 1\{K_x\ge k+1\}]}{\mathbb P(K_x\ge k)}&(\text{the first term in }B\text{ is at time }k+1, \text{so the change does not affect the expectation})\\ &=\frac{\mathbb E[B\mathbf 1\{K_x\ge k+1\}]}{\mathbb P(K_x\ge k+1)}\cdot\frac{\mathbb P(K_x\ge k+1)}{\mathbb P(K_x\ge k)}\\ &=\mathbb E[B|K_x\ge k+1]\cdot\mathbb P(K_x\ge k+1|K_x\ge k)\\ &=p_{x+k}\mathbb E[B|K_x\ge k+1]\\ &=p_{x+k}\mathbb E[vL^n_{k+1}|K_x\ge k+1]\\ &=vp_{x+k}\mathbb E[L^n_{k+1}|K_x\ge k+1]\\ &=vp_{x+k}\;_{k+1}V.\\ \end{align} [[/math]]

The result follows.

■

To explain the proof more intuitively, consider the following diagram:

• Consider the policy value at time [math]k[/math]: [math]_k V[/math]. It is the APV of future benefits minus the APV of future premiums.
• We can split the future benefits and future premiums into two parts:

1. benefit at time [math]k+1[/math] and premium at time [math]k[/math]
2. benefits at time [math]k+2,k+3,\dotsc[/math] and premiums at [math]k+1,k+2,\dotsc[/math]

• For the second part, they are incorporated by the policy value at time [math]k+1[/math] [math]_{k+1}V[/math]. But of course the policy value at time [math]k+1[/math] gives the value at time [math]k+1[/math], but not the value at time [math]k[/math] (which is what we want). Hence, we need to actuarially discount [math]_{k+1}V[/math] back to time [math]k[/math] (multiply [math]vp_x[/math]).
• To incorporate the first part, we add the APV of death benefit at time [math]k+1[/math] ([math]vb_{k+1}q_{x+k}[/math]), and then subtract the premium at time [math]k[/math] ([math]P_k[/math]).

Example

A discrete whole life insurance of 1,000,000 is issued to a life aged [math] x[/math] with premiums payable at the beginning of the first 20 years after policy issue. It is given that

• [math]i=0.05[/math]
• the policy value at time 18 is [math]_{18}V=351200[/math].
• [math]q_{x+18}=0.012[/math]
• [math]q_{x+19}=0.014[/math]
• [math]q_{x+20}=0.016[/math]
• the annual premium is 22100.

Calculate the policy value at time 21, [math]_{21}V[/math].

Solution.

By the recursion relation, we have

[[math]] \begin{align} &&_{19}V&=\frac{351200+22100-(1.05)^{-1}(0.012)(1000000)}{(1.05)^{-1}(1-0.012)}\approx 384579.96\\ &\Rightarrow&_{20}V&\approx\frac{384579.96+22100-(1.05)^{-1}(0.014)(1000000)}{(1.05)^{-1}(1-0.014)}\approx 418878.25\\ &\Rightarrow&_{21}V&\approx\frac{418878.25+22100-(1.05)^{-1}(0.016)(1000000)}{(1.05)^{-1}(1-0.016)}\approx 454295.90.\\ \end{align} [[/math]]

Example

A 20-year discrete endowment insurance with death benefit of 1000 and survival benefit of 5000 is issued to a life aged 30. It is given that

• [math]i=0.04[/math]
• [math]q_{48}=0.009[/math]
• [math]q_{49}=0.01[/math]
• premiums are paid at the beginning of each year, with amount [math]250+k[/math] at time [math]k[/math].

Calculate the policy value at time 18, [math]_{18} V[/math].

Solution.

First, notice that the policy value at time 20 is simply the amount of survival benefit, i.e., [math]_{20}V=5000[/math]. Then, we can use backward recursion to calculate [math]_{18}V[/math]:

[[math]] \begin{align} && _{19}V&=(1.04)^{-1}(1-0.01)(5000)+(1.04)^{-1}(0.01)(1000)-(250+19)\approx 4500.231 \\ &\Rightarrow& _{18}V&\approx (1.04)^{-1}(1-0.009)(4500.231)+(1.04)^{-1}(0.009)(1000)-(250+18)\approx 4028.855. \end{align} [[/math]]

General References

• Wikibooks contributors. "Fundamental_Actuarial_Mathematics/Premium_and_Policy_Value_Calculation_for_Long-Term_Insurance_Coverages". Wikibooks. Wikibooks. Retrieved 14 January 2024.