guide:A112646061

Insurances payable at the moment of death

In this section, we will model some types of insurances payable at the moment of death, which is associated with the random variable [math]T_x[/math], and all insurances mentioned in this section are payable at the moment of death unless stated otherwise. In practice, the insurance is not payable at the moment of death, since it is infeasible. However, with this theoretical assumption, some calculations can be more convenient.

Before modeling the insurances, we need to introduce a fundamental random variable: present-value random variable.

Definition (Present-value random variable)

The present-value random variable [math]Z=b_Tv_T[/math], in which [math]b_T[/math] and [math]v_T[/math] are benefit function and discount function of [math]T[/math] ([math]T=T_x[/math]), respectively.

In the models discussed in this section, they differ in only the definitions of [math]b_T[/math] and [math]v_T[/math], and the model for [math]n[/math]-year term life insurance is the basic one, and other models are just some modifications on this model. Because of this, it is important to understand the [math]n[/math]-year term life insurance model clearly.

We often want to know the expected value of the present-value random variable so that we would somehow predict how much benefit will be paid, in the present value term. As a result, we have a special name for such expected value:

Definition (Actuarial present value)

The actuarial present value (APV) is [math]\mathbb E[Z][/math], the expected value of the present-value random variable.

For simplicity, we will assume the benefit amount is one in the following models unless otherwise specified. If we want to change the benefit amount to other values, then we can just multiply it accordingly. For the insurances for which the benefit amount is varying, we can also change the benefit amounts "together" through appropriate multiplication.

n-year term life insurance

Definition ([math]n[/math]-year term life insurnace)

A [math]n[/math]-year term life insurance provides a payment if the insured dies within the [math]n[/math]-year term, starting from the time of policy issue, and does not provide any payment otherwise.

For [math]n[/math]-year term life insurance, we have

[[math]] b_T=\begin{cases}1,& T\le n;\\ 0,&T \gt n,\end{cases} [[/math]]

and [math] v_T=v^T,\quad T\ge 0 [/math] ([math]v[/math] is the discount factor which is [math]\frac{1}{1+i}[/math], in which [math]i[/math] is the (annual) effective interest rate). Hence,

[[math]]Z=\begin{cases}v^T,&T\le n\\ 0,&T \gt n\end{cases}[[/math]]

.

In this case, the actuarial present value, denoted by [math]\bar A^1_{x:\overline n|}[/math], is

[[math]]\mathbb E[Z]=\int_{0}^{n}v^tf_x(t)\,dt=\int_{0}^{n}v^t{}_tp_x \mu_{x+t}\,dt.[[/math]]

Here, we use the result [math]f_x(t)={}_tp_x\mu_{x+t}[/math] from the mortality models chapter.

The notation for the APV may seem weird at first, but after knowing the meaning of each of symbols involved, the notation will make more sense. Indeed, the other notations for the APV in other types of life insurance are constructed in a similar way. The meaning of the symbols involved is as follows:

• [math]A[/math] means "a life insurance".
• [math]\bar{}[/math] (on top of [math]A[/math]) means this APV is "in a continuous manner" (since the benefit is paid at the moment of death, the APV is "somehow continuous").
• [math]x[/math] means the insured is aged [math]x[/math] at the time of policy issue.
• [math]:\overline n|[/math] means the term of the life insurance is [math]n[/math] years.
• [math]1[/math] on top of [math]x[/math] (and "before" [math]:\overline n|[/math]) means the benefit of amount 1 is paid to the insured (aged [math]x[/math] at the time of policy issue), if he dies before [math]n[/math] years passed from the time of policy issue.

Example

Consider a 10-year term life insurance with benefit of 1, issued to a life aged 60. Suppose the pdf of [math]T_x[/math] is [math]f_x(t)=\frac{1}{100},\quad 0\le t\le 100[/math], and the annual force of interest (the force of interest in the following will be annual unless otherwise specified) is (a constant) [math]\delta=0.05[/math]. Then,

• The APV is denoted by [math]\bar A^1_{60:\overline {10|}}[/math]
• The discount function is [math]v^t=e^{-\delta t}=e^{-0.05 t}[/math]
• The value of APV is thus [math]\int_{0}^{10}e^{-0.05 t}\cdot\frac{1}{100}\,dt=\frac{1}{100(-0.05)}[e^{-0.05t}]_0^{10}=-\frac{1}{5}(e^{-0.5}-1)=0.0787[/math].

• This means it is "expected" that benefit with present value of 0.0787 will be paid for each insurance issued.
• It may be intuitive that the insurance should also cost 0.0787 when the life aged 60 purchases it immediately after reaching age 60. However, this may not necessarily be the case, since there is also some cost for handling the purchase of insurance, and also the insurance company selling it will also want to make some profits. As a result, the resultant cost may be higher than this APV.

• If the force of interest is not constant, the calculation will be more complicated.
• Thus, for simplicity, the force of interest will be assumed to be constant unless otherwise specified in the following.

Example

Amy, aged 30, purchases a 20-year term life insurance with benefit 1,000,000 from XYZ life insurance company. Suppose the survival distribution for Amy at aged [math]x[/math] is [math]S_x(t)=e^{-0.05 t}[/math], and the force of interest is 7% (constant).

(a) What is the expression for the APV of this life insurance?

(b) Suppose the premium of this policy is the APV of this life insurance plus 1000. Calculate the premium of this policy.

Solution:

(a) [math]1000000\bar A^1_{30:\overline{20}|}[/math].

(b) First, given the survival function, we know that [math]_t p_{30}=e^{-0.05 t}[/math]. Also, the force of mortality is [math]\mu=0.05[/math] which is constant (so we are actually assuming constant force of mortality). The premium is

[[math]]1000000\bar A^1_{30:\overline{20}|}+1000=1000000\int_{0}^{20}e^{-0.07 t}{}_t p_{30}\mu_{30+t}\,dt+1000 =50000\int_{0}^{20}e^{-0.12 t}\,dt+1000 =\frac{50000}{-0.12}[e^{-0.12 t}]_0^{20}+1000 \approx 379867.52. [[/math]]

Whole life insurance

For whole life insurance, it can be interpreted as a "[math]\infty[/math]-year term life insurance", and so payment will be eventually provided since no one lives for eternity. To be more precise, its definition is as follows:

Definition (Whole life insurance)

A whole life insurance provides a payment following the death of the insured (at any time in the future).

For whole life insurance, we have [math]b_T=1,\quad t\ge 0[/math], [math]v_T=v^T,\quad T\ge 0[/math], and thus [math]Z=v^T,\quad t\ge 0[/math]. The APV, denoted by [math]\bar A_x[/math], is [math]\int_{0}^{\infty}v^t{}_tp_x\mu_{x+t}\,dt[/math].

In the notation, we omit the "[math]1[/math]" and "[math]:\overline n|[/math]" appearing in the notation of APV for [math]n[/math]-year term life insurance., since for whole life insurnace, the "term" does not exist (or is "infinite"). Also, the benefit must be paid eventually, and so there is no need to emphasize the benefit payment, unlike above, where the benefit may or may not be paid, depending on how long the insured live.

Example

(Formula of [math]\bar A_x[/math] with constant force of interest and force of mortality) Given the force of interest is [math]\delta[/math] and the force of mortality is [math]\mu[/math], [math]\bar A_x=\frac{\mu}{\mu+\delta}[/math].

Proof

When the force of mortality is [math]\mu[/math],

[[math]]_t p_x=\frac{S_0(x+t)}{S_0(x)}=\frac{e^{-\int_{0}^{x+t}\mu\,ds}}{e^{-\int_{0}^{x}\mu\,ds}}=\frac{e^{-(x+t)\mu}}{e^{-x\mu}}=e^{-\mu t}[[/math]]

. Thus,

[[math]] \begin{aligned} \bar A_x=\int_{0}^{\infty}v^t{}_tp_x\mu_{x+t}\,dt =\int_{0}^{\infty}e^{-\delta t}{}_tp_x(\mu)\,dt &=\mu\int_{0}^{\infty}e^{-\delta t}e^{-\mu t}\,dt \\ &=\mu\int_{0}^{\infty}e^{(-\delta + \mu)t} \,dt \\ &=\frac{\mu}{-(\delta + \mu)}[e^{(-\delta + \mu)t}]_0^{\infty} \\ &=\frac{\mu}{-(\delta +\mu)}(0-1) \\ &=\frac{\mu}{\mu+\delta}. \end{aligned} [[/math]]

• We can see that when [math]\delta=0[/math], then [math]\bar A_x=1[/math] for each nonzero [math]\mu[/math] ([math]\mu[/math] should not be zero, or else the life will never die (the survival function is always equal to 1)).
• This is intuitive, since for whole life insurance, the benefit must be paid eventually (since the life will die eventually), and if the interest rate is always zero, then the present value of the benefit is always one. Thus, its expected value is also one.

[math]n[/math]-year pure endowment

The [math]n[/math]-year pure endowment is similar to the [math]n[/math]-year term life insurance in some sense, but the death benefit in the [math]n[/math]-year term life insurance is replaced by the survival benefit (i.e. benefit is paid when the insured survives for, but not dies within, [math]n[/math] years) in the [math]n[/math]-year pure endowment.

Definition ([math]n[/math]-year pure endowment)

The [math]n[/math]-year pure endowment provides a payment at the end of the [math]n[/math] years when the insured survives for [math]n[/math] years from the time of policy issue, and does not provide any payment otherwise.

For [math]n[/math]-year pure endowment, we have

[[math]]b_T=\begin{cases}0,&T\le n;\\ 1,&T \gt n\end{cases}[[/math]]

, [math]v_T=v^n,\quad T\ge 0[/math] . Hence,

[[math]]Z=\begin{cases}0,&T \le n;\\ v^n,&T \gt n.\end{cases}[[/math]]

. The APV, denoted by [math]A^{\;\;1}_{x:\overline n|}[/math], is

[[math]]\int_{n}^{\infty}v^nf_x(t)\,dt=v^n\int_{n}^{\infty}f_x(t)\,dt=v^n\mathbb P(T_x \gt n)=v^n{}_np_x[[/math]]

.

Since this notation may look a bit clumsy, there is an alternative notation: [math]_n E_x[/math].

In the notation, there is no [math]\bar{}[/math] on top of [math]A[/math], since the benefit is paid at a fixed timing, so the APV is "not quite in a continuous manner". Also, the "[math]1[/math]" is placed on top of "[math]:\overline n|[/math]", since the benefit (if exists) is paid at the end of [math]n[/math]th year (or time [math]n[/math]).

[math]n[/math]-year endowment insurance

The [math]n[/math]-year endowment insurance is not purely endowment. Instead, it is a mixture between [math]n[/math]-year term life insurance and [math]n[/math]-year endowment. That is, both death and survival benefits exist. Because of this, this type of insurance is similar to to whole life insurance, in the sense that benefit must be paid.

Definition ([math]n[/math]-year endowment insurance)

A [math]n[/math]-year endowment insurance provides an payment either following the death of the insured when the insured dies within [math]n[/math] years, or at the end of [math]n[/math] years when the insured survives for [math]n[/math] years.

For [math]n[/math]-year endowment insurance, we have

[[math]]b_T=1,\quad T\ge 0[[/math]]

,

[[math]]v_T=\begin{cases}v^T,&T\le n;\\ v^n,&T \gt n\end{cases}[[/math]]

, and thus

[[math]]Z=\begin{cases}v^T,& T\le n;\\ v^n,&T \gt n.\end{cases}[[/math]]

We can observe that [math]Z[/math] in this case is the sum of [math]Z[/math] for [math]n[/math]-year term life insurance and [math]Z[/math] for [math]n[/math]-year pure endowment. It follows that the APV is also the sum of the two corresponding APV's, that is, the APV for [math]n[/math]-year endowment insurance is

[[math]]\bar A_{x:\overline n|}^1+A_{x:\overline n|}^{\;\;1}[[/math]]

. Such APV is denoted by [math]\bar A_{x:\overline n|}[/math].

In the notation, we can see that there is a [math]\bar{}[/math] on top of [math]A[/math], since the benefit may be paid at the moment of the death of the insured, so the APV is somehow "in a continuous manner". Also, the "[math]1[/math]" is omitted, with the same reason for whole life insurance: the benefit must be paid.

[math]m[/math]-year deferred whole life insurance

As suggested by its name, this type of insurance is a deferred whole life insurance, i.e. the "start" of the insurance takes place in some years after the policy issue. To be more precise, we have the following definition.

Definition ([math]m[/math]-year deferred whole life insurance)

A [math]m[/math]-year deferred whole life insurance provides a payment when the insured dies at least [math]m[/math] years following policy issue.

For [math]m[/math]-year deferred insurance, we have

[[math]]b_T=\begin{cases}0,&T\le m;\\1,&T \gt m\end{cases}[[/math]]

, [math]v_T=v^T,\quad T\ge 0[/math] , and thus [math]Z=\begin{cases}0,&T\le m;\\v^T,&T \gt m.\end{cases}[/math]

The APV, denoted by [math]_{m|}\bar A_x[/math], is

[[math]]\int_{m}^{\infty}v^t{}_tp_x\mu_{x+t}\,dt[[/math]]

, which is similar to the one for whole life insurance, except that the lower bound of the integral is replaced by [math]m[/math]. The "[math]m|[/math]" in the notation refers to deferring [math]m[/math] years, and since the insurance does not have a term, "[math]:\overline n|[/math]" is omitted.

[math]m[/math]-year deferred [math]n[/math]-year term life insurance

In a similar manner, we can also defer a [math]n[/math]-year term life insurance.

Definition ([math]m[/math]-year deferred [math]n[/math]-year term life insurance)

A [math]m[/math]-year deferred [math]n[/math]-year term life insurance provides a payment when the insured survives for at least [math]m[/math] years following policy issue, and then dies within the coming [math]n[/math] years. The insurance does not provide any payment otherwise.

• That is, the insurance provides payment when the insured dies between [math]m[/math] years and [math]m+n[/math] years following policy issue, and does not provide payment otherwise.

For such insurance, we have

[[math]]b_T=\begin{cases}0,& T\le m;\\1,& m \lt T\le m+n;\\ 0,&T \gt m+n\end{cases}[[/math]]

, [math]v_T=v^T,\quad T\ge 0[/math] .

Thus,

[[math]]Z=\begin{cases}0,& T\le m;\\v^T,&m \lt T\le m+n;\\0,&T \gt m+n.\end{cases}[[/math]]

The APV, denoted by [math]_{m|n}\bar A_x[/math], is [math]\int_{m}^{m+n}v^t{}_tp_x\mu_{x+t}\,dt[/math], which is similar to the one for the [math]n[/math]-year term life insurance, except that both the lower and upper bound is added by [math]m[/math]. In the notation, [math]m|n[/math] means that [math]m[/math] years are deferred and the term is [math]n[/math] years after the deferral, i.e. the insurance lasts for [math]n[/math] years after deferred by [math]m[/math] years. This has the similar meaning as the "[math]m|n[/math]" in "[math]_{m|n}q_x[/math]". Indeed, this is how "[math]m|n[/math]" means in actuarial notations.

Annually increasing whole life insurance

Starting from this section, we will discuss the life insurances for which the benefit amount is varying.

Definition (Annually increasing whole life insurance)

An annually increasing whole life insurance provides payment of 1, 2, ... at the moment of death during the first, second year, etc., respectively.

For the annually increasing whole life insurance, we have

[[math]]b_T=\lfloor T\rfloor +1,\quad T\ge 0[[/math]]

, [math]v_T=v^T,\quad T\ge 0[/math], and thus

[[math]]Z=(\lfloor T\rfloor +1)v^T,\quad T\ge 0[[/math]]

.

Graphically, the value of benefit function [math]b_T[/math] is illustrated below:

The APV, denoted by [math](I\bar A)_x[/math], is

[[math]]\int_{0}^{\infty}(\lfloor t\rfloor+1) v^t{}_tp_x\mu_{x+t}\,dt[[/math]]

. In practice, since it is difficult to integrate "[math]\lfloor t\rfloor[/math]" directly, we will split the integration interval to [math][0,1),[1,2),\dotsc[/math], and multiple integrals are created from this, so that in each of these intervals, [math]\lfloor t\rfloor[/math] equals an integer only. That is, we split the integral like this:

[[math]]\int_{0}^{\infty}(\lfloor t\rfloor+1) v^t{}_tp_x\mu_{x+t}\,dt=\int_{0}^{1}v^t{}_tp_x\mu_{x+t}\,dt+\int_{1}^{2}2v^t{}_tp_x\mu_{x+t}\,dt+\int_{2}^{3}3v^t{}_tp_x\mu_{x+t}\,dt+\dotsb[[/math]]

, which is an infinite sum.

In the notation, the "[math]I[/math]" stands for "increasing" (annually), and we add a bracket so that the notation is not to be confused with [math]I\cdot \bar A_x[/math].

Annually increasing [math]n[/math]-year term life insurance

When we "strip off" the benefit starting from year [math]n+1[/math] and onward, we obtain an annually increasing [math]n[/math]-year insurance. To be more precise, we have the following definition:

Definition (Annually increasing [math]n[/math]-year term life insurance)

An annually increasing [math]n[/math]-year insurance provides payment of 1, 2, ..., [math]n[/math] at the moment of death during the first, second, ..., [math]n[/math]th year respectively.

For this insurance, we have a slightly different benefit function:

[[math]]b_T=\begin{cases}\lfloor T\rfloor+1,& T\le n;\\ 0,& T \gt n\end{cases}[[/math]]

and [math]v_T=v^T,\quad t\ge 0[/math]. Thus,

[[math]]Z=\begin{cases}(\lfloor T\rfloor+1) v^T,& T\le n;\\ 0,& T \gt n.\end{cases}[[/math]]

Graphically, the benefit function looks like:

The APV, denoted by [math](I\bar A)_{x:\overline n|}^1=\int_{0}^{n}(\lfloor t\rfloor+1) v^t{}_tp_x\mu_{x+t}\,dt[/math]. We have "[math]x:\overline n|[/math]" instead of [math]x[/math] in the notation, since this is a term life insurance.

Annually decreasing [math]n[/math]-year term life insurance

Similarly, we have annually decreasing [math]n[/math]-year insurance, but the benefit does not "start" at 1.

Definition (Annually decreasing [math]n[/math]-year term life insurance)

An annually decreasing [math]n[/math]-year term life insurance provides payment of [math]n[/math], [math]n-1[/math], ... , 1 at the moment of death during the first, second year, ..., [math]n[/math]th year.

The benefit function is

[[math]]b_T=\begin{cases}n-\lfloor T\rfloor,& T\le n;\\ 0,& T \gt n.\end{cases}[[/math]]

, the discount function is [math]v_T=v^T,\quad T\ge 0[/math]. Thus,

[[math]]Z=\begin{cases}(n-\lfloor T\rfloor)v^T,& T\le n;\\ 0,& T \gt n.\end{cases}[[/math]]

Graphically, the benefit function looks like:

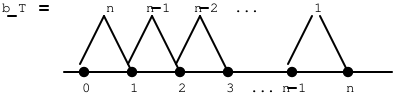
The APV, denoted by [math](D\bar A)_{x:\overline n|}^1[/math], equals [math]\int_{0}^{n}(n-\lfloor t\rfloor)v^t{}_tp_x\mu_{x+t}\,dt[/math]. We have "[math]D[/math]" instead of "[math]I[/math]" in the notation to reflect that the insurance is decreasing rather than increasing.

[math]m[/math]-thly increasing whole life insurance

This is a "more frequent" version of the annually increasing whole life insurance.

Definition ([math]m[/math]-thly increasing whole life insurance)

A [math]m[/math]-thly increasing whole life insurance provides payment of [math]1/m[/math], [math]2/m[/math], ... at the moment of death during the first [math]1/m[/math] of year, second [math]1/m[/math] of year, etc., respectively.

The benefit function is

[[math]]b_T=\frac{\lfloor mT\rfloor+1}{m},\quad T\ge 0[[/math]]

, the discount function is [math]v_T=v^T,\quad T\ge 0[/math], and thus

[[math]]Z=\frac{\lfloor mT\rfloor+1}{m}v^T,\quad T\ge 0[[/math]]

. Graphically, the benefit function looks like:

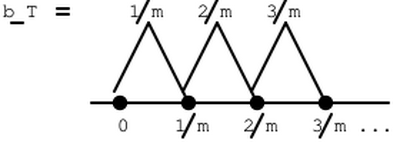
The APV, denoted by [math](I^{(m)}\bar A)_x[/math], is [math]\int_{0}^{\infty}\frac{\lfloor mt\rfloor+1}{m}v^t{}_tp_x\mu_{x+t}\,dt[/math]. The "[math]I^{(m)}[/math]" in the notation reflects that the insurance is increasing [math]m[/math]-thly.

Continuously increasing whole life insurance

We can further increasing the frequency and obtain a "continuous" version of the annually increasing whole life insurance. This version is a bit theoretical, and there may not be such kind of insurance in real life. However, the calculation is simpler using this continuous model, as we will see.

Definition (Continuously increasing whole life insurance)

A continuously increasing whole life insurance provides a payment of [math]t[/math] when the time of death is [math]t[/math].

• The benefit function is [math]b_T=T,\quad T\ge 0[/math], and
• the discount function is [math]v_T=v^T,\quad T\ge 0[/math], and
• thus, [math]Z=Tv^T,\quad T\ge 0[/math].

Its APV, denoted by [math](\bar I\bar A)_x[/math], is [math]\int_{0}^{\infty}tv^t{}_t p_x\mu_{x+t}\,dt[/math]. There is a "[math]\bar{}[/math]" in the notation, since the increase is continuous.

Example: (Alternative formula for APV of continuously increasing whole life insurance)

Show that [math](\bar I\bar A)_x=\int_{0}^{\infty}{}_{s|}\bar A_x\,ds[/math].

Proof

[[math]] \begin{align} (\bar I\bar A)_x&=\int_{0}^{\infty}{\color{darkgreen}t}v^t{}_tp_x\mu_{x+t}\,dt\\ &=\int_{0}^{\infty}v^t{}_tp_x\mu_{x+t}{\color{darkgreen}\int_{0}^{t}\,ds}\,dt\\ &=\int_{0}^{\infty}\int_{0}^{t}v^t{}_tp_x\mu_{x+t}\,ds\,dt&\text{since }v^t{}_tp_x\mu_{x+t}\text{ is independent from }s\\ &=\int_{0}^{\infty}{\color{blue}\int_{s}^{\infty}v^t{}_tp_x\mu_{x+t}\,dt}\,ds&\text{by changing the expression of the integration region}\\ &=\int_{0}^{\infty}{}_{s|}\bar A_x\,ds.\\ \end{align} [[/math]]

[math]m[/math]-thly and continuously increasing [math]n[/math]-year term life insurance

We can modify slightly [math]m[/math]-thly/continuously increasing whole life insurance to [math]m[/math]thly/continuously increasing [math]n[/math]-year term life insurance, which is similar to the previous case for modifying annually increasing whole life insurance to annually increasing [math]n[/math]-year term life insurance.

Despite their definitions are quite similar to the whole life insurance counterparts, we still include their definition as follows for completeness.

Definition ([math]m[/math]-thly increasing [math]n[/math]-year term life insurance)

A [math]m[/math]-thly increasing [math]n[/math]-year term life insurance provides payment of [math]1/m[/math], [math]2/m[/math], ... at the moment of death during the first [math]1/m[/math] of year, second [math]1/m[/math] of year, ... , [math]mn[/math]th [math]1/m[/math] of year respectively.

Definition (Continuously increasing [math]n[/math]-year term life insurance)

A continuously increasing [math]n[/math]-year term life insurance provides a payment of [math]t[/math] when the time of death is [math]t\le n[/math].

For [math]m[/math]-thly increasing [math]n[/math]-year term life insurance, the benefit function is

[[math]]b_T=\begin{cases}\frac{\lfloor mT\rfloor+1}{m},& T\le n;\\0,&T \gt n\end{cases}[[/math]]

, the discount function is

[[math]]v_T=v^T,\quad T\ge 0[[/math]]

, and thus

[[math]]Z=\begin{cases}\frac{\lfloor mT\rfloor+1}{m}v^T,& T\le n;\\0,&T \gt n.\end{cases}[[/math]]

Hence, the APV, denoted by [math](I^{(m)}\bar A)_{x:\overline n|}[/math], is [math]\int_{0}^{n}\frac{\lfloor mt\rfloor+1}{m}v^t{}_t p_x\mu_{x+t}\,dt[/math] ("[math]:\overline n|[/math]" is added to the notation to represent the [math]n[/math]-year term).

For continuously increasing [math]n[/math]-year whole life insurance, the benefit function is

[[math]]b_T=\begin{cases}T,& T\le n;\\ 0,& T \gt n\\\end{cases}[[/math]]

, the discount function is [math]v_T=v^T,\quad T\ge 0[/math]. Thus,

[[math]]Z=\begin{cases}Tv^T,&T\le n;\\0,&T \gt n.\end{cases}[[/math]]

Hence, the APV, denoted by [math](\bar I\bar A)_{x:\overline n|}[/math], is [math]\int_{0}^{n}tv^t{}_t p_x\mu_{x+t}\,dt.[/math]

Of course, we can also have [math]m[/math]-thly/continuously decreasing whole/[math]n[/math]-year term life insurance, and their APV notations are constructed in a similar manner. But, to avoid being repetitive, these insurances are omitted here.

Rule of moments

We have discussed how to calculate the actuarial present value, which is [math]\mathbb E[Z][/math]. How about the higher moments: [math]\mathbb E[Z^2],\mathbb E[Z^3],\dotsc[/math]? We will provide a convenient way (for some type of insurance) below to calculate those moments by using the actuarial present value ([math]\mathbb E[Z][/math]), namely rule of moments.

Theorem (Rule of moments)

For insurances with one payment with unit amount (i.e. payment of 1), then [math]\mathbb E[Z^j][/math] when the force of interest is [math]\delta_t[/math] (a function of [math]t[/math]) equals [math]\mathbb E[Z][/math] when the force of interest is [math]j\delta_t[/math] ([math]j=2,3,\dotsc[/math]) .

Show Proof

We assume the insurance concerned is a whole life insurance of benefit 1. For other types of insurance (that satisfy the conditions, i.e. the benefit is a single payment of 1), we can just change the integration region below suitably, and we will get the same result.

For whole life insurance, with force of interest [math]\delta_t[/math], we have

[[math]]\mathbb E[Z^j]=\mathbb E[v^{jT}]=\int_{0}^{\infty}\big(v^{T}\big)^j{}_tp_x\mu_{x+t}\,dt =\int_{0}^{\infty}\left(e^{-\int_{0}^{t}\delta_s\,ds}\right)^{{\color{darkgreen}j}}{}_tp_x\mu_{x+t}\,dt =\int_{0}^{\infty}e^{-{\color{darkgreen}j}\int_{0}^{t}\delta_s\,ds}{}_tp_x\mu_{x+t}\,dt, =\int_{0}^{\infty}e^{-\int_{0}^{t}{\color{darkgreen}j}\delta_s\,ds}{}_tp_x\mu_{x+t}\,dt, [[/math]]

which is [math]\mathbb E[Z][/math] when the force of interest is [math]j\delta_t[/math].

■

• When the benefit payment is not 1, we cannot apply this rule directly. We can see from the proof that the benefit payment needs to satisfy [math]b^j_T=b_T[/math] for this rule to hold. In this case, we have [math]Z^j=(b_Tv_T)^j=b_Tv_T^j[/math]. When [math]b_T[/math] is nonzero (benefit payment should not be zero for an insurance), when [math]b_T=1[/math], this is satisfied, and for other (positive) values of [math]b_T[/math], this is not satisfied.
• For values of benefit payment other than one, we need to perform some procedure so that we can still use the rule of moments, as follows:

• When the benefit payment is [math]b_T[/math] ([math]\ne 1[/math]), we have [math]\mathbb E[Z^j]=\mathbb E[(b_Tv_T)^j]=b_T^j\mathbb E[v_T^j][/math].
• After that, the random variable inside the expectation is [math]Z[/math] with payment 1, and we can use the rule of moments.

Because of this result, we introduce some special notation for the higher moment: we add a "[math]j[/math]" in the upper left corner of the notation when we are discussing the [math]j[/math]th moment of [math]Z[/math], rather than actuarial present value of the concerning insurance.

For example, we use [math]^2 \bar A_x[/math] to denote [math]\mathbb E[Z^2][/math] in which [math]Z[/math] is the present-value random variable for the whole life insurance .

Example

Recall that [math]\bar A_x=\frac{\mu}{\mu+\delta}[/math] under the constant force of interest [math]\delta[/math] and constant force of mortality [math]\mu[/math]. By rule of moments, we have [math]^2\bar A_x=\frac{\mu}{\mu+2\delta}[/math].

Summary of insurance types

Summary

Insurance name	benefit function [math]b_T[/math]	discount function [math]v_T[/math]	present-value random variable [math]Z[/math]	APV notation
Whole life insurance	[math]1,\quad T\ge 0[/math]	[math]v^{T},\quad T\ge 0[/math]	[math]v^{T},\quad T\ge 0[/math]	[math]\bar A_x[/math]
[math]n[/math]-year term life insurance	[math]\begin{cases}1,& T\le n;\\0,&T \gt n\\\end{cases}[/math]	[math]v^{T},\quad T\ge 0[/math]	[math]\begin{cases}v^{T},& T\le n;\\0,&T \gt n\end{cases}[/math]	[math]\bar A^1_{x:\overline n|}[/math]
[math]n[/math]-year pure endowment	[math]\begin{cases}0,& T\le n;\\1,&T \gt n\\\end{cases}[/math]	[math]v^{n},\quad T\ge 0[/math]	[math]\begin{cases}0,& T\le n;\\v^n,&T \gt n\end{cases}[/math]	[math]\bar A^{\;\;1}_{x:\overline n|}[/math] or [math]_nE_x[/math]
[math]n[/math]-year endowment insurance	[math]1,\quad T\ge 0[/math]	[math]\begin{cases}v^{T},& T\le n;\\v^n,&T \gt n\\\end{cases}[/math]	[math]\begin{cases}v^{T},& T\le n;\\v^n,&T \gt n\end{cases}[/math]	[math]\bar A_{x:\overline n|}[/math]
[math]m[/math]-year deferred whole life insurance	[math]\begin{cases}0,& T\le n;\\1,&T \gt n\\\end{cases}[/math]	[math]v^{T},\quad T\ge 0[/math]	[math]\begin{cases}v^{T},& T\le n;\\0,&T \gt n\end{cases}[/math]	[math]_{m|}\bar A_{x}[/math]
[math]m[/math]-year deferred [math]n[/math]-year term life insurance	[math]\begin{cases}0,&T\le m;\\1,& m \lt T\le m+n;\\0,&T \gt m+n,\\\end{cases}[/math]	[math]v^{T},\quad T\ge 0[/math]	[math]\begin{cases}0,&T\ge 0;\\v^{T},& m \lt T\le m+n;\\0,&T \gt m+n\\\end{cases}[/math]	[math]_{m|n}\bar A_x[/math]
Annually increasing whole life insurance	[math]\lfloor T\rfloor +1,\quad T\ge 0[/math]	[math]v^{T},\quad T\ge 0[/math]	[math](\lfloor T\rfloor +1)v^{T},\quad T\ge 0[/math]	[math](I\bar A)_x[/math]
Annually increasing [math]n[/math]-year term life insurance	[math] \begin{cases}\lfloor T\rfloor+1,& T\le n\;\\ 0,& T \gt n\\\end{cases} [/math]	[math]v^{T},\quad T\ge 0[/math]	[math] \begin{cases}(\lfloor T\rfloor+1)v^{T},& T\le n\;\\ 0,& T \gt n\\ \end{cases} [/math]	[math](I\bar A)_{x:\overline n|}^1[/math]
Annually decreasing [math]n[/math]-year term life insurance	[math] \begin{cases}n-\lfloor T\rfloor,& T\le n\;\\ 0,& T \gt n\\\end{cases} [/math]	[math]v^{T},\quad T\ge 0[/math]	[math] \begin{cases}(n-\lfloor T\rfloor)v^{T},& T\le n\;\\ 0,& T \gt n\\ \end{cases} [/math]	[math](D\bar A)_{x:\overline n|}^1[/math]
[math]m[/math]-thly increasing whole life insurance	[math]\frac{\lfloor mT\rfloor+1}{m},\quad T\ge 0[/math]	[math]v^T,\quad T\ge 0[/math]	[math]\frac{\lfloor mT\rfloor +1}{m}v^T,\quad T\ge 0[/math]	[math](I^{(m)}\bar A)_x[/math]
[math]m[/math]-thly increasing [math]n[/math]-year term life insurance	[math]\begin{cases}\frac{\lfloor mT\rfloor+1}{m},& T\le n;\\ 0,& T \gt n\end{cases}[/math]	[math]v^T,\quad T\ge 0[/math]	[math]\begin{cases}\frac{\lfloor mT\rfloor +1}{m}v^T,& T\le n;\\ 0,& T \gt n\end{cases}[/math]	[math](I^{(m)}\bar A)_{x:\overline n|}[/math]
Continuously increasing whole life insurance	[math]T,\quad T\ge 0[/math]	[math]v^T,\quad T\ge 0[/math]	[math]Tv^T,\quad T\ge 0[/math]	[math](\bar I\bar A)_x[/math]
Continuously increasing [math]n[/math]-year term life insurance	[math]\begin{cases}T,& T\le n;\\ 0,& T \gt n\end{cases}[/math]	[math]v^T,\quad T\ge 0[/math]	[math]\begin{cases}Tv^T,&T\le n;\\ 0,& T \gt n\end{cases}[/math]	[math](\bar I\bar A)_{x:\overline n|}[/math]

General References

• Wikibooks contributors. "Fundamental Actuarial Mathematics/Present Value Random Variables for Long-Term Insurance Coverages". Wikibooks. Wikibooks. Retrieved 14 January 2024.