guide:A6f1984402: Difference between revisions
No edit summary |
mNo edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\NA}{{\rm NA}} | |||
\newcommand{\mat}[1]{{\bf#1}} | |||
\newcommand{\exref}[1]{\ref{##1}} | |||
\newcommand{\secstoprocess}{\all} | |||
\newcommand{\NA}{{\rm NA}} | |||
\newcommand{\mathds}{\mathbb}</math></div> | |||
In [[exercise:0d25d46ede|Exercise]], the distribution of the time | |||
of the last equalization in the symmetric random walk was determined. If we let <math>\alpha_{2k, 2m}</math> | |||
denote the probability that a random walk of length <math>2m</math> has its last equalization at time | |||
<math>2k</math>, then we have | |||
<math display="block"> | |||
\alpha_{2k, 2m} = u_{2k}u_{2m-2k}\ . | |||
</math> | |||
We shall now show how one can approximate the distribution of the <math>\alpha</math>'s with a simple | |||
function. We recall that | |||
<math display="block"> | |||
u_{2k} \sim {1\over{\sqrt {\pi k}}}\ . | |||
</math> | |||
Therefore, as both <math>k</math> and <math>m</math> go to <math>\infty</math>, we have | |||
<math display="block"> | |||
\alpha_{2k, 2m} \sim {1\over{\pi \sqrt{k(m-k)}}}\ . | |||
</math> | |||
This last expression can be written as | |||
<math display="block"> | |||
{1\over{\pi m \sqrt{(k/m)(1 - k/m)}}}\ . | |||
</math> | |||
Thus, if we define | |||
<math display="block"> | |||
f(x) = {1\over{\pi \sqrt{x(1-x)}}}\ , | |||
</math> | |||
for <math>0 < x < 1</math>, then we have | |||
<math display="block"> | |||
\alpha_{2k, 2m} \approx {1\over m}f\biggl({k\over m}\biggr)\ . | |||
</math> | |||
The reason for the <math>\approx</math> sign is that we no longer require that <math>k</math> get large. This means | |||
that we can replace the discrete <math>\alpha_{2k, 2m}</math> distribution by the continuous density <math>f(x)</math> on | |||
the interval <math>[0, 1]</math> and obtain a good approximation. In particular, if <math>x</math> is a fixed real | |||
number between 0 and 1, then we have | |||
<math display="block"> | |||
\sum_{k < xm}\alpha_{2k, 2m} \approx \int_0^x f(t)\,dt\ . | |||
</math> | |||
It turns out that <math>f(x)</math> has a nice antiderivative, so we can write | |||
<math display="block"> | |||
\sum_{k < xm}\alpha_{2k, 2m} \approx {2\over \pi}\arcsin \sqrt x\ . | |||
</math> | |||
One can see from the graph of this last function that it has a minimum at <math>x = 1/2</math> and is | |||
symmetric about that point. As noted in the exercise, this implies that half of the walks of | |||
length <math>2m</math> have no equalizations after time <math>m</math>, a fact which probably would not be guessed. | |||
It turns out that the arc sine density comes up in the answers to many other questions | |||
concerning random walks on the line. Recall that in [[guide:Ff217e6881|Random Walks in Euclidean Space]], a random walk could be | |||
viewed as a polygonal line connecting <math>(0,0)</math> with <math>(m, S_m)</math>. Under this interpretation, we | |||
define <math>b_{2k, 2m}</math> to be the probability that a random walk of length <math>2m</math> has exactly <math>2k</math> of | |||
its <math>2m</math> polygonal line segments above the <math>t</math>-axis. | |||
The probability <math>b_{2k, 2m}</math> is frequently interpreted in terms of a two-player game. (The | |||
reader will recall the game Heads or Tails, in [[guide:4f3a4e96c3#exam 1.3 |Example]].) Player A is said to be in | |||
the lead at time | |||
<math>n</math> if the random walk is above the | |||
<math>t</math>-axis at that time, or if the random walk is on the <math>t</math>-axis at time <math>n</math> but above the | |||
<math>t</math>-axis at time | |||
<math>n-1</math>. (At time 0, neither player is in the lead.) One can ask what is the most probable number | |||
of times that player A is in the lead, in a game of length <math>2m</math>. Most people will say that the | |||
answer to this question is <math>m</math>. However, the following theorem says that <math>m</math> is the least likely | |||
number of times that player A is in the lead, and the most likely number of times in the | |||
lead is 0 or <math>2m</math>. | |||
{{proofcard|Theorem|thm_12.3.1|If Peter and Paul play a game of Heads or Tails of length <math>2m</math>, the probability that Peter will | |||
be in the lead exactly <math>2k</math> times is equal to | |||
<math display="block"> | |||
\alpha_{2k, 2m}\ . | |||
</math>|To prove the theorem, we need to show that | |||
<span id{{=}}"eq 12.3.1"/> | |||
<math display="block"> | |||
\begin{equation} | |||
b_{2k, 2m} = \alpha_{2k, 2m}\ . | |||
\label{eq 12.3.1} | |||
\end{equation} | |||
</math> | |||
[[exercise:9e4fe88535|Exercise]] shows that <math>b_{2m, 2m} = u_{2m}</math> and <math>b_{0, 2m} = u_{2m}</math>, | |||
so we only need to prove that Equation \ref{eq 12.3.1} holds for <math>1 \le k \le m-1</math>. We can obtain a | |||
recursion involving the <math>b</math>'s and the <math>f</math>'s (defined in [[guide:Ff217e6881|Random Walks in Euclidean Space]]) by counting the | |||
number of paths of length <math>2m</math> that have exactly <math>2k</math> of their segments above the <math>t</math>-axis, where <math>1 | |||
\le k \le m-1</math>. To count this collection of paths, we assume that the first return occurs at time | |||
<math>2j</math>, where | |||
<math>1 \le j \le m-1</math>. There are two cases to consider. Either during the first <math>2j</math> outcomes the | |||
path is above the <math>t</math>-axis or below the <math>t</math>-axis. In the first case, it must be true that the | |||
path has exactly <math>(2k - 2j)</math> line segments above the <math>t</math>-axis, between <math>t = 2j</math> and <math>t = 2m</math>. | |||
In the second case, it must be true that the path has exactly <math>2k</math> line segments above the | |||
<math>t</math>-axis, between <math>t = 2j</math> and <math>t = 2m</math>. | |||
We now count the number of paths of the various types | |||
described above. The number of paths of length <math>2j</math> all of whose line segments lie above the | |||
<math>t</math>-axis and which return to the origin for the first time at time <math>2j</math> equals | |||
<math>(1/2)2^{2j}f_{2j}</math>. This also equals the number of paths of length <math>2j</math> all of whose line | |||
segments lie below the <math>t</math>-axis and which return to the origin for the first time at time <math>2j</math>. | |||
The number of paths of length <math>(2m - 2j)</math> which have exactly <math>(2k - 2j)</math> line segments above the | |||
<math>t</math>-axis is <math>b_{2k-2j, 2m-2j}</math>. Finally, the number of paths of length <math>(2m-2j)</math> which have | |||
exactly <math>2k</math> line segments above the <math>t</math>-axis is <math>b_{2k,2m-2j}</math>. Therefore, we have | |||
<math display="block"> | |||
b_{2k,2m} = {1\over 2} \sum_{j = 1}^k f_{2j}b_{2k-2j, 2m-2j} + | |||
{1\over 2}\sum_{j = 1}^{m-k} f_{2j}b_{2k, 2m-2j}\ . | |||
</math> | |||
We now assume that Equation \ref{eq 12.3.1} is true for <math>m < n</math>. Then we have | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
b_{2k, 2n} &=& {1\over 2} \sum_{j = 1}^k f_{2j}\alpha_{2k-2j, 2m-2j} + | |||
{1\over 2}\sum_{j = 1}^{m-k} f_{2j}\alpha_{2k, 2m - 2j}\\ | |||
&=& {1\over 2}\sum_{j = 1}^k f_{2j}u_{2k-2j}u_{2m-2k} + | |||
{1\over 2}\sum_{j = 1}^{m-k} f_{2j}u_{2k}u_{2m - 2j - 2k}\\ | |||
&=& {1\over 2}u_{2m-2k}\sum_{j = 1}^k f_{2j}u_{2k - 2j} + | |||
{1\over 2}u_{2k}\sum_{j = 1}^{m-k} f_{2j}u_{2m - 2j - 2k}\\ | |||
&=& {1\over 2}u_{2m - 2k}u_{2k} + {1\over 2}u_{2k}u_{2m - 2k}\ , | |||
\end{eqnarray*} | |||
</math> | |||
where the last equality follows from [[guide:Ff217e6881#thm 12.1.2 |Theorem]]. Thus, we have | |||
<math display="block"> | |||
b_{2k, 2n} = \alpha_{2k, 2n}\ , | |||
</math> | |||
which completes the proof.}} | |||
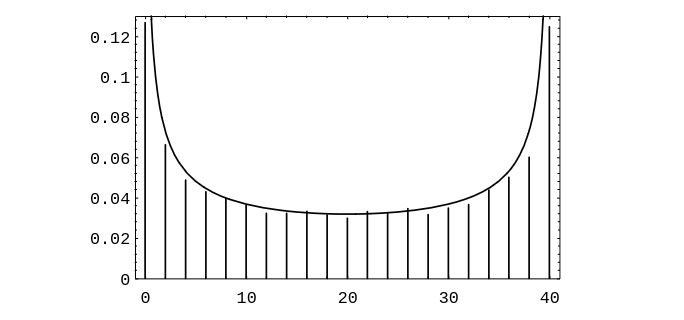
We illustrate the above theorem by simulating 10,00 games of Heads or Tails, with each game | |||
consisting of 40 tosses. The distribution of the number of times that Peter is in the lead is given in [[#fig 12.2|Figure]], together with the arc sine density. | |||
<div id="fig 12.2" class="d-flex justify-content-center"> | |||
[[File:guide_e6d15_PSfig12-2.png | 600px | thumb |Times in the lead.]] | |||
</div> | |||
We end this section by stating two other results in which the arc sine density appears. | |||
Proofs of these results may be found in Feller.<ref group="Notes" >W. Feller, op. cit., pp. 93--94.</ref> | |||
{{proofcard|Theorem|thm_12.3.2|Let <math>J</math> be the random variable which, for a given random walk of length <math>2m</math>, gives the | |||
smallest subscript <math>j</math> such that <math>S_{j} = S_{2m}</math>. (Such a subscript <math>j</math> must be even, | |||
by parity considerations.) Let <math>\gamma_{2k, 2m}</math> be the probability that <math>J = 2k</math>. Then we | |||
have | |||
<math display="block"> | |||
\gamma_{2k, 2m} = \alpha_{2k, 2m}\ . | |||
</math>|}} | |||
The next theorem says that the arc sine density is applicable to a wide range of | |||
situations. A continuous distribution function <math>F(x)</math> is said to | |||
be ''symmetric'' if <math>F(x) = 1 - F(-x)</math>. (If <math>X</math> is a continuous random variable | |||
with a symmetric distribution function, then for any real <math>x</math>, we have <math>P(X \le x) = P(X | |||
\ge -x)</math>.) We imagine that we have a random walk of length <math>n</math> in which each summand | |||
has the distribution | |||
<math>F(x)</math>, where <math>F</math> is continuous and symmetric. The subscript of the ''first | |||
maximum'' of such a walk is the unique subscript <math>k</math> such that | |||
<math display="block"> | |||
S_k > S_0,\ \ldots,\ S_k > S_{k-1},\ S_k \ge S_{k+1},\ \ldots,\ S_k \ge S_n\ . | |||
</math> | |||
We define the random variable <math>K_n</math> to be the subscript of the | |||
first maximum. We can now state the following theorem concerning the random variable <math>K_n</math>. | |||
{{proofcard|Theorem|thm_12.3.3|Let <math>F</math> be a symmetric continuous distribution function, and let <math>\alpha</math> be a fixed real number strictly between 0 and 1. Then as <math>n \rightarrow \infty</math>, we have | |||
<math display="block"> | |||
P(K_n < n\alpha) \rightarrow {2\over \pi} \arcsin\sqrt \alpha\ . | |||
</math>|}} | |||
A version of this theorem that holds for a symmetric random walk can also be found in Feller. | |||
==General references== | |||
{{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | |||
==Notes== | |||
{{Reflist|group=Notes}} | |||
Latest revision as of 01:56, 12 June 2024
In Exercise, the distribution of the time of the last equalization in the symmetric random walk was determined. If we let [math]\alpha_{2k, 2m}[/math] denote the probability that a random walk of length [math]2m[/math] has its last equalization at time [math]2k[/math], then we have
We shall now show how one can approximate the distribution of the [math]\alpha[/math]'s with a simple function. We recall that
Therefore, as both [math]k[/math] and [math]m[/math] go to [math]\infty[/math], we have
This last expression can be written as
Thus, if we define
for [math]0 \lt x \lt 1[/math], then we have
The reason for the [math]\approx[/math] sign is that we no longer require that [math]k[/math] get large. This means that we can replace the discrete [math]\alpha_{2k, 2m}[/math] distribution by the continuous density [math]f(x)[/math] on the interval [math][0, 1][/math] and obtain a good approximation. In particular, if [math]x[/math] is a fixed real number between 0 and 1, then we have
It turns out that [math]f(x)[/math] has a nice antiderivative, so we can write
One can see from the graph of this last function that it has a minimum at [math]x = 1/2[/math] and is symmetric about that point. As noted in the exercise, this implies that half of the walks of length [math]2m[/math] have no equalizations after time [math]m[/math], a fact which probably would not be guessed.
It turns out that the arc sine density comes up in the answers to many other questions
concerning random walks on the line. Recall that in Random Walks in Euclidean Space, a random walk could be
viewed as a polygonal line connecting [math](0,0)[/math] with [math](m, S_m)[/math]. Under this interpretation, we
define [math]b_{2k, 2m}[/math] to be the probability that a random walk of length [math]2m[/math] has exactly [math]2k[/math] of
its [math]2m[/math] polygonal line segments above the [math]t[/math]-axis.
The probability [math]b_{2k, 2m}[/math] is frequently interpreted in terms of a two-player game. (The reader will recall the game Heads or Tails, in Example.) Player A is said to be in the lead at time [math]n[/math] if the random walk is above the [math]t[/math]-axis at that time, or if the random walk is on the [math]t[/math]-axis at time [math]n[/math] but above the [math]t[/math]-axis at time [math]n-1[/math]. (At time 0, neither player is in the lead.) One can ask what is the most probable number of times that player A is in the lead, in a game of length [math]2m[/math]. Most people will say that the answer to this question is [math]m[/math]. However, the following theorem says that [math]m[/math] is the least likely number of times that player A is in the lead, and the most likely number of times in the lead is 0 or [math]2m[/math].
If Peter and Paul play a game of Heads or Tails of length [math]2m[/math], the probability that Peter will be in the lead exactly [math]2k[/math] times is equal to
To prove the theorem, we need to show that
Exercise shows that [math]b_{2m, 2m} = u_{2m}[/math] and [math]b_{0, 2m} = u_{2m}[/math], so we only need to prove that Equation \ref{eq 12.3.1} holds for [math]1 \le k \le m-1[/math]. We can obtain a recursion involving the [math]b[/math]'s and the [math]f[/math]'s (defined in Random Walks in Euclidean Space) by counting the number of paths of length [math]2m[/math] that have exactly [math]2k[/math] of their segments above the [math]t[/math]-axis, where [math]1 \le k \le m-1[/math]. To count this collection of paths, we assume that the first return occurs at time [math]2j[/math], where [math]1 \le j \le m-1[/math]. There are two cases to consider. Either during the first [math]2j[/math] outcomes the path is above the [math]t[/math]-axis or below the [math]t[/math]-axis. In the first case, it must be true that the path has exactly [math](2k - 2j)[/math] line segments above the [math]t[/math]-axis, between [math]t = 2j[/math] and [math]t = 2m[/math]. In the second case, it must be true that the path has exactly [math]2k[/math] line segments above the [math]t[/math]-axis, between [math]t = 2j[/math] and [math]t = 2m[/math].
We now count the number of paths of the various types
described above. The number of paths of length [math]2j[/math] all of whose line segments lie above the
[math]t[/math]-axis and which return to the origin for the first time at time [math]2j[/math] equals
[math](1/2)2^{2j}f_{2j}[/math]. This also equals the number of paths of length [math]2j[/math] all of whose line
segments lie below the [math]t[/math]-axis and which return to the origin for the first time at time [math]2j[/math].
The number of paths of length [math](2m - 2j)[/math] which have exactly [math](2k - 2j)[/math] line segments above the
[math]t[/math]-axis is [math]b_{2k-2j, 2m-2j}[/math]. Finally, the number of paths of length [math](2m-2j)[/math] which have
exactly [math]2k[/math] line segments above the [math]t[/math]-axis is [math]b_{2k,2m-2j}[/math]. Therefore, we have
We now assume that Equation \ref{eq 12.3.1} is true for [math]m \lt n[/math]. Then we have
where the last equality follows from Theorem. Thus, we have
We illustrate the above theorem by simulating 10,00 games of Heads or Tails, with each game consisting of 40 tosses. The distribution of the number of times that Peter is in the lead is given in Figure, together with the arc sine density.
We end this section by stating two other results in which the arc sine density appears. Proofs of these results may be found in Feller.[Notes 1]
Let [math]J[/math] be the random variable which, for a given random walk of length [math]2m[/math], gives the smallest subscript [math]j[/math] such that [math]S_{j} = S_{2m}[/math]. (Such a subscript [math]j[/math] must be even, by parity considerations.) Let [math]\gamma_{2k, 2m}[/math] be the probability that [math]J = 2k[/math]. Then we have
The next theorem says that the arc sine density is applicable to a wide range of situations. A continuous distribution function [math]F(x)[/math] is said to be symmetric if [math]F(x) = 1 - F(-x)[/math]. (If [math]X[/math] is a continuous random variable with a symmetric distribution function, then for any real [math]x[/math], we have [math]P(X \le x) = P(X \ge -x)[/math].) We imagine that we have a random walk of length [math]n[/math] in which each summand has the distribution [math]F(x)[/math], where [math]F[/math] is continuous and symmetric. The subscript of the first maximum of such a walk is the unique subscript [math]k[/math] such that
We define the random variable [math]K_n[/math] to be the subscript of the first maximum. We can now state the following theorem concerning the random variable [math]K_n[/math].
Let [math]F[/math] be a symmetric continuous distribution function, and let [math]\alpha[/math] be a fixed real number strictly between 0 and 1. Then as [math]n \rightarrow \infty[/math], we have
A version of this theorem that holds for a symmetric random walk can also be found in Feller.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.