exercise:2b544d7e7a: Difference between revisions
From Stochiki
(Created page with "<div class="d-none"><math> \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}</math></div> A rat runs through the maze shown in Figure \ref{fig 11.6.5}. At each step it leaves the room it is in by choosing at random one of the doors out of the room. <div id="PSfig11-6-5" class="d-flex justify-content-center"> File:guide_e6d15_PSfig...") |
No edit summary |
||
| Line 5: | Line 5: | ||
\newcommand{\secstoprocess}{\all} | \newcommand{\secstoprocess}{\all} | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
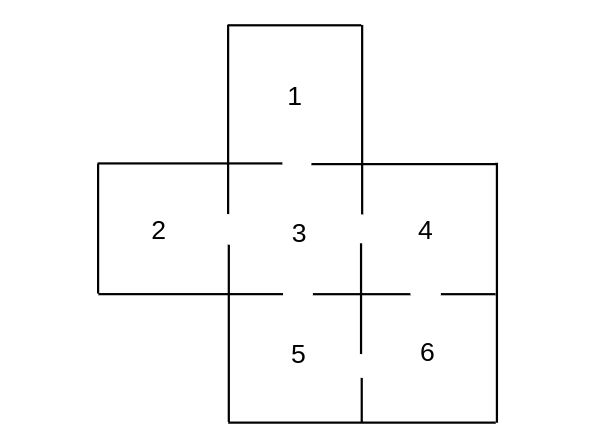
\newcommand{\mathds}{\mathbb}</math></div> A rat runs through the maze shown in | \newcommand{\mathds}{\mathbb}</math></div> A rat runs through the maze shown in [[#fig11.6.5|Figure]]. At each step it leaves the room it is in by choosing at random one of the doors out of the room. | ||
<div id="fig11.6.5" class="d-flex justify-content-center"> | |||
At each step it leaves the room it is in by choosing at random one of the doors | [[File:guide_e6d15_PSfig11-6-5.png | 400px ]] | ||
out of the room. | |||
<div id=" | |||
[[File:guide_e6d15_PSfig11-6-5. | |||
</div> | </div> | ||
<ul><li> Give the transition matrix <math>\mat{P}</math> for this Markov chain. | <ul style="list-style-type:lower-alpha"><li> Give the transition matrix <math>\mat{P}</math> for this Markov chain. | ||
</li> | </li> | ||
<li> Show that it is an ergodic chain but not a regular chain. | <li> Show that it is an ergodic chain but not a regular chain. | ||
Latest revision as of 01:20, 15 June 2024
[math]
\newcommand{\NA}{{\rm NA}}
\newcommand{\mat}[1]{{\bf#1}}
\newcommand{\exref}[1]{\ref{##1}}
\newcommand{\secstoprocess}{\all}
\newcommand{\NA}{{\rm NA}}
\newcommand{\mathds}{\mathbb}[/math]
A rat runs through the maze shown in Figure. At each step it leaves the room it is in by choosing at random one of the doors out of the room.
- Give the transition matrix [math]\mat{P}[/math] for this Markov chain.
- Show that it is an ergodic chain but not a regular chain.
- Find the fixed vector.
- Find the expected number of steps before reaching Room 5 for the first time, starting in Room 1.