guide:Baa5a33dd4: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
\newcommand{\mathds}{\mathbb}</math></div> | \newcommand{\mathds}{\mathbb}</math></div> | ||
===Historical Background=== | ===Historical Background=== | ||
| Line 13: | Line 12: | ||
Until recently it was thought that the theory of branching processes originated | Until recently it was thought that the theory of branching processes originated | ||
with the following problem posed by Francis Galton in the ''Educational | with the following problem posed by Francis Galton in the ''Educational | ||
Times'' in 1873.<ref group="Notes" >D. | Times'' in 1873.<ref group="Notes" >D.G. Kendall, “Branching Processes Since | ||
1873,” ''Journal of London Mathematics Society,'' vol. | 1873,” ''Journal of London Mathematics Society,'' vol.41 (1966), p.386.</ref> | ||
<blockquote> | <blockquote> | ||
Problem 4001: A large nation, of whom we will only concern ourselves with the | Problem 4001: A large nation, of whom we will only concern ourselves with the | ||
| Line 26: | Line 26: | ||
held by <math>m</math> persons. | held by <math>m</math> persons. | ||
</blockquote> | </blockquote> | ||
The first attempt at a solution was given by Reverend H. W. Watson. | The first attempt at a solution was given by Reverend H. W. Watson. | ||
Because of a mistake in algebra, he incorrectly concluded that a family name would always | Because of a mistake in algebra, he incorrectly concluded that a family name would always | ||
| Line 40: | Line 41: | ||
following translation from Bienaymé's paper: | following translation from Bienaymé's paper: | ||
<blockquote> | <blockquote> | ||
If | If ... the mean of the number of male children who replace the number of males of the preceding generation were less than unity, it would be easily | ||
males of the preceding generation were less than unity, it would be easily | realized that families are dying out due to the disappearance of the members of which they are composed. However, the analysis shows further that when this mean is equal to unity families tend to disappear, although less rapidly ... | ||
realized that families are dying out due to the disappearance of the members of | |||
which they are composed. However, the analysis shows further that when this | |||
mean is equal to unity families tend to disappear, although less rapidly | |||
The analysis also shows clearly that if the mean ratio is greater than unity, | The analysis also shows clearly that if the mean ratio is greater than unity, | ||
the probability of the extinction of families with the passing of time no | the probability of the extinction of families with the passing of time no longer reduces to certainty. It only approaches a finite limit, which is | ||
longer reduces to certainty. It only approaches a finite limit, which is | fairly simple to calculate and which has the singular characteristic of being given by one of the roots of the equation (in which the number of generations | ||
fairly simple to calculate and which has the singular characteristic of being | is made infinite) which is not relevant to the question when the mean ratio is less than unity.<ref group="Notes" >ibid., pp. 117--118.</ref> | ||
given by one of the roots of the equation (in which the number of generations | |||
is made infinite) which is not relevant to the question when the mean ratio is | |||
less than unity.<ref group="Notes" >ibid., pp. 117--118.</ref> | |||
</blockquote> | </blockquote> | ||
Although Bienaymé does not give his reasoning for these results, he did | Although Bienaymé does not give his reasoning for these results, he did | ||
indicate that he intended to publish a special paper on the problem. The paper | indicate that he intended to publish a special paper on the problem. The paper | ||
| Line 78: | Line 74: | ||
===Problem of Extinction=== | ===Problem of Extinction=== | ||
We turn now to the first problem posed by Galton (i.e., the problem of finding | We turn now to the first problem posed by Galton (i.e., the problem of finding the probability of extinction for a branching process). We start in the | ||
the probability of extinction for a branching process). We start in the | 0th generation with 1 male parent. In the first generation we shall have 0, 1,2, 3, ... male offspring with probabilities <math>p_0,p_1,p_2,p_3,\ldots</math> If in the first generation there are <math>k</math> offspring, then in the | ||
0th generation with 1 male parent. In the first generation we shall have 0, 1, | |||
2, 3, | |||
second generation there will be <math>X_1 + X_2 +\cdots+ X_k</math> offspring, where | second generation there will be <math>X_1 + X_2 +\cdots+ X_k</math> offspring, where | ||
<math>X_1 | <math>X_1, X_2, \ldots, X_k</math> are independent random variables, each with the common distribution <math>p_0, p_1, p_2, \ldots</math>. This description enables us to construct a tree, and a tree measure, for any number of generations. | ||
common distribution <math>p_0 | |||
construct a tree, and a tree measure, for any number of generations. | |||
===Examples=== | ===Examples=== | ||
| Line 92: | Line 83: | ||
'''Example''' | '''Example''' | ||
Assume that <math>p_0 = 1/2</math>, <math>p_1 = 1/4</math>, and <math>p_2 = 1/4</math>. Then the tree measure | Assume that <math>p_0 = 1/2</math>, <math>p_1 = 1/4</math>, and <math>p_2 = 1/4</math>. Then the tree measure | ||
for the first two generations is shown in | for the first two generations is shown in [[#fig 10.1|Figure]]. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig10-1. | <div id="fig 10.1" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig10-1.png | 600px | thumb | Tree diagram for [[#exam 10.2.1|Example]]. ]] | |||
</div> | </div> | ||
Note that we use the theory of sums of independent random variables to assign | |||
branch probabilities. For example, if there are two offspring in the first | Note that we use the theory of sums of independent random variables to assign branch probabilities. For example, if there are two offspring in the first | ||
generation, the probability that there will be two in the second generation is | generation, the probability that there will be two in the second generation is | ||
| Line 108: | Line 100: | ||
</math> | </math> | ||
We now study the probability that our process dies out (i.e., that at some generation there are no offspring). | |||
We now study the probability that our process dies out (i.e., that at some | |||
generation there are no offspring). | |||
Let <math>d_m</math> be the probability that the process dies out by the <math>m</math>th | Let <math>d_m</math> be the probability that the process dies out by the <math>m</math>th | ||
generation. Of course, <math>d_0 = 0</math>. In our example, <math>d_1 = 1/2</math> and <math>d_2 = 1/2 | generation. Of course, <math>d_0 = 0</math>. In our example, <math>d_1 = 1/2</math> and <math>d_2 = 1/2 | ||
+ 1/8 + 1/16 = 11/16</math> (see | + 1/8 + 1/16 = 11/16</math> (see [[#fig 10.1|Figure]]). Note that we must add the | ||
probabilities for all paths that lead to 0 by the <math>m</math>th generation. It is | probabilities for all paths that lead to 0 by the <math>m</math>th generation. It is | ||
clear from the definition that | clear from the definition that | ||
| Line 144: | Line 133: | ||
h(z) = p_0 + p_1z + p_2z^2 +\cdots\ . | h(z) = p_0 + p_1z + p_2z^2 +\cdots\ . | ||
</math> | </math> | ||
Using this generating function, we can rewrite | Using this generating function, we can rewrite Equation \ref{eq 10.2.1} in the form | ||
<span id{{=}}"eq 10.2.2"/> | <span id{{=}}"eq 10.2.2"/> | ||
| Line 154: | Line 143: | ||
</math> | </math> | ||
Since <math>d_m \to d</math>, by | Since <math>d_m \to d</math>, by Equation \ref{eq 10.2.2} we see that the value <math>d</math> that we are | ||
looking for satisfies the equation | looking for satisfies the equation | ||
| Line 171: | Line 160: | ||
</math> | </math> | ||
This is where Watson made his mistake. He assumed that 1 was the only solution | This is where Watson made his mistake. He assumed that 1 was the only solution | ||
to | to Equation \ref{eq 10.2.3}. To examine this question more carefully, we first note | ||
that solutions to | that solutions to Equation \ref{eq 10.2.3} represent intersections of the graphs of | ||
<math display="block"> | <math display="block"> | ||
| Line 200: | Line 189: | ||
Therefore the graph of <math>y = h(z)</math> can intersect the line <math>y = z</math> in at most two | Therefore the graph of <math>y = h(z)</math> can intersect the line <math>y = z</math> in at most two | ||
points. Since we know it must intersect the line <math>y = z</math> at <math>(1,1)</math>, we know | points. Since we know it must intersect the line <math>y = z</math> at <math>(1,1)</math>, we know | ||
that there are just three possibilities, as shown in | that there are just three possibilities, as shown in [[#fig 10.2|Figure]]. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig10-2. | <div id="fig 10.2" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig10-2.png | 600px | thumb | Graphs of <math>y = z</math> and <math>y = h(z)</math>. ]] | |||
</div> | </div> | ||
In case (a) the equation <math>d = h(d)</math> has roots <math>\{d,1\}</math> with <math>0 \leq d < | In case (a) the equation <math>d = h(d)</math> has roots <math>\{d,1\}</math> with <math>0 \leq d < | ||
| Line 214: | Line 203: | ||
From | From Equation \ref{eq 10.2.4} we see that | ||
<math display="block"> | <math display="block"> | ||
| Line 223: | Line 212: | ||
our three cases correspond to <math>m > 1</math>, <math>m = 1</math>, and <math>m < 1</math>. We assume now | our three cases correspond to <math>m > 1</math>, <math>m = 1</math>, and <math>m < 1</math>. We assume now | ||
that <math>m > 1</math>. Recall that <math>d_0 = 0</math>, <math>d_1 = h(d_0) = p_0</math>, <math>d_2 = h(d_1)</math>, | that <math>m > 1</math>. Recall that <math>d_0 = 0</math>, <math>d_1 = h(d_0) = p_0</math>, <math>d_2 = h(d_1)</math>, | ||
\ldots, and <math>d_n = h(d_{n - 1})</math>. We can construct these values geometrically, | \ldots, and <math>d_n = h(d_{n - 1})</math>. We can construct these values geometrically, as shown in [[#fig 10.3|Figure]]. | ||
as shown in | |||
<div id=" | <div id="fig 10.3" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig10-3. | [[File:guide_e6d15_PSfig10-3.png | 600px | thumb | Geometric determination of <math>d</math>. ]] | ||
</div> | </div> | ||
We can see geometrically, as indicated for <math>d_0</math>, <math>d_1</math>, <math>d_2</math>, and <math>d_3</math> in | We can see geometrically, as indicated for <math>d_0</math>, <math>d_1</math>, <math>d_2</math>, and <math>d_3</math> in | ||
[[#fig 10.3|Figure]], that the points <math>(d_i,h(d_i))</math> will always lie above the line <math>y = | |||
z</math>. Hence, they must converge to the first intersection of the curves <math>y = z</math> | z</math>. Hence, they must converge to the first intersection of the curves <math>y = z</math> | ||
and <math>y = h(z)</math> (i.e., to the root <math>d < 1</math>). This leads us to the following | and <math>y = h(z)</math> (i.e., to the root <math>d < 1</math>). This leads us to the following | ||
| Line 247: | Line 236: | ||
This makes it easy to compute these probabilities. | This makes it easy to compute these probabilities. | ||
The program ''' Branch''' calculates the values of <math>d_n</math>. We have run this program for 12 generations for the case that a parent can produce at most two offspring and the probabilities for the number produced are <math>p_0 = .2</math>, <math>p_1 = .5</math>, and <math>p_2 = .3</math>. The results are given in [[#table 10.1 |Table]]. | |||
<span id="table 10.1"/> | <span id="table 10.1"/> | ||
{|class="table" | {|class="table" | ||
|+ Probability of dying out. | |+ Probability of dying out. | ||
|- | |- | ||
| | | Generation || Probability of dying out | ||
|- | |- | ||
|1 || .2 | |||
|- | |- | ||
|2 || .312 | |||
|- | |- | ||
|3 || .385203 | |||
|- | |- | ||
|4 || .437116 | |||
|- | |- | ||
|5 || .475879 | |||
|- | |- | ||
|6 || .505878 | |||
|- | |- | ||
|7 || .529713 | |||
|- | |- | ||
|8 || .549035 | |||
|- | |- | ||
|9 || .564949 | |||
|- | |- | ||
|10 || .578225 | |||
|- | |- | ||
|11 || .589416 | |||
|- | |- | ||
|12 || .598931 | |||
|} | |} | ||
We see that the probability of dying out by 12 generations is about .6. We | We see that the probability of dying out by 12 generations is about .6. We shall see in the next example that the probability of eventually dying out | ||
shall see in the next example that the probability of eventually dying out | is 2/3, so that even 12 generations is not enough to give an accurate estimate for this probability. | ||
is 2/3, so that even 12 generations is not enough to give an accurate estimate | |||
for this probability. | |||
We now assume that at most two offspring can be produced. Then | We now assume that at most two offspring can be produced. Then | ||
| Line 310: | Line 293: | ||
we have a double root <math>d = 1</math>. If <math>p_0 < p_2</math>, <math>m > 1</math> and the second root <math>d</math> | we have a double root <math>d = 1</math>. If <math>p_0 < p_2</math>, <math>m > 1</math> and the second root <math>d</math> | ||
is less than 1 and represents the probability that the process will die out. | is less than 1 and represents the probability that the process will die out. | ||
<span id="exam 10.2.3"/> | <span id="exam 10.2.3"/> | ||
'''Example''' | '''Example''' | ||
Keyfitz<ref group="Notes" >N. Keyfitz, ''Introduction to the Mathematics of | Keyfitz<ref group="Notes" >N. Keyfitz, ''Introduction to the Mathematics of Population,'' rev. ed. (Reading, PA: Addison Wesley, 1977).</ref> compiled and | ||
Population,'' rev. ed. | analyzed data on the continuation of the female family line among Japanese women. His estimates at the basic probability distribution for the number of | ||
analyzed data on the continuation of the female family line among Japanese | |||
women. His estimates at the basic probability distribution for the number of | |||
female children born to Japanese women of ages 45--49 in 1960 are given in [[#table 10.2 |Table]]. | female children born to Japanese women of ages 45--49 in 1960 are given in [[#table 10.2 |Table]]. | ||
<span id="table 10.2"/> | <span id="table 10.2"/> | ||
{|class="table" | {| class="table" | ||
|+ Distribution of number of female children. | |+Distribution of number of female children. | ||
|- | |- | ||
||| | |<math>p_0</math> || = .2092 | ||
|- | |- | ||
|<math> | | <math>p_1</math> || = .2584 | ||
|- | |- | ||
| | | <math>p_2</math> || = .2360 | ||
|- | |- | ||
| | | <math>p_3</math> || = .1593 | ||
|- | |- | ||
| | | <math>p_4</math> || = .0828 | ||
|- | |- | ||
| | | <math>p_5</math> || = .0357 | ||
|- | |- | ||
| | | <math>p_6</math> || = .0133 | ||
|- | |- | ||
| | | <math>p_7</math> || = .0042 | ||
|- | |- | ||
| | | <math>p_8</math> || = .0011 | ||
|- | |- | ||
| | | <math>p_9</math> || = .0002 | ||
|- | |- | ||
|10 || .0000 | | <math>p_{10}</math> || = .0000 | ||
|} | |} | ||
The expected number of girls in a family is then 1.837 so the probability <math>d</math> | The expected number of girls in a family is then 1.837 so the probability <math>d</math> | ||
of extinction is less than 1. If we run the program ''' Branch''', we can estimate | of extinction is less than 1. If we run the program ''' Branch''', we can estimate | ||
that <math>d</math> is in fact only about .324. | that <math>d</math> is in fact only about .324. | ||
===Distribution of Offspring=== | ===Distribution of Offspring=== | ||
| Line 378: | Line 357: | ||
<math>X_j</math> has the same integer-valued distribution <math>(p_j)</math> with generating function | <math>X_j</math> has the same integer-valued distribution <math>(p_j)</math> with generating function | ||
<math>k(z) = p_0 + p_1z + p_2z^2 +\cdots.</math> Let <math>k_n(z)</math> be the generating function | <math>k(z) = p_0 + p_1z + p_2z^2 +\cdots.</math> Let <math>k_n(z)</math> be the generating function | ||
of <math>S_n</math>. Then using one of the properties of ordinary generating functions | of <math>S_n</math>. Then using one of the properties of ordinary generating functions discussed in [[guide:04b2b9c99f|Generating Functions for Discrete Distributions]], we have | ||
discussed in | |||
<math display="block"> | <math display="block"> | ||
| Line 422: | Line 400: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
If we differentiate | If we differentiate Equation \ref{eq 10.2.5} and use the chain rule we have | ||
<math display="block"> | <math display="block"> | ||
| Line 460: | Line 438: | ||
easily carry out the calculation of <math>h_n(z)</math> by this method. However, there is | easily carry out the calculation of <math>h_n(z)</math> by this method. However, there is | ||
one special case in which this can be done. | one special case in which this can be done. | ||
<span id="exam 10.2.4"/> | <span id="exam 10.2.4"/> | ||
'''Example''' | '''Example''' | ||
Assume that the probabilities <math>p_1 | Assume that the probabilities <math>p_1, p_2, \ldots</math> form a geometric series: | ||
<math>p_k = bc^{k - 1}</math>, <math>k = 1 | <math>p_k = bc^{k - 1}</math>, <math>k = 1, 2, \ldots,</math> with <math>0 < b \leq 1 - c</math> and <math>0 < c < 1</math>. Then we have | ||
<math display="block"> | <math display="block"> | ||
| Line 556: | Line 535: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Solving | |||
Solving \ref{eq 10.2.7} and \ref{eq 10.2.8} for <math>b</math> and <math>c</math> gives | |||
<math display="block"> | <math display="block"> | ||
| Line 570: | Line 550: | ||
Keyfitz example. Using these values, we obtain <math>b = .3666</math> and <math>c = .5533</math>. | Keyfitz example. Using these values, we obtain <math>b = .3666</math> and <math>c = .5533</math>. | ||
Note that <math>(1 - c)^2 < b < 1 - c</math>, as required. In [[#table 10.3 |Table]] | Note that <math>(1 - c)^2 < b < 1 - c</math>, as required. In [[#table 10.3 |Table]] | ||
we give for | we give for comparison the probabilities <math>p_0</math> through <math>p_8</math> as calculated by the geometric | ||
comparison the probabilities <math>p_0</math> through <math>p_8</math> as calculated by the geometric | |||
distribution versus the empirical values. | distribution versus the empirical values. | ||
<span id="table 10.3"/> | <span id="table 10.3"/> | ||
{|class="table" | {|class="table" | ||
|+ Comparison of observed and expected frequencies. | |+ Comparison of observed and expected frequencies. | ||
|- | |- | ||
|<math>p_j</math> ||Data || Geometric Model | |||
|<math>p_j</math> ||Data || Model | |||
|- | |- | ||
|0 || .2092 || .1816 | |0 || .2092 || .1816 | ||
| Line 638: | Line 616: | ||
We have run this program for the Keyfitz example, carrying out 10 simulations | We have run this program for the Keyfitz example, carrying out 10 simulations | ||
and graphing the results in | and graphing the results in [[#fig 10.4|Figure]]. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig10-4. | <div id="fig 10.4" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig10-4.png | 400px | thumb | Simulation of <math>Z_n/m^n</math> for the Keyfitz example. ]] | |||
</div> | </div> | ||
| Line 712: | Line 691: | ||
buyer then crosses off the name at the top of the list and adds her own name at | buyer then crosses off the name at the top of the list and adds her own name at | ||
the bottom in each letter before it is sold again. | the bottom in each letter before it is sold again. | ||
Let us first assume that the buyer may sell the letter only to a single | Let us first assume that the buyer may sell the letter only to a single | ||
person. If you buy the letter you will want to compute your expected | person. If you buy the letter you will want to compute your expected | ||
| Line 722: | Line 702: | ||
your expected winnings are <math>-100 + 50p + 50p^{12}</math>. Thus the chain in this | your expected winnings are <math>-100 + 50p + 50p^{12}</math>. Thus the chain in this | ||
situation is a highly unfavorable game. | situation is a highly unfavorable game. | ||
It would be more reasonable to allow each person involved to make a copy of the | It would be more reasonable to allow each person involved to make a copy of the | ||
list and try to sell the letter to at least 2 other people. Then you would | list and try to sell the letter to at least 2 other people. Then you would | ||
| Line 730: | Line 711: | ||
generation consists of the letters sold by members of the first generation, and | generation consists of the letters sold by members of the first generation, and | ||
so forth. | so forth. | ||
Let us assume that the probabilities that each individual sells letters to | Let us assume that the probabilities that each individual sells letters to | ||
0, 1, or 2 others are <math>p_0</math>, <math>p_1</math>, and <math>p_2</math>, respectively. Let <math>Z_1</math>, <math>Z_2</math>, | 0, 1, or 2 others are <math>p_0</math>, <math>p_1</math>, and <math>p_2</math>, respectively. Let <math>Z_1</math>, <math>Z_2</math>, | ||
| Line 766: | Line 748: | ||
this happening?) | this happening?) | ||
To simulate this game, we need only simulate a branching process for 12 | To simulate this game, we need only simulate a branching process for 12 | ||
generations. Using a slightly modified version of our program ''' | generations. Using a slightly modified version of our program '''BranchingSimulation''' we carried out twenty such simulations, giving the | ||
BranchingSimulation''' we carried out twenty such simulations, giving the | |||
results shown in [[#table 10.4 |Table]]. | results shown in [[#table 10.4 |Table]]. | ||
Note that we were quite lucky on a few runs, but we came out ahead only a | Note that we were quite lucky on a few runs, but we came out ahead only a | ||
| Line 773: | Line 754: | ||
in 12 out of the 20 experiments, in good agreement with the probability <math>d_{12} | in 12 out of the 20 experiments, in good agreement with the probability <math>d_{12} | ||
= .599</math> that we calculated using the program ''' Branch'''. | = .599</math> that we calculated using the program ''' Branch'''. | ||
<span id="table 10.4"/> | |||
{|class="table" | {|class="table" | ||
|+ Simulation of chain letter (finite distribution case). | |+ Simulation of chain letter (finite distribution case). | ||
|- | |- | ||
| | |<math>Z_{1}</math>||<math>Z_{2}</math>||<math> Z_{3}</math>|| <math>Z_{4}</math>|| <math>Z_{5}</math>|| <math>Z_{6}</math>|| <math>Z_{7}</math>|| <math>Z_{8}</math>|| <math>Z_{9}</math>||<math> Z_{10}</math>||<math> Z_{11}</math>|| <math>Z_{12}</math>|| Profit | ||
|- | |- | ||
|1 ||0 ||0 ||0 ||0 || 0 || 0 ||0 ||0 ||0 ||0 ||0 ||-50 | |1 ||0 ||0 ||0 ||0 || 0 || 0 ||0 ||0 ||0 ||0 ||0 ||-50 | ||
| Line 819: | Line 801: | ||
|1 ||0 ||0 ||0 || 0 || 0 || 0 ||0 ||0 ||0 ||0 ||0 || -50 | |1 ||0 ||0 ||0 || 0 || 0 || 0 ||0 ||0 ||0 ||0 ||0 || -50 | ||
|} | |} | ||
Let us modify the assumptions about our chain letter to let the buyer sell the | Let us modify the assumptions about our chain letter to let the buyer sell the | ||
letter to as many people as she can instead of to a maximum of two. We shall | letter to as many people as she can instead of to a maximum of two. We shall | ||
| Line 845: | Line 828: | ||
The expected number of letters that an individual passes on is <math>m</math>, and again | The expected number of letters that an individual passes on is <math>m</math>, and again | ||
to be favorable we must have <math>m > 1</math>. Let us assume again that <math>m = 1.1</math>. | to be favorable we must have <math>m > 1</math>. Let us assume again that <math>m = 1.1</math>. | ||
Then we can find again the probability <math>1 - d_{12}</math> of a bonus from ''' | Then we can find again the probability <math>1 - d_{12}</math> of a bonus from '''Branch'''. The result is .232. Although the expected winnings are the same, the variance is larger in this case, and the buyer has a better chance for a | ||
Branch'''. The result is .232. Although the expected winnings are the same, the | |||
variance is larger in this case, and the buyer has a better chance for a | |||
reasonably large profit. We again carried out 20 simulations using the Poisson | reasonably large profit. We again carried out 20 simulations using the Poisson | ||
distribution with mean 1.1. The results are shown in [[#table 10.5 |Table]]. | distribution with mean 1.1. The results are shown in [[#table 10.5 |Table]]. | ||
| Line 854: | Line 835: | ||
|+ Simulation of chain letter (Poisson case). | |+ Simulation of chain letter (Poisson case). | ||
|- | |- | ||
| | |<math>Z_{1}</math>||<math>Z_{2}</math>||<math> Z_{3}</math>|| <math>Z_{4}</math>|| <math>Z_{5}</math>|| <math>Z_{6}</math>|| <math>Z_{7}</math>|| <math>Z_{8}</math>|| <math>Z_{9}</math>||<math> Z_{10}</math>||<math> Z_{11}</math>|| <math>Z_{12}</math>|| Profit | ||
|- | |- | ||
|1 ||2 ||6 ||7 ||7 || 8 || 11 ||9 ||7 ||6 ||6 ||5 || 200 | |1 ||2 ||6 ||7 ||7 || 8 || 11 ||9 ||7 ||6 ||6 ||5 || 200 | ||
| Line 902: | Line 883: | ||
This is again in reasonable agreement with our calculation of a probability | This is again in reasonable agreement with our calculation of a probability | ||
.232 for this happening. | .232 for this happening. | ||
==General references== | ==General references== | ||
Latest revision as of 17:38, 11 June 2024
Historical Background
In this section we apply the theory of generating functions to the study of an important chance process called a branching process. Until recently it was thought that the theory of branching processes originated with the following problem posed by Francis Galton in the Educational Times in 1873.[Notes 1]
Problem 4001: A large nation, of whom we will only concern ourselves with the adult males, [math]N[/math] in number, and who each bear separate surnames, colonise a district. Their law of population is such that, in each generation, [math]a_0[/math] per cent of the adult males have no male children who reach adult life; [math]a_1[/math] have one such male child; [math]a_2[/math] have two; and so on up to [math]a_5[/math] who have five. Find (1) what proportion of the surnames will have become extinct after [math]r[/math] generations; and (2) how many instances there will be of the same surname being held by [math]m[/math] persons.
The first attempt at a solution was given by Reverend H. W. Watson. Because of a mistake in algebra, he incorrectly concluded that a family name would always die out with probability 1. However, the methods that he employed to solve the problems were, and still are, the basis for obtaining the correct solution.
Heyde and Seneta discovered an earlier communication by
Bienaymé (1845) that anticipated Galton and Watson by 28 years.
Bienaymé showed, in fact, that he was aware of the correct solution to Galton's problem.
Heyde and Seneta in their book I. J. Bienaymé: Statistical Theory
Anticipated,[Notes 2] give the
following translation from Bienaymé's paper:
If ... the mean of the number of male children who replace the number of males of the preceding generation were less than unity, it would be easily realized that families are dying out due to the disappearance of the members of which they are composed. However, the analysis shows further that when this mean is equal to unity families tend to disappear, although less rapidly ... The analysis also shows clearly that if the mean ratio is greater than unity, the probability of the extinction of families with the passing of time no longer reduces to certainty. It only approaches a finite limit, which is fairly simple to calculate and which has the singular characteristic of being given by one of the roots of the equation (in which the number of generations is made infinite) which is not relevant to the question when the mean ratio is less than unity.[Notes 3]
Although Bienaymé does not give his reasoning for these results, he did indicate that he intended to publish a special paper on the problem. The paper was never written, or at least has never been found. In his communication Bienaymé indicated that he was motivated by the same problem that occurred to Galton. The opening paragraph of his paper as translated by Heyde and Seneta says,
A great deal of consideration has been given to the possible multiplication of the numbers of mankind; and recently various very curious observations have been published on the fate which allegedly hangs over the aristocrary and middle classes; the families of famous men, etc. This fate, it is alleged, will inevitably bring about the disappearance of the so-called families fermées.[Notes 4]
A much more extensive discussion of the history of branching processes may be found in two papers by David G. Kendall.[Notes 5] Branching processes have served not only as crude models for population growth but also as models for certain physical processes such as chemical and nuclear chain reactions.
Problem of Extinction
We turn now to the first problem posed by Galton (i.e., the problem of finding the probability of extinction for a branching process). We start in the 0th generation with 1 male parent. In the first generation we shall have 0, 1,2, 3, ... male offspring with probabilities [math]p_0,p_1,p_2,p_3,\ldots[/math] If in the first generation there are [math]k[/math] offspring, then in the second generation there will be [math]X_1 + X_2 +\cdots+ X_k[/math] offspring, where [math]X_1, X_2, \ldots, X_k[/math] are independent random variables, each with the common distribution [math]p_0, p_1, p_2, \ldots[/math]. This description enables us to construct a tree, and a tree measure, for any number of generations.
Examples
Example Assume that [math]p_0 = 1/2[/math], [math]p_1 = 1/4[/math], and [math]p_2 = 1/4[/math]. Then the tree measure for the first two generations is shown in Figure.
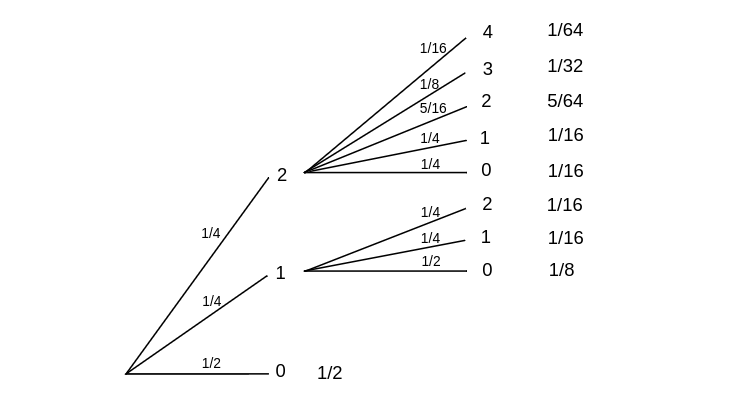
Note that we use the theory of sums of independent random variables to assign branch probabilities. For example, if there are two offspring in the first generation, the probability that there will be two in the second generation is
We now study the probability that our process dies out (i.e., that at some generation there are no offspring).
Let [math]d_m[/math] be the probability that the process dies out by the [math]m[/math]th generation. Of course, [math]d_0 = 0[/math]. In our example, [math]d_1 = 1/2[/math] and [math]d_2 = 1/2 + 1/8 + 1/16 = 11/16[/math] (see Figure). Note that we must add the probabilities for all paths that lead to 0 by the [math]m[/math]th generation. It is clear from the definition that
Hence, [math]d_m[/math] converges to a limit [math]d[/math], [math]0 \leq d \leq 1[/math], and [math]d[/math] is the probability that the process will ultimately die out. It is this value that we wish to determine. We begin by expressing the value [math]d_m[/math] in terms of all possible outcomes on the first generation. If there are [math]j[/math] offspring in the first generation, then to die out by the [math]m[/math]th generation, each of these lines must die out in [math]m - 1[/math] generations. Since they proceed independently, this probability is [math](d_{m - 1})^j[/math]. Therefore
Let [math]h(z)[/math] be the ordinary generating function for the [math]p_i[/math]:
Using this generating function, we can rewrite Equation \ref{eq 10.2.1} in the form
Since [math]d_m \to d[/math], by Equation \ref{eq 10.2.2} we see that the value [math]d[/math] that we are looking for satisfies the equation
One solution of this equation is always [math]d = 1[/math], since
This is where Watson made his mistake. He assumed that 1 was the only solution to Equation \ref{eq 10.2.3}. To examine this question more carefully, we first note that solutions to Equation \ref{eq 10.2.3} represent intersections of the graphs of
and
Thus we need to study the graph of [math]y = h(z)[/math]. We note that [math]h(0) = p_0[/math]. Also,
and
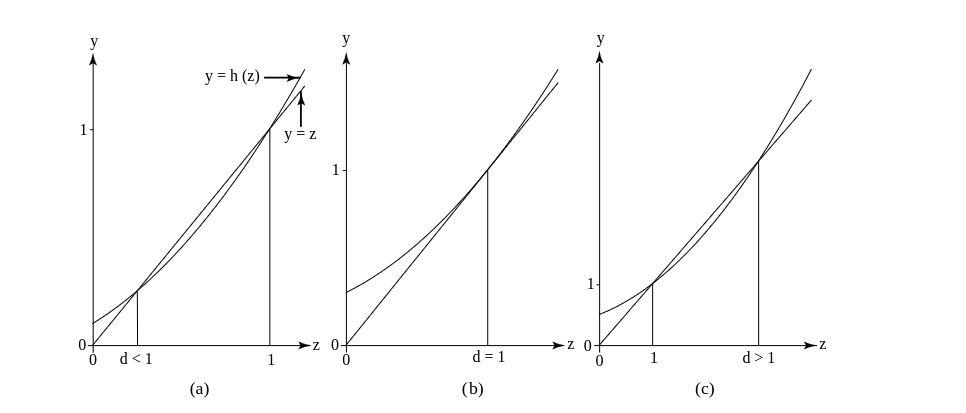
From this we see that for [math]z \geq 0[/math], [math]h'(z) \geq 0[/math] and [math]h''(z) \geq 0[/math]. Thus for nonnegative [math]z[/math], [math]h(z)[/math] is an increasing function and is concave upward. Therefore the graph of [math]y = h(z)[/math] can intersect the line [math]y = z[/math] in at most two points. Since we know it must intersect the line [math]y = z[/math] at [math](1,1)[/math], we know that there are just three possibilities, as shown in Figure.
In case (a) the equation [math]d = h(d)[/math] has roots [math]\{d,1\}[/math] with [math]0 \leq d \lt 1[/math]. In the second case (b) it has only the one root [math]d = 1[/math]. In case (c) it has two roots [math]\{1,d\}[/math] where [math]1 \lt d[/math]. Since we are looking for a solution [math]0 \leq d \leq 1[/math], we see in cases (b) and (c) that our only solution is 1. In these cases we can conclude that the process will die out with probability 1. However in case (a) we are in doubt. We must study this case more carefully.
From Equation \ref{eq 10.2.4} we see that
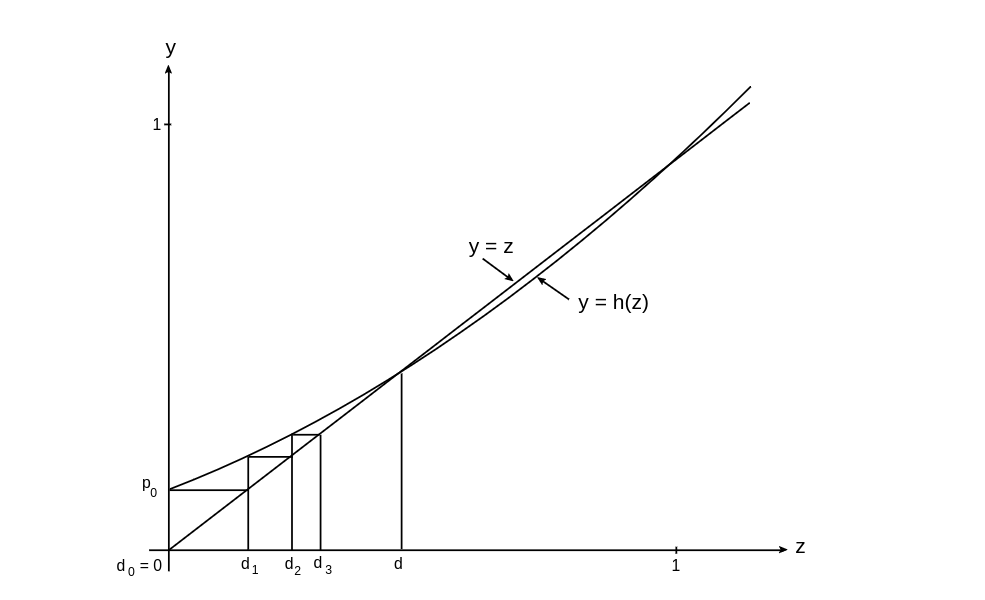
where [math]m[/math] is the expected number of offspring produced by a single parent. In case (a) we have [math]h'(1) \gt 1[/math], in (b) [math]h'(1) = 1[/math], and in (c) [math]h'(1) \lt 1[/math]. Thus our three cases correspond to [math]m \gt 1[/math], [math]m = 1[/math], and [math]m \lt 1[/math]. We assume now that [math]m \gt 1[/math]. Recall that [math]d_0 = 0[/math], [math]d_1 = h(d_0) = p_0[/math], [math]d_2 = h(d_1)[/math], \ldots, and [math]d_n = h(d_{n - 1})[/math]. We can construct these values geometrically, as shown in Figure.
We can see geometrically, as indicated for [math]d_0[/math], [math]d_1[/math], [math]d_2[/math], and [math]d_3[/math] in
Figure, that the points [math](d_i,h(d_i))[/math] will always lie above the line [math]y =
z[/math]. Hence, they must converge to the first intersection of the curves [math]y = z[/math]
and [math]y = h(z)[/math] (i.e., to the root [math]d \lt 1[/math]). This leads us to the following
theorem.
Consider a branching process with generating function [math]h(z)[/math] for the number of offspring of a given parent. Let [math]d[/math] be the smallest root of the equation [math]z = h(z)[/math]. If the mean number [math]m[/math] of offspring produced by a single parent is [math]{} \leq 1[/math], then [math]d = 1[/math] and the process dies out with probability 1. If [math]m \gt 1[/math] then [math]d \lt 1[/math] and the process dies out with probability [math]d[/math].
We shall often want to know the probability that a branching process dies out by a particular generation, as well as the limit of these probabilities. Let [math]d_n[/math] be the probability of dying out by the [math]n[/math]th generation. Then we know that [math]d_1 = p_0[/math]. We know further that [math]d_n = h(d_{n - 1})[/math] where [math]h(z)[/math] is the generating function for the number of offspring produced by a single parent. This makes it easy to compute these probabilities.
The program Branch calculates the values of [math]d_n[/math]. We have run this program for 12 generations for the case that a parent can produce at most two offspring and the probabilities for the number produced are [math]p_0 = .2[/math], [math]p_1 = .5[/math], and [math]p_2 = .3[/math]. The results are given in Table.
| Generation | Probability of dying out |
| 1 | .2 |
| 2 | .312 |
| 3 | .385203 |
| 4 | .437116 |
| 5 | .475879 |
| 6 | .505878 |
| 7 | .529713 |
| 8 | .549035 |
| 9 | .564949 |
| 10 | .578225 |
| 11 | .589416 |
| 12 | .598931 |
We see that the probability of dying out by 12 generations is about .6. We shall see in the next example that the probability of eventually dying out
is 2/3, so that even 12 generations is not enough to give an accurate estimate for this probability.
We now assume that at most two offspring can be produced. Then
In this simple case the condition [math]z = h(z)[/math] yields the equation
which is satisfied by [math]d = 1[/math] and [math]d = p_0/p_2[/math]. Thus, in addition to the root [math]d = 1[/math] we have the second root [math]d = p_0/p_2[/math]. The mean number [math]m[/math] of offspring produced by a single parent is
Thus, if [math]p_0 \gt p_2[/math], [math]m \lt 1[/math] and the second root is [math]{} \gt 1[/math]. If [math]p_0 = p_2[/math], we have a double root [math]d = 1[/math]. If [math]p_0 \lt p_2[/math], [math]m \gt 1[/math] and the second root [math]d[/math] is less than 1 and represents the probability that the process will die out.
Example Keyfitz[Notes 6] compiled and analyzed data on the continuation of the female family line among Japanese women. His estimates at the basic probability distribution for the number of female children born to Japanese women of ages 45--49 in 1960 are given in Table.
| [math]p_0[/math] | = .2092 |
| [math]p_1[/math] | = .2584 |
| [math]p_2[/math] | = .2360 |
| [math]p_3[/math] | = .1593 |
| [math]p_4[/math] | = .0828 |
| [math]p_5[/math] | = .0357 |
| [math]p_6[/math] | = .0133 |
| [math]p_7[/math] | = .0042 |
| [math]p_8[/math] | = .0011 |
| [math]p_9[/math] | = .0002 |
| [math]p_{10}[/math] | = .0000 |
The expected number of girls in a family is then 1.837 so the probability [math]d[/math] of extinction is less than 1. If we run the program Branch, we can estimate that [math]d[/math] is in fact only about .324.
Distribution of Offspring
So far we have considered only the first of the two problems raised by Galton, namely the probability of extinction. We now consider the second problem, that is, the distribution of the number [math]Z_n[/math] of offspring in the [math]n[/math]th generation. The exact form of the distribution is not known except in very special cases. We shall see, however, that we can describe the limiting behavior of [math]Z_n[/math] as [math]n \to \infty[/math].
We first show that the generating function [math]h_n(z)[/math] of the distribution
of [math]Z_n[/math] can be obtained from [math]h(z)[/math] for any branching process.
We recall that the value of the generating function at the value [math]z[/math] for any
random variable [math]X[/math] can be written as
That is, [math]h(z)[/math] is the expected value of an experiment which has outcome [math]z^j[/math] with probability [math]p_j[/math].
Let [math]S_n = X_1 + X_2 +\cdots+ X_n[/math] where each
[math]X_j[/math] has the same integer-valued distribution [math](p_j)[/math] with generating function
[math]k(z) = p_0 + p_1z + p_2z^2 +\cdots.[/math] Let [math]k_n(z)[/math] be the generating function
of [math]S_n[/math]. Then using one of the properties of ordinary generating functions discussed in Generating Functions for Discrete Distributions, we have
since the [math]X_j[/math]'s are independent and all have the same distribution.
Consider now the branching process [math]Z_n[/math]. Let [math]h_n(z)[/math] be the generating
function of [math]Z_n[/math]. Then
If [math]Z_n = k[/math], then [math]Z_{n + 1} = X_1 + X_2 +\cdots+ X_k[/math] where [math]X_1[/math], [math]X_2[/math], \ldots, [math]X_k[/math] are independent random variables with common generating function [math]h(z)[/math]. Thus
and
But
Thus,
If we differentiate Equation \ref{eq 10.2.5} and use the chain rule we have
Putting [math]z = 1[/math] and using the fact that [math]h(1) = 1[/math], [math]h'(1) = m[/math], and [math]h_n'(1) = m_n = {}[/math]the mean number of offspring in the [math]n[/math]'th generation, we have
Thus, [math]m_2 = m \cdot m = m^2[/math], [math]m_3 = m^2 \cdot m = m^3[/math], and in general
Thus, for a branching process with [math]m \gt 1[/math], the mean number of offspring grows exponentially at a rate [math]m[/math].
Examples
Example For the branching process of Example we have
The probabilities for the number of offspring in the second generation agree with those obtained directly from the tree measure (see Figure 1).
It is clear that even in the simple case of at most two offspring, we cannot easily carry out the calculation of [math]h_n(z)[/math] by this method. However, there is one special case in which this can be done.
Example Assume that the probabilities [math]p_1, p_2, \ldots[/math] form a geometric series: [math]p_k = bc^{k - 1}[/math], [math]k = 1, 2, \ldots,[/math] with [math]0 \lt b \leq 1 - c[/math] and [math]0 \lt c \lt 1[/math]. Then we have
The generating function [math]h(z)[/math] for this distribution is
From this we find
and
We know that if [math]m \leq 1[/math] the process will surely die out and [math]d = 1[/math]. To find the probability [math]d[/math] when [math]m \gt 1[/math] we must find a root [math]d \lt 1[/math] of the equation
or
This leads us to a quadratic equation. We know that [math]z = 1[/math] is one solution. The other is found to be
It is easy to verify that [math]d \lt 1[/math] just when [math]m \gt 1[/math]. It is possible in this case to find the distribution of [math]Z_n[/math]. This is done by first finding the generating function [math]h_n(z)[/math].[Notes 7] The result for [math]m \ne 1[/math] is:
The coefficients of the powers of [math]z[/math] give the distribution for [math]Z_n[/math]:
and
for [math]j \geq 1[/math].
Example Let us re-examine the Keyfitz data to see if a distribution of the type considered in Example could reasonably be used as a model for this population. We would have to estimate from the data the parameters [math]b[/math] and [math]c[/math] for the formula [math]p_k = bc^{k - 1}[/math]. Recall that
and the probability [math]d[/math] that the process dies out is
Solving \ref{eq 10.2.7} and \ref{eq 10.2.8} for [math]b[/math] and [math]c[/math] gives
and
We shall use the value 1.837 for [math]m[/math] and .324 for [math]d[/math] that we found in the Keyfitz example. Using these values, we obtain [math]b = .3666[/math] and [math]c = .5533[/math]. Note that [math](1 - c)^2 \lt b \lt 1 - c[/math], as required. In Table we give for comparison the probabilities [math]p_0[/math] through [math]p_8[/math] as calculated by the geometric distribution versus the empirical values.
| [math]p_j[/math] | Data | Geometric Model |
| 0 | .2092 | .1816 |
| 1 | .2584 | .3666 |
| 2 | .2360 | .2028 |
| 3 | .1593 | .1122 |
| 4 | .0828 | .0621 |
| 5 | .0357 | .0344 |
| 6 | .0133 | .0190 |
| 7 | .0042 | .0105 |
| 8 | .0011 | .0058 |
| 9 | .0002 | .0032 |
| 10 | .0000 | .0018 |
The geometric model tends to favor the larger numbers of offspring but is
similar enough to show that this modified geometric distribution might be
appropriate to use for studies of this kind.
Recall that if [math]S_n = X_1 + X_2 +\cdots+ X_n[/math] is the sum of independent random
variables with the same distribution then the Law of Large Numbers states that
[math]S_n/n[/math] converges to a constant, namely [math]E(X_1)[/math]. It is natural to ask if
there is a similar limiting theorem for branching processes.
Consider a branching process with [math]Z_n[/math] representing the number of offspring
after [math]n[/math] generations. Then we have seen that the expected value of [math]Z_n[/math]
is [math]m^n[/math]. Thus we can scale the random variable [math]Z_n[/math] to have expected value 1
by considering the random variable
In the theory of branching processes it is proved that this random variable [math]W_n[/math] will tend to a limit as [math]n[/math] tends to infinity. However, unlike the case of the Law of Large Numbers where this limit is a constant, for a branching process the limiting value of the random variables [math]W_n[/math] is itself a random variable. Although we cannot prove this theorem here we can illustrate it by simulation. This requires a little care. When a branching process survives, the number of offspring is apt to get very large. If in a given generation there are 1000 offspring, the offspring of the next generation are the result of 1000 chance events, and it will take a while to simulate these 1000 experiments. However, since the final result is the sum of 1000 independent experiments we can use the Central Limit Theorem to replace these 1000 experiments by a single experiment with normal density having the appropriate mean and variance. The program BranchingSimulation carries out this process.
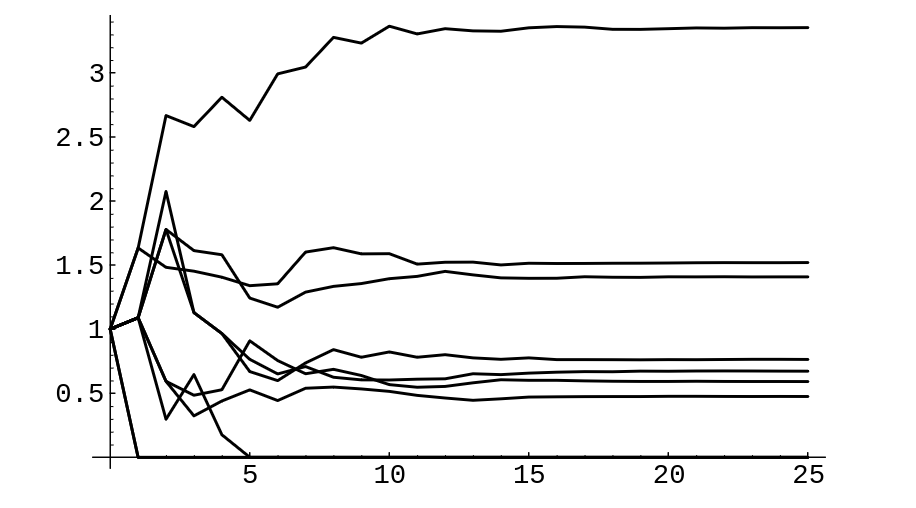
We have run this program for the Keyfitz example, carrying out 10 simulations
and graphing the results in Figure.
The expected number of female offspring per female is 1.837, so that we are graphing the outcome for the random variables [math]W_n = Z_n/(1.837)^n[/math]. For three of the simulations the process died out, which is consistent with the value [math]d = .3[/math] that we found for this example. For the other seven simulations the value of [math]W_n[/math] tends to a limiting value which is different for each simulation.
Example We now examine the random variable [math]Z_n[/math] more closely for the case [math]m \lt 1[/math] (see Example). Fix a value [math]t \gt 0[/math]; let [math][tm^n][/math] be the integer part of [math]tm^n[/math]. Then
where [math]|a| \leq 2[/math]. Thus, as [math]n \to \infty[/math],
For [math]t = 0[/math],
We can compare this result with the Central Limit Theorem for sums [math]S_n[/math] of integer-valued independent random variables (see Theorem), which states that if [math]t[/math] is an integer and [math]u = (t - n\mu)/\sqrt{\sigma^2 n}[/math], then as [math]n \to \infty[/math],
We see that the form of these statements are quite similar. It is possible to prove a limit theorem for a general class of branching processes that states that under suitable hypotheses, as [math]n \to \infty[/math],
for [math]t \gt 0[/math], and
However, unlike the Central Limit Theorem for sums of independent random variables, the function [math]k(t)[/math] will depend upon the basic distribution that determines the process. Its form is known for only a very few examples similar to the one we have considered here.
Chain Letter Problem
Example An interesting example of a branching process was suggested by Free Huizinga.[Notes 8] In 1978, a chain letter called the “Circle of Gold,” believed to have started in California, found its way across the country to the theater district of New York. The chain required a participant to buy a letter containing a list of 12 names for 100 dollars. The buyer gives 50 dollars to the person from whom the letter was purchased and then sends 50 dollars to the person whose name is at the top of the list. The buyer then crosses off the name at the top of the list and adds her own name at the bottom in each letter before it is sold again.
Let us first assume that the buyer may sell the letter only to a single person. If you buy the letter you will want to compute your expected winnings. (We are ignoring here the fact that the passing on of chain letters through the mail is a federal offense with certain obvious resulting penalties.) Assume that each person involved has a probability [math]p[/math] of selling the letter. Then you will receive 50 dollars with probability [math]p[/math] and another 50 dollars if the letter is sold to 12 people, since then your name would have risen to the top of the list. This occurs with probability [math]p^{12}[/math], and so your expected winnings are [math]-100 + 50p + 50p^{12}[/math]. Thus the chain in this situation is a highly unfavorable game.
It would be more reasonable to allow each person involved to make a copy of the list and try to sell the letter to at least 2 other people. Then you would have a chance of recovering your 100 dollars on these sales, and if any of the letters is sold 12 times you will receive a bonus of 50 dollars for each of these cases. We can consider this as a branching process with 12 generations. The members of the first generation are the letters you sell. The second generation consists of the letters sold by members of the first generation, and so forth.
Let us assume that the probabilities that each individual sells letters to 0, 1, or 2 others are [math]p_0[/math], [math]p_1[/math], and [math]p_2[/math], respectively. Let [math]Z_1[/math], [math]Z_2[/math], \ldots, [math]Z_{12}[/math] be the number of letters in the first 12 generations of this branching process. Then your expected winnings are
where [math]m = p_1 + 2p_2[/math] is the expected number of letters you sold. Thus to be favorable we just have
or
But this will be true if and only if [math]m \gt 1[/math]. We have seen that this will occur in the quadratic case if and only if [math]p_2 \gt p_0[/math]. Let us assume for example that [math]p_0 = .2[/math], [math]p_1 = .5[/math], and [math]p_2 = .3[/math]. Then [math]m = 1.1[/math] and the chain would be a favorable game. Your expected profit would be
The probability that you receive at least one payment from the 12th generation is [math]1 - d_{12}[/math]. We find from our program Branch that [math]d_{12} = .599[/math]. Thus, [math]1 - d_{12} = .401[/math] is the probability that you receive some bonus. The maximum that you could receive from the chain would be [math]50(2 + 2^{12}) = 204,00[/math] if everyone were to successfully sell two letters. Of course you can not always expect to be so lucky. (What is the probability of this happening?) To simulate this game, we need only simulate a branching process for 12 generations. Using a slightly modified version of our program BranchingSimulation we carried out twenty such simulations, giving the results shown in Table. Note that we were quite lucky on a few runs, but we came out ahead only a little less than half the time. The process died out by the twelfth generation in 12 out of the 20 experiments, in good agreement with the probability [math]d_{12} = .599[/math] that we calculated using the program Branch.
| [math]Z_{1}[/math] | [math]Z_{2}[/math] | [math] Z_{3}[/math] | [math]Z_{4}[/math] | [math]Z_{5}[/math] | [math]Z_{6}[/math] | [math]Z_{7}[/math] | [math]Z_{8}[/math] | [math]Z_{9}[/math] | [math] Z_{10}[/math] | [math] Z_{11}[/math] | [math]Z_{12}[/math] | Profit |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 1 | 2 | 3 | 2 | 3 | 2 | 1 | 2 | 3 | 3 | 6 | 250 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -100 |
| 2 | 4 | 4 | 2 | 3 | 4 | 4 | 3 | 2 | 2 | 1 | 1 | 50 |
| 1 | 2 | 3 | 5 | 4 | 3 | 3 | 3 | 5 | 8 | 6 | 6 | 250 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -100 |
| 2 | 3 | 2 | 2 | 2 | 1 | 2 | 3 | 3 | 3 | 4 | 6 | 300 |
| 1 | 2 | 1 | 1 | 1 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | -50 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -100 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 2 | 3 | 2 | 3 | 3 | 3 | 5 | 9 | 12 | 12 | 13 | 15 | 750 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 2 | 2 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 6 | 4 | 5 | 200 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 1 | 2 | 3 | 3 | 4 | 2 | 3 | 3 | 3 | 3 | 2 | 50 |
| 1 | 2 | 4 | 6 | 6 | 9 | 10 | 13 | 16 | 17 | 15 | 18 | 850 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
Let us modify the assumptions about our chain letter to let the buyer sell the letter to as many people as she can instead of to a maximum of two. We shall assume, in fact, that a person has a large number [math]N[/math] of acquaintances and a small probability [math]p[/math] of persuading any one of them to buy the letter. Then the distribution for the number of letters that she sells will be a binomial distribution with mean [math]m = Np[/math]. Since [math]N[/math] is large and [math]p[/math] is small, we can assume that the probability [math]p_j[/math] that an individual sells the letter to [math]j[/math] people is given by the Poisson distribution
The generating function for the Poisson distribution is
The expected number of letters that an individual passes on is [math]m[/math], and again
to be favorable we must have [math]m \gt 1[/math]. Let us assume again that [math]m = 1.1[/math].
Then we can find again the probability [math]1 - d_{12}[/math] of a bonus from Branch. The result is .232. Although the expected winnings are the same, the variance is larger in this case, and the buyer has a better chance for a
reasonably large profit. We again carried out 20 simulations using the Poisson
distribution with mean 1.1. The results are shown in Table.
| [math]Z_{1}[/math] | [math]Z_{2}[/math] | [math] Z_{3}[/math] | [math]Z_{4}[/math] | [math]Z_{5}[/math] | [math]Z_{6}[/math] | [math]Z_{7}[/math] | [math]Z_{8}[/math] | [math]Z_{9}[/math] | [math] Z_{10}[/math] | [math] Z_{11}[/math] | [math]Z_{12}[/math] | Profit |
| 1 | 2 | 6 | 7 | 7 | 8 | 11 | 9 | 7 | 6 | 6 | 5 | 200 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -100 |
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 4 | 9 | 7 | 9 | 7 | 300 |
| 2 | 3 | 3 | 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | 4 | 7 | 11 | 17 | 14 | 11 | 11 | 10 | 16 | 25 | 1300 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -100 |
| 1 | 2 | 2 | 1 | 1 | 3 | 1 | 0 | 0 | 0 | 0 | 0 | -50 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -100 |
| 2 | 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
| 3 | 4 | 4 | 7 | 10 | 11 | 9 | 11 | 12 | 14 | 13 | 10 | 550 |
| 1 | 3 | 3 | 4 | 9 | 5 | 7 | 9 | 8 | 8 | 6 | 3 | 100 |
| 1 | 0 | 4 | 6 | 6 | 9 | 10 | 13 | 0 | 0 | 0 | 0 | -50 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -50 |
We note that, as before, we came out ahead less than half the time, but we also
had one large profit. In only 6 of the 20 cases did we receive any profit.
This is again in reasonable agreement with our calculation of a probability
.232 for this happening.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- D.G. Kendall, “Branching Processes Since 1873,” Journal of London Mathematics Society, vol.41 (1966), p.386.
- C. C. Heyde and E. Seneta, I. J. Bienaymé: Statistical Theory Anticipated (New York: Springer Verlag, 1977).
- ibid., pp. 117--118.
- ibid., p. 118.
- D. G. Kendall, “Branching Processes Since 1873,” pp. 385--406; and “The Genealogy of Genealogy: Branching Processes Before (and After) 1873,” Bulletin London Mathematics Society, vol. 7 (1975), pp. 225--253.
- N. Keyfitz, Introduction to the Mathematics of Population, rev. ed. (Reading, PA: Addison Wesley, 1977).
- T. E. Harris, The Theory of Branching Processes (Berlin: Springer, 1963), p. 9.
- Private communication.