guide:Ebe68e8408: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 33: | Line 33: | ||
</math></div> | </math></div> | ||
This section contains a number of theorems which provide an important technique for finding the limit of the quotient of two functions. These theorems are usually referred to collectively as L'H\ôpital's Rule. Two examples of problems which are readily solved by this technique are the computations of the limits: | This section contains a number of theorems which provide an important technique for finding the limit of the quotient of two functions. These theorems are usually referred to collectively as L'H\ôpital's Rule. Two examples of problems which are readily solved by this technique are the computations of the limits: | ||
| Line 42: | Line 41: | ||
Properly speaking, this section is a continuation of Section 5, since all the results are corollaries of Rolle's Theorem and of the Mean Value Theorem. | Properly speaking, this section is a continuation of Section 5, since all the results are corollaries of Rolle's Theorem and of the Mean Value Theorem. | ||
The following proposition, known as the Generalized Mean Value Theorem, is the basic lemma used in proving the theorems which make up L'H\ôpital's Rule. (A lemma is a theorem included as a reference in proving other theorems.) | The following proposition, known as the Generalized Mean Value Theorem, is the basic lemma used in proving the theorems which make up L'H\ôpital's Rule. (A lemma is a theorem included as a reference in proving other theorems.) | ||
{{proofcard| | {{proofcard|GENERALIZED MEAN VALUE THEOREM|theorem-1|Assume that <math>a < b</math>, and let <math>f</math> and <math>g</math> be functions which are continuous on the closed interval <math>[a, b]</math> and differentiable on the open interval <math>(a, b)</math>. If <math>g'(x) \neq 0</math> for every<math> x</math> in <math>(a, b)</math>, then there exists a real number <math>c</math> in <math>(a, b)</math> such that | ||
<math display="block"> | <math display="block"> | ||
| Line 64: | Line 63: | ||
0 = f'(c) - {\frac{f(b) - f(a)}{g(b) - g(a)}} g'(c), | 0 = f'(c) - {\frac{f(b) - f(a)}{g(b) - g(a)}} g'(c), | ||
</math> | </math> | ||
We first present L'H\ôpital's Rule as a theorem about one-sided limits. | We first present L'H\ôpital's Rule as a theorem about one-sided limits. | ||
{{proofcard| | {{proofcard|L'HÔPITAL'S RULE I|theorem-2|Let <math>f</math> and <math>g</math> be functions which are differentiable on a nonempty open interval <math>(a, b)</math> with <math>g'(x) \neq 0</math> for every <math>x</math> in <math>(a, b)</math>. If, in addition, | ||
| Line 85: | Line 84: | ||
</math> | </math> | ||
for some number <math>y</math> in <math>(a, x)</math>. As <math>x</math> approaches a from the right, so also does <math>y</math>, and hence <math>\lim_{x \rightarrow a+} \frac{f(x)}{g(x)} = \lim_{y \rightarrow a+}\frac{f'(y)}{g'(x)} = L</math>. This completes the proof.}} | for some number <math>y</math> in <math>(a, x)</math>. As <math>x</math> approaches a from the right, so also does <math>y</math>, and hence <math>\lim_{x \rightarrow a+} \frac{f(x)}{g(x)} = \lim_{y \rightarrow a+}\frac{f'(y)}{g'(x)} = L</math>. This completes the proof.}} | ||
'''Example''' | '''Example''' | ||
| Line 104: | Line 104: | ||
It is a simple matter to verify that Theorem (7.2) remains true if <math>(a, b)</math> is replaced throughout by <math>(b, a)</math>, and <math>\lim_{x \rightarrow a+}</math> is replaced throughout by <math>\lim_{x \rightarrow a-}</math>. This fact, significant in itself, also implies the following two-sided form of L'H\ôpital's Rule. | It is a simple matter to verify that Theorem (7.2) remains true if <math>(a, b)</math> is replaced throughout by <math>(b, a)</math>, and <math>\lim_{x \rightarrow a+}</math> is replaced throughout by <math>\lim_{x \rightarrow a-}</math>. This fact, significant in itself, also implies the following two-sided form of L'H\ôpital's Rule. | ||
{{proofcard| | {{proofcard|L'HÔPITAL'S RULE II|theorem-3|Consider an open interval containing the number <math>a</math>, and let <math>f</math> and <math>g</math> be functions differentiable and with <math>g'(x) \neq 0</math> at every point of the interval except possibly at <math>a</math>. If | ||
\item[i] <math>\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) = 0</math>, | \item[i] <math>\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) = 0</math>, | ||
| Line 126: | Line 126: | ||
</math> | </math> | ||
'''Example''' | '''Example''' | ||
| Line 182: | Line 181: | ||
</math> | </math> | ||
A variation of (7.2), not difficult to prove, is the following: | A variation of (7.2), not difficult to prove, is the following: | ||
{{proofcard| | {{proofcard|L'HÔPITAL'S RULE III|theorem-4|Let <math>f</math> and <math>g</math> be differentiable on an open interval <math>(a, \infty)</math> with <math>g'(x) \neq 0</math> for <math>x > a</math>. If | ||
\item[i] <math>\lim_{x \rightarrow \infty} f(x) = \lim_{x \rightarrow \infty} g(x) = 0</math>, | \item[i] <math>\lim_{x \rightarrow \infty} f(x) = \lim_{x \rightarrow \infty} g(x) = 0</math>, | ||
| Line 222: | Line 220: | ||
= \lim_{x \rightarrow \infty} \frac{f'(x)}{g'(x)} = L. | = \lim_{x \rightarrow \infty} \frac{f'(x)}{g'(x)} = L. | ||
</math> | </math> | ||
By L' | By L'Hôpital's Rule I it follows that <math>\lim_{t \rightarrow 0+} \frac{F(t)}{G(t)} = L</math>. Hence | ||
<math display="block"> | <math display="block"> | ||
| Line 228: | Line 226: | ||
</math> | </math> | ||
and the proof is complete.}} | and the proof is complete.}} | ||
An important observation is that all the forms of L' | An important observation is that all the forms of L'Hôpital's Rule developed so far are valid whether <math>L</math> is finite or not. This fact requires no new proof and has really already been established. The reason is that the basic conclusion of Theorem (7.2) is the equation | ||
<math display="block"> | <math display="block"> | ||
| Line 234: | Line 232: | ||
</math> | </math> | ||
and this holds good whether or not <math>\lim_{x \rightarrow a+}\frac{f'(x)}{g'(x)}</math> is finite or infinite. | and this holds good whether or not <math>\lim_{x \rightarrow a+}\frac{f'(x)}{g'(x)}</math> is finite or infinite. | ||
There is another significant variation of L'Hôpital's Rule, whose proof, although requiring only the Generalized Mean Value Theorem, cannot (as far as we know) be obtained from (7.2) by a simple substitution. It states that the several forms of condition (i), <math>\lim f(x) = \lim g(x)= 0</math>, can be replaced by <math>\lim |g(x)| = \infty</math>. The specific statement which we prove is the following: | |||
{{proofcard|L'HÔPITAL'S RULE IV|theorem-5|Let <math>f</math> and <math>g</math> be functions which are differentiable on a nonempty open interval <math>(a, b)</math> with <math>g'(x) \neq 0</math> for every <math>x</math> in <math>(a, b)</math>. If | |||
<ul style{{=}}"list-style-type:lower-roman"> | |||
<li> | |||
<math>\lim_{t \rightarrow a+} |g(x)| = \infty</math>, | |||
</li> | |||
<li> | |||
<math>\lim_{t \rightarrow a+} \frac{f'(x)}{g'(x)} = L</math>, | |||
</li> | |||
</ul> | |||
then | then | ||
| Line 250: | Line 254: | ||
<math display="block"> | <math display="block"> | ||
\Big| \frac{f'(x)}{g'(x)} - L \Big| < \varepsilon, \;\;\; \mbox{for every $x$ in | \Big| \frac{f'(x)}{g'(x)} - L \Big| < \varepsilon, \;\;\; \mbox{for every $x$ in $(a, c)$}. | ||
</math> | </math> | ||
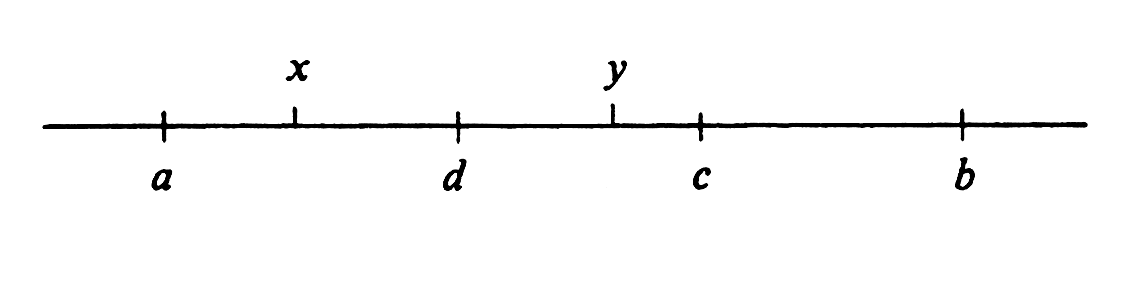
By hypothesis (i) there exists a real number <math>d</math> in <math>(a, b)</math>, which we shall for convenience assume to be in <math>(a, c)</math>, such that, for every <math>x</math> in <math>(a, d)</math>, the following three inequalities hold: | By hypothesis (i) there exists a real number <math>d</math> in <math>(a, b)</math>, which we shall for convenience assume to be in <math>(a, c)</math>, such that, for every <math>x</math> in <math>(a, d)</math>, the following three inequalities hold: | ||
| Line 258: | Line 262: | ||
</math> | </math> | ||
(see [[#fig 2.22|Figure]]). | (see [[#fig 2.22|Figure]]). | ||
<div id="fig 2.22" class="d-flex justify-content-center"> | |||
<div id{{=}}"fig 2.22" class{{=}}"d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig2_22.png | 400px | thumb | ]] | [[File:guide_c5467_scanfig2_22.png | 400px | thumb | ]] | ||
</div> | </div> | ||
It is a consequence of the last inequality that | It is a consequence of the last inequality that | ||
<math display="block"> | <math display="block"> | ||
\Big| 1 - \frac{g(c)}{g(x)} \Big| < 1 + \varepsilon, \;\;\; \mbox{for every $x$ in | \Big| 1 - \frac{g(c)}{g(x)} \Big| < 1 + \varepsilon, \;\;\; \mbox{for every $x$ in $(a, d)$}. | ||
</math> | </math> | ||
| Line 300: | Line 306: | ||
Since the right side of this inequality can be made arbitrarily small by taking <math>\varepsilon</math> sufficiently small, it follows that <math>\lim_{t \rightarrow a+} \frac{f(x)}{g(x)} = L</math>, and the proof is complete.}} | Since the right side of this inequality can be made arbitrarily small by taking <math>\varepsilon</math> sufficiently small, it follows that <math>\lim_{t \rightarrow a+} \frac{f(x)}{g(x)} = L</math>, and the proof is complete.}} | ||
It is not difficult to derive variations of the preceding theorem analogous to the modified versions of (7.2) described above. Thus, with the obvious changes in the hypotheses, this last form of L'H\ôpital's Rule also holds for two-sided limits and with <math>a</math> or <math>L</math> (or both) replaced by <math>\pm \infty</math>. | It is not difficult to derive variations of the preceding theorem analogous to the modified versions of (7.2) described above. Thus, with the obvious changes in the hypotheses, this last form of L'H\ôpital's Rule also holds for two-sided limits and with <math>a</math> or <math>L</math> (or both) replaced by <math>\pm \infty</math>. | ||
'''Example''' | '''Example''' | ||
| Line 316: | Line 323: | ||
The several forms of L'H\ôpital's Rule which we have derived in this section fall naturally into two types, symbolically denoted as the <math>\frac{0}{0}</math> type and the <math>\frac{*}{\infty}</math> type. Theorems (7.2), (7.3), and (7.4) are all examples of the first type, whereas the harder Theorem (7.5) is the prototype of the second type. The full power of the <math>\frac{*}{\infty}</math> forms will be realized later in the book in conjunction with the logarithmic, exponential, and trigonometric functions. | The several forms of L'H\ôpital's Rule which we have derived in this section fall naturally into two types, symbolically denoted as the <math>\frac{0}{0}</math> type and the <math>\frac{*}{\infty}</math> type. Theorems (7.2), (7.3), and (7.4) are all examples of the first type, whereas the harder Theorem (7.5) is the prototype of the second type. The full power of the <math>\frac{*}{\infty}</math> forms will be realized later in the book in conjunction with the logarithmic, exponential, and trigonometric functions. | ||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | {{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | ||
Revision as of 02:26, 5 November 2024
This section contains a number of theorems which provide an important technique for finding the limit of the quotient of two functions. These theorems are usually referred to collectively as L'H\ôpital's Rule. Two examples of problems which are readily solved by this technique are the computations of the limits:
Properly speaking, this section is a continuation of Section 5, since all the results are corollaries of Rolle's Theorem and of the Mean Value Theorem. The following proposition, known as the Generalized Mean Value Theorem, is the basic lemma used in proving the theorems which make up L'H\ôpital's Rule. (A lemma is a theorem included as a reference in proving other theorems.) {{proofcard|GENERALIZED MEAN VALUE THEOREM|theorem-1|Assume that [math]a \lt b[/math], and let [math]f[/math] and [math]g[/math] be functions which are continuous on the closed interval [math][a, b][/math] and differentiable on the open interval [math](a, b)[/math]. If [math]g'(x) \neq 0[/math] for every[math] x[/math] in [math](a, b)[/math], then there exists a real number [math]c[/math] in [math](a, b)[/math] such that
Note that [math]g(b)-g(a) \neq 0[/math]. For otherwise the Mean Value Theorem would imply that [math]g'(x) = 0[/math] for some [math]x[/math] in [math](a, b)[/math], which is contrary to hypothesis. |Let [math]h[/math] be the function defined by
for every [math]x[/math] in [math][a, b][/math]. The function [math]h[/math] is continuous on [math][a, b][/math], differentiable on [math](a, b)[/math], and, in addition, [math]h(a) = h(b) = 0[/math]. Hence, by Rolle's Theorem, there exists a real number [math]c[/math] in [math](a, b)[/math] such that [math]h'(c) = 0[/math]. Since
we obtain
We first present L'H\ôpital's Rule as a theorem about one-sided limits.
Let [math]f[/math] and [math]g[/math] be functions which are differentiable on a nonempty open interval [math](a, b)[/math] with [math]g'(x) \neq 0[/math] for every [math]x[/math] in [math](a, b)[/math]. If, in addition,
\item[i] [math]\lim_{x \rightarrow a+} f(x) = \lim_{x \rightarrow a+} g(x)= 0[/math],]
\item[(ii) [math]\lim_{x \rightarrow a+} \frac{f'(x)}{g'(x)} = L[/math],
then
We may assume that [math]f(a) = g(a) = 0[/math]. (If this is not the case to begin with, we simply define, or redefine, the values of [math]f[/math] and [math]g[/math] to be zero at [math]a[/math].) Thus we ensure that [math]f[/math] and [math]g[/math] are continuous on [math][a, b)[/math]. Let [math]x[/math] be an arbitrary number in [math](a, b)[/math]. Then [math]f[/math] and [math]g[/math] are continuous on [math][a, x][/math] (recall that differentiability at a point implies continuity) and are differentiable on [math](a, x)[/math]. Moreover, the derivative [math]g'[/math] does not take on the value zero in [math](a, x)[/math]. Hence, by the Generalized Mean Value Theorem and the fact that [math]f(a) = g(a) = 0[/math], we obtain
Example
Compute [math]\lim_{x \rightarrow 2+}\frac{\sqrt x - \sqrt 2}{\sqrt{x-2}}.[/math] Let [math]f (x) = \sqrt x - \sqrt 2[/math] and [math]g(x) = \sqrt {x - 2}[/math]. Obviously, [math]\lim_{x \rightarrow 2+} f(x) = \lim_{x \rightarrow 2+} g(x) = 0[/math], and, since
[math]f[/math] and [math]g[/math] are differentiable, and [math]g'[/math] does not take on the value zero on any open interval with left endpoint equal to 2. We obtain
And it follows by L'H\ôpital's Rule that [math]\lim_{x \rightarrow 2+} \frac{\sqrt x - \sqrt 2}{\sqrt{x-2}} = 0[/math]. It is a simple matter to verify that Theorem (7.2) remains true if [math](a, b)[/math] is replaced throughout by [math](b, a)[/math], and [math]\lim_{x \rightarrow a+}[/math] is replaced throughout by [math]\lim_{x \rightarrow a-}[/math]. This fact, significant in itself, also implies the following two-sided form of L'H\ôpital's Rule.
Consider an open interval containing the number [math]a[/math], and let [math]f[/math] and [math]g[/math] be functions differentiable and with [math]g'(x) \neq 0[/math] at every point of the interval except possibly at [math]a[/math]. If
\item[i] [math]\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) = 0[/math], \item[ii] [math]\lim_{x \rightarrow a} \frac{f'(x)}{g'(x)} = L[/math],
then
The hypotheses of (7.3) have been taken as weak as possible. If, as frequently happens, the functions [math]f[/math] and [math]g[/math] are also continuous at [math]a[/math], then (i) can be replaced by the simpler condition [math]f(a) = g(a) = 0[/math].
Example
Evaluate [math]\lim_{x \rightarrow a}\frac{x^{1/2} - a^{1/2}}{x^{1/3} - a^{1/3}}[/math], where [math]a \gt 0[/math]. If [math]f(x) = x^{1/2} - a^{1/2}[/math] and if [math]g(x) = x^{1/3} - a^{1/3}[/math], then the derivatives are given by [math]f' (x) = \frac{1}{2x^{1/2}}[/math] and [math]g'(x) = \frac{1}{3x^{2/3}}[/math], and it is clear that [math]f[/math] and [math]g[/math] are differentiable (and hence continuous) and [math]g'[/math] is not zero on an open interval containing [math]a[/math]. Moreover, [math]f(a) = g(a) = 0[/math]. Hence, by L'H\ôpital's Rule,
Example
Compute [math]\lim_{x \rightarrow a}\frac{x - a}{x^2 - a^2}[/math] where [math]a \neq 0 [/math]. Doing this problem by L'H\ôpital's Rule is somewhat akin to smashing a peanut with a sledgehammer. The fact that
immediately implies that
Of course, the same answer is obtained by L'H\ôpital's Rule. If we let [math]f(x) = x - a[/math] and [math]g(x) = x^2 - a^2[/math], then [math]f(a) = g(a) = 0[/math] and [math]f'(x) = 1[/math] and [math]g'(x) = 2x[/math]. Hence
It is important to realize that L'H\ôpital's Rule II can be applied only if the function [math]\frac{f(x)}{g(x)}[/math] is unclefined at [math]x = a[/math] and if [math]\lim_{x \rightarrow a}f(x) = \lim_{x \rightarrow a} g(x) = 0.[/math] For example, if [math]f(x) = x^2 + 3x - 10[/math] and [math]g(x) = 3x[/math], then
but
If the hypotheses of Theorem (7.3) are satisfied for the functions [math]f'[/math] and [math]g'[/math], that is, for the derivatives of [math]f[/math] and [math]g[/math], respectively, then we can conclude that
This fact suggests the possibility of applying L'H\ôpital's Rule more than once, and in some problems it is necessary to take second or higher derivatives to find the limit. Example
Evaluate [math]\lim_{x \rightarrow 1}\frac{ 3x^{1/3} - x - 2}{3x^2 - 6x + 3}[/math]. Let [math]f(x) = 3x^{1/3} - x - 2[/math] and [math]g(x) = 3x^2 - 6x + 3[/math]. Then [math]f(1) = g(1) = 0[/math], and the derivatives are given by [math]f'(x) = x^{-2/3} - 1[/math] and [math]g'(x) = 6x - 6[/math]. However, the value of
is not obvious because [math]f'(1) = g'(1) = 0[/math]. Taking derivatives again, we get [math]f''(x) = - \frac{2}{3}x^{-5/3}[/math] and [math]g''(x) = 6[/math], and it follows that
Thus two applications of L'H\ôpital's Rule yield
A variation of (7.2), not difficult to prove, is the following:
Let [math]f[/math] and [math]g[/math] be differentiable on an open interval [math](a, \infty)[/math] with [math]g'(x) \neq 0[/math] for [math]x \gt a[/math]. If
\item[i] [math]\lim_{x \rightarrow \infty} f(x) = \lim_{x \rightarrow \infty} g(x) = 0[/math], \item[ii] [math]\lim_{x \rightarrow \infty}\frac{ f'(x)}{g'(x)} = L[/math],
then
An analogous theorem holds if [math](a, \infty)[/math] is replaced by [math](-\infty, a)[/math] and if [math]\lim_{x \rightarrow \infty}[/math] is replaced throughout by [math]\lim_{x \rightarrow -\infty}[/math].
The result is a corollary of (7.2) and the Chain Rule. Let [math]t = \frac{1}{x}[/math], and set [math]F(t) = f \Bigl( \frac{1}{t} \Bigr) = f(x)[/math] and [math]G(t) = g \Bigl( \frac{1}{t} \Bigr) = g(x)[/math]. Since [math]t[/math] approaches 0 from the right if and only if [math]x[/math] increases without bound,
An important observation is that all the forms of L'Hôpital's Rule developed so far are valid whether [math]L[/math] is finite or not. This fact requires no new proof and has really already been established. The reason is that the basic conclusion of Theorem (7.2) is the equation
and this holds good whether or not [math]\lim_{x \rightarrow a+}\frac{f'(x)}{g'(x)}[/math] is finite or infinite.
There is another significant variation of L'Hôpital's Rule, whose proof, although requiring only the Generalized Mean Value Theorem, cannot (as far as we know) be obtained from (7.2) by a simple substitution. It states that the several forms of condition (i), [math]\lim f(x) = \lim g(x)= 0[/math], can be replaced by [math]\lim |g(x)| = \infty[/math]. The specific statement which we prove is the following:
Let [math]f[/math] and [math]g[/math] be functions which are differentiable on a nonempty open interval [math](a, b)[/math] with [math]g'(x) \neq 0[/math] for every [math]x[/math] in [math](a, b)[/math]. If
- [math]\lim_{t \rightarrow a+} |g(x)| = \infty[/math],
- [math]\lim_{t \rightarrow a+} \frac{f'(x)}{g'(x)} = L[/math],
then
Let [math]\varepsilon[/math] be an arbitrary positive number. By hypothesis (ii), there exists a real number [math]c[/math] in [math](a, b)[/math] such that
It is a consequence of the last inequality that
Now let [math]x[/math] be an arbitrary real number in [math](a, d)[/math]. By the Generalized Mean Value Theorem, there exists a real number [math]y[/math] in [math](x, c)[/math] such that
It is not difficult to derive variations of the preceding theorem analogous to the modified versions of (7.2) described above. Thus, with the obvious changes in the hypotheses, this last form of L'H\ôpital's Rule also holds for two-sided limits and with [math]a[/math] or [math]L[/math] (or both) replaced by [math]\pm \infty[/math].
Example
Compute [math]\lim_{t \rightarrow \infty} \frac{\sqrt[3]{x + 1}}{x + 4} [/math]. Let [math]f[/math] and [math]g[/math] be the functions defined by [math]f(x) = \sqrt[3]{x + 1}[/math] and [math]g(x) = x + 4[/math], respectively. Since [math]f'(x) = \frac{1}{3(x + 1)^{2/3}}[/math] and [math]g'(x) = 1[/math], we see that [math]f[/math] and [math]g[/math] are differentiable on the interval [math](1, \infty)[/math] and that [math]g'(x) \neq 0[/math]. Moreover, [math]\lim_{t \rightarrow \infty} |g(x)| = \lim_{t \rightarrow \infty} |x + 4| = \infty[/math], and
It follows by L'H\ôpital's Rule that
The several forms of L'H\ôpital's Rule which we have derived in this section fall naturally into two types, symbolically denoted as the [math]\frac{0}{0}[/math] type and the [math]\frac{*}{\infty}[/math] type. Theorems (7.2), (7.3), and (7.4) are all examples of the first type, whereas the harder Theorem (7.5) is the prototype of the second type. The full power of the [math]\frac{*}{\infty}[/math] forms will be realized later in the book in conjunction with the logarithmic, exponential, and trigonometric functions.
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.