guide:08d5919107: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 32: | Line 32: | ||
\newcommand{\mathds}{\mathbb} | \newcommand{\mathds}{\mathbb} | ||
</math></div> | </math></div> | ||
Special among infinite series which contain both positive and negative terms are those whose terms alternate in sign. More precisely, we define the series <math>\sum_{i=m}^\infty a_i</math> to be \textbf{alternating} if <math>a_{i}a_{i+1} < 0</math> for every integer <math>i \geq m</math>. It follows from this definition that an alternating series is one which can be written in one of the two forms | Special among infinite series which contain both positive and negative terms are those whose terms alternate in sign. More precisely, we define the series <math>\sum_{i=m}^\infty a_i</math> to be \textbf{alternating} if <math>a_{i}a_{i+1} < 0</math> for every integer <math>i \geq m</math>. It follows from this definition that an alternating series is one which can be written in one of the two forms | ||
| Line 47: | Line 47: | ||
{{proofcard|Theorem|theorem-1|The alternuting series <math>\sum_{i=m}^\infty a_i</math> concerges if: | {{proofcard|Theorem|theorem-1|The alternuting series <math>\sum_{i=m}^\infty a_i</math> concerges if: | ||
<ul style{{=}}"list-style-type:lower-roman"> | |||
<li> <math>|a_{n + 1}| \leq |a_n|, \;\;\; \mathrm{for every integer} n \geq m, \;\mathrm{and}</math> </li> | |||
<li><math>\lim_{n \rightarrow \infty} a_n = 0 \;\mathrm{(or, equivalently,} \; \lim_{n \rightarrow \infty} |a_n| = 0).</math></li> | |||
</ul> | |||
|We shall assume for convenience and with no loss of generality that <math>m = 0</math> and that <math>a_i = (-1)^{i} b_i</math>, with <math>b_i > 0</math> for every integer <math>i \geq 0</math>. The series is therefore <math>\sum_{i=0}^\infty (-1)^{i} b_i</math>, and the hypotheses (i) and (ii) become | |We shall assume for convenience and with no loss of generality that <math>m = 0</math> and that <math>a_i = (-1)^{i} b_i</math>, with <math>b_i > 0</math> for every integer <math>i \geq 0</math>. The series is therefore <math>\sum_{i=0}^\infty (-1)^{i} b_i</math>, and the hypotheses (i) and (ii) become | ||
<ul style{{=}}"list-style-type:lower-roman"> | |||
<li><math>b_{n + 1} \leq b_n, \;\;\; \mbox{for every integer $n \geq 0$, and}</math> </li> | |||
<li><math>\lim_{n \rightarrow \infty} b_n = 0.</math></li> | |||
</ul> | |||
The proof is completed by showing the convergence of the sequence <math>\{s_n \}</math> of partial sums, which is defined recursively by the equations | The proof is completed by showing the convergence of the sequence <math>\{s_n \}</math> of partial sums, which is defined recursively by the equations | ||
| Line 66: | Line 69: | ||
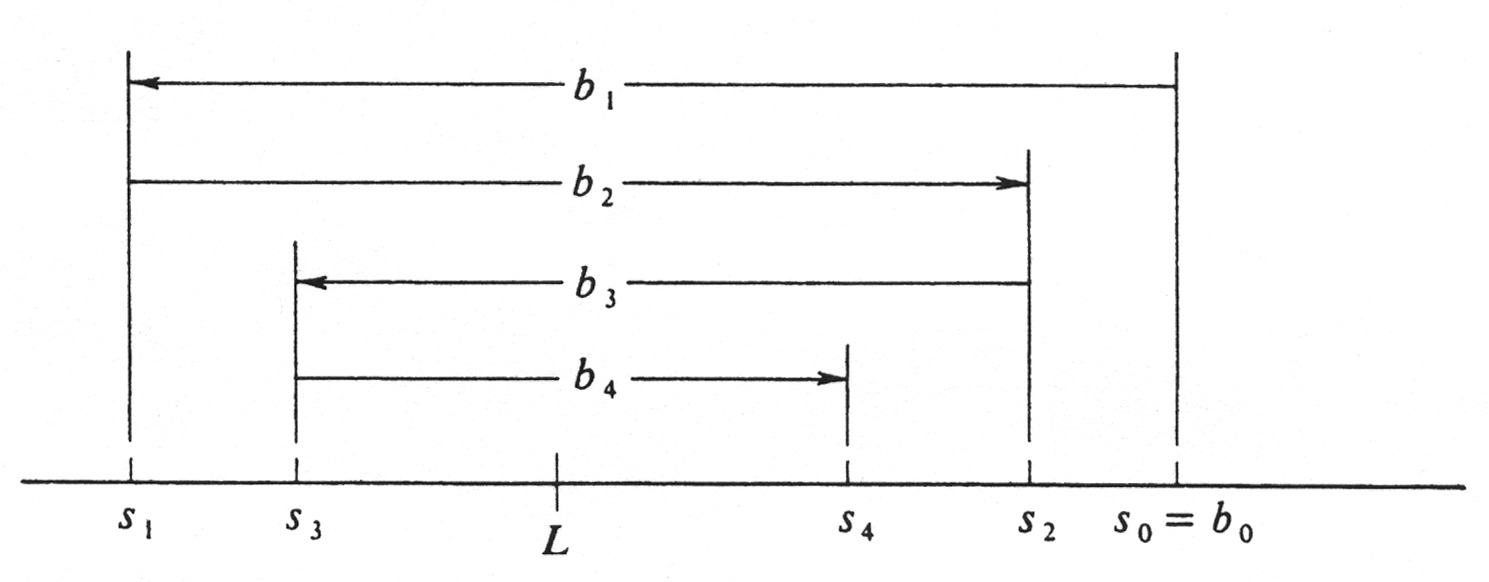
The best proof that <math>\lim_{n \rightarrow \infty} s_n</math>, exists is obtained by an illustration. In Figure 5 we first plot the point <math>s_0 = b_0</math> and then the point <math>s_1 = s_0 - b_1</math>. Next we | The best proof that <math>\lim_{n \rightarrow \infty} s_n</math>, exists is obtained by an illustration. In Figure 5 we first plot the point <math>s_0 = b_0</math> and then the point <math>s_1 = s_0 - b_1</math>. Next we | ||
plot <math>s_2 = s_1 + b_2</math> and observe that, since <math>b_2 \leq b_1</math>, we have <math>s_2 \leq s_0</math>. After that comes <math>s_3 = s_2 - b_3</math> and, since <math>b_3 \leq b_2</math> it follows that <math>s_1 \leq s_3</math>. Continuing in this way, we see that the odd-numbered points of the sequence <math>\{s_n\}</math> form an increasing subsequence: | plot <math>s_2 = s_1 + b_2</math> and observe that, since <math>b_2 \leq b_1</math>, we have <math>s_2 \leq s_0</math>. After that comes <math>s_3 = s_2 - b_3</math> and, since <math>b_3 \leq b_2</math> it follows that <math>s_1 \leq s_3</math>. Continuing in this way, we see that the odd-numbered points of the sequence <math>\{s_n\}</math> form an increasing subsequence: | ||
<div id="fig 9.5" class="d-flex justify-content-center"> | <div id{{=}}"fig 9.5" class{{=}}"d-flex justify-content-center"> | ||
[[File:guide_c5467_scanfig9_5.png | 400px | thumb | ]] | [[File:guide_c5467_scanfig9_5.png | 400px | thumb | ]] | ||
</div> | </div> | ||
| Line 122: | Line 125: | ||
\sum_{ i=1}^\infty (-1)^{i + 1} \frac{1}{i} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots . | \sum_{ i=1}^\infty (-1)^{i + 1} \frac{1}{i} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots . | ||
</math> | </math> | ||
The hypotheses of the theorem are obviously satisfied: | The hypotheses of the theorem are obviously satisfied: | ||
<ul style="list-style-type:lower-roman"> | |||
<li><math>\frac{1}{n + 1} \leq \frac{1}{n}, \;\;\; \mbox{for every integer $n \geq 1$, and}</math></li> | |||
<li><math>\lim_{n \rightarrow \infty} (-1)^{n+1} \frac{1}{n} = \lim_{n \rightarrow \infty} \frac{1}{n} = 0.</math></li> | |||
</ul> | |||
Hence it follows that the alternating harmonic series is convergent. It is interesting to compare this series with the ordinary harmonic series | Hence it follows that the alternating harmonic series is convergent. It is interesting to compare this series with the ordinary harmonic series | ||
| Line 168: | Line 172: | ||
</math> | </math> | ||
and the proof is complete.}} | and the proof is complete.}} | ||
==General references== | ==General references== | ||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | {{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | ||
Latest revision as of 02:35, 20 November 2024
Special among infinite series which contain both positive and negative terms are those whose terms alternate in sign. More precisely, we define the series [math]\sum_{i=m}^\infty a_i[/math] to be \textbf{alternating} if [math]a_{i}a_{i+1} \lt 0[/math] for every integer [math]i \geq m[/math]. It follows from this definition that an alternating series is one which can be written in one of the two forms
where [math]b_i \gt 0[/math] for every integer [math]i \geq m[/math]. An example is the alternating harmonic series
An alternating series converges under surprisingly weak conditions. The next theorem gives two simple hypotheses whose conjunction is sufficient to imply convergence.
The alternuting series [math]\sum_{i=m}^\infty a_i[/math] concerges if:
- [math]|a_{n + 1}| \leq |a_n|, \;\;\; \mathrm{for every integer} n \geq m, \;\mathrm{and}[/math]
- [math]\lim_{n \rightarrow \infty} a_n = 0 \;\mathrm{(or, equivalently,} \; \lim_{n \rightarrow \infty} |a_n| = 0).[/math]
We shall assume for convenience and with no loss of generality that [math]m = 0[/math] and that [math]a_i = (-1)^{i} b_i[/math], with [math]b_i \gt 0[/math] for every integer [math]i \geq 0[/math]. The series is therefore [math]\sum_{i=0}^\infty (-1)^{i} b_i[/math], and the hypotheses (i) and (ii) become
- [math]b_{n + 1} \leq b_n, \;\;\; \mbox{for every integer $n \geq 0$, and}[/math]
- [math]\lim_{n \rightarrow \infty} b_n = 0.[/math]
The proof is completed by showing the convergence of the sequence [math]\{s_n \}[/math] of partial sums, which is defined recursively by the equations
The best proof that [math]\lim_{n \rightarrow \infty} s_n[/math], exists is obtained by an illustration. In Figure 5 we first plot the point [math]s_0 = b_0[/math] and then the point [math]s_1 = s_0 - b_1[/math]. Next we
plot [math]s_2 = s_1 + b_2[/math] and observe that, since [math]b_2 \leq b_1[/math], we have [math]s_2 \leq s_0[/math]. After that comes [math]s_3 = s_2 - b_3[/math] and, since [math]b_3 \leq b_2[/math] it follows that [math]s_1 \leq s_3[/math]. Continuing in this way, we see that the odd-numbered points of the sequence [math]\{s_n\}[/math] form an increasing subsequence:
We have shown that both the odd-numbered subsequences [math]\{s_{2n-1} \}[/math] and the even-numbered subsequence [math]\{ s_{2n} \}[/math] converge to the same limit [math]L[/math]. This implies that [math]\lim_{n \rightarrow \infty} s_n = L[/math]. For, given an arbitrary real number [math] \epsilon \gt 0[/math], we have proved that there exist integers [math]N_1[/math], and [math]N_2[/math], such that
As an application of Theorem (4.1) consider the alternating harmonic series
The hypotheses of the theorem are obviously satisfied:
- [math]\frac{1}{n + 1} \leq \frac{1}{n}, \;\;\; \mbox{for every integer $n \geq 1$, and}[/math]
- [math]\lim_{n \rightarrow \infty} (-1)^{n+1} \frac{1}{n} = \lim_{n \rightarrow \infty} \frac{1}{n} = 0.[/math]
Hence it follows that the alternating harmonic series is convergent. It is interesting to compare this series with the ordinary harmonic series [math] \sum_{i=1}^\infty \frac{1}{i} = 1 + \frac{1}{2} + \frac{1}{3} +\frac{1}{4} + \cdots [/math], which we have shown to be divergent. We see that the alternating harmonic series is a convergent infinite series [math]\sum_{i=m}^{\infty} a_i[/math] for which the corresponding series of absolute values [math]\sum_{i=m}^{\infty} |a_i|[/math] fail diverges. For practical purposes, the value of a convergent infinite series [math]\sum_{i=m}^{\infty} a_i[/math] is usually approximated by a partial [math]\sum_{i=m}^{\infty} a_i[/math]. The error in the approximation, denoted by [math]E_n[/math], is the absolute value of the difference between the true value of the series and the approximating partial sum; i.e.,
ln general, it is a difficult problem to know how large [math]n[/math] must be chosen to cosure that the error [math]E_n[/math] be less than a given size. However, for those alternating series which satisfy the hypotheses of Theorem (4.1), the problem is an easy one.
If the ulternating series [math]\sum_{i=m}^{\infty} a_i[/math] satisfies hypotheses (i) and (ii) of Theorem (4.1), then the error [math]E_n[/math] is less than or equal to the absolute value of the first omitted term. That is,
We shall use the same notation as in the proof of (4.1). Thus we assume that [math] m = 0[/math] and that [math]a_i = (-1)^{i} b_i[/math] where [math]b_i \gt 0[/math] for every integer [math]i \geq 0[/math]. The value of the series is the number [math]L[/math], and the error [math]E_n[/math] is therefore given by
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.