exercise:27313b016d: Difference between revisions
From Stochiki
(Created page with "<div class="d-none"><math> \newcommand{\indexmark}[1]{#1\markboth{#1}{#1}} \newcommand{\red}[1]{\textcolor{red}{#1}} \newcommand{\NOTE}[1]{$^{\textcolor{red}\clubsuit}$\marginpar{\setstretch{0.5}$^{\scriptscriptstyle\textcolor{red}\clubsuit}$\textcolor{blue}{\bf\tiny #1}}} \newcommand\xoverline[2][0.75]{% \sbox{\myboxA}{$\m@th#2$}% \setbox\myboxB\null% Phantom box \ht\myboxB=\ht\myboxA% \dp\myboxB=\dp\myboxA% \wd\myboxB=#1\wd\myboxA% Scale phantom...") |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | <div class="d-none"><math> | ||
\newcommand{\smallfrac}[2]{\frac{#1}{#2}} | |||
\newcommand{\medfrac}[2]{\frac{#1}{#2}} | |||
\newcommand{\textfrac}[2]{\frac{#1}{#2}} | |||
\newcommand{\smallfrac}[2] | |||
\newcommand{\medfrac}[2] | |||
\newcommand{\textfrac}[2] | |||
\newcommand{\tr}{\operatorname{tr}} | \newcommand{\tr}{\operatorname{tr}} | ||
\newcommand{\e}{\operatorname{e}} | \newcommand{\e}{\operatorname{e}} | ||
\newcommand{\B}{\operatorname{B}} | \newcommand{\B}{\operatorname{B}} | ||
\newcommand{\Bbar}{\ | \newcommand{\Bbar}{\overline{\operatorname{B}}} | ||
\newcommand{\pr}{\operatorname{pr}} | \newcommand{\pr}{\operatorname{pr}} | ||
\newcommand{\dd}{\operatorname{d}\hspace{-1pt}} | \newcommand{\dd}{\operatorname{d}\hspace{-1pt}} | ||
| Line 33: | Line 12: | ||
\newcommand{\V}{\operatorname{V}} | \newcommand{\V}{\operatorname{V}} | ||
\newcommand{\Cov}{\operatorname{Cov}} | \newcommand{\Cov}{\operatorname{Cov}} | ||
\newcommand{\Bigsum}[2] | \newcommand{\Bigsum}[2]{\mathop{\textstyle\sum}_{#1}^{#2}} | ||
\newcommand{\ran}{\operatorname{ran}} | \newcommand{\ran}{\operatorname{ran}} | ||
\newcommand{\card}{\#} | \newcommand{\card}{\#} | ||
\ | \renewcommand{\P}{\operatorname{P}} | ||
\renewcommand{\L}{\operatorname{L}} | |||
\newcommand{\mathds}{\mathbb}</math></div> | |||
Replicate the results of [[guide:6588b14666#SEP-FIG-2|Figure]]. More precisely, run the code from [[guide:6588b14666#PROBL-6-2 |Problem]] for different dimensions <math>d</math> and different distance functions <math>\Delta=\Delta(d)</math>, e.g., <math>\Delta\equiv c > 0</math>, <math>\Delta=2\sqrt{d}</math>, <math>\Delta=d^{0.3}</math> or <math>\Delta=d^{1/4}</math>. Plot the rate of correctly classified data points as a function of the dimension. Simulate also the case <math>\Delta=2d^{0.2}</math> and confirm that this leads to a low correct classification rate which decreases for large dimensions. | |||
<span id{{=}}"SEP-FIG-4"/> | |||
Replicate the results of [[#SEP-FIG-2|Figure]]. More precisely, run the code from [[#PROBL-6-2 |Problem]] for different dimensions <math>d</math> and different distance functions <math>\Delta=\Delta(d)</math>, e.g., <math>\Delta\equiv c > 0</math>, <math>\Delta=2\sqrt{d}</math>, <math>\Delta=d^{0.3}</math> or <math>\Delta=d^{1/4}</math>. Plot the rate of correctly classified data points as a function of the dimension. Simulate also the case <math>\Delta=2d^{0.2}</math> and confirm that this leads to a low correct classification rate which decreases for large dimensions. | <div class{{=}}"d-flex justify-content-center"> | ||
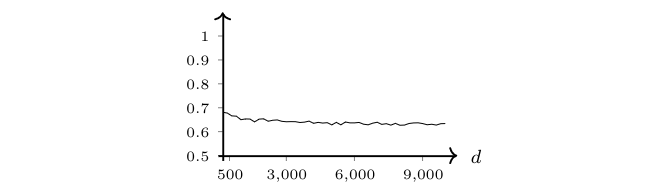
[[File:tikzebf95.png | 600px | thumb | Average rate of correctly classified data points for <math>\Delta=2d^{0.2}</math>.]] | |||
</div> | |||
Latest revision as of 03:24, 2 June 2024
[math]
\newcommand{\smallfrac}[2]{\frac{#1}{#2}}
\newcommand{\medfrac}[2]{\frac{#1}{#2}}
\newcommand{\textfrac}[2]{\frac{#1}{#2}}
\newcommand{\tr}{\operatorname{tr}}
\newcommand{\e}{\operatorname{e}}
\newcommand{\B}{\operatorname{B}}
\newcommand{\Bbar}{\overline{\operatorname{B}}}
\newcommand{\pr}{\operatorname{pr}}
\newcommand{\dd}{\operatorname{d}\hspace{-1pt}}
\newcommand{\E}{\operatorname{E}}
\newcommand{\V}{\operatorname{V}}
\newcommand{\Cov}{\operatorname{Cov}}
\newcommand{\Bigsum}[2]{\mathop{\textstyle\sum}_{#1}^{#2}}
\newcommand{\ran}{\operatorname{ran}}
\newcommand{\card}{\#}
\renewcommand{\P}{\operatorname{P}}
\renewcommand{\L}{\operatorname{L}}
\newcommand{\mathds}{\mathbb}[/math]
Replicate the results of Figure. More precisely, run the code from Problem for different dimensions [math]d[/math] and different distance functions [math]\Delta=\Delta(d)[/math], e.g., [math]\Delta\equiv c \gt 0[/math], [math]\Delta=2\sqrt{d}[/math], [math]\Delta=d^{0.3}[/math] or [math]\Delta=d^{1/4}[/math]. Plot the rate of correctly classified data points as a function of the dimension. Simulate also the case [math]\Delta=2d^{0.2}[/math] and confirm that this leads to a low correct classification rate which decreases for large dimensions.