guide:87cf36f969: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
\newcommand{\mathds}{\mathbb}</math></div> | \newcommand{\mathds}{\mathbb}</math></div> | ||
The subject of Markov chains is best studied by considering special types of | The subject of Markov chains is best studied by considering special types of | ||
Markov chains. The first type that we shall study is called an ''absorbing | Markov chains. The first type that we shall study is called an ''absorbing | ||
Markov chain.'' | Markov chain.'' | ||
{{defncard|label=|id=|A state | {{defncard|label=|id=|A state <math>s_i</math> of a Markov chain is called ''absorbing'' if it is impossible | ||
to leave | to leave | ||
it (i.e., | it (i.e., | ||
| Line 24: | Line 24: | ||
<span id="exam 11.2.1"/> | <span id="exam 11.2.1"/> | ||
'''Example''' | '''Example''' | ||
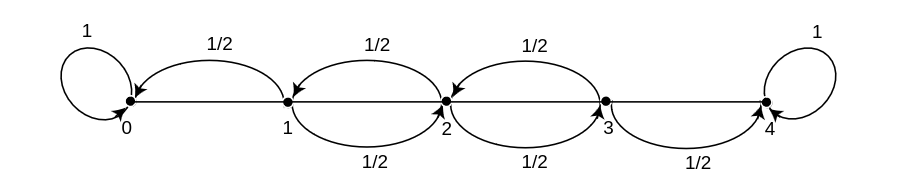
A man walks along a four-block stretch of Park Avenue (see | A man walks along a four-block stretch of Park Avenue (see [[#fig | ||
11.3 | 11.3|Figure]]). If he is | ||
at corner 1, 2, or 3, then he walks to the left or right with equal | at corner 1, 2, or 3, then he walks to the left or right with equal | ||
probability. | probability. | ||
| Line 60: | Line 60: | ||
transient state? The answers to all these questions depend, in general, on the | transient state? The answers to all these questions depend, in general, on the | ||
state from which the process starts as well as the transition probabilities. | state from which the process starts as well as the transition probabilities. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig11-3. | <div id="fig 11.3" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig11-3.png | 400px | thumb | Drunkard's walk. ]] | |||
</div> | </div> | ||
===Canonical Form=== | ===Canonical Form=== | ||
Consider an arbitrary absorbing Markov chain. Renumber the states so that the | Consider an arbitrary absorbing Markov chain. Renumber the states so that the | ||
| Line 84: | Line 84: | ||
are absorbing. | are absorbing. | ||
In [[guide:52e01d4de7|Introduction]], we saw that the entry <math>p_{ij}^{(n)}</math> of the matrix | |||
In | |||
<math>\mat{P}^n</math> is the probability of being in the state <math>s_j</math> after <math>n</math> steps, | <math>\mat{P}^n</math> is the probability of being in the state <math>s_j</math> after <math>n</math> steps, | ||
when | when | ||
| Line 254: | Line 253: | ||
expected number of times in states 1, 2, and 3 before being absorbed | expected number of times in states 1, 2, and 3 before being absorbed | ||
are 1, 2, and 1. | are 1, 2, and 1. | ||
===Time to Absorption=== | ===Time to Absorption=== | ||
| Line 302: | Line 300: | ||
Another proof of this is given in | Another proof of this is given in [[exercise:Ef04d1ba60 |Exercise]]. | ||
<span id="exam 11.2.3"/> | <span id="exam 11.2.3"/> | ||
'''Example''' | '''Example''' | ||
continued) | ([[#exam 11.2.2|Example]] continued) | ||
In the Drunkard's Walk example, we found that | In the Drunkard's Walk example, we found that | ||
| Line 374: | Line 374: | ||
probability 3/4 | probability 3/4 | ||
of absorption in state <math>0</math> and 1/4 of absorption in state <math>4</math>. | of absorption in state <math>0</math> and 1/4 of absorption in state <math>4</math>. | ||
===Computation=== | ===Computation=== | ||
| Line 439: | Line 438: | ||
Note that the probability of reaching the bar before reaching home, starting | Note that the probability of reaching the bar before reaching home, starting | ||
at <math>x</math>, is <math>x/5</math> (i.e., proportional to the distance of home from the starting | at <math>x</math>, is <math>x/5</math> (i.e., proportional to the distance of home from the starting | ||
point). (See | point). (See [[exercise:087f70d94a |Exercise]].) | ||
==General references== | ==General references== | ||
{{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | {{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | ||
Revision as of 22:32, 11 June 2024
The subject of Markov chains is best studied by considering special types of Markov chains. The first type that we shall study is called an absorbing Markov chain.
A state [math]s_i[/math] of a Markov chain is called absorbing if it is impossible to leave it (i.e., [math]p_{ii} = 1[/math]). A Markov chain is absorbing if it has at least one absorbing state, and if from every state it is possible to go to an absorbing state (not necessarily in one step).
In an absorbing Markov chain, a state which is not absorbing is called transient.
Drunkard's Walk
Example A man walks along a four-block stretch of Park Avenue (see [[#fig 11.3|Figure]]). If he is at corner 1, 2, or 3, then he walks to the left or right with equal probability. He continues until he reaches corner 4, which is a bar, or corner 0, which is his home. If he reaches either home or the bar, he stays there.
We form a Markov chain with states 0, 1, 2, 3, and 4. States 0 and 4 are
absorbing states. The transition matrix is then
The states 1, 2, and 3 are transient states, and from any of these it is possible to reach the absorbing states 0 and 4. Hence the chain is an absorbing chain. When a process reaches an absorbing state, we shall say that it is absorbed.
The most obvious question that can be asked about such a chain is: What is the probability that the process will eventually reach an absorbing state? Other interesting questions include: (a) What is the probability that the process will end up in a given absorbing state? (b) On the average, how long will it take for the process to be absorbed? (c) On the average, how many times will the process be in each transient state? The answers to all these questions depend, in general, on the state from which the process starts as well as the transition probabilities.
Canonical Form
Consider an arbitrary absorbing Markov chain. Renumber the states so that the transient states come first. If there are [math]r[/math] absorbing states and [math]t[/math] transient states, the transition matrix will have the following canonical form
Here [math]\mat{I}[/math] is an [math]r[/math]-by-[math]r[/math] indentity matrix, [math]\mat{0}[/math] is an [math]r[/math]-by-[math]t[/math] zero matrix, [math]\mat{R}[/math] is a nonzero [math]t[/math]-by-[math]r[/math] matrix, and [math]\mat{Q}[/math] is an [math]t[/math]-by-[math]t[/math] matrix. The first [math]t[/math] states are transient and the last [math]r[/math] states are absorbing.
In Introduction, we saw that the entry [math]p_{ij}^{(n)}[/math] of the matrix [math]\mat{P}^n[/math] is the probability of being in the state [math]s_j[/math] after [math]n[/math] steps, when the chain is started in state [math]s_i[/math]. A standard matrix algebra argument shows that [math]\mat{P}^n[/math] is of the form
where the asterisk [math]*[/math] stands for the [math]t[/math]-by-[math]r[/math] matrix in the upper right-hand corner of [math]\mat{P}^n.[/math] (This submatrix can be written in terms of [math]\mat{Q}[/math] and [math]\mat{R}[/math], but the expression is complicated and is not needed at this time.) The form of [math]\mat{P}^n[/math] shows that the entries of [math]\mat{Q}^n[/math] give the probabilities for being in each of the transient states after [math]n[/math] steps for each possible transient starting state. For our first theorem we prove that the probability of being in the transient states after [math]n[/math] steps approaches zero. Thus every entry of [math]\mat{ Q}^n[/math] must approach zero as [math]n[/math] approaches infinity (i.e, [math]\mat{Q}^n \to \mat{ 0}[/math]).
Probability of Absorption
In an absorbing Markov chain, the probability that the process will be absorbed is 1 (i.e., [math]\mat{Q}^n \to \mat{0}[/math] as [math]n \to \infty[/math]).\n
Show ProofFrom each nonabsorbing state [math]s_j[/math] it is possible to reach an absorbing state. Let [math]m_j[/math] be the minimum number of steps required to reach an absorbing state, starting from [math]s_j[/math]. Let [math]p_j[/math] be the probability that, starting from [math]s_j[/math], the process will not reach an absorbing state in [math]m_j[/math] steps. Then [math]p_j \lt 1[/math]. Let [math]m[/math] be the largest of the [math]m_j[/math] and let [math]p[/math] be the largest of [math]p_j[/math]. The probability of not being absorbed in [math]m[/math] steps is less than or equal to [math]p[/math], in [math]2m[/math] steps less than or equal to [math]p^2[/math], etc. Since [math]p \lt 1[/math] these probabilities tend to 0. Since the probability of not being absorbed in [math]n[/math] steps is monotone decreasing, these probabilities also tend to 0, hence [math]\lim_{n \rightarrow \infty } \mat{Q}^n = 0.[/math]
The Fundamental Matrix
For an absorbing Markov chain the matrix [math]\mat{I} - \mat{Q}[/math] has an inverse [math]\mat{N}[/math] and [math]\mat{N} =\mat{I} + \mat{Q} + \mat{Q}^{2} + \cdots\ [/math]. The [math]ij[/math]-entry [math]n_{ij}[/math] of the matrix [math]\mat{N}[/math] is the expected number of times the chain is in state [math]s_j[/math], given that it starts in state [math]s_i[/math]. The initial state is counted if [math]i = j[/math].\n
Show ProofLet [math](\mat{I} - \mat{Q})\mat{x}~=~0;[/math] that is [math]\mat{x}~=~\mat{Q}\mat{x}.[/math] Then, iterating this we see that [math]\mat{x}~=~\mat{Q}^{n}\mat x.[/math] Since [math]\mat{Q}^{n} \rightarrow \mat{0}[/math], we have [math]\mat{Q}^n\mat{x} \rightarrow \mat{0}[/math], so [math]\mat{x}~=~\mat{0}[/math]. Thus [math](\mat{I} - \mat{Q})^{-1}~=~\mat{N}[/math] exists. Note next that
Let [math]s_i[/math] and [math]s_j[/math] be two transient states, and assume throughout the remainder of the proof that [math]i[/math] and [math]j[/math] are fixed. Let [math]X^{(k)}[/math] be a random variable which equals 1 if the chain is in state [math]s_j[/math] after [math]k[/math] steps, and equals 0 otherwise. For each [math]k[/math], this random variable depends upon both [math]i[/math] and [math]j[/math]; we choose not to explicitly show this dependence in the interest of clarity. We have
The expected number of times the chain is in state [math]s_j[/math] in the first [math]n[/math]
steps,
given that it starts in state [math]s_i[/math], is clearly
For an absorbing Markov chain [math]\mat{P}[/math], the matrix [math]\mat{N} = (\mat{I} - \mat{Q})^{-1}[/math] is called the fundamental matrix for [math]\mat{P}[/math]. The entry [math]n_{ij}[/math] of [math]\mat{N}[/math] gives the expected number of times that the process is in the transient state [math]s_j[/math] if it is started in the transient state [math]s_i[/math].
Example (Example continued) In the Drunkard's Walk example, the transition matrix in canonical form is
From this we see that the matrix [math]\mat{Q}[/math] is
and
Computing [math](\mat{I} - \mat{Q})^{-1}[/math], we find
From the middle row of [math]\mat{N}[/math], we see that if we start in state 2, then the expected number of times in states 1, 2, and 3 before being absorbed are 1, 2, and 1.
Time to Absorption
We now consider the question: Given that the chain starts in state [math]s_i[/math], what is the expected number of steps before the chain is absorbed? The answer is given in the next theorem.
Let [math]t_i[/math] be the expected number of steps before the chain is absorbed, given that the chain starts in state [math]s_i[/math], and let [math]\mat{t}[/math] be the column vector whose [math]i[/math]th entry is [math]t_i[/math]. Then
If we add all the entries in the [math]i[/math]th row of [math]\mat{N}[/math], we will have the expected number of times in any of the transient states for a given starting state [math]s_i[/math], that is, the expected time required before being absorbed. Thus, [math]t_i[/math] is the sum of the entries in the [math]i[/math]th row of [math]\mat{N}[/math]. If we write this statement in matrix form, we obtain the theorem.
Absorption Probabilities
Let [math]b_{ij}[/math] be the probability that an absorbing chain will be absorbed in the absorbing state [math]s_j[/math] if it starts in the transient state [math]s_i[/math]. Let [math]\mat{B}[/math] be the matrix with entries [math]b_{ij}[/math]. Then [math]\mat{B}[/math] is an [math]t[/math]-by-[math]r[/math] matrix, and
We have
Another proof of this is given in Exercise.
Example (Example continued)
In the Drunkard's Walk example, we found that
Hence,
Thus, starting in states 1, 2, and 3, the expected times to absorption are 3, 4, and 3, respectively.
From the canonical form,
Hence,
Here the first row tells us that, starting from state [math]1[/math], there is
probability 3/4
of absorption in state [math]0[/math] and 1/4 of absorption in state [math]4[/math].
Computation
The fact that we have been able to obtain these three descriptive quantities in matrix form makes it very easy to write a computer program that determines these quantities for a given absorbing chain matrix. The program AbsorbingChain calculates the basic descriptive quantities of an absorbing Markov chain. We have run the program AbsorbingChain for the example of the drunkard's walk (Example) with 5 blocks. The results are as follows:
Note that the probability of reaching the bar before reaching home, starting at [math]x[/math], is [math]x/5[/math] (i.e., proportional to the distance of home from the starting point). (See Exercise.)
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.