guide:8be2f96c1e: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
\newcommand{\mathds}{\mathbb}</math></div> | \newcommand{\mathds}{\mathbb}</math></div> | ||
In this section we consider two closely related descriptive quantities of | In this section we consider two closely related descriptive quantities of | ||
interest for ergodic chains: the mean time to return to a state and the mean | interest for ergodic chains: the mean time to return to a state and the mean | ||
time to go from one state to another state. | time to go from one state to another state. | ||
Let <math>\mat{P}</math> be the transition matrix of an ergodic chain with states | Let <math>\mat{P}</math> be the transition matrix of an ergodic chain with states | ||
<math>s_1 | <math>s_1, s_2, \ldots, s_r</math>. Let <math>\mat {w} = (w_1,w_2,\ldots,w_r)</math> be the | ||
unique | unique | ||
probability vector such that <math>\mat {w} \mat {P} = \mat {w}</math>. Then, by the Law | probability vector such that <math>\mat {w} \mat {P} = \mat {w}</math>. Then, by the Law | ||
| Line 54: | Line 53: | ||
passage time'' from <math>s_i</math> to <math>s_j</math>. | passage time'' from <math>s_i</math> to <math>s_j</math>. | ||
It is denoted by <math>m_{ij}</math>. By convention <math>m_{ii} = 0</math>.}} | It is denoted by <math>m_{ij}</math>. By convention <math>m_{ii} = 0</math>.}} | ||
<span id="exam 11.5.1"/> | <span id="exam 11.5.1"/> | ||
'''Example''' | '''Example''' | ||
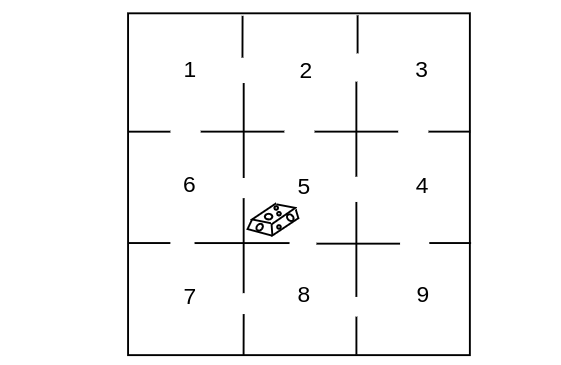
Let us return to the maze example ( | Let us return to the maze example ([[guide:E5c38a1e8a#exam 11.3.3|Example]]). We shall make this ergodic chain into an absorbing chain by making state 5 an absorbing state. For example, we might assume that food is placed in the center of the maze and | ||
11.3.3 | once the rat finds the food, he stays to enjoy it (see [[#fig 11.5|Figure]]). | ||
We shall make this ergodic chain into an absorbing chain by making state 5 an | |||
absorbing state. | <div id="fig 11.5" class="d-flex justify-content-center"> | ||
For example, we might assume that food is placed in the center of the maze and | [[File:guide_e6d15_PSfig11-5.png | 400px | thumb | The maze problem. ]] | ||
once the rat finds the food, he stays to enjoy it (see | |||
<div id=" | |||
[[File:guide_e6d15_PSfig11-5. | |||
</div> | </div> | ||
| Line 69: | Line 66: | ||
The new transition matrix in canonical form is | The new transition matrix in canonical form is | ||
<pre> | |||
<math display="block"> | <math display="block"> | ||
\mat {P}\;= \bordermatrix{& | \mat {P}\;= \bordermatrix{& | ||
| Line 94: | Line 92: | ||
& 1}\ . | & 1}\ . | ||
</math> | </math> | ||
</pre> | |||
If we compute the fundamental matrix <math>\mat{N}</math>, we obtain | If we compute the fundamental matrix <math>\mat{N}</math>, we obtain | ||
<pre> | |||
<math display="block"> | <math display="block"> | ||
\mat {N} = \frac18 \pmatrix{ | \mat {N} = \frac18 \pmatrix{ | ||
| Line 107: | Line 108: | ||
2 & 3 & 4 & 9 & 3 & 4 & 9 & 14 \cr}\ . | 2 & 3 & 4 & 9 & 3 & 4 & 9 & 14 \cr}\ . | ||
</math> | </math> | ||
</pre> | |||
The expected time to absorption for different starting states is given by the | The expected time to absorption for different starting states is given by the | ||
vector <math>\mat {N} \mat {c}</math>, where | vector <math>\mat {N} \mat {c}</math>, where | ||
| Line 121: | Line 124: | ||
instance, we note that the expected number of times in the starting state is | instance, we note that the expected number of times in the starting state is | ||
14/8 regardless of the state in which we start. | 14/8 regardless of the state in which we start. | ||
===Mean Recurrence Time=== | ===Mean Recurrence Time=== | ||
| Line 170: | Line 172: | ||
\end{eqnarray} | \end{eqnarray} | ||
</math> | </math> | ||
===Mean First Passage Matrix and Mean Recurrence Matrix=== | ===Mean First Passage Matrix and Mean Recurrence Matrix=== | ||
| Line 178: | Line 178: | ||
of <math>\mat{M}</math> is the mean first passage time to go from <math>s_i</math> to <math>s_j</math> if <math>i \ne | of <math>\mat{M}</math> is the mean first passage time to go from <math>s_i</math> to <math>s_j</math> if <math>i \ne | ||
j</math>; | j</math>; | ||
the diagonal entries are 0. The matrix <math>\mat{M}</math> is called the ''mean | the diagonal entries are 0. The matrix <math>\mat{M}</math> is called the ''mean first passage matrix.'' | ||
first passage | The matrix <math>\mat{D}</math> is the matrix with all | ||
matrix.'' | |||
entries 0 except | entries 0 except | ||
the diagonal entries <math>d_{ii} = r_i</math>. The matrix <math>\mat{D}</math> is called the ''mean recurrence | the diagonal entries <math>d_{ii} = r_i</math>. The matrix <math>\mat{D}</math> is called the ''mean recurrence | ||
| Line 187: | Line 185: | ||
Let <math>\mat {C}</math> be an <math>r \times r</math> matrix with all entries 1. Using | Let <math>\mat {C}</math> be an <math>r \times r</math> matrix with all entries 1. Using | ||
Equation \ref{eq 11.5.1} for the case <math>i \ne j</math> and Equation \ref{eq 11.5.2} for the case <math>i = j</math>, we obtain | |||
the case <math>i \ne j</math> and | |||
the matrix equation | the matrix equation | ||
| Line 207: | Line 204: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Equation \ref{eq 11.5.4} with <math>m_{ii} = 0</math> implies Equation \ref{eq 11.5.1} and Equation \ref{eq 11.5.2}. We are now in a position to prove our first basic theorem. | |||
theorem. | |||
{{proofcard|Theorem|theorem-1|For an ergodic Markov chain, the mean recurrence time for state <math>s_i</math> is <math>r_i = | {{proofcard|Theorem|theorem-1|For an ergodic Markov chain, the mean recurrence time for state <math>s_i</math> is <math>r_i = | ||
1/w_i</math>, where <math>w_i</math> is the <math>i</math>th component of the fixed probability vector for | 1/w_i</math>, where <math>w_i</math> is the <math>i</math>th component of the fixed probability vector for | ||
the transition matrix. | the transition matrix.|Multiplying both sides of Equation \ref{eq 11.5.4} by <math>\mat{w}</math> and using the | ||
fact | fact | ||
that | that | ||
| Line 240: | Line 237: | ||
{{proofcard|Corollary|cor_11.5.17|For an ergodic Markov chain, the components of the fixed probability | {{proofcard|Corollary|cor_11.5.17|For an ergodic Markov chain, the components of the fixed probability | ||
vector ''' | vector ''' | ||
w''' are strictly positive. | w''' are strictly positive.|We know that the values of <math>r_i</math> are finite and so <math>w_i = 1/r_i</math> cannot be 0.}} | ||
'''Example''' | '''Example''' | ||
In [[guide:E5c38a1e8a#exam 11.3.3 |Example]] we found the fixed probability vector for the maze | In [[guide:E5c38a1e8a#exam 11.3.3 |Example]] we found the fixed probability vector for the maze | ||
| Line 257: | Line 254: | ||
Returning to the Land of Oz, we found that the weather in the Land of Oz could | Returning to the Land of Oz, we found that the weather in the Land of Oz could | ||
be represented by a Markov chain with states rain, nice, and snow. In | be represented by a Markov chain with states rain, nice, and snow. In [[guide:E5c38a1e8a|Ergodic Markov Chains]] we found that the limiting vector was <math>\mat {w} = | ||
(2/5,1/5,2/5)</math>. From this we see that the mean number of days between rainy | (2/5,1/5,2/5)</math>. From this we see that the mean number of days between rainy | ||
days | days | ||
| Line 297: | Line 293: | ||
restriction of the transition matrix to the set of transient states, then the | restriction of the transition matrix to the set of transient states, then the | ||
fundamental | fundamental | ||
matrix \mat {N} could be written as | matrix <math>\mat {N}</math> could be written as | ||
<math display="block"> | <math display="block"> | ||
| Line 315: | Line 311: | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\mat {I} + (\mat {P} -\mat {W}) + (\mat {P}^2 - \mat{W}) + \cdots\ .\label{eq | \mat {I} + (\mat {P} -\mat {W}) + (\mat {P}^2 - \mat{W}) + \cdots\ .\label{eq 11.5.8} | ||
11.5.8} | |||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
We now use special properties of \mat {P} and \mat {W} to rewrite this series. | We now use special properties of <math>\mat {P}</math> and <math>\mat {W}</math> to rewrite this series. | ||
The special | The special | ||
properties are: 1) <math>\mat {P}\mat {W} = \mat {W}</math>, and 2) <math>\mat {W}^k = \mat | properties are: 1) <math>\mat {P}\mat {W} = \mat {W}</math>, and 2) <math>\mat {W}^k = \mat | ||
{W}</math> for all | {W}</math> for all | ||
positive integers <math>k</math>. These facts are easy to verify, and are left as an | positive integers <math>k</math>. These facts are easy to verify, and are left as an | ||
exercise (see | exercise (see [[exercise:2e4acd3b92 |Exercise]]). Using these facts, we see that | ||
<math display="block"> | <math display="block"> | ||
| Line 346: | Line 340: | ||
</math> | </math> | ||
for all <math>n \ge 1</math>. | for all <math>n \ge 1</math>. | ||
We can now rewrite the series in \ref{eq 11.5.8} as | We can now rewrite the series in \ref{eq 11.5.8} as | ||
| Line 368: | Line 361: | ||
<math>\mat {I} - \mat | <math>\mat {I} - \mat | ||
{P} + \mat {W}</math> still has an inverse, as we will now show. | {P} + \mat {W}</math> still has an inverse, as we will now show. | ||
{{proofcard|Proposition|proposition-1|Let \mat {P} be the transition matrix of an ergodic chain, and let \mat {W} be | {{proofcard|Proposition|proposition-1|Let <math>\mat {P}</math> be the transition matrix of an ergodic chain, and let \mat {W} be | ||
the matrix all | the matrix all | ||
of whose rows are the fixed probability row vector for \mat {P}. Then the | of whose rows are the fixed probability row vector for <math>\mat {P}</math>. Then the | ||
matrix | matrix | ||
| Line 376: | Line 369: | ||
\mat {I} - \mat {P} + \mat {W} | \mat {I} - \mat {P} + \mat {W} | ||
</math> | </math> | ||
has an inverse. | has an inverse.|Let <math>\mat{x}</math> be a column vector such that | ||
<math display="block"> | <math display="block"> | ||
| Line 410: | Line 403: | ||
the ''fundamental matrix'' for the ergodic chain with transition | the ''fundamental matrix'' for the ergodic chain with transition | ||
matrix \mat {P}, and we will | matrix \mat {P}, and we will | ||
use \mat {Z} to denote this fundamental matrix. | use <math>\mat {Z}</math> to denote this fundamental matrix. | ||
<span id="exam 11.5.2"/> | <span id="exam 11.5.2"/> | ||
'''Example''' | '''Example''' | ||
| Line 443: | Line 437: | ||
</math> | </math> | ||
==Using the Fundamental Matrix to Calculate the Mean First Passage Matrix== | |||
We shall show how one can obtain the mean first passage matrix \mat{M} from the | We shall show how one can obtain the mean first passage matrix <math>\mat{M}</math> from the | ||
fundamental | fundamental matrix \mat{Z} for an ergodic Markov chain. Before stating the theorem which | ||
matrix \mat{Z} for an ergodic Markov chain. Before stating the theorem which | |||
gives the first | gives the first | ||
passage times, we need a few facts about \mat{Z}. | passage times, we need a few facts about \mat{Z}. | ||
| Line 465: | Line 458: | ||
<math display="block"> | <math display="block"> | ||
\mat{Z}(\mat{I} - \mat{P}) = \mat{I} - \mat{W}\ . | \mat{Z}(\mat{I} - \mat{P}) = \mat{I} - \mat{W}\ . | ||
</math> | </math>|Since <math>\mat{P}\mat{c} = \mat{c}</math> and <math>\mat{W}\mat{c} = \mat{c}</math>, | ||
<math display="block"> | <math display="block"> | ||
| Line 513: | Line 506: | ||
<math display="block"> | <math display="block"> | ||
m_{ij} = \frac{z_{jj} - z_{ij}}{w_j}\ . | m_{ij} = \frac{z_{jj} - z_{ij}}{w_j}\ . | ||
</math> | </math>|We showed in Equation \ref{eq 11.5.4} that | ||
<math display="block"> | <math display="block"> | ||
| Line 560: | Line 553: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
From | From \ref{eq 11.5.6} and \ref{eq 11.5.7}, we have | ||
<math display="block"> | <math display="block"> | ||
| Line 599: | Line 592: | ||
10/3 & 4 & 0\cr}\ . | 10/3 & 4 & 0\cr}\ . | ||
</math> | </math> | ||
===Computation=== | ===Computation=== | ||
| Line 610: | Line 602: | ||
We obtain: | We obtain: | ||
<pre> | |||
<math display="block"> | <math display="block"> | ||
\mat {P} = \bordermatrix{ | \mat {P} = \bordermatrix{ | ||
| Line 619: | Line 612: | ||
4 & .0000 & .0000 & .0000 & 1.0000& .0000}\ ; | 4 & .0000 & .0000 & .0000 & 1.0000& .0000}\ ; | ||
</math> | </math> | ||
</pre> | |||
<math display="block"> | <math display="block"> | ||
| Line 656: | Line 649: | ||
===Ehrenfest Model=== | ===Ehrenfest Model=== | ||
'''Example''' | '''Example''' | ||
Let us consider the Ehrenfest model (see | Let us consider the Ehrenfest model (see [[guide:52e01d4de7#exam 11.1.6|Example]]) for gas diffusion for the general case of <math>2n</math> balls. Every second, one of the <math>2n</math> balls is chosen at random and moved from the urn it was in to the other urn. If there are | ||
11.1.6 | <math>i</math> balls in the first urn, then with probability <math>i/2n</math> we take one of them out and put | ||
for gas | it in the second urn, and | ||
diffusion for the general case of <math>2n</math> balls. Every second, one of the <math>2n</math> | |||
balls is chosen | |||
at random and moved from the urn it was in to the other urn. If there are | |||
<math>i</math> balls | |||
in the first urn, then with probability <math>i/2n</math> we take one of them out and put | |||
it | |||
in the second urn, and | |||
with probability <math>(2n - i)/2n</math> we take a ball from the second urn and put it in | with probability <math>(2n - i)/2n</math> we take a ball from the second urn and put it in | ||
the first urn. At each second we let the number <math>i</math> of balls in the first urn | the first urn. At each second we let the number <math>i</math> of balls in the first urn | ||
| Line 714: | Line 701: | ||
to | to | ||
<math>i - 1</math> if <math>i > n</math> and <math>i</math> to <math>i + 1</math> if <math>i < n</math>. | <math>i - 1</math> if <math>i > n</math> and <math>i</math> to <math>i + 1</math> if <math>i < n</math>. | ||
<div id=" | <div id="fig 11.6" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig11-6. | [[File:guide_e6d15_PSfig11-6.png | 600px | thumb | Ehrenfest simulation. ]] | ||
</div> | </div> | ||
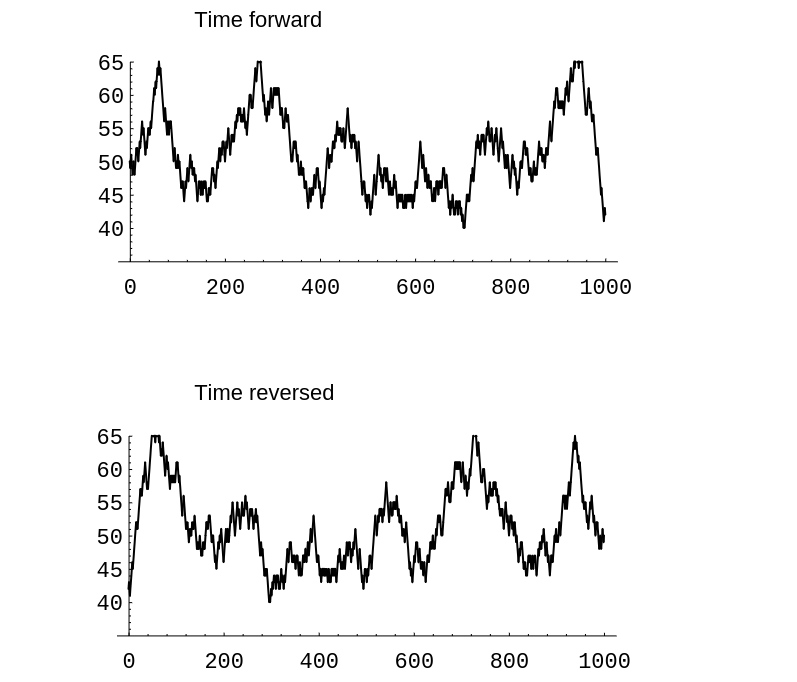
In [[#fig 11.6|Figure]] we show the results of simulating the Ehrenfest urn model for the case of <math>n = 50</math> and 1000 time units, using the program '''EhrenfestUrn'''. The top graph shows these results graphed in the order in which they occurred and the bottom graph shows the same results but with time reversed. There is no apparent difference. | |||
We note that if we had not started in equilibrium, the two graphs would typically look quite different. | |||
We note that if we had not started in equilibrium, the two graphs would | |||
typically | |||
look quite different. | |||
===Reversibility=== | ===Reversibility=== | ||
| Line 787: | Line 764: | ||
equilibrium, the pairs <math>(i, i - 1)</math> and <math>(i - 1, i)</math> should occur with the same | equilibrium, the pairs <math>(i, i - 1)</math> and <math>(i - 1, i)</math> should occur with the same | ||
frequency. While many of the Markov chains that occur in applications are | frequency. While many of the Markov chains that occur in applications are | ||
reversible, this is a very strong condition. In | reversible, this is a very strong condition. In [[exercise:20a3e63037 |Exercise]] you are asked to find an example of a Markov chain which is not reversible. | ||
you | |||
are asked to find an example of a Markov chain which is not reversible. | |||
===The Central Limit Theorem for Markov Chains=== | ===The Central Limit Theorem for Markov Chains=== | ||
| Line 805: | Line 779: | ||
that the expected value of the random variable <math>S^{(n)}_j</math>, as <math>n \rightarrow | that the expected value of the random variable <math>S^{(n)}_j</math>, as <math>n \rightarrow | ||
\infty</math>, is | \infty</math>, is | ||
asymptotic to <math>nw_j</math>, and it is easy to show that this is the case (see | asymptotic to <math>nw_j</math>, and it is easy to show that this is the case (see [[exercise:2ab75d75ba|Exercise]]). | ||
Exercise | |||
It is also natural to ask whether there is a limiting distribution of the | It is also natural to ask whether there is a limiting distribution of the random variables | ||
random variables | |||
<math>S^{(n)}_j</math>. The answer is yes, and in fact, this limiting distribution is the | <math>S^{(n)}_j</math>. The answer is yes, and in fact, this limiting distribution is the | ||
normal | normal | ||
| Line 836: | Line 806: | ||
following | following | ||
theorem. | theorem. | ||
{{proofcard|Theorem|thm_11.5.20|''' (Central Limit Theorem for Markov | {{proofcard|Theorem|thm_11.5.20|''' (Central Limit Theorem for Markov Chains)''' | ||
Chains)''' | |||
For an ergodic chain, for any real numbers <math>r < s</math>, we have | For an ergodic chain, for any real numbers <math>r < s</math>, we have | ||
| Line 848: | Line 817: | ||
as <math>n \rightarrow \infty</math>, for any choice of starting state, where | as <math>n \rightarrow \infty</math>, for any choice of starting state, where | ||
<math>\sigma_j^2</math> is | <math>\sigma_j^2</math> is | ||
the quantity defined in | the quantity defined in Equation \ref{eq 11.5.9}.|}} | ||
===Historical Remarks=== | ===Historical Remarks=== | ||
| Line 887: | Line 855: | ||
Markov chain with transition matrix | Markov chain with transition matrix | ||
<pre> | |||
<math display="block"> | <math display="block"> | ||
\bordermatrix{ | \bordermatrix{ | ||
| Line 893: | Line 862: | ||
\mbox{consonant} & .663 & .337}\ . | \mbox{consonant} & .663 & .337}\ . | ||
</math> | </math> | ||
</pre> | |||
The fixed vector for this chain is <math>(.432, .568)</math>, indicating that we should | The fixed vector for this chain is <math>(.432, .568)</math>, indicating that we should | ||
| Line 901: | Line 870: | ||
Claude Shannon considered an interesting extension of this idea in his book | Claude Shannon considered an interesting extension of this idea in his book | ||
'' | ''The Mathematical Theory of Communication,''<ref group="Notes" >C. E. Shannon and W. Weaver, ''The Mathematical Theory of Communication'' (Urbana: | ||
The Mathematical Theory of Communication,''<ref group="Notes" >C. E. | Univ. of Illinois Press, 1964).</ref> in which he developed the information-theoretic concept of entropy. Shannon considers a series of Markov chain approximations to | ||
Shannon and W. Weaver, ''The Mathematical Theory of Communication'' (Urbana: | |||
Univ. | |||
Illinois Press, 1964).</ref> in which he developed the | |||
concept | |||
of entropy. Shannon considers a series of Markov chain approximations to | |||
English | English | ||
prose. He does this first by chains in which the states are letters and then | prose. He does this first by chains in which the states are letters and then | ||
| Line 913: | Line 877: | ||
presents first a simulation where the words are chosen independently but with | presents first a simulation where the words are chosen independently but with | ||
appropriate frequencies. | appropriate frequencies. | ||
<blockquote> | <blockquote> | ||
| Line 932: | Line 895: | ||
</blockquote> | </blockquote> | ||
A simulation like the last one is carried out by opening a book and choosing the first word, say it is ''the.'' Then the book is read until the word | |||
A simulation like the last one is carried out by opening a book and choosing | ''the'' appears again and the word after this is chosen as the second word, which turned out to be | ||
the first word, say it is ''the.'' Then the book is read until the word | ''head.'' The book is then read until the word ''head'' appears again and the next | ||
''the'' | |||
appears again and the word after this is chosen as the second word, which | |||
turned out to be | |||
''head.'' The book is then read until the word ''head'' appears again | |||
and the next | |||
word, ''and,'' is chosen, and so on. | word, ''and,'' is chosen, and so on. | ||
Other early examples of the use of Markov chains occurred in Galton's study of the problem of survival of family names in 1889 and in the Markov chain | |||
Other early examples of the use of Markov chains occurred in Galton's study of | introduced by P. and T. Ehrenfest in 1907 for diffusion. Poincaré in 1912 dicussed card shuffling in terms of an ergodic Markov | ||
the problem of survival of family names in 1889 and in the Markov chain | chain defined on a permutation group. Brownian motion, a continuous time version of random walk, | ||
introduced by P. and T. Ehrenfest in 1907 for diffusion. | was introducted in 1900--1901 by L. Bachelier in his study of the stock market, and in 1905--1907 in the works of A. Einstein and M. Smoluchowsky in their study of physical processes. | ||
chain defined | |||
on a permutation group. Brownian motion, a continuous time version of random | |||
walk, | |||
was introducted in 1900--1901 by L. Bachelier in his study of the stock | |||
market, | |||
and in 1905--1907 in the works of A. Einstein and M. Smoluchowsky in their | |||
study of | |||
physical processes. | |||
One of the first systematic studies of finite Markov chains was carried out by | One of the first systematic studies of finite Markov chains was carried out by | ||
| Line 972: | Line 920: | ||
ergodic chains appeared first in the work of Frechet, who used it to find the | ergodic chains appeared first in the work of Frechet, who used it to find the | ||
limiting variance for the central limit theorem for Markov chains. | limiting variance for the central limit theorem for Markov chains. | ||
==General references== | |||
{{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | {{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | ||
==Notes== | ==Notes== | ||
{{Reflist|group=Notes}} | {{Reflist|group=Notes}} | ||
Revision as of 23:31, 11 June 2024
In this section we consider two closely related descriptive quantities of interest for ergodic chains: the mean time to return to a state and the mean time to go from one state to another state.
Let [math]\mat{P}[/math] be the transition matrix of an ergodic chain with states [math]s_1, s_2, \ldots, s_r[/math]. Let [math]\mat {w} = (w_1,w_2,\ldots,w_r)[/math] be the unique probability vector such that [math]\mat {w} \mat {P} = \mat {w}[/math]. Then, by the Law of Large Numbers for Markov chains, in the long run the process will spend a fraction [math]w_j[/math] of the time in state [math]s_j[/math]. Thus, if we start in any state, the chain will eventually reach state [math]s_j[/math]; in fact, it will be in state [math]s_j[/math] infinitely often.
Another way to see this is the following: Form a new Markov chain by making
[math]s_j[/math] an
absorbing state, that is, define [math]p_{jj} = 1[/math]. If we start at any state other
than [math]s_j[/math],
this new process will behave exactly like the original chain up to the first
time that state
[math]s_j[/math] is reached. Since the original chain was an ergodic chain, it was
possible to reach
[math]s_j[/math] from any other state. Thus the new chain is an absorbing chain with a
single absorbing
state [math]s_j[/math] that will eventually be reached. So if we start the original chain
at a state
[math]s_i[/math] with [math]i \ne j[/math], we will eventually reach the state [math]s_j[/math].
Let [math]\mat{N}[/math] be the fundamental matrix for the new chain. The entries
of [math]\mat{N}[/math]
give the expected number of times in each state before absorption. In terms of
the original chain, these quantities give the expected number of times in each
of the states before reaching state [math]s_j[/math] for the first time. The [math]i[/math]th
component of the vector [math]\mat {N} \mat {c}[/math] gives the expected number of steps
before
absorption in the new chain, starting in state [math]s_i[/math]. In terms of the old
chain, this is the expected number of steps required to reach state [math]s_j[/math] for
the first time starting at state [math]s_i[/math].
Mean First Passage Time
If an ergodic Markov chain is started in state [math]s_i[/math], the expected number of steps to reach state [math]s_j[/math] for the first time is called the mean first passage time from [math]s_i[/math] to [math]s_j[/math]. It is denoted by [math]m_{ij}[/math]. By convention [math]m_{ii} = 0[/math].
Example Let us return to the maze example (Example). We shall make this ergodic chain into an absorbing chain by making state 5 an absorbing state. For example, we might assume that food is placed in the center of the maze and once the rat finds the food, he stays to enjoy it (see Figure).
The new transition matrix in canonical form is
<math display="block">
\mat {P}\;= \bordermatrix{&
\hbox{1}&\hbox{2}&\hbox{3}&\hbox{4}&\hbox{6}&\hbox{7}&\hbox{8}
&\hbox{9}&\omit\hfil&\hbox{5}\cr
\hbox{1}\strut & 0 &1/2 & 0 & 0 & 1/2 & 0 & 0
& 0 &\srule & 0 \cr
\hbox{2}\strut &1/3 & 0 &1/3 & 0 & 0 & 0 & 0
& 0 &\srule &1/3\cr
\hbox{3}\strut & 0 &1/2 & 0 & 1/2 & 0 & 0 & 0
& 0 &\srule & 0 \cr
\hbox{4}\strut & 0 & 0 &1/3 & 0 & 0 &1/3 & 0
& 1/3 &\srule &1/3\cr
\hbox{6}\strut &1/3 & 0 & 0 & 0 & 0 & 0 & 0
& 0 &\srule &1/3\cr
\hbox{7}\strut & 0 & 0 & 0 & 0 &1/2 & 0 & 1/2
& 0 &\srule &0 \cr
\hbox{8}\strut & 0 & 0 & 0 & 0 & 0 &1/3 & 0
& 1/3 &\srule &1/3\cr
\hbox{9}\strut & 0 & 0 & 0 &1/2 & 0 & 0 & 1/2&
0 &\srule & 0 \cr
\middlehrule{8}{1}
\hbox{5}\strut & 0 & 0 & 0 & 0 & 0 & 0 & 0
& 0 &\srule
& 1}\ .
</math>
If we compute the fundamental matrix [math]\mat{N}[/math], we obtain
<math display="block">
\mat {N} = \frac18 \pmatrix{
14 & 9 & 4 & 3 & 9 & 4 & 3 & 2 \cr
6 & 14 & 6 & 4 & 4 & 2 & 2 & 2 \cr
4 & 9 & 14 & 9 & 3 & 2 & 3 & 4 \cr
2 & 4 & 6 & 14 & 2 & 2 & 4 & 6 \cr
6 & 4 & 2 & 2 & 14 & 6 & 4 & 2 \cr
4 & 3 & 2 & 3 & 9 & 14 & 9 & 4 \cr
2 & 2 & 2 & 4 & 4 & 6 & 14 & 6 \cr
2 & 3 & 4 & 9 & 3 & 4 & 9 & 14 \cr}\ .
</math>
The expected time to absorption for different starting states is given by the vector [math]\mat {N} \mat {c}[/math], where
We see that, starting from compartment 1, it will take on the average six steps to reach food. It is clear from symmetry that we should get the same answer for starting at state 3, 7, or 9. It is also clear that it should take one more step, starting at one of these states, than it would starting at 2, 4, 6, or 8. Some of the results obtained from [math]\mat{N}[/math] are not so obvious. For instance, we note that the expected number of times in the starting state is 14/8 regardless of the state in which we start.
Mean Recurrence Time
A quantity that is closely related to the mean first passage time is the mean recurrence time, defined as follows. Assume that we start in state [math]s_i[/math]; consider the length of time before we return to [math]s_i[/math] for the first time. It is clear that we must return, since we either stay at [math]s_i[/math] the first step or go to some other state [math]s_j[/math], and from any other state [math]s_j[/math], we will eventually reach [math]s_i[/math] because the chain is ergodic.
If an ergodic Markov chain is started in state [math]s_i[/math], the expected number of steps to return to [math]s_i[/math] for the first time is the mean recurrence time for [math]s_i[/math]. It is denoted by [math]r_i[/math].
We need to develop some basic properties of the mean first passage time. Consider the mean first passage time from [math]s_i[/math] to [math]s_j[/math]; assume that [math]i \ne j[/math]. This may be computed as follows: take the expected number of steps required given the outcome of the first step, multiply by the probability that this outcome occurs, and add. If the first step is to [math]s_j[/math], the expected number of steps required is 1; if it is to some other state [math]s_k[/math], the expected number of steps required is [math]m_{kj}[/math] plus 1 for the step already taken. Thus,
or, since [math]\sum_k p_{ik} = 1[/math],
Similarly, starting in [math]s_i[/math], it must take at least one step to return.
Considering all possible first steps gives us
Mean First Passage Matrix and Mean Recurrence Matrix
Let us now define two matrices [math]\mat{M}[/math] and [math]\mat{D}[/math]. The [math]ij[/math]th entry [math]m_{ij}[/math] of [math]\mat{M}[/math] is the mean first passage time to go from [math]s_i[/math] to [math]s_j[/math] if [math]i \ne j[/math]; the diagonal entries are 0. The matrix [math]\mat{M}[/math] is called the mean first passage matrix. The matrix [math]\mat{D}[/math] is the matrix with all entries 0 except the diagonal entries [math]d_{ii} = r_i[/math]. The matrix [math]\mat{D}[/math] is called the mean recurrence matrix.
Let [math]\mat {C}[/math] be an [math]r \times r[/math] matrix with all entries 1. Using Equation \ref{eq 11.5.1} for the case [math]i \ne j[/math] and Equation \ref{eq 11.5.2} for the case [math]i = j[/math], we obtain the matrix equation
or
Equation \ref{eq 11.5.4} with [math]m_{ii} = 0[/math] implies Equation \ref{eq 11.5.1} and Equation \ref{eq 11.5.2}. We are now in a position to prove our first basic theorem.
For an ergodic Markov chain, the mean recurrence time for state [math]s_i[/math] is [math]r_i = 1/w_i[/math], where [math]w_i[/math] is the [math]i[/math]th component of the fixed probability vector for the transition matrix.
Show ProofMultiplying both sides of Equation \ref{eq 11.5.4} by [math]\mat{w}[/math] and using the fact that
gives
For an ergodic Markov chain, the components of the fixed probability vector w are strictly positive.
Show ProofWe know that the values of [math]r_i[/math] are finite and so [math]w_i = 1/r_i[/math] cannot be 0.
Example In Example we found the fixed probability vector for the maze example to be
Hence, the mean recurrence times are given by the reciprocals of these probabilities. That is,
Returning to the Land of Oz, we found that the weather in the Land of Oz could be represented by a Markov chain with states rain, nice, and snow. In Ergodic Markov Chains we found that the limiting vector was [math]\mat {w} = (2/5,1/5,2/5)[/math]. From this we see that the mean number of days between rainy days is 5/2, between nice days is 5, and between snowy days is 5/2.
Fundamental Matrix
We shall now develop a fundamental matrix for ergodic chains that will play a role similar to that of the fundamental matrix [math]\mat {N} = (\mat {I} - \mat {Q})^{-1}[/math] for absorbing chains. As was the case with absorbing chains, the fundamental matrix can be used to find a number of interesting quantities involving ergodic chains. Using this matrix, we will give a method for calculating the mean first passage times for ergodic chains that is easier to use than the method given above. In addition, we will state (but not prove) the Central Limit Theorem for Markov Chains, the statement of which uses the fundamental matrix.
We begin by considering the case that \mat{P} is the transition matrix of a
regular
Markov chain. Since there are no absorbing states, we might be tempted to try
[math]\mat {Z} = (\mat {I} - \mat {P})^{-1}[/math] for a fundamental matrix. But [math]\mat
{I} - \mat {P}[/math]
does not have an inverse. To see this, recall that a matrix [math]\mat{R}[/math] has an
inverse if and
only if [math]\mat {R} \mat {x} = \mat {0}[/math] implies [math]\mat {x} = \mat {0}[/math]. But
since [math]\mat {P}
\mat {c} = \mat {c}[/math] we have [math](\mat {I} - \mat {P})\mat {c} = \mat {0}[/math], and so
[math]\mat {I} -
\mat {P}[/math] does not have an inverse.
We recall that if we have an absorbing Markov chain, and \mat{Q} is the
restriction of the transition matrix to the set of transient states, then the
fundamental
matrix [math]\mat {N}[/math] could be written as
The reason that this power series converges is that [math]\mat {Q}^n \rightarrow 0[/math], so this series acts like a convergent geometric series.
This idea might prompt one to try to find a similar series for regular chains.
Since we
know that [math]\mat {P}^n \rightarrow \mat {W}[/math], we might consider the series
We now use special properties of [math]\mat {P}[/math] and [math]\mat {W}[/math] to rewrite this series. The special properties are: 1) [math]\mat {P}\mat {W} = \mat {W}[/math], and 2) [math]\mat {W}^k = \mat {W}[/math] for all positive integers [math]k[/math]. These facts are easy to verify, and are left as an exercise (see Exercise). Using these facts, we see that
If we expand the expression [math](1-1)^n[/math], using the Binomial Theorem, we obtain the expression in parenthesis above, except that we have an extra term (which equals 1). Since [math](1-1)^n = 0[/math], we see that the above expression equals -1. So we have
for all [math]n \ge 1[/math].
We can now rewrite the series in \ref{eq 11.5.8} as
Since the [math]n[/math]th term in this series is equal to [math]\mat {P}^n - \mat {W}[/math], the [math]n[/math]th term goes to 0 as [math]n[/math] goes to infinity. This is sufficient to show that this series converges, and sums to the inverse of the matrix [math]\mat {I} - \mat {P} + \mat {W}[/math]. We call this inverse the fundamental matrix associated with the chain, and we denote it by \mat {Z}.
In the case that the chain is ergodic, but not regular, it is not true that
[math]\mat {P}^n
\rightarrow \mat {W}[/math] as [math]n \rightarrow \infty[/math]. Nevertheless, the matrix
[math]\mat {I} - \mat
{P} + \mat {W}[/math] still has an inverse, as we will now show.
Let [math]\mat {P}[/math] be the transition matrix of an ergodic chain, and let \mat {W} be the matrix all of whose rows are the fixed probability row vector for [math]\mat {P}[/math]. Then the matrix
Let [math]\mat{x}[/math] be a column vector such that
But this means that [math]\mat {x} = \mat {P} \mat {x}[/math] is a fixed column vector for [math]\mat{P}[/math]. By Theorem, this can only happen if [math]\mat{x}[/math] is a constant vector. Since [math]\mat {w}\mat {x} = 0[/math], and \mat {w} has strictly positive entries, we see that [math]\mat {x} = \mat {0}[/math]. This completes the proof.
As in the regular case, we will call the inverse of the matrix [math]\mat {I} - \mat
{P} + \mat {W}[/math]
the fundamental matrix for the ergodic chain with transition
matrix \mat {P}, and we will
use [math]\mat {Z}[/math] to denote this fundamental matrix.
Example Let [math]\mat{P}[/math] be the transition matrix for the weather in the Land of Oz. Then
so
Using the Fundamental Matrix to Calculate the Mean First Passage Matrix
We shall show how one can obtain the mean first passage matrix [math]\mat{M}[/math] from the fundamental matrix \mat{Z} for an ergodic Markov chain. Before stating the theorem which gives the first passage times, we need a few facts about \mat{Z}.
Let [math]\mat{Z} = (\mat{I} - \mat{P} + \mat{W})^{-1}[/math], and let [math]\mat{c}[/math] be a column vector of all 1's. Then
Since [math]\mat{P}\mat{c} = \mat{c}[/math] and [math]\mat{W}\mat{c} = \mat{c}[/math],
Similarly, since [math]\mat{w}\mat{P} = \mat{w}[/math] and [math]\mat{w}\mat{W} = \mat{w}[/math],
Finally, we have
The following theorem shows how one can obtain the mean first passage times from the fundamental matrix.
The mean first passage matrix [math]\mat{M}[/math] for an ergodic chain is determined from the fundamental matrix [math]\mat{Z}[/math] and the fixed row probability vector [math]\mat{w}[/math] by
We showed in Equation \ref{eq 11.5.4} that
Example In the Land of Oz example, we find that
We have also seen that [math]\mat {w} = (2/5,1/5, 2/5)[/math]. So, for example,
by Theorem. Carrying out the calculations for the other entries of [math]\mat{M}[/math], we obtain
Computation
The program ErgodicChain calculates the fundamental matrix, the fixed vector, the mean recurrence matrix [math]\mat{D}[/math], and the mean first passage matrix [math]\mat{M}[/math]. We have run the program for the Ehrenfest urn model (Example). We obtain:
<math display="block">
\mat {P} = \bordermatrix{
& 0 & 1 & 2 & 3 & 4 \cr
0 & .0000 & 1.0000 & .0000 & .0000 & .0000\cr
1 & .2500 & .0000 & .7500 & .0000 & .0000\cr
2 & .0000 & .5000 & .0000 & .5000 & .0000\cr
3 & .0000 & .0000 & .7500 & .0000 & .2500\cr
4 & .0000 & .0000 & .0000 & 1.0000& .0000}\ ;
</math>
From the mean first passage matrix, we see that the mean time to go from 0 balls in urn 1 to 2 balls in urn 1 is 2.6667 steps while the mean time to go from 2 balls in urn 1 to 0 balls in urn 1 is 18.6667. This reflects the fact that the model exhibits a central tendency. Of course, the physicist is interested in the case of a large number of molecules, or balls, and so we should consider this example for [math]n[/math] so large that we cannot compute it even with a computer.
Ehrenfest Model
Example Let us consider the Ehrenfest model (see Example) for gas diffusion for the general case of [math]2n[/math] balls. Every second, one of the [math]2n[/math] balls is chosen at random and moved from the urn it was in to the other urn. If there are [math]i[/math] balls in the first urn, then with probability [math]i/2n[/math] we take one of them out and put it in the second urn, and with probability [math](2n - i)/2n[/math] we take a ball from the second urn and put it in the first urn. At each second we let the number [math]i[/math] of balls in the first urn be the state of the system. Then from state [math]i[/math] we can pass only to state [math]i - 1[/math] and [math]i + 1[/math], and the transition probabilities are given by
This defines the transition matrix of an ergodic, non-regular Markov chain
(see Exercise). Here the physicist is interested in
long-term
predictions about the state occupied. In Example, we gave an
intuitive reason for expecting that the fixed vector [math]\mat{w}[/math] is the binomial
distribution with parameters [math]2n[/math] and [math]1/2[/math]. It is easy to check that this is
correct. So,
Thus the mean recurrence time for state [math]i[/math] is
Consider in particular the central term [math]i = n[/math]. We have seen that this term
is
approximately [math]1/\sqrt{\pi n}[/math]. Thus we may approximate [math]r_n[/math] by [math]\sqrt{\pi
n}[/math].
This model was used to explain the concept of reversibility in physical
systems. Assume that we let our system run until it is in equilibrium. At
this
point, a movie is made, showing the system's progress. The movie is then shown
to you, and you are asked to tell if the movie was shown in the forward or
the reverse direction. It would seem that there
should always be a tendency to move toward an equal proportion of balls so that
the correct order of time should be the one with the most transitions from [math]i[/math]
to
[math]i - 1[/math] if [math]i \gt n[/math] and [math]i[/math] to [math]i + 1[/math] if [math]i \lt n[/math].
In Figure we show the results of simulating the Ehrenfest urn model for the case of [math]n = 50[/math] and 1000 time units, using the program EhrenfestUrn. The top graph shows these results graphed in the order in which they occurred and the bottom graph shows the same results but with time reversed. There is no apparent difference.
We note that if we had not started in equilibrium, the two graphs would typically look quite different.
Reversibility
If the Ehrenfest model is started in equilibrium, then the process has no apparent time direction. The reason for this is that this process has a property called reversibility. Define [math]X_n[/math] to be the number of balls in the left urn at step [math]n[/math]. We can calculate, for a general ergodic chain, the reverse transition probability:
In general, this will depend upon [math]n[/math], since [math]P(X_n = j)[/math] and also [math]P(X_{n - 1}
= j)[/math] change with [math]n[/math]. However, if we start with the vector [math]\mat{w}[/math] or wait
until equilibrium is reached, this will not be the case. Then we can define
as a transition matrix for the process watched with time reversed.
Let us calculate a typical transition probability for the reverse chain [math]\mat{
P}^* = \{p_{ij}^*\}[/math] in the Ehrenfest model. For example,
Similar calculations for the other transition probabilities show that [math]\mat
{P}^*
= \mat {P}[/math]. When this occurs the process is called reversible.
Clearly,
an ergodic chain is reversible if, and only if, for every pair of states
[math]s_i[/math] and [math]s_j[/math], [math]w_i p_{ij} = w_j p_{ji}[/math]. In particular, for the Ehrenfest
model
this means that [math]w_i p_{i,i - 1} = w_{i - 1} p_{i - 1,i}[/math]. Thus, in
equilibrium, the pairs [math](i, i - 1)[/math] and [math](i - 1, i)[/math] should occur with the same
frequency. While many of the Markov chains that occur in applications are
reversible, this is a very strong condition. In Exercise you are asked to find an example of a Markov chain which is not reversible.
The Central Limit Theorem for Markov Chains
Suppose that we have an ergodic Markov chain with states [math]s_1, s_2, \ldots, s_k[/math]. It is natural to consider the distribution of the random variables [math]S^{(n)}_j[/math], which denotes the number of times that the chain is in state [math]s_j[/math] in the first [math]n[/math] steps. The [math]j[/math]th component [math]w_j[/math] of the fixed probability row vector [math]\mat{w}[/math] is the proportion of times that the chain is in state [math]s_j[/math] in the long run. Hence, it is reasonable to conjecture that the expected value of the random variable [math]S^{(n)}_j[/math], as [math]n \rightarrow \infty[/math], is asymptotic to [math]nw_j[/math], and it is easy to show that this is the case (see Exercise).
It is also natural to ask whether there is a limiting distribution of the random variables [math]S^{(n)}_j[/math]. The answer is yes, and in fact, this limiting distribution is the normal distribution. As in the case of independent trials, one must normalize these random variables. Thus, we must subtract from [math]S^{(n)}_j[/math] its expected value, and then divide by its standard deviation. In both cases, we will use the asymptotic values of these quantities, rather than the values themselves. Thus, in the first case, we will use the value [math]nw_j[/math]. It is not so clear what we should use in the second case. It turns out that the quantity
represents the asymptotic variance. Armed with these ideas, we can state the following theorem.
(Central Limit Theorem for Markov Chains) For an ergodic chain, for any real numbers [math]r \lt s[/math], we have
Historical Remarks
Markov chains were introduced by Andre\u i Andreevich Markov (1856--1922) and were named in his honor. He was a talented undergraduate who received a gold medal for his undergraduate thesis at St. Petersburg University. Besides being an active research mathematician and teacher, he was also active in politics and patricipated in the liberal movement in Russia at the beginning of the twentieth century. In 1913, when the government celebrated the 300th anniversary of the House of Romanov family, Markov organized a counter-celebration of the 200th anniversary of Bernoulli's discovery of the Law of Large Numbers.
Markov was led to develop Markov chains as a natural extension of sequences of
independent random variables. In his first paper, in 1906, he proved that for
a Markov chain with positive transition probabilities and numerical states the
average of the outcomes converges to the expected value of the limiting
distribution (the fixed vector). In a later paper he proved the central limit
theorem for such chains. Writing about Markov, A. P. Youschkevitch remarks:
Markov arrived at his chains starting from the internal needs of probability theory, and he never wrote about their applications to physical science. For him the only real examples of the chains were literary texts, where the two states denoted the vowels and consonants.[Notes 1]
In a paper written in 1913,[Notes 2] Markov chose a sequence
of 20,00 letters from Pushkin's Eugene Onegin to see if this
sequence can be approximately considered a simple chain. He obtained the
Markov chain with transition matrix
<math display="block">
\bordermatrix{
& \mbox{vowel} & \mbox{consonant} \cr
\mbox{vowel} & .128 & .872 \cr
\mbox{consonant} & .663 & .337}\ .
</math>
The fixed vector for this chain is [math](.432, .568)[/math], indicating that we should expect about 43.2 percent vowels and 56.8 percent consonants in the novel, which was borne out by the actual count.
Claude Shannon considered an interesting extension of this idea in his book
The Mathematical Theory of Communication,[Notes 3] in which he developed the information-theoretic concept of entropy. Shannon considers a series of Markov chain approximations to
English
prose. He does this first by chains in which the states are letters and then
by chains in which the states are words. For example, for the case of words he
presents first a simulation where the words are chosen independently but with
appropriate frequencies.
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
He then notes the increased resemblence to ordinary English text when the words
are chosen as a Markov chain, in which case he obtains
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRI\-TER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
A simulation like the last one is carried out by opening a book and choosing the first word, say it is the. Then the book is read until the word the appears again and the word after this is chosen as the second word, which turned out to be head. The book is then read until the word head appears again and the next word, and, is chosen, and so on.
Other early examples of the use of Markov chains occurred in Galton's study of the problem of survival of family names in 1889 and in the Markov chain introduced by P. and T. Ehrenfest in 1907 for diffusion. Poincaré in 1912 dicussed card shuffling in terms of an ergodic Markov chain defined on a permutation group. Brownian motion, a continuous time version of random walk, was introducted in 1900--1901 by L. Bachelier in his study of the stock market, and in 1905--1907 in the works of A. Einstein and M. Smoluchowsky in their study of physical processes.
One of the first systematic studies of finite Markov chains was carried out by M. Frechet.[Notes 4] The treatment of Markov chains in terms of the two fundamental matrices that we have used was developed by Kemeny and Snell [Notes 5] to avoid the use of eigenvalues that one of these authors found too complex. The fundamental matrix [math]\mat{N}[/math] occurred also in the work of J. L. Doob and others in studying the connection between Markov processes and classical potential theory. The fundamental matrix [math]\mat{Z}[/math] for ergodic chains appeared first in the work of Frechet, who used it to find the limiting variance for the central limit theorem for Markov chains.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- See Dictionary of Scientific Biography, ed. C. C. Gillespie (New York: Scribner's Sons, 1970), pp. 124--130.
- A. A. Markov, “An Example of Statistical Analysis of the Text of Eugene Onegin Illustrating the Association of Trials into a Chain,” Bulletin de l'Acadamie Imperiale des Sciences de St. Petersburg, ser. 6, vol. 7 (1913), pp. 153--162.
- C. E. Shannon and W. Weaver, The Mathematical Theory of Communication (Urbana: Univ. of Illinois Press, 1964).
- M. Frechet, “Théorie des événements en chaine dans le cas d'un nombre fini d'états possible,” in Recherches théoriques Modernes sur le calcul des probabilités, vol. 2 (Paris, 1938).
- J. G. Kemeny and J. L. Snell, Finite Markov Chains.