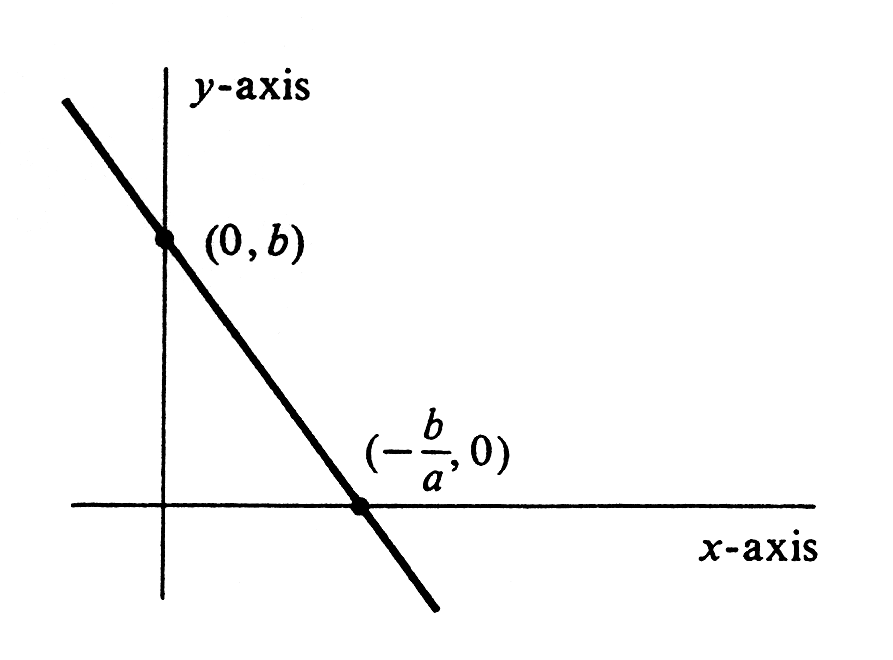guide:D0085fde68: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
==<span id="sec 1.3"></span>Operations with Functions.== | |||
If <math>f</math> and <math>g</math> are two functions, | |||
a new function <math>f(g)</math>, | |||
called the '''composition''' of <math>g</math> with <math>f</math>, | |||
is defined by | |||
<math display="block"> | |||
(f(g))(x) = f(g(x)). | |||
</math> | |||
For example, | |||
if <math>f(x) = x^3 - 1</math> and <math>g(x) = \frac{x + 1}{x - 1}</math>, | |||
then | |||
<span id{{=}}"eq1.3.1"/> | |||
<math display="block"> | |||
\begin{eqnarray} | |||
\label{eq1.3.1} | |||
(f(g))(x) | |||
&=& f(g(x)) | |||
= (g(x))^3 - 1 \\ | |||
&=& \biggl( \frac{x + 1}{x - 1}\biggr)^3 - 1 | |||
= \frac{2(3x^2 + 1)}{(x - 1)^3} . | |||
\end{eqnarray} | |||
</math> | |||
The composition of two functions | |||
is the function obtained by applying one after the other. | |||
If <math>f</math> and <math>g</math> are regarded as computing machines, | |||
then <math>f(g)</math> is the composite machine | |||
constructed by feeding the output of <math>g</math> | |||
into the input of <math>f</math> | |||
as indicated in [[#fig 1.17|Figure]]. | |||
<div id="fig 1.17" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_17.png | 400px | thumb | ]] | |||
</div> | |||
In general it is not true that <math>f(g) = g(f)</math>. | |||
In the above example we have | |||
<span id{{=}}"eq1.3.2"/> | |||
<math display="block"> | |||
\begin{eqnarray} | |||
\label{eq1.3.2} | |||
(g(f))(x) | |||
&=& g(f(x)) | |||
= \frac{f(x) + 1}{f(x) - 1} \\ | |||
&=& \frac{(x^3 - 1) + 1}{(x^3 - 1) - 1} | |||
= \frac{x^3}{x^3 - 2} , | |||
\end{eqnarray} | |||
</math> | |||
and the two functions are certainly not the same. | |||
In terms of ordered pairs the composition <math>f(g)</math> of <math>g</math> with <math>f</math> | |||
is formally defined to be | |||
the set of all ordered pairs <math>(a, c)</math> | |||
for which there is an element <math>b</math> | |||
such that <math>b = g(a)</math> and <math>c = f(b)</math>. | |||
If <math>f</math> and <math>g</math> are two real-valued functions, | |||
we can perform the usual arithmetic operations of | |||
addition, subtraction, multiplication, and division. | |||
Thus for the functions | |||
<math>f(x) = x^3 - 1</math> and <math>g(x) = \frac{x + 1}{x - 1}</math>, | |||
we have | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
f(x) + g(x) | |||
&=& x^3 - 1 + \frac{x + 1}{x - 1} , \\ | |||
f(x) - g(x) | |||
&=& x^3 - 1 - \frac{x + 1}{x - 1} , \\ | |||
f(x)g(x) | |||
&=& (x^3 -1) \frac{x + 1}{x - 1} , \\ | |||
&=& (x^2 + x + 1)(x + 1) \provx{if $x \neq 1$}, \\ | |||
f(x)/g(x) | |||
&=& \frac{x^3 - 1}{\frac{x + 1}{x - 1}} \\ | |||
&=& \frac{(x^3 - 1)(x - 1)}{x + 1}. | |||
\end{eqnarray*} | |||
</math> | |||
Just as with the composition of two functions, | |||
each arithmetic operation | |||
provides a method of constructing a new function | |||
from the two given functions <math>f</math> and <math>g</math>. | |||
The natural notations for these new functions are | |||
<math>f + g</math>, <math>f - g</math>, <math>fg</math>, and <math>\frac{f}{g}</math>. | |||
They are defined by the formulas | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
(f + g)(x) | |||
&=& f(x) + g(x), \\ | |||
(f - g)(x) | |||
&=& f(x) - g(x), \\ | |||
(fg)(x) | |||
&=& f(x)g(x), \\ | |||
{\frac{f}{g}}(x) | |||
&=& \frac{f(x)}{g(x)} \provx{if $g(x) \neq 0$}. | |||
\end{eqnarray*} | |||
</math> | |||
The product function <math>fg</math> should not be confused with | |||
the composite function <math>f(g)</math>. | |||
For example, if <math>f(x) = x^5</math> and <math>g(x) = x^3</math>, | |||
then we have <math>(fg)(x) = f(x)g(x) = {x^5} \cdot {x^3} = x^8</math>, | |||
whereas | |||
<math display="block"> | |||
(f(g))(x) = f(g(x)) = (x^3)^5 = x^{15}. | |||
</math> | |||
We may also form the product <math>af</math> of an arbitrary real number <math>a</math> | |||
and real-valued function <math>f</math>. | |||
The product function is defined by | |||
<math display="block"> | |||
(af)(x)= af(x). | |||
</math> | |||
<span id="exam 1.3.1"/> | |||
'''Example''' | |||
\label{exam 1.3.1} | |||
Let functions <math>f</math> and <math>g</math> be defined by | |||
<math>f(x) = x - 2</math> and <math>g(x) = x^2 - 5x + 6</math>. | |||
Draw the graphs of <math>f</math>, <math>g</math>, <math>2f</math>, and <math>f + g</math>. | |||
We compute the function values | |||
corresponding to several different numbers <math>x</math> in | |||
[[#table 1.3 |Tables]] [[#table 1.4 |and]]. | |||
The resulting graphs of <math>f</math> and <math>g</math> are, respectively, | |||
the straight line and parabola shown in [[#fig 1.18|Figure]](a). | |||
<div id="fig 1.18" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_18.png | 400px | thumb | ]] | |||
</div> | |||
It turns out that the graphs of <math>2f</math> and <math>f + g</math> | |||
are also a straight line and a parabola. | |||
They are drawn in [[#fig 1.18|Figure]](b). | |||
To see why the graph of <math>f + g</math> is a parabola, | |||
observe that | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
(f + g)(x) | |||
&=& f(x) + g(x) | |||
= (x - 2) + (x^2 - 5x + 6) = x^2 - 4x + 4 \\ | |||
&=& (x - 2)^2. | |||
\end{eqnarray*} | |||
</math> | |||
It follows that <math>f + g</math> is very much like | |||
the function defined by <math>y = x^2</math>. | |||
Instead of simply squaring a number, | |||
<math>f + g</math> first subtracts <math>2</math> and then squares. | |||
Its graph will be just like that of <math>y = x^2</math> | |||
except that it will be shifted two units to the right. | |||
\begin{table} | |||
<math display="block"> | |||
\begin{array}{r|r|c} | |||
\hline | |||
x & f(x) & 2f(x) \\ | |||
\hline | |||
0 & -2 & -4 \\ | |||
1 & -1 & -2 \\ | |||
2 & 0 & 0 \\ | |||
3 & 1 & 2 \\ | |||
\hline | |||
\end{array} | |||
</math> | |||
\caption{} | |||
\label{table 1.3} | |||
\end{table} | |||
\begin{table} | |||
\centering | |||
<math display="block"> | |||
\begin{array}{r|c} | |||
\hline | |||
x & g(x) \\ | |||
\hline | |||
0 & 6 \\ | |||
5 & 6 \\ | |||
\frac{5}{2} & -\frac{1}{4} \\ | |||
1 & 2 \\ | |||
4 & 2 \\ | |||
\hline | |||
\end{array} | |||
</math> | |||
\caption{} | |||
\label{table 1.4} | |||
\end{table} | |||
Up to this point | |||
we have used the letters | |||
<math>f</math>, <math>g</math>, <math>h</math>, <math>F</math>, <math>G</math>, and <math>H</math> | |||
to denote functions, | |||
and the letters <math>x</math>, <math>y</math>, <math>a</math>, <math>b</math>, and <math>c</math> | |||
to denote elements of sets---usually real numbers. | |||
However, the letters in the second set | |||
are sometimes also used as functions. | |||
This occurs, for example, | |||
when we speak of <math>x</math> as a real variable. | |||
As such, it not only is the name of a real number | |||
but also can take on many different values: | |||
<math>5</math>, or <math>-7</math>, or <math>\pi</math>, or \ldots. | |||
Thus the variable <math>x</math> is a function. | |||
Specifically, it is the very simple function | |||
that assigns the value <math>5</math> to the number <math>5</math>, | |||
the value <math>-7</math> to the number <math>-7</math>, | |||
the value <math>\pi</math> to <math>\pi</math>, \ldots. | |||
For every real number <math>a</math>, we have | |||
<math display="block"> | |||
x(a) = a. | |||
</math> | |||
This function is called the '''identity function'''. | |||
Suppose, for example, | |||
that <math>s</math> is used to denote the distance | |||
that a stone falling freely in space has fallen. | |||
The value of <math>s</math> increases as the stone falls | |||
and depends on the length of time <math>t</math> that it has fallen | |||
according to the equation | |||
<math>s= {\frac{1}{2}}g{t^2}</math>, | |||
where <math>g</math> is the constant gravitational acceleration. | |||
(This formula assumes no air resistance, | |||
that the stone was at rest at time <math>t = 0</math>, | |||
and that distance is measured from the starting point.) | |||
Thus <math>s</math> has the value <math>{\frac{9}{2}}g</math> | |||
if <math>t</math> has the value <math>3</math>, | |||
and, more generally, | |||
the value <math>{\frac{1}{2}}g{a^2}</math> | |||
when <math>t</math> has the value <math>a</math>. | |||
If we consider <math>t</math> to be another name for the identity function, | |||
then <math>s</math> may be regarded as the function whose value is | |||
<math display="block"> | |||
s(a) = {\frac{1}{2}}{g{a^2}} = {\frac{1}{2}}{g(t(a))^2} | |||
</math> | |||
for every real number <math>a</math>. | |||
The original equation <math>s = {\frac{1}{2}}g{t^2}</math> then states | |||
the relation between the two functions <math>s</math> and <math>t</math>. | |||
The fact that <math>s</math> and <math>t</math> take on different values | |||
is also expressed by referring to them as variables. | |||
A '''variable''' is simply a name of a function. | |||
In our example <math>s</math> is called a dependent variable, | |||
and <math>t</math> an independent variable, | |||
because the values of <math>s</math> depend on those of <math>t</math> | |||
according to <math>s = {\frac{1}{2}}g{t^2}</math>. | |||
Thus an '''independent variable''' | |||
is a name for the identity function, | |||
and a '''dependent variable''' is one that is not independent. | |||
A real variable is therefore a name of a real-valued function. | |||
Since the arithmetic operations of | |||
addition, subtraction, multiplication, and division | |||
have been defined for real-valued functions, | |||
they are automatically defined for real variables. | |||
We shall generally use the letter <math>x</math> | |||
to denote an independent variable. | |||
This raises the question: | |||
How does one tell whether an occurrence of <math>x</math> | |||
denotes a real number or the identity function? | |||
The answer is that the notation alone does not tell, | |||
but the context and the reader's understanding should. | |||
However, a more practical reply | |||
is that it doesn't really make much difference. | |||
We may regard <math>f(x)</math> as either | |||
the value of the function <math>f</math> at the number <math>x</math> | |||
or as the composition of <math>f</math> with the variable <math>x</math>. | |||
If <math>x</math> is an independent variable, | |||
the function <math>f(x)</math> is then the same thing as <math>f</math>. | |||
<span id="exam 1.3.2"/> | |||
'''Example''' | |||
\label{exam 1.3.2} | |||
The conventions that we have adopted | |||
concerning the use of variables | |||
give our notations a flexibility | |||
that is both consistent and extremely useful. | |||
Consider, for example, the equation | |||
<math display="block"> | |||
y= 2x^2 - 3x. | |||
</math> | |||
On the one hand, | |||
we may consider the subset of <math>\R^2</math>, pictured in | |||
[[#fig 1.19 |Fifure]], | |||
<div id="fig 1.19" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_19.png | 400px | thumb | ]] | |||
</div> | |||
that consists of all ordered pairs <math>(x, y)</math> such that <math>y = 2x^2 - 3x</math>. | |||
This subset is a function <math>f</math> | |||
whose value at an arbitrary real number <math>x</math> | |||
is the real number <math>f(x) = 2x^2 - 3x</math>. | |||
Alternatively, | |||
we may regard <math>x</math> as an independent variable, | |||
i.e., the identity function. | |||
The composition of <math>f</math> with <math>x</math> is then the | |||
function <math>f(x) = 2x^2 - 3x</math>, whose value at <math>2</math>, | |||
for instance, is | |||
<math display="block"> | |||
(f(x))(2) = f(x(2)) = f(2) = 8 - 6 = 2. | |||
</math> | |||
A third interpretation | |||
is that <math>y</math> is a dependent variable that depends on <math>x</math> | |||
according to the equation <math>y = 2x^2 - 3x</math>. | |||
That is, <math>y</math> is the name of the function <math>2x^2 - 3x</math>. | |||
<span id="exam 1.3.3"/> | |||
'''Example''' | |||
\label{exam 1.3.3} | |||
Let <math>F</math> be the function defined by | |||
<math>F(x) = x^3 + x + 1</math>. If <math>u = \sqrt{x - 2}</math>, | |||
then | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
F(u) | |||
&=& u^3 + u + 1 \\ | |||
&=& (x - 2)^{3/2} + (x - 2)^{1/2} + 1. | |||
\end{eqnarray*} | |||
</math> | |||
If we denote the function <math>F(x)</math> by <math>w</math>, then | |||
<math display="block"> | |||
u + w = \sqrt{x - 2} + x^3 + x + 1, | |||
</math> | |||
<math display="block"> | |||
uw = (x - 2)^{1/2} (x^3 + x + 1). | |||
</math> | |||
On the other hand, | |||
we may let <math>G</math> be the function defined by | |||
<math>G(x) = \sqrt{x - 2}</math> | |||
for every real number <math>x \geq 2</math>. | |||
Then <math>G + F</math> and <math>GF</math> are the functions defined, respectively, by | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
(G + F)(x) | |||
&=& G(x) + F(x) \\ | |||
&=& \sqrt{x - 2} + x^3 + x + 1, \\ | |||
(GF)(x) | |||
&=& G(x)F(x) \\ | |||
&=& (x - 2)^{1/2} (x^3 + x + 1). | |||
\end{eqnarray*} | |||
</math> | |||
To say that <math>a</math> is a real '''constant''' | |||
means first that it is a real number. | |||
Second, it may or may not matter which real number <math>a</math> is, | |||
but it is fixed for the duration of the discussion in which it occurs. | |||
Similarly, a '''constant function''' is one which takes on just one value; | |||
i.e., its range consists of a single element. | |||
For example, consider the constant function <math>f</math> defined by | |||
<math display="block"> | |||
f(x) = 5, \;\;\; - \infty < x < \infty. | |||
</math> | |||
The graph of <math>f</math> is the straight line parallel to the <math>x</math>-axis | |||
that intersects the <math>y</math>-axis in the point (0, 5); | |||
see [[#fig 1.20|Figure]]. | |||
<div id="fig 1.20" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_20.png | 400px | thumb | ]] | |||
</div> | |||
We shall commonly use lower-case letters | |||
at the beginning of the alphabet, | |||
e.g., <math>a</math>, <math>b</math>, <math>c</math>,..., | |||
to denote both constants and constant functions. | |||
<span id="exam 1.3.4"/> | |||
'''Example''' | |||
\label{exam 1.3.4} | |||
Consider the function <math>ax + b</math>, | |||
where <math>a</math> and <math>b</math> are constants, | |||
<math>a \neq 0</math>, | |||
and <math>x</math> is an independent variable. | |||
The graph of this function is a straight line | |||
that cuts the <math>y</math>-axis at <math>b</math> and the <math>x</math>-axis at <math>-\frac{b}{a}</math>. | |||
It is drawn in [[#fig 1.21|Figure]]. | |||
<div id="fig 1.21" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig1_21.png | 400px | thumb | ]] | |||
</div> | |||
This function is the sum of the constant function <math>b</math> | |||
and the function which is the product of the constant function <math>a</math> | |||
and the identity function <math>x</math>. | |||
\end{exercise} | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Revision as of 01:06, 3 November 2024
Operations with Functions.
If [math]f[/math] and [math]g[/math] are two functions, a new function [math]f(g)[/math], called the composition of [math]g[/math] with [math]f[/math], is defined by
For example, if [math]f(x) = x^3 - 1[/math] and [math]g(x) = \frac{x + 1}{x - 1}[/math], then
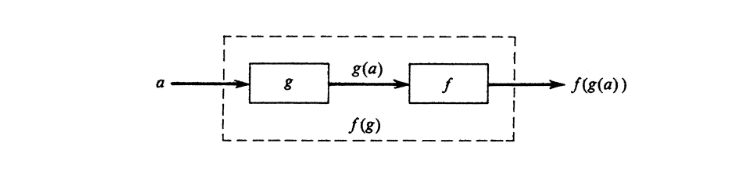
The composition of two functions is the function obtained by applying one after the other. If [math]f[/math] and [math]g[/math] are regarded as computing machines, then [math]f(g)[/math] is the composite machine constructed by feeding the output of [math]g[/math] into the input of [math]f[/math] as indicated in Figure.
In general it is not true that [math]f(g) = g(f)[/math]. In the above example we have
and the two functions are certainly not the same. In terms of ordered pairs the composition [math]f(g)[/math] of [math]g[/math] with [math]f[/math] is formally defined to be the set of all ordered pairs [math](a, c)[/math] for which there is an element [math]b[/math] such that [math]b = g(a)[/math] and [math]c = f(b)[/math]. If [math]f[/math] and [math]g[/math] are two real-valued functions, we can perform the usual arithmetic operations of addition, subtraction, multiplication, and division. Thus for the functions [math]f(x) = x^3 - 1[/math] and [math]g(x) = \frac{x + 1}{x - 1}[/math], we have
Just as with the composition of two functions, each arithmetic operation provides a method of constructing a new function from the two given functions [math]f[/math] and [math]g[/math]. The natural notations for these new functions are [math]f + g[/math], [math]f - g[/math], [math]fg[/math], and [math]\frac{f}{g}[/math]. They are defined by the formulas
The product function [math]fg[/math] should not be confused with the composite function [math]f(g)[/math]. For example, if [math]f(x) = x^5[/math] and [math]g(x) = x^3[/math], then we have [math](fg)(x) = f(x)g(x) = {x^5} \cdot {x^3} = x^8[/math], whereas
We may also form the product [math]af[/math] of an arbitrary real number [math]a[/math] and real-valued function [math]f[/math]. The product function is defined by
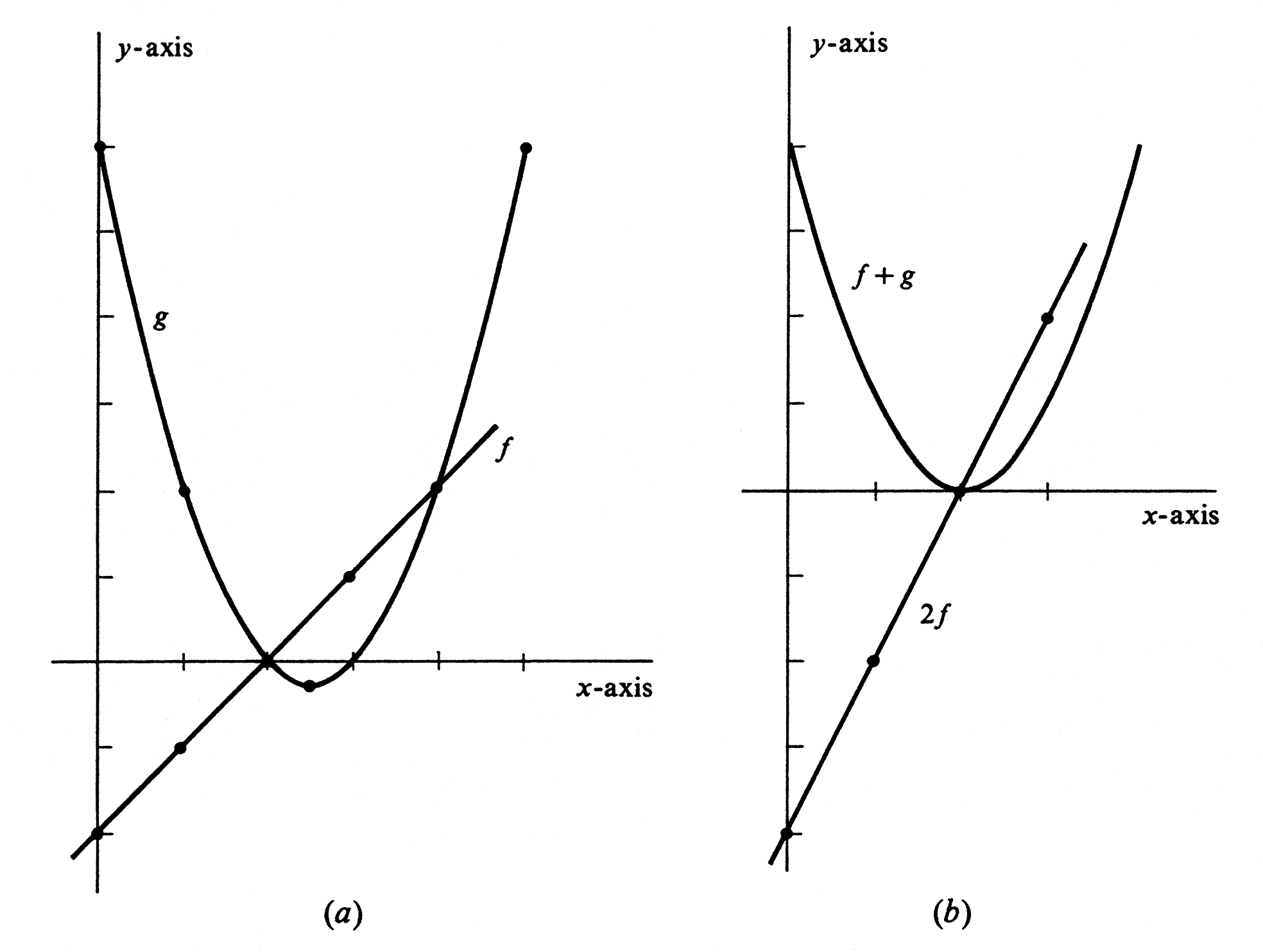
Example \label{exam 1.3.1} Let functions [math]f[/math] and [math]g[/math] be defined by [math]f(x) = x - 2[/math] and [math]g(x) = x^2 - 5x + 6[/math]. Draw the graphs of [math]f[/math], [math]g[/math], [math]2f[/math], and [math]f + g[/math]. We compute the function values corresponding to several different numbers [math]x[/math] in Tables and. The resulting graphs of [math]f[/math] and [math]g[/math] are, respectively, the straight line and parabola shown in Figure(a).
It turns out that the graphs of [math]2f[/math] and [math]f + g[/math] are also a straight line and a parabola. They are drawn in Figure(b). To see why the graph of [math]f + g[/math] is a parabola, observe that
It follows that [math]f + g[/math] is very much like the function defined by [math]y = x^2[/math]. Instead of simply squaring a number, [math]f + g[/math] first subtracts [math]2[/math] and then squares. Its graph will be just like that of [math]y = x^2[/math] except that it will be shifted two units to the right.
\begin{table}
\caption{} \label{table 1.3} \end{table} \begin{table} \centering
\caption{} \label{table 1.4} \end{table} Up to this point we have used the letters [math]f[/math], [math]g[/math], [math]h[/math], [math]F[/math], [math]G[/math], and [math]H[/math] to denote functions, and the letters [math]x[/math], [math]y[/math], [math]a[/math], [math]b[/math], and [math]c[/math] to denote elements of sets---usually real numbers. However, the letters in the second set are sometimes also used as functions. This occurs, for example, when we speak of [math]x[/math] as a real variable. As such, it not only is the name of a real number but also can take on many different values: [math]5[/math], or [math]-7[/math], or [math]\pi[/math], or \ldots. Thus the variable [math]x[/math] is a function. Specifically, it is the very simple function that assigns the value [math]5[/math] to the number [math]5[/math], the value [math]-7[/math] to the number [math]-7[/math], the value [math]\pi[/math] to [math]\pi[/math], \ldots. For every real number [math]a[/math], we have
This function is called the identity function. Suppose, for example, that [math]s[/math] is used to denote the distance that a stone falling freely in space has fallen. The value of [math]s[/math] increases as the stone falls and depends on the length of time [math]t[/math] that it has fallen according to the equation [math]s= {\frac{1}{2}}g{t^2}[/math], where [math]g[/math] is the constant gravitational acceleration. (This formula assumes no air resistance, that the stone was at rest at time [math]t = 0[/math], and that distance is measured from the starting point.) Thus [math]s[/math] has the value [math]{\frac{9}{2}}g[/math] if [math]t[/math] has the value [math]3[/math], and, more generally, the value [math]{\frac{1}{2}}g{a^2}[/math] when [math]t[/math] has the value [math]a[/math]. If we consider [math]t[/math] to be another name for the identity function, then [math]s[/math] may be regarded as the function whose value is
for every real number [math]a[/math]. The original equation [math]s = {\frac{1}{2}}g{t^2}[/math] then states the relation between the two functions [math]s[/math] and [math]t[/math]. The fact that [math]s[/math] and [math]t[/math] take on different values is also expressed by referring to them as variables. A variable is simply a name of a function. In our example [math]s[/math] is called a dependent variable, and [math]t[/math] an independent variable, because the values of [math]s[/math] depend on those of [math]t[/math] according to [math]s = {\frac{1}{2}}g{t^2}[/math]. Thus an independent variable is a name for the identity function, and a dependent variable is one that is not independent. A real variable is therefore a name of a real-valued function. Since the arithmetic operations of addition, subtraction, multiplication, and division have been defined for real-valued functions, they are automatically defined for real variables. We shall generally use the letter [math]x[/math] to denote an independent variable. This raises the question: How does one tell whether an occurrence of [math]x[/math] denotes a real number or the identity function? The answer is that the notation alone does not tell, but the context and the reader's understanding should. However, a more practical reply is that it doesn't really make much difference. We may regard [math]f(x)[/math] as either the value of the function [math]f[/math] at the number [math]x[/math] or as the composition of [math]f[/math] with the variable [math]x[/math]. If [math]x[/math] is an independent variable, the function [math]f(x)[/math] is then the same thing as [math]f[/math].
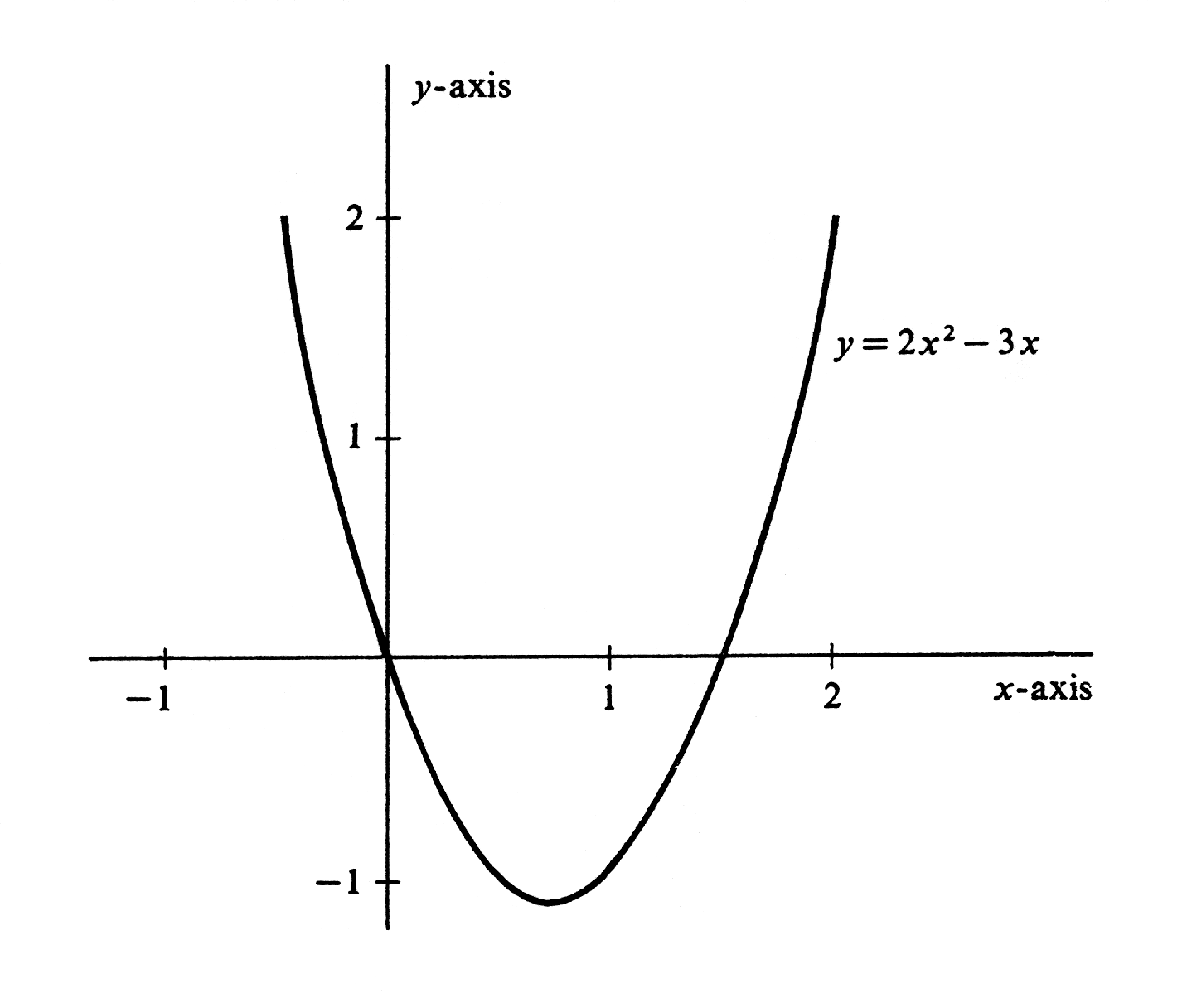
Example \label{exam 1.3.2} The conventions that we have adopted concerning the use of variables give our notations a flexibility that is both consistent and extremely useful. Consider, for example, the equationthat consists of all ordered pairs [math](x, y)[/math] such that [math]y = 2x^2 - 3x[/math]. This subset is a function [math]f[/math] whose value at an arbitrary real number [math]x[/math] is the real number [math]f(x) = 2x^2 - 3x[/math]. Alternatively, we may regard [math]x[/math] as an independent variable, i.e., the identity function. The composition of [math]f[/math] with [math]x[/math] is then the function [math]f(x) = 2x^2 - 3x[/math], whose value at [math]2[/math], for instance, is
Example \label{exam 1.3.3} Let [math]F[/math] be the function defined by [math]F(x) = x^3 + x + 1[/math]. If [math]u = \sqrt{x - 2}[/math], then
To say that [math]a[/math] is a real constant
means first that it is a real number.
Second, it may or may not matter which real number [math]a[/math] is,
but it is fixed for the duration of the discussion in which it occurs.
Similarly, a constant function is one which takes on just one value;
i.e., its range consists of a single element.
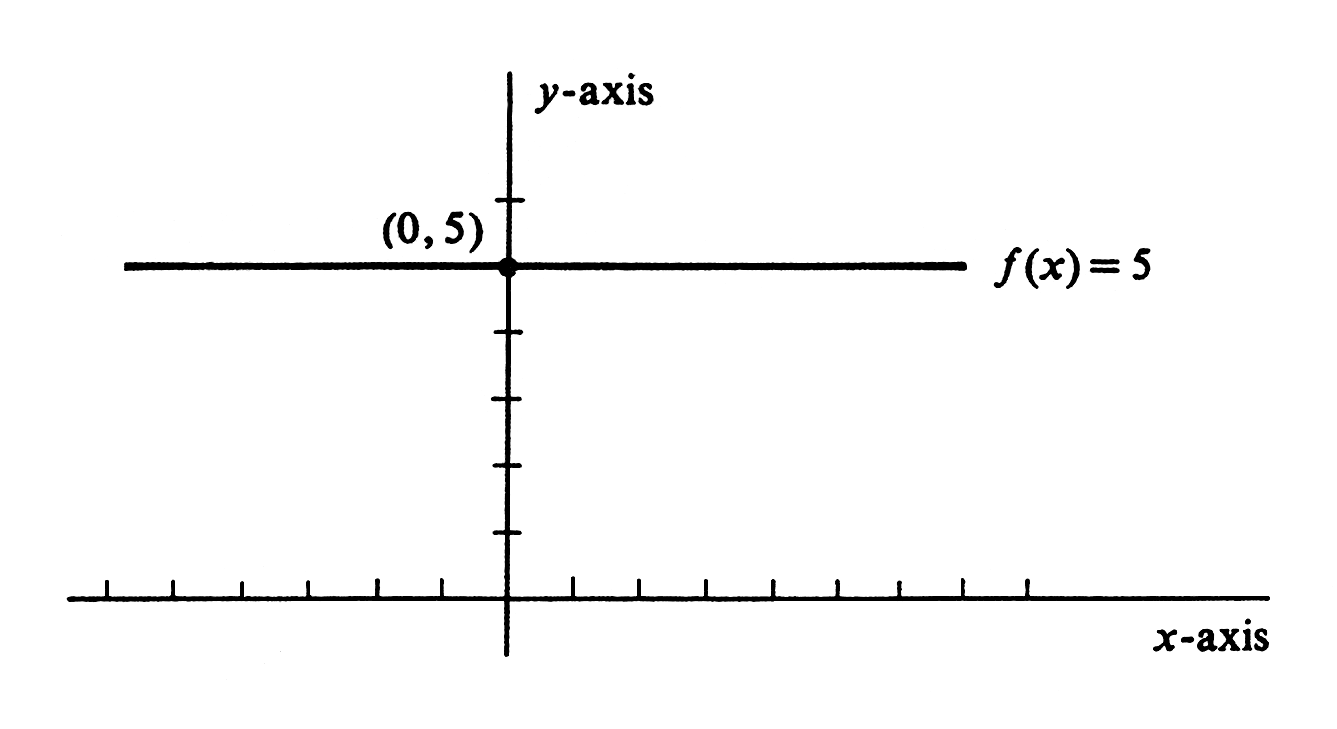
For example, consider the constant function [math]f[/math] defined by
We shall commonly use lower-case letters at the beginning of the alphabet, e.g., [math]a[/math], [math]b[/math], [math]c[/math],..., to denote both constants and constant functions. Example \label{exam 1.3.4} Consider the function [math]ax + b[/math], where [math]a[/math] and [math]b[/math] are constants, [math]a \neq 0[/math], and [math]x[/math] is an independent variable. The graph of this function is a straight line that cuts the [math]y[/math]-axis at [math]b[/math] and the [math]x[/math]-axis at [math]-\frac{b}{a}[/math]. It is drawn in Figure.
This function is the sum of the constant function [math]b[/math] and the function which is the product of the constant function [math]a[/math] and the identity function [math]x[/math].
\end{exercise}
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.