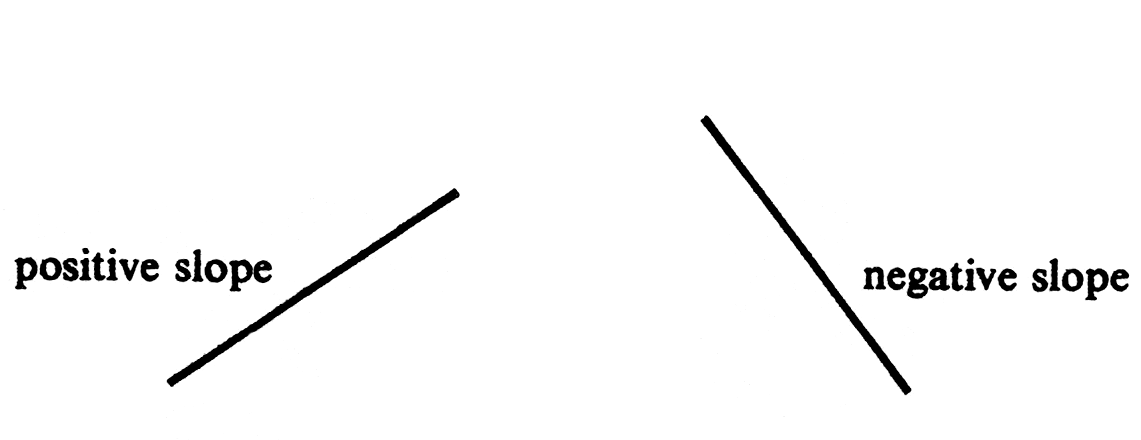guide:0d227dcd1c

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

Straight Lines and Their Equations.

We shall define a straight line in [math]\R^2[/math] to be any subset [math]L[/math] consisting of all ordered pairs [math](x, y)[/math] such that

[[math]] \begin{equation} ax + by + c = 0, \;\;\; \mbox{where} \;\;\; a^2 + b^2 \gt 0. \label{eq1.5.0} \end{equation} [[/math]]

The inequality [math]a^2 + b^2 \gt 0[/math] simply says that the constants [math]a[/math] and [math]b[/math] are not both equal to zero. Of course two different equations can define the same line. For example, the set of all ordered pairs [math](x, y)[/math] such that [math]4x - 3y + 5 = 0[/math] is the same line as the set of pairs for which [math]28x = 21y - 35[/math]. For this reason, we speak of an equation of a straight line and not the equation.

Proposition

Suppose that straight lines [math]L_1[/math] and [math]L_2[/math] are defined, respectioely, by

[[math]] \begin{array}{ll} a_{1}x + b_{1}y + c_1 = 0, & {a_1}^2 + {b_1}^2 \gt 0,\\ a_{2}x + b_{2}y + c_2 = 0, & {a_2}^2 + {b_2}^2 \gt 0. \end{array} [[/math]]

Then [math]L_{1} = L_{2}[/math] if and only if there is a nonzero constant [math]k[/math] such that

[[math]] \begin{eqnarray*} a_2 &=& ka_{1}, \\ b_2 &=& kb_{1}, \\ c_2 &=& kc_{1}. \end{eqnarray*} [[/math]]

Show Proof

If such a [math]k[/math] exists, then the two equations are equivalent, and so [math]L_1 = L_2[/math]. Conversely, suppose that [math]L_1 = L_2[/math]. We may assume without loss of generality that [math]b_{1} \neq 0[/math]. Then the point [math]\Bigl(0, -\frac{c_1}{b_1} \Bigr)[/math] lies on [math]L_1[/math] since it satisfies the first equation; i.e.,

[[math]] a_{1} \cdot 0 + b_{1} \Bigl(- \frac{c_1}{b_1} \Bigr) + c_{1} = 0. [[/math]]

Because the two lines are equal, the point also lies on [math]L_2[/math], and so

[[math]] a_2 \cdot 0 + b_2 \Bigl( - \frac{c_1}{b_1} \Bigr) + c_2 = 0. [[/math]]

Hence

[[math]] c_2 = \Bigl( \frac{b_2}{b_1} \Bigr) c_1. [[/math]]

In addition, the point [math]\Bigl(1, - \frac{a_1 + c_1}{b_1} \Bigr)[/math] lies on [math]L_1[/math] because

[[math]] a_1 + b_{1} \Bigl( \frac{- a_1 - c_1}{ b_1} \Bigr) + c_1 = 0. [[/math]]

This point then also lies on [math]L_2[/math], and this fact means that

[[math]] a_2 + b_{2} \Bigl(\frac{- a_1 - c_1}{b_1} \Bigr) + c_2 = 0. [[/math]]

Hence

[[math]] a_2 = {\frac{b_2}{b_1}} a_{1} + {\frac{b_2}{b_1}} c_1 - c_2 = \Bigl( \frac{b_2}{b_1} \Bigr) a_{1}. [[/math]]

Since [math]b_2 = \Bigl( \frac{b_2}{b_1} \Bigr) b_1[/math] trivially, we obtain the desired conclusion by setting [math]k = \frac{b_2}{b_1}[/math]. Note that [math]k \neq 0[/math], for if it were zero, we would get [math]a_2 = b_2 = 0[/math], contrary to assumption.

■

One consequence of Theorem is that it enables us to recognize at a glance whether or not different equations define the same straight line. Another corollary arises in connection with the following definitions: A line [math]L[/math] defined by an equation [math]ax + by + c = 0[/math] with [math]a^2 + b^2 \gt 0[/math] will be called vertical if [math]b = 0[/math] and horizontal if [math]a = 0[/math]. It follows from the theorem that [math]b[/math] must equal zero for every such equation which defines a vertical line and that [math]a[/math] must equal zero for every such equation which defines a horizontal line. Thus the definitions are not dependent on the particular equation which defines [math]L[/math]. 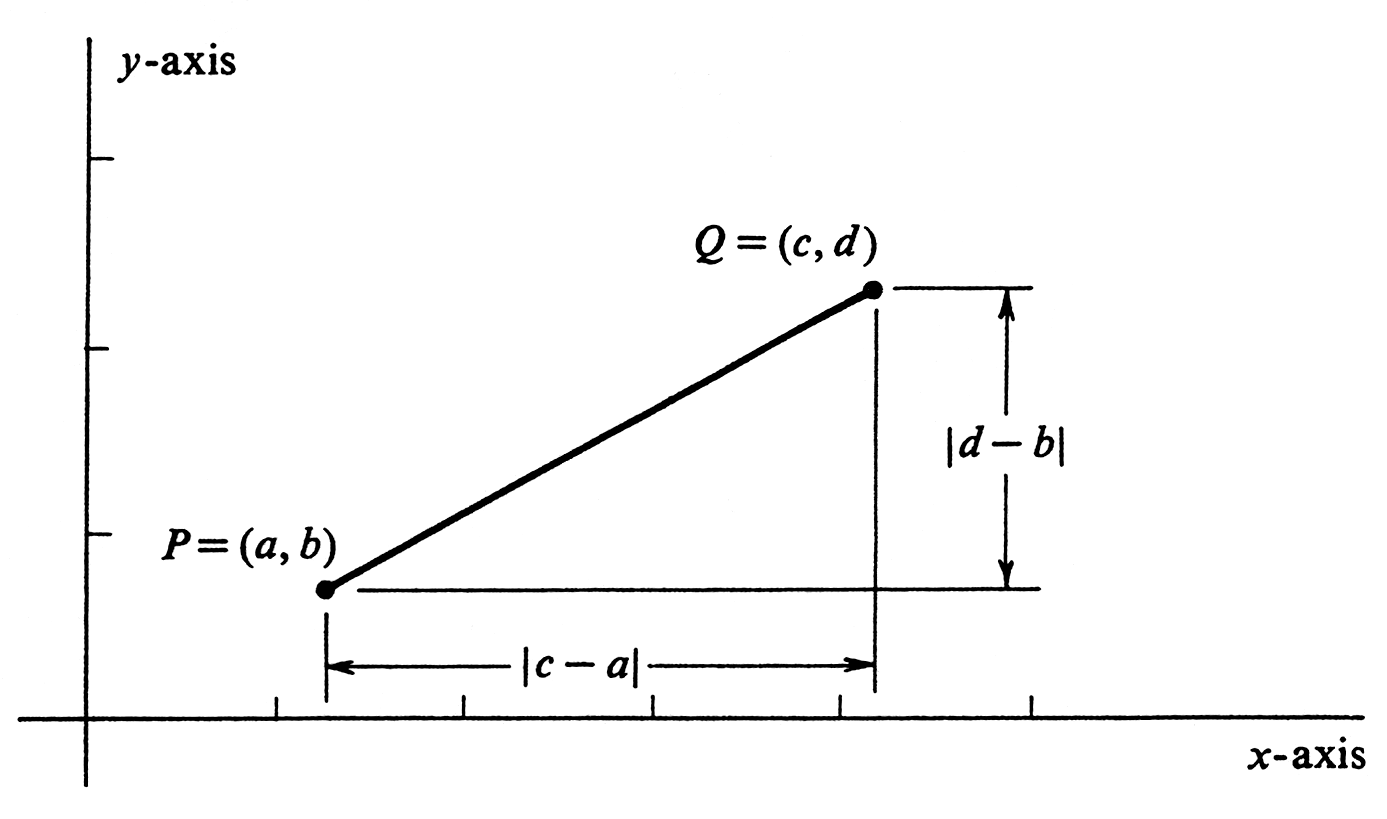If [math]P = (a, b)[/math] and [math]Q = (c, d)[/math] are two points in [math]\R^2[/math] and [math]a \neq c[/math], the slope of the line segment joining [math]P[/math] to [math]Q[/math] is, by definition,

[[math]] m(P, Q) = \frac{d - b}{c - a} . [[/math]]

Note that

[[math]] m(P, Q) = \frac{d - b}{c - a} = \frac{b - d}{a - c} = m(Q, P) . [[/math]]

The absolute value of [math]m(P, Q)[/math] is the ratio of the vertical to horizontal distance between [math]P[/math] and [math]Q[/math] (see Figure). It is simply a measure of steepness. A segment with positive slope goes up as it goes to the right; one with negative slope goes down as it goes to the right (Figure). If [math]a = c[/math], the segment is vertical, and the slope is not defined.

File:Guide c5467 scanfig1 30.png

Proposition

Let [math]L[/math] be the straight line defined by the equation [math]ax + by + c = 0[/math], where [math]b \neq 0[/math]. If [math]P[/math] and [math]Q[/math] are any two distinct points on the line, then [math]m(P, Q) = -\frac{a}{b}[/math].

Show Proof

Let [math]P = (x_1, y_1)[/math] and [math]Q = (x_2, y_2)[/math]. An equation equivalent to the original one is

[[math]] \begin{equation} y = - \Bigl( \frac{a}{b} \Bigr) x - \frac{c}{b} . \label{eq1.5.1} \end{equation} [[/math]]

It follows that [math]x_1 \neq x_2[/math], since, otherwise, substitution in this equation would yield [math]y_1 = y_2[/math], which would then imply [math]P = Q[/math]. We obtain

[[math]] m(P, Q) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ - \frac{a}{b} x_2 - \frac{c}{b} + \frac{a}{b} x_1 + \frac{c}{b}} {x_2 - x_1} = -\frac{a}{b} , [[/math]]

and this completes the proof.

■

File:Guide c5467 scanfig1 31.png

As a result of Theorems and, we can unambiguously define the slope of a nonvertical line [math]L[/math], which we shall denote by [math]m_{L}[/math], as follows: For any pair of distinct points [math]P[/math] and [math]Q[/math] on [math]L[/math], we define

[[math]] m_{L} = m(P, Q). [[/math]]

It follows at once that [math]m_{L}[/math] depends only on the line [math]L[/math]. For if [math]P'[/math] and [math]Q'[/math] are any other two distinct points on the line, then

[[math]] m(P, Q) = - \frac{a}{b} = m(P', Q'). [[/math]]

(Since [math]L[/math] is not vertical, [math]b \neq 0[/math].) Furthermore, any other equation defining [math]L[/math] can be written [math]kax + kby + kc = 0[/math] with [math]k \neq 0[/math], and, of course, [math]-\frac{ka}{kb} = -\frac{a}{b}[/math]. We note that the slope of a vertical line is not defined.

Example

\label{exam 1.5.1} Find an equation of the straight line [math]L[/math] through the point [math](a, b)[/math] and with slope [math]m[/math]. If [math](x, y)[/math] is any other point on the line, then

[[math]] m = \frac{y - b}{x - a}, [[/math]]

which implies

[[math]] \begin{equation} y - b = m(x - a). \label{eq1.5.2} \end{equation} [[/math]]

This is an equation of the line. For suppose [math]L[/math] were defined by some equation [math]a_{1}x + b_{1}y + c_1 = 0[/math]. An equivalent equation is

[[math]] y = -\Bigl( \frac {a_1}{b_1} \Bigr) x -\frac{c_1}{b_1}, [[/math]]

or, since [math]m = -\frac{a_1}{b_1}[/math],

[[math]] \begin{equation} y = mx - \frac{c_1}{b_1}. \label{eq1.5.3} \end{equation} [[/math]]

Since we are given that [math](a, b)[/math] lies on [math]L[/math], we get [math]b = ma - \frac{c_1}{b_1}[/math], or

[[math]] \frac{c_1}{b_1} = ma - b. [[/math]]

Substitution in yields [math]y = mx - ma + b[/math], which is equivalent to.

Suppose that [math]S[/math] is an arbitrary subset of [math]\R^2[/math] with the following three properties:

\item[i]] [math]S[/math] contains a point [math](a, b)[/math]; i.e., [math]S[/math] is a nonempty set. \item[(ii)] The slope [math]m(P, Q)[/math] is defined and is equal to the same fixed number [math]m[/math], for every pair of distinct points [math]P[/math] and [math]Q[/math] in [math]S[/math]. \item[(iii)] [math]S[/math] contains every point [math](x, y)[/math] in [math]\R^2[/math] which is connected to [math](a, b)[/math] by a line segment of slope [math]m[/math].

These are certainly the geometric properties of a nonvertical straight line. It follows from (i) and (ii) that the coordinates of every point [math](x, y)[/math] in [math]S[/math] satisfy the equation

[[math]] \begin{equation} y - b = m(x - a). \label{eq1.5.4} \end{equation} [[/math]]

Conversely, it follows from (iii) that, for every pair of real numbers [math]x[/math] and [math]y[/math] which satisfy (4), the point [math](x, y)[/math] must lie in [math]S[/math]. Thus the set [math]S[/math] is the graph of (4), and, as such, it is a straight line. Since nonvertical straight lines, as we have defined them, have the above three properties, we conclude that our definition coincides with the natural geometric one. We define two lines [math]L_1[/math] and [math]L_2[/math] to be parallel if they are both vertical or if they have the same slope. 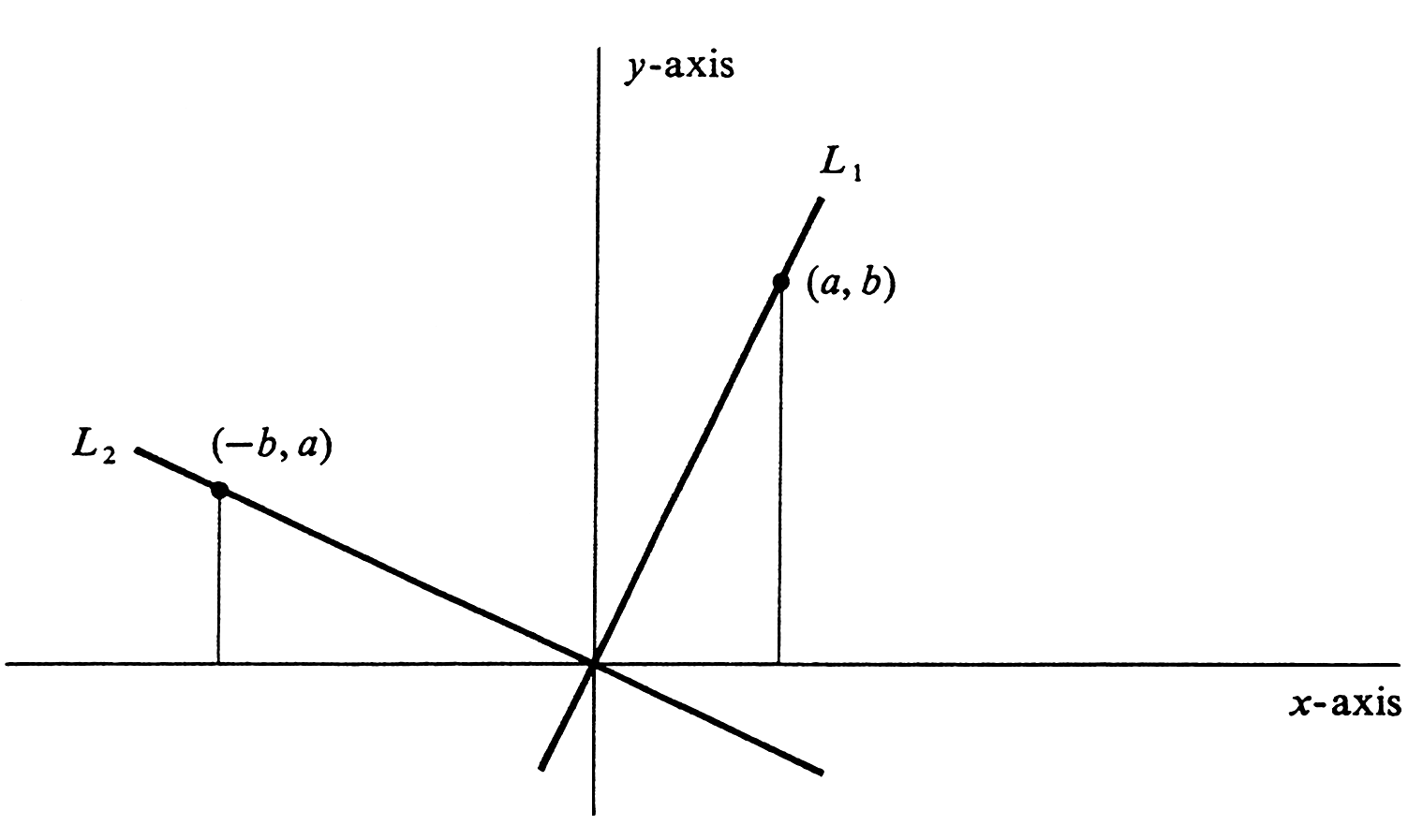The following fact, which we shall prove later using trigonometry, can also be deduced from Figure by the methods of plane geometry.

File:Guide c5467 scanfig1 32.png

Proposition

Two nonvertical lines [math]L_1[/math] and [math]L_2[/math] with slopes [math]m_1[/math] and [math]m_2[/math], respectively, are perpendicular if and only if [math]m_{1}m_{2} = -1[/math].

Example

\label{exam 1.5.2} (a) Write an equation of the straight line [math]L_1[/math] that passes through [math](-2, 4)[/math] and (3, 7). (b) Write an equation of the line [math]L_2[/math] passing through [math](5, -2)[/math] and parallel to [math]L_1[/math]. (c) Write an equation defining the line [math]L_3[/math] that passes through [math](-1, -3)[/math] and is perpendicular to [math]L_1[/math]. The slope of the segment joining [math](-2, 4)[/math] and (3, 7) is [math]\frac{7 - 4}{3 + 2} = \frac{3}{5}[/math]. An arbitrary point [math](x, y)[/math] other than (3, 7) belongs to [math]L_1[/math] if and only if

[[math]] \frac{y - 7}{x - 3} = \frac{3}{5}. \ Hence an equation defining $L_1$ is \ltmath\gt5(y - 7) = 3(x - 3)[[/math]]

, or, equivalently,

[[math]] 3x - 5y + 26 = 0. [[/math]]

The line [math]L_2[/math] also has slope 5. Since it passes through [math](5, -2)[/math], it is defined by

[[math]] \frac{y + 2}{x - 5} = \frac{3}{5} \;\;\; \mbox{if} \;\;\; x \neq 5, [[/math]]

or, more generally, by [math]5(y + 2) = 3(x - 5)[/math], which is equivalent to

[[math]] 3x - 5y - 25 = 0. [[/math]]

The slope of the perpendicular is [math]-\frac{5}{3}[/math]. Hence we obtain the equation

[[math]] \frac{y + 3}{x + 1} = - \frac{5}{3}, \;\;\; x \neq -1, [[/math]]

or [math]3y + 9 = -5x - 5[/math], as an equation of [math]L_3[/math].

What functions have graphs that are straight lines? The answer is an easy one. If [math]f[/math] is defined by

[[math]] f(x) = ax + b, \;\;\; - \infty \lt x \lt \infty, [[/math]]

then its graph, which is the set of all ordered pairs [math](x, y)[/math] such that [math]y = ax + b[/math], is certainly a straight line. Conversely, if the graph of an arbitrary function [math]f[/math] is a straight line, then the equation [math]y = f(x)[/math] is equivalent to one of the form

[[math]] \begin{equation} a_{1}x + b_{1}y + c_1 = 0, \;\;\; {a_1}^2 + {b_1}^2 \gt 0. \label{eq1.5.5} \end{equation} [[/math]]

If [math]b_1[/math] were zero, both points [math]\Bigl( - \frac{c_1}{b_1}, 0 \Bigr)[/math] and [math]\Bigl( -\frac{ c_1}{b_1}, 1 \Bigr)[/math] would satisfy (5), but the definition of function makes this impossible for the equation [math]y = f(x)[/math]. We conclude that [math]b_1 \neq 0[/math] and that (5) is therefore equivalent to

[[math]] y = - \Bigl(\frac{a_1}{b_1} \Bigr) x - \frac{c_1}{b_1}. [[/math]]

It follows [see Theorem] that the functions [math]f(x)[/math] and [math]-\Bigl( \frac{a_1}{b_1} \Bigr) x -\frac{c_1}{b_1}[/math] are equal. Thus the functions whose graphs are straight lines are precisely those of the form [math]ax + b[/math]. These are the polynomials of degree less than 2, the linear functions.

\end{exercise}

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.