guide:27efc1ff17: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\ex}[1]{\item } | |||
\newcommand{\sx}{\item} | |||
\newcommand{\x}{\sx} | |||
\newcommand{\sxlab}[1]{} | |||
\newcommand{\xlab}{\sxlab} | |||
\newcommand{\prov}[1] {\quad #1} | |||
\newcommand{\provx}[1] {\quad \mbox{#1}} | |||
\newcommand{\intext}[1]{\quad \mbox{#1} \quad} | |||
\newcommand{\R}{\mathrm{\bf R}} | |||
\newcommand{\Q}{\mathrm{\bf Q}} | |||
\newcommand{\Z}{\mathrm{\bf Z}} | |||
\newcommand{\C}{\mathrm{\bf C}} | |||
\newcommand{\dt}{\textbf} | |||
\newcommand{\goesto}{\rightarrow} | |||
\newcommand{\ddxof}[1]{\frac{d #1}{d x}} | |||
\newcommand{\ddx}{\frac{d}{dx}} | |||
\newcommand{\ddt}{\frac{d}{dt}} | |||
\newcommand{\dydx}{\ddxof y} | |||
\newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} | |||
\newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} | |||
\newcommand{\dist}{\mathrm{distance}} | |||
\newcommand{\arccot}{\mathrm{arccot\:}} | |||
\newcommand{\arccsc}{\mathrm{arccsc\:}} | |||
\newcommand{\arcsec}{\mathrm{arcsec\:}} | |||
\newcommand{\arctanh}{\mathrm{arctanh\:}} | |||
\newcommand{\arcsinh}{\mathrm{arcsinh\:}} | |||
\newcommand{\arccosh}{\mathrm{arccosh\:}} | |||
\newcommand{\sech}{\mathrm{sech\:}} | |||
\newcommand{\csch}{\mathrm{csch\:}} | |||
\newcommand{\conj}[1]{\overline{#1}} | |||
\newcommand{\mathds}{\mathbb} | |||
</math></div> | |||
==<span id="sec 8.3"></span>Numerical Approximations (Continued).== | |||
Two additional methods of integration by numerical approximations, which we shall describe in this section, are the Midpoint Rule and Simpson's Rule. | |||
In the Midpoint Rule the approximation to the integral <math>\int_a^b f</math> is a Riemann sum <math>\sum_{i=1}^{n} f(x_i^*)(x_i - x_{i-1})</math> in which each <math>x_i^*</math> is taken to be the midpoint of the subinterval <math>[x_{i-1}, x_i]</math>. In more detail: Let <math>f</math> be a function which is integrable over <math>[a, b]</math>. For every positive integer <math>n</math>, let <math>h = \frac{b - a}{n}</math>, and let <math>\sigma_n = \{ x_0, . . ., x_n \}</math> be the partition defined by | |||
<math display="block"> | |||
x_i = a + ih, \;\;\; i = 0, ... , n. | |||
</math> | |||
As a result, it follows that | |||
<math display="block"> | |||
x_i - x_{i-1} = h, \;\;\; i = 1, ... , n. | |||
</math> | |||
If we take <math>x_i^*</math> to be the midpoint of the subinterval <math>[x_{i-1}, x_i]</math>, then | |||
<math display="block"> | |||
x_i^* = \frac{x_{i-1} + x_i}{2}, \;\;\; i = 1, ... , n. | |||
</math> | |||
The Riemann sum used as the approximation to the integral in the Midpoint Rule will be denoted by <math>M_n</math>. It is given by | |||
<math display="block"> | |||
M_n = \sum_{i=1}^n f(x_i^*)(x_i - x_{i-1}) = h \sum_{i=1}^n f \Bigl(\frac{x_{i-1}+ x_i}{2} \Bigr) . | |||
</math> | |||
In studying the Trapezoid Rule, we found it convenient to use the abbreviation <math>y_i = f(x_i)</math>, for <math>i = 0, ... , n.</math> By analogy, we shall here let | |||
<math display="block"> | |||
y_{i-1/2} = f \Bigl( \frac{x_{i-1} + x_i}{2} \Bigr), \;\;\; i = 1, ... , n . | |||
</math> | |||
Then | |||
<math display="block"> | |||
M_n = h \sum_{i=1}^n y_{i-1/2} = h (y_{1/2} + y_{3/2} + \cdots + y_{n-1/2}), | |||
</math> | |||
and we express the '''Midpoint Rule''' for numerical integration by the formula | |||
{{proofcard|Theorem|theorem-1| | |||
<math display="block"> | |||
\int_a^b f \approx M_n = h (y_{1/2} + y_{3/2} + \cdots + y_{n-1/2}) . | |||
</math>|}} | |||
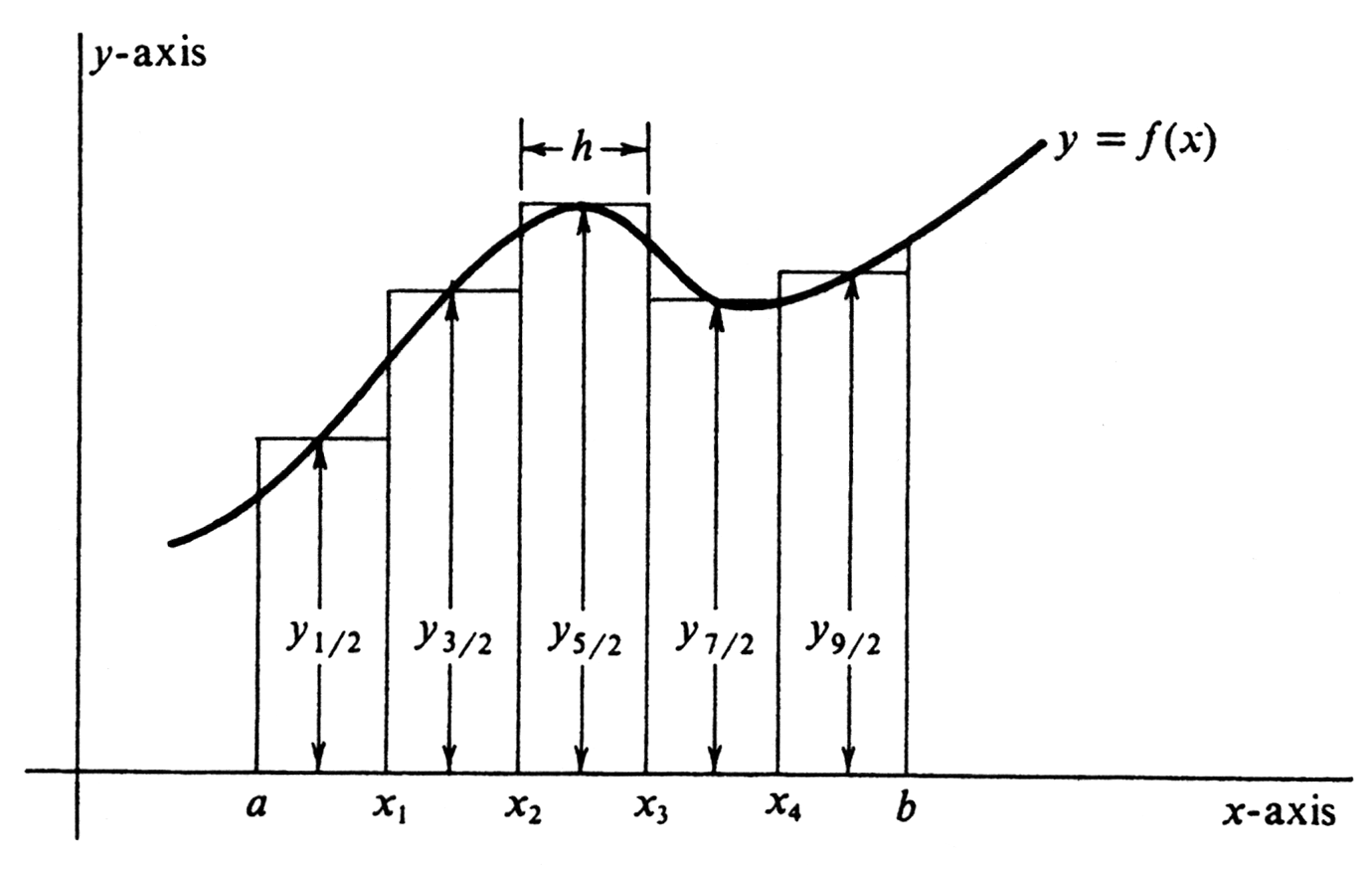
If <math>f(x) \geq 0</math> for every <math>x</math> in <math>[a, b]</math>, the Midpoint Rule approximates the integral <math>\int_a^b f</math>, which is the area under the curve, by a sum of areas of rectangles, as illustrated in Figure 6. | |||
<div id="fig 8.6" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_6.png | 400px | thumb | ]] | |||
</div> | |||
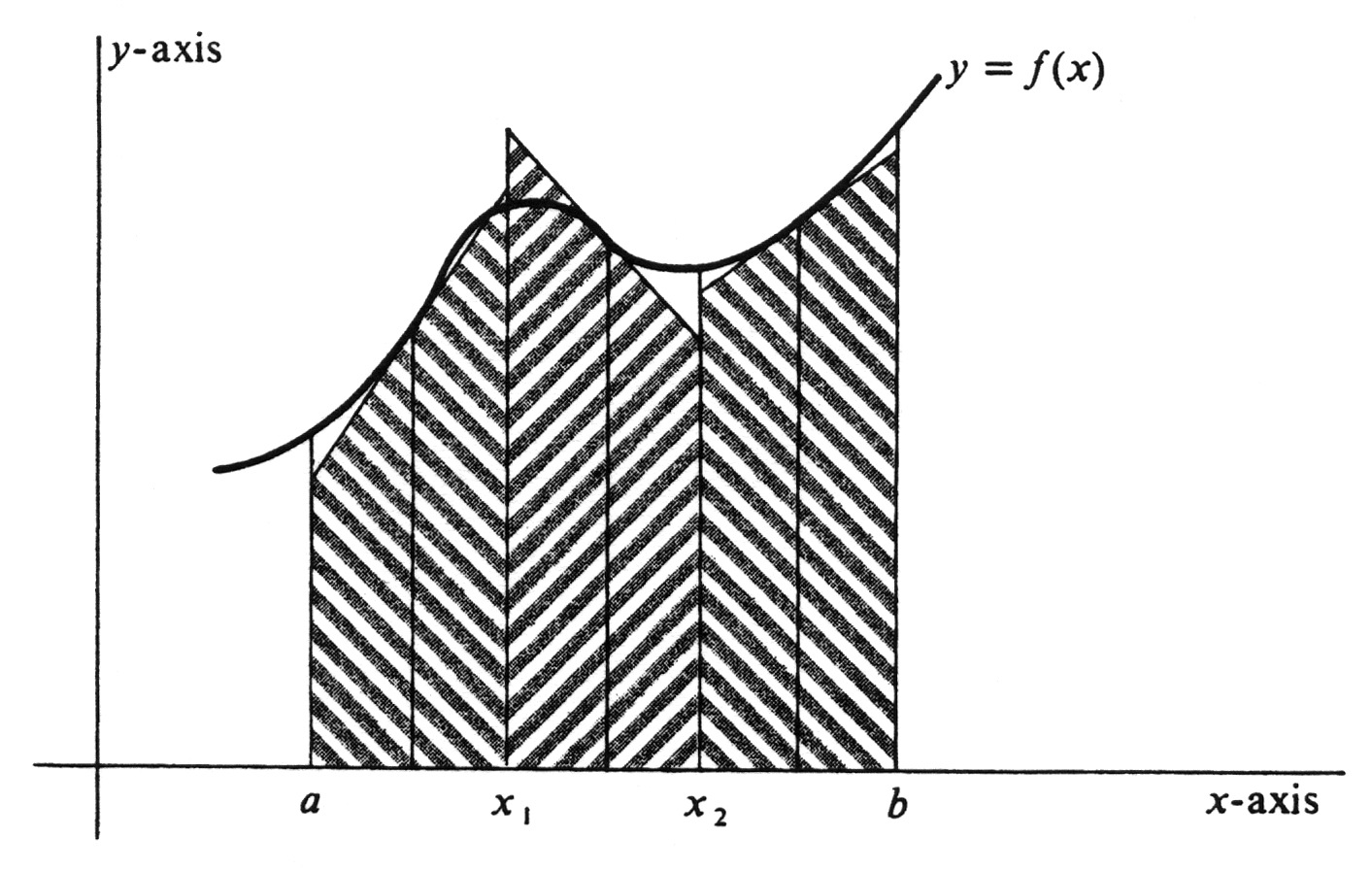
An alternative to approximating the integral by a Riemann sum is to use straight-line segments which are tangent to the curve <math>y = f(x)</math> at the midpoints of the subintervals. An example is shown in Figure 7, in which | |||
<div id="fig 8.7" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_7.png | 400px | thumb | ]] | |||
</div> | |||
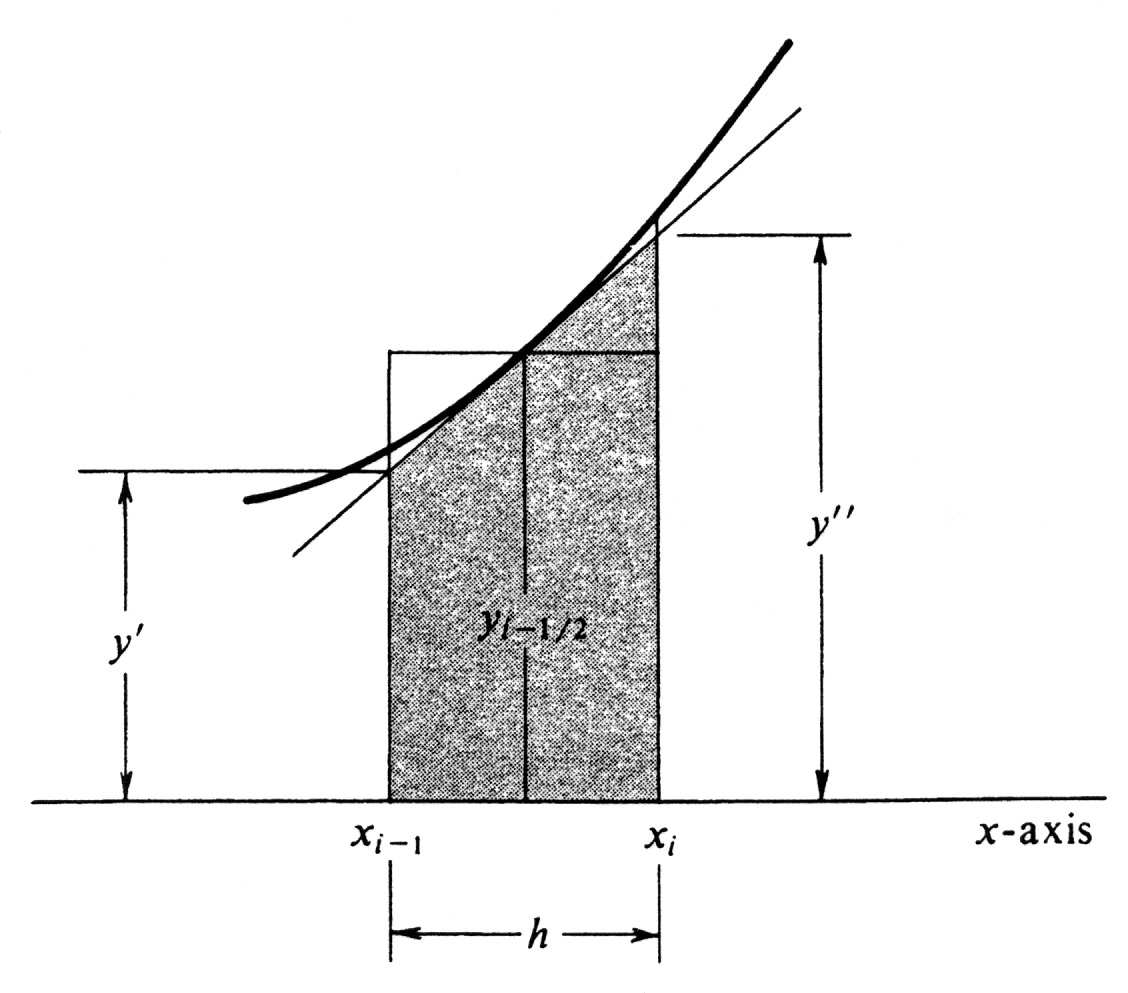
<math>\int_a^b f</math> is approximated by the sum of the areas of the three shaded trapezoids. This method yields the so-called '''Tangent Formula.''' It turns out, however, that the Tangent Formula is the same as the Midpoint Rule. The reason can be seen by looking at Figure 8, in which the area of the shaded trapezoid with one side tangent to the curve is the ith term in the approximating sum used in the Tangent Formula. The area of this trapezoid is equal to <math>\frac{h}{2} (y' + y'')</math>, where <math>y'</math> and <math>y''</math> are the lengths of the bases. However, by elementary geometry the trapezoid can be seen to have the same area as the rectangle with base <math>[x_{i-1}, x_i]</math> and altitude <math>y_{i-1/2}</math> The area of the rectangle is <math>h \cdot y_{i-1/2}</math>, and so | |||
<div id="fig 8.8" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_8.png | 400px | thumb | ]] | |||
</div> | |||
<math display="block"> | |||
\frac{h}{2} (y' + y'') = h \cdot y_{i-1/2}. | |||
</math> | |||
(Incidentally, note that this equation is true regardless of whether <math>y'</math>, <math>y''</math>, and <math>y_{i-1/2}</math> are positive, negative, or zero.) Since the product <math>h \cdot y_{i-1/2}</math> is the ith term in the midpoint approximation <math>M_n</math>, we conclude that the Tangent Formula and the Midpoint Rule, although differently motivated, are in fact the same. | |||
<span id="table 8.2"/> | |||
'''Example''' | |||
Approximate <math>\int_{-1}^1 (x^2 + x^3) dx</math> using the Midpoint Rule. This is the same integral which we evaluated in Section 2 by the Trapezoid Rule. To compare the two methods, we shall again take <math>n = 8</math> and | |||
<math display="block"> | |||
h = \frac{1- (-1)}{8} = \frac{1}{4}. | |||
</math> | |||
Since, for an arbitrary interval <math>[a, b]</math>, we have | |||
<math display="block"> | |||
x_i = a + ih, \;\;\; i = 0, ... ,n, | |||
</math> | |||
it follows that | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
x_i^{*} &=& \frac{x_{i-1} + x_i}{2} = \frac{[a + (i - 1)h] + (a + ih)}{2}\\ | |||
&=& a + (i - \frac{1}{2})h | |||
\end{eqnarray*} | |||
</math> | |||
In addition, since <math>y_{i-1/2} = f(x_i^{*})</math>, we have a pair of useful formulas: | |||
<math display="block"> | |||
\begin{array}{rl} | |||
x_i^{*} &= a + (i - \frac{1}{2})h \\ | |||
y_{i-1/2} &= f(a + (i - \frac{1}{2})h) | |||
\end{array} | |||
\} i = 1, ... , n. | |||
</math> | |||
In the present example, <math>a = -1</math>, <math>h = \frac{1}{4}</math>, and <math>f(x) = x^2 + x^3</math>. Hence | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
x_i^{*} &=& -1 + (i - \frac{1}{2})\frac{1}{4} = \frac{2i - 9}{8}, \\ | |||
y_{i- 1/2} &=& \Bigl( \frac{2i - 9}{8} \Bigr)^2 + \Bigl( \frac{2i - 9}{8} \Bigr)^3 = \frac{8(2i - 9)^2 + (2i - 9)^3}{8^3} \\ | |||
&=& \frac{(2i - 9)^2(2i - 1)}{8^3} . | |||
\end{eqnarray*} | |||
</math> | |||
Table 2 contains the numbers for the computation of <math>M_8</math>. | |||
<span id="table 8.2"/> | |||
{|class="table" | |||
|- | |||
|<math>i</math>|| <math>y_{i - 1/2} = \frac{(2i - 9)^2(2i - 1)}{8^3}</math> \vspace {1ex} | |||
|- | |||
|1 || <math>y_{1/2} = \frac{49}{8^3}</math> | |||
|- | |||
|2 || <math>y_{3/2} = \frac{25 \cdot 3}{8^3} = \frac{75}{8^3}</math> | |||
|- | |||
|3 || <math>y_{5/2} = \frac{9 \cdot 5}{8^3} = \frac{45}{8^3}</math> | |||
|- | |||
|4 || <math>y_{7/2} = \frac{7}{8^3}</math> | |||
|- | |||
|5 || <math>y_{9/2} = \frac{9}{8^3}</math> | |||
|- | |||
|6 || <math>y_{11/2} = \frac{9 \cdot 11}{8^3} = \frac{99}{8^3}</math> | |||
|- | |||
|7 || <math>y_{13/2} = \frac{25 \cdot 13}{8^3} = \frac{325}{8^3}</math> | |||
|- | |||
|8 || <math>y_{15/2} = \frac{49 \cdot 15}{8^3} = \frac{735}{8^3}</math> | |||
|} | |||
Hence we obtain | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
M_8 &=& \frac{1}{4}(y_{1/2} + \cdots + y_{15/2})\\ | |||
&=& \frac{1}{4 \cdot 8^3} (49 + 75 + 45 + 7 + 9 + 99 + 325 + 735) \\ | |||
&=& \frac{1344}{ 4 \cdot 8^3} = \frac{21}{32} | |||
\end{eqnarray*} | |||
</math> | |||
as an approximation to the integral <math>\int_{-1}^1 (x^2 + x^3) dx</math>. The value obtained earlier with the Trapezoid Rule was <math>T_8 = \frac{11}{16}</math>. Since the true value is given by | |||
<math display="block"> | |||
\int_{-1}^1 (x^2 + x^3) dx = \frac{2}{3}, | |||
</math> | |||
it follows that the error using the Midpoint Rule is equal to | |||
<math display="block"> | |||
| \frac{2}{3} - \frac{21}{32} | = \frac{1}{96} . | |||
</math> | |||
This is one half the error obtained using the Trapezoid Rule with the same value of <math>h</math>. | |||
In any application of the Midpoint Rule, the error <math>| \int_a^b f - M_n |</math> can be made arbitrarily small by taking <math>n</math> sufficiently large. That is, we assert that | |||
{{proofcard|Theorem|theorem-2| | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} M_n = \int_a^b f . | |||
</math>|}} | |||
This theorem is easier to prove than the corresponding one for the Trapezoid Rule because every approximation <math>M_n</math> is, as it stands, a Riemann sum of <math>f</math> relative to the partition <math>\sigma_n</math> of <math>[a, b]</math>. Since <math>|| \sigma_n || \rightarrow 0</math> as <math>n \rightarrow \infty</math>, it is a direct corollary of the fundamental theorem on the limit of Riemann sums [(2.1), page 414] that <math>\lim_{n \rightarrow \infty} M_n = \int_a^b f</math>. | |||
A means of estimating the error <math>| \int_a^b f - M_n |</math> in a particular application of the Midpoint Rule is provided by the following theorem: | |||
{{proofcard|Theorem|theorem-3|If the second derivative <math>f''</math> is continuous at every point of <math>[a, b]</math>, then there exists a number <math>c</math> such that <math>a < c < b</math> and | |||
<math display="block"> | |||
\int_a^b f = M_n + \frac{b - a}{24} f''(c) h^2. | |||
</math>|}} | |||
As with the analogous theorem for the Trapezoid Rule [(2.4), page 419], this theorem can be proved by first reducing it to the case <math>n = 1</math>. A discussion of the error term can be found in <math>R</math>. Courant and F. John, ''Introduction to Calculus and Analysis'', Volume I, Interscience Publishers (Wiley), 1965, pages 486 and 487. | |||
Theorem (3.3) can be used to obtain an upper bound on the error <math>|\int_a^b f - M_n|</math> provided the second derivative <math>f''</math> is bounded on the interval <math>[a, b]</math>. That is, if there exists a real number <math>K</math> such that | |||
<math display="block"> | |||
| f''(x) | \leq K, \;\;\; \mbox{for every $x$ in <math>[a, b]</math>,} | |||
</math> | |||
then, in particular <math>|f''(c)| \leq K</math>, and so | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\Big| \int_a^b f - M_n \Big| &=& \frac{(b - a)h^2}{24} | f''(c) | \\ | |||
&\leq& \frac{(b - a)K}{24} h^2 . | |||
\end{eqnarray*} | |||
</math> | |||
For the one integral we computed by both methods, the Midpoint Rule gave a better approximation than the Trapezoid Rule by a factor of 2. Comparison of Theorem (3.3) with (2.4) shows that in general this ratio can be expected. | |||
Geometrically, the different methods of numerical integration described thus far in this and the preceding section are all based on approximating the area under a curve by a sum of areas of rectangles or trapezoids. Analytically, in each method the approximation to <math>\int_a^b f</math> has been obtained by replacing <math>f</math> over every subinterval by a linear function. In Simpson's Rule, however, we shall replace <math>f</math> over each subinterval by a quadratic polynomial <math>Ax^2 + Bx + C</math>. The corresponding area problem is the simple one of finding the area under a parabola (or a straight line, if <math>A = 0</math>). For most integrals, Simpson's Rule gives much greater accuracy for the same value of <math>h</math>. | |||
Let <math>f</math> be a function which is integrable over the interval <math>[a, b]</math>. The procedure differs from the others in that we consider only partitions of <math>[a, b]</math> into an even number of subintervals. Thus for an arbitrary ''even'' integer <math>n > 0</math>, we set <math>h = \frac{b - a}{n}</math>, and let | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
x_i &=& a + ih,\\ | |||
y_i &=& f (x_i), \;\;\; \mbox{for}\; i = 0, . . ., n. | |||
\end{eqnarray*} | |||
</math> | |||
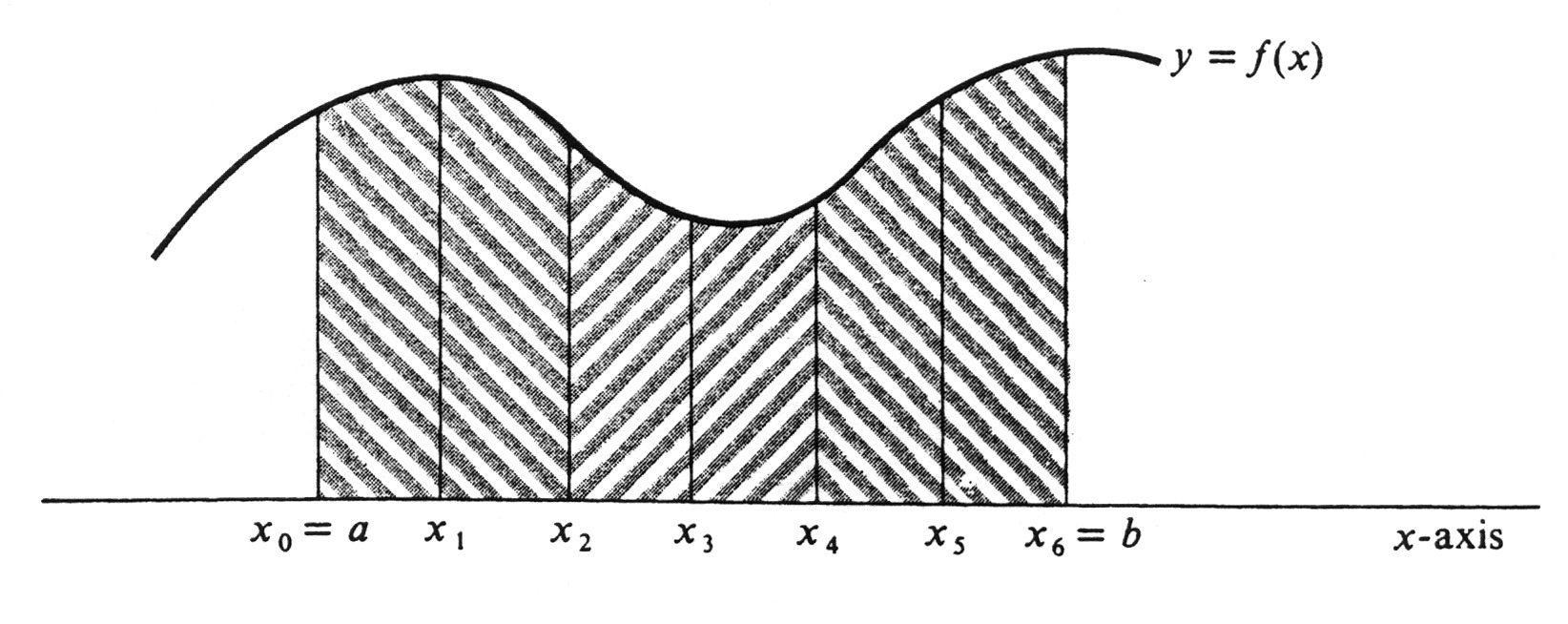
Since <math>n</math> is even, there is an integral number of “double” intervals <math>[x_{2i-2}, x_{2i}], i = 1, ... , \frac{n}{2}</math> as illustrated in Figure 9, and | |||
<div id="fig 8.9" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_9.png | 400px | thumb | ]] | |||
</div> | |||
<math display="block"> | |||
\int_a^b f(x) dx= \sum_{i=1}^{n/2} \int_{x_{2i-2}}^{x_{2i}} f(x) dx. | |||
</math> | |||
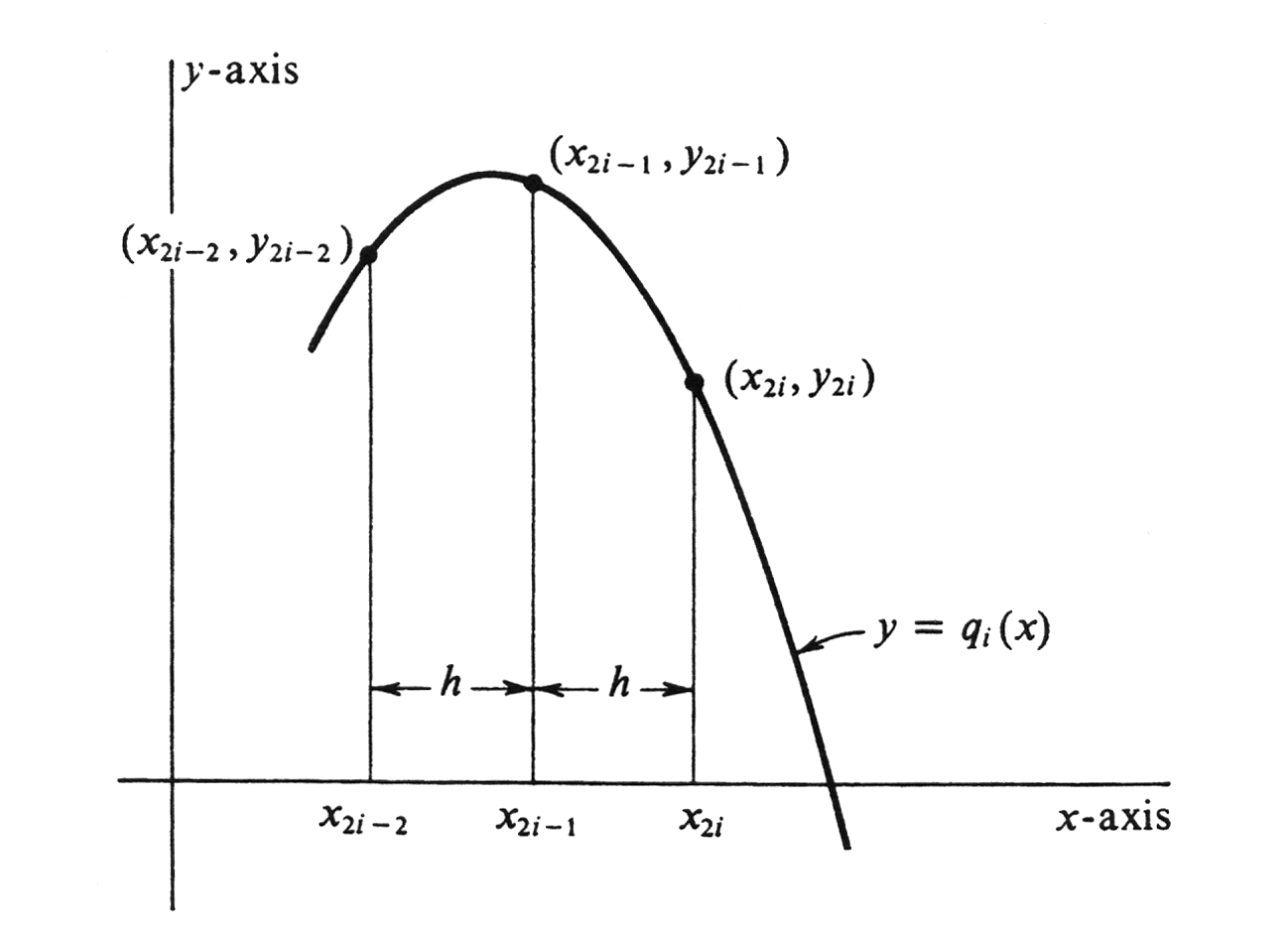
There exists one and only one polynomial <math>q_i(x) = A_i x^2 + B_i x + C_i</math> of degree less than three whose graph passes through the three points <math>(x_{2i-2}, y_{2i-2}), (x_{2i-1}, y_{2i-1})</math>, and <math>(x_{2i}, y_{2i})</math> (see Figure 10). Over each double interval <math>[x_{2i-2}, x_{2i}]</math> we shall approximate the integral of <math>f</math> by the integral of <math>q_i</math>. Let us assume for the moment, and later prove, the fact that | |||
<span id{{=}}"eq8.3.1"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\int_{x_{2i-2}}^{x_{2i}} q_i(x) dx = \frac{h}{3} (y_{2i-2} + 4y_{2i-1} + y_{2i}). | |||
\label{eq8.3.1} | |||
\end{equation} | |||
</math> | |||
<div id="fig 8.10" class="d-flex justify-content-center"> | |||
[[File:guide_c5467_scanfig8_10.png | 400px | thumb | ]] | |||
</div> | |||
The sum of these integrals, which we shall denote <math>S_n</math>, is the approximation to <math>\int_a^b f</math> prescribed by Simpson's Rule. Hence | |||
<math display="block"> | |||
S_n = \frac{h}{3} \sum_{i=1}^{n/2} (y_{2i-2} + 4y_{2i-1} + y_{2i}) . | |||
</math> | |||
If this sum is expanded, note the pattern of the coefficient of the <math>y_i</math>'s: If <math>i</math> is odd, the coefficient of <math>y_i</math> is 4. If <math>i</math> is even, the coefficient is 2, with the exception of <math>y_0</math> and <math>y_n</math>, each of which has coefficient 1. Thus '''Simpson's Rule''' is expressed in the formula | |||
{{proofcard|Theorem|theorem-4| | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
\int_a^b f \approx S_n &=& \frac{h}{3} (y_0 + 4y_1 + 2y_2 + 4y_3 + 2y_4\\ | |||
&& + \cdots + 2y_{n-2} + 4y_{n-1} + y_n) . | |||
\end{eqnarray*} | |||
</math>|}} | |||
We now prove equation (1). The algebra is significantly simpler if we write <math>q_{i}(x)</math> in terms of <math>x - x_{2i-1}</math> instead of <math>x</math> (see Figure 10). Hence we let | |||
<span id{{=}}"eq8.3.2"/> | |||
<math display="block"> | |||
\begin{equation} | |||
q_i(x) = \alpha_i(x - x_{2i-1})^2 + \beta_i(x- x_{2i-1}) + \gamma_i. | |||
\label{eq8.3.2} | |||
\end{equation} | |||
</math> | |||
The integral <math>\int_{x_{2i-2}}^{x_{2i}} q_i (x) dx</math> may be computed by substituting <math>u = x - x_{2i-1}</math> and using the Change of Variable Theorem for Definite Integrals (see page 215). Since <math>x_{2i-2} - x_{2i-1} = - h</math> and <math>x_{2i} - x_{2i-1} = h</math>, the result is | |||
<span id{{=}}"eq8.3.3"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\begin{array}{ll} | |||
\int_{x_{2i-2}}^{x_{2i}} q_i (x) dx | |||
&= \int_{-h}^h (\alpha_i u^2 + \beta_i u + \gamma_i) du \\ | |||
&= \Bigl( \frac{\alpha_i u^3}{3} + \frac{\beta_i u^2}{2} + \gamma_i u \Bigr) \big|_{-h}^h \\ | |||
&= \frac{h}{3} (2\alpha_i h^2 + 6\gamma_i). | |||
\end{array} | |||
\label{eq8.3.3} | |||
\end{equation} | |||
</math> | |||
Setting first <math>x = x_{2i-1}</math> in equation (2), we obtain | |||
<math display="block"> | |||
y_{2i-1} = q_i(x_{2i-1}) = \alpha_i \cdot 0^2 + \beta_i \cdot 0 + \gamma_i = \gamma_i. | |||
</math> | |||
Next we let <math>x = x_{2i-2}</math> and <math>x = x_{2i}</math> to get | |||
<math display="block"> | |||
y_{2i-2} = q_i(x_{2i-2}) = \alpha_i h^2 - \beta_{i}h + \gamma_i, | |||
</math> | |||
and | |||
<math display="block"> | |||
y_{2i} = q_i(x_{2i}) = \alpha_i h^2 + \beta_i h + \gamma_i. | |||
</math> | |||
Adding, we obtain | |||
<math display="block"> | |||
y_{2i-2} + y_{2i} = 2\alpha_i h^2 + 2\gamma_i. | |||
</math> | |||
Since <math>\gamma_i = y_{2i-1}</math>, it follows that | |||
<math display="block"> | |||
2\alpha_i h^2 + 6\gamma_i = y_{2i-2} + 4y_{2i-1} + y_{2i}. | |||
</math> | |||
Substituting this result in (3) yields the desired result (1), and the derivation of Simpson's Rule is complete. | |||
<span id="table 8.3"/> | |||
'''Example''' | |||
Using <math>n = 4</math>, find an approximate value of <math>\int_0^1 \frac{1}{1+ x^2} dx</math> by Simpson's Rule. We have <math>h = \frac{1 - 0}{4} = \frac{1}{4}</math>, | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
x_i &=& \frac{i}{4}, \;\;\; i = 0,1,..., 4,\\ | |||
y_i &=& \frac{1}{1 + x_i^2} = \frac{1}{1 + \frac{i^2}{16}} = \frac{16}{16 + i^2}, \;\;\; i = 0, 1,..., 4. | |||
\end{eqnarray*} | |||
</math> | |||
Table 3 contains the numbers necessary for the computation. | |||
<span id="table 8.3"/> | |||
{|class="table" | |||
|- | |||
|<math>i</math>|| 0 || 1 || 2 || 3 || 4\vspace {1ex} | |||
|- | |||
|<math>y_i = \frac{16}{16 + i^2}</math> || 1 ||<math>\frac{16}{17}</math>||<math>\frac{16}{20}</math>||<math>\frac{16}{25}</math>||<math>\frac{16}{32}</math> \vspace {1ex} | |||
|} | |||
Hence | |||
<math display="block"> | |||
\begin{eqnarray*} | |||
S_4 &=& \frac{h}{3} - (y_0 + 4y_1 + 2y_2 + 4y_3 + y_4)\\ | |||
&=& \frac{1}{12} (1 + \frac{64}{17} + \frac{32}{20} + \frac{64}{25} + \frac{16}{32}) \\ | |||
&=& 0.785392.... | |||
\end{eqnarray*} | |||
</math> | |||
We know that | |||
<math display="block"> | |||
\int_0^1\frac{1}{1 + x^2} dx = \arctan x \big|_0^1 = \frac{\pi}{4} = 0.785398.... | |||
</math> | |||
Hence the error <math>|\int_a^b f - S_4|</math> is approximately 0.000006. | |||
Just as with the other two methods of integration by numerical approximation, the error <math>| \int_a^b f - S_n |</math> can be made arbitrarily small by taking <math>n</math> aufficiently large. That is, we have the following theorem, which we state without proof. | |||
{{proofcard|Theorem|theorem-5| | |||
<math display="block"> | |||
\lim_{n \rightarrow \infty} S_n = \int_a^b f . | |||
</math>|}} | |||
In addition, the next theorem can be used to estimate the error in a particular application of Simpson's Rule. | |||
{{proofcard|Theorem|theorem-6|If the fourth derivative <math>f^{(4)}</math> is continuous at every point of <math>[a, b]</math>, then there exists a number <math>c</math> such that <math>a < c < b</math> and | |||
<math display="block"> | |||
\int_a^b f = S_n - \frac{b - a}{180} f^{(4)} (c)h^4. | |||
</math>|}} | |||
For an outline of a proof, see J. M. H. Olmsted, Advanced Calculus, Appleton-Century-Crofts, 1961, page 119. | |||
The fourth derivative of every cubic polynomial is identically zero, for if | |||
<math display="block"> | |||
f(x) = a_{3}x^3 + a_{2}x^2 + a_{1}x + a_0, | |||
</math> | |||
then <math>f^{(4)} (x) = 0</math>. It is therefore a rather surprising corollary of Theorem(3.6) that Simpson's Rule will always give the exact value of the integral when applied to any polynomial of degree less than 4. | |||
\end{exercise} | |||
==General references== | |||
{{cite web |title=Crowell and Slesnick’s Calculus with Analytic Geometry|url=https://math.dartmouth.edu/~doyle/docs/calc/calc.pdf |last=Doyle |first=Peter G.|date=2008 |access-date=Oct 29, 2024}} | |||
Revision as of 01:09, 3 November 2024
Numerical Approximations (Continued).
Two additional methods of integration by numerical approximations, which we shall describe in this section, are the Midpoint Rule and Simpson's Rule. In the Midpoint Rule the approximation to the integral [math]\int_a^b f[/math] is a Riemann sum [math]\sum_{i=1}^{n} f(x_i^*)(x_i - x_{i-1})[/math] in which each [math]x_i^*[/math] is taken to be the midpoint of the subinterval [math][x_{i-1}, x_i][/math]. In more detail: Let [math]f[/math] be a function which is integrable over [math][a, b][/math]. For every positive integer [math]n[/math], let [math]h = \frac{b - a}{n}[/math], and let [math]\sigma_n = \{ x_0, . . ., x_n \}[/math] be the partition defined by
As a result, it follows that
If we take [math]x_i^*[/math] to be the midpoint of the subinterval [math][x_{i-1}, x_i][/math], then
The Riemann sum used as the approximation to the integral in the Midpoint Rule will be denoted by [math]M_n[/math]. It is given by
In studying the Trapezoid Rule, we found it convenient to use the abbreviation [math]y_i = f(x_i)[/math], for [math]i = 0, ... , n.[/math] By analogy, we shall here let
Then
and we express the Midpoint Rule for numerical integration by the formula
If [math]f(x) \geq 0[/math] for every [math]x[/math] in [math][a, b][/math], the Midpoint Rule approximates the integral [math]\int_a^b f[/math], which is the area under the curve, by a sum of areas of rectangles, as illustrated in Figure 6.
An alternative to approximating the integral by a Riemann sum is to use straight-line segments which are tangent to the curve [math]y = f(x)[/math] at the midpoints of the subintervals. An example is shown in Figure 7, in which
[math]\int_a^b f[/math] is approximated by the sum of the areas of the three shaded trapezoids. This method yields the so-called Tangent Formula. It turns out, however, that the Tangent Formula is the same as the Midpoint Rule. The reason can be seen by looking at Figure 8, in which the area of the shaded trapezoid with one side tangent to the curve is the ith term in the approximating sum used in the Tangent Formula. The area of this trapezoid is equal to [math]\frac{h}{2} (y' + y'')[/math], where [math]y'[/math] and [math]y''[/math] are the lengths of the bases. However, by elementary geometry the trapezoid can be seen to have the same area as the rectangle with base [math][x_{i-1}, x_i][/math] and altitude [math]y_{i-1/2}[/math] The area of the rectangle is [math]h \cdot y_{i-1/2}[/math], and so
(Incidentally, note that this equation is true regardless of whether [math]y'[/math], [math]y''[/math], and [math]y_{i-1/2}[/math] are positive, negative, or zero.) Since the product [math]h \cdot y_{i-1/2}[/math] is the ith term in the midpoint approximation [math]M_n[/math], we conclude that the Tangent Formula and the Midpoint Rule, although differently motivated, are in fact the same.
ExampleApproximate [math]\int_{-1}^1 (x^2 + x^3) dx[/math] using the Midpoint Rule. This is the same integral which we evaluated in Section 2 by the Trapezoid Rule. To compare the two methods, we shall again take [math]n = 8[/math] and
In addition, since [math]y_{i-1/2} = f(x_i^{*})[/math], we have a pair of useful formulas:
Table 2 contains the numbers for the computation of [math]M_8[/math].
| [math]i[/math] | [math]y_{i - 1/2} = \frac{(2i - 9)^2(2i - 1)}{8^3}[/math] \vspace {1ex} |
| 1 | [math]y_{1/2} = \frac{49}{8^3}[/math] |
| 2 | [math]y_{3/2} = \frac{25 \cdot 3}{8^3} = \frac{75}{8^3}[/math] |
| 3 | [math]y_{5/2} = \frac{9 \cdot 5}{8^3} = \frac{45}{8^3}[/math] |
| 4 | [math]y_{7/2} = \frac{7}{8^3}[/math] |
| 5 | [math]y_{9/2} = \frac{9}{8^3}[/math] |
| 6 | [math]y_{11/2} = \frac{9 \cdot 11}{8^3} = \frac{99}{8^3}[/math] |
| 7 | [math]y_{13/2} = \frac{25 \cdot 13}{8^3} = \frac{325}{8^3}[/math] |
| 8 | [math]y_{15/2} = \frac{49 \cdot 15}{8^3} = \frac{735}{8^3}[/math] |
Hence we obtain
as an approximation to the integral [math]\int_{-1}^1 (x^2 + x^3) dx[/math]. The value obtained earlier with the Trapezoid Rule was [math]T_8 = \frac{11}{16}[/math]. Since the true value is given by
In any application of the Midpoint Rule, the error [math]| \int_a^b f - M_n |[/math] can be made arbitrarily small by taking [math]n[/math] sufficiently large. That is, we assert that
This theorem is easier to prove than the corresponding one for the Trapezoid Rule because every approximation [math]M_n[/math] is, as it stands, a Riemann sum of [math]f[/math] relative to the partition [math]\sigma_n[/math] of [math][a, b][/math]. Since [math]|| \sigma_n || \rightarrow 0[/math] as [math]n \rightarrow \infty[/math], it is a direct corollary of the fundamental theorem on the limit of Riemann sums [(2.1), page 414] that [math]\lim_{n \rightarrow \infty} M_n = \int_a^b f[/math]. A means of estimating the error [math]| \int_a^b f - M_n |[/math] in a particular application of the Midpoint Rule is provided by the following theorem:
If the second derivative [math]f''[/math] is continuous at every point of [math][a, b][/math], then there exists a number [math]c[/math] such that [math]a \lt c \lt b[/math] and
As with the analogous theorem for the Trapezoid Rule [(2.4), page 419], this theorem can be proved by first reducing it to the case [math]n = 1[/math]. A discussion of the error term can be found in [math]R[/math]. Courant and F. John, Introduction to Calculus and Analysis, Volume I, Interscience Publishers (Wiley), 1965, pages 486 and 487. Theorem (3.3) can be used to obtain an upper bound on the error [math]|\int_a^b f - M_n|[/math] provided the second derivative [math]f''[/math] is bounded on the interval [math][a, b][/math]. That is, if there exists a real number [math]K[/math] such that
The sum of these integrals, which we shall denote [math]S_n[/math], is the approximation to [math]\int_a^b f[/math] prescribed by Simpson's Rule. Hence
We now prove equation (1). The algebra is significantly simpler if we write [math]q_{i}(x)[/math] in terms of [math]x - x_{2i-1}[/math] instead of [math]x[/math] (see Figure 10). Hence we let
Setting first [math]x = x_{2i-1}[/math] in equation (2), we obtain
Using [math]n = 4[/math], find an approximate value of [math]\int_0^1 \frac{1}{1+ x^2} dx[/math] by Simpson's Rule. We have [math]h = \frac{1 - 0}{4} = \frac{1}{4}[/math],
Table 3 contains the numbers necessary for the computation.
| [math]i[/math] | 0 | 1 | 2 | 3 | 4\vspace {1ex} |
| [math]y_i = \frac{16}{16 + i^2}[/math] | 1 | [math]\frac{16}{17}[/math] | [math]\frac{16}{20}[/math] | [math]\frac{16}{25}[/math] | [math]\frac{16}{32}[/math] \vspace {1ex} |
Hence
Just as with the other two methods of integration by numerical approximation, the error [math]| \int_a^b f - S_n |[/math] can be made arbitrarily small by taking [math]n[/math] aufficiently large. That is, we have the following theorem, which we state without proof.
In addition, the next theorem can be used to estimate the error in a particular application of Simpson's Rule.
If the fourth derivative [math]f^{(4)}[/math] is continuous at every point of [math][a, b][/math], then there exists a number [math]c[/math] such that [math]a \lt c \lt b[/math] and
For an outline of a proof, see J. M. H. Olmsted, Advanced Calculus, Appleton-Century-Crofts, 1961, page 119. The fourth derivative of every cubic polynomial is identically zero, for if
\end{exercise}
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.