guide:F22a4e9424

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

If a function [math]f[/math] is continuous at every point of an interval [math][a, b][/math], then we know that [math]f[/math] is integrable over [math][a, b][/math] [see Theorem (5.1), page 199]. Continuity is certainly the most important criterion for integrability that we have. For example, in the fundamental theorem of calculus it is assumed that the integrand is continuous over the interval of integration. However, it is important to realize that a function does not have to be continuous to be integrable and that there are many simple discontinuous functions which can be integrated. We begin with the following theorem:

Theorem

If [math]f[/math] is bounded on [math][a, b][/math] and is continuous at every point of [math][a, b][/math] except possibly at the endpoints, then [math]f[/math] is integrable over [math][a, b][/math].

Show Proof

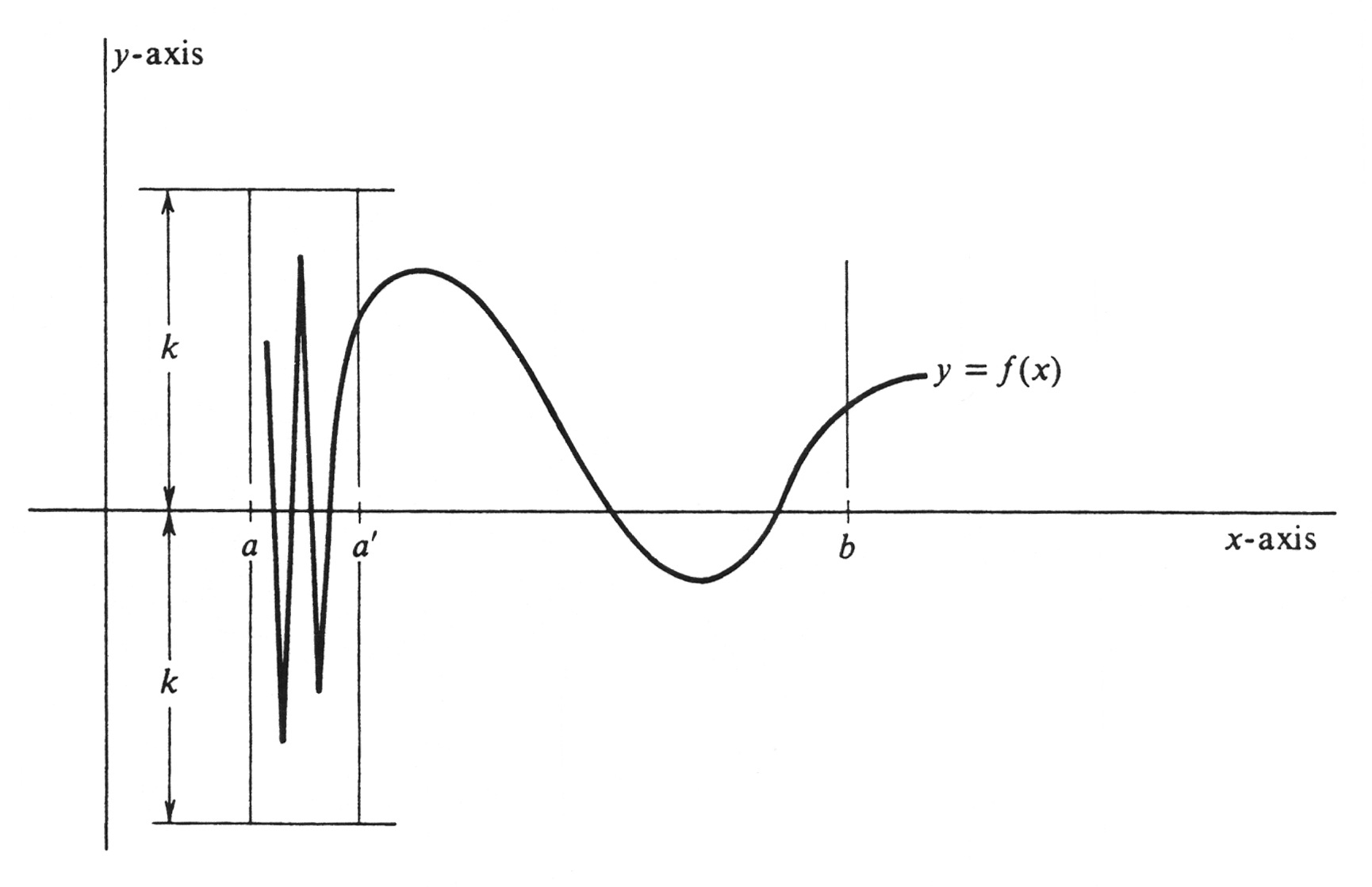
If [math]a = b[/math], the conclusion follows at once since [math]\int_a^b f = \int_a^a f = 0[/math]. Hence we shall assume that [math]a \lt b[/math]. To be specific, we shall furthermore assume that [math]f[/math] is continuous at every point of [math][a, b][/math] except at [math]a[/math]. The necessary mod)fication in the argument if a discontinuity occurs at [math]b[/math] (or at both [math]a[/math] and [math]b[/math]) should be obvious. According to the definition of integrability (page 168), it is sufficient to prove that there exist partitions [math]\sigma[/math] and [math]\tau[/math] of [math][a, b][/math] such that [math]U_\sigma - L_\tau[/math], the difference between the corresponding upper and lower sums, is arbitrarily small. For this purpose, we choose an arbitrary positive number [math]\epsilon[/math]. Since [math]f[/math] is bounded on [math][a, b][/math], there exists a positive number [math]k[/math] such that [math]|f(x)| \leq k[/math], for every [math]x[/math] in [math][a, b][/math]. We next pick a point [math]a'[/math] which is in [math][a, b][/math] and sufficiently close to a that

[[math]] 0 \lt a' - a \lt \frac{\epsilon}{3k} [[/math]]

(see Figure 26). Since [math]f[/math] is continuous on the smaller interval [math][a', b][/math], we know that [math]f[/math] is integrable over it. Hence there exist partitions [math]\sigma'[/math] and [math]\tau'[/math] of [math][a', b][/math] such that the upper sum [math]U_{\sigma'}[/math], and lower sum [math]L_{\tau'}[/math] for [math]f[/math] satisfy

[[math]] \begin{equation} | U_{\sigma'} - L_{\tau'} | \lt \frac{\epsilon}{3}. \label{eq8.6.1} \end{equation} [[/math]]

Let [math]\sigma[/math] and [math]\tau[/math] be the partitions of [math][a, b][/math] obtained from [math]\sigma'[/math] and [math]\tau'[/math] respectively, by adjoining the point [math]a[/math]; i.e., [math]\sigma = \sigma' \cup \{ a \}[/math] and [math]\tau = \tau' \cup \{ a \}[/math]. Since the maximum value of [math]|f(x)|[/math] on the subinterval [math][a, a'][/math] is less than or equal to [math]k[/math], it follows that

[[math]] \begin{equation} | U_\sigma - U_{\sigma'} | \leq k (a' - a) \lt k \cdot \frac{\epsilon}{3k} = \frac{\epsilon}{3} . \label{eq8.6.2} \end{equation} [[/math]]

By the same argument, we have

[[math]] \begin{equation} | L_{\tau'} - L_{\tau} | \leq k (a' - a) \lt k \cdot \frac{\epsilon}{3k} = \frac{\epsilon}{3} . \label{eq8.6.3} \end{equation} [[/math]]

Next, consider the algebraic identity

[[math]] U_\sigma - L_\tau = (U_\sigma - U_{\sigma'}) + (L_{\tau'} - L_\tau) + (U_{\sigma'} - L_{\tau'}). [[/math]]

The sum of three numbers is always less than or equal to the sum of their absolute values. Using this fact and the inequalities (1), (2), and (3), we obtain

[[math]] \begin{eqnarray*} U_\sigma - L_\tau &\leq& | U_\sigma - U_{\sigma'} | + | L_{\tau'} - L_\tau | + | U_{\sigma'} - L_{\tau'} | \\ & \lt & \frac{\epsilon}{3} + \frac{\epsilon}{3} + \frac{\epsilon}{3} = \epsilon . \end{eqnarray*} [[/math]]

Thus there exist upper and lower sums Iying arbitrarily close to each other, and the proof is complete.

■

Example

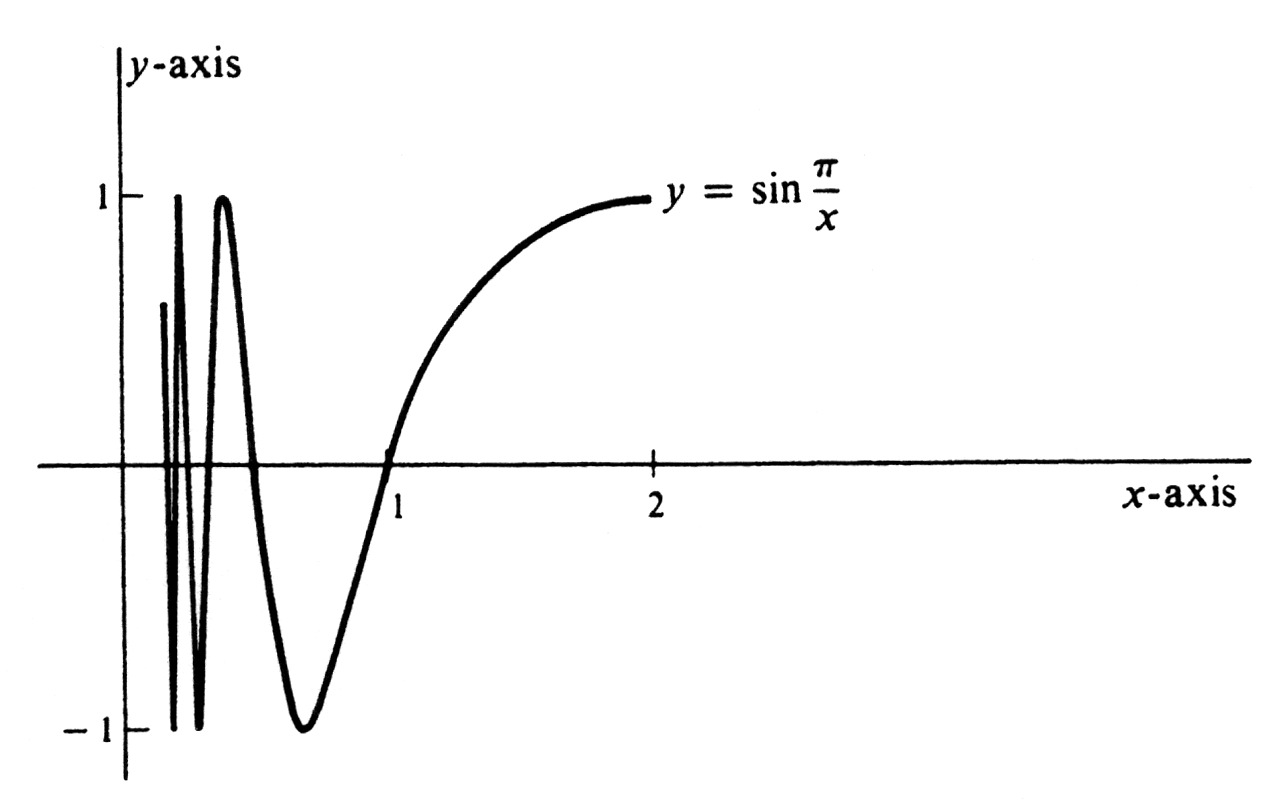
Let [math]f[/math] be the function defined by

[[math]] f(x) = \left\{ \begin{array}{ll} \sin \frac{\pi}{x}, &\;\;\;\mbox{if}\; x \neq 0,\\ 0 &\;\;\;\mbox{if}\; x = 0. \end{array} \right . [[/math]]

This function is continuous everywhere except at 0, and its values oscillate wildly as [math]x[/math] approaches 0. The graph, for values of [math]x[/math] in the interval [0, 2], is shown in Figure 27. Since [math]|f(x)| \leq 1[/math] for every [math]x[/math], the function is bounded on every interval. It therefore follows by Theorem (6.1) that [math]f[/math] is integrable over [0,2].

An important extension of Theorem (6.1) is the following:

Theorem

If [math]f[/math] is bounded on [math][a, b][/math] and is continuous at all but a finite number of points in the interval, then [math]f[/math] is integrable over [math][a, b][/math]. Furthermore, if [math]a_1, ..., a_n[/math] are the points of discontinuity and if [math]a \leq a_1 \leq \cdots \leq a_n \leq b[/math], then

[[math]] \int_a^b f = \int_a^{a_1} f + \int_{a_1}^{a_2} f + \cdots + \int_{a_n}^b f. [[/math]]

Show Proof

It is a direct corollary of (6.1) that [math]f[/math] is integrable over each subinterval [math][a, a_1], [a_1, a_2], ... , [a_n, b][/math]. By repeated applications of Theorem (4.2), page 191, we may then conclude that [math]f[/math] is integrable over [math][a, b][/math] and that

[[math]] \int_a^b f = \int_a^{a_1} f + \cdots + \int_{a_n}a^b f. [[/math]]

This completes the proof.

■

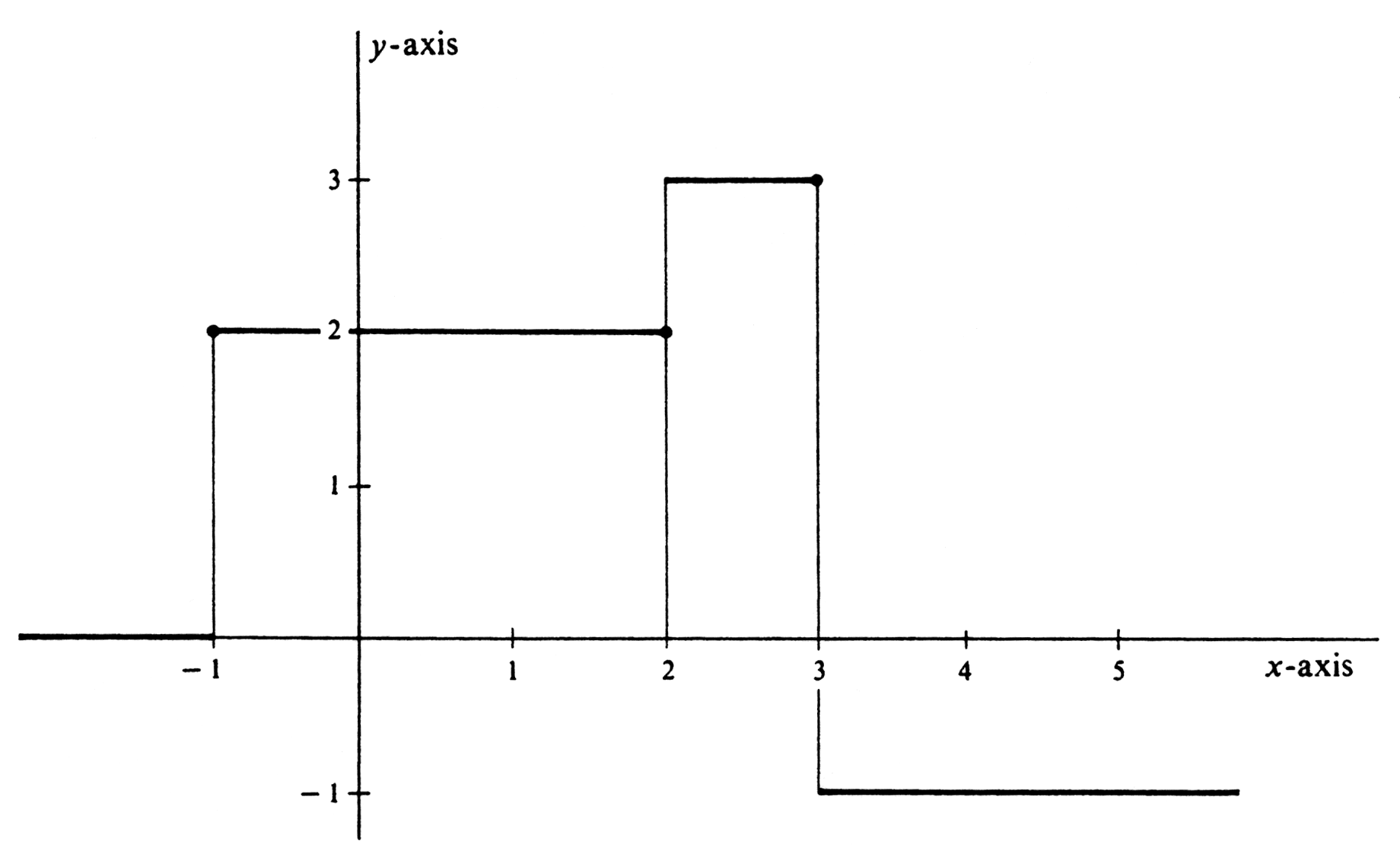
Consider the function [math]f[/math], whose graph is shown in Figure 28, and which is defined by

[[math]] f(x) = \left\{ \begin{array}{rc} 0 & -\infty \lt x \lt -1, \\ 2 & -1 \leq x \leq 2, \\ 3 & 2 \lt x \leq 3, \\ -1 & 3 \lt x \lt \infty. \end{array} \right . [[/math]]

This function, which is constant over certain intervals, is an example of a step function. A function whose domain is the entire set of real numbers is a step function if every bounded interval is the union of a finite number of subintervals on each of which the function is a constant. A step function is bounded on any bounded interval and is continuous there at all but possibly a finite number of points. In the present example the only discontinuities occur at [math]-1[/math], 2, and 3. Hence, Theorem (6.2) implies that [math]f[/math] is integrable over any interval [math][a, b][/math]. In particular,

[[math]] \int_0^4 f = \int_0^2 f + \int_2^3 f + \int_3^4 f. [[/math]]

For each of the three integrals on the right side of the preceding equation, the integrand [math]f[/math] is constant on the interval of integration except possibly at the endpoints. If we think of an integral as area or as an average value, we shall almost certainly support the conjecture that the value of an integral is not affected by isolated discontinuities in the integrand. Thus we expect that

[[math]] \begin{eqnarray*} \int_0^4 f &=& \int_0^2 f + \int_2^3 f + \int_3^4 f\\ &=& 2 \cdot (2 - 0) + 3 \cdot (3 - 2) + (- 1)(4 - 3) = 6. \end{eqnarray*} [[/math]]

This conjecture is correct (hence, so is the preceding computation), and is implied by the next theorem.

Theorem

Let [math][a, b][/math] be a subset of the domains of two functions [math]f[/math] and [math]g[/math], and let [math]f (x) = g(x)[/math] for all but afinite number of values of [math]x[/math] in [math][a, b][/math]. If [math]f[/math] is integrable over [math][a, b][/math], then so is [math]g[/math] and [math]\int_a^b f = \int_a^b g.[/math]

Show Proof

It is sufficient to prove this theorem under the assumption that the values of [math]f[/math] and [math]g[/math] differ at only a single point [math]c[/math] in the interval [math][a, b][/math] (because the result can then be iterated). To be specific, we shall assume that [math]f(c) \lt g(c)[/math]. The proof is completed if we can show that there exist upper and lower sums for [math]g[/math] which differ from the integral [math]\int_a^b f[/math] by an arbitrarily small amount. For this purpose, we choose an arbitrary positive number [math]\epsilon[/math]. Since [math]f[/math] is, by hypothesis, integrable over [math][a, b][/math], there exists a partition [math]\tau[/math] of [math][a, b][/math] such that the corresponding lower sum for [math]f[/math], which we denote by [math]L_\tau (f)[/math], satisfies

[[math]] \int_a^b f L_\tau (f) \lt \epsilon. [[/math]]

However, every lower sum for [math]f[/math] is also a lower sum for [math]g[/math]. Hence we may substitute [math]L_\tau (g)[/math] for [math]L_\tau (f)[/math] in the preceding inequality and obtain

[[math]] \begin{equation} \int_a^b f - L_\tau (g) \lt \epsilon. \label{eq8.6.4} \end{equation} [[/math]]

We next derive a similar inequality involving an upper sum for [math]g[/math]. The integrability of [math]f[/math] also implies the existence of a partition [math]\sigma'[/math] of [math][a, b][/math] such that the corresponding upper sum for [math]f[/math] satisfies

[[math]] U_{\sigma'} (f) - \int_a^b f \lt \frac{\epsilon}{2}. [[/math]]

By possibly adjoining to [math]\sigma'[/math] a point on either side of [math]c[/math], we can assure ourselves of getting a partition [math]\sigma = \{ x_0, ..., x_n \}[/math] of [math][a, b][/math] with the property that if [math]c[/math] lies in the ith subinterval [math][x_{i-1}, x_i][/math], then

[[math]] \begin{equation} x_i - x_{i-1} \lt \frac{\epsilon}{2[g(c) - f(c)]} . \label{eq8.6.5} \end{equation} [[/math]]

We have already shown [see the proof of (1.1), page 168] that if one partition [math]\sigma[/math] is a refinement of another [math]\sigma'[/math] (i.e., if [math]\sigma'[/math] is a subset of [math]\sigma[/math]), then [math]U_\sigma \leq U_{\sigma'}[/math]. Thus [math]U_\sigma (f)[/math] is, if anything, a better approximation to [math]\int_a^b f[/math] than [math]U_{\sigma'} (f)[/math]. Hence

[[math]] \begin{equation} U_\sigma (f) - \int_a^b f \lt \frac{\epsilon}{2} \label{eq8.6.6} \end{equation} [[/math]]

Let [math]M_i[/math] and [math]N_i[/math] be the least upper bounds of the values of [math]f[/math] and [math]g[/math], respectively, on [math][x_{i-1}, x_i][/math]. Since [math]f(x) = g(x)[/math] except at [math]c[/math], it follows that

[[math]] U_\sigma (g) - U_\sigma (f) = (N_i - M_i)(x_i - x_{i-1}). [[/math]]

But the difference [math]N_i - M_i[/math] can be no more than [math]g(c) - f(c)[/math]. Hence

[[math]] U_\sigma (g) - U_\sigma (f) \leq [g(c) - f (c)](x_i - x_{i-1}), [[/math]]

and this inequality combined with (5) yields

[[math]] \begin{equation} U_\sigma (g) - U_\sigma (f) \lt \frac{\epsilon}{2} . \label{eq8.6.7} \end{equation} [[/math]]

Finally, adding the inequalities (6) and (7), we obtain

[[math]] U_\sigma (g) - \int_a^b f \lt \epsilon . [[/math]]

This is the analogue of (4) and completes the proof.

■

Example

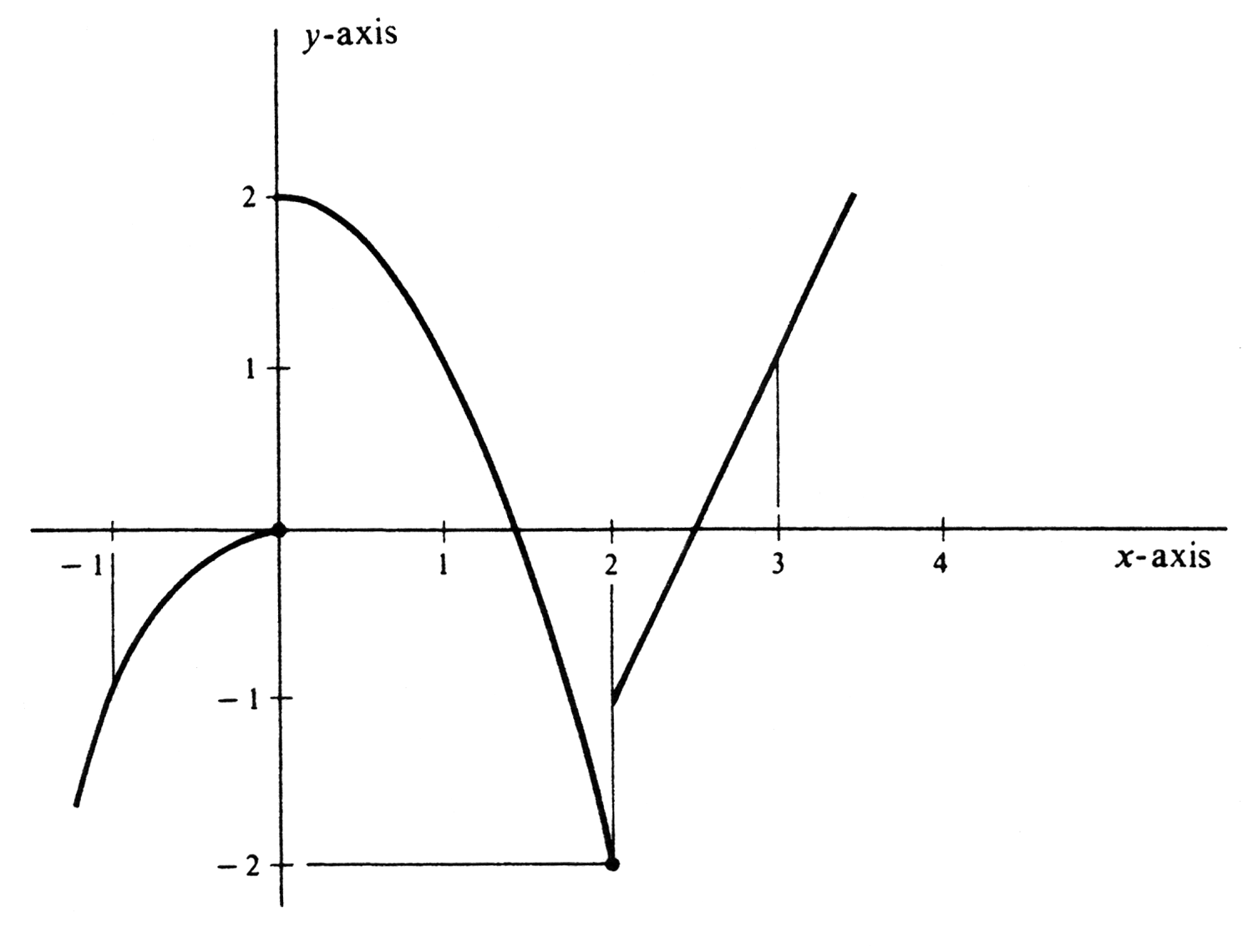
Let [math]f[/math] be the function defined by

[[math]] f(x) = \left\{ \begin{array}{lc} x^3 & -\infty \lt x \leq 0, \\ 2 - x^2 & 0 \lt x \leq 2, \\ 2x - 5 & 2 \lt x \lt \infty. \end{array} \right . [[/math]]

The graph of [math]f[/math] is drawn in Figure 29. The function is clearly continuous except at 0 and at 2, and is bounded on any bounded interval. It follows by Theorem (6.2) that [math]f[/math] is integrable over the interval [math][-1, 3][/math] and that

[[math]] \int_{-1}^3 f = \int_{-1}^0 f + \int_0^2 f + \int_2^3 f . [[/math]]

For every [math]x[/math] in [math][-1, 0][/math], we have [math]f(x) = x^3[/math], and so

[[math]] \int_{-1}^0 f = \int_{-1}^0 x^3 dx = \frac{x^4}{4} \Big|_{-1}^0 = - \frac{1}{4}. [[/math]]

For every [math]x[/math] in [math][0, 2][/math], we have [math]f(x) = 2 - x^2[/math] except that [math]f(0) = 0[/math]. Hence, by Theorem (6.3),

[[math]] \int_0^2 f = \int_0^2 (2 - x^2) dx = (2x - \frac{x^3}{3}) \Big|_0^2 = \frac{4}{3}. [[/math]]

Similarly, [math]f(x) = 2x - 5[/math] for every [math]x[/math] in [2, 3] except that [math]f(2) = - 2[/math]. Again, by Theorem (6.3),

[[math]] \int_2^3 f = \int_2^3 (2x - 5) dx = (x^2 - 5x)\big|_2^3 = - 6 - (- 6)= 0. [[/math]]

Hence

[[math]] \int_{-1}^3 f = -\frac{1}{4} + \frac{4}{3} + 0 = \frac{13}{12}. [[/math]]

Example Is each of the following integrals defined?

• [math]\int_0^1 \sin \frac{1}{x} dx,[/math]
• [math]\int_1^2 \frac{\ln x}{1 - x} dx,[/math]
• [math]\int_0^{\pi/2} \tan x dx.[/math]

This is the same as asking whether or not each function is integrable over its proposed interval of integration. Strictly speaking, the answer is no in every case, because each function fails to be defined at one of the endpoints of the interval. However, Theorem (6.3) shows that this answer is based on a technicality and misses the real point of the question. If a function [math]f[/math] is bounded on an open interval [math](a, b)[/math] and if [math]f(a)[/math] end [math]f(b)[/math] are any real numbers whatever, then [math]f[/math] is also bounded on the closed interval [math][a, b][/math]. Let us suppose, therefore, that [math]f[/math] is bounded and continuous on the open interval [math](a, b)[/math]. We may choose values [math]f(a)[/math] and [math]f(b)[/math] completely arbitrarily, and the resulting function will be integrable over [math][a, b][/math] as a result of Theorem (6.1). Furthermore, by Theorem (6.3), the integral [math]\int_a^b f[/math] is independent of the choice of [math]f(a)[/math] and [math]f(b)[/math]. Hence, if [math]f[/math] is bounded and continuous on [math](a, b)[/math], we shall certainly adopbt the point of view that [math]f[/math] is integrable over [math][a, b][/math] and, equivalently, that [math]\int_a^b f[/math] is defined.

Following this convention, we see that the function [math]\sin \frac{1}{x}[/math] is bounded and continuous on (0, 1), and so [math]\int_0^1 \sin \frac{1}{x} dx[/math] is defined. Using L'Hôpital's Rule (page 123), one can easily show that

[[math]] \lim_{x \rightarrow 1_{+}} \frac{\ln x}{1 - x} = - 1 . [[/math]]

Hence, [math]\frac{\ln x}{1 - x}[/math] is bounded and continuous on (1, 2), and so [math]\int_1^2 \frac{\ln x}{1 - x} dx[/math] exists. On the other hand,

[[math]] \lim_{x \rightarrow (\pi/2)_{-}} \tan x = \infty, [[/math]]

and we therefore conclude that tan [math]x[/math] is not integrable over the interval [math][0, \frac{\pi}{2}][/math].

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.