guide:68fbdee177: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"><math> | |||
\newcommand{\R}{\mathbb{R}} | |||
\newcommand{\A}{\mathcal{A}} | |||
\newcommand{\B}{\mathcal{B}} | |||
\newcommand{\N}{\mathbb{N}} | |||
\newcommand{\C}{\mathbb{C}} | |||
\newcommand{\Rbar}{\overline{\mathbb{R}}} | |||
\newcommand{\Bbar}{\overline{\mathcal{B}}} | |||
\newcommand{\Q}{\mathbb{Q}} | |||
\newcommand{\E}{\mathbb{E}} | |||
\newcommand{\p}{\mathbb{P}} | |||
\newcommand{\one}{\mathds{1}} | |||
\newcommand{\0}{\mathcal{O}} | |||
\newcommand{\mat}{\textnormal{Mat}} | |||
\newcommand{\sign}{\textnormal{sign}} | |||
\newcommand{\CP}{\mathcal{P}} | |||
\newcommand{\CT}{\mathcal{T}} | |||
\newcommand{\CY}{\mathcal{Y}} | |||
\newcommand{\F}{\mathcal{F}} | |||
\newcommand{\mathds}{\mathbb}</math></div> | |||
\begin{thm}[Central limit theorem (CLT)] | |||
Let <math>(\Omega,\A,\p)</math> be a probability space. Let <math>(X_n)_{n\geq 1}</math> be a sequence of iid r.v.'s with values in <math>\R</math>. We assume that <math>\E[X_k^2] < \infty</math> (i.e. <math>X_k\in L^2(\Omega,\A,\p)</math>) and let <math>\sigma^2=Var(X_k)</math> for all <math>k\in\{1,...,n\}</math>. Then for all <math>k\in\{1,...,n\}</math> we get | |||
<math display="block"> | |||
\sqrt{n}\left(\frac{1}{n}\sum_{i=0}^nX_i-\E[X_k]\right)\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,\sigma^2). | |||
</math> | |||
Equivalently, for all <math>a,b\in\bar\R</math> with <math>a < b</math> and for all <math>k\in\{1,...,n\}</math> we get | |||
<math display="block"> | |||
\lim_{n\to\infty}\p\left[\sum_{i=0}^nX_i\in \left[n\E[X_k]+a\sqrt{n},n\E[X_k]+b\sqrt{n}\right]\right]=\frac{1}{\sigma\sqrt{2\pi}}\int_a^be^{-\frac{x^2}{2\sigma^2}}dx. | |||
</math> | |||
\end{thm} | |||
'''Example''' | |||
If <math>\E[X_k]=0</math> for all <math>k\in\{1,...,n\}</math>, then | |||
<math display="block"> | |||
\lim_{n\to\infty}\p\left[\frac{\sum_{i=1}^nX_i-n\E[X_k]}{\sqrt{n}}\in[a,b]\right]=\frac{1}{\sigma\sqrt{2\pi}}\int_a^be^{-\frac{x^2}{2\sigma^2}}dx. | |||
</math> | |||
\begin{proof} | |||
Without loss of generality we can assume that <math>\E[X_k]=0</math>, for all <math>k\in\{1,...,n\}</math>. Define now a sequence <math>Z_n=\frac{\sum_{i=1}^nX_i}{\sqrt{n}}</math>. Then we can obtain | |||
<math display="block"> | |||
\Phi_{Z_n}(\xi)=\E\left[e^{i\xi Z_n}\right]=\E\left[e^{i\xi \left(\frac{\sum_{i=1}^nX_i}{\sqrt{n}}\right)}\right]=\prod_{j=1}^n\E\left[e^{i\xi \frac{X_j}{\sqrt{n}}}\right]=\E\left[e^{i\xi\frac{X_k}{\sqrt{n}}}\right]^n=\Phi_{X_k}^n(\xi). | |||
</math> | |||
We have already seen that | |||
<math display="block"> | |||
\Phi_{X_k}(\xi)=1+n\xi\E[X_k]-\frac{1}{2}\xi^2\E[X_k^2]+O(\xi^2)=1-\frac{\sigma^2}{2}\xi^2+O(\xi^2). | |||
</math> | |||
Finally, for fixed <math>\xi</math>, we have | |||
<math display="block"> | |||
\Phi_{X_k}\left(\frac{\xi}{\sqrt{n}}\right)=1-\frac{\sigma^2\xi^2}{2n}+O\left(\frac{1}{n}\right) | |||
</math> | |||
<math display="block"> | |||
\lim_{n\to\infty}\Phi_{X_k}^n(\xi)=\lim_{n\to\infty}\left(1-\frac{\sigma^2\xi^2}{2}+O\left(\frac{1}{n}\right)\right)^n=\E\left[e^{i\xi \mathcal{N}(0,\sigma^2)}\right]. | |||
</math> | |||
\end{proof} | |||
<div id="" class="d-flex justify-content-center"> | |||
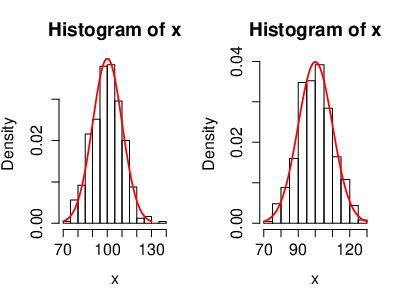
[[File:guide_fe641_CLT_Histx_0.png | 400px | thumb | For the illustration of the CLT, the distribution of a Gaussian distributed r.v. <math>X</math> with <math>\mu=100</math> and <math>\sigma=10</math> (<math>X\sim \mathcal{N}(\mu,\sigma^2)</math>). ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
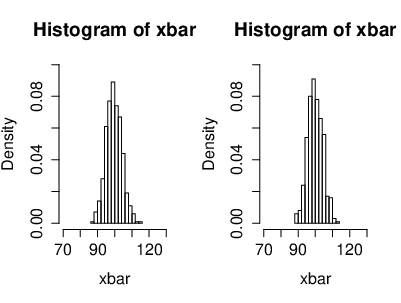
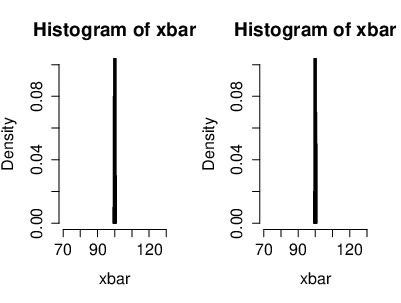
[[File:guide_fe641_CLT_xbar_n5.png | 400px | thumb | The distribution of the mean of <math>n=5</math> i.i.d. Gaussian r.v.'s <math>(X_n)</math> with <math>\mu=100</math> and <math>\sigma^2=10</math> (<math>X_k\sim \mathcal{N}(\mu,\sigma^2)</math>). The figure illustrates the behavior of the distribution of the mean, which is given by <math>\bar X_n=\frac{1}{n}\sum_{k=1}^nX_k</math>. ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
[[File:guide_fe641_CLT_xbar_n20.png | 400px | thumb | The distribution of the mean of <math>n=20</math> i.i.d. Gaussian r.v.'s <math>(X_n)</math> with <math>\mu=100</math> and <math>\sigma^2=10</math> (<math>X_k\sim \mathcal{N}(\mu,\sigma^2)</math>). The figure illustrates the behavior of the distribution of the mean, which is given by <math>\bar X_n=\frac{1}{n}\sum_{k=1}^nX_k</math>. ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
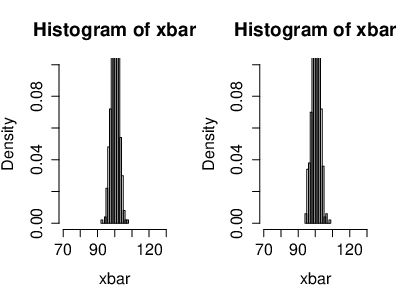
[[File:guide_fe641_CLT_xbar_n100.png | 400px | thumb | The distribution of the mean of <math>n=100</math> i.i.d. Gaussian r.v.'s <math>(X_n)</math> with <math>\mu=100</math> and <math>\sigma^2=10</math> (<math>X_k\sim \mathcal{N}(\mu,\sigma^2)</math>). The figure illustrates the behavior of the distribution of the mean, which is given by <math>\bar X_n=\frac{1}{n}\sum_{k=1}^nX_k</math>. ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
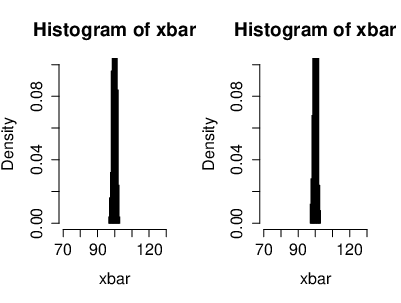
[[File:guide_fe641_CLT_xbar_n1000.png | 400px | thumb | The distribution of the mean of <math>n=1000</math> i.i.d. Gaussian r.v.'s <math>(X_n)</math> with <math>\mu=100</math> and <math>\sigma^2=10</math> (<math>X_k\sim \mathcal{N}(\mu,\sigma^2)</math>). The figure illustrates the behavior of the distribution of the mean, which is given by <math>\bar X_n=\frac{1}{n}\sum_{k=1}^nX_k</math>. Clearly we see that it's converging to <math>\mu</math> for <math>n\to\infty</math>. ]] | |||
</div> | |||
{{proofcard|Theorem|thm-1|Let <math>(X_n)_{n\geq 1}</math> be independent r.v.'s but not necessarily i.i.d. We assume that <math>\E[X_j]=0</math> and that <math>\E[X_j^2]=\sigma_j^2 < \infty</math>, for all <math>j\in\{1,...,n\}</math>. Assume further that <math>\sup_n\E[\vert X_n\vert^{2+\delta}] < \infty</math> for some <math>\delta > 0</math>, and that <math>\sum_{j=1}^\infty \sigma_j^2 < \infty.</math> Then | |||
<math display="block"> | |||
\frac{\sum_{j=1}^nX_j}{\sqrt{\sum_{j=1}^n \sigma_j^2}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1). | |||
</math>|}} | |||
'''Example''' | |||
We got the following examples: | |||
<ul style{{=}}"list-style-type:lower-roman"><li>Let <math>(X_n)_{n\geq 1}</math> be i.i.d. r.v.'s with <math>\p[X_n=1]=p</math> and <math>\p[X_n=0]=1-p</math>. Then <math>S_n=\sum_{i=1}^nX_i</math> is a binomial r.v. <math>\B(p,n)</math>. We have <math>\E[S_n]=np</math> and <math>Var(S_n)=np(1-p)</math>. Now with the strong law of large numbers we get <math>\frac{S_n}{n}\xrightarrow{n\to\infty\atop a.s.}p</math> and with the central limit theorem we get | |||
<math display="block"> | |||
\frac{S_n-np}{\sqrt{np(1-p)}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1). | |||
</math> | |||
</li> | |||
<li>Let <math>\mathcal{P}</math> be the set of prime numbers. For <math>p\in\mathcal{P}</math>, define <math>\B_p</math> as <math>\p[\B_p=1]=\frac{1}{p}</math> and <math>\p[\B_p=0]=1-\frac{1}{p}</math>. We take the <math>(\B_p)_{p\in\mathcal{P}}</math> to be independent and | |||
<math display="block"> | |||
W_n=\sum_{\mathcal{P}\subset\N\atop p\in\mathcal{P}}\B_p, | |||
</math> | |||
the probabilistic model for the total numbers of distinct prime divisors of <math>n:=W(0)</math>. It's a simple exercise to check that <math>(W_n)_{n\geq 1}</math> satisfies the assumption of theorem 13.2 and using the fact that <math>\sum_{p\leq n\atop p\in\mathcal{P}}\frac{1}{p}\sim \log\log n</math> and we obtain | |||
<math display="block"> | |||
\frac{W_n-\log\log n}{\sqrt{\log\log n}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1). | |||
</math> | |||
<div id="" class="d-flex justify-content-center"> | |||
[[File:guide_fe641_CLT_cdfs_exp_n2.png | 400px | thumb | An illustration of the CLT, where the r.v.'s <math>(X_n)</math> are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have <math>n=2</math> exponentially distributed r.v's <math>\left(X_k\sim \lambda e^{-\lambda}\right)</math>. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. <math>Y</math> with <math>\mu=0</math> (<math>Y\sim\mathcal{N}(0,\sigma^2)</math>). On the right side, the black curve represents the cumulative distribution function of the r.v.'s <math>X_k</math> and the red curve represents the cumulative distribution function of a Gaussian r.v. <math>Y</math>. ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
[[File:guide_fe641_CLT_cdfs_exp_n4.png | 400px | thumb | An illustration of the CLT, where the r.v.'s <math>(X_n)</math> are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have <math>n=4</math> exponentially distributed r.v's <math>\left(X_k\sim \lambda e^{-\lambda}\right)</math>. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. <math>Y</math> with <math>\mu=0</math> (<math>Y\sim\mathcal{N}(0,\sigma^2)</math>). On the right side, the black curve represents the cumulative distribution function of the r.v.'s <math>X_k</math> and the red curve represents the cumulative distribution function of a Gaussian r.v. <math>Y</math>. ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
[[File:guide_fe641_CLT_cdfs_exp_n10.png | 400px | thumb | An illustration of the CLT, where the r.v.'s <math>(X_n)</math> are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have <math>n=10</math> exponentially distributed r.v's <math>\left(X_k\sim \lambda e^{-\lambda}\right)</math>. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. <math>Y</math> with <math>\mu=0</math> (<math>Y\sim\mathcal{N}(0,\sigma^2)</math>). On the right side, the black curve represents the cumulative distribution function of the r.v.'s <math>X_k</math> and the red curve represents the cumulative distribution function of a Gaussian r.v. <math>Y</math>. ]] | |||
</div> | |||
<div id="" class="d-flex justify-content-center"> | |||
[[File:guide_fe641_CLT_cdfs_exp_n20.png | 400px | thumb | An illustration of the CLT, where the r.v.'s <math>(X_n)</math> are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have <math>n=20</math> exponentially distributed r.v's <math>\left(X_k\sim \lambda e^{-\lambda}\right)</math>. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. <math>Y</math> with <math>\mu=0</math> (<math>Y\sim\mathcal{N}(0,\sigma^2)</math>). On the right side, the black curve represents the cumulative distribution function of the r.v.'s <math>X_k</math> and the red curve represents the cumulative distribution function of a Gaussian r.v. <math>Y</math>. Now we can see that both, the density and the cumulative distribution function, are converging to a Gaussian density and a Gaussian cumulative distribution function for <math>n\to\infty</math>. ]] | |||
</div> | |||
{{proofcard|Theorem (Erdös-Kac)|thm-2|Let <math>N_n</math> be a r.v. with uniformly distribution in <math>\{1,...,n\}</math>, then | |||
<math display="block"> | |||
\frac{W(N_n)-\log\log n}{\sqrt{\log\log n}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1), | |||
</math> | |||
where <math>W(n)=\sum_{p\leq n\atop p\in\mathcal{P}}\one_{p|n}</math>.|}} | |||
</li> | |||
<li>Suppose that <math>(X_n)_{n\geq 1}</math> are i.i.d. r.v.'s with distribution function <math>F(x)=\p[X_1\leq x]</math>. Let <math>Y_n(x)=\one_{X_n\leq x}</math>, where <math>(Y_n)_{n\geq 1}</math> are i.i.d. Define <math>F_n(x)=\frac{1}{n}\sum_{k=1}^nY_k(x)=\frac{1}{n}\sum_{k=1}^n\one_{X_k\leq x}</math>. <math>F_n</math> is called the empirical distribution function. With the strong law of large numbers we get <math>\lim_{n\to\infty\atop a.s.}F_n(x)=\E[Y_1(x)]</math> and | |||
<math display="block"> | |||
\E[Y_1(x)]=\E[\one_{X_1\leq x}]=\p[X_1\leq x]=F(x). | |||
</math> | |||
In fact, it is a theorem (Gliwenko-Cantelli) which says that | |||
<math display="block"> | |||
\sup_{x\in\R}\vert F_n(x)-F(x)\vert\xrightarrow{n\to\infty\atop a.s.}0. | |||
</math> | |||
Next we note that | |||
<math display="block"> | |||
\sqrt{n}(F_n(x)-F(x))=\sqrt{n}\left(\frac{1}{n}\sum_{k=1}^nY_k(x)-\E[Y_1(x)]\right)=\frac{1}{\sqrt{n}}\left(\sum_{k=1}^nY_k(x)-n\E[Y_1(x)]\right) | |||
</math> | |||
Now with the central limit theorem we get | |||
<math display="block"> | |||
\sqrt{n}(F_n(x)-F(x))\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,\sigma^2(x)), | |||
</math> | |||
where <math>\sigma^2(x)=Var(Y_1)=\E[Y_1^2(x)]=\E[Y_1(x)]=F(x)-F^2(x)=F(x)(1-F(x))</math>. Hence | |||
<math display="block"> | |||
\sqrt{n}(F_n(x)-F(x))\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,F(x)(1-F(x))). | |||
</math> | |||
</li> | |||
</ul> | |||
{{proofcard|Theorem (Berry-Esseen)|thm-3|Let <math>(X_n)_{n\geq 1}</math> be i.i.d. r.v's and suppose that <math>\E[\vert X_k\vert^3] < \infty</math>, <math>\forall k\in\{1,...,n\}</math>. Let | |||
<math display="block"> | |||
G_n(x)=\p\left[\frac{\sum_{i=1}^nX_i-n\E[X_k]}{\sigma\sqrt{n}}\leq x\right],\forall k\in\{1,...,n\}, | |||
</math> | |||
where <math>\sigma^2=\E[X_k^2]</math> <math>\forall k\in\{1,...,n\}</math> and <math>\Phi(x)=\p\left[\mathcal{N}(0,1)\leq x\right]=\int_{-\infty}^xe^{-\frac{u^2}{2}}\frac{1}{\sqrt{2\pi}}du</math>. Then | |||
<math display="block"> | |||
\sup_{x\in\R}\vert G_n(x)-\Phi(x)\vert\leq C\frac{\E[\vert X_k\vert^3]}{\sigma^3\sqrt{n}},\forall k\in\{1,...,n\} | |||
</math> | |||
where <math>C</math> is a universal constant.|}} | |||
==General references== | |||
{{cite arXiv|last=Moshayedi|first=Nima|year=2020|title=Lectures on Probability Theory|eprint=2010.16280|class=math.PR}} | |||
Revision as of 00:53, 8 May 2024
\begin{thm}[Central limit theorem (CLT)] Let [math](\Omega,\A,\p)[/math] be a probability space. Let [math](X_n)_{n\geq 1}[/math] be a sequence of iid r.v.'s with values in [math]\R[/math]. We assume that [math]\E[X_k^2] \lt \infty[/math] (i.e. [math]X_k\in L^2(\Omega,\A,\p)[/math]) and let [math]\sigma^2=Var(X_k)[/math] for all [math]k\in\{1,...,n\}[/math]. Then for all [math]k\in\{1,...,n\}[/math] we get
Equivalently, for all [math]a,b\in\bar\R[/math] with [math]a \lt b[/math] and for all [math]k\in\{1,...,n\}[/math] we get
\end{thm}
Example
If [math]\E[X_k]=0[/math] for all [math]k\in\{1,...,n\}[/math], then
\begin{proof} Without loss of generality we can assume that [math]\E[X_k]=0[/math], for all [math]k\in\{1,...,n\}[/math]. Define now a sequence [math]Z_n=\frac{\sum_{i=1}^nX_i}{\sqrt{n}}[/math]. Then we can obtain
We have already seen that
Finally, for fixed [math]\xi[/math], we have
\end{proof}
Let [math](X_n)_{n\geq 1}[/math] be independent r.v.'s but not necessarily i.i.d. We assume that [math]\E[X_j]=0[/math] and that [math]\E[X_j^2]=\sigma_j^2 \lt \infty[/math], for all [math]j\in\{1,...,n\}[/math]. Assume further that [math]\sup_n\E[\vert X_n\vert^{2+\delta}] \lt \infty[/math] for some [math]\delta \gt 0[/math], and that [math]\sum_{j=1}^\infty \sigma_j^2 \lt \infty.[/math] Then
Example
We got the following examples:
- Let [math](X_n)_{n\geq 1}[/math] be i.i.d. r.v.'s with [math]\p[X_n=1]=p[/math] and [math]\p[X_n=0]=1-p[/math]. Then [math]S_n=\sum_{i=1}^nX_i[/math] is a binomial r.v. [math]\B(p,n)[/math]. We have [math]\E[S_n]=np[/math] and [math]Var(S_n)=np(1-p)[/math]. Now with the strong law of large numbers we get [math]\frac{S_n}{n}\xrightarrow{n\to\infty\atop a.s.}p[/math] and with the central limit theorem we get
[[math]] \frac{S_n-np}{\sqrt{np(1-p)}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1). [[/math]]
- Let [math]\mathcal{P}[/math] be the set of prime numbers. For [math]p\in\mathcal{P}[/math], define [math]\B_p[/math] as [math]\p[\B_p=1]=\frac{1}{p}[/math] and [math]\p[\B_p=0]=1-\frac{1}{p}[/math]. We take the [math](\B_p)_{p\in\mathcal{P}}[/math] to be independent and
[[math]] W_n=\sum_{\mathcal{P}\subset\N\atop p\in\mathcal{P}}\B_p, [[/math]]the probabilistic model for the total numbers of distinct prime divisors of [math]n:=W(0)[/math]. It's a simple exercise to check that [math](W_n)_{n\geq 1}[/math] satisfies the assumption of theorem 13.2 and using the fact that [math]\sum_{p\leq n\atop p\in\mathcal{P}}\frac{1}{p}\sim \log\log n[/math] and we obtain[[math]] \frac{W_n-\log\log n}{\sqrt{\log\log n}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1). [[/math]]
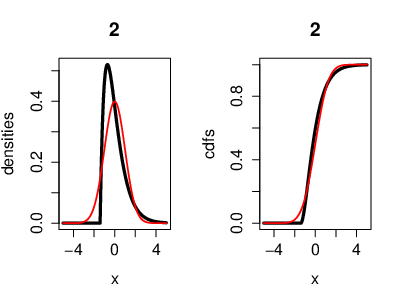
An illustration of the CLT, where the r.v.'s [math](X_n)[/math] are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have [math]n=2[/math] exponentially distributed r.v's [math]\left(X_k\sim \lambda e^{-\lambda}\right)[/math]. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. [math]Y[/math] with [math]\mu=0[/math] ([math]Y\sim\mathcal{N}(0,\sigma^2)[/math]). On the right side, the black curve represents the cumulative distribution function of the r.v.'s [math]X_k[/math] and the red curve represents the cumulative distribution function of a Gaussian r.v. [math]Y[/math]. 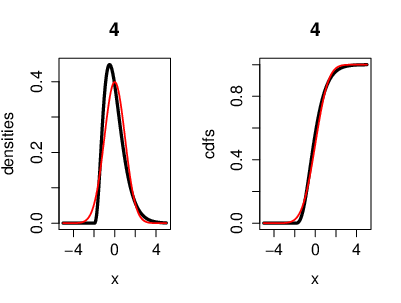
An illustration of the CLT, where the r.v.'s [math](X_n)[/math] are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have [math]n=4[/math] exponentially distributed r.v's [math]\left(X_k\sim \lambda e^{-\lambda}\right)[/math]. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. [math]Y[/math] with [math]\mu=0[/math] ([math]Y\sim\mathcal{N}(0,\sigma^2)[/math]). On the right side, the black curve represents the cumulative distribution function of the r.v.'s [math]X_k[/math] and the red curve represents the cumulative distribution function of a Gaussian r.v. [math]Y[/math]. 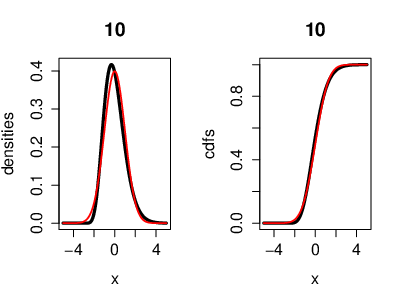
An illustration of the CLT, where the r.v.'s [math](X_n)[/math] are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have [math]n=10[/math] exponentially distributed r.v's [math]\left(X_k\sim \lambda e^{-\lambda}\right)[/math]. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. [math]Y[/math] with [math]\mu=0[/math] ([math]Y\sim\mathcal{N}(0,\sigma^2)[/math]). On the right side, the black curve represents the cumulative distribution function of the r.v.'s [math]X_k[/math] and the red curve represents the cumulative distribution function of a Gaussian r.v. [math]Y[/math]. 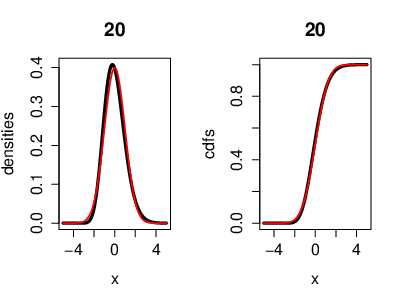
An illustration of the CLT, where the r.v.'s [math](X_n)[/math] are i.i.d. exponentially distributed. Also with the cumulative distribution functions. Here we have [math]n=20[/math] exponentially distributed r.v's [math]\left(X_k\sim \lambda e^{-\lambda}\right)[/math]. On the left side, the black curve represents the density function of the r.v.'s and the red curve represents the density of a Gaussian r.v. [math]Y[/math] with [math]\mu=0[/math] ([math]Y\sim\mathcal{N}(0,\sigma^2)[/math]). On the right side, the black curve represents the cumulative distribution function of the r.v.'s [math]X_k[/math] and the red curve represents the cumulative distribution function of a Gaussian r.v. [math]Y[/math]. Now we can see that both, the density and the cumulative distribution function, are converging to a Gaussian density and a Gaussian cumulative distribution function for [math]n\to\infty[/math]. Theorem (Erdös-Kac)Let [math]N_n[/math] be a r.v. with uniformly distribution in [math]\{1,...,n\}[/math], then
[[math]] \frac{W(N_n)-\log\log n}{\sqrt{\log\log n}}\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,1), [[/math]]where [math]W(n)=\sum_{p\leq n\atop p\in\mathcal{P}}\one_{p|n}[/math]. - Suppose that [math](X_n)_{n\geq 1}[/math] are i.i.d. r.v.'s with distribution function [math]F(x)=\p[X_1\leq x][/math]. Let [math]Y_n(x)=\one_{X_n\leq x}[/math], where [math](Y_n)_{n\geq 1}[/math] are i.i.d. Define [math]F_n(x)=\frac{1}{n}\sum_{k=1}^nY_k(x)=\frac{1}{n}\sum_{k=1}^n\one_{X_k\leq x}[/math]. [math]F_n[/math] is called the empirical distribution function. With the strong law of large numbers we get [math]\lim_{n\to\infty\atop a.s.}F_n(x)=\E[Y_1(x)][/math] and
[[math]] \E[Y_1(x)]=\E[\one_{X_1\leq x}]=\p[X_1\leq x]=F(x). [[/math]]In fact, it is a theorem (Gliwenko-Cantelli) which says that[[math]] \sup_{x\in\R}\vert F_n(x)-F(x)\vert\xrightarrow{n\to\infty\atop a.s.}0. [[/math]]Next we note that[[math]] \sqrt{n}(F_n(x)-F(x))=\sqrt{n}\left(\frac{1}{n}\sum_{k=1}^nY_k(x)-\E[Y_1(x)]\right)=\frac{1}{\sqrt{n}}\left(\sum_{k=1}^nY_k(x)-n\E[Y_1(x)]\right) [[/math]]Now with the central limit theorem we get[[math]] \sqrt{n}(F_n(x)-F(x))\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,\sigma^2(x)), [[/math]]where [math]\sigma^2(x)=Var(Y_1)=\E[Y_1^2(x)]=\E[Y_1(x)]=F(x)-F^2(x)=F(x)(1-F(x))[/math]. Hence[[math]] \sqrt{n}(F_n(x)-F(x))\xrightarrow{n\to\infty\atop law}\mathcal{N}(0,F(x)(1-F(x))). [[/math]]
Let [math](X_n)_{n\geq 1}[/math] be i.i.d. r.v's and suppose that [math]\E[\vert X_k\vert^3] \lt \infty[/math], [math]\forall k\in\{1,...,n\}[/math]. Let
where [math]\sigma^2=\E[X_k^2][/math] [math]\forall k\in\{1,...,n\}[/math] and [math]\Phi(x)=\p\left[\mathcal{N}(0,1)\leq x\right]=\int_{-\infty}^xe^{-\frac{u^2}{2}}\frac{1}{\sqrt{2\pi}}du[/math]. Then
General references
Moshayedi, Nima (2020). "Lectures on Probability Theory". arXiv:2010.16280 [math.PR].