guide:96d478d44f

[math] \newcommand{\varitem}[1]{\vspace{0.1cm}\hspace*{1cm}\raisebox{0.1cm}{ \tikz[baseline=(SebastianoItem.base),remember picture]{% \node[fill=green!20,inner sep=4pt,font=\sffamily] (SebastianoItem){#1};}\hspace{0.25cm} \vspace*{0.1cm}}} \newcommand{\SebastianoHighlight}{\tikz[overlay,remember picture]{% \fill[red!20] ([yshift=-20pt,xshift=-\pgflinewidth]SebastianoItem.east) -- ++(2pt,-2pt) -- ++(-2pt,-2pt) -- cycle; }} \newcommand{\rz}[1]{\displaystyle\stackrel{#1}{\phantom{.}}} % to raise exponent just a bit \newcommand{\CC}{C\nolinebreak\hspace{-.05em}\raisebox{.4ex}{\tiny\bf +}\nolinebreak\hspace{-.10em}\raisebox{.4ex}{\tiny\bf +}} \newcommand{\bm}[1]{\boldsymbol{#1}} \newcommand{\sectionbreak}{\clearpage} \newcommand\pythonstyle{\lstset{ language=Python, basicstyle=\ttm, otherkeywords={self},  % Add keywords here keywordstyle=\ttb\color{deepblue}, emph={MyClass,__init__},  % Custom highlighting emphstyle=\ttb\color{deepred},  % Custom highlighting style stringstyle=\color{deepgreen}, frame=tb,  % Any extra options here showstringspaces=false  % }} \newcommand\pythoninline[1]{{\pythonstyle\lstinline!#1!}} \DeclareMathOperator{\sign}{sign} \newcommand{\mathds}{\mathbb}[/math]

\label{sec:RL} In the previous sections, we have introduced data-based learning, where we are given a dataset [math]\{\bm{x}_i\}[/math] for training. Depending on whether we are given labels [math]y_i[/math] with each data point, we have further divided our learning task as either being supervised or unsupervised, respectively. The aim of machine learning is then to classify unseen data (supervised), or extract useful information from the data and generate new data resembling the data in the given dataset (unsupervised). However, the concept of learning as commonly understood certainly encompasses other forms of learning that are not falling into these data-driven categories. An example for a form of learning not obviously covered by supervised or unsupervised learning is learning how to walk: in particular, a child that learns how to walk does not first collect data on all possible ways of successfully walking to extract rules on how to walk best. Rather, the child performs an action, sees what happens, and then adjusts their actions accordingly. This kind of learning thus happens best ‘on-the-fly’, in other words while performing the attempted task. Reinforcement learning formalizes this different kind of learning and introduces suitable (computational) methods.

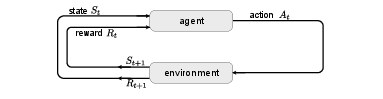
As we will explain in the following, the framework of reinforcement learning considers an agent, that interacts with an environment through actions, which, on the one hand, changes the state of the agent and on the other hand, leads to a reward. Whereas we tried to minimize a loss function in the previous sections, the main goal of reinforcement learning is to maximize this reward by learning an appropriate policy. One way of reformulating this task is to find a value function, which associates to each state (or state-action pair) a value, or expected total reward. Note that, importantly, to perform our learning task we do not require knowledge, a model, of the environment. All that is needed is feedback to our actions in the form of a reward signal and a new state. We stress again that we study in the following methods that learn at each time step. One could also devise methods, where an agent tries a policy many times and judges only the final outcome. The framework of reinforcement learning is very powerful and versatile. Examples include:

• We can train a robot to perform a task, such as using an arm to collect samples. The state of the agent is the position of the robot arm, the actions move the arm, and the agent receives a reward for each sample collected.
• We can use reinforcement learning to optimize experiments, such as chemical reactions. In this case, the state contains the experimental conditions, such as temperature, solvent composition, or pH and the actions are all possible ways of changing these state variables. The reward is a function of the yield, the purity, or the cost. Note that reinforcement learning can be used at several levels of this process: While one agent might be trained to target the experimental conditions directly, another agent could be trained to reach the target temperature by adjusting the current running through a heating element.
• We can train an agent to play a game, with the state being the current state of the game and a reward is received once for winning. The most famous example for such an agent is Google's AlphaGo, which outperforms humans in the game of Go. A possible way of applying reinforcement learning in the sciences is to phrase a problem as a game. An example, where such rephrasing was successfully applied, is error correction for (topological) quantum computers.
• In the following, we will use a toy example to illustrate the concepts introduced: We want to train an agent to help us with the plants in our lab: in particular, the state of the agent is the water level. The agent can turn on and off a growth lamp and it can send us a message if we need to show up to water the plants. Obviously, we would like to optimize the growth of the plants and not have them die.

As a full discussion of reinforcement learning goes well beyond the scope of this lecture, we will focus in the following on the main ideas and terminology with no claim of completeness.

Exploration versus exploitation

We begin our discussion with a simple example that demonstrates some important aspects of reinforcement learning. In particular, we discuss a situation, where the reward does not depend on a state, but only on the action taken. The agent is a doctor, who has to choose from [math]n[/math] actions, the treatments, for a given disease, with the reward depending on the recovery of the patient. The doctor ‘learns on the job’ and tries to find the best treatment. The value of a treatment [math]a\in\mathcal{A}[/math] is denoted by [math]q_* (a) = E( r ) [/math], the expectation value of our reward. Unfortunately, there is an uncertainty in the outcome of each treatment, such that it is not enough to perform each treatment just once to know the best one. Rather, only by performing a treatment many times we find a good estimate [math]Q_t(a) \approx q_*(a)[/math]. Here, [math]Q_t(a)[/math] is our estimate of the value of [math]a[/math] after [math]t[/math] (time-) steps. Obviously, we should not perform a bad treatment many times, only to have a better estimate for its failure. We could instead try each action once and then continue for the rest of the time with the action that performed best. This strategy is called a greedy method and exploits our knowledge of the system. Again, this strategy bears risks, as the uncertainty in the outcome of the treatment means that we might use a suboptimal treatment. It is thus crucial to explore other actions. This dilemma is called the ‘conflict between exploration and exploitation’. A common strategy is to use the best known action [math]a_* = {\rm argmax}_a Q_t(a)[/math] most of the time, but with probability [math]\epsilon[/math] chose randomly one of the other actions. This strategy of choosing the next action is called [math]\epsilon[/math]-greedy.

Finite Markov decision process

Markov decision process. Schematic of the agent-environment interaction.

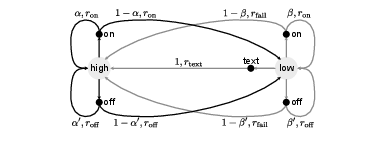
After this introductory example, we introduce the idealized form of reinforcement learning with a Markov decision process (MDP). At each time step [math]t[/math], the agent starts from a state [math]S_t\in \mathcal{S}[/math], performs an action [math]A_t\in\mathcal{A}[/math], which, through interaction with the environment, leads to a reward [math]R_{t+1}\in \mathcal{R}[/math] and moves the agent to a new state [math]S_{t+1}[/math]. This agent-environment interaction is schematically shown in Fig.~fig:mdp. Note that we assume the space of all actions, states, and rewards to be finite, such that we talk about a finite MDP. For our toy example, the sensor we have only shows whether the water level is high (h) or low (l), so that the state space of our agent is [math]\mathcal{S} = \{ {\rm h}, {\rm l} \}[/math]. In both cases, our agent can choose to turn the growth lamps on or off, or in the case of low water, he can choose to send us a message so we can go and water the plants. The available actions are thus [math]\mathcal{A} = \{{\rm on}, {\rm off}, {\rm text}\}[/math]. When the growth lamps are on, the plants grow faster, which leads to a bigger reward, [math]r_{\rm on} \gt r_{\rm off} \gt 0[/math]. Furthermore, there is a penalty for texting us, but an even bigger penalty for letting the plants die, [math]0 \gt r_{\rm text} \gt r_{\rm fail}[/math]. A model of the environment provides the probability of ending in state [math]s'[/math] with reward [math]r[/math], starting from a state [math]s[/math] and choosing the action [math]a[/math], [math]p(s', r | s, a)[/math]. In this case, the dynamics of the Markov decision process is completely characterized. Note that the process is a Markov process, since the next state and reward only depend on the current state and chosen action. In our toy example, being in state ‘high’ and having the growth lamp on will provide a reward of [math]r_{\rm on}[/math] and keep the agent in ‘high’ with probability [math]p({\rm h}, r_{\rm on} | \rm {h}, {\rm on}) = \alpha[/math], while with [math]1-\alpha[/math] the agent will end up with a low water level. However, if the agent turns the lamps off, the reward is [math]r_{\rm off}[/math] and the probability of staying in state ‘high’ is [math]\alpha' \gt \alpha[/math]. For the case of a low water level, the probability of staying in low despite the lamps on is [math]p({\rm l}, r_{\rm on} | \rm {l}, {\rm on}) = \beta[/math], which means that with probability [math]1 - \beta[/math], our plants run out of water. In this case, we will need to get new plants and we will water them , of course, such that [math]p({\rm h}, r_{\rm fail} | \rm {l}, {\rm on}) = 1-\beta[/math]. As with high water levels, turning the lamps off reduces our rewards, but increases our chance of not losing the plants, [math]\beta' \gt \beta[/math]. Finally, if the agent should choose to send us a text, we will refill the water, such that [math]p({\rm h}, r_{\rm text} | {\rm l}, {\rm text}) = 1[/math]. The whole Markov process is summarized in the transition graph in Fig.~fig:mdp_example. From the probability for the next reward and state, we can also calculate the expected reward starting from state [math]s[/math] and choosing action [math]a[/math], namely

[[math]] \begin{equation} r(s, a) = \sum_{r\in\mathcal{R}} r \sum_{s'\in\mathcal{S}} p(s', r | s, a). \end{equation} [[/math]]

Obviously, the value of an action now depends on the state the agent is in, such that we write [math]q_* (s, a)[/math]. Alternatively, we can also assign to each state a value [math]v_*(s)[/math], which quantizes the optimal reward from this state.

Transition graph of the MDP for the plant-watering agent. The states ‘high’ and ‘low’ are denoted with large circles, the actions with small black circles, and the arrows correspond to the probabilities and rewards.

Finally, we can define what we want to accomplish by learning: knowing our current state [math]s[/math], we want to know what action to choose such that our future total reward is maximized. Importantly, we want to accomplish this without any prior knowledge of how to optimize rewards directly. This poses yet another question: what is the total reward? We usually distinguish tasks with a well-defined end point [math]t=T[/math], so-called episodic tasks, from continuous tasks that go on for ever. The total reward for the former is simply the total return

[[math]] \begin{equation} G_t = R_{t+1} + R_{t+2} + R_{t+3} + \cdots + R_T. \end{equation} [[/math]]

As such a sum is not guaranteed to converge for a continuous task, the total reward is the discounted return

[[math]] \begin{equation} G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^\infty \gamma^k R_{t+k+1}, \label{eq:disc_return} \end{equation} [[/math]]

with [math]0 \leq \gamma \lt 1[/math] the discount rate. Equation~\eqref{eq:disc_return} is more general and can be used for an episodic task by setting [math]\gamma = 1[/math] and [math]R_t = 0[/math] for [math]t \gt T[/math]. Note that for rewards which are bound, this sum is guaranteed to converge to a finite value.

Policies and value functions

A policy [math]\pi(a | s)[/math] is the probability of choosing the action [math]a[/math] when in state [math]s[/math]. We can thus formulate our learning task as finding the policy that maximizes our reward and reinforcement learning as adapting an agent's policy as a result of its experience. For a given policy, we can define the value function of a state [math]s[/math] as the expected return from starting in that state and using the policy function [math]\pi[/math] for choosing all our future actions. We can write this as

[[math]] \begin{equation} v_\pi(s) \equiv E_\pi (G_t | S_t = s). \label{eq:value_function} \end{equation} [[/math]]

Alternatively, we can define the action-value function of [math]\pi[/math] as

[[math]] \begin{equation} q_\pi (s, a) \equiv E_\pi(G_t | S_t = s, A_t = a). \end{equation} [[/math]]

This is the expectation value for the return starting in state [math]s[/math] and choosing action [math]a[/math], but using the policy [math]\pi[/math] for all future actions. Note that one of the key ideas of reinforcement learning is to use such value functions, instead of the policy, to organize our learning process. The value function of Eq.~\eqref{eq:value_function} satisfies a self-consistency equation,

[[math]] \begin{align} v_\pi(s) &= E_\pi ( R_{t+1} + \gamma G_{t+1} | S_t = s)\label{eq:BE_expect}\\ &= \sum_a \pi(a | s) \sum_{s', r} p(s', r | s, a) [ r + \gamma v_\pi (s')]. \end{align} [[/math]]

This equation, known as the Bellman equation, relates the value of state [math]s[/math] to the expected reward and the (discounted) value of the next state after having chosen an action under the policy [math]\pi(a|s)[/math]. As an example, we can write the Bellman equation for the strategy of always leaving the lamps on in our toy model. Then, we find the system of linear equations

[[math]] \begin{align} v_{\rm on}({\rm h}) &= p({\rm h}, r_{\rm on} | {\rm h}, {\rm on}) [r_{\rm on} + \gamma v_{\rm on} ({\rm h})] + p({\rm l}, r_{\rm on} | {\rm h}, {\rm on}) [r_{\rm on} + \gamma v_{\rm on} ({\rm l})] \nonumber\\ & = r_{\rm on} + \gamma [\alpha v_{\rm on}({\rm h}) + (1-\alpha) v_{\rm on}({\rm l})],\\ v_{\rm on}({\rm l}) &= \beta[r_{\rm on} + \gamma v_{\rm on}({\rm l})] + (1-\beta) [r_{\rm fail} + \gamma v_{\rm on}({\rm h})], \end{align} [[/math]]

from which we can solve easily for [math]v_{\rm on}({\rm h})[/math] and [math]v_{\rm on}({\rm l})[/math]. Instead of calculating the value function for all possible policies, we can directly try and find the optimal policy [math]\pi_*[/math], for which [math]v_{\pi_*}(s) \gt v_{\pi'}(s)[/math] for all policies [math]\pi'[/math] and [math]s\in\mathcal{S}[/math]. For this policy, we find the Bellman optimality equations

[[math]] \begin{align} v_*(s) &= \max_a q_{\pi_*}(s, a)\nonumber\\ &= \max_a E(R_{t+1} + \gamma v_*(S_{t+1}) | S_t = s, A_t = a)\label{eq:bellman-optimality-1a}\\ &=\max_a \sum_{s', r} p(s', r | s, a) [ r + \gamma v_* (s')]. \label{eq:bellman-optimality-1b} \end{align} [[/math]]

Importantly, the Bellman optimality equations do not depend on the actual policy anymore. As such, Eq.~\eqref{eq:bellman-optimality-1b} defines a non-linear system of equations, which for a sufficiently simple MDP can be solved explicitly. For our toy example, the two equations for the value functions are

[[math]] \begin{equation} v_*({\rm h}) = \max \left\{\begin{array}{l} r_{\rm on} + \gamma [\alpha v_*({\rm h}) + (1-\alpha) v_*({\rm l})] \\ r_{\rm off} + \gamma [\alpha' v_*({\rm h}) + (1-\alpha') v_*({\rm l})] \end{array}\right. \end{equation} [[/math]]

and

[[math]] \begin{equation} v_*({\rm l}) = \max \left\{\begin{array}{l} \beta[r_{\rm on} + \gamma v_*({\rm l})] + (1-\beta) [r_{\rm fail} + \gamma v_*({\rm h})] \\ \beta'[r_{\rm off} + \gamma v_*({\rm l})] + (1-\beta') [r_{\rm fail} + \gamma v_*({\rm h})]\\ r_{\rm text} + \gamma v_*({\rm h})\end{array}\right. . \end{equation} [[/math]]

Note that equivalent equations to Eqs.~\eqref{eq:bellman-optimality-1a} and \eqref{eq:bellman-optimality-1b} hold for the state-action value function

[[math]] \begin{align} q_*(s, a) &= E(R_{t+1} + \gamma \max_{a'} q_*(S_{t+1},a'))\\ &= \sum_{s', r} p(s', r | s, a) [ r + \gamma \max_{a'} q_* (s', a')]. \label{eq:bellman-optimality-2} \end{align} [[/math]]

Once we know [math]v_*[/math], the optimal policy [math]\pi_* (a| s)[/math] is the greedy policy that chooses the action [math]a[/math] that maximizes the right-hand side of Eq.~\eqref{eq:bellman-optimality-1b}. If, instead, we know [math]q_*(s,a)[/math], then we can directly choose the action which maximizes [math]q_*(s,a)[/math], namely [math]\pi_*(a | s) = {\rm argmax}_{a'} q_*(s, a')[/math], without looking one step ahead. While Eqs~\eqref{eq:bellman-optimality-1b} or \eqref{eq:bellman-optimality-2} can be solved explicitly for a sufficiently simple system, such an approach, which corresponds to an exhaustive search, is often not feasible. In the following, we distinguish two levels of complexity: First, if the explicit solution is too hard, but we can still keep track of all possible value functions---we can choose either the state or the state-action value function---we can use a tabular approach. A main difficulty in this case is the evaluation of a policy, or prediction, which is needed to improve on the policy. While various methods for policy evaluation and policy improvement exist, we will discuss in the following an approach called temporal-difference learning. Second, in many cases the space of possible states is much too large to allow for a complete knowledge of all value functions. In this case, we additionally need to approximate the value functions. For this purpose, we can use the methods encountered in the previous chapters, such as (deep) neural networks.

Temporal-difference learning

If we cannot explicitly solve the Bellman optimality equations---the case most often encountered---then we need to find the optimal policy by some other means. If the state space is still small enough to keep track of all value functions, we can tabulate the value function for all the states and a given policy and thus, speak of tabular methods. The most straight-forward approach, referred to as policy iteration, proceeds in two steps: First, given a policy [math]\pi(a|s)[/math], the value function [math]v_{\pi}(s)[/math] is evaluated. Second, after this policy evaluation, we can improve on the given policy [math]\pi(a|s)[/math] using the greedy policy

[[math]] \begin{equation} \pi'(a|s) = {\rm argmax}_a \sum_{s', r} p(s', r| s, a) [r + \gamma v_\pi(s')]. \label{eq:greedy_improvement} \end{equation} [[/math]]

This second step is called policy improvement. The full policy iteration then proceeds iteratively

[[math]] \begin{equation} \pi_0 \rightarrow v_{\pi_0} \rightarrow \pi_1 \rightarrow v_{\pi_1} \rightarrow \pi_2 \rightarrow \cdots \end{equation} [[/math]]

until convergence to [math]v_*[/math] and hence [math]\pi_*[/math]. Note that, indeed, the Bellman optimality equation~\eqref{eq:bellman-optimality-1b} is the fixed-point equation for this procedure. Policy iteration requires a full evaluation of the value function of [math]\pi_k[/math] for every iteration [math]k[/math], which is usually a costly calculation. Instead of fully evaluating the value function under a fixed policy, we can also directly try and calculate the optimal value function by iteratively solving the Bellman optimality equation,

[[math]] \begin{equation} v^{[k+1]} (s) = \max_a \sum_{s', r} p(s', r| s, a) [r + \gamma v^{[k]}(s')]. \end{equation} [[/math]]

Note that once we have converged to the optimal value function, the optimal policy is given by the greedy policy corresponding to the right-hand side of Eq.~\eqref{eq:greedy_improvement} An alternative way of interpreting this iterative procedure is to perform policy improvement every time we update the value function, instead of finishing the policy evaluation each time before policy improvement. This procedure is called value iteration and is an example of a generalized policy iteration, the idea of allowing policy evaluation and policy improvement to interact while learning. In the following, we want to use such a generalized policy iteration scheme for the (common) case, where we do not have a model for our environment. In this model-free case, we have to perform the (generalized) policy improvement using only our interactions with the environment. It is instructive to first think about how to evaluate a policy. We have seen in Eqs.~\eqref{eq:value_function} and \eqref{eq:BE_expect} that the value function can also be written as an expectation value,

[[math]] \begin{align} v_{\pi} (s) &= E_\pi (G_t | S_t = s)\\ &= E_\pi (R_{t+1} + \gamma v_{\pi}(S_{t+1})| S_t = s).\label{eq:policy_evaluation} \end{align} [[/math]]

We can thus either try to directly sample the expectation value of the first line---this can be done using Monte Carlo sampling over possible state-action sequences---or we try to use the second line to iteratively solve for the value function. In both cases, we start from state [math]S_t[/math] and choose an action [math]A_t[/math] according to the policy we want to evaluate. The agent's interaction with the environment results in the reward [math]R_{t+1}[/math] and the new state [math]S_{t+1}[/math]. Using the second line, Eq.~\eqref{eq:policy_evaluation}, goes under the name temporal-difference learning and is in many cases the most efficient method. In particular, we make the following updates

[[math]] \begin{equation} v_\pi^{[k+1]} (S_t) = v_\pi^{[k]}(S_t) + \alpha [R_{t+1} + \gamma v_\pi^{[k]} (S_{t+1}) - v_\pi^{[k]} (S_{t}) ]. \label{eq:policy_evaluation_modelfree} \end{equation} [[/math]]

The expression in the brackets is the difference between our new estimate and the old estimate of the value function and [math]\alpha \lt 1[/math] is a learning rate. As we look one step ahead for our new estimate, the method is called one-step temporal difference method. We now want to use generalized policy iteration to find the optimal value. We already encountered a major difficulty when improving a policy using a value function based on experience in Sec.~sec:expl_v_expl: it is difficult to maintain enough exploration over possible action-state pairs and not end up exploiting the current knowledge. However, this sampling is crucial for both Monte Carlo methods and the temporal-difference learning we discuss here. In the following, we will discuss two different methods of performing the updates, both working on the state-action value function, instead of the value function. Both have in common that we look one step ahead to update the state-action value function. A general update should then be of the form

[[math]] \begin{equation} q^{[k+1]} (S_t, a) = q^{[k]}(S_t, a) + \alpha [R_{t+1} + \gamma q^{[k]} (S_{t+1}, a') - q^{[k]} (S_{t}, a) ] \end{equation} [[/math]]

and the question is then what action [math]a[/math] we should take for the state-action pair and what action [math]a'[/math] should be taken in the new state [math]S_{t+1}[/math]. Starting from a state [math]S_0[/math], we first choose an action [math]A_0[/math] according to a policy derived from the current estimate of the state-action value function~, such as an [math]\epsilon[/math]-greedy policy. For the first approach, we perform updates as

[[math]] \begin{equation} q^{[k+1]} (S_t, A_t) = q^{[k]}(S_t, A_t) + \alpha [R_{t+1} + \gamma q^{[k]} (S_{t+1}, A_{t+1}) - q^{[k]} (S_{t}, A_t) ]. \end{equation} [[/math]]

As above, we are provided a reward [math]R_{t+1}[/math] and a new state [math]S_{t+1}[/math] through our interaction with the environment. To choose the action [math]A_{t+1}[/math], we again use a policy derived from [math]Q^{[k]}(s=S_{t+1}, a)[/math]. Since we are using the policy for choosing the action in the next state [math]S_{t+1}[/math], this approach is called on-policy. Further, since in this particular case, we use the quintuple [math]S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}[/math], this algorithm is referred to as Sarsa. Finally, note that for the next step, we use [math]S_{t+1}, A_{t+1}[/math] as the state-action pair for which [math]q^{[k]}(s,a)[/math] is updated. Alternatively, we only keep the state [math]S_t[/math] from the last step and first choose the action [math]A_t[/math] for the update using the current policy. Then, we choose our action from state [math]S_{t+1}[/math] in greedy fashion, which effectively uses [math]Q^{[k]}(s=S_t, a)[/math] as an approximation for [math]q_*(s=S_t, a)[/math]. This leads to

[[math]] \begin{equation} q^{[k+1]} (S_t, A_t) = q^{[k]}(S_t, A_t) + \alpha [R_{t+1} + \gamma \max_a q^{[k]} (S_{t+1}, a) - q^{[k]} (S_{t}, A_t) ]. \end{equation} [[/math]]

and is a so-called off-policy approach. The algorithm, a variant of which is used in AlphaGo, is called Q-learning.

Function approximation

When the state-action space becomes very large, we face two problems: First, we can not use tabular methods anymore, since we can not store all values. Second and more important, even if we could store all the values, the probability of visiting all state-action pairs with the above algorithms becomes increasingly unlikely, in other words most states will never be visited during training. Ideally, we should thus identify states that are ‘similar’, assign them ‘similar’ value, and choose ‘similar’ actions when in these states. This grouping of similar states is exactly the kind of generalization we tried to achieve in the previous sections. Not surprisingly, reinforcement learning is most successful when combined with neural networks. In particular, we can parametrize a value function [math]\hat{v}_\pi(s; \theta)[/math] and try to find parameters [math]\theta[/math] such that [math]\hat{v}_\pi(s; \theta) \approx v_\pi(s)[/math]. This approximation can be done using the supervised-learning methods encountered in the previous sections, where the target, or label, is given by the new estimate. In particular, we can use the mean squared value error to formulate a gradient descent method for an update procedure analogous to Eq.~\eqref{eq:policy_evaluation_modelfree}. Starting from a state [math]S[/math] and choosing an action [math]A[/math] according to the policy [math]\pi(a|S)[/math], we update the parameters

[[math]] \begin{equation} \theta^{[k+1]} = \theta^{[k]} + \alpha [R +\gamma \hat{v}_\pi(S'; \theta^{[k]}) - \hat{v}_\pi(S; \theta^{[k]}) ] \nabla \hat{v}_\pi (S;\theta^{[k]}) \end{equation} [[/math]]

with [math]0 \lt \alpha \lt 1[/math] again the learning rate. Note that, even though the new estimate also depends on [math]\theta^{[k]}[/math], we only take the derivative with respect to the old estimate. This method is thus referred to as semi-gradient method. In an similar fashion, we can reformulate the Sarsa algorithm introduced for generalized gradient iteration.

General references

Neupert, Titus; Fischer, Mark H; Greplova, Eliska; Choo, Kenny; Denner, M. Michael (2022). "Introduction to Machine Learning for the Sciences". arXiv:2102.04883 [physics.comp-ph].