Overview

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

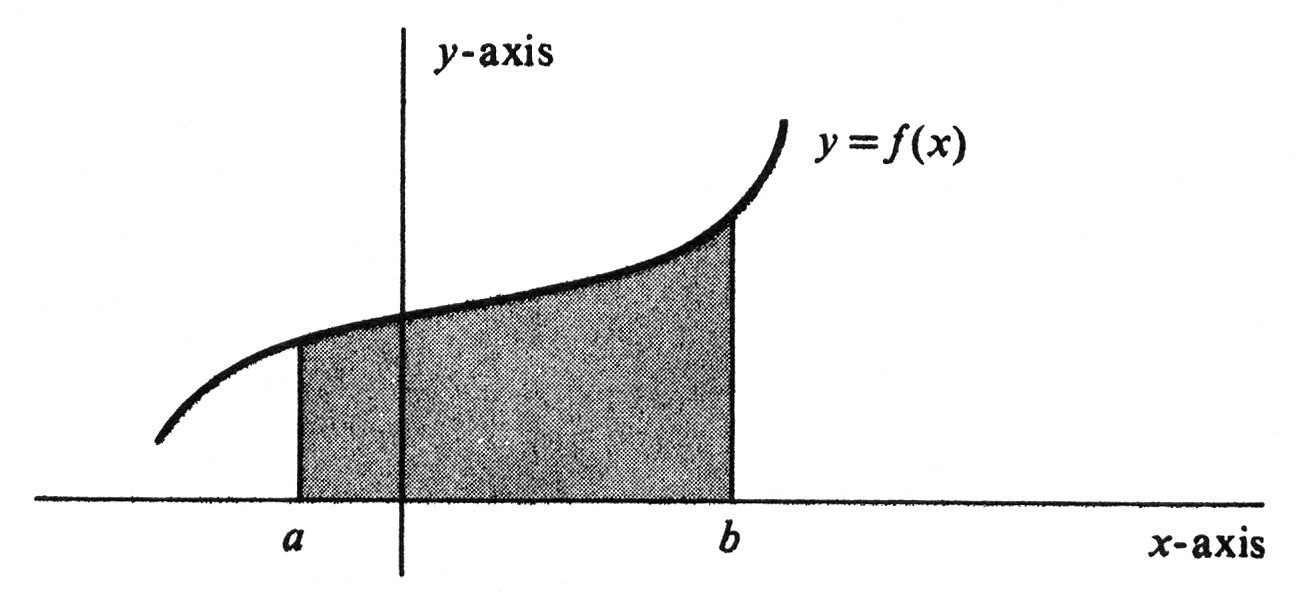
\chapter{Integration}\label{chp 4} There are two major topics in calculus, differentiation and integration. The theory of integration at first appears to have little connection with differentiation. However, we shall see that the two processes are indeed closely related. Differentiation deals with derivatives of real-valued functions, integration with integrals of real-valued functions defined on closed intervals. In this chapter we shall define and study the definite integral from [math]a[/math] to [math]b[/math] of a real-valued function [math]f[/math], which is denoted by [math]\int_{a}^{b} f[/math]. The integral has countless applications both in mathematics and the sciences. One of the most important enables us to find the area of a region more involved than those studied in plane geometry. If [math]f(x) \geq 0[/math] for every [math]x[/math] in [math][a, b][/math], then we shall see that [math]\int_{a}^{b} f[/math] is equal to the area of the region lying above the [math]x[/math]-axis, below the graph of [math]f[/math], and between the vertical lines [math]x = a[/math] and [math]x = b[/math] (see Figure). Thus the areas of many irregularly shaped regions can be found by integration.

File:Guide c5467 scanfig4 1.png

Another interesting application enables us to find the distance traveled by a particle which moves in a straight line. If the particle moves with a velocity equal to [math]v(t)[/math] at time [math]t[/math], then the distance travelbed during the interval of time from [math]t = a[/math] to [math]t = b[/math] is given by the integral [math]\int_{a}^{b} |v|[/math]. It will be useful to recall some of the elementary ideas and notations of set theory. In particular, the union of two sets [math]P[/math] and [math]Q[/math], denoted by [math]P \cup Q[/math], is the set of elements that belong either to [math]P[/math], or to [math]Q[/math], or to both. The intersection of [math]P[/math] and [math]Q[/math], denoted by [math]P \cap Q[/math], is the set of elements that belong to both [math]P[/math] and [math]Q[/math]. If [math]P[/math] and [math]Q[/math] have no points in common, they are said to be disjoint. The set which contains no elements is called the empty set and will be denoted by [math]\phi[/math]. Thus [math]P[/math] and [math]Q[/math] are disjoint if and only if [math]P \cap Q = \phi[/math]. Finally, the difference, [math]P - Q[/math], is the set of all elements of [math]P[/math] which do not belong to [math]Q[/math].

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.