The Complex Exponential Function $e^{z}$

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

Consider the function [math]\varphi[/math] defined by

[[math]] \varphi(x) = \cos x + i \sin x, [[/math]]

for every real number [math]x[/math]. This is a complex-valued function of a real variable. The domain of [math]\varphi[/math] is the set [math]R[/math] of all real numbers. For every real number [math]x[/math], we have

[[math]] |\varphi(x)| = \sqrt{\cos^{2}x + \sin^{2}x} = \sqrt{1} = 1. [[/math]]

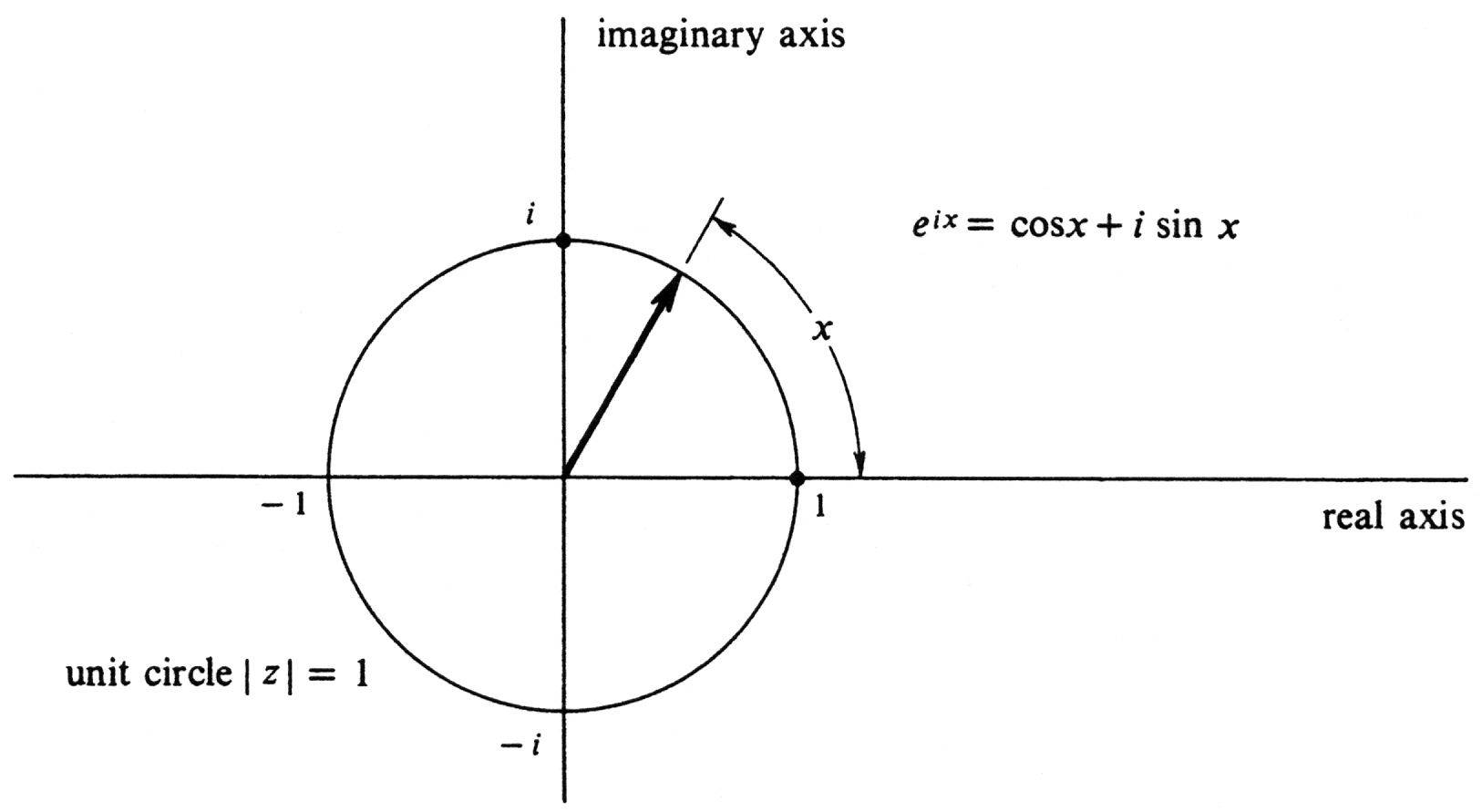
It follows that [math]\varphi (x)[/math] is a point on the unit circle in the complex plane, i.e., the circle with center at the origin and radius 1. Conversely, every point on the unit circle is equal to [math](\cos x, \sin x)[/math], for some real number [math]x[/math], and we know that [math](\cos x, \sin x) = \cos x + i \sin x[/math]. It follows that the range of [math]\varphi[/math] is the unit circle. The function [math]\varphi[/math] has the following properties:

Theorem

[[math]] \begin{array}{lrcl} \mathrm{( 7.1 )}& \varphi (0) &=& 1. \\ \mathrm{( 7.2 )}& \varphi (a) \varphi (b) &=& \varphi (a + b).\\ \mathrm{( 7.3 )}& \frac{\varphi (a)}{\varphi (b)} &=& \varphi (a - b).\\ \mathrm{( 7.4 )}& \varphi( -a) &=& \frac{1}{\varphi (a)}. \end{array} [[/math]]

Show Proof

The proofs are completely straightforward. Thus (7.1) follows from the equations

[[math]] \varphi(0) = \cos 0 + i \sin 0 = \cos 0 = 1. [[/math]]

To prove (7.2), we write

[[math]] \begin{eqnarray*} \varphi (a) \varphi (b) &=& (\cos a + i \sin a)(\cos b + i \sin b)\\ &=& \cos a \cos b - \sin a \sin b + i(\sin a \cos b + \cos a \sin b). \end{eqnarray*} [[/math]]

The trigonometric identities for the cosine and sine of the sum of two numbers then imply that

[[math]] \varphi (a) \varphi (b) = \cos(a + b) + i \sin(a + b), [[/math]]

and the right side is by definition equal to [math]\varphi (a + b)[/math]. Thus (7.2) is proved. As a special case of (7.2), we have

[[math]] \varphi (a - b) \varphi (b) = \varphi (a - b + b) = \varphi (a). [[/math]]

On dividing by [math]\varphi(b)[/math], which is never zero, we get (7.3). The last result, (7.4), is obtained by taking [math]a = 0[/math] in (7.3) and then substituting 1 for [math]\varphi (0)[/math] in accordance with (7.1). Thus

[[math]] \begin{eqnarray*} \frac{\varphi (0)}{\varphi (b)} &=& \varphi (0 - b),\\ \frac{1}{\varphi (b)} &=& \varphi (-b). \end{eqnarray*} [[/math]]

■

The above four properties of [math]\varphi[/math] are also shared by the real-valued exponential function [math]\exp[/math] [we recall that [math]\exp(x) = e^{x}[/math]]. This fact suggests the possibility of extending the domain and range of [math]\exp[/math] into the complex plane. That is, it suggests that the functions [math]\varphi[/math] and [math]\exp[/math] can be combined to give a complex-valued exponential function of a complex variable which will have the property that when its domain is restricted to the real numbers, it is simply [math]\exp[/math]. We define such a function now. For every complex number [math]z = x + iy[/math], let [math]\mbox{Exp}[/math] be the function defined by

[[math]] \mbox{Exp}(z) = \exp(x) \varphi(y). [[/math]]

Thus

[[math]] \mbox{Exp}(z) = e^{x}(\cos y + i \sin y). [[/math]]

If [math]z = x + i0[/math], then [math]z = x[/math] and [math]\mbox{Exp}(z) = \exp(x) \varphi (0) = \exp(x)[/math]. Hence the function $\mbox{Exp}$ is an extension of the function $\exp$. It is a routine matter to show that the function [math]\mbox{Exp}[/math] has the exponential properties listed above for [math]\varphi[/math]. Following the practice for the real-valued exponential, we shall write [math]\mbox{Exp}(z)[/math] as [math]e^z[/math]. In this notation therefore, if [math]z = x + iy[/math], the definition reads

[[math]] e^z = e^{x}(\cos y + i \sin y). [[/math]]

The exponential properties are

Theorem

[[math]] \begin{array}{lrcl} \mathrm{( 7.1')}& e^0 &=& 1. \\ \mathrm{( 7.2')}& e^{z_{1}}e^{z_{2}} &=& e^{z_{1} + z_{2}}.\\ \mathrm{( 7.3')}& \frac{e^{z_1}}{e^{z_2}} &=& e^{z_{1} - z_{2}}.\\ \mathrm{( 7.4')}& \frac{1}{e^z} &=& e^{-z}. \end{array} [[/math]]

Show Proof

The proofs simply use the fact that the functions [math]\exp[/math] and [math]e^z[/math] separately have these properties. Thus

[[math]] e^0 = e^{0+i0} = \exp(0) \varphi(0) = 1 \cdot 1 = 1. [[/math]]

Letting [math]z_{1} = x_{1} + iy_{1}[/math] and [math]z_{2} = x_{2} + iy_{2}[/math], we have

[[math]] \begin{eqnarray*} e^{z_{1}}e^{z_{2}} &=& \exp(x_{1}) \varphi (y_{1}) \exp(x_{2})\varphi(y_{2})\\ &=& \exp(x_{1} + x_{2}) \varphi (y_{1} + y_{2}). \end{eqnarray*} [[/math]]

Since [math]z_{1} + z_{2} = (x_{1} + x_{2}) + i(y_{1} + y_{2})[/math], the right side is by definition equal to [math]\mbox{Exp}(z_{1} + z_{2})[/math], which is [math]e^{z_{1}+z_2}[/math]. The last two propositions, (7.3') and (7.4'), are corollaries of (7.1') and (7.2') in exactly the same way that (7.3) and (7.4) follow from (7.1) and (7.2).

■

If [math]x[/math] is an arbitrary real number, then

[[math]] e^{ix} = e^{0+ix} = e^{0}(\cos x + i \sin x). [[/math]]

Thus we have the equation

Theorem

[[math]] e^{ix} = \cos x + i \sin x, \;\;\;\mathrm{for~every~real~number}\; x. [[/math]]

File:Guide c5467 scanfig6 20.png

Thus if [math]x[/math] is any real number, the complex number [math]e^{ix}[/math] is the ordered pair [math](\cos x, \sin x)[/math]. Hence [math]e^{ix}[/math] is the point on the unit circle obtained by starting at the complex number 1 and measuring along the circle at a distance equal to the absolute value of [math]x[/math], measuring in the counterclockwise direction if [math]x[/math] is positive and in the clockwise direction if it is negative (see Figure 20). In terms of angle, [math]x[/math] is the radian measure of the angle whose initial side is the positive half of the real axis and whose terminal side contains the arrow representing [math]z[/math]. Letting [math]x = \pi[/math] in (7.5), we get [math]e^{i\pi} = \cos \pi + i \sin \pi[/math]. Since [math]\cos \pi = -1[/math] and [math]\sin \pi = 0[/math], it follows that [math]e^{i\pi} = - 1[/math], which is equivalent to the equation

[[math]] e^{i \pi} + 1 = 0 . [[/math]]

This equation is most famous since it combines in a simple formula the three special numbers [math]\pi[/math], [math]e[/math], and [math]i[/math] with the additive and multiplicative identities 0 and 1. One of the most important features of the complex exponential function is that it provides an alternative way of writing complex numbers. We have

Theorem

Every complex number [math]z[/math] can be written in the form [math]z = |z| e^{it}[/math], for some real number [math]t[/math]. Furthermore, if [math]z = x + iy[/math] and [math]z \neq 0[/math], then [math]z = |z| e^{it}[/math] if and only if [math]\cos t = \frac{x}{|z|}[/math] and [math]\sin t = \frac{y}{|z|}[/math].

Show Proof

If [math]z = 0[/math], then [math]|z| = 0[/math], and so [math]0 = z = |z|e^{it}[/math], for every real number [math]t[/math]. Next we suppose that [math]z \neq 0[/math]. Then [math]|z| \neq 0[/math], and [math]\frac{z}{|z|}[/math] is defined and lies on the unit circle because

[[math]] | \frac{z}{ |z|} | = \frac{|z|}{|z|} =1. [[/math]]

Hence there exists a real number [math]t[/math] such that [math]\frac{z}{|z|} = e^{it}[/math], and this proves the first statement in the theorem. Suppose that [math]z = x + iy[/math] and that [math]z \neq 0[/math]. If [math]z = |z|e^{it}[/math], then

[[math]] x + iy = |z|e^{it} = |z|(\cos t + i \sin t). [[/math]]

Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Hence [math]x = |z| \cos t[/math] and [math]y =|z| \sin t[/math]. Since [math]|z| \neq 0[/math], we conclude that [math]\cos t = \frac{x}{|z|}[/math] and [math]\sin t = \frac{y}{|z|}[/math] . Conversely, if we start from the last two equations, it follows that

[[math]] x + iy = |z|(\cos t + i \sin t). [[/math]]

The left side is equal to [math]z[/math], and the right side to [math]|z|e^{it}[/math]. This completes the proof of the theorem.

■

A complex number written as [math]z = |z| e^{it}[/math] is said to be in exponential form. The number [math]|z|[/math] is, of course, the absolute value of [math]z[/math], and the number [math]t[/math] is called the angle, or argument, of [math]z[/math]. The latter is not uniquely determined by [math]z[/math]. Since the trigonometric functions [math]\sin[/math] and [math]\cos[/math] have period [math]2\pi[/math], it follows that

[[math]] z = |z|e^{it} = |z|e^{i(t +2\pi n)}, [[/math]]

for every integer [math]n[/math]. Consider two complex numbers written in exponential form:

[[math]] z_{1} = |z_1| e^{it_1} \;\;\; \mbox{and} \;\;\; z_{2} = |z_{2}| e^{it_{2}}. [[/math]]

The product and ratio are given by

[[math]] z_{1}z_{2} = |z_1| |z_2| e^{it_1} e^{it_2}, \;\;\; \frac{z_1}{z_2} = \frac{|z_1|}{z_2} \frac{e^{it_1}}{e^{it_2}}. [[/math]]

Hence by formulas (7.2') and (7.3') for the product and ratio of exponentials, we have

[[math]] z_{1}z_{2} = |z_{1}| |z_{2}| e^{i (t_{1} + t_{2})},\;\;\; \frac{ z_{1}}{z_{2}} = e^{i (t_{1} - t_{2})}. [[/math]]

That is, two complex numbers are multiplied by multiplying their absolute values and adding their angles. They are divided by dividing their absolute values and subtracting their angles.

Example

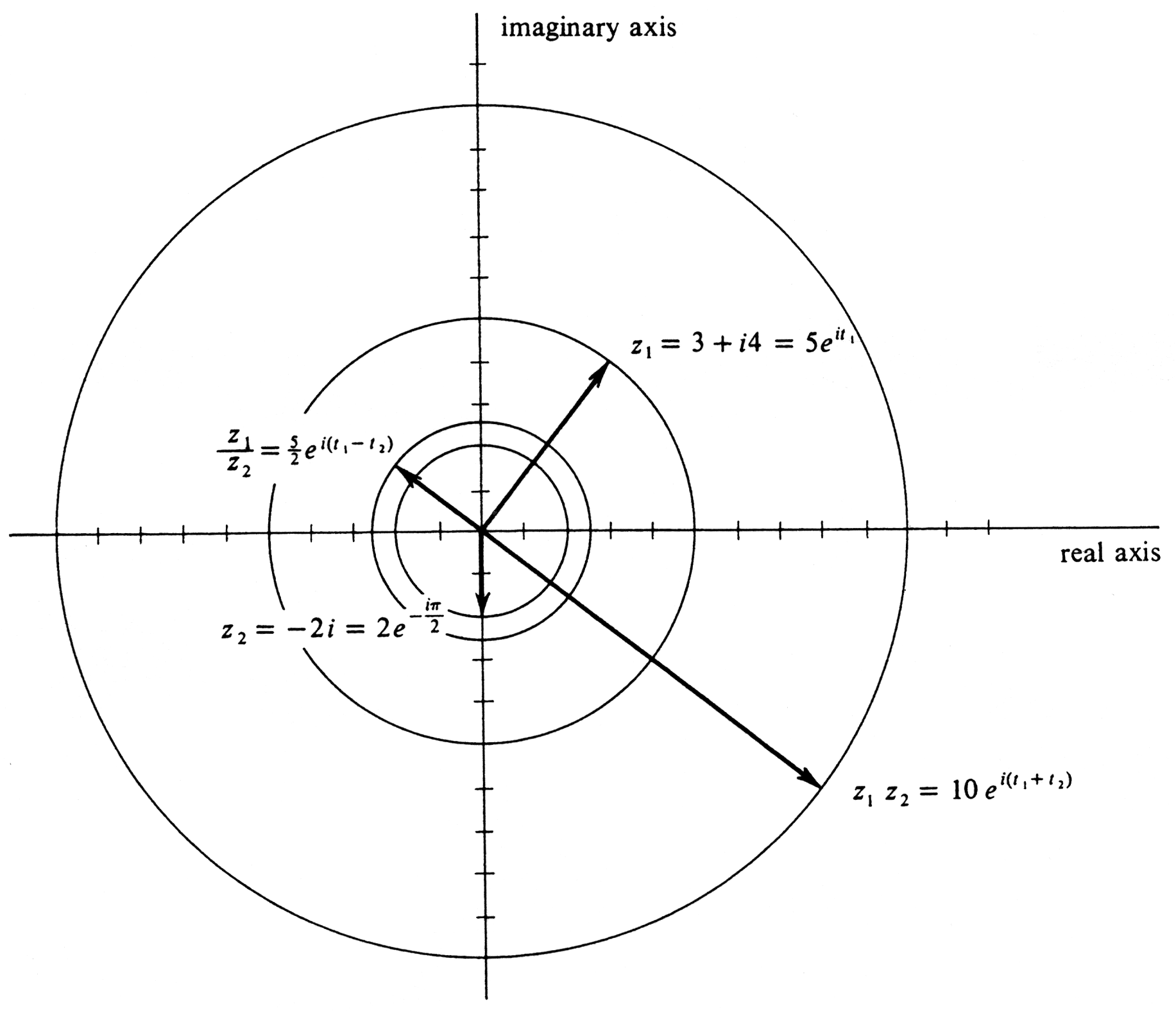
Let [math]z_{1} = 3 + i4[/math] and [math]z_{2} = -2i[/math]. Express [math]z_{1}, z_{2}, z_{1}z_{2}[/math], and [math]\frac{z_{1}}{z_{2}}[/math] in the exponential form [math]|z| e^{it}[/math], and plot the resulting arrows in the complex plane. To begin with,

[[math]] \begin{eqnarray*} |z_{1}| &=& \sqrt{3^2 + 4^2} = 5,\\ |z_{2}| &=& \sqrt{0^2 + (-2)^2} = 2. \end{eqnarray*} [[/math]]

We next seek a real number [math]t_{1}[/math] such that [math]\cos t_{1} = \frac{3}{5}[/math] and [math]\sin t_{1} = \frac{4}{5}[/math], and also a number [math]t_{2}[/math] such that [math]\cos t_{2} = 0[/math] and [math]\sin t_{2} = - 1[/math]. These are given by

[[math]] \begin{eqnarray*} t_{1} &=& \arccos \frac{3}{5} = 0.93 \;\mbox{(approximately),} \\ t_{2} &=& \arcsin(-1) = - \frac{\pi}{2}. \end{eqnarray*} [[/math]]

Then

[[math]] \begin{eqnarray*} z_{1} &=& |z_{1}| e^{it_{1}} = 5e^{i(0.93)},\\ z_{2} &=& |z_{2}| e^{it_{2}} = 2e^{-i(\pi/2)}. \end{eqnarray*} [[/math]]

Since [math]t_{1} + t_{2} = 0.93 - \frac{\pi}{2} = - 0.64[/math] (approximately) and [math]t_{1} - t_{2} = 0.93 - \Bigl(-\frac{\pi}{2}\Bigr) = 2.50[/math] (approximately), we obtain

[[math]] \begin{eqnarray*} z_{1}z_{2} &=& |z_{1}| |z_{2}| e^{i(t_{1} + t_{2})} = 10 e^{-i(0.64)}, \\ \frac{z_1}{z_2} &=& \frac{|z_1|}{|z_2|} e^{i(t_{1} - t_{2})} = \frac{5}{2} e^{i(2.50)} . \end{eqnarray*} [[/math]]

File:Guide c5467 scanfig6 21.png

The arrows representing [math]z_{1}, z_{2}, z_{1}z_{2}[/math] and [math]\frac{z_{1}}{z_{2}}[/math] are shown in Figure 21. To locate these numbers geometrically using a ruler and protractor marked off in degrees, we would compute

[[math]] \begin{eqnarray*} t_{1} &=& 0.93 \;\;\mbox{radian} = 53 \;\mbox{degrees}, \\ t_{2} &=& - \frac{\pi}{2} \; \;\mbox{radians} = - 90 \; \;\mbox{degrees},\\ t_{1} + t_{2} &=& - 0.64 \;\;\mbox{radian} = - 37 \; \;\mbox{degrees},\\ t_{1} - t_{2} &=& 2.50 \;\;\mbox{radians} = 143 \; \;\mbox{degrees}. \end{eqnarray*} [[/math]]

Of course, we can find the real and imaginary parts of [math]z_{1}z_{2}[/math] and [math]\frac{z_{1}}{z_{2}}[/math] by the computations

[[math]] \begin{eqnarray*} z_{1}z_{2} &=& (3 + i4)(-2i) = 8 - i6, \\ \frac{z_{1}}{z_{2}} &=& \frac{ 3 + i4}{-2i} = \frac{ 3 + i4}{- 2i} \frac{2i}{2i} = \frac{-8 + i6}{4} = -2 + i \frac{3}{2} . \end{eqnarray*} [[/math]]

If [math]z[/math] is a complex number, then [math]z^n[/math] can be defined inductively, for every nonnegative integer [math]n[/math], by

[[math]] \begin{equation} z^0 = 1, \label{eq6.7.1} \end{equation} [[/math]]

[[math]] \begin{equation} z^n = z(z^{n - 1}),\;\;\;\mbox{for}\; n \gt 0. \label{eq6.7.2} \end{equation} [[/math]]

Another useful property of the complex exponential function is

Theorem

[[math]] (e^z)^n = e^{nz}, \;\;\;\mbox{for every nonnegative integer}\; n. [[/math]]

Show Proof

By induction. If [math]n = 0[/math], then [math](e^z)^n = (e^z)^0[/math]. Since [math]e^z[/math] is a complex number, [math](e^z)^0 = 1[/math], by equation (1). Moreover, in this case, [math]e^{nz} = e^{0z} = 1[/math], by (7.1'). Next suppose that [math]n \gt 0[/math]. By equation (2), we have [math](e^z)^n = e^{z}(e^z)^{n-1}[/math], and by hypothesis of induction [math](e^z)^{n-1} = e^{(n-1)z} = e^{(n - 1)z}[/math]. Hence, by (7.2'),

[[math]] (e^z)^n = e^{z}e^{(n-1)z} = e^{z+(n-1)z}, [[/math]]

and, since [math]z + (n - 1)z = nz[/math], the proof is finished.

■

Let [math]z[/math] be a complex number and [math]n[/math] a positive integer. A complex number [math]w[/math] is said to be an [math]\bf{n}[/math]^th root of [math]z[/math] if [math]w^n = z[/math]. We shall now show that

Theorem

If [math]z \neq 0[/math], then there exist [math]n[/math] distinct [math]n[/math]th roots of [math]z[/math].

Show Proof

Let us write [math]z[/math] in exponential form: [math]z = |z| e^{it}[/math]. By [math]|z|^{1/n}[/math] we mean the positive [math]n[/math]th root of the real number [math]|z|[/math] (which we assume exists and is unique). Consider the complex number

[[math]] w_0 = |z|^{1/n} e^{i(t/n)}. [[/math]]

It is easy to see that [math]w_0[/math] is an nth root of [math]z[/math], since

[[math]] \begin{eqnarray*} w_{0}^{n} &=& (|z|^{1/n})^{n} (e^{i(t/n)})^n \\ &=& |z|e^{it} \\ &=& z . \end{eqnarray*} [[/math]]

However, [math]w_0[/math] is not the only [math]n[/math]th root. We have already observed that

[[math]] z = |z| e^{it} = |z| e^{i(t + 2\pi k)}, [[/math]]

for every integer [math]k[/math]. If we set

[[math]] w_{k} = |z|^{1/n} e^{i\frac{i + 2\pi k}{n}} , [[/math]]

then all these numbers are seen to be nth roots of [math]z[/math], since each one satisfies the equation [math]w_{k}^{n} = z[/math]. However, they are not all different. Note that [math]w_{k+1}[/math] is equal to the product [math]w_{k}e^{i(2\pi/n)}[/math]. The angle of [math]e^{i(2\pi/n)}[/math] is [math]\frac{2\pi}{n}[/math] radians, and [math]\frac{2\pi}{n}[/math] is one [math]n[/math]th the entire circumference of the unit circle. Thus [math]w_{k+1}[/math] is obtained from [math]w_k[/math] by adding an angle of [math]\frac{2\pi}{n}[/math] radians, or, equivalently, by rotating [math]w_k[/math] exactly [math]\frac{1}{n}[/math] of an entire rotation. If we begin with [math]w_k[/math] and form [math]w_{k+1}, w_{k+2}, . . . [/math] by successive rotations, when we get to [math]w_{k+n}[/math] we will be back at [math]wk[/math], where we started. Thus there are only [math]n[/math] distinct complex numbers among all the [math]w[/math]'s. In particular,

[[math]] w_{k} = |z|^{1/n} e^{i\frac{i + 2\pi k}{n}}, \;\;\; k = 0, . . ., n - 1, [[/math]]

are [math]n[/math] distinct nth roots of [math]z[/math]. This completes the proof.

■

An [math]n[/math]th root of [math]z[/math] is a solution of the complex polynomial equation [math]w^n - z = 0[/math]. It is a well-known theorem of algebra that a polynomial equation of degree [math]n[/math] cannot have more than [math]n[/math] roots. Hence we can strengthen the statement of (7.8) to read that every nonzero complex number [math]z[/math] has precisely [math]n[/math] distinct nth roots.

File:Guide c5467 scanfig6 22.png

Example

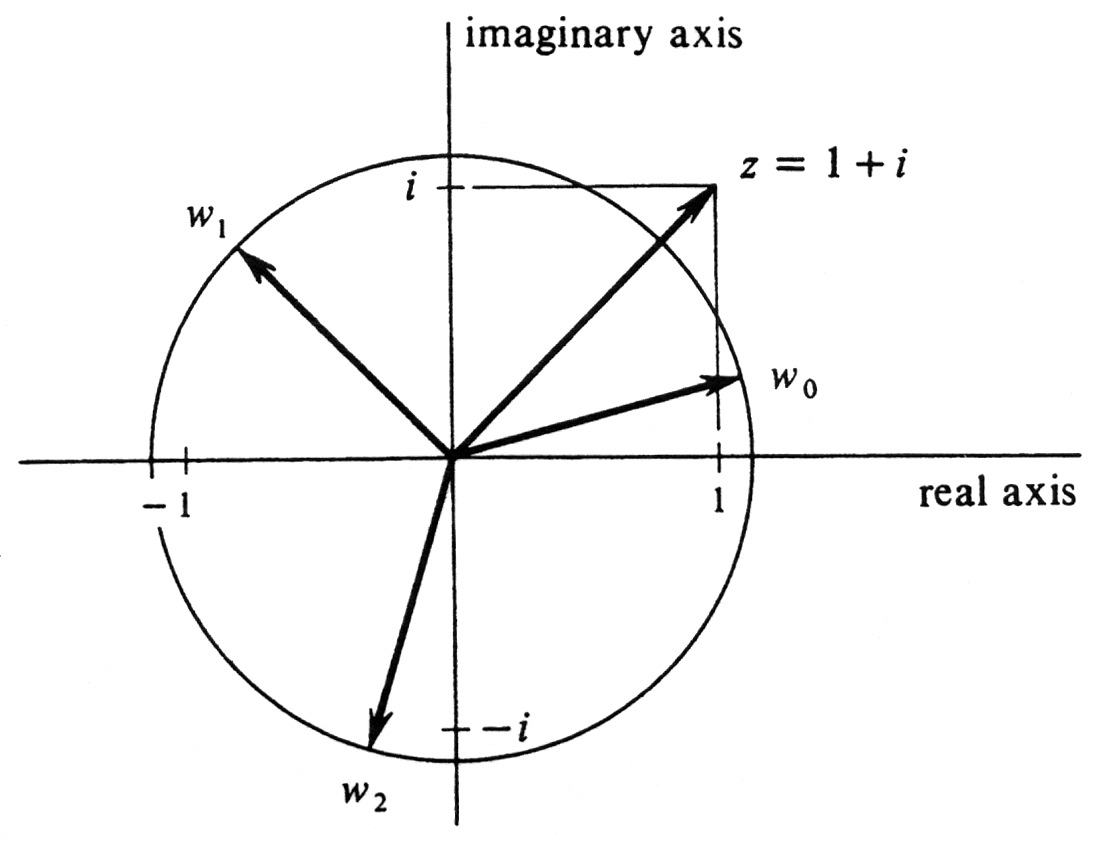
Find the three cube roots of the complex number [math]z = 1 + i[/math], and plot them in the complex plane. Writing [math]z[/math] in exponential form, we have

[[math]] z = \sqrt{2} e^{i(\pi/4)} [[/math]]

(see Figure 22). Hence the three cube roots are

[[math]] w_k = (\sqrt 2)^{1/3} e ^{i \frac{\pi/4 + 2\pi k}{3}}, \;\;\; k = 0, 1, 2. [[/math]]

Since [math](\sqrt 2)^{1/3} = 2^{1/6} = 1.12[/math] (approximately) and [math]\frac{1}{3} \Bigl(\frac{\pi}{4}\Bigr)[/math] radius = 15 degrees, we see that [math]w_0[/math] is the complex number lying on the circle of radius 1.12 about the origin and making an angle of 15 degrees with the positive [math]x[/math]-axis. The other two roots lie on the same circle and have angles of 15 + 120 degrees and 15 + 240 degrees, respectively. The three roots are thus [math]\sqrt[6]{2} e^{i(\pi/12)}[/math], [math]\sqrt[6]{2} e^{i(3\pi/4)}[/math], and [math]\sqrt[6]{2} e^{i(17 \pi/12)}[/math].

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.