Bagging, Boosting, and Random Forests

[math] \DeclareMathOperator*{\argmax}{argmax} \newcommand{\D}{\mathcal{D}_n} \newcommand{\T}{\Theta} \newcommand{\Pt}{\mathbb{P}_{\Theta}} \newcommand{\Vt}{\mathbb{V}_{\Theta}} \newcommand{\Et}{\mathbb{E}_{\Theta}} \newcommand{\E}{\mathbb{E}} \newcommand{\V}{\mathbb{V}} \renewcommand{\P}{\mathbb{P}} \newcommand{\LL}{\mathbb{L}} \newcommand{\Ccal}{\mathcal{C}} \newcommand{\Pcal}{\mathcal{P}} \newcommand{\N}{\mathbb{N}} \newcommand{\e}{\varepsilon} \newcommand{\R}{\mathbb{R}} \newcommand{\bX}{{\bf X}} \newcommand{\bx}{{\bf x}} \newcommand{\bz}{{\bf z}} \newcommand{\smallO}[1]{\ensuremath{\mathop{}\mathopen{}o\mathopen{}\left(#1\right)}} \newcommand{\Mtry}{\mathcal{M}_{\textrm{try}}} \newcommand{\Pfin}{\mathcal{P}_{\textrm{final}}} \newcommand{\mtry}{\texttt{mtry}} [/math]

Bootstrap aggregating, also called bagging (from bootstrap aggregating), is a machine learning ensemble meta-algorithm designed to improve the stability and accuracy of machine learning algorithms used in statistical classification and regression. It also reduces variance and helps to avoid overfitting. Although it is usually applied to decision tree methods, it can be used with any type of method. Bagging is a special case of the model averaging approach.

Description of the technique

Given a standard training set [math]D[/math] of size [math]n[/math], bagging generates [math]m[/math] new training sets [math]D_i[/math], each of size [math]n[/math], by sampling from [math]D[/math] uniformly and with replacement. By sampling with replacement, some observations may be repeated in each [math]D_i[/math]. If [math]n=n'[/math], then for large [math]n[/math] the set [math]D_i[/math] is expected to have the fraction (1 - 1/e) (≈63.2%) of the unique examples of [math]D[/math], the rest being duplicates. This kind of sample is known as a bootstrap sample. Sampling with replacement ensures each bootstrap is independent from its peers, as it does not depend on previous chosen samples when sampling. Then, [math]m[/math] models are fitted using the above [math]m[/math] bootstrap samples and combined by averaging the output (for regression) or voting (for classification).

An illustration for the concept of bootstrap aggregating

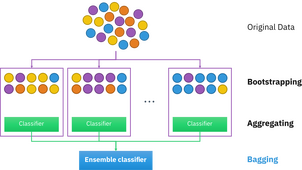
Bagging leads to "improvements for unstable procedures", which include, for example, artificial neural networks, classification and regression trees, and subset selection in linear regression. Bagging was shown to improve preimage learning. On the other hand, it can mildly degrade the performance of stable methods such as K-nearest neighbors.

Creating the bootstrap dataset

The bootstrap dataset is made by randomly picking objects from the original dataset. Also, it must be the same size as the original dataset. However, the difference is that the bootstrap dataset can have duplicate objects. Here is simple example to demonstrate how it works along with the illustration below:

Bootstrap Example

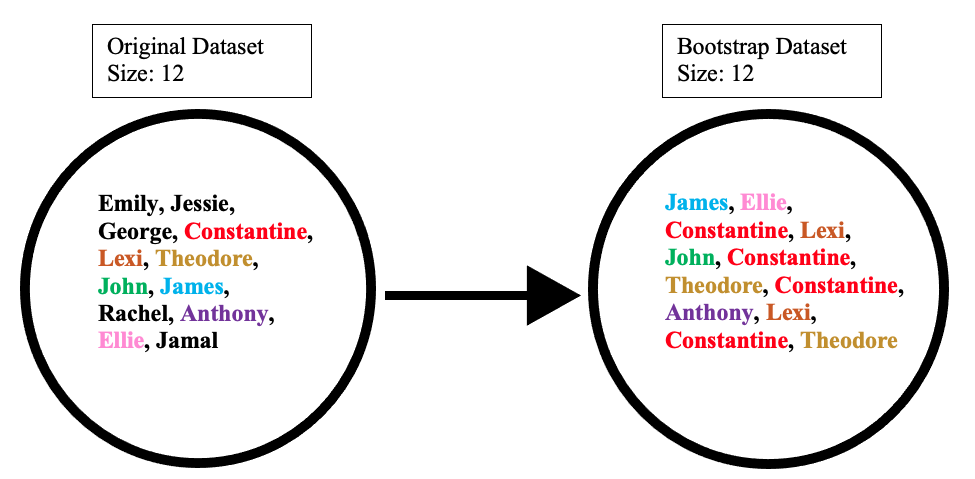
Suppose the original dataset is a group of 12 people. These guys are Emily, Jessie, George, Constantine, Lexi, Theodore, John, James, Rachel, Anthony, Ellie, and Jamal.

By randomly picking a group of names, let us say our bootstrap dataset had James, Ellie, Constantine, Lexi, John, Constantine, Theodore, Constantine, Anthony, Lexi, Constantine, and Theodore. In this case, the bootstrap sample contained four duplicates for Constantine, and two duplicates for Lexi, and Theodore.

Creating the out-of-bag dataset

The out-of-bag dataset represents the remaining people who were not in the bootstrap dataset. It can be calculated by taking the difference between the original and the bootstrap datasets. In this case, the remaining samples who were not selected are Emily, Jessie, George, Rachel, and Jamal. Keep in mind that since both datasets are sets, when taking the difference the duplicate names are ignored in the bootstrap dataset. The illustration below shows how the math is done:

Complete Example

Example: ozone data

To illustrate the basic principles of bagging, below is an analysis on the relationship between ozone and temperature (data from Rousseeuw and Leroy (1986), analysis done in R).

The relationship between temperature and ozone appears to be nonlinear in this data set, based on the scatter plot. To mathematically describe this relationship, LOESS smoothers (with bandwidth 0.5) are used. Rather than building a single smoother for the complete data set, 100 bootstrap samples were drawn. Each sample is composed of a random subset of the original data and maintains a semblance of the master set’s distribution and variability. For each bootstrap sample, a LOESS smoother was fit. Predictions from these 100 smoothers were then made across the range of the data. The black lines represent these initial predictions. The lines lack agreement in their predictions and tend to overfit their data points: evident by the wobbly flow of the lines.

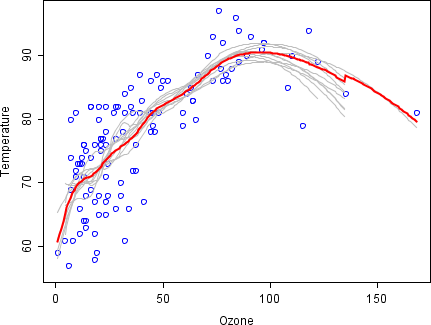
By taking the average of 100 smoothers, each corresponding to a subset of the original data set, we arrive at one bagged predictor (red line). The red line's flow is stable and does not overly conform to any data point(s).

Boosting

In machine learning, boosting is an ensemble meta-algorithm for primarily reducing bias, and also variance in supervised learning, and a family of machine learning algorithms that convert weak learners to strong ones. Boosting is based on the question posed by Kearns and Valiant (1988, 1989): "Can a set of weak learners create a single strong learner?" A weak learner is defined to be a classifier that is only slightly correlated with the true classification (it can label examples better than random guessing). In contrast, a strong learner is a classifier that is arbitrarily well-correlated with the true classification.

Robert Schapire's affirmative answer in a 1990 paper to the question of Kearns and Valiant has had significant ramifications in machine learning and statistics, most notably leading to the development of boosting.

When first introduced, the hypothesis boosting problem simply referred to the process of turning a weak learner into a strong learner. "Informally, [the hypothesis boosting] problem asks whether an efficient learning algorithm […] that outputs a hypothesis whose performance is only slightly better than random guessing [i.e. a weak learner] implies the existence of an efficient algorithm that outputs a hypothesis of arbitrary accuracy [i.e. a strong learner]." Algorithms that achieve hypothesis boosting quickly became simply known as "boosting". Freund and Schapire's arcing (Adapt[at]ive Resampling and Combining), as a general technique, is more or less synonymous with boosting.

Boosting algorithms

While boosting is not algorithmically constrained, most boosting algorithms consist of iteratively learning weak classifiers with respect to a distribution and adding them to a final strong classifier. When they are added, they are weighted in a way that is related to the weak learners' accuracy. After a weak learner is added, the data weights are readjusted, known as "re-weighting". Misclassified input data gain a higher weight and examples that are classified correctly lose weight. Thus, future weak learners focus more on the examples that previous weak learners misclassified.

An illustration presenting the intuition behind the boosting algorithm, consisting of the parallel learners and weighted dataset.

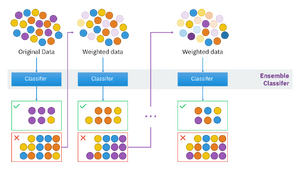
There are many boosting algorithms. The original ones, proposed by Robert Schapire (a recursive majority gate formulation) and Yoav Freund (boost by majority), were not adaptive and could not take full advantage of the weak learners. Schapire and Freund then developed AdaBoost, an adaptive boosting algorithm that won the prestigious Gödel Prize.

The main variation between many boosting algorithms is their method of weighting training data points and hypotheses. AdaBoost is very popular and the most significant historically as it was the first algorithm that could adapt to the weak learners. It is often the basis of introductory coverage of boosting in university machine learning courses. There are many more recent algorithms such as LPBoost, TotalBoost, BrownBoost, xgboost, MadaBoost, LogitBoost, and others. Many boosting algorithms fit into the AnyBoost framework, which shows that boosting performs gradient descent in a function space using a convex cost function.

Random Forests

This section is based on . To take advantage of the sheer size of modern data sets, we now need learning algorithms that scale with the volume of information, while maintaining sufficient statistical efficiency. Random forests, devised by L. Breiman in the early 2000s ,are part of the list of the most successful methods currently available to handle data in these cases. This supervised learning procedure, influenced by the early work of , , and , operates according to the simple but effective divide and conquer principle: sample fractions of the data, grow a randomized tree predictor on each small piece, then paste (aggregate) these predictors together.

What has greatly contributed to the popularity of forests is the fact that they can be applied to a wide range of prediction problems and have few parameters to tune. Aside from being simple to use, the method is generally recognized for its accuracy and its ability to deal with small sample sizes and high-dimensional feature spaces. At the same time, it is easily parallelizable and has therefore the potential to deal with large real-life systems.

Basic Principles

As mentioned above, the forest mechanism is versatile enough to deal with both supervised classification and regression tasks. However, to keep things simple, we focus in this introduction on regression analysis, and only briefly survey the classification case. Our objective in this section is to provide a concise but mathematically precise presentation of the algorithm for building a random forest. The general framework is nonparametric regression estimation, in which an input random vector [math]\bX \in \mathcal{X} \subset \mathbb{R}^p[/math] is observed, and the goal is to predict the square integrable random response [math]Y\in \mathbb R[/math] by estimating the regression function [math]m(\bx)=\mathbb E[Y|\bX=\bx][/math]. With this aim in mind, we assume we are given a training sample [math]\mathcal D_n=((\bX_1,Y_1), \ldots, (\bX_n,Y_n))[/math] of independent random variables distributed as the independent prototype pair [math](\bX, Y)[/math]. The goal is to use the data set [math]\mathcal D_n[/math] to construct an estimate [math]m_n: \mathcal{X} \to \mathbb R[/math] of the function [math]m[/math]. In this respect, we say that the regression function estimate [math]m_n[/math] is (mean squared error) consistent if [math]\mathbb E [m_n(\bX)-m(\bX)]^2 \to 0[/math] as [math]n \to \infty[/math] (the expectation is evaluated over [math]\bX[/math] and the sample [math]\mathcal D_n[/math]).

A random forest is a predictor consisting of a collection of [math]M[/math] randomized regression trees. For the [math]j[/math]-th tree in the family, the predicted value at the query point [math]\bx[/math] is denoted by [math]m_n(\bx; \Theta_j,\mathcal D_n)[/math], where [math]\Theta_1, \ldots,\Theta_M[/math] are independent random variables, distributed the same as a generic random variable [math]\Theta[/math] and independent of [math]\mathcal D_n[/math]. In practice, the variable [math]\Theta[/math] is used to resample the training set prior to the growing of individual trees and to select the successive directions for splitting---more precise definitions will be given later. In mathematical terms, the [math]j[/math]-th tree estimate takes the form

[[math]] \begin{align*} m_n(\bx; \Theta_j,\mathcal D_n) = \sum_{i \in \mathcal{D}^{\star}_n(\Theta_j)} \frac{\mathbb{1}_{\bX_i \in A_n(\bx; \Theta_j, \mathcal{D}_n) }Y_i}{N_n(\bx; \Theta_j,\mathcal{D}_n)}, \end{align*} [[/math]]

where [math]\mathcal{D}_n^{\star}(\Theta_j)[/math] is the set of data points selected prior to the tree construction, [math]A_n(\bx; \Theta_j, \mathcal{D}_n)[/math] is the cell containing [math]\bx[/math], and [math]N_n(\bx; \Theta_j, \mathcal{D}_n)[/math] is the number of (preselected) points that fall into [math]A_n(\bx; \Theta_j, \mathcal{D}_n)[/math].

At this stage, we note that the trees are combined to form the (finite) forest estimate

[[math]] \begin{equation} m_{M,n}(\bx; \Theta_1, \ldots, \Theta_M, \mathcal{D}_n)=\frac{1}{M}\sum_{j=1}^M m_n(\bx; \Theta_j,\mathcal D_n).\label{chapitre0_finite_forest} \end{equation} [[/math]]

In the R package randomForest, the default value of [math]M[/math] (the number of trees in the forest) is ntree = 500. Since [math]M[/math] may be chosen arbitrarily large (limited only by available computing resources), it makes sense, from a modeling point of view, to let [math]M[/math] tends to infinity, and consider instead of (\ref{chapitre0_finite_forest}) the (infinite) forest estimate \begin{align*} m_{\infty, n}(\bx; \mathcal{D}_n)=\mathbb E_{\Theta}\left [m_n(\bx;\Theta,\mathcal D_n)\right]. \end{align*} In this definition, [math]\mathbb E_{\Theta}[/math] denotes the expectation with respect to the random parameter [math]\Theta[/math], conditional on [math]\mathcal D_n[/math]. In fact, the operation [math]M \to \infty[/math] is justified by the law of large numbers, which asserts that almost surely, conditional on [math]\mathcal{D}_n[/math],

[[math]] \lim\limits_{M \to \infty} m_{M,n}(\bx; \Theta_1, \ldots, \Theta_M, \mathcal{D}_n) = m_{\infty, n}(\bx; \mathcal{D}_n)[[/math]]

(see for instance , and , for more information on this limit calculation). In the following, to lighten notation we will simply write [math]m_{\infty, n}(\bx)[/math] instead of [math]m_{\infty, n}(\bx;\mathcal{D}_n)[/math].

Algorithm

We now provide some insight on how the individual trees are constructed and how randomness kicks in. In Breiman’s original forests, each node of a single tree is associated with a hyperrectangular cell. The root of the tree is [math]\mathcal{X}[/math] itself and, at each step of the tree construction, a node (or equivalently its corresponding cell) is split in two parts. The terminal nodes (or leaves), taken together, form a partition of [math]\mathcal{X}[/math].

The algorithm works by growing [math]M[/math] different (randomized) trees as follows. Prior to the construction of each tree, [math]a_n[/math] observations are drawn at random with (or without) replacement from the original data set. These---and only these---[math]a_n[/math] observations (with possible repetitions) are taken into account in the tree building. Then, at each cell of each tree, a split is performed by maximizing the CART-criterion (see below) over mtry directions chosen uniformly at random among the [math]p[/math] original ones. (The resulting subset of selected coordinates is called [math]\Mtry[/math].) Lastly, construction of individual trees is stopped when each cell contains less than nodesize points. For any query point [math]\bx \in \mathcal X[/math], each regression tree predicts the average of the [math]Y_i[/math] (that were among the [math]a_n[/math] points) for which the corresponding [math]\bX_i[/math] falls into the cell of [math]\bx[/math]. We draw attention to the fact that growing the tree and making the final estimation only depends on the [math]a_n[/math] preselected data points. Algorithm 1 describes in full detail how to compute a forest's prediction.

Breiman's random forest

Input: Training set [math]\mathcal{D}_n[/math], number of trees [math]M\gt0[/math], [math]a_n \in \{1, \ldots, n \}[/math], [math]\texttt{mtry} \in \{1, \ldots, p \}[/math], [math]\texttt{nodesize} \in \{1, \ldots, a_n \}[/math], and [math]\bx \in \mathcal{X}[/math].

Output: Prediction of the random forest at [math]\bx[/math].

For [math]j=1,\ldots,M[/math] do

1. Select [math]a_n[/math] points, with (or without) replacement, uniformly in [math]\mathcal{D}_n[/math]. In the following steps, only these [math]a_n[/math] observations are used.
2. Set [math]\mathcal{P} = (\mathcal{X})[/math] the list containing the cell associated with the root of the tree.
3. Set [math]\Pfin = \emptyset[/math] an empty list.

While: [math]\mathcal{P} \neq \emptyset [/math] do

Let [math]A[/math] be the first element of [math]\mathcal{P}[/math]

If [math]A[/math] contains less than nodesize points or if all [math]\bX_i \in A[/math] are equal
then

1. Remove the cell [math]A[/math] from the list [math]\mathcal{P}[/math].
2. [math]\Pfin \leftarrow Concatenate (\Pfin , A)[/math].

else

1. Select uniformly, without replacement, a subset [math]\Mtry \subset[/math] [math] \{1,\ldots,[/math] [math]p\}[/math] of cardinality [math]\mtry[/math].
2. Select the best split in [math]A[/math] by optimizing the CART-split criterion along the coordinates in [math]\mathcal{M}_{\textrm{try}}[/math] (see text for details).
3. Cut the cell [math]A[/math] according to the best split. Call [math]A_L[/math] and [math]A_R[/math] the two resulting cells.
4. Remove the cell [math]A[/math] from the list [math]\mathcal{P}[/math].
5. [math]\mathcal{P} \leftarrow Concatenate( \mathcal{P}, A_L, A_R)[/math].

end

Compute the predicted value [math]m_n(\bx; \Theta_j, \mathcal{D}_n)[/math] at [math]\bx[/math] equal to the average of the [math]Y_i[/math] falling in the cell of [math]\bx[/math] in partition [math]\Pfin[/math].

end

Compute the random forest estimate [math]m_{M,n}(\bx; \Theta_1, \ldots, \Theta_M, \mathcal{D}_n)[/math] at the query point [math]\bx[/math] according to (\ref{chapitre0_finite_forest}).

Algorithm 1 may seem a bit complicated at first sight, but the underlying ideas are simple. We start by noticing that this algorithm has three important parameters:

• [math]a_n \in \{1, \ldots, n \}[/math]: the number of sampled data points in each tree;
• [math]\mtry \in \{1, \ldots, p \}[/math]: the number of possible directions for splitting at each node of each tree;
• [math]\texttt{nodesize} \in \{1, \ldots, a_n \}[/math]: the number of examples in each cell below which the cell is not split.

By default, in the regression mode of the R package randomForest, the parameter [math]\mtry[/math] is set to [math]\lceil p/3 \rceil[/math] ([math]\lceil \cdot \rceil[/math] is the ceiling function), [math]a_n[/math] is set to [math]n[/math], and nodesize is set to [math]5[/math]. The role and influence of these three parameters on the accuracy of the method will be thoroughly discussed in the next section.

We still have to describe how the CART-split criterion operates. As for now, we consider for the ease of understanding a tree with no subsampling, which uses the entire and original data set [math]\mathcal{D}_n[/math] for its construction. Also, we let [math]A[/math] be a generic cell and denote by [math]N_n(A)[/math] the number of data points falling in [math]A[/math]. A cut in [math]A[/math] is a pair [math](j,z)[/math], where [math]j[/math] is some value (dimension) from [math]\{1, \ldots, p\}[/math] and [math]z[/math] the position of the cut along the [math]j[/math]-th coordinate, within the limits of [math]A[/math]. Let [math]\mathcal{C}_A[/math] be the set of all such possible cuts in [math]A[/math]. Then, with the notation [math]\bX_i = (\bX_i^{(1)}, \ldots, \bX_i^{(p)} )[/math], for any [math](j,z) \in \mathcal{C}_A[/math], the CART-split criterion takes the form

[[math]] \begin{align} L_{\textrm{reg}, n}(j,z) = & \frac{1}{N_n(A)} \sum_{i=1}^n (Y_i - \bar{Y}_{A})^2\mathbb{1}_{\bX_i \in A} \nonumber \\ & - \frac{1}{N_n(A)} \sum_{i=1}^n (Y_i - \bar{Y}_{A_{L}} \mathbb{1}_{\bX_i^{(j)} \lt z} - \bar{Y}_{A_{R}} \mathbb{1}_{\bX_i^{(j)} \geq z})^2 \mathbb{1}_{\bX_i \in A}, \label{chapitre0_definition_empirical_CART_criterion} \end{align} [[/math]]

where [math]A_L = \{ \bx \in A: \bx^{(j)} \lt z\}[/math], [math]A_R = \{ \bx \in A: \bx^{(j)} \geq z\}[/math], and [math]\bar{Y}_{A}[/math] (resp., [math]\bar{Y}_{A_{L}}[/math], [math]\bar{Y}_{A_{R}}[/math]) is the average of the [math]Y_i[/math] belonging to [math]A[/math] (resp., [math]A_{L}[/math], [math]A_{R}[/math]), with the convention that the average is equal to [math]0[/math] when no point [math]\bX_i[/math] belongs to [math]A[/math] (resp., [math]A_{L}[/math], [math]A_{R}[/math]). For each cell [math]A[/math], the best cut [math](j_n^{\star},z_n^{\star})[/math] is selected by maximizing [math]L_{\textrm{reg}, n}(j,z)[/math] over [math]\Mtry[/math] and [math]\mathcal{C}_A[/math]; that is,

[[math]] \begin{align*} (j_n^{\star},z_n^{\star}) \in \argmax\limits_{\substack{j \in \Mtry\\(j,z) \in \mathcal{C}_A }} L_{\textrm{reg}, n}(j,z). \end{align*} [[/math]]

(To remove some of the ties in the argmax, the best cut is always performed in the middle of two consecutive data points.) Let us finally notice that the above optimization program extends effortlessly to the resampling case, by optimizing over the [math]a_n[/math] preselected observations instead of the original data set [math]\mathcal{D}_n[/math].

Thus, at each cell of each tree, the algorithm chooses uniformly at random [math]\mtry[/math] coordinates in [math]\{1, \ldots, p\}[/math], evaluates criterion (\ref{chapitre0_definition_empirical_CART_criterion}) over all possible cuts along the directions in [math]\Mtry[/math], and returns the best one. The quality measure (\ref{chapitre0_definition_empirical_CART_criterion}) is the criterion used in the influential CART algorithm of . This criterion computes the (renormalized) difference between the empirical variance in the node before and after a cut is performed. There are three essential differences between CART and a tree of Breiman's forest. First of all, in Breiman's forests, the criterion (\ref{chapitre0_definition_empirical_CART_criterion}) is evaluated over a subset [math]\Mtry[/math] of randomly selected coordinates, and not over the whole range [math]\{1, \ldots, p\}[/math]. Besides, the individual trees are not pruned, and the final cells do not contain more than nodesize observations (unless all data points in the cell have the same [math]\bX_i[/math]). At last, each tree is constructed on a subset of [math]a_n[/math] examples picked within the initial sample, not on the whole sample [math]\mathcal D_n[/math]; and only these [math]a_n[/math] observations are used to calculate the estimation. When [math]a_n=n[/math] (and the resampling is done with replacement), the algorithm runs in bootstrap mode, whereas [math]a_n \lt n[/math] corresponds to subsampling (with or without replacement).

Supervised classification

For simplicity, we only consider here the binary classification problem, keeping in mind that random forests are intrinsically capable of dealing with multi-class problems . In this setting , the random response [math]Y[/math] takes values in [math]\{0, 1\}[/math] and, given [math]\bX[/math], one has to guess the value of [math]Y[/math]. A classifier, or classification rule, [math]m_n[/math] is a Borel measurable function of [math]\bX[/math] and [math]\mathcal D_n[/math] that attempts to estimate the label [math]Y[/math] from [math]\bX[/math] and [math]\mathcal D_n[/math]. In this framework, one says that the classifier [math]m_n[/math] is consistent if its conditional probability of error

[[math]] L(m_n)=\mathbb P[m_n(\bX)\neq Y] \underset{n\to \infty}{\to} L^{\star}, [[/math]]

where [math]L^{\star}[/math] is the error of the optimal---but unknown---Bayes classifier:

[[math]] m^{\star} (\bx) = \left\{ \begin{array}{ll} 1 & \textrm{if} \,\, \mathbb P[Y=1| \bX=\bx] \gt \mathbb P[Y=0| \bX=\bx]\\ 0 & \mbox{ otherwise.} \end{array} \right. [[/math]]

In the classification context, the random forest classifier is obtained via a majority vote among the classification trees, that is,

[[math]] \begin{equation*} m_{M,n}(\bx; \Theta_1, \ldots, \Theta_M, \mathcal{D}_n) = \left\{ \begin{array}{ll} 1 & \textrm{if}\,\, \frac{1}{M}\sum_{j=1}^M m_n(\bx; \Theta_j,\mathcal D_n) \gt 1/2\\ 0 & \mbox{ otherwise.} \end{array} \right. \end{equation*} [[/math]]

If a leaf represents region [math]A[/math], then a randomized tree classifier takes the simple form

[[math]] \begin{eqnarray*} m_n (\bx;\Theta_j,\mathcal D_n) = \left\{ \begin{array}{ll} 1 & \mbox{ if $\sum_{i \in \mathcal{D}_n^{\star}(\Theta)} \mathbf 1_{\bX_i \in A, Y_i =1} \gt \sum_{i \in \mathcal{D}_n^{\star}(\Theta)} \mathbf 1_{\bX_i \in A, Y_i =0}$, $\bx\in A$}\\ 0 & \mbox{ otherwise,} \end{array} \right. \end{eqnarray*} [[/math]]

where [math]\mathcal{D}^{\star}_n(\Theta)[/math] contains the data points selected in the resampling step. That is, in each leaf, a majority vote is taken over all [math](\bX_i,Y_i)[/math] for which [math]\bX_i[/math] is in the same region. Ties are broken, by convention, in favor of class 0. Algorithm 1 can be easily adapted to do classification by modifying the CART-split criterion for the binary setting. To see this, let us consider a single tree with no subsampling step. For any generic cell [math]A[/math], let [math]p_{0,n}(A)[/math] (resp., [math]p_{1,n}(A)[/math]) be the empirical probability of a data point in the cell [math]A[/math] having label [math]0[/math] (resp., label [math]1[/math]). Then, for any [math](j,z) \in \mathcal{C}_A[/math], the classification CART-split criterion reads

[[math]] \begin{align*} L_{\textrm{class}, n}(j,z) & = p_{0,n}(A)p_{1,n}(A) - \frac{N_n(A_L)}{N_n(A)} \times p_{0,n}(A_L)p_{1,n}(A_L)\nonumber\\ & \qquad - \frac{N_n(A_R)}{N_n(A)} \times p_{0,n}(A_R)p_{1,n}(A_R). \end{align*} [[/math]]

This criterion is based on the so-called Gini impurity measure [math]2p_{0,n}(A)p_{1,n}(A)[/math] , which has the following simple interpretation. To classify a data point that falls in cell [math]A[/math], one uses the rule that assigns a point, uniformly selected from [math]\{\bX_i \in A: (\bX_i, Y_i)\in \mathcal{D}_n\}[/math], to label [math]\ell[/math] with probability [math]p_{\ell,n}(A)[/math], for [math]j \in \{0,1\}[/math]. The estimated probability that the item has actually label [math]\ell[/math] is [math]p_{\ell,n}(A)[/math]. Therefore the estimated error under this rule is the Gini index [math]2p_{0,n}(A)p_{1,n}(A)[/math].

We note that whenever [math]Y \in \{0,1\}[/math], optimizing the classification criterion [math]L_{\textrm{class}, n}[/math] is equivalent to optimizing its regression counterpart [math]L_{\textrm{reg}, n}[/math]. Thus, in this case, the trees obtained with [math]L_{\textrm{class}, n}[/math] and [math]L_{\textrm{reg}, n}[/math] are identical. However, the prediction strategy is different: in the classification regime, each tree uses a local majority vote, whereas in regression the prediction is achieved by a local averaging.

When dealing with classification problems, it is usually recommended to set [math]\texttt{nodesize} = 1[/math] and [math]\mtry=\sqrt{p}[/math] .

We draw attention to the fact that regression estimation may also have an interest in the context of dichotomous and multicategory outcome variables (in this case, it is often termed probability estimation). For example, estimating outcome probabilities for individuals is important in many areas of medicine, with applications to surgery, oncology, internal medicine, pathology, pediatrics, and human genetics. We refer the interested reader to and to the survey papers by and .

Parameter tuning

Literature focusing on tuning the parameters [math]M[/math], mtry, nodesize and [math]a_n[/math] is unfortunately rare, with the notable exception of , , and . According to , tuning the forest parameters may result in a computational burden, in particular for big data sets, with hundreds and thousands of samples and variables. To circumvent this issue, implement a fast version of the original algorithm, which they name Random Jungle.

It is easy to see that the forest's variance decreases as [math]M[/math] grows. Thus, more accurate predictions are likely to be obtained by choosing a large number of trees. Interestingly, picking a large [math]M[/math] does not lead to overfitting. In effect, following an argument of , we have

[[math]] \begin{align*} \lim_{n \to \infty}\mathbb{E}[m_{M,n}(\bX; \Theta_1, \ldots, \Theta_M) - m(\bX)]^2 = \mathbb{E}[m_{\infty,n}(\bX) - m(\bX)]^2. \end{align*} [[/math]]

However, the computational cost for inducing a forest increases linearly with [math]M[/math], so a good choice results from a trade-off between computational complexity ([math]M[/math] should not be too large for the computations to finish in a reasonable time) and accuracy ([math]M[/math] must be large enough for predictions to be stable). In this respect, argue that the value of [math]M[/math] is irrelevant (provided that [math]M[/math] is large enough) in a prediction problem involving microarray data sets, where the aim is to classify patients according to their genetic profiles (typically, less than one hundred patients for several thousand genes). For more details we refer the reader to , who offer a thorough discussion on the choice of this parameter in various regression problems. Another interesting and related approach is by , who propose a simple procedure that determines a priori a minimum number of tree estimates to combine in order to obtain a prediction accuracy level similar to that of a larger forest. Their experimental results show that it is possible to significantly limit the number of trees. \medskip

In the R package randomForest, the default value of the parameter nodesize is 1 for classification and 5 for regression. These values are often reported to be good choices despite the fact that this is not supported by solid theory. A simple algorithm to tune the parameter nodesize in the classification setting is discussed in .

The effect of [math]\mtry[/math] is thoroughly investigated in , who show that this parameter has a little impact on the performance of the method, though larger values may be associated with a reduction in the predictive performance. On the other hand, claim that the default value of [math]\mtry[/math] is either optimal or too small. Therefore, a conservative approach is to take [math]\mtry[/math] as large as possible (limited by available computing resources) and set [math]\mtry=p[/math] (recall that [math]p[/math] is the dimension of the [math]\bX_i[/math]). A data-driven choice of mtry is implemented in the algorithm Forest-RK of .

Let us finally notice that even if there is no theoretical guarantee to support the default values of the parameters, they are nevertheless easy to tune without requiring an independent validation set. Indeed, the procedure accuracy is estimated internally, during the run, as follows. Since each tree is constructed using a different bootstrap sample from the original data, about one-third of the observations are left out of the bootstrap sample and not used in the construction of the [math]j[/math]-th tree. In this way, for each tree, a test set---disjoint from the training set---is obtained, and averaging over all these left-out data points and over all trees is known as the out-of-bag error estimate. Thus, the out-of-bag error, computed on the observations set aside by the resampling prior to the tree building, offers a simple way to adjust the parameters without the need of a validation set. (e.g.,).

Variable importance measures

Random forests can be used to rank the importance of variables in regression or classification problems via two measures of significance. The first, called Mean Decrease Impurity (see ), is based on the total decrease in node impurity from splitting on the variable, averaged over all trees. The second, referred to as Mean Decrease Accuracy (MDA), first defined by , stems from the idea that if the variable is not important, then rearranging its values should not degrade prediction accuracy.

Set [math]\bX = (X^{(1)}, \ldots, X^{(p)} )[/math]. For a forest resulting from the aggregation of [math]M[/math] trees, the MDI of the variable [math]X^{(j)}[/math] is defined by

[[math]] \begin{align*} \widehat{\mbox{MDI}}(X^{(j)}) = \frac{1}{M} \sum_{{\ell}=1}^M \sum_{\substack{t \in \mathcal{T}_{\ell}\\ j_{n,t}^{\star} = j}} p_{n,t} L_{{\scriptsize \mbox{reg}}, n}(j_{n,t}^{\star}, z_{n,t}^{\star}), \end{align*} [[/math]]

where [math]p_{n,t}[/math] is the fraction of observations falling in the node [math]t[/math], [math]\{\mathcal{T}_{\ell}\}_{1\leq {\ell} \leq M}[/math] the collection of trees in the forest, and [math](j_{n,t}^{\star}, z_{n,t}^{\star})[/math] the split that maximizes the empirical criterion (\ref{chapitre0_definition_empirical_CART_criterion}) in node [math]t[/math]. Note that the same formula holds for classification random forests by replacing the criterion [math]L_{{\scriptsize \mbox{reg}}, n}[/math] by its classification version [math]L_{{\scriptsize \mbox{class}}, n}[/math]. Thus, the MDI of [math]X^{(j)}[/math] computes the weighted decrease of impurity corresponding to splits along the variable [math]X^{(j)}[/math] and averages this quantity over all trees.

The MDA relies on a different principle and uses the out-of-bag error estimate (see Section [math]2.4[/math]). To measure the importance of the [math]j[/math]-th feature, we randomly permute the values of variable [math]X^{(j)}[/math] in the out-of-bag observations and put these examples down the tree. The MDA of [math]X^{(j)}[/math] is obtained by averaging the difference in out-of-bag error estimation before and after the permutation over all trees. In mathematical terms, consider a variable [math]X^{(j)}[/math] and denote by [math]\mathcal{D}_{{\ell},n}[/math] the out-of-bag data set of the [math]{\ell}[/math]-th tree and [math]{\mathcal{D}}^j_{{\ell},n}[/math] the same data set where the values of [math]X^{(j)}[/math] have been randomly permuted. Recall that [math]m_n(\cdot; \Theta_{\ell})[/math] stands for the [math]{\ell}[/math]-th tree estimate. Then, by definition,

[[math]] \begin{align} \widehat{\mbox{MDA}}(X^{(j)})= \frac{1}{M} \sum_{{\ell}=1}^M \bigg[ R_n\big[m_{n}(\cdot; \Theta_{\ell}),{\mathcal{D}}^j_{{\ell},n}\big] - R_n\big[m_{n}(\cdot; \Theta_{\ell}),\mathcal{D}_{{\ell},n}\big] \bigg], \label{test_bis} \end{align} [[/math]]

where [math]R_n[/math] is defined for [math]\mathcal D=\mathcal{D}_{{\ell},n}[/math] or [math]\mathcal D={\mathcal{D}}^j_{{\ell},n}[/math] by

[[math]] \begin{align} R_n\big[m_{n}(\cdot; \Theta_{\ell}), \mathcal{D}\big] = \frac{1}{|\mathcal{D}|} \sum_{i: (\bX_i, Y_i) \in \mathcal{D}} (Y_i - m_{n}(\bX_i; \Theta_{\ell}) )^2. \label{test_bisb} \end{align} [[/math]]

It is easy to see that the population version of [math]\widehat{\mbox{MDA}}(X^{(j)}) [/math] is

[[math]] \begin{align*} \mbox{MDA}^{\star}(X^{(j)}) = \mathbb{E} \big[ Y - m_n(\bX'_{j}; \Theta) \big]^2 - \mathbb{E} \big[ Y - m_n(\bX;\Theta) \big]^2, \end{align*} [[/math]]

where [math]\bX'_{j} = (X^{(1)}, \ldots, X'^{(j)} , \ldots, X^{(p)})[/math] and [math]X'^{(j)}[/math] is an independent copy of [math]X^{(j)}[/math]. For classification purposes, the MDA still satisfies (\ref{test_bis}) and (\ref{test_bisb}) since [math]Y_i \in \{0,1\}[/math] (so, [math]R_n(m_n(\cdot; \Theta),\mathcal{D})[/math] is also the proportion of points that are correctly classified by [math]m_n(\cdot; \Theta)[/math] in [math]\mathcal{D}[/math]).

Further Reading

• Breiman, Leo (1996). "Bagging predictors". Machine Learning 24 (2): 123–140. doi:10.1007/BF00058655. 
• Alfaro, E., Gámez, M. and García, N. (2012). "adabag: An R package for classification with AdaBoost.M1, AdaBoost-SAMME and Bagging". 
• Kotsiantis, Sotiris (2014). "Bagging and boosting variants for handling classifications problems: a survey". Knowledge Eng. Review 29 (1): 78–100. doi:10.1017/S0269888913000313. 
• Boehmke, Bradley; Greenwell, Brandon (2019). "Bagging". Hands-On Machine Learning with R. Chapman & Hall. pp. 191–202. ISBN 978-1-138-49568-5.

Wikipedia References

• Wikipedia contributors. "Bootstrap aggregating". Wikipedia. Wikipedia. Retrieved 17 August 2022.
• Wikipedia contributors. "Boosting (machine learning)". Wikipedia. Wikipedia. Retrieved 17 August 2022.
• Wikipedia contributors. "Random forest". Wikipedia. Wikipedia. Retrieved 17 August 2022.