Partial Identification of Probability Distributions

[math] \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\cov}{Cov} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\Sel}{Sel} \DeclareMathOperator{\Bel}{Bel} \DeclareMathOperator{\cl}{cl} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\essinf}{essinf} \DeclareMathOperator{\esssup}{esssup} \newcommand{\mathds}{\mathbb} \renewcommand{\P}{\mathbb{P}} [/math]

The literature reviewed in this chapter starts with the analysis of what can be learned about functionals of probability distributions that are well-defined in the absence of a model. The approach is nonparametric, and it is typically constructive, in the sense that it leads to “plug-in” formulae for the bounds on the functionals of interest.

Selectively Observed Data

As in , suppose that a researcher is interested in learning the probability that an individual who is homeless at a given date has a home six months later. Here the population of interest is the people who are homeless at the initial date, and the outcome of interest [math]\ey[/math] is an indicator of whether the individual has a home six months later (so that [math]\ey=1[/math]) or remains homeless (so that [math]\ey=0[/math]). A random sample of homeless individuals is interviewed at the initial date, so that individual background attributes [math]\ex[/math] are observed, but six months later only a subset of the individuals originally sampled can be located. In other words, attrition from the sample creates a ’'selection problem whereby [math]\ey[/math] is observed only for a subset of the population. Let [math]\ed[/math] be an indicator of whether the individual can be located (hence [math]\ed=1[/math]) or not (hence [math]\ed=0[/math]). The question is what can the researcher learn about [math]\E_\sQ(\ey|\ex=x)[/math], with [math]\sQ[/math] the distribution of [math](\ey,\ex)[/math]? showed that [math]\E_\sQ(\ey|\ex=x)[/math] is not point identified in the absence of additional assumptions, but informative nonparametric bounds on this quantity can be obtained. In this section I review his approach, and discuss several important extensions of his original idea. Throughout the chapter, I formally state the structure of the problem under study as an “Identification Problem”, and then provide a solution, either in the form of a sharp identification region, or of an outer region. To set the stage, and at the cost of some repetition, I do the same here, slightly generalizing the question stated in the previous paragraph.

Identification Problem (Conditional Expectation of Selectively Observed Data)

Let [math]\ey \in \mathcal{Y}\subset \R[/math] and [math]\ex \in \mathcal{X}\subset \R^d[/math] be, respectively, an outcome variable and a vector of covariates with support [math]\cY[/math] and [math]\cX[/math] respectively, with [math]\cY[/math] a compact set. Let [math]\ed \in \{0,1\}[/math]. Suppose that the researcher observes a random sample of realizations of [math](\ex,\ed)[/math] and, in addition, observes the realization of [math]\ey[/math] when [math]\ed=1[/math]. Hence, the observed data is [math](\ey\ed,\ed,\ex)\sim \sP[/math]. Let [math]g:\cY\mapsto\R[/math] be a measurable function that attains its lower and upper bounds [math]g_0=\min_{y\in\cY}g(y)[/math] and [math]g_1=\max_{y\in\cY}g(y)[/math], and assume that [math]-\infty \lt g_0 \lt g_1 \lt \infty[/math]. Let [math]y_{j}\in\cY[/math] be such that [math]g(y_j)=g_j[/math], [math]j=0,1[/math]. In the absence of additional information, what can the researcher learn about [math]\E_\sQ(g(\ey)|\ex=x)[/math], with [math]\sQ[/math] the distribution of [math](\ey,\ex)[/math]?

’s analysis of this problem begins with a simple application of the law of total probability, that yields

[[math]] \begin{align} \sQ(\ey|\ex=x) = \sP(\ey|\ex=x,\ed=1)\sP(\ed=1|\ex=x)+\sR(\ey|\ex=x,\ed=0)\sP(\ed=0|\ex=x).\label{eq:LTP_md} \end{align} [[/math]]

Equation \eqref{eq:LTP_md} lends a simple but powerful anatomy of the selection problem. While [math]\sP(\ey|\ex=x,\ed=1)[/math] and [math]\sP(\ed|\ex=x)[/math] can be learned from the observable distribution [math]\sP(\ey\ed,\ed,\ex)[/math], under the maintained assumptions the sampling process reveals nothing about [math]\sR(\ey|\ex=x,\ed=0)[/math]. Hence, [math]\sQ(\ey|\ex=x)[/math] is not point identified. If one were to assume exogenous selection (or data missing at random conditional on [math]\ex[/math]), i.e., [math]\sR(\ey|\ex,\ed=0)=\sP(\ey|\ex,\ed=1)[/math], point identification would obtain. However, that assumption is non-refutable and it is well known that it may fail in applications . Let [math]\cT[/math] denote the space of all probability measures with support in [math]\cY[/math]. The unknown functional vector is [math]\{\tau(x),\upsilon(x)\}\equiv \{\sQ(\ey|\ex=x),\sR(\ey|\ex=x,\ed=0)\}[/math]. What the researcher can learn, in the absence of additional restrictions on [math]\sR(\ey|\ex=x,\ed=0)[/math], is the region of observationally equivalent distributions for [math]\ey|\ex=x[/math], and the associated set of expectations taken with respect to these distributions.

Theorem (Conditional Expectations of Selectively Observed Data)

Under the assumptions in Identification Problem,

[[math]] \begin{multline} \idr{\E_\sQ(g(\ey)|\ex=x)} = \Big[\E_\sP(g(\ey)|\ex=x,\ed=1)\sP(\ed=1|\ex=x)+ g_0P(\ed=0|\ex=x),\\ \E_\sP(g(\ey)|\ex=x,\ed=1)\sP(\ed=1|\ex=x)+ g_1\sP(\ed=0|\ex=x)\Big]\label{eq:bounds:mean:md} \end{multline} [[/math]]

is the sharp identification region for [math]\E_\sQ(g(\ey)|\ex=x)[/math].

Show Proof

Due to the discussion following equation \eqref{eq:LTP_md}, the collection of observationally equivalent distribution functions for [math]\ey|\ex=x[/math] is

[[math]] \begin{multline} \idr{\sQ(\ey|\ex=x)}=\Big\{ \tau(x) \in \cT: \tau(x) = \sP(\ey|\ex=x,\ed=1)\sP(\ed=1|\ex=x)\\ +\upsilon(x)\sP(\ed=0|\ex=x),~\text{for some } \upsilon(x)\in\cT\Big\}.\label{eq:Tau_md} \end{multline} [[/math]]

Next, observe that the lower bound in equation \eqref{eq:bounds:mean:md} is achieved by integrating [math]g(\ey)[/math] against the distribution [math]\tau(x)[/math] that results when [math]\upsilon(x)[/math] places probability one on [math]y_0[/math]. The upper bound is achieved by integrating [math]g(\ey)[/math] against the distribution [math]\tau(x)[/math] that results when [math]\upsilon(x)[/math] places probability one on [math]y_1[/math]. Both are contained in the set [math]\idr{\sQ(\ey|\ex=x)}[/math] in equation \eqref{eq:Tau_md}.

■

These are the worst case bounds, so called because assumptions free and therefore representing the widest possible range of values for the parameter of interest that are consistent with the observed data. A simple “plug-in” estimator for [math]\idr{\E_\sQ(g(\ey)|\ex=x)}[/math] replaces all unknown quantities in \eqref{eq:bounds:mean:md} with consistent estimators, obtained, e.g., by kernel or sieve regression. I return to consistent estimation of partially identified parameters in Section. Here I emphasize that identification problems are fundamentally distinct from finite sample inference problems. The latter are typically reduced as sample size increase (because, e.g., the variance of the estimator becomes smaller). The former do not improve, unless a different and better type of data is collected, e.g. with a smaller prevalence of missing data (see ).

shows that the proof of Theorem SIR- can be extended to obtain the smallest and largest points in the sharp identification region of any parameter that respects stochastic dominance. This is especially useful to bound the quantiles of [math]\ey|\ex=x[/math]. For any given [math]\alpha \in (0,1)[/math], let [math]\sq_{\sP}^{g(\ey)}(\alpha,1,x)\equiv \left\{\min t:\sP(g(\ey)\le t|\ed=1,\ex=x)\ge \alpha\right\}[/math]. Then the smallest and largest admissible values for the [math]\alpha[/math]-quantile of [math]g(\ey)|\ex=x[/math] are, respectively,

[[math]] \begin{align*} r(\alpha,x)&\equiv \begin{cases} \sq_{\sP}^{g(\ey)}\left(\left[1-\frac{(1-\alpha)}{\sP(\ed=1|\ex=x)}\right],1,x\right) & \text{if } \sP(\ed=1|\ex=x) \gt 1-\alpha,\\ g_0 & \text{otherwise}; \end{cases}\\ s(\alpha,x)&\equiv \begin{cases} \sq_{\sP}^{g(\ey)}\left(\left[\frac{\alpha}{\sP(\ed=1|\ex=x)}\right],1,x\right) & \text{if } \sP(\ed=1|\ex=x)\ge\alpha,\\ g_1 & \text{otherwise}. \end{cases} \end{align*} [[/math]]

The lower bound on [math]\E_\sQ(g(\ey)|\ex=x)[/math] is informative only if [math]g_0 \gt -\infty[/math], and the upper bound is informative only if [math]g_1 \lt \infty[/math]. By comparison, for any value of [math]\alpha[/math], [math]r(\alpha,x)[/math] and [math]s(\alpha,x)[/math] are generically informative if, respectively, [math]\sP(\ed=1|\ex=x) \gt 1-\alpha[/math] and [math]\sP(\ed=1|\ex=x) \ge \alpha[/math], regardless of the range of [math]g[/math]. further extends partial identification analysis to the study of spread parameters in the presence of missing data (as well as interval data, data combinations, and other applications). These parameters include ones that respect second order stochastic dominance, such as the variance, the Gini coefficient, and other inequality measures, as well as other measures of dispersion which do not respect second order stochastic dominance, such as interquartile range and ratio. shows that the sharp identification region for these parameters can be obtained by fixing the mean or quantile of the variable of interest at a specific value within its sharp identification region, and deriving a distribution consistent with this value which is ``compressed" with respect to the ones which bound the cumulative distribution function (CDF) of the variable of interest, and one which is ``dispersed" with respect to them. Heuristically, the compressed distribution minimizes spread, while the dispersed one maximizes it (the sense in which this optimization occurs is formally defined in the paper). The intuition for this is that a compressed CDF is first below and then above any non-compressed one; a dispersed CDF is first above and then below any non-dispersed one. Second-stage optimization over the possible values of the mean or the quantile delivers unconstrained bounds. The main results of the paper are sharp identification regions for the expectation and variance, for the median and interquartile ratio, and for many other combinations of parameters.

Key Insight (Identification is not a binary event): Identification Problem is mathematically simple, but it puts forward a new approach to empirical research. The traditional approach aims at finding a sufficient (possibly minimal) set of assumptions guaranteeing point identification of parameters, viewing identification as an “all or nothing” notion, where either the functional of interest can be learned exactly or nothing of value can be learned. The partial identification approach pioneered by points out that much can be learned from combination of data and assumptions that restrict the functionals of interest to a set of observationally equivalent values, even if this set is not a singleton. Along the way, points out that in Identification Problem the observed outcome is the singleton [math]\ey[/math] when [math]\ed=1[/math], and the set [math]\cY[/math] when [math]\ed=0[/math]. This is a random closed set, see Definition. I return to this connection in Section Interval Data.

Despite how transparent the framework in Identification Problem is, important subtleties arise even in this seemingly simple context. For a given [math]t\in\R[/math], consider the function [math]g(\ey)=\one(\ey\le t)[/math], with [math]\one(A)[/math] the indicator function taking the value one if the logical condition in parentheses holds and zero otherwise. Then equation \eqref{eq:bounds:mean:md} yields ’'pointwise-sharp bounds on the CDF of [math]\ey[/math] at any fixed [math]t\in\R[/math]:

[[math]] \begin{multline} \label{eq:pointwise_bounds_F_md} \idr{\sQ(\ey\le t|\ex=x)} = \left[\sP(\ey\le t|\ex=x,\ed=1)\sP(\ed=1|\ex=x)\right.,\\ \left.\sP(\ey\le t|\ex=x,\ed=1)\sP(\ed=1|\ex=x)+ \sP(\ed=0|\ex=x)\right]. \end{multline} [[/math]]

Yet, the collection of CDFs that belong to the band defined by \eqref{eq:pointwise_bounds_F_md} is not the sharp identification region for the CDF of [math]\ey|\ex=x[/math]. Rather, it constitutes an outer region, as originally pointed out by .

Theorem (Cumulative Distribution Function of Selectively Observed Data)

Let [math]\cC[/math] denote the collection of cumulative distribution functions on [math]\cY[/math]. Then, under the assumptions in Identification Problem,

[[math]] \begin{multline} \label{eq:outer_cdf_md} \outr{\sF(\ey|\ex=x)}=\left\{\sF\in\cC:~\sP(\ey\le t|\ex=x,\ed=1)\sP(\ed=1|\ex=x)\le\sF(t|x)\le \right. \\ \left.\sP(\ey\le t|\ex=x,\ed=1)\sP(\ed=1|\ex=x)+ \sP(\ed=0|\ex=x)~\forall t\in\R \right\} \end{multline} [[/math]]

is an outer region for the CDF of [math]\ey|\ex=x[/math].

Show Proof

Any admissible CDF for [math]\ey|\ex=x[/math] belongs to the family of functions in equation \eqref{eq:outer_cdf_md}. However, the bound in equation \eqref{eq:outer_cdf_md} does not impose the restriction that for any [math]t_0\le t_1[/math],

[[math]] \begin{align} \label{eq:CDF_md_Kinterval} \sQ(t_0\le\ey\le t_1|\ex=x)\ge \sP(t_0\le\ey\le t_1|\ex=x,\ed=1)\sP(\ed=1|\ex=x). \end{align} [[/math]]

This restriction is implied by the maintained assumptions, but is not necessarily satisfied by all CDFs in [math]\outr{\sF(\ey|\ex=x)}[/math], as illustrated in the following simple example.

■

The tube defined by inequalities \eqref{eq:pointwise_bounds_F_md} in the set-up of Example, and the CDF in \eqref{eq:CDF_counterexample_md}.

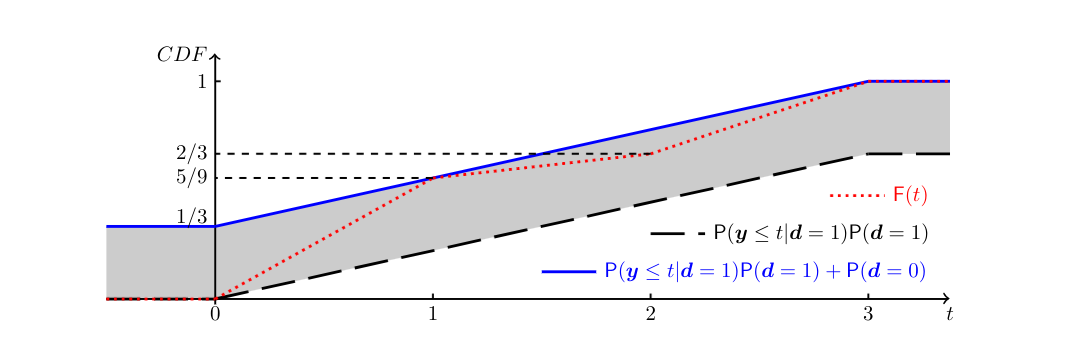
Example

Omit [math]\ex[/math] for simplicity, let [math]\sP(\ed=1)=\frac{2}{3}[/math], and let

[[math]] \sP(\ey\le t|\ed=1)\left\{ \begin{array}{lll} 0 & \textrm{if} & t \lt 0,\\ \frac{1}{3}t & \textrm{if} & 0\le t \lt 3,\\ 1 & \textrm{if} & t\ge 3. \end{array} \right. [[/math]]

The bounding functions and associated tube from the inequalities in \eqref{eq:pointwise_bounds_F_md} are depicted in Figure. Consider the cumulative distribution function

[[math]] \begin{align} \label{eq:CDF_counterexample_md} \sF(t)= \left\{ \begin{array}{lll} 0 & \textrm{if}\,\, & t \lt 0,\\ \frac{5}{9}t & \textrm{if} & 0\le t \lt 1,\\ \frac{1}{9}t+\frac{4}{9} & \textrm{if} & 1\le t \lt 2,\\ \frac{1}{3}t & \textrm{if} & 2\le t \lt 3,\\ 1 & \textrm{if} & t\ge 3. \end{array} \right. \end{align} [[/math]]

For each [math]t\in\R[/math], [math]\sF(t)[/math] lies in the tube defined by equation \eqref{eq:pointwise_bounds_F_md}. However, it cannot be the CDF of [math]\ey[/math], because [math]\sF(2)-\sF(1)=\frac{1}{9} \lt \sP(1\le\ey\le 2|\ed=1)\sP(\ed=1)[/math], directly contradicting equation \eqref{eq:CDF_md_Kinterval}.

How can one characterize the sharp identification region for the CDF of [math]\ey|\ex=x[/math] under the assumptions in Identification Problem? In general, there is not a single answer to this question: different methodologies can be used. Here I use results in and , which yield an alternative characterization of [math]\idr{\sQ(\ey|\ex=x)}[/math] that translates directly into a characterization of [math]\idr{\sF(\ey|\ex=x)}[/math].

Theorem (Conditional Distribution and CDF of Selectively Observed Data)

Given [math]\tau\in\cT[/math], let [math]\tau_K(x)[/math] denote the probability that distribution [math]\tau[/math] assigns to set [math]K[/math] conditional on [math]\ex=x[/math], with [math]\tau_y(x)\equiv\tau_{\{y\}}(x)[/math]. Under the assumptions in Identification Problem,

[[math]] \begin{align} \idr{\sQ(\ey|\ex=x)}&=\Big\{\tau(x) \in \cT: \tau_K(x) \ge \sP(\ey\in K|\ex=x,\ed=1)\sP(\ed=1|\ex=x),\,\forall K\subset \cY \Big\},\label{eq:sharp_id_P_md_Manski} \end{align} [[/math]]

where [math]K[/math] is measurable. If [math]\cY[/math] is countable,

[[math]] \begin{align} \idr{\sQ(\ey|\ex=x)}&=\Big\{\tau(x) \in \cT: \tau_y(x) \ge \sP(\ey=y|\ex=x,\ed=1)\sP(\ed=1|\ex=x),\,\forall y\in \cY \Big\}.\label{eq:sharp_id_P_md_discrete} \end{align} [[/math]]

If [math]\cY[/math] is a bounded interval,

[[math]] \begin{multline} \idr{\sQ(\ey|\ex=x)}=\Big\{\tau(x) \in \cT: \tau_{[t_0,t_1]}(x) \ge \\ \sP(t_0\le\ey\le t_1|\ex=x,\ed=1)\sP(\ed=1|\ex=x),\,\forall t_0\le t_1, t_0,t_1\in\cY \Big\}.\label{eq:sharp_id_P_md_interval} \end{multline} [[/math]]

Show Proof

The characterization in \eqref{eq:sharp_id_P_md_Manski} follows from equation \eqref{eq:Tau_md}, observing that if [math]\tau(x)\in\idr{\sQ(\ey|\ex=x)}[/math] as defined in equation \eqref{eq:Tau_md}, then there exists a distribution [math]\upsilon(x)\in\cT[/math] such that [math]\tau(x) = \sP(\ey|\ex=x,\ed=1)\sP(\ed=1|\ex=x)+\upsilon(x)\sP(\ed=0|\ex=x)[/math]. Hence, by construction [math]\tau_K(x) \ge \sP(\ey\in K|\ex=x,\ed=1)\sP(\ed=1|\ex=x)[/math], [math]\forall K\subset \cY[/math]. Conversely, if one has [math]\tau_K(x) \ge \sP(\ey\in K|\ex=x,\ed=1)\sP(\ed=1|\ex=x)[/math], [math]\forall K\subset \cY[/math], one can define [math]\upsilon(x)=\frac{\tau(x) - \sP(\ey|\ex=x,\ed=1)\sP(\ed=1|\ex=x)}{\sP(\ed=0|\ex=x)}[/math]. The resulting [math]\upsilon(x)[/math] is a probability measure, and hence [math]\tau(x)\in\idr{\sQ(\ey|\ex=x)}[/math] as defined in equation \eqref{eq:Tau_md}. When [math]\cY[/math] is countable, if [math]\tau_y(x) \ge \sP(\ey=y|\ex=x,\ed=1)\sP(\ed=1|\ex=x)[/math] it follows that for any [math]K\subset\cY[/math],

[[math]] \begin{multline} \tau_K(x)=\sum_{y\in K}\tau_y(x) \ge \sum_{y\in K}\sP(\ey=y|\ex=x,\ed=1)\sP(\ed=1|\ex=x)\\ =\sP(\ey\in K|\ex=x,\ed=1)\sP(\ed=1|\ex=x).\notag \end{multline} [[/math]]

The result in equation \eqref{eq:sharp_id_P_md_interval} is proven in using elements of random set theory, to which I return in Section Interval Data. Using elements of random set theory it is also possible to show that the characterization in \eqref{eq:sharp_id_P_md_Manski} requires only to check the inequalities for [math]K[/math] the compact subsets of [math]\cY[/math].

■

This section provides sharp identification regions and outer regions for a variety of functionals of interest. The computational complexity of these characterizations varies widely. Sharp bounds on parameters that respect stochastic dominance only require computing the parameters with respect to two probability distributions. An outer region on the CDF can be obtained by evaluating all tail probabilities of a certain distribution. A sharp identification region on the CDF requires evaluating the probability that a certain distribution assigns to all intervals. I return to computational challenges in partial identification in Section.

Treatment Effects with and without Instrumental Variables

The discussion of partial identification of probability distributions of selectively observed data naturally leads to the question of its implications for program evaluation. The literature on program evaluation is vast. The purpose of this section is exclusively to show how the ideas presented in Section Selectively Observed Data can be applied to learn features of treatment effects of interest, when no assumptions are imposed on treatment selection and outcomes. I also provide examples of assumptions that can be used to tighten the bounds. To keep this chapter to a manageable length, I discuss only partial identification of the average response to a treatment and of the average treatment effect (ATE). There are many different parameters that received much interest in the literature. Examples include the local average treatment effect of and the marginal treatment effect of . For thorough discussions of the literature on program evaluation, I refer to the textbook treatments in and , to the Handbook chapters by and , and to the review articles by and .

Using standard notation (e.g., ), let [math]\ey:\T \mapsto \cY[/math] be an individual-specific response function, with [math]\T=\{0,1,\dots,T\}[/math] a finite set of mutually exclusive and exhaustive treatments, and let [math]\es[/math] denote the individual's received treatment (taking its realizations in [math]\T[/math]). The researcher observes data [math](\ey,\es,\ex)\sim\sP[/math], with [math]\ey\equiv\ey(\es)[/math] the outcome corresponding to the received treatment [math]\es[/math], and [math]\ex[/math] a vector of covariates. The outcome [math]\ey(t)[/math] for [math]\es\neq t[/math] is counterfactual, and hence can be conceptualized as missing. Therefore, we are in the framework of Identification Problem and all the results from Section Selectively Observed Data apply in this context too, subject to adjustments in notation. For example, using Theorem SIR-,

[[math]] \begin{align} \idr{\E_\sQ(\ey(t)|\ex=x)}= \Big[\E_\sP&(\ey|\ex=x,\es=t)\sP(\es=t|\ex=x)+ y_0P(\es\neq t|\ex=x),\notag\\ &\E_\sP(\ey|\ex=x,\es=t)\sP(\es=t|\ex=x)+ y_1P(\es\neq t|\ex=x)\Big],\label{eq:WCB:treat} \end{align} [[/math]]

where [math]y_0\equiv\inf_{y\in\cY}y[/math], [math]y_1\equiv\sup_{y\in\cY}y[/math]. If [math]y_0 \lt \infty[/math] and/or [math]y_1 \lt \infty[/math], these worst case bounds are informative. When both are infinite, the data is uninformative in the absence of additional restrictions. If the researcher is interested in an Average Treatment Effect (ATE), e.g.

[[math]] \begin{multline*} \E_\sQ(\ey(t_1)|\ex=x)-\E_\sQ(\ey(t_0)|\ex=x)=\\ \E_\sP(\ey|\ex=x,\es=t_1)\sP(\es=t_1|\ex=x)+\E_\sQ(\ey(t_1)|\ex=x,\es\neq t_1)\sP(\es\neq t_1|\ex=x)\\ -\E_\sP(\ey|\ex=x,\es=t_0)\sP(\es=t_0|\ex=x)-\E_\sQ(\ey(t_0)|\ex=x,\es\neq t_0)\sP(\es\neq t_0|\ex=x), \end{multline*} [[/math]]

with [math]t_0,t_1\in\T[/math], sharp worst case bounds on this quantity can be obtained as follows. First, observe that the empirical evidence reveals [math]\E_\sP(\ey|\ex=x,\es=t_j)[/math] and [math]\sP(\es|\ex=x)[/math], but is uninformative about [math]\E_\sQ(\ey(t_j)|\ex=x,\es\neq t_j)[/math], [math]j=0,1[/math]. Each of the latter quantities (the expectations of [math]\ey(t_0)[/math] and [math]\ey(t_1)[/math] conditional on different realizations of [math]\es[/math] and [math]\ex=x[/math]) can take any value in [math][y_0,y_1][/math]. Hence, the sharp lower bound on the ATE is obtained by subtracting the upper bound on [math]\E_\sQ(\ey(t_0)|\ex=x)[/math] from the lower bound on [math]\E_\sQ(\ey(t_1)|\ex=x)[/math]. The sharp upper bound on the ATE is obtained by subtracting the lower bound on [math]\E_\sQ(\ey(t_0)|\ex=x)[/math] from the upper bound on [math]\E_\sQ(\ey(t_1)|\ex=x)[/math]. The resulting bounds have width equal to [math](y_1-y_0)[2-\sP(\es=t_1|\ex=x)-\sP(\es=t_0|\ex=x)]\in[(y_1-y_0),2(y_1-y_0)][/math], and hence are informative only if both [math]y_0 \gt -\infty[/math] and [math]y_1 \lt \infty[/math]. As the largest logically possible value for the ATE (in the absence of information from data) cannot be larger than [math](y_1-y_0)[/math], and the smallest cannot be smaller than [math]-(y_1-y_0)[/math], the sharp bounds on the ATE always cover zero.

Key Insight: How should one think about the finding on the size of the worst case bounds on the ATE? On the one hand, if both [math]y_0 \lt \infty[/math] and [math]y_1 \lt \infty[/math] the bounds are informative, because they are a strict subset of the ATE's possible realizations. On the other hand, they reveal that the data alone are silent on the sign of the ATE. This means that assumptions play a crucial role in delivering stronger conclusions about this policy relevant parameter. The partial identification approach to empirical research recommends that as assumptions are added to the analysis, one systematically reports how each contributes to shrinking the bounds, making transparent their role in shaping inference.

What assumptions may researchers bring to bear to learn more about treatment effects of interest? The literature has provided a wide array of well motivated and useful restrictions. Here I consider two examples. The first one entails shape restrictions on the treatment response function, leaving selection unrestricted. obtains bounds on treatment effects under the assumption that the response functions are monotone, semi-monotone, or concave-monotone. These restrictions are motivated by economic theory, where it is commonly presumed, e.g., that demand functions are downward sloping and supply functions are upward sloping. Let the set [math]\T[/math] be ordered in terms of degree of intensity. Then 's monotone treatment response assumption requires that

[[math]] \begin{align*} t_1\ge t_0 \Rightarrow \sQ(\ey(t_1)\ge\ey(t_0))=1~~\forall t_0,t_1\in\T. \end{align*} [[/math]]

Under this assumption, one has a sharp characterization of what can be learned about [math]\ey(t)[/math]:

[[math]] \begin{align} \ey(t)\in \begin{cases} (-\infty,\ey]\cap\cY & \text{if } t \lt \es,\\ \{\ey\} & \text{if } t=\es,\\ [\ey,\infty)\cap\cY & \text{if } t \gt \es. \end{cases}\label{eq:RCS:MTR} \end{align} [[/math]]

Hence, the sharp bounds on [math]\E_\sQ(\ey(t)|\ex=x)[/math] are

[[math]] \begin{align} \idr{\E_\sQ(\ey(t)|\ex=x)}= \Big[\E_\sP&(\ey|\ex=x,\es\le t)\sP(\es\le t|\ex=x)+ y_0P(\es \gt t|\ex=x),\notag\\ &\E_\sP(\ey|\ex=x,\es\ge t)\sP(\es \ge t|\ex=x)+ y_1P(\es \lt t|\ex=x)\Big].\label{eq:MTR:treat} \end{align} [[/math]]

This finding highlights some important facts. Under the monotone treatment response assumption, the bounds on [math]\E_\sQ(\ey(t)|\ex=x)[/math] are obtained using information from all [math](\ey,\es)[/math] pairs (given [math]\ex=x[/math]), while the bounds in \eqref{eq:WCB:treat} only use the information provided by [math](\ey,\es)[/math] pairs for which [math]\es=t[/math] (given [math]\ex=x[/math]). As a consequence, the bounds in \eqref{eq:MTR:treat} are informative even if [math]\sP(\es= t|\ex=x)=0[/math], whereas the worst case bounds are not. Concerning the ATE with [math]t_1 \gt t_0[/math], under monotone treatment response its lower bound is zero, and its upper bound is obtained by subtracting the lower bound on [math]\E_\sQ(\ey(t_0)|\ex=x)[/math] from the upper bound on [math]\E_\sQ(\ey(t_1)|\ex=x)[/math], where both bounds are obtained as in \eqref{eq:MTR:treat} . The second example of assumptions used to tighten worst case bounds is that of exclusion restrictions, as in, e.g., . Suppose the researcher observes a random variable [math]\ez[/math], taking its realizations in [math]\cZ[/math], such that

[[math]] \begin{align} \E_\sQ(\ey(t)|\ez,\ex)=\E_\sQ(\ey(t)|\ex)~~\forall t \in\T,~\ex\text{-a.s.}.\label{eq:ass:MI} \end{align} [[/math]]

This assumption is treatment-specific, and requires that the treatment response to [math]t[/math] is mean independent with [math]\ez[/math]. It is easy to show that under the assumption in \eqref{eq:ass:MI}, the bounds on [math]\E_\sQ(\ey(t)|\ex=x)[/math] become

[[math]] \begin{multline} \idr{\E_\sQ(\ey(t)|\ex=x)}=\Big[\mathrm{ess}\sup_\ez\E_\sP(\ey|\ex=x,\es=t,\ez)\sP(\es=t|\ex=x,\ez)+ y_0P(\es\neq t|\ex=x,\ez),\\ \mathrm{ess}\inf_\ez\E_\sP(\ey|\ex=x,\es=t,\ez)\sP(\es=t|\ex=x,\ez)+ y_1P(\es\neq t|\ex=x,\ez)\Big].\label{eq:intersection:bounds} \end{multline} [[/math]]

These are called intersection bounds because they are obtained as follows. Given [math]\ex[/math] and [math]\ez[/math], one uses \eqref{eq:WCB:treat} to obtain sharp bounds on [math]\E_\sQ(\ey(t)|\ez=z,\ex=x)[/math]. Due to the mean independence assumption in \eqref{eq:ass:MI}, [math]\E_\sQ(\ey(t)|\ex=x)[/math] must belong to each of these bounds [math]\ez[/math]-a.s., hence to their intersection. The expression in \eqref{eq:intersection:bounds} follows. If the instrument affects the probability of being selected into treatment, or the average outcome for the subpopulation receiving treatment [math]t[/math], the bounds on [math]\E_\sQ(\ey(t)|\ex=x)[/math] shrink. If the bounds are empty, the mean independence assumption can be refuted (see Section for a discussion of misspecification in partial identification). generalize the notion of instrumental variable to monotone instrumental variable, and show how these can be used to obtain tighter bounds on treatment effect parameters. They also show how shape restrictions and exclusion restrictions can jointly further tighten the bounds. generalizes these findings to the case where treatment response may have social interactions -- that is, each individual's outcome depends on the treatment received by all other individuals.

Interval Data

Identification Problem, as well as the treatment evaluation problem in Section Treatment Effects with and without Instrumental Variables, is an instance of the more general question of what can be learned about (functionals of) probability distributions of interest, in the presence of interval valued outcome and/or covariate data. Such data have become commonplace in Economics. For example, since the early 1990s the Health and Retirement Study collects income data from survey respondents in the form of brackets, with degenerate (singleton) intervals for individuals who opt to fully reveal their income (see, e.g., ). Due to concerns for privacy, public use tax data are recorded as the number of tax payers which belong to each of a finite number of cells (see, e.g., ). The Occupational Employment Statistics (OES) program at the Bureau of Labor Statistics collects wage data from employers as intervals, and uses these data to construct estimates for wage and salary workers in more than 800 detailed occupations. and document the extensive prevalence of rounding in survey responses to probabilistic expectation questions, and propose to use a person's response pattern across different questions to infer his rounding practice, the result being interpretation of reported numerical values as interval data. Other instances abound. Here I focus first on the case of interval outcome data.

Identification Problem (Interval Outcome Data)

Assume that in addition to being compact, either [math]\cY[/math] is countable or [math]\cY=[y_0,y_1][/math], with [math]y_0=\min_{y\in\cY}y[/math] and [math]y_1=\max_{y\in\cY}y[/math]. Let [math](\yL,\yU,\ex)\sim\sP[/math] be observable random variables and [math]\ey[/math] be an unobservable random variable whose distribution (or features thereof) is of interest, with [math]\yL,\yU,\ey\in\cY[/math]. Suppose that [math](\yL,\yU,\ey)[/math] are such that [math]\sR(\yL\le\ey\le\yU)=1[/math]. In the absence of additional information, what can the researcher learn about features of [math]\sQ(\ey|\ex=x)[/math], the conditional distribution of [math]\ey[/math] given [math]\ex=x[/math]?

It is immediate to obtain the sharp identification region

[[math]] \begin{align*} \idr{\E_\sQ(\ey|\ex=x)} = \left[\E_\sP(\yL|\ex=x),\E_\sP(\yU|\ex=x)\right]. \end{align*} [[/math]]

As in the previous section, it is also easy to obtain sharp bounds on parameters that respect stochastic dominance, and pointwise-sharp bounds on the CDF of [math]\ey[/math] at any fixed [math]t\in\R[/math]:

[[math]] \begin{align} \label{eq:pointwise_bounds_F} \sP(\yU\le t|\ex=x)\le\sQ(\ey\le t|\ex=x)\le\sP(\yL\le t|\ex=x). \end{align} [[/math]]

In this case too, however, as in Theorem OR-, the tube of CDFs satisfying equation \eqref{eq:pointwise_bounds_F} for all [math]t\in\R[/math] is an outer region for the CDF of [math]\ey|\ex=x[/math], rather than its sharp identification region. Indeed, also in this context it is easy to construct examples similar to Example. How can one characterize the sharp identification region for the probability distribution of [math]\ey|\ex[/math] when one observes [math](\yL,\yU,\ex)[/math] and assumes [math]\sR(\yL\le\ey\le\yU)=1[/math]? Again, there is not a single answer to this question. Depending on the specific problem at hand, e.g., the specifics of the interval data and whether [math]\ey[/math] is assumed discrete or continuous, different methods can be applied. I use random set theory to provide a characterization of [math]\idr{\sQ(\ey|\ex=x)}[/math]. Let

[[math]] \begin{align*} \eY\equiv [\yL,\yU]\cap\cY. \end{align*} [[/math]]

Then [math]\eY[/math] is a random closed set according to Definition. The requirement [math]\sR(\yL\le\ey\le\yU)=1[/math] can be equivalently expressed as

[[math]] \begin{align} \label{eq:y_in_Y} \ey\in\eY~~\text{almost surely.} \end{align} [[/math]]

Equation \eqref{eq:y_in_Y}, together with knowledge of [math]\sP[/math], exhausts all the information in the data and maintained assumptions. In order to harness such information to characterize the set of observationally equivalent probability distributions for [math]\ey[/math], one can leverage a result due to (and ), reported in Theorem in Appendix, which allows one to translate \eqref{eq:y_in_Y} into a collection of conditional moment inequalities. Specifically, let [math]\cT[/math] denote the space of all probability measures with support in [math]\cY[/math].

Theorem (Conditional Distribution of Interval-Observed Outcome Data)

Given [math]\tau\in\cT[/math], let [math]\tau_K(x)[/math] denote the probability that distribution [math]\tau[/math] assigns to set [math]K[/math] conditional on [math]\ex=x[/math]. Under the assumptions in Identification Problem, the sharp identification region for [math]\sQ(\ey|\ex=x)[/math] is

[[math]] \begin{align} \idr{\sQ(\ey|\ex=x)}=\Big\{\tau(x) \in \cT: \tau_K(x) \ge \sP(\eY\subset K|\ex=x),\,\forall K\subset \cY,\,K\text{ compact} \Big\}\label{eq:sharp_id_P_interval_1} \end{align} [[/math]]

When [math]\cY=[y_0,y_1][/math], equation \eqref{eq:sharp_id_P_interval_1} becomes

[[math]] \begin{align} \idr{\sQ(\ey|\ex=x)}=\Big\{\tau(x) \in \cT: \tau_{[t_0,t_1]}(x) \ge \sP(\yL\ge t_0,\yU\le t_1|\ex=x),\,\forall t_0\le t_1,\, t_0,t_1 \in \cY \Big\}.\label{eq:sharp_id_P_interval_2} \end{align} [[/math]]

Show Proof

Theorem yields \eqref{eq:sharp_id_P_interval_1}. If [math]\cY=[y_0,y_1][/math], show that it suffices to verify the inequalities in \eqref{eq:sharp_id_P_interval_2} for sets [math]K[/math] that are intervals.

■

Compare equation \eqref{eq:sharp_id_P_interval_1} with equation \eqref{eq:sharp_id_P_md_Manski}. Under the set-up of Identification Problem, when [math]\ed=1[/math] we have [math]\eY=\{\ey\}[/math] and when [math]\ed=0[/math] we have [math]\eY=\cY[/math]. Hence, for any [math]K \subsetneq \cY[/math], [math]\sP(\eY \subset K|\ex=x)=\sP(\ey\in K|\ex=x,\ed=1)\sP(\ed=1)[/math]. It follows that the characterizations in \eqref{eq:sharp_id_P_interval_1} and \eqref{eq:sharp_id_P_md_Manski} are equivalent. If [math]\cY[/math] is countable, it is easy to show that \eqref{eq:sharp_id_P_interval_1} simplifies to \eqref{eq:sharp_id_P_md_Manski} (see, e.g., ).

Key Insight (Random set theory and partial identification):The mathematical framework for the analysis of random closed sets embodied in random set theory is naturally suited to conduct identification analysis and statistical inference in partially identified models. This is because, as argued by and , lack of point identification can often be traced back to a collection of random variables that are consistent with the available data and maintained assumptions. In turn, this collection of random variables is equal to the family of selections of a properly specified random closed set, so that random set theory applies. The interval data case is a simple example that illustrates this point. More examples are given throughout this chapter. As mentioned in the Introduction, the exercise of defining the random closed set that is relevant for the problem under consideration is routinely carried out in partial identification analysis, even when random set theory is not applied. For example, in the case of treatment effect analysis with monotone response function, derived the set in the right-hand-side of \eqref{eq:RCS:MTR}, which satisfies Definition def:rcs.

An attractive feature of the characterization in \eqref{eq:sharp_id_P_interval_1} is that it holds regardless of the specific assumptions on [math]\yL,\,\yU[/math], and [math]\cY[/math]. Later sections in this chapter illustrate how Theorem delivers the sharp identification region in other more complex instances of partial identification of probability distributions, as well as in structural models. In Chapter XXX in this Volume, apply Theorem to obtain sharp identification regions for functionals of interest in the important class of generalized instrumental variable models. To avoid repetitions, I do not systematically discuss that class of models in this chapter. When addressing questions about features of [math]\sQ(\ey|\ex=x)[/math] in the presence of interval outcome data, an alternative approach (e.g. ) looks at all (random) mixtures of [math]\yL,\yU[/math]. The approach is based on a random variable [math]\eu[/math] (a selection mechanism that picks an element of [math]\eY[/math]) with values in [math][0,1][/math], whose distribution conditional on [math]\yL,\yU[/math] is left completely unspecified. Using this random variable, one defines

[[math]] \begin{align} \ey_\eu=\eu\yL+(1-\eu)\yU.\label{eq:y_s} \end{align} [[/math]]

The sharp identification region in Theorem SIR- can be characterized as the collection of conditional distributions of all possible random variables [math]\ey_\eu[/math] as defined in \eqref{eq:y_s}, given [math]\ex=x[/math]. This is because each [math]\ey_\eu[/math] is a (stochastic) convex combination of [math]\yL,\yU[/math], hence each of these random variables satisfies [math]\sR(\yL\le\ey_\eu\le\yU)=1[/math]. While such characterization is sharp, it can be of difficult implementation in practice, because it requires working with all possible random variables [math]\ey_\eu[/math] built using all possible random variables [math]\eu[/math] with support in [math][0,1][/math]. Theorem allows one to bypass the use of [math]\eu[/math], and obtain directly a characterization of the sharp identification region for [math]\sQ(\ey|\ex=x)[/math] based on conditional moment inequalities. study nonparametric conditional prediction problems with missing outcome and/or missing covariate data. Their analysis shows that this problem is considerably more pernicious than the case where only outcome data are missing. For the case of interval covariate data, provide a set of sufficient conditions under which simple and elegant sharp bounds on functionals of [math]\sQ(\ey|\ex)[/math] can be obtained, even in this substantially harder identification problem. Their assumptions are listed in Identification Problem, and their result (with proof) in Theorem SIR-.

Identification Problem (Interval Covariate Data)

Let [math](\ey,\xL,\xU)\sim\sP[/math] be observable random variables in [math]\R\times\R\times\R[/math] and [math]\ex\in\R[/math] be an unobservable random variable. Suppose that [math]\sR[/math], the joint distribution of [math](\ey,\ex,\xL,\xU)[/math], is such that: (I) [math]\sR(\xL\le\ex\le\xU)=1[/math]; (M) [math]\E_\sQ(\ey|\ex=x)[/math] is weakly increasing in [math]x[/math]; and (MI) [math]\E_{\sR}(\ey|\ex,\xL,\xU)=\E_\sQ(\ey|\ex)[/math]. In the absence of additional information, what can the researcher learn about [math]\E_\sQ(\ey|\ex=x)[/math] for given [math]x\in\cX[/math]?

Compared to the earlier discussion for the interval outcome case, here there are two additional assumptions. The monotonicity condition (M) is a simple shape restrictions, which however requires some prior knowledge about the joint distribution of [math](\ey,\ex)[/math]. The mean independence restriction (MI) requires that if [math]\ex[/math] were observed, knowledge of [math](\xL,\xU)[/math] would not affect the conditional expectation of [math]\ey|\ex[/math]. The assumption is not innocuous, as pointed out by the authors. For example, it may fail if censoring is endogenous.

Theorem (Conditional Expectation with Interval-Observed Covariate Data)

Under the assumptions of Identification Problem, the sharp identification region for [math]\E_\sQ(\ey|\ex=x)[/math] for given [math]x\in\cX[/math] is

[[math]] \begin{align} \label{eq:man:tam:nonpar} \idr{\E_\sQ(\ey|\ex=x)}=\left[\sup_{\xU\le x}\E_\sP(\ey|\xL,\xU),\inf_{\xL \ge x}\E_\sP(\ey|\xL,\xU)\right]. \end{align} [[/math]]

Show Proof

The law of iterated expectations and the independence assumption yield [math]\E_\sP(\ey|\xL,\xU)=\int \E_\sQ(\ey|\ex)d\sR(\ex|\xL,\xU)[/math]. For all [math]\underline{x}\le \bar{x}[/math], the monotonicity assumption and the fact that [math]\ex\in[\xL,\xU][/math]-a.s. yield [math]\E_\sQ(\ey|\ex=\underline{x})\le \int \E_\sQ(\ey|\ex)d\sR(\ex|\xL=\underline{x},\xU=\bar{x}) \le \E_\sQ(\ey|\ex=\bar{x})[/math]. Putting this together with the previous result, [math]\E_\sQ(\ey|\ex=\underline{x})\le \E_\sP(\ey|\xL=\underline{x},\xU=\bar{x}) \le \E_\sQ(\ey|\ex=\bar{x})[/math]. Then (using again the monotonicity assumption) for any [math]x\ge \bar{x}[/math], [math]\E_{\sP}(\ey|\xL=\underline{x},\xU=\bar{x}) \le \E_\sQ(\ey|\ex=x)[/math] so that the lower bound holds. The bound is weakly increasing as a function of [math]x[/math], so that the monotonicity assumption on [math]\E_\sQ(\ey|\ex=x)[/math] holds and the bound is sharp. The argument for the upper bound can be concluded similarly.

■

Learning about functionals of [math]\sQ(\ey|\ex=x)[/math] naturally implies learning about predictors of [math]\ey|\ex=x[/math]. For example, [math]\idr{\E_\sQ(\ey|\ex=x)}[/math] yields the collection of values for the best predictor under square loss; [math]\idr{\M_\sQ(\ey|\ex=x)}[/math], with [math]\M_\sQ[/math] the median with respect to distribution [math]\sQ[/math], yields the collection of values for the best predictor under absolute loss. And so on. A related but distinct problem is that of parametric conditional prediction. Often researchers specify not only a loss function for the prediction problem, but also a parametric family of predictor functions, and wish to learn the member of this family that minimizes expected loss. To avoid confusion, let me clarify that here I am not referring to a parametric assumption on the best predictor, e.g., that [math]\E_\sQ(\ey|\ex)[/math] is a linear function of [math]\ex[/math]. I return to such assumptions at the end of this section. For now, in the example of linearity and square loss, I am referring to best linear prediction, i.e., best linear approximation to [math]\E_\sQ(\ey|\ex)[/math]. discusses what can be learned about the best linear predictor of [math]\ey[/math] conditional on [math]\ex[/math], when only interval data on [math](\ey,\ex)[/math] is available. I treat first the case of interval outcome and perfectly observed covariates.

Identification Problem (Parametric Prediction with Interval Outcome Data)

Maintain the same assumptions as in Identification Problem. Let [math](\yL,\yU,\ex)\sim\sP[/math] be observable random variables and [math]\ey[/math] be an unobservable random variable, with [math]\sR(\yL\le\ey\le\yU)=1[/math]. In the absence of additional information, what can the researcher learn about the best linear predictor of [math]\ey[/math] given [math]\ex=x[/math]?

For simplicity suppose that [math]\ex[/math] is a scalar, and let [math]\theta=[\theta_0~\theta_1]^\top\in\Theta\subset\R^2[/math] denote the parameter vector of the best linear predictor of [math]\ey|\ex[/math]. Assume that [math]Var(\ex) \gt 0[/math]. Combining the definition of best linear predictor with a characterization of the sharp identification region for the joint distribution of [math](\ey,\ex)[/math], we have that

[[math]] \begin{equation} \idr{\theta}=\left\{ \vartheta =\arg \min \int \left( y-\theta_0-\theta_1x\right)^2 d\eta ,~\eta \in \idr{\sQ(\ey,\ex)}\right\} , \label{eq:manski_blp} \end{equation} [[/math]]

where, using an argument similar to the one in Theorem SIR-,

[[math]] \begin{multline} \idr{\sQ(\ey,\ex)}= \Big\{\eta : \eta_{([t_0,t_1],(-\infty,s])}\ge \sP(\yL\ge t_0,\yU\le t_1,\ex \le s)\\ \forall t_0\le t_1,t_0,t_1\in\R,\forall s\in \R\Big\}. \label{eq:Qyx} \end{multline} [[/math]]

show that \eqref{eq:manski_blp} can be re-written in an intuitive way that generalizes the well-known formula for the best linear predictor that arises when [math]\ey[/math] is perfectly observed. Define the random segment [math]\eG[/math] and the matrix [math]\Sigma_\sP[/math] as

[[math]] \begin{align} \eG=\left\{ \begin{pmatrix} \ey\\ \ey\ex \end{pmatrix}  :\; \ey \in \Sel(\eY)\right\}\subset\R^2, ~~\text{and}~~ \Sigma_\sP=\E_\sP \begin{pmatrix} 1 & \ex\\ \ex & \ex^2 \end{pmatrix},\label{eq:G_and_Sigma} \end{align} [[/math]]

where [math]\Sel(\eY)[/math] is the set of all measurable selections from [math]\eY[/math], see Definition. Then,

Theorem (Best Linear Predictor with Interval Outcome Data)

Under the assumptions of Identification Problem, the sharp identification region for the parameters of the best linear predictor of [math]\ey|\ex[/math] is

[[math]] \begin{equation} \label{eq:ThetaI_BLP} \idr{\theta}= \Sigma_\sP^{-1} \E_\sP\eG, \end{equation} [[/math]]

with [math]\E_\sP\eG[/math] the Aumann (or selection) expectation of [math]\eG[/math] as in Definition.

Show Proof

By Theorem, [math](\tilde\ey,\tilde\ex)\in(\eY\times\ex)[/math] (up to an ordered coupling as discussed in Appendix), if and only if the distribution of [math](\tilde\ey,\tilde\ex)[/math] belongs to [math]\idr{\sQ(\ey,\ex)}[/math]. The result follows.

■

In either representation \eqref{eq:manski_blp} or \eqref{eq:ThetaI_BLP}, [math]\idr{\theta}[/math] is the collection of best linear predictors for each selection of [math]\eY[/math]. Why should one bother with the representation in \eqref{eq:ThetaI_BLP}? The reason is that [math]\idr{\theta}[/math] is a convex set, as it can be evinced from representation \eqref{eq:ThetaI_BLP}: [math]\eG[/math] has almost surely convex realizations that are segments and the Aumann expectation of a convex set is convex. Hence, it can be equivalently represented through its support function [math]h_{\idr{\theta}}[/math], see Definition and equation eq:rocka. In particular, in this example,

[[math]] \begin{align} \label{eq:supfun:BLP} h_{\idr{\theta}}(u)=\E_\sP[(\yL\one(f(\ex,u) \lt 0)+\yU\one(f(\ex,u)\ge 0))f(\ex,u)],~~u\in\mathbb{S}, \end{align} [[/math]]

where [math]f(\ex,u)\equiv [1~\ex]\Sigma_\sP^{-1}u[/math]. The characterization in \eqref{eq:supfun:BLP} results from Theorem, which yields [math]h_{\idr{\theta}}(u)=h_{\Sigma_\sP^{-1} \E_\sP\eG}(u)=\E_\sP h_{\Sigma_\sP^{-1} \eG}(u)[/math], and the fact that [math]\E_\sP h_{\Sigma_\sP^{-1} \eG}(u)[/math] equals the expression in \eqref{eq:supfun:BLP}. As I discuss in Section below, because the support function fully characterizes the boundary of [math]\idr{\theta}[/math], \eqref{eq:supfun:BLP} allows for a simple sample analog estimator, and for inference procedures with desirable properties. It also immediately yields sharp bounds on linear combinations of [math]\theta[/math] by judicious choice of [math]u[/math]. and provide the same characterization as in \eqref{eq:supfun:BLP} using, respectively, direct optimization and the Frisch-Waugh-Lovell theorem.

A natural generalization of Identification Problem allows for both outcome and covariate data to be interval valued.

Identification Problem (Parametric Prediction with Interval Outcome and Covariate Data)

Maintain the same assumptions as in Identification Problem, but with [math]\ex\in\cX\subset\R[/math] unobservable. Let the researcher observe [math](\yL,\yU,\xL,\xU)[/math] such that [math]\sR(\yL \leq \ey \leq \yU , \xL \leq \ex \leq \xU)=1[/math]. Let [math]\eX\equiv [\xL,\xU][/math] and let [math]\cX[/math] be bounded. In the absence of additional information, what can the researcher learn about the best linear predictor of [math]\ey[/math] given [math]\ex=x[/math]?

Abstractly, [math]\idr{\theta}[/math] is as given in \eqref{eq:manski_blp}, with

[[math]] \begin{align*} \idr{\sQ(\ey,\ex)}= \left\{\eta : \eta_K\ge \sP((\eY\times\eX)\subset K) ~\forall \text{ compact } K\subset \cY\times\cX\right\} \end{align*} [[/math]]

replacing \eqref{eq:Qyx} by an application of Theorem. While this characterization is sharp, it is cumbersome to apply in practice, see . On the other hand, when both [math]\ey[/math] and [math]\ex[/math] are perfectly observed, the best linear predictor is simply equal to the parameter vector that yields a mean zero prediction error that is uncorrelated with [math]\ex[/math]. How can this basic observation help in the case of interval data? The idea is that one can use the same insight applied to the set-valued data, and obtain [math]\idr{\theta}[/math] as the collection of [math]\theta[/math]'s for which there exists a selection [math](\tilde{\ey},\tilde{\ex}) \in \Sel(\eY \times \eX)[/math], and associated prediction error [math]\eps_\theta=\tilde{\ey}-\theta_0-\theta_1 \tilde{\ex}[/math], satisfying [math]\E_\sP \eps_\theta=0[/math] and [math]\E_\sP (\eps_\theta \tilde{\ex})=0[/math] (as shown by ). To obtain the formal result, define the [math]\theta[/math]-dependent set

[[math]]\Eps_\theta = \left\lbrace \begin{pmatrix} \tilde{\ey}-\theta_0-\theta_1 \tilde{\ex} \\ (\tilde{\ey}-\theta_0-\theta_1 \tilde{\ex})\tilde{\ex} \end{pmatrix} \: : \, (\tilde{\ey},\tilde{\ex}) \in \Sel(\eY \times\eX) \right\rbrace. [[/math]]

Theorem (Best Linear Predictor with Interval Outcome and Covariate Data)

Under the assumptions of Identification Problem, the sharp identification region for the parameters of the best linear predictor of [math]\ey|\ex[/math] is

[[math]] \begin{align} \label{eq:ThetaI:BLP} \idr{\theta} = \{\theta\in\Theta:\mathbf{0}\in \E_\sP\Eps_\theta\} = \left\{\theta\in\Theta:~ \min_{u \in \Ball}\E_\sP h_{\Eps_\theta}(u) = 0 \right\}, \end{align} [[/math]]

where [math]h_{\Eps_\theta}(u) = \max_{y\in\eY,x\in\eX} [u_1(y-\theta_0-\theta_1 x)+ u_2(yx-\theta_0 x-\theta_1 x^2)][/math] is the support function of the set [math]\Eps_\theta[/math] in direction [math]u\in\Sphere[/math], see Definition.

Show Proof

By Theorem, [math](\tilde\ey,\tilde\ex)\in(\eY\times\eX)[/math] (up to an ordered coupling as discussed in Appendix), if and only if the distribution of [math](\tilde\ey,\tilde\ex)[/math] belongs to [math]\idr{\sQ(\ey,\ex)}[/math]. For given [math]\theta[/math], one can find [math](\tilde\ey,\tilde\ex)\in(\eY\times\eX)[/math] such that [math]\E_\sP \eps_\theta=0[/math] and [math]\E_\sP (\eps_\theta \tilde{\ex})=0[/math] with [math]\eps_\theta\in\Eps_\theta[/math] if and only if the zero vector belongs to [math]\E_\sP \Eps_\theta[/math]. By Theorem, [math]\E_\sP \Eps_\theta[/math] is a convex set and by eq:dom_Aumann, [math]\mathbf{0} \in \E_\sP \Eps_\theta[/math] if and only if [math]0 \leq h_{\E_\sP \Eps_\theta}(u) \,\forall \, u \in \Ball[/math]. The final characterization follows from eq:supf.

■

The support function [math]h_{\Eps_\theta}(u)[/math] is an easy to calculate convex sublinear function of [math]u[/math], regardless of whether the variables involved are continuous or discrete. The optimization problem in (eq:ThetaI:BLP), determining whether [math]\theta \in \idr{\theta}[/math], is a convex program, hence easy to solve. See for example the CVX software by . It should be noted, however, that the set [math]\idr{\theta}[/math] itself is not necessarily convex. Hence, tracing out its boundary is non-trivial. I discuss computational challenges in partial identification in Section. I conclude this section by discussing parametric regression. study identification of parametric regression models under the assumptions in Identification Problem; Theorem SIR- below reports the result. The proof is omitted because it follows immediately from the proof of Theorem SIR-.

Identification Problem (Parametric Regression with Interval Covariate Data)

Let [math](\ey,\xL,\xU,\ew)\sim\sP[/math] be observable random variables in [math]\R\times\R\times\R\times\R^d[/math], [math]d \lt \infty[/math], and let [math]\ex\in\R[/math] be an unobservable random variable. Assume that the joint distribution [math]\sR[/math] of [math](\ey,\ex,\xL,\xU)[/math] is such that [math]\sR(\xL\le\ex\le\xU)=1[/math] and [math]\E_{\sR}(\ey|\ew,\ex,\xL,\xU)=\E_\sQ(\ey|\ew,\ex)[/math]. Suppose that [math]\E_\sQ(\ey|\ew,\ex)=f(\ew,\ex;\theta)[/math], with [math]f:\R^d\times\R\times\Theta \mapsto \R[/math] a known function such that for each [math]w\in\R[/math] and [math]\theta\in\Theta[/math], [math]f(w,x;\theta)[/math] is weakly increasing in [math]x[/math]. In the absence of additional information, what can the researcher learn about [math]\theta[/math]?

Theorem (Parametric Regression with Interval Covariate Data)

Under the Assumptions of Identification Problem, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{multline} \idr{\theta}=\big\{\vartheta\in \Theta: f(\ew,\xL;\vartheta)\le \E_\sP(\ey|\ew,\xL,\xU) \le f(\ew,\xU;\vartheta),~(\ew,\xL,\xU)\text{-a.s.} \big\}.\label{eq:ThetaI_man:tam02_param} \end{multline} [[/math]]

study Identification Problem for the case of missing covariate data without imposing the mean independence restriction of (Assumption MI in Identification Problem). As discussed in footnote, restriction MI is undesirable in this context because it implies the assumption that data are missing at random. characterize [math]\idr{\theta}[/math] under the weaker assumptions, but face the problem that this characterization is usually too complex to compute or to use for inference. They therefore provide outer regions that are easier to compute, and they show that these regions are informative and relatively easy to use.

Measurement Error and Data Combination

One of the first examples of bounding analysis appears in , to assess the impact in linear regression of covariate measurement error. This analysis was substantially extended in , , and . The more recent literature in partial identification has provided important advances to learn features of probability distributions when the observed variables are error-ridden measures of the variables of interest. Here I briefly mention some of the papers in this literature, and refer to Chapter XXX in this Volume by for a thorough treatment of identification and inference with mismeasured and unobserved variables. In an influential paper, study what can be learned about features of the distribution of [math]\ey|\ex[/math] in the presence of contaminated or corrupted outcome data. Whereas a contaminated sampling model assumes that data errors are statistically independent of sample realizations from the population of interest, the corrupted sampling model does not. These models are regularly used in the important literature on robust estimation (e.g., ). However, the goal of that literature is to characterize how point estimators of population parameters behave when data errors are generated in specified ways. As such, the inference problem is approached ex-ante: before collecting the data, one looks for point estimators that are not greatly affected by error. The question addressed by is conceptually distinct. It asks what can be learned about specific population parameters ex-post, that is, after the data has been collected. For example, whereas the mean is well known not to be a robust estimator in the presence of contaminated data, show that it can be (non-trivially) bounded provided the probability of contamination is strictly less than one. and extend the results of to allow for (partial) verification of the distribution from which the data are drawn. They apply the resulting sharp bounds to learn about school performance when the observed test scores may not be valid for all students. provides sharp bounds on the distribution of a misclassified outcome variable under an array of different assumptions on the extent and type of misclassification.

A completely different problem is that of data combination. Applied economists often face the problem that no single data set contains all the variables that are necessary to conduct inference on a population of interest. When this is the case, they need to integrate the information contained in different samples; for example, they might need to combine survey data with administrative data (see ). From a methodological perspective, the problem is that while the samples being combined might contain some common variables, other variables belong only to one of the samples. When the data is collected at the same aggregation level (e.g., individual level, household level, etc.), if the common variables include a unique and correctly recorded identifier of the units constituting each sample, and there is a substantial overlap of units across all samples, then exact matching of the data sets is relatively straightforward, and the combined data set provides all the relevant information to identify features of the population of interest. However, it is rather common that there is a limited overlap in the units constituting each sample, or that variables that allow identification of units are not available in one or more of the input files, or that one sample provides information at the individual or household level (e.g., survey data) while the second sample provides information at a more aggregate level (e.g., administrative data providing information at the precinct or district level). Formally, the problem is that one observes data that identify the joint distributions [math]\sP(\ey,\ex)[/math] and [math]\sP(\ex,\ew)[/math], but not data that identifies the joint distribution [math]\sQ(\ey,\ex,\ew)[/math] whose features one wants to learn. The literature on statistical matching has aimed at using the common variable(s) [math]\ex[/math] as a bridge to create synthetic records containing [math](\ey,\ex,\ew)[/math] (see, e.g., ). As points out, the inherent assumption at the base of statistical matching is that conditional on [math]\ex[/math], [math]\ey[/math] and [math]\ew[/math] are independent. This conditional independence assumption is strong and untestable. While it does guarantee point identification of features of the conditional distributions [math]\sQ(\ey|\ex,\ew)[/math], it often finds very little justification in practice. Early on, provided numerical illustrations on how one can bound the object of interest, when both [math]\ey[/math] and [math]\ew[/math] are binary variables. provide a general analysis of the problem. They obtain bounds on the long regression [math]\E_\sQ(\ey|\ex,\ew)[/math], under the assumption that [math]\ew[/math] has finite support. They show that sharp bounds on [math]\E_\sQ(\ey|\ex,\ew=w)[/math] can be obtained using the results in , thereby establishing a connection with the analysis of contaminated data. They then derive sharp identification regions for [math][\E_\sQ(\ey|\ex=x,\ew=w),x\in\cX,w\in\cW][/math]. They show that these bounds are sharp when [math]\ey[/math] has finite support, and establish sharpness without this restriction. address the question of what can be learned about counterfactual distributions and treatment effects under the data scenario just described, but with [math]\ex[/math] replaced by [math]\es[/math], a binary indicator for the received treatment (using the notation of the previous section). In this case, the exogenous selection assumption (conditional on [math]\ew[/math]) does not suffice for point identification of the objects of interest. The authors derive, however, sharp bounds on these quantities using monotone rearrangement inequalities. provides partial identification results for the coefficients in the linear projection of [math]\ey[/math] on [math](\ex,\ew)[/math].

Further Theoretical Advances and Empirical Applications

In order to discuss the partial identification approach to learning features of probability distributions in some level of detail while keeping this chapter to a manageable length, I have focused on a selection of papers. In this section I briefly mention several other excellent theoretical contributions that could be discussed more closely, as well as several papers that have applied partial identification analysis to answer important empirical questions.

While selectively observed data are commonplace in observational studies, in randomized experiments subjects are randomly placed in designated treatment groups conditional on [math]\ex[/math], so that the assumption of exogenous selection is satisfied with respect to the assigned treatment. Yet, identification of some highly policy relevant parameters can remain elusive in the absence of strong assumptions. One challenge results from noncompliance, where individuals' received treatments differs from the randomly assigned ones. derive sharp bounds on the ATE in this context, when [math]\cY=\T=\{0,1\}[/math]. Even if one is interested in the intention-to-treat parameter, selectively observed data may continue to be a problem. For example, studies the wage effects of the Job Corps training program, which randomly assigns eligibility to participate in the program. Individuals randomized to be eligible were not compelled to receive treatment, hence focuses on the intention-to-treat effect. Because wages are only observable when individuals are employed, a selection problem persists despite the random assignment of eligibility to treatment, as employment status may be affected by the training program. obtains sharp bounds on the intention-to-treat effect, through a trimming procedure that leverages results in . analyzes the problem of identification of the ATE and other treatment effects, when the received treatment is unobserved for a subset of the population. Missing treatment data may be due to item or survey nonresponse in observational studies, or noncompliance with randomly assigned treatments that are not directly monitored. She derives sharp worst case bounds leveraging results in , and she shows that these are a function of the available prior information on the distribution of missing treatments. If the response function is assumed monotone as in \eqref{eq:MTR:treat}, she obtains informative bounds without restrictions on the distribution of missing treatments.

Even randomly assigned treatments and perfect compliance with no missing data may not suffice for point identification of all policy relevant parameters. Important examples are given by and . show that features of the joint distribution of the potential outcomes of treatment and control, including the distribution of treatment effects impacts, cannot be point identified in the absence of strong restrictions. This is because although subjects are randomized to treatment and control, nobody's outcome is observed under both states. Nonetheless, the authors obtain bounds for the functionals of interest. derives related bounds on the probability that the potential outcome of one treatment is larger than that of the other treatment, and applies these results to health economics problems. shows that features of outcome distributions under treatment rules in which treatment may vary within groups cannot be point identified in the absence of strong restrictions. This is because data resulting from randomized experiments with perfect compliance allow for point identification of the outcome distributions under treatment rules that assign all persons with the same [math]\ex[/math] to the same treatment group. However, such data only allow for partial identification of outcome distributions under rules in which treatment may vary within groups. derives sharp bounds for functionals of these distributions.

Analyses of data resulting from natural experiments also face identification challenges. study what can be learned about treatment effects when one uses a contaminated instrumental variable, i.e. when a mean-independence assumption holds in a population of interest, but the observed population is a mixture of the population of interest and one in which the assumption doesn't hold. They extend the results of to learn about the causal effect of teenage childbearing on a teen mother's subsequent outcomes, using the natural experiment of miscarriages to form an instrumental variable for teen births. This instrument is contaminated because miscarriges may not occur randomly for a subset of the population (e.g., higher miscarriage rates are associated with smoking and drinking, and these behaviors may be correlated with the outcomes of interest).

Of course, analyses of selectively observed data present many challenges, including but not limited to the ones described in Section Selectively Observed Data. generalize the difference-in-difference (DID) design to a changes-in-changes (CIC) model, where the distribution of the unobservables is allowed to vary across groups, but not overtime within groups, and the additivity and linearity assumptions of the DID are dispensed with. For the case that the outcomes have a continuous distribution, provide conditions for point identification of the entire counterfactual distribution of effects of the treatment on the treatment group as well as the distribution of effects of the treatment on the control group, without restricting how these distributions differ from each other. For the case that the outcome variables are discrete, they provide partial identification results, as well as additional conditions compared to their baseline model under which point identification attains.

Motivated by the question of whether the age-adjusted mortality rate from cancer in 2000 was lower than that in the early 1970s, study partial identification of competing risk models (see ). To answer this question, they need to contend with the fact that mortality rate from cardiovascular disease declined substantially over the same period of time, so that individuals that in the early 1970s might have died from cardiovascular disease before being diagnosed with cancer, do not in 2000. In this context, it is important to carry out the analysis without assuming that the underlying risks are independent. show that bounds for the parameters of interest can be obtained as the solution to linear programming problems. The estimated bounds suggest much larger improvements in cancer mortality rates than previously estimated.

use UK data to study changes over time in the distribution of male and female wages, and in wage inequality. Because the composition of the workforce changes over time, it is difficult to disentangle that effect from changes in the distribution of wages, given that the latter are observed only for people in the workforce. begin their empirical analysis by reporting worst case bounds (as in ) on the CDF of wages conditional on covariates. They then consider various restrictions on treatment selection, e.g., a first order stochastic dominance assumption according to which people with higher wages are more likely to work, and derive tighter bounds under this assumption (and under weaker ones). Finally, they bring to bear shape restrictions. At each step of the analysis, they report the resulting bounds, thereby illuminating the role played by each assumption in shaping the inference. provide best linear approximations to the identification region for the quantile gender wage gap using Current Population Survey repeated cross-sections data from 1975-2001, using treatment selection assumptions in the spirit of as well as exclusion restrictions. study the effect of Swan-Ganz catheterization on subsequent mortality. Previous research had shown, using propensity score matching (assuming that there are no unobserved differences between catheterized and non catheterized patients) that Swan-Ganz catheterization increases the probability that patients die within 180 days from admission to the intensive care unit. re-analyze the data using (and extending) bounds results obtained by . These results are based on exclusion restrictions combined with a threshold crossing structure for both the treatment and the outcome variables in problems where [math]\cY=\cT=\{0,1\}[/math].

use as instrument for Swan-Ganz catheterization the day of the week that the patient was admitted to the intensive care unit. The reasoning is that patients are less likely to be catheterized on the weekend, but the admission day to the intensive care unit is plausibly uncorrelated with subsequent mortality. Their results confirm that for some diagnoses, Swan-Ganz catheterization increases mortality at 30 days after catheterization and beyond. use data from Maryland, Virginia and Illinois to learn about the impact of laws allowing individuals to carry concealed handguns (right-to-carry laws) on violent and property crimes. Point identification of these treatment effects is possible under invariance assumptions that certain features of treatment response are constant across states and years. propose the use of weaker but more credible restrictions according to which these features exhibit bounded variation -- the invariance case being the limit where the bound on variation equals zero. They carry out their analysis under different combinations of the bounded variation assumptions, and at each step they report the resulting bounds, thereby illuminating the role played by each assumption in shaping the inference.

provide sharp bounds on the joint distribution of potential (binary) outcomes in a Roy model with sector specific unobserved heterogeneity and self selection based on potential outcomes. The key maintained assumption is that the researcher has access to data that includes a stochastically monotone instrumental variable. This is a selection shifter that is restricted to affect potential outcomes monotonically. An example is parental education, which may not be independent from potential wages, but plausibly does not negatively affect future wages. Under this assumption, show that all observable implications of the model are embodied in the stochastic monotonicity of observed outcomes in the instrument, hence Roy selection behavior can be tested by checking this stochastic monotonicity. They apply the method to estimate a Roy model of college major choice in Canada and Germany, with special interest in the under-representation of women in STEM. provide a general method to obtain sharp bounds on a certain class of treatment effects parameters. This class is comprised of parameters that can be expressed as weighted averages of marginal treatment effects .

provides a general method, based on copulas, to obtain sharp bounds on treatment effect parameters in semiparametric binary models. A notable feature of both and is that the bounds are obtained as solutions to convex (even linear) optimization problems, rendering them computationally attractive. provide partial identification results and inference methods for a linear functional [math]\ell(g)[/math] when [math]g:\cX\mapsto\R[/math] is such that [math]\ey=g(\ex)+\epsilon[/math] and [math]\E(\ey|\ez)=0[/math]. The instrumental variable [math]\ez[/math] and regressor [math]\ex[/math] have discrete distributions, and [math]\ez[/math] has fewer points of support than [math]\ex[/math], so that [math]\ell(g)[/math] can only be partially identified. They impose shape restrictions on [math]g[/math] (e.g., monotonicity or convexity) to achieve interval identification of [math]\ell(g)[/math], and they show that the lower and upper points of the interval can be obtained by solving linear programming problems. They also show that the bootstrap can be used to carry out inference.

General references

Molinari, Francesca (2020). "Microeconometrics with Partial Identification". arXiv:2004.11751 [econ.EM].