Partial Identification of Structural Models

[math] \newcommand{\edis}{\stackrel{d}{=}} \newcommand{\fd}{\stackrel{f.d.}{\rightarrow}} \newcommand{\dom}{\operatorname{dom}} \newcommand{\eig}{\operatorname{eig}} \newcommand{\epi}{\operatorname{epi}} \newcommand{\lev}{\operatorname{lev}} \newcommand{\card}{\operatorname{card}} \newcommand{\comment}{\textcolor{Green}} \newcommand{\B}{\mathbb{B}} \newcommand{\C}{\mathbb{C}} \newcommand{\G}{\mathbb{G}} \newcommand{\M}{\mathbb{M}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\T}{\mathbb{T}} \newcommand{\R}{\mathbb{R}} \newcommand{\E}{\mathbb{E}} \newcommand{\W}{\mathbb{W}} \newcommand{\bU}{\mathfrak{U}} \newcommand{\bu}{\mathfrak{u}} \newcommand{\bI}{\mathfrak{I}} \newcommand{\cA}{\mathcal{A}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cD}{\mathcal{D}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cG}{\mathcal{G}} \newcommand{\cg}{\mathcal{g}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cO}{\mathcal{O}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cQ}{\mathcal{Q}} \newcommand{\cR}{\mathcal{R}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cU}{\mathcal{U}} \newcommand{\cu}{\mathcal{u}} \newcommand{\cV}{\mathcal{V}} \newcommand{\cW}{\mathcal{W}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cZ}{\mathcal{Z}} \newcommand{\sF}{\mathsf{F}} \newcommand{\sM}{\mathsf{M}} \newcommand{\sG}{\mathsf{G}} \newcommand{\sT}{\mathsf{T}} \newcommand{\sB}{\mathsf{B}} \newcommand{\sC}{\mathsf{C}} \newcommand{\sP}{\mathsf{P}} \newcommand{\sQ}{\mathsf{Q}} \newcommand{\sq}{\mathsf{q}} \newcommand{\sR}{\mathsf{R}} \newcommand{\sS}{\mathsf{S}} \newcommand{\sd}{\mathsf{d}} \newcommand{\cp}{\mathsf{p}} \newcommand{\cc}{\mathsf{c}} \newcommand{\cf}{\mathsf{f}} \newcommand{\eU}{{\boldsymbol{U}}} \newcommand{\eb}{{\boldsymbol{b}}} \newcommand{\ed}{{\boldsymbol{d}}} \newcommand{\eu}{{\boldsymbol{u}}} \newcommand{\ew}{{\boldsymbol{w}}} \newcommand{\ep}{{\boldsymbol{p}}} \newcommand{\eX}{{\boldsymbol{X}}} \newcommand{\ex}{{\boldsymbol{x}}} \newcommand{\eY}{{\boldsymbol{Y}}} \newcommand{\eB}{{\boldsymbol{B}}} \newcommand{\eC}{{\boldsymbol{C}}} \newcommand{\eD}{{\boldsymbol{D}}} \newcommand{\eW}{{\boldsymbol{W}}} \newcommand{\eR}{{\boldsymbol{R}}} \newcommand{\eQ}{{\boldsymbol{Q}}} \newcommand{\eS}{{\boldsymbol{S}}} \newcommand{\eT}{{\boldsymbol{T}}} \newcommand{\eA}{{\boldsymbol{A}}} \newcommand{\eH}{{\boldsymbol{H}}} \newcommand{\ea}{{\boldsymbol{a}}} \newcommand{\ey}{{\boldsymbol{y}}} \newcommand{\eZ}{{\boldsymbol{Z}}} \newcommand{\eG}{{\boldsymbol{G}}} \newcommand{\ez}{{\boldsymbol{z}}} \newcommand{\es}{{\boldsymbol{s}}} \newcommand{\et}{{\boldsymbol{t}}} \newcommand{\ev}{{\boldsymbol{v}}} \newcommand{\ee}{{\boldsymbol{e}}} \newcommand{\eq}{{\boldsymbol{q}}} \newcommand{\bnu}{{\boldsymbol{\nu}}} \newcommand{\barX}{\overline{\eX}} \newcommand{\eps}{\varepsilon} \newcommand{\Eps}{\mathcal{E}} \newcommand{\carrier}{{\mathfrak{X}}} \newcommand{\Ball}{{\mathbb{B}}^{d}} \newcommand{\Sphere}{{\mathbb{S}}^{d-1}} \newcommand{\salg}{\mathfrak{F}} \newcommand{\ssalg}{\mathfrak{B}} \newcommand{\one}{\mathbf{1}} \newcommand{\Prob}[1]{\P\{#1\}} \newcommand{\yL}{\ey_{\mathrm{L}}} \newcommand{\yU}{\ey_{\mathrm{U}}} \newcommand{\yLi}{\ey_{\mathrm{L}i}} \newcommand{\yUi}{\ey_{\mathrm{U}i}} \newcommand{\xL}{\ex_{\mathrm{L}}} \newcommand{\xU}{\ex_{\mathrm{U}}} \newcommand{\vL}{\ev_{\mathrm{L}}} \newcommand{\vU}{\ev_{\mathrm{U}}} \newcommand{\dist}{\mathbf{d}} \newcommand{\rhoH}{\dist_{\mathrm{H}}} \newcommand{\ti}{\to\infty} \newcommand{\comp}[1]{#1^\mathrm{c}} \newcommand{\ThetaI}{\Theta_{\mathrm{I}}} \newcommand{\crit}{q} \newcommand{\CS}{CS_n} \newcommand{\CI}{CI_n} \newcommand{\cv}[1]{\hat{c}_{n,1-\alpha}(#1)} \newcommand{\idr}[1]{\mathcal{H}_\sP[#1]} \newcommand{\outr}[1]{\mathcal{O}_\sP[#1]} \newcommand{\idrn}[1]{\hat{\mathcal{H}}_{\sP_n}[#1]} \newcommand{\outrn}[1]{\mathcal{O}_{\sP_n}[#1]} \newcommand{\email}[1]{\texttt{#1}} \newcommand{\possessivecite}[1]{\citeauthor{#1}'s \citeyear{#1}} \newcommand\xqed[1]{% \leavevmode\unskip\penalty9999 \hbox{}\nobreak\hfill \quad\hbox{#1}} \newcommand\qedex{\xqed{$\triangle$}} \newcommand\independent{\perp\!\!\!\perp} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\cov}{Cov} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\Sel}{Sel} \DeclareMathOperator{\Bel}{Bel} \DeclareMathOperator{\cl}{cl} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\essinf}{essinf} \DeclareMathOperator{\esssup}{esssup} \newcommand{\mathds}{\mathbb} \renewcommand{\P}{\mathbb{P}} [/math]

In this section I focus on the literature concerned with learning features of structural econometric models. These are models where economic theory is used to postulate relationships among observable outcomes [math]\ey[/math], observable covariates [math]\ex[/math], and unobservable variables [math]\nu[/math]. For example, economic theory may guide assumptions on economic behavior (e.g., utility maximization) and equilibrium that yield a mapping from [math](\ex,\nu)[/math] to [math]\ey[/math]. The researcher is interested in learning features of these relationships (e.g., utility function, distribution of preferences), and to this end may supplement the data and economic theory with functional form assumptions on the mapping of interest and distributional assumptions on the observable and unobservable variables. The earlier literature on partial identification of features of structural models includes important examples of nonparametric analysis of random utility models and revealed preference extrapolation, e.g. , , , , , , and others.

The earlier literature also addresses semiparametric analysis, where the underlying models are specified up to parameters that are finite dimensional (e.g., preference parameters) and parameters that are infinite dimensional (e.g., distribution functions); important examples include , , , , , , , , , , , , and others. Contrary to the nonparametric bounds results discussed in Section, and especially in the case of semiparametric models, structural partial identification often yields an identification region that is not constructive. Indeed, the boundary of the set is not obtained in closed form as a functional of the distribution of the observable data. Rather, the identification region can often be characterized as a level set of a properly specified criterion function. The recent spark of interest in partial identification of structural microeconometric models was fueled by the work of , and , and . Each of these papers has advanced the literature in fundamental ways, studying conceptually very distinct problems. are concerned with partial identification of the decision process yielding binary outcomes in a semiparametric model, when one of the explanatory variables is interval valued.

Hence, the root cause of the identification problem they study is that the data is incomplete.

and are concerned with identification (and estimation) of simultaneous equation models with dummy endogeneous variables which are representations of two-player entry games with multiple equilibria. are concerned with nonparametric identification and estimation of the distribution of valuations in a model of English auctions under weak assumptions on bidders' behavior. In both cases, the root cause of the identification problem is that the structural model is incomplete. This is because the model makes multiple predictions for the observed outcome variables (respectively: the players' actions; and the bidders' bids), but does not specify how one of them is selected to yield the observed data.

Set-valued predictions for the observable outcome (endogenous variables) are a key feature of partially identified structural models. The goal of this section is to explain how they result in a wide array of theoretical frameworks, and how sharp identification regions can be characterized using a unified approach based on random set theory. Although the work of , and , and has spurred many of the developments discussed in this section, for pedagogical reasons I organize the presentation based on application topic rather than chronologically. The work of and further stimulated a large empirical literature that applies partial identification methods to a wide array of questions of substantive economic importance, to which I return in Section Further Theoretical Advances and Empirical Applications.

Discrete Choice in Single Agent Random Utility Models

Let [math]\cI[/math] denote a population of decision makers and [math]\cY=\{c_1,\dots,c_{|\cY|}\}[/math] a finite universe of potential alternatives (feasible set henceforth). Let [math]\bU[/math] be a family of real valued functions defined over the elements of [math]\cY[/math]. Let [math]\in^* [/math] denote ‘`is chosen from." Then observed choice is consistent with a ’'random utility model if there exists a function [math]\bu_i[/math] drawn from [math]\bU[/math] according to some probability distribution, such that [math]\P(c \in^* C)=\P(\bu_i(c) \ge \bu_i(b)\forall b \in C)[/math] for all [math]c\in C[/math], all non empty sets [math]C \subset \cY[/math], and all [math]i\in\cI[/math] . See for a textbook presentation of this class of models, and for a review of sufficient conditions for point identification of nonparametric and semiparametric limited dependent variables models. As in the seminal work of , assume that the decision makers and alternatives are characterized by observable and unobservable vectors of real valued attributes. Denote the observable attributes by [math]\ex_i \equiv \{\ex_i^1,(\ex_{ic}^2,c\in\cY)\},i\in\cI[/math]. These include attribute vectors [math]\ex_i^1[/math] that are specific to the decision maker, as well as attribute vectors [math]\ex_{ic}^2[/math] that include components that are specific to the alternative and components that are indexed by both. Denote the unobservable attributes (preferences) by [math]\nu_i\equiv(\zeta_i,\{\epsilon_{ic},c\in\cY\}),i\in\cI[/math]. These are idiosyncratic to the decision maker and similarly may include alternative and decision maker specific terms. Denote [math]\cX,\cV[/math] the supports of [math]\ex,\nu[/math], respectively. In what follows, I label ‘`standard" a random utility model that maintains some form of exogeneity for [math]\ex_i[/math] (e.g., mean or quantile or statistical independence with [math]\nu_i[/math]) and presupposes observation of data that include [math]\{(\eC_i,\ey_i,\ex_i):\ey_i \in^* \eC_i\}, i=1,\dots,n[/math], with [math]\eC_i[/math] the choice set faced by decision maker [math]i[/math] and [math]|\eC_i|\ge 2[/math] (e.g., ). Often it is also assumed that all members of the population face the same choice set, [math]\eC_i=D[/math] for all [math]i\in\cI[/math] and some known [math]D\subseteq\cY[/math], although this requirement is not critical to identification analysis.

Semiparametric Binary Choice Models with Interval Valued Covariates

provide inference methods for nonparametric, semiparametric, and parametric conditional expectation functions when one of the conditioning variables is interval valued. I have discussed their nonparametric and parametric sharp bounds on conditional expectations with interval valued covariates in Identification Problems and, and Theorems SIR- and SIR-, respectively. Here I focus on their analysis of semiparametric binary choice models. Compared to the generic notation set forth at the beginning of Section Discrete Choice in Single Agent Random Utility Models, I let [math]\eC_i=\cY=\{0,1\}[/math] for all [math]i\in\cI[/math], and with some abuse of notation I denote the vector of observed covariates [math](\xL,\xU,\ew)[/math].

Identification Problem (Semiparametric Binary Regression with Interval Covariate Data)

Let [math](\ey,\xL,\xU,\ew)\sim\sP[/math] be observable random variables in [math]\{0,1\}\times\R\times\R\times\R^d[/math], [math]d \lt \infty[/math], and let [math]\ex\in\R[/math] be an unobservable random variable. Let [math]\ey=\one(\ew\theta + \delta\ex +\epsilon \gt 0)[/math]. Assume [math]\delta \gt 0[/math], and further normalize [math]\delta=1[/math] because the threshold-crossing condition is invariant to the scale of the parameters. Here [math]\epsilon[/math] is an unobserved heterogeneity term with continuous distribution conditional on [math](\ew,\ex,\xL,\xU)[/math], [math](\ew,\ex,\xL,\xU)[/math]-a.s., and [math]\theta\in\Theta\subset\R^d[/math] is a parameter vector representing decision makers’ preferences, with compact parameter space [math]\Theta[/math]. Assume that [math]\sR[/math], the joint distribution of [math](\ey,\ex,\xL,\xU,\ew,\epsilon)[/math], is such that [math]\sR(\xL\le\ex\le\xU)=1[/math]; [math] \sR(\epsilon |\ew,\ex,\xL,\xU)=\sR(\epsilon|\ew,\ex)[/math]; and for a specified [math]\alpha \in (0,1)[/math], [math]\sq_{\sR}^\epsilon(\alpha,\ew,\ex)=0[/math] and [math]\sR(\epsilon \le 0|\ew,\ex)=\alpha[/math], [math](\ew,\ex)[/math]-a.s.. In the absence of additional information, what can the researcher learn about [math]\theta[/math]?

Compared to Identification Problem (see p.\pageref{IP:interval_covariate}), here one continues to impose [math]\ex\in[\xL,\xU][/math] a.s. The sign restriction on [math]\delta[/math] replaces the monotonicity restriction (M) in Identification Problem, but does not imply it unless the distribution of [math]\epsilon[/math] is independent of [math]\ex[/math] conditional on [math]\ew[/math]. The quantile independence restriction is inspired by . For given [math]\theta\in\Theta[/math], this model yields set valued predictions because [math]\ey=1[/math] can occur whenever [math]\epsilon \gt -\ew\theta-\xU[/math], whereas [math]\ey=0[/math] can occur whenever [math]\epsilon\le -\ew\theta-\xL[/math], and [math]-\ew\theta-\xU \le -\ew\theta-\xL[/math]. Conversely, observation of [math]\ey=1[/math] allows one to conclude that [math]\epsilon\in(-\ew\theta-\xU,+\infty)[/math], whereas observation of [math]\ey=0[/math] allows one to conclude that [math]\epsilon\in(-\infty,-\ew\theta-\xL][/math], and these regions of possible realizations of [math]\epsilon[/math] overlap. In contrast, when [math]\ex[/math] is observed the prediction is unique because the value [math]-\ew\theta-\ex[/math] partitions the space of realizations of [math]\epsilon[/math] in two disjoint sets, one associated with [math]\ey=1[/math] and the other with [math]\ey=0[/math]. Figure depicts the model's set-valued predictions for [math]\ey[/math] given [math](\ew,\xL,\xU)[/math] as a function of [math]\epsilon[/math], and the model's set valued predictions for [math]\epsilon[/math] given [math](\ew,\xL,\xU)[/math] as a function of [math]\ey[/math]. Why does this set-valued prediction hinder point identification? The reason is that the distribution of the observable data relates to the model structure in an incomplete manner. The model predicts [math]\sM(\ey=1|\ew,\xL,\xU)=\int \sR(\ey=1|\ew,\ex,\xL,\xU)d\sR(\ex|\ew,\xL,\xU)=\int \sR(\epsilon \gt -\ew\theta-\ex|\ew,\ex)d\sR(\ex|\ew,\xL,\xU),(\ew,\xL,\xU)[/math]-a.s. Because the distribution [math]\sR(\ex|\ew,\xL,\xU)[/math] is left completely unspecified, one can find multiple values for [math](\theta,\sR(\ex|\ew,\xL,\xU),\sR(\epsilon|\ew,\ex))[/math], satisfying the assumptions in Identification Problem, such that [math]\sM(\ey=1|\ew,\xL,\xU)=\sP(\ey=1|\ew,\xL,\xU),(\ew,\xL,\xU)[/math]-a.s. Nonetheless, in general, not all values of [math]\theta\in\Theta[/math] can be paired with some [math]\sR(\ex|\ew,\xL,\xU)[/math] and [math]\sR(\epsilon|\ew,\ex)[/math] so that they are compatible with [math]\sP(\ey=1|\ew,\xL,\xU),(\ew,\xL,\xU)[/math]-a.s. and with the maintained assumptions. Hence, [math]\theta[/math] can be partially identified using the information in the model and observed data.

Predicted value of [math]\ey[/math] as a function of [math]\epsilon[/math], and admissible values of [math]\epsilon[/math] for each realization of [math]\ey[/math], in Identification Problem, conditional on [math](\ew,\xL,\xU)[/math].

Theorem (Semiparametric Binary Regression with Interval Covariate Data)

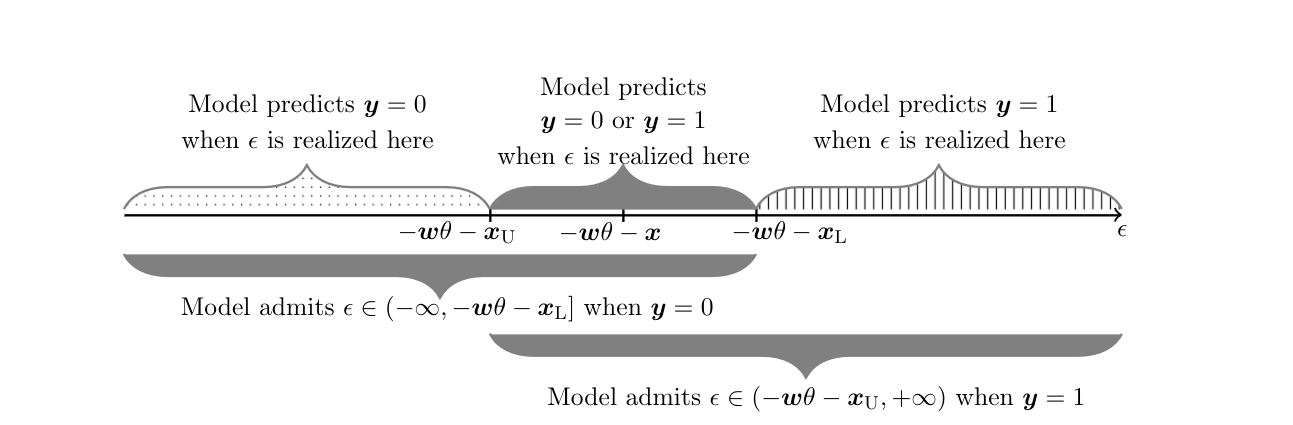
Under the Assumptions of Identification Problem, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{multline} \idr{\theta}=\Big\{\vartheta\in \Theta: \sP\Big((\ew,\xL,\xU):\, \{0\le\ew\vartheta+\xL\cap \sP(\ey=1|\ew,\xL,\xU)\le 1-\alpha\}\\ \cup \{\ew\vartheta+\xU\le 0\cap \sP(\ey=1|\ew,\xL,\xU)\ge 1-\alpha\}\Big) = 0 \Big\}.\label{eq:ThetaI_man:tam02_binary} \end{multline} [[/math]]

Show Proof

For any [math]\vartheta\in\Theta[/math], define the set of possible values for the unobservable associated with the possible realizations of [math](\ey,\ew,\xL,\xU)[/math], illustrated in Figure, as

[[math]] \begin{align} \Eps_\vartheta(\ey,\ew,\xL,\xU) =\left \{ \begin{tabular}{ll} \ltmath\gt(-\infty,-\ew\vartheta-\xL][[/math]]

& if [math]\ey=0[/math],\\ [math][-\ew\vartheta-\xU,+\infty)[/math] & if [math]\ey=1[/math]. \end{tabular} \right.\label{eq:def_Epsilon:man:tam} \end{align} </math> Then [math]\Eps_\vartheta(\ey,\ew,\xL,\xU)[/math] is a random closed set as per Definition. To simplify notation, let [math]\Eps_\vartheta(\ey)\equiv\Eps_\vartheta(\ey,\ew,\xL,\xU)[/math] suppressing the dependence on [math](\ew,\xL,\xU)[/math]. Let [math](\Eps_\vartheta(\ey),\ew,\xL,\xU)=\Eps_\vartheta(\ey)\times(\ew,\xL,\xU)=\{(\mathbf{e},\ew,\xL,\xU):\mathbf{e}\in\Eps_\vartheta(\ey)\}[/math]. If the model is correctly specified, for the data generating value [math]\theta[/math], [math](\epsilon,\ew,\xL,\xU) \in (\Eps_\theta(\ey),\ew,\xL,\xU)[/math] a.s. By Theorem and Theorem 2.33 in , this occurs if and only if

[[math]] \begin{align} \sR(\epsilon\in C|\ew,\xL,\xU)&\ge \sP(\Eps_\theta(\ey)\subset C|\ew,\xL,\xU),(\ew,\xL,\xU)\text{-a.s.}\forall C\in\cF,\label{eq:Artstein_on_man:tam} \end{align} [[/math]]

where [math]\cF[/math] here denotes the collection of closed subsets of [math]\R[/math]. We then have that [math]\vartheta[/math] is observationally equivalent to [math]\theta[/math] if and only if \eqref{eq:Artstein_on_man:tam} holds for [math]\Eps_\vartheta(\ey)[/math] as defined in \eqref{eq:def_Epsilon:man:tam}. The condition can be rewritten as

[[math]] \begin{align*} \int \sR(\epsilon\in C|\ew,\ex,\xL,\xU)d\sR(\ex|\ew,\xL,\xU)&\ge \sP(\Eps_\vartheta(\ey)\subset C|\ew,\xL,\xU),(\ew,\xL,\xU)\text{-a.s.}\forall C\in\cF. \end{align*} [[/math]]

The assumption that [math]\sR(\epsilon|\ew,\ex,\xL,\xU)=\sR(\epsilon|\ew,\ex)[/math] yields that the above system of inequalities reduces to

[[math]] \begin{align*} \int \sR(\epsilon\in C|\ew,\ex)d\sR(\ex|\ew,\xL,\xU)&\ge \sP(\Eps_\vartheta(\ey)\subset C|\ew,\xL,\xU),(\ew,\xL,\xU)\text{-a.s.}\forall C\in\cF. \end{align*} [[/math]]

Next, note that given the possible realizations of [math]\Eps_\vartheta(\ey)[/math], the above inequality is trivially satisfied unless [math]C=(-\infty,t][/math] or [math]C=[t,\infty)[/math] for some [math]t\in\R[/math]. Finally, the only restriction on the distribution of [math]\epsilon[/math] is the quantile independence condition, hence it suffices to consider [math]t=0[/math]. To see why this is the case, let for example [math]t \gt 0[/math] and fix a realization [math](w,x_L,x_U)[/math] for [math](\ew,\xL,\xU)[/math]. Then for the inequality not to be trivially satisfied it must be that either [math]w\vartheta+x_L\ge -t[/math] or [math]w\vartheta+x_U\le -t[/math] (both are not possible because [math]w\vartheta+x_L\le w\vartheta+x_U[/math]). If [math]w\vartheta+x_U\le -t[/math], it must be that [math]t\in(0,-w\vartheta-x_U][/math] and [math]-w\vartheta-x_U \gt 0[/math]. Then a distribution [math]\sR[/math] such that [math]\int \sR(\epsilon\in [0,t)|\ew=w,\ex)d\sR(\ex|\ew=w,\xL=x_L,\xU=x_U)=0[/math] is always feasible for [math]t\in(0,-w\vartheta-x_U][/math]. A similar argument holds if [math]w\vartheta+x_L\ge -t[/math]; and also if [math]t \lt 0[/math]. We then have that if the inequalities are satisfied for [math]t=0[/math], they are satisfied also for [math]t\neq 0[/math]. Finally, using the definition of [math]\Eps_\vartheta(\ey)[/math], for [math]t=0[/math] we have

[[math]] \begin{align} 1-\alpha &\ge \sP(\ey=1|\ew,\xL,\xU)\text{for all}(\ew,\xL,\xU)\text{such that } \ew\vartheta+\xU\le 0,\label{eq:key_sharp:man:tam02_1}\\ 1-\alpha & \le \sP(\ey=1|\ew,\xL,\xU)\text{for all}(\ew,\xL,\xU)\text{such that } \ew\vartheta+\xL \ge 0.\label{eq:key_sharp:man:tam02_2} \end{align} [[/math]]

Any given [math]\vartheta\in\Theta[/math], [math]\vartheta\neq\theta[/math], violates the above conditions if and only if [math]\sP\big((\ew,\xL,\xU):\, \{0\le\ew\vartheta+\xL\cap \sP(\ey=1|\ew,\xL,\xU)\le 1-\alpha\}\cup \{\ew\vartheta+\xU\le 0\cap \sP(\ey=1|\ew,\xL,\xU)\ge 1-\alpha\}\big) \gt 0[/math].

■

Key Insight: The analysis in systematically studies what can be learned under increasingly strong sets of assumptions. These include both assumptions that constrain the model from fully nonparametric to semiparametric to parametric, as well as assumptions that constrain the distribution of the observable covariates. For example, provide sufficient conditions on the joint distribution of [math](\ew,\xL,\xU)[/math] that allow for identification of the sign of components of [math]\theta[/math], as well as for point identification of [math]\theta[/math]. The careful analysis of the identifying power of increasingly stronger assumptions is the pillar of the partial identification approach to empirical research proposed by Manski, as illustrated in Section. The work of was the first example of this kind in semiparametric structural models.

Revisiting study of Identification Problem nearly 20 years later yields important insights on the differences between point and partial identification analysis. It is instructive to take as a point of departure the analysis of , which under the additional assumption that [math](\ey,\ew,\ex)[/math] is observed yields

[[math]] \begin{align*} \ew\theta+\ex \gt 0 \Leftrightarrow \sP(\ey=1|\ew,\ex) \gt 1-\alpha. \end{align*} [[/math]]

In this case, [math]\theta[/math] is identified relative to [math]\vartheta\in\Theta[/math] if

[[math]] \begin{align} \sP\left((\ew,\ex):\, \{\ew\theta+\ex\le 0 \lt \ew\vartheta+\ex\} \cup \{\ew\vartheta+\ex\le 0 \lt \ew\theta+\ex\}\right) \gt 0.\label{eq:manski85} \end{align} [[/math]]

extend this reasoning to the case that [math]\ex[/math] is unobserved, but known to satisfy [math]\ex\in [\xL,\xU][/math] a.s. The first part of their analysis, collected in their Proposition 2, characterizes the collection of values that cannot be distinguished from [math]\theta[/math] on the basis of [math]\sP(\ew,\xL,\xU)[/math] alone, through a clear generalization of \eqref{eq:manski85}:

[[math]] \begin{align} \{\vartheta\in \Theta: \sP\left((\ew,\xL,\xU):\, \{\ew\theta+\xU\le 0 \lt \ew\vartheta+\xL\} \cup \{\ew\vartheta+\xU\le 0 \lt \ew\theta+\xL\}\right) = 0\}.\label{eq:region:man:tam02:potential} \end{align} [[/math]]

It is worth emphasizing that the characterization in \eqref{eq:region:man:tam02:potential} depends on [math]\theta[/math], and makes no use of the information in [math]\sP(\ey|\ew,\xL,\xU)[/math]. The Corollary to Proposition 2 yields conditions on [math]\sP(\ew,\xL,\xU)[/math] under which either the sign of components of [math]\theta[/math], or [math]\theta[/math] itself, can be identified, regardless of the distribution of [math]\ey|\ew,\xL,\xU[/math]. provide a second characterization, which presupposes knowledge of [math]\sP(\ey,\ew,\xL,\xU)[/math], yields a set smaller than the one in \eqref{eq:region:man:tam02:potential}, and coincides with the result in Theorem SIR-. use the same notation for the two sets, although the sets are conceptually and mathematically distinct. The result in Theorem SIR- is due to , but the proof provided here is new, as is the use of random set theory in this application.

Key Insight:The preceding discussion allows me to draw a novel connection between the two characterizations in , and the distinction put forward by and in partial identification between potential observational equivalence and observational equivalence. Applying 's definition, parameter vectors [math]\theta[/math] and [math]\vartheta[/math] are potentially observationally equivalent if there exists some distribution of [math]\ey|\ew,\xL,\xU[/math] for which conditions \eqref{eq:key_sharp:man:tam02_1}-\eqref{eq:key_sharp:man:tam02_2} hold. Simple algebra confirms that this yields the region in \eqref{eq:region:man:tam02:potential}. This notion of potential observational equivalence parallels one of the notions used to obtain sufficient conditions for point identification in the semiparametric literature (as in, e.g. ). Both notions, as explained in , make no reference to the conditional distribution of outcomes given covariates delivered by the process being studied. To obtain that parameters [math]\theta[/math] and [math]\vartheta[/math] are observationally equivalent one requires instead that conditions \eqref{eq:key_sharp:man:tam02_1}-\eqref{eq:key_sharp:man:tam02_2} hold for the observed distribution [math]\sP(\ey=1|\ew,\xL,\xU)[/math] (as opposed to ‘`for some distribution" as in the case of potential observational equivalence). This yields the sharp identification region in \eqref{eq:ThetaI_man:tam02_binary}.

studies random ’'expected utility models, where agents choose the alternative that maximizes their expected utility. The core difference with standard models is that does not fully specify the subjective beliefs that agents use to form their expectations, but only a set of such beliefs. shows that the resulting, partially identified, discrete choice model can be formulated similarly to how treat interval valued covariates, and leverages their results to obtain bounds on preference parameters.

consider a different but closely related model to the semiparametric binary response model studied by . They assume that an instrumental variable [math]\ez[/math] is available, that [math]\epsilon[/math] is independent of [math]\ex[/math] conditional on [math](\ew,\ez)[/math], and that [math]Corr(\ez,\epsilon)=0[/math]. They assume that the distribution of [math]\ex[/math] is absolutely continuous with support [math][v_1,v_k][/math], and that [math]\ex[/math] is not a deterministic linear function of [math](\ew,\ez)[/math]. They consider the case that [math]\ex[/math] is unobserved but known to belong to one of the fixed (and known) intervals [math][v_i,v_{i+1})[/math], [math]i=1,\dots,k-1[/math], with [math]\sR[\ex\in[v_i,v_{i+1})|\ew,\ez] \gt 0[/math] almost surely for all [math]i[/math]. Finally, they assume that [math](-\ew\theta-\epsilon)\in [v_1,v_k][/math] with probability one. They do not, however, make quantile independence assumptions. Their point of departure is the fact that under these conditions, if [math]\ex[/math] were observed, one could employ a transformation proposed by for the binary outcome [math]\ey[/math], such that [math]\theta[/math] can be identified through a simple linear moment condition. Specifically, let

[[math]] \begin{align*} \tilde{\ey}=\frac{\ey - \one_{\ex \gt 0}}{f_\ex(\ex|\ew,\ez)}, \end{align*} [[/math]]

where [math]f_\ex(\cdot|\ew,\ez)[/math] is the conditional density function of [math]\ex[/math]. Then, using the assumption that [math]\ez[/math] and [math]\epsilon[/math] are uncorrelated, one has

[[math]] \begin{align} \E_\sP(\ez \tilde{\ey})-\E_\sP(\ez \ew^\top) \theta = 0.\label{eq:sem-bin} \end{align} [[/math]]

With interval valued [math]\ex[/math], denote by [math]\ex^*[/math] the random variable that takes value [math]i\in\{1,\dots,k-1\}[/math] if [math]\ex\in[v_i,v_{i+1})[/math], so that the observed data are draws from the joint distribution of [math](\ey,\ew,\ez,\ex^*)[/math]. They let [math]\delta(\ex^*)=v_{\ex^*+1}-v_{\ex^*}[/math] denote the length of the [math]\ex^*[/math]-th interval, and define the transformed outcome variable:

[[math]] \ey^*=\frac{\delta(\ex^*)}{\sP(\ex^*=i|\ew,\ez)}\ey-v_k. [[/math]]

The assumptions on [math]\ex[/math] yield that, given [math]\ez[/math] and [math]\ew[/math], [math]\epsilon[/math] does not depend on [math]\ex^*[/math]. Moreover, [math]\sP(\ey=1|\ex^*,\ew,\ez)[/math] is non-decreasing in [math]\ex^*[/math] and [math]\sF_\epsilon(\cdot|\ez,\ew,\ex,\ex^*)=\sF_\epsilon(\cdot|\ez,\ew)[/math]. show that the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align} \idr{\theta}=\E_\sP(\ez \ew^\top)^{-1}\E_\sP(\ez \ey^* + \ez \eU),\label{eq:SIR:mag:mau} \end{align} [[/math]]

where [math]\E_\sP(\ez \ey^* + \ez \eU)[/math] is the Aumann (or selection) expectation of the random interval [math]\ez \ey^* + \ez \eU[/math], see Definition, with

[[math]] \begin{align*} \eU=\left[-\sum_{i=1}^{k-1}(r_i(\ew,\ez)-r_{i-1}(\ew,\ez))(v_{i+1}-v_i), \sum_{i=1}^{k-1}(r_{i+1}(\ew,\ez)-r_i(\ew,\ez))(v_{i+1}-v_i) \right]. \end{align*} [[/math]]

In this expression, [math]r_{\ex^*}(\ew,\ez)\equiv\sP(\ey=1|\ex^*,\ew,\ez)[/math] and by convention [math]r_0(\ew,\ez)=0[/math] and [math]r_K(\ew,\ez)=1[/math], see . If [math]r_i(\ew,\ez),i=0,\dots,k[/math], were observed, this characterization would be very similar to the one provided by for Identification Problem, see equation eq:ThetaI_BLP. However, these random functions need to be estimated. While the first-stage estimation of [math]r_i(\ew,\ez),i=0,\dots,k[/math], does not affect the identification arguments, it does complicate inference, see and the discussion in Section.

Endogenous Explanatory Variables

Whereas the standard random utility model presumes some form of exogeneity for [math]\ex[/math], in practice often some explanatory variables are endogenous. This problem has been addressed in the literature to obtain point identification of the model through a combination of several assumptions, including large support conditions, special regressors, control function restrictions, and more (see, e.g., ). analyze the distinct but related problem of identification in a censored regression model with endogeneous explanatory variables, and provide sufficient conditions for point identification. Here I discuss how to carry out identification analysis in the absence of such assumptions when instrumental variables [math]\ez[/math] are available, as proposed by . They consider a more general case than I do here, with utility function that is not parametrically specified and not restricted to be separable in the unobservables. Even in that more general case, the identification analysis follows through similar steps as reported here. \begin{IP}[Discrete Choice with Endogenous Explanatory Variables]\label{IP:discrete:choice:endogenous} Let [math](\ey,\ex,\ez)\sim\sP[/math] be observable random variables in [math]\cY\times\cX\times\cZ[/math]. Let all members of the population face the same choice set [math]\cY[/math]. Suppose that each alternative has one unobservable attribute [math]\epsilon_c,c\in\cY[/math] and let [math]\nu\equiv(\epsilon_{c_1},\dots,\epsilon_{c_{|\cY|}})[/math]. Let [math]\nu\sim\sQ[/math] and assume that [math]\nu\independent\ez[/math]. Suppose [math]\sQ[/math] belongs to a nonparametric family of distributions [math]\cT[/math], and that the conditional distribution of [math]\nu|\ex,\ez[/math], denoted [math]\sR(\nu|\ex,\ez)[/math], is absolutely continuous with respect to Lebesgue measure with everywhere positive density on its support, [math](\ex,\ez)[/math]-a.s. Suppose utility is separable in unobservables and has a functional form known up to finite dimensional parameter vector [math]\theta\in\Theta\subset\R^m[/math], so that [math]\bu_i(c)=g(\ex_c;\theta)+\epsilon_c[/math], [math](\ex_c,\epsilon_c)[/math]-a.s., for all [math]c\in\cY[/math]. Maintain the normalizations [math]g(\ex_{c_{|\cY|}};\theta)=0[/math] for all [math]\theta\in\Theta[/math] and all [math]\ex\in\cX[/math], and [math]g(x_c^0;\theta)=\bar{g}[/math] for known [math](x_c^0,\bar{g})[/math] for all [math]\theta\in\Theta[/math] and [math]c\in\cY[/math]. Given [math](\ex,\ez,\nu)[/math], suppose [math]\ey[/math] is the utility maximizing choice in [math]\cY[/math]. In the absence of additional information, what can the researcher learn about [math](\theta,\sQ)[/math]? \qedex }} The key challenge to identification here results because the distribution of [math]\nu[/math] can vary across different values of [math]\ex[/math], both conditional and unconditional on [math]\ez[/math]. Why does this fact hinder point identification? For a given [math]\vartheta\in\Theta[/math] and for any [math]c\in\cY[/math] and [math]x\in\cX[/math], the model yields that [math]c[/math] is optimal, and hence chosen, if and only if [math]\nu[/math] realizes in the set

[[math]] \begin{align} \cE_\vartheta(c,x)=\{e\in\cV:g(x_c;\vartheta)+e_c\ge g(x_d;\vartheta)+e_d\forall d\in\cY\}.\label{eq:che:ros:E} \end{align} [[/math]]

Figure plots the set [math]\cE_\vartheta(\ey,\ex)[/math] in a stylized example with [math]\cY=\{1,2,3\}[/math] and [math]\cX=\{x^1,x^2\}[/math], as a function of [math](\epsilon_1-\epsilon_3,\epsilon_2-\epsilon_3)[/math]. Consider the model implied distribution, denoted [math]\sM[/math] below, of the optimal choice. Then, recalling the restriction [math]\ez\independent\nu[/math], we have

[[math]] \begin{align} \sM(c|\ex\in R_x,\ez;\vartheta)&=\int_{x\in R_x}\sR(\cE_\vartheta(c,\ex)|\ex=x,\ez)d\sP(x|z),\forallR_x\subseteq\cX,\ez\text{-a.s.}\label{eq:che:ros:model:distrib}\\ \sQ(F)&=\int_{x\in\cX}\sR(F|\ex=x,\ez)d\sP(x|z),\forallF\subseteq\cV,\ez\text{-a.s.},\label{eq:che:ros:instrument} \end{align} [[/math]]

Because the joint distribution of [math](\ex,\nu)[/math] conditional on [math]\ez[/math] is left completely unrestricted (other than \eqref{eq:che:ros:instrument}), one can find multiple triplets [math](\vartheta,\sQ,\sR(\nu|\ex,\ez))[/math] satisfying the maintained assumptions and with [math]\sM(c|\ex\in R_x,\ez;\vartheta)=\sP(c|\ex\in R_x,\ez)[/math] for all [math]c\in\cY[/math] and [math]R_x\subseteq\cX[/math], [math]\ez[/math]-a.s.

The set [math]\cE_\vartheta[/math] in equation \eqref{eq:che:ros:E} and the corresponding admissible values for [math](\ey,\ex)[/math] as a function of [math](\epsilon_1-\epsilon_3,\epsilon_2-\epsilon_3)[/math] under the simplifying assumption that [math]\cX=\{x^1,x^2\}[/math] and [math]\cY=\{1,2,3\}[/math]. The admissible values for [math](\ey,\ex)[/math] are [math]\{(c,x^1)\}[/math] in the gray area, and [math]\{(c,x^2)\}[/math] in the area with vertical lines. Because the two areas overlap, the model has set-valued predictions for [math](\ey,\ex)[/math].

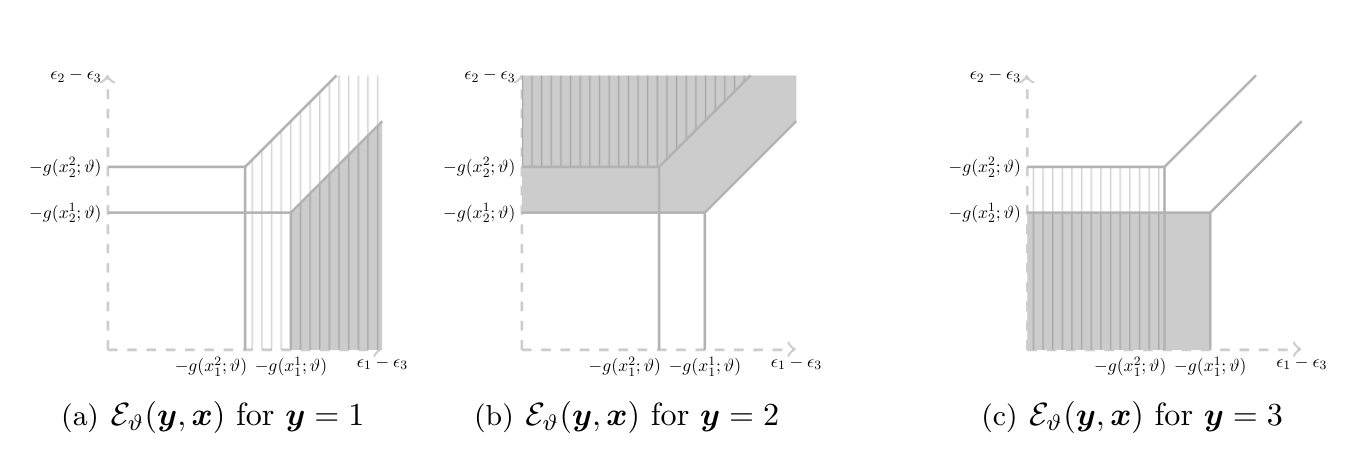
It is instructive to compare \eqref{eq:che:ros:model:distrib}-\eqref{eq:che:ros:instrument} with conditional logit. Under the standard assumptions, [math]\ex\independent\nu[/math] so that no instrumental variables are needed. This yields [math]\sQ(\nu)=\sR(\nu|\ex)[/math] [math]\ex[/math]-a.s., and in addition [math]\sQ[/math] is typically known, with corresponding simplifications in \eqref{eq:che:ros:model:distrib}. The resulting system of equalities can be inverted under standard order and rank conditions to yield point identification of [math]\theta[/math]. Further insights can be gained by looking at Figure. As the value of [math]\ex[/math] changes from [math]x^1[/math] to [math]x^2[/math], the region of values where, say, alternative 1 is optimal changes. When [math]\ex[/math] is exogenous, say independent of [math]\nu[/math], this yields a system of equalities relating [math](\theta,\sQ)[/math] to the observed distribution [math]\sP(\ey,\ex)[/math] which, as stated above, can be inverted to obtain point identification. When [math]\ex[/math] is endogenous, this reasoning breaks down because the conditional distribution [math]\sR(\nu|\ex,\ez)[/math] may change across realizations of [math]\ex[/math]. Figure also offers an instructive way to connect Identification Problem with the identification problem studied in Section Semiparametric Binary Choice Models with Interval Valued Covariates (as well as with those in Sections Static, Simultaneous-Move Finite Games with Multiple Equilibria-Auction Models with Independent Private Values below). In the latter, the model has set-valued predictions for the outcome variable given realizations of the covariates and unobserved heterogeneity terms, which overlap across realizations of the unobserved heterogeneity terms. In the problem studied here, the model has singleton-valued predictions for the outcome variable of interest [math]\ey[/math] as a function of the observable explanatory variables [math]\ex[/math] and unobservables [math]\nu[/math]. However, for given realization of [math]\nu[/math], the model admits sets of values for the endogenous variables [math](\ey,\ex)[/math], which overlap across realizations of [math]\nu[/math]. Because the model is silent on the joint distribution of [math](\ex,\nu)[/math] (except for requiring that the marginal distribution of [math]\nu[/math] does not depend on [math]\ez[/math]), partial identification results. It is possible to couple the maintained assumptions with the observed data to learn features of [math](\theta,\sQ)[/math]. Because the observed choice [math]\ey[/math] is assumed to maximize utility, for the data generating [math](\theta,\sQ)[/math] the model yields

[[math]] \begin{align} \nu\in \cE_\theta(\ey,\ex)\text{-a.s.},\label{eq:che:ros:e_in_E} \end{align} [[/math]]

with [math]\cE_\theta(\ey,\ex)[/math] a random closed set as per Definition. Equation \eqref{eq:che:ros:e_in_E} exhausts the modeling content of Identification Problem. Theorem (as expressed in eq:dom-c) can then be leveraged to extract its empirical content from the observed distribution [math]\sP(\ey,\ex,\ez)[/math]. As a preparation for doing so, note that for given [math]F\in\cF[/math] (with [math]\cF[/math] the collection of closed subsets of [math]\cV[/math]) and [math]\vartheta\in\Theta[/math], we have

[[math]] \begin{align*} \sP(\cE_\vartheta(\ey,\ex)\subseteq F|\ez)=\int_{x\in\cX}\sum_{c\in\cY}\one(\cE_\vartheta(c,x)\subseteq F)\sP(\ey=c|\ex=x,\ez)d\sP(x|\ez), \end{align*} [[/math]]

so that this probability can be learned from the observed data.

Discrete Choice with Endogenous Explanatory Variables

Under the assumptions of Identification Problem, the sharp identification region for [math](\theta,\sQ)[/math] is

[[math]] \begin{align} \idr{\theta,\sQ}=\left\{\vartheta\in\Theta,\tilde\sQ\in\cT:\tilde\sQ(F)\ge \sP(\cE_\vartheta(\ey,\ex)\subseteq F|\ez),\forall F\in\cF,\ez\text{-a.s.}\right\}.\label{eq:SIR:discrete:choice:endogenous} \end{align} [[/math]]

Show Proof

To simplify notation, I write [math]\cE_\vartheta\equiv\cE_\vartheta(\ey,\ex)[/math]. Let [math](\cE_\vartheta,\ex,\ez)=\{(\mathbf{e},\ex,\ez):\mathbf{e}\in\cE_\vartheta\}[/math]. If the model is correctly specified, [math](\nu,\ex,\ez)\in(\cE_\theta,\ex,\ez)[/math]-a.s. for the data generating value of [math](\theta,\sQ)[/math]. Using Theorem and Theorem 2.33 in , it follows that [math](\vartheta,\tilde\sQ)[/math] is observationally equivalent to [math](\theta,\sQ)[/math] if and only if

[[math]] \begin{align*} \tilde\sQ(F|\ex,\ez)\ge \sP(\cE_\vartheta(\ey,\ex)\subseteq F|\ex,\ez),\forall F\in\cF,(\ex,\ez)\text{-a.s.} \end{align*} [[/math]]

As the distribution of [math]\nu[/math] is only restricted so that [math]\nu\independent\ez[/math], one can integrate both sides of the inequality with respect to [math]\ex[/math]. The final result follows because [math]\tilde\sQ[/math] does not depend on [math]\ez[/math].

■

While Theorem SIR- relies on checking inequality \eqref{eq:SIR:discrete:choice:endogenous} for all [math]F\in\cF[/math], the results in and can be used to obtain a smaller collection of sets over which to verify it. In particular, if [math]\ex[/math] has a discrete distribution, it suffices to use a finite collection of sets. For example, in the case depicted in Figure with [math]\cX=\{x^1,x^2\}[/math], show that [math]\idr{\theta,\sQ}[/math] is obtained by checking at most twelve inequalities in \eqref{eq:SIR:discrete:choice:endogenous}. The left hand side of these inequalities is a linear function of six values that the distribution [math]\tilde\sQ[/math] assigns to each of the component regions depicted in Figure (the one where [math]\cE_\vartheta(1,x^1)\cap\cE_\vartheta(1,x^2)[/math] realizes; the one where [math]\cE_\vartheta(1,x^1)\cap\cE_\vartheta(3,x^2)[/math] realizes; etc.) Hence, in this example, [math](\vartheta,\tilde\sQ)\in\idr{\theta,\sQ}[/math] if and only if [math]\tilde\sQ[/math] assigns to these six regions a probability mass such that for [math]\vartheta[/math] the twelve inequalities characterized by hold.

Key Insight: A conceptual contribution of is to show that one can frame models with endogenous explanatory variables as incomplete models. Incompleteness here results from the fact that the model does not specify how the endogenous variables [math]\ex[/math] are determined. One can then think of these as models with set-valued predictions for the endogeneous variables ([math]\ey[/math] and [math]\ex[/math] in this application), even though the outcome of the model ([math]\ey[/math]) is uniquely predicted by the realization of the observed explanatory variables ([math]\ex[/math]) and the unobserved heterogeneity terms ([math]\nu[/math]). Random set theory can again be leveraged to characterize sharp identification regions. discuss related generalized instrumental variables models where random set methods are used to obtain characterizations of sharp identification regions in the presence of endogenous explanatory variables.

Unobserved Heterogeneity in Choice Sets and/or Consideration Sets

Compared to the general framework set forth at the beginning of Section Discrete Choice in Single Agent Random Utility Models, as pointed out in , often the researcher observes [math](\ey_i,\ex_i)[/math] but not [math]\eC_i[/math], [math]i=1,\dots,n[/math]. Even when [math]\eC_i[/math] is observable, the researcher may be unaware of which of its elements the decision maker actually evaluates before selecting one. In what follows, to shorten expressions, I refer to both the measurement problem of unobserved choice sets and the (cognitive) problem of limited consideration as ‘`unobserved heterogeneity in choice sets."

Learning features of preferences using discrete choice data in the presence of unobserved heterogeneity in choice sets is a formidable task. When a decision maker chooses an alternative, this may be because her choice set equals the feasible set and the chosen alternative is the one yielding the highest utility. Then observed choice reveals preferences. But it can also be that the decision maker has access to/considers only the chosen alternative (e.g., ). Then observed choice is driven entirely by choice set composition, and is silent about preferences. A plethora of scenarios between these extremes is possible, but the researcher does not know which has generated the observed data. This fundamental identification problem calls either for restrictions on the random utility model and consideration set formation process, or for collection of richer data that eliminates unobserved heterogeneity in [math]\eC_i[/math] or allows for enhanced modeling of it (see, e.g., ).

A sizable literature spanning behavioral economics, econometrics, experimental economics, marketing, microeconomics, and psychology, has put forward different models to formalize the complex process that leads to the formation of the set of alternatives that the agent considers or can choose from (see, e.g., ). proposes both a general econometric model where decision makers draw choice sets from an unknown distribution, as well as a specific model of choice set formation, independent from preferences, and studies their implications for the distributional structure of random utility models.

However, assumptions about the choice set formation process are often rooted in a desire to achieve point identification rather than in information contained in the model or observed data. It is then important to ask what can be learned about decision maker’s preferences under minimal assumptions on the choice set formation process. Allowing for unrestricted dependence between choice sets and preferences, while challenging for identification analysis, is especially relevant. Indeed, decision makers' unobserved attributes may determine both their preferences and which items in the feasible set they pay attention to or are available to them (e.g., through unobserved liquidity constraints, unobserved characteristics such as religious preferences in the context of school choice, or behavioral phenomena such as aversion to extremes, salience, etc.). Here I use the framework put forward by to study identification of discrete choice models with unobserved heterogeneity in choice sets and preferences.

\begin{IP}[Discrete Choice with Unobserved Heterogeneity in Choice Sets and Preferences]\label{IP:BCMT} Let [math](\ey,\ex)\sim \sP[/math] be observable random variables in [math]\cY\times\cX[/math]. Assume that there exists a real valued function [math]g[/math], which for simplicity I posit known up to parameter [math]\delta\in\Delta\subset\R^m[/math] and continuous in its second argument, such that [math]\bu_i(c)=g(\ex_{ic},\nu_i;)[/math], [math](\ex_{ic},\nu_i)[/math]-a.s., for all [math]c\in\cY,i\in\cI[/math], where [math]\ex_{ic}[/math] denotes the vectors of attributes relevant to alternative [math]c[/math], and includes attributes that are alternative invariant and ones that are alternative specific (respectively, [math]\ex_i^1[/math] and [math]\ex_{ic}^2[/math] in the general notation laid out in Section Discrete Choice in Single Agent Random Utility Models). Suppose that [math]\ey=\arg\max_{c\in \eC}g(\ex_c,\nu;\delta)[/math], where ties are assumed to occur with probability zero and [math]\eC[/math] is an unobservable choice set drawn from the subsets of [math]\cY[/math] according to some unknown probability distribution. Suppose [math]\sR(|\eC|\ge\kappa)=1[/math] for some known constant [math]\kappa\ge 2[/math]. Let [math]\sQ[/math] denote the distribution of [math]\nu[/math], and assume that it is known up to a finite dimensional parameter [math]\gamma\in\Gamma\subset\R^k[/math]. For simplicity, assume that [math]\nu\independent\ex[/math]. In the absence of additional information, what can the researcher learn about [math]\theta\equiv[\delta;\gamma][/math]? \qedex }}

Predicted value of [math]\ey[/math] in Identification Problem as a function of [math]\nu[/math] for [math]\kappa=|\cY|-1[/math]. In this case, [math]\eC=\cY\setminus\{c\}[/math] for some [math]c\in\cY[/math], and the model predicts either the first or the second best alternative in [math]\cY[/math].

The model just laid out has set valued predictions for the decision maker's optimal choice, because different alternatives might be optimal depending on which choice set the decision maker draws. Figure, which is based on the analysis in , illustrates the set valued predictions in a stylized example. In the figure [math]\nu[/math] is assumed to be a scalar; [math]\bar{\nu}_{j,m}[/math] denotes the threshold value of [math]\nu[/math] above which [math]c_j[/math] yields higher utility than [math]c_m[/math] and below which [math]c_m[/math] yields higher utility than [math]c_j[/math] (the threshold's dependence on [math](\ex;\delta)[/math] is suppressed for notational convenience). Consider the case that [math]\nu\in[\bar{\nu}_{2,3},\bar{\nu}_{1,2}][/math], so that [math]c_2[/math] is the option yielding the highest utility among all options in [math]\cY[/math]. When [math]\kappa=|\cY|-1[/math], the agent may draw a choice set that does not include one of the alternatives in [math]\cY[/math]. If the excluded alternative is not [math]c_2[/math] (or if [math]\eC[/math] realizes equal to [math]\cY[/math]), the model predicts that the decision maker chooses [math]c_2[/math]. If [math]\eC[/math] realizes equal to [math]\cY\setminus\{c_2\}[/math], the model predicts that the decision maker chooses the second best: [math]c_1[/math] if [math]\nu\in[\bar{\nu}_{1,3},\bar{\nu}_{1,2}][/math], and [math]c_3[/math] if [math]\nu\in[\bar{\nu}_{2,3},\bar{\nu}_{1,3}][/math]. Conversely, observation of [math]\ey=c_1[/math] allows one to conclude that [math]\nu\ge\bar\nu_{1,3}[/math], and [math]\ey=c_2[/math] that [math]\nu\ge\bar\nu_{2,4}[/math], with [math]\bar\nu_{2,4}\le\bar\nu_{1,3}[/math], and these regions of possible realizations of [math]\nu[/math] overlap.

Why does this set valued prediction hinder point identification? The reason is similar to the explanation given for Identification Problem: the distribution of the observable data relates to the model structure in an incomplete manner, because the distribution of the (unobserved) choice sets is left completely unspecified. show that one can find multiple candidate distributions for [math]\eC[/math] and parameter vectors [math]\vartheta[/math], such that together they yield a model implied distribution for [math]\ey|\ex[/math] that matches [math]\sP(\ey|\ex)[/math], [math]\ex[/math]-a.s. propose to work directly with the set of model implied optimal choices given [math](\ex,\nu)[/math] associated with each possible realization of [math]\eC[/math], which is depicted in Figure for a specific example. The key idea is that, according to the model, the observed choice maximizes utility among the alternatives in [math]\eC[/math]. Hence, for the data generating value of [math]\theta[/math], it belongs to the set of model implied optimal choices. With this, the authors are able to characterize [math]\idr{\theta}[/math] through Theorem as the collection of parameter vectors that satisfy a finite number of conditional moment inequalities.

Key Insight: show that working directly with the set of model implied optimal choices given [math](\ex,\nu)[/math] allows one to dispense with considering all possible distributions of choice sets that are allowed for in Identification Problem to complete the model. Such distributions may depend on [math]\nu[/math] even after conditioning on observables and may constitute an infinite dimensional nuisance parameter, which creates great difficulties for the computation of [math]\idr{\theta}[/math] and for inference.

Identification Problem sets up a structure where preferences include idiosyncratic components [math]\nu[/math] that are decision maker specific and can depend on [math]\eC[/math], and where heterogeneity in [math]\eC[/math] can be driven either by a measurement problem, or by the decision maker's limited attention to the options available to her. However, for computational and finite sample inference reasons, it restricts the family of utility functions to be known up to a finite dimensional parameter vector [math]\delta[/math].

A rich literature in decision theory has analyzed a different framework, where the decision maker's choice set is observable to the researcher, but the decision maker does not consider all alternatives in it (for recent contributions see, e.g., ). In this literature, the utility function is left completely unspecified, so that interest focuses on identification of preference orderings of the available options. Unobserved heterogeneity in preferences is assumed away, so that heterogeneous choice is driven by randomness in consideration sets. If the consideration set formation process is left unspecified or is subject only to weak restrictions, point identification of the preference orderings is not possible even if preferences are homogeneous and the researcher observes a representative agent facing multiple distinct choice problems with varying choice sets.

propose a general model for the consideration set formation process where the only restriction is a weak and intuitive monotonicity condition: the probability that any particular consideration set is drawn does not decrease when the number of possible consideration sets decreases. Within this framework, they provide revealed preference theory and testable implications for observable choice probabilities. \begin{IP}[Homogeneous Preference Orderings in Random Attention Models]\label{IP:RAM} Let [math](\ey,\eC)\sim\sP[/math] be a pair of observable random variable and random set in [math]\cY\times\mathfrak{D}[/math], where [math]\mathfrak{D}=\{D:D\subseteq\cY\}\setminus\emptyset[/math]. Let [math]\mu:\mathfrak{D}\times\mathfrak{D}\to[0,1][/math] denote an attention rule such that [math]\mu(A|G)\ge 0[/math] for all [math]A\subseteq G[/math], [math]\mu(A|G)=0[/math] for all [math]A\nsubseteq G[/math], and [math]\sum_{A\subset G}\mu(A|G)=1[/math], [math]A,G\in\mathfrak{D}[/math]. Assume that for any [math]b\in G\setminus A[/math],

[[math]] \begin{align} \label{eq:RAM:monotonicity} \mu(A|G)\le\mu(A|G\setminus\{b\}), \end{align} [[/math]]

and that the decision maker has a strict preference ordering [math]\succ[/math] on [math]\cY[/math]. In the absence of additional information, what can the researcher learn about [math]\succ[/math]? \qedex }} posit that an observed distribution of choice [math]\sP(\ey|\eC)[/math] has a random attention representation, and hence they name it a random attention model, if there exists a preference ordering [math]\succ[/math] over [math]\cY[/math] and a monotonic attention rule [math]\mu[/math] such that

[[math]] \begin{align} \cp(c|G)\equiv\sP(\ey=c|\eC=G)=\sum_{A\subseteq G}\one(c\text{ is }\succ\text{-best in }A)\mu(A|G),\forall c\in G,\forall G\in\mathfrak{D}.\label{eq:RAM} \end{align} [[/math]]

The sharp identification region for the preference ordering, denoted [math]\idr{\succ}[/math] henceforth, is given by the collection of preference orderings for which one can find a monotonic attention rule to pair it with, so that \eqref{eq:RAM} holds. Of course, an observed distribution of choice can be represented by multiple preference orderings and attention rules. The authors, however, show in their Lemma 1 that if for some [math]G\in\mathfrak{D}[/math] with [math]\{b,c\}\in G[/math],

[[math]] \begin{align} \cp(c|G) \gt \cp(c|G\setminus \{b\}),\label{eq:RAM_violation_reg} \end{align} [[/math]]

then [math]c \succ b[/math] for any [math]\succ[/math] for which one can find a monotonic attention rule [math]\mu[/math] such that \eqref{eq:RAM} holds. Because of preference transitivity, one can also learn [math]a\succ b[/math] if in addition to the above condition one has [math]\cp(a|G^\prime) \gt \cp(a|G^\prime\setminus \{c\})[/math] for some [math]c\in G^\prime[/math] and [math]G^\prime\in\mathfrak{D}[/math]. The authors further show in their Theorem 1 that the collection of preference relations associated with all possible instances of \eqref{eq:RAM_violation_reg} for all [math]c\in G[/math] and [math]G\in\mathfrak{D}[/math] yield all information about preferences given the observed choice probabilities. This yields a system of linear inequalities in [math]\cp(c|G)[/math] that fully characterize [math]\idr{\succ}[/math]. Let [math]\vec{\cp}[/math] denote the vector with elements [math][\cp(c|G):c\in G,G\in\mathfrak{D}][/math] and [math]\Pi_\succ[/math] denote a conformable matrix collecting the constraints on [math]\sP(\ey|\eC)[/math] embodied in \eqref{eq:RAM_violation_reg} and its generalizations based on transitive closure. Then

[[math]] \begin{align} \idr{\succ}=\{\succ: \Pi_\succ \vec{\cp}\le 0\}.\label{eq:SIR:RAM} \end{align} [[/math]]

The authors show that for any given preference ordering [math]\succ[/math], the matrix [math]\Pi_\succ[/math] characterizing whether [math]\succ \in \idr{\succ}[/math] through the system of linear inequalities in \eqref{eq:SIR:RAM} is unique, and they provide a simple algorithm to compute it. They also show that mild additional assumptions, such as, for example, that decision makers facing binary choice sets pay attention to both alternatives frequently enough, can substantially increase the informational content of the data (i.e., substantially tighten [math]\idr{\succ}[/math]).

Key Insight: show that learning features of preference orderings in Identification Problem requires the existence in the data of choice problems where the choice probabilities satisfy \eqref{eq:RAM_violation_reg}. The latter is a violation of the principle of ‘`regularity" according to which the probability of choosing an alternative from any set is at least as large as the probability of choosing it from any of its supersets. Regularity is a monotonicity property of choice probabilities, and it is implied by a wide array of models of decision making. The monotonicity of attention rules in \eqref{eq:RAM:monotonicity} can be viewed as regularity of the process that chooses a consideration set from the subsets of the choice set. show that it is implied by various models of limited attention. While the violation required in \eqref{eq:RAM_violation_reg} is weak in that it needs only to occur for some [math]G[/math], it sheds a different light on the severity of the identification problem described at the beginning of this section. Regularity of choice probabilities and (partial) identification of preference orderings can co-exist only under restrictions on the consideration set formation process that are stronger than the regularity of attention rules in \eqref{eq:RAM:monotonicity}.

and provide different sets of sufficient conditions for point identification of models of limited consideration. In both cases, the authors posit specific models of consideration set formation and provide sufficient conditions for point identification under exclusion and large support assumptions. assume that unobserved heterogeneity in preferences and in consideration sets are independent. They exploit violations of Slutsky symmetry that result from inattention, assuming that for each alternative there is an observable characteristic with large support that does not affect the consideration probability of the other options.

provide a thorough analysis of the extent of dependency between consideration and preferences under which semi-nonparametric point identification of the distribution of preferences and consideration attains. They exploit a requirement of standard economic theory --the Spence-Mirrlees single crossing property of utility functions-- coupled with a mild strengthening of the classic conditions for semi-nonparametric identification of discrete choice models with full consideration and identical choice sets (see, e.g., ), assuming that there is at least one decision maker-specific characteristic with large support that affects utility but not consideration.

Prediction of Choice Behavior with Counterfactual Choice Sets

Building on , studies a question related but distinct from those in Identification problem - problem. He is concerned with prediction of choice behavior when decision makers face counterfactual choice sets. frames this question as one of predicting treatment response (see Section Treatment Effects with and without Instrumental Variables). Here the collection of potential treatments is given by [math]\mathfrak{D}[/math], the nonempty subsets of the universe of feasible alternatives [math]\cY[/math], and the response function specifies the alternative chosen by a decision maker when facing choice set [math]G\in\mathfrak{D}[/math]. assumes that the researcher observes realized choice sets and chosen alternatives, [math](\ey,\eC)\sim\sP[/math]. Under the standard assumptions laid out at the beginning of Section Discrete Choice in Single Agent Random Utility Models, specifically if utility functions are (say) linear in [math]\epsilon_{ic}[/math] and the distribution of [math]\epsilon_{ic}[/math] is (say) Type I extreme value or multivariate normal, prediction of choice behavior with counterfactual choice sets is immediate (and point identified). , however, leaves utility functions completely unspecified, and in fact works directly with preference orderings, which he labels decision maker’s types. He places no restriction on the distribution of preference types, except requiring that they are independent of the observed choice sets. shows that under these rather weak assumptions, the distribution of predicted choices from counterfactual choice sets can be partially identified, and characterized as the solution to linear programs.

Specifically, let [math]\ey^*(G)[/math] denote the decision maker's optimal choice when facing choice set [math]G\in\mathfrak{D}[/math]. Assume [math]\ey^*(\cdot)\independent\eC[/math], and let [math]y_k[/math] denote the choice function for a decision maker of type [math]k[/math] --that is, a decision maker with a specific preference ordering labeled [math]k[/math]. One example of such preference ordering might be [math]c_1\succ c_2\succ\dots\succ c_{|\cY|}[/math]. If a decision maker of this type faces, say, choice set [math]G=\{c_2,c_3,c_4\}[/math], then she chooses alternative [math]c_2[/math]. Let [math]K[/math] denote the set of logically possible types, and [math]\theta_k[/math] the probability that a decision maker in the population is of type [math]k[/math]. Suppose that the researcher posits a behavioral model specifying [math]K[/math], [math]\{y_k,k=1,\dots,K\}[/math], and restrictions that constrain [math]\theta[/math] to lie in some specified set of distributions. Let [math]\Theta[/math] denote the values of [math]\vartheta[/math] that satisfy these requirements plus the conditions [math]\vartheta_k\ge 0[/math] for all [math]k\in K[/math] and [math]\sum_{k\in K}\vartheta_k=1[/math]. Then for any [math]c\in\cY[/math] and [math]\vartheta\in\Theta[/math], the model predicts

[[math]] \begin{align*} \sQ(\ey^*(G)=c)=\sum_{k\in K}\one(y_k(G)=c)\vartheta_k. \end{align*} [[/math]]

How can one partially identify this probability based on the observed data? Suppose [math]\eC[/math] is observed to take realizations [math]D_1,\dots,D_m[/math]. Then the data reveal

[[math]] \begin{align*} \sP(\ey(D_j)=d_j)=\sum_{k\in K}\one(y_k(D_j)=d_j)\theta_k\forall d_j\in D_j,j=1,\dots,m.\end{align*} [[/math]]

This yields that the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align*} \idr{\theta}=\{\vartheta\in\Theta:\sP(\ey(D_j)=d_j)=\sum_{k\in K}\one(y_k(D_j)=d_j)\vartheta_k\forall d_j\in D_j,j=1,\dots,m\}. \end{align*} [[/math]]

If the behavioral model is correctly specified, [math]\idr{\theta}[/math] is non-empty. In turn, the sharp identification region for each choice probability is

[[math]] \begin{align*} \idr{\sQ(\ey^*(G)=c)}=\left\{\sum_{k\in K}\one(y_k(G)=c)\vartheta_k:\vartheta\in\idr{\theta}\right\}, \end{align*} [[/math]]

and its extreme points can be obtained by solving linear programs.

provide closely related sharp bounds on features of counterfactual choices in the nonparametric random utility model of demand, where observable choices are repeated cross-sections and one allows for unrestricted, unobserved heterogeneity. Their approach builds on the work of , who test weather agents' behavior is consistent with the Axiom of Revealed Stochastic Preference (SARP) in a random utility model in which the utility function of each consumer over commodity bundles is assumed to satisfy only the basic restriction that ‘`more is better" with no satiation. Because the testing exercise is to be carried out using repeated cross-sections data, the authors maintain the assumption that multiple populations of consumers who face distinct choice sets have the same distribution of preferences. With this structure in place, de facto the task is to test the full implications of rationality without functional form restrictions. ’s approach is based on several novel ideas. As a first step, they leverage an earlier insight of to discretize the data without loss of information, so that they can define a large but finite set of rational preferences types. As a second step, they show that this implies that rationality can be tested by checking whether observed behavior lies in a cone corresponding to positive linear combinations of preference types. While the problem is discrete, its dimension is at first sight prohibitive. Nonetheless, Kitamura and Stoye are able to develop novel computational methods that render the problem tractable. They apply their method to the U.K. Household Expenditure Survey, adapting to their framework results on nonparametric instrumental variable analysis by so that they can handle price endogeneity.

builds on to learn program effects when agents are randomly assigned to control or treatment. The treatment group is provided access to the program, while the control group is not. However, members of the control group may receive access to the program from outside the experiment, leading to noncompliance with the randomly assigned treatment. The researcher wants to learn about the average effect of program access on the decision to participate in the program and on the subsequent outcome. While sufficiently rich data may allow the researcher to learn these effects, is concerned with the identification problem that arises when the researcher only observes the treatment assignment status, the program participation decision, and the outcome, but not the receipt of program access for every agent. formalizes this problem as one where the received treatment is selected from a choice set that depends on the assigned treatment and is unobservable to the researcher, and the agents optimally choose whether to participate in the program by maximizing their utility function over their choice set. Importantly, the utility functions are not subject to parametric restrictions, similarly to . But while assumed independence of choice sets and preference types, allows them to be arbitrarily dependent on each other, as in . approach leverages specific assumptions on random assignment of treatments and on compliance (or lack thereof) of participants to obtain nonparametric bounds on the treatment effects of interest that can be characterized using tractable linear programs.

Static, Simultaneous-Move Finite Games with Multiple Equilibria

An Inference Approach Robust to the Presence of Multiple Equilibria

and substantially enlarge the scope of partial identification analysis of structural models by showing how to apply it to learn features of payoff functions in static, simultaneous-move finite games of complete information with multiple equilibria. extend the approach and considerations that follow to games of incomplete information. To start, here I focus on two-player entry games with complete information.

Identification Problem (Complete Information Two Player Entry Game)

Let [math](\ey_1,\ey_2,\ex_1,\ex_2)\sim\sP[/math] be observable random variables in [math]\{0,1\}\times\{0,1\}\times\R^d\times\R^d[/math], [math]d \lt \infty[/math]. Suppose that [math](\ey_1,\ey_2)[/math] result from simultaneous move, pure strategy Nash play (PSNE) in a game where the payoffs are [math]\bu_j(\ey_j,\ey_{3-j},\ex_j;\beta_j,\delta_j)\equiv \ey_j(\ex_j\beta_j+\delta_j\ey_{3-j}+\eps_j)[/math], [math]j=1,2[/math] and the strategies are ‘`enter" ([math]\ey_j=1[/math]) or ``stay out" ([math]\ey_j=0[/math]). Here [math](\ex_1,\ex_2)[/math] are observable payoff shifters, [math](\eps_1,\eps_2)[/math] are payoff shifters observable to the players but not to the econometrician, [math]\delta_1\le 0,\delta_2\le 0[/math] are interaction effect parameters, and [math]\beta_1,\beta_2[/math] are parameter vectors in [math]B\subset\R^d[/math] reflecting the effect of the observable covariates on payoffs. Each player enters the market if and only if entering yields non-negative payoff, so that [math]\ey_j=\one(\ex_j\beta_j+\delta_j\ey_{3-j}+\eps_j\ge 0)[/math]. For simplicity, assume that [math]\eps\equiv(\eps_1,\eps_2)[/math] is independent of [math]\ex\equiv(\ex_1,\ex_2)[/math] and has bivariate Normal distribution with mean vector zero, variances equal to one (a normalization required by the threshold crossing nature of the model), and correlation [math]\rho\in [-1,1][/math]. In the absence of additional information, what can the researcher learn about [math]\theta=[\delta_1\delta_2\beta_1\beta_2\rho][/math]?

From the econometric perspective, this is a generalization of a standard discrete choice model to a bivariate simultaneous response model which yields a stochastic representation of equilibria in a two player, two action game. Generically, for a given value of [math]\theta[/math] and realization of the payoff shifters, the model just laid out admits multiple equilibria (existence of PSNE is guaranteed because the interaction parameters are non-positive). In other words, it yields set valued predictions as depicted in Figure. Why does this set valued prediction hinder point identification? Intuitively, the challenge can be traced back to the fact that for different values of [math]\theta\in\Theta[/math], one may find different ways to assign the probability mass in [math][-\ex_1\beta_1,-\ex_1\beta_1-\delta_1)\times [-\ex_2\beta_2,-\ex_2\beta_2-\delta_2)[/math] to [math](0,1)[/math] and [math](1,0)[/math], so as to match the observed distribution [math]\sP(\ey_1,\ey_2|\ex_1,\ex_2)[/math]. More formally, for fixed [math]\vartheta\in\Theta[/math] and given [math](\ex,\eps)[/math] and [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math], let

[[math]] \begin{align*} \cE_\vartheta[(1,0),(0,1);\ex]&\equiv[-\ex_1\beta_1,-\ex_1\beta_1-\delta_1)\times [-\ex_2\beta_2,-\ex_2\beta_2-\delta_2),\\ \cE_\vartheta[(y_1,y_2);\ex]&\equiv\{(\eps_1,\eps_2):(y_1,y_2)\text{is the unique equilibrium}\}, \end{align*} [[/math]]

so that in Figure [math]\cE_\vartheta[(1,0),(0,1);\ex][/math] is the gray region, [math]\cE_\vartheta[(0,1);\ex][/math] is the dotted region, etc. Let [math]\sR(y_1,y_2|\ex,\eps)[/math] be a ’'selection mechanism that assigns to each possible outcome of the game [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math] the probability that it is played conditional on observable and unobservable payoff shifters. In order to be admissible, [math]\sR(y_1,y_2|\ex,\eps)[/math] must be such that [math]\sR(y_1,y_2|\ex,\eps)\ge 0[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math], [math]\sum_{(y_1,y_2)\in\{0,1\}\times\{0,1\}}\sR(y_1,y_2|\ex,\eps)=1[/math], and

[[math]] \begin{align} \forall \eps\in\cE_\vartheta[(1,0),(0,1);\ex],&\sR(0,0|\ex,\eps)=\sR(1,1|\ex,\eps)=0 \label{eq:games:sel:mec:1}\\ \forall\eps\in\cE_\vartheta[(y_1,y_2);\ex],&\sR(\tilde y_1,\tilde y_2|\ex,\eps)=0 \forall(\tilde y_1,\tilde y_2)\in\{0,1\}\times\{0,1\}\text{s.t. }(\tilde y_1,\tilde y_2)\neq(y_1,y_2).\label{eq:games:sel:mec:2} \end{align} [[/math]]

Let [math]\Phi_r[/math] denote the probability distribution of a bivariate Normal random variable with zero means, unit variances, and correlation [math]r\in[-1,1][/math]. Let [math]\sM(y_1,y_2|\ex)[/math] denote the model predicted probability that the outcome of the game realizes equal to [math](y_1,y_2)[/math]. Then the model yields

[[math]] \begin{align} \sM(y_1,y_2|\ex)&=\int\sR(y_1,y_2|\ex,\eps)d\Phi_r\notag\\ &=\int_{(\eps_1,\eps_2)\in\cE_\vartheta[(y_1,y_2);\ex]}d\Phi_r+\int_{\eps_1,\eps_2\in\cE_\vartheta[(1,0),(0,1);\ex]}\sR(y_1,y_2|\ex,\eps)d\Phi_r.\label{eq:games_model:pred} \end{align} [[/math]]

Because [math]\sR(\cdot|\ex,\eps)[/math] is left completely unspecified, other than the basic restrictions listed above that render it an admissible selection mechanism, one can find multiple values for [math](\vartheta,\sR(\cdot|\ex,\eps))[/math] such that [math]\sM(y_1,y_2|\ex)=\sP(y_1,y_2|\ex)[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math] [math]\ex[/math]-a.s.

PSNE outcomes of the game in Identification Problem as a function of [math](\eps_1,\eps_2)[/math].

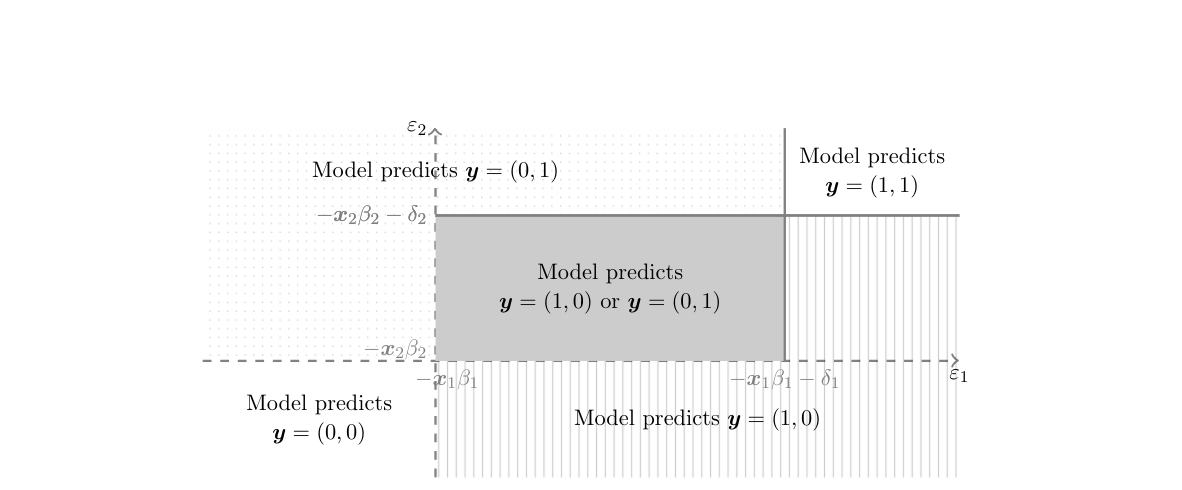
Multiplicity of equilibria implies that the mapping from the model's exogenous variables [math](\ex_1,\ex_2,\eps_1,\eps_2)[/math] to outcomes [math](\ey_1,\ey_2)[/math] is a correspondence rather than a function. This violates the classical “principal assumptions” or “coherency conditions” for simultaneous discrete response models discussed extensively in the econometrics literature (e.g., ). Such coherency conditions require the existence of a unique reduced form, mapping the model's exogenous variables and parameters to a unique realization of the endogenous variable; hence, they constrain the model to be recursive or triangular in nature. As pointed out by , however, the coherency conditions shut down exactly the social interaction effect of interest by requiring, e.g., that [math]\delta_1\delta_2=0[/math], so that at least one player's action has no impact on the other player's payoff.

The desire to learn about interaction effects coupled with the difficulties generated by multiplicity of equilibria prompted the earlier literature to provide at least two different ways to achieve point identification. The first one relies on imposing simplifying assumptions that shift focus to outcome features that are common across equilibria. For example, and study entry games where the number, though not the identities, of entrants is uniquely predicted by the model in equilibrium. Unfortunately, however, these simplifying assumptions substantially constrain the amount of heterogeneity in player's payoffs that the model allows for. The second approach relies on explicitly modeling a selection mechanism which specifies the equilibrium played in the regions of multiplicity. For example, assume it to be a constant; assume a more flexible, covariate dependent parametrization; and considers two possible selection mechanism specifications, one where the incumbent moves first, and the other where the most profitable player moves first. Unfortunately, however, the chosen selection mechanism can have non-trivial effects on inference, and the data and theory might be silent on which is more appropriate. A nice example of this appears in . review and extend a number of results on the identification of entry models extensively used in the empirical literature. discusses the observable implications of models with multiple equilibria, and within the analysis of a model with homogeneous preferences shows that partial identification is possible (see ). I refer to for a review of the literature on econometric analysis of games with multiple equilibria.

show, on the other hand, that it is possible to partially identify entry models that allow for rich heterogeneity in payoffs and for any possible selection mechanism (even ones that are arbitrarily dependent on the unobservable payoff shifters after conditioning on the observed payoff shifters). In addition, provides sufficient conditions for point identification based on exclusion restrictions and large support assumptions. analyze partial identification of nonparametric models of entry in a two-player model, drawing connections with the program evaluation literature.

Key Insight: An important conceptual contribution of is to clarify the distinction between a model which is incoherent, so that no reduced form exists, and a model which is incomplete, so that multiple reduced forms may exist. Models with multiple equilibria belong to the latter category. Whereas the earlier literature in partial identification had been motivated by measurement problems, e.g., missing or interval data, the work of and is motivated by the fact that economic theory often does not specify how an equilibrium is selected in the regions of the exogenous variables which admit multiple equilibria. This is a conceptually completely distinct identification problem.

propose to use simple and tractable implications of the model to learn features of the structural parameters of interest. Specifically, they point out that the probability of observing any outcome of the game cannot be smaller than the model's implied probability that such outcome is the unique equilibrium of the game, and cannot be larger than the model's implied probability that such outcome is one of the possible equilibria of the game. Looking at Figure this means, for example, that the observed [math]\sP((\ey_1,\ey_2)=(0,1)|\ex_1,\ex_2)[/math] cannot be smaller than the probability that [math](\eps_1,\eps_2)[/math] realizes in the dotted region, and cannot be larger than the probability that it realizes either in the dotted region or in the gray region. Compared to the model predicted distribution in \eqref{eq:games_model:pred}, this means that [math]\sP((\ey_1,\ey_2)=(0,1)|\ex_1,\ex_2)[/math] cannot be smaller than the expression obtained setting, for [math]\eps\in\Eps_\vartheta[(1,0);(0,1);\ex][/math], [math]\sR(0,1|\ex,\eps)=0[/math], and cannot be larger than that obtained with [math]\sR(0,1|\ex,\eps)=1[/math]. Denote by [math]\Phi(A_1,A_2;\rho)[/math] the probability that the bivariate normal with mean vector zero, variances equal to one, and correlation [math]\rho[/math] assigns to the event [math]\{\eps_1\in A_1,\eps_2\in A_2\}[/math]. Then show that any [math]\vartheta=[d_1,d_2,b_1,b_2,r][/math] that is observationally equivalent to the data generating value [math]\theta[/math] satisfies, [math](\ex_1,\ex_2)[/math]-a.s.,

[[math]] \begin{align} \sP((\ey_1,\ey_2)=(0,0)|\ex_1,\ex_2)&=\Phi((-\infty,-\ex_1b_1),(-\infty,-\ex_2b_2);r)\label{eq:CT_00}\\ \sP((\ey_1,\ey_2)=(1,1)|\ex_1,\ex_2)&=\Phi([-\ex_1b_1-d_1,\infty),[-\ex_2b_2-d_2,\infty);r)\label{eq:CT_11}\\ \sP((\ey_1,\ey_2)=(0,1)|\ex_1,\ex_2)&\le\Phi((-\infty,-\ex_1b_1-d_1),(-\ex_2b_2,\infty);r)\label{eq:CT_01U}\\ \sP((\ey_1,\ey_2)=(0,1)|\ex_1,\ex_2)&\ge\Big\{\Phi((-\infty,-\ex_1b_1-d_1),(-\ex_2b_2,\infty);r)\notag\\ &\quad\quad-\Phi((-\ex_1b_1,-\ex_1b_1-d_1),(-\ex_2b_2,-\ex_2b_2-d_2);r)\Big\}\label{eq:CT_01L} \end{align} [[/math]]

While the approach of is summarized here for a two player entry game, it extends without difficulty to any finite number of players and actions and to solution concepts other than pure strategy Nash equilibrium.

build on the insights of to study what is the identification power of equilibrium in games. To do so, they compare the set-valued model predictions and what can be learned about [math]\theta[/math] when one assumes only level-[math]k[/math] rationality as opposed to Nash play. In static entry games of complete information, they find that the model's predictions when [math]k\ge 2[/math] are similar to those obtained with Nash behavior and allowing for multiple equilibria and mixed strategies. extend the analysis of to the class of supermodular games.

The collections of parameter vectors satisfying (in)equalities \eqref{eq:CT_00}-\eqref{eq:CT_01L} yields the sharp identification region [math]\idr{\theta}[/math] in the case of two player entry games with pure strategy Nash equilibrium as solution concept, as shown by . When there are more than two players or more than two actions (or with different solutions concepts, such as, e.g., mixed strategy Nash equilibrium; correlated equilibrium; or rationality of level [math]k[/math] as in ), the characterization in obtained by extending the reasoning just laid out yields an outer region. use elements of random set theory to provide a general and computationally tractable characterization of the identification region that is sharp, regardless of the number of players and actions, or the solution concept adopted. For the case of PSNE with any finite number of players or actions, provide a computationally tractable sharp characterization of the identification region using elements of optimal transportation theory.

Characterization of Sharpness through Random Set Theory

provide a general approach based on random set theory that delivers sharp identification regions on parameters of structural semiparametric models with set valued predictions. Here I summarize it for the case of static, simultaneous move finite games of complete information, first with PSNE as solution concept and then with mixed strategy Nash equilibrium. Then I discuss games of incomplete information.

For a given [math]\vartheta\in\Theta[/math], denote the set of pure strategy Nash equilibria (depicted in Figure) as [math]\eY_\vartheta(\ex,\eps)[/math]. It is easy to show that [math]\eY_\vartheta(\ex,\eps)[/math] is a random closed set as in Definition. Under the assumption in Identification Problem that [math]\ey[/math] results from simultaneous move, pure strategy Nash play, at the true DGP value of [math]\theta\in\Theta[/math], one has

[[math]] \begin{align} \ey\in\eY_\theta\text{a.s.}\label{eq:y_in_Y_games} \end{align} [[/math]]

Equation \eqref{eq:y_in_Y_games} exhausts the modeling content of Identification Problem. Theorem can be leveraged to extract its empirical content from the observed distribution [math]\sP(\ey,\ex)[/math]. For a given [math]\vartheta\in\Theta[/math] and [math]K\subset\cY[/math], let [math]\sT_{\eY_{\vartheta}(\ex,\eps)}(K;\Phi_r)[/math] denote the probability of the event [math]\{\eY_\vartheta(\ex,\eps)\cap K\neq \emptyset\}[/math] implied when [math]\eps\sim\Phi_r[/math], [math]\ex[/math]-a.s.

Theorem (Structural Parameters in Static, Simultaneous Move Finite Games of Complete Information with PSNE)

Under the assumptions of Identification Problem, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align} \idr{\theta}=\{\vartheta\in\Theta:\sP(\ey\in K|\ex)\le \sT_{\eY_{\vartheta}(\ex,\eps)}(K;\Phi_r)\,\forall K\subset\cY, \, \ex\text{-a.s.}\}.\label{eq:SIR:entry_game} \end{align} [[/math]]

Show Proof

To simplify notation, let [math]\eY_\vartheta\equiv \eY_\vartheta(\ex,\eps)[/math]. In order to establish sharpness, it suffices to show that [math]\vartheta\in \idr{\theta}[/math] if and only if one can complete the model with an admissible selection mechanism [math]\sR(y_1,y_2|\ex,\eps)[/math] such that [math]\sR(y_1,y_2|\ex,\eps)\ge 0[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math], [math]\sum_{(y_1,y_2)\in\{0,1\}\times\{0,1\}}\sR(y_1,y_2|\ex,\eps)=1[/math], and satisfying \eqref{eq:games:sel:mec:1}-\eqref{eq:games:sel:mec:2}, so that [math]\sM(y_1,y_2|\ex)=\sP(y_1,y_2|\ex)[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math] [math]\ex[/math]-a.s., with [math]\sM(y_1,y_2|\ex)[/math] defined in \eqref{eq:games_model:pred}. Suppose first that [math]\vartheta[/math] is such that a selection mechanism with these properties is available. Then there exists a selection of [math]\eY_\vartheta[/math] which is equal to the prediction selected by the selection mechanism and whose conditional distribution is equal to [math]\sP(\ey|\ex)[/math], [math]\ex[/math]-a.s., and therefore [math]\vartheta \in \idr{\theta}[/math]. Next take [math]\vartheta \in \idr{\theta}[/math]. Then by Theorem, [math]\ey[/math] and [math]\eY_\vartheta[/math] can be realized on the same probability space as random elements [math]\ey'[/math] and [math]\eY'_\vartheta[/math], so that [math]\ey'[/math] and [math]\eY'_\vartheta[/math] have the same distributions, respectively, as [math]\ey[/math] and [math]\eY_\vartheta[/math], and [math]\ey' \in \Sel(\eY'_\vartheta)[/math], where [math]\Sel(\eY'_\vartheta)[/math] is the set of all measurable selections from [math]\eY'_\vartheta[/math], see Definition. One can then complete the model with a selection mechanism that picks [math]\ey'[/math] with probability 1, and the result follows.

■

The characterization provided in Theorem SIR- for games with multiple PSNE, taken from , is equivalent to the one in . When [math]J=2[/math] and [math]\cY=\{0,1\}\times\{0,1\}[/math], the inequalities in \eqref{eq:SIR:entry_game} reduce to \eqref{eq:CT_00}-\eqref{eq:CT_01L}. With more players and/or more actions, the inequalities in \eqref{eq:SIR:entry_game} are a superset of those in \eqref{eq:CT_00}-\eqref{eq:CT_01L}, with the latter comprised of the ones in \eqref{eq:SIR:entry_game} for [math]K=\{k\}[/math] and [math]k=\cY\setminus\{k\}[/math], for all [math]k\in\cY[/math]. Hence, the inequalities in \eqref{eq:SIR:entry_game} are more informative. Of course, the computational cost incurred to characterize [math]\idr{\theta}[/math] may grow with the number of inequalities involved. I discuss computational challenges in partial identification in Section.

Key Insight:(Random set theory and partial identification -- continued) In Identification Problem lack of point identification can be traced back to the set valued predictions delivered by the model, which in turn derive from the model incompleteness defined by . As stated in the Introduction, constructing the (random) set of model predictions delivered by the maintained assumptions is an exercise typically carried out in identification analysis, regardless of whether random set theory is applied. Indeed, for the problem studied in this section, put forward the set of admissible outcomes of the game. propose to work directly with this random set to characterize [math]\idr{\theta}[/math]. The fundamental advantage of this approach is that it dispenses with considering the possible selection mechanisms that may complete the model. Selection mechanisms may depend on the model's unobservables even after conditioning on observables and may constitute an infinite dimensional nuisance parameter, which creates great difficulties for the computation of [math]\idr{\theta}[/math] and for inference.

Next, I discuss the case that the outcome of the game results from simultaneous move, mixed strategy Nash play. When mixed strategies are allowed for, the model predicts multiple mixed strategy Nash equilibria (MSNE). But whereas when only pure strategies are allowed for, if the model is correctly specified, the observed outcome of the game is one of the predicted PSNE, with mixed strategy it is only the result of a random mixing draw from one of the predicted MSNE. Hence, the identification problem is more complex, and in order to obtain a tractable characterization of [math]\theta[/math]'s sharp identification region one needs to use different tools from random set theory.

To keep the treatment simple here I continue to consider the case of two players with two strategies, as in Identification Problem, with mixed strategies allowed for, and refer to for the general case. Fix [math]\vartheta\in\Theta[/math]. Let [math]\sigma_j:\{0,1\}\to [0,1][/math] denote the probability that player [math]j[/math] enters the market, with [math]1-\sigma_j[/math] the probability that she stays out. With some abuse of notation, let [math]\bu_j(\sigma_j,\sigma_{-j},\ex_j,\eps_j,\vartheta)[/math] denote the expected payoff associated with the mixed strategy profile [math]\sigma=(\sigma_1,\sigma_2)[/math]. For a given realization [math](x,e)[/math] of [math](\ex,\eps)[/math] and a given value of [math]\vartheta\in\Theta[/math], the set of mixed strategy Nash equilibria is

[[math]] \begin{multline*} S_\vartheta(x,e) =\bigg\{\sigma \in [0,1]^2:\; \bu_j(\sigma_j,\sigma_{-j},x_j,e_j;\vartheta) \geq \bu_j(\tilde{\sigma}_j,\sigma_{-j},x_j,e_j;\vartheta)\;\, \forall \tilde{\sigma}_j\in [0,1]\; j=1,2\bigg\}. \end{multline*} [[/math]]

show that [math]\eS_\vartheta\equiv S_\vartheta(\ex,\eps)[/math] is a random closed set in [math][0,1]^2[/math]. Its realizations are illustrated in Panel (a) of Figure as a function of [math](\eps_1,\eps_2)[/math].

MSNE strategies ([math]\eS_\vartheta[/math]), set of multinomial distributions over outcomes of the game ([math]\eQ_\vartheta[/math]), and its support function ([math]h_{\eQ_\vartheta}[/math]), as a function of [math](\eps_1,\eps_2)[/math], where [math]\sigma_1^*\equiv\frac{-\eps_2-\ex_2\beta_2}{\vartheta_2},\sigma_2^*\equiv\frac{-\eps_1-\ex_1\beta_1}{\vartheta_1}[/math].

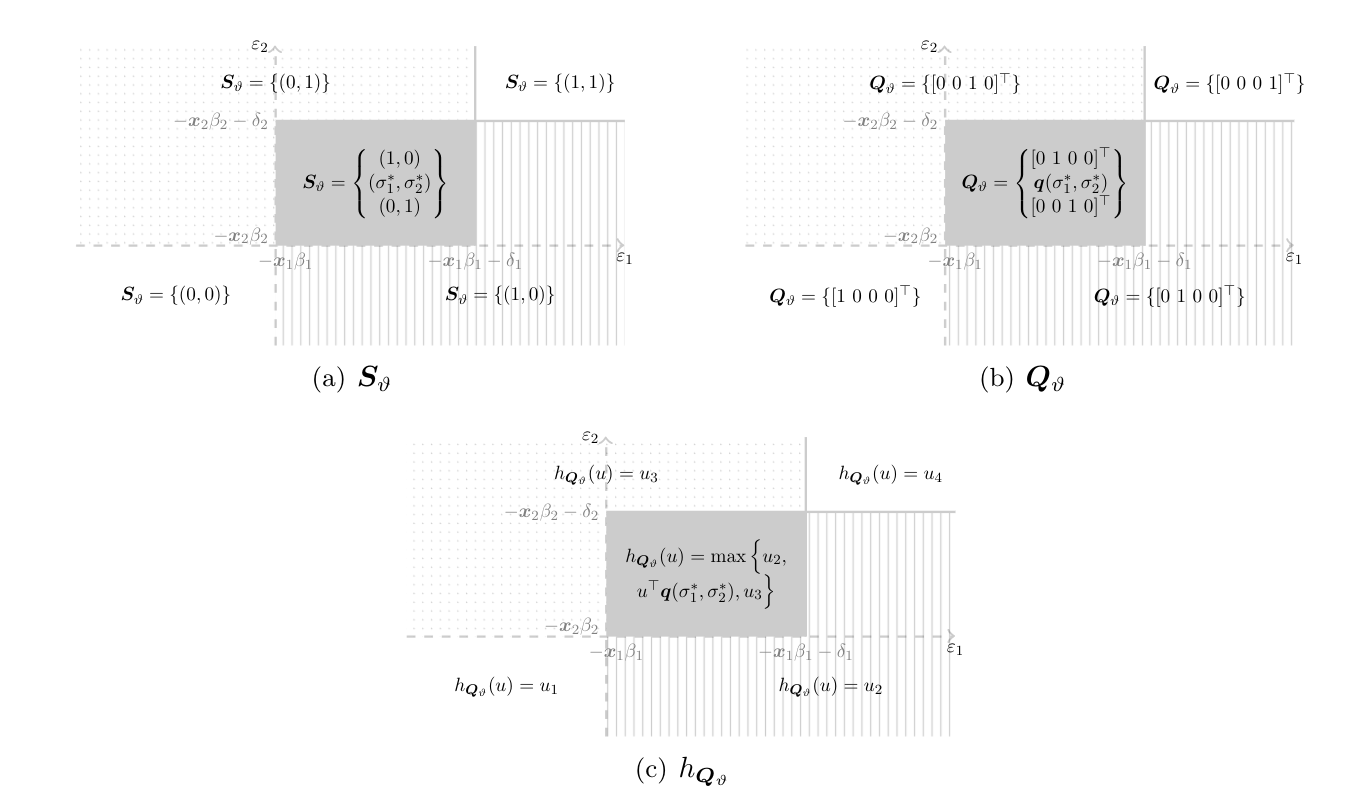
Define the set of possible multinomial distributions over outcomes of the game associated with the selections [math]\sigma[/math] of each possible realization of [math]\eS_{\vartheta}[/math] as

[[math]] \begin{equation} \label{eq:Q-set} \eQ_\vartheta=\left\{\eq(\sigma)\equiv \begin{bmatrix} (1-\sigma_1)(1-\sigma_2)\\ \sigma_1(1-\sigma_2)\\ (1-\sigma_1)\sigma_2\\ \sigma_1\sigma_2 \end{bmatrix}:\, \sigma \in \eS_\vartheta\right\}. \end{equation} [[/math]]

As [math]\eQ_\vartheta[/math] is the image of a continuous map applied to the random compact set [math]\eS_\vartheta[/math], it is a random compact set. Its realizations are plotted in Panel (b) of Figure as a function of [math](\eps_1,\eps_2)[/math].

The multinomial distribution over outcomes of the game determined by a given [math]\sigma\in\eS_\vartheta[/math] is a function of [math]\eps[/math]. To obtain the predicted distribution over outcomes of the game conditional on observed payoff shifters only, one needs to integrate out the unobservable payoff shifters [math]\eps[/math]. Doing so requires care, as it needs to be done for each [math]\eq(\sigma)\in\eQ_\vartheta[/math]. First, observe that all the [math]\eq(\sigma)\in\eQ_\vartheta[/math] are contained in the [math]3[/math] dimensional unit simplex, and are therefore integrable. Next, define the conditional selection expectation (see Definition) of [math]\eQ_\vartheta[/math] as

[[math]] \E_{\Phi_r}(\eQ_\vartheta|\ex)=\Big\{\E_{\Phi_r}(\eq(\sigma)|\ex):\; \sigma \in \Sel(\eS_\vartheta)\Big\}, [[/math]]

where [math]\Sel(\eS_\vartheta)[/math] is the set of all measurable selections from [math]\eS_\vartheta[/math], see Definition. By construction, [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] is the set of probability distributions over action profiles conditional on [math]\ex[/math] which are consistent with the maintained modeling assumptions, i.e., with all the model's implications (including the assumption that [math]\eps\sim\Phi_r[/math]). If the model is correctly specified, there exists at least one vector [math]\theta\in\Theta[/math] such that the observed conditional distribution [math]\cp(\ex)\equiv[\sP(\ey=y^1|\ex),\dots,\sP(\ey=y^4|\ex)]^\top[/math] almost surely belongs to the set [math]\E_{\Phi_\rho}(\eQ_\theta|\ex)[/math]. Indeed, by the definition of [math]\E_{\Phi_\rho}(\eQ_\theta|\ex)[/math], [math]\cp(\ex)\in \E_{\Phi_\rho}(\eQ_\theta|\ex)[/math] almost surely if and only if there exists [math]\eq\in \Sel(\eQ_\theta)[/math] such that [math]\E_{\Phi_\rho}(\eq|\ex)=\cp(\ex)[/math] almost surely, with [math]\Sel(\eQ_\theta)[/math] the set of all measurable selections from [math]\eQ_\theta[/math]. Hence, the collection of parameter vectors [math]\vartheta\in\Theta[/math] that are observationally equivalent to the data generating value [math]\theta[/math] is given by the ones that satisfy [math]\cp(\ex)\in \E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] almost surely. In turn, observing that by Theorem the set [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] is convex, we have that [math]\cp(\ex)\in \E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] if and only if [math]u^\top \cp(\ex)\leq h_{\E_{\Phi_r}(\eQ_\vartheta|\ex)}(u)[/math] for all [math]u[/math] in the unit ball (see, e.g., ), where [math]h_{\E_{\Phi_r}(\eQ_\vartheta|\ex)}(u)[/math] is the support function of [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math], see Definition.

Theorem (Structural Parameters in Static, Simultaneous Move Finite Games of Complete Information with MSNE)

Under the assumptions in Identification Problem, allowing for mixed strategies and with the observed outcomes of the game resulting from mixed strategy Nash play, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align} \idr{\theta} &=\bigg\{\vartheta\in \Theta:\; \max_{u\in\mathbb{B}^{|\cY|}}\left( u^\top \cp(\ex) -\E_{\Phi_r}[h_{\eQ_\vartheta}(u)|\ex]\right)=0,\, \ex\text{-a.s.}\bigg\} \label{eq:SIR_sharp_mixed_sup}\\ &=\bigg\{\vartheta \in \Theta:\; \int_{\mathbb{B}^{|\cY|}} (u^\top \cp(\ex) -\E_{\Phi_r}[h_{\eQ_\vartheta}(u)|\ex])_+ \mathrm{d}\mu(u)=0,\, \ex\text{-a.s.}\bigg\} \label{eq:SIR_sharp_mixed_int}, \end{align} [[/math]]

where [math]\mu[/math] is any probability measure on [math]\mathbb{B}^{|\cY|}[/math], and [math]|\cY|=4[/math] in this case.

Show Proof

Theorem (equation eq:dom_Aumann:cond) yields \eqref{eq:SIR_sharp_mixed_sup}, because by the arguments given before the theorem, [math]\idr{\theta}=\{\vartheta \in \Theta:\;\cp(\ex)\in \E_{\Phi_r}(\eQ_\vartheta|\ex),\ex\text{-a.s.}\}[/math]. The result in \eqref{eq:SIR_sharp_mixed_int} follows because the integrand in \eqref{eq:SIR_sharp_mixed_int} is continuous in [math]u[/math] and both conditions inside the curly brackets are satisfied if and only if [math]u^\top \cp(\ex)-\E_{\Phi_r}[h_{\eQ_\vartheta}(u)|\ex]\leq 0[/math] [math]\forall u\in \mathbb{B}^{|\cY|}[/math] [math]\ex[/math]-a.s.

■

For a fixed [math]u\in\mathbb{B}^4[/math], the possible realizations of [math]h_{\eQ_\vartheta}(u)[/math] are plotted in Panel (c) of Figure as a function of [math](\eps_1,\eps_2)[/math]. The expectation of [math]h_{\eQ_\vartheta}(u)[/math] is quite straightforward to compute, whereas calculating the set [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] is computationally prohibitive in many cases. Hence, the characterization in \eqref{eq:SIR_sharp_mixed_sup} is computationally attractive, because for each [math]\vartheta\in\Theta[/math] it requires to maximize an easy-to-compute superlinear, hence concave, function over a convex set, and check if the resulting objective value vanishes. Several efficient algorithms in convex programming are available to solve this problem, see for example the MatLab software for disciplined convex programming CVX . Nonetheless, [math]\idr{\theta}[/math] itself is not necessarily convex, hence tracing out its boundary is non-trivial. I return to computational challenges in partial identification in Section.\medskip

Key Insight: Random set theory and partial identification -- continued provide a general characterization of sharp identification regions for models with convex moment predictions. These are models that for a given [math]\vartheta\in\Theta[/math] and realization of observable variables, predict a set of values for a vector of variables of interest. This set is not necessarily convex, as exemplified by [math]\eY_\vartheta[/math] and [math]\eQ_\vartheta[/math], which are finite. No restriction is placed on the manner in which, in the DGP, a specific model prediction is selected from this set. When the researcher takes conditional expectations of the resulting elements of this set, the unrestricted process of selection yields a convex set of moments for the model variables (all possible mixtures). This is the model's convex set of moment predictions. If this set were almost surely single valued, the researcher would learn (features of) [math]\theta[/math] by solving moment equality conditions involving the observed variables and predicted ones. The approach reviewed in this section is a set-valued method of moments that extends the singleton-valued one commonly used in econometrics.

I conclude this section discussing the case of static, simultaneous move finite games of incomplete information, using the results in . For clarity, I formalize the maintained assumptions.

Identification Problem (Structural Parameters in Static, Simultaneous Move Finite Games of Incomplete Information with multiple BNE)

Impose the same structure on payoffs, entry decision rule, outcome space, parameter space, and observable variables as in Identification Problem. Assume that the observed outcome of the game results from simultaneous move, pure strategy Bayesian Nash play. Both players and the researcher observe [math](\ex_1,\ex_2)[/math]. However, [math]\eps_j[/math] is private information to player [math]j=1,2[/math] and unobservable to the researcher, with [math]\eps_1\independent\eps_2|(\ex_1,\ex_2)[/math]. Assume that players have correct common prior [math]\sF_\gamma[/math] on the distribution of [math](\eps_1,\eps_2)[/math] and the researcher knows this distribution up to [math]\gamma[/math], a finite dimensional parameter vector. Under these assumptions, multiple Bayesian Nash equilibria (BNE) may result. In the absence of additional information, what can the researcher learn about [math]\theta=[\delta_1\delta_2\beta_1\beta_2\gamma][/math]?

With incomplete information, players' strategies are decision rules that map the support of [math](\eps,\ex)[/math] into [math]\{0,1\}[/math]. The non-negativity condition on expected payoffs that determines each player's decision to enter the market results in equilibrium mappings (decision rules) that are step functions determined by a threshold: [math]y_j(\eps_j) =\one(\eps_j\geq t_j), j=1,2[/math]. As a result, player [math]j[/math]'s beliefs about player [math]3-j[/math]'s probability of entry under the common prior assumption is [math]\int y_{3-j}(\eps_{3-j}) d\sF_\gamma(\eps_{3-j}|\ex) =1-\sF_\gamma(t_{3-j}|\ex)[/math], and therefore player [math]j[/math]'s best response cutoff is

[[math]] \begin{align*} t_j^b(t_{3-j},\ex;\theta)=-\ex_j\beta_j-\delta_j(1-\sF_\gamma(t_{3-j}|\ex)). \end{align*} [[/math]]

Hence, the set of equilibria can be defined as the set of cutoff rules:

[[math]] \begin{equation*} \eT_{\theta}(\ex)=\left\{(t_1,t_2\right):t_j=t_j^b(t_{3-j},\ex;\theta),j=1,2\}. \end{equation*} [[/math]]

The equilibrium thresholds are functions of [math]\ex[/math] and [math]\theta[/math] only. The set [math]\eT_{\theta}(\ex)[/math] might contain a finite number of equilibria (e.g., if the common prior is the Normal distribution), or a continuum of equilibria. For ease of notation I suppress its dependence on [math]\ex[/math] in what follows. Given the equilibrium decision rules (the selections of the set [math]\eT_\theta[/math]), it is possible to determine their associated action profiles. Because in the simple two-player entry game that I consider actions and outcomes coincide, I denote the set of admissible action profiles by [math]\eY_\theta[/math]:

[[math]] \begin{align} \eY_\theta=\left\{ \ey(\et)\equiv \begin{bmatrix} \one(\eps_1 \lt \et_1,\eps_2 \lt \et_2)\\ \one(\eps_1\ge\et_1,\eps_2 \lt \et_2)\\ \one(\eps_1 \lt \et_1,\eps_2\ge\et_2)\\ \one(\eps_1\ge\et_1,\eps_2\ge\et_2) \end{bmatrix} :\et\in\Sel(\eT_\theta) \right\},\label{eq:q_incomplete} \end{align} [[/math]]

with [math]\Sel(\eT_\theta)[/math] the set of all measurable selections from [math]\eT_\theta[/math], see Definition. To obtain the predicted set of multinomial distributions for the outcomes of the game, one needs to integrate out [math]\eps[/math] conditional on [math]\ex[/math]. Again this can be done by using the conditional Aumann expectation:

[[math]] \begin{equation*} \E_{\sF_\gamma}(\eY_\theta|\ex)=\{\E_{\sF_\gamma}(\ey(\et)|\ex):\et\in\Sel(\eT_\theta)\}. \end{equation*} [[/math]]

This set is closed and convex. Regardless of whether [math]\eT_\theta[/math] contains a finite number of equilibria or a continuum, [math]\eY_\theta[/math] can take on only a finite number of realizations corresponding to each of the vertices of the three dimensional simplex, because the vectors [math]\ey(\et)[/math] in \eqref{eq:q_incomplete} collect threshold decision rules. This implies that [math]\E_{\sF_\gamma}(\eY_\theta|\ex)[/math] is a closed convex polytope [math]\ex[/math]-a.s., fully characterized by a finite number of supporting hyperplanes. Hence, it is possible to determine whether [math]\vartheta\in\idr{\theta}[/math] using efficient algorithms in linear programming.

Theorem (Structural Parameters in Static, Simultaneous Move Finite Games of Incomplete Information with BNE)

Under the assumptions in Identification Problem, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align} \idr{\theta} &=\bigg\{\vartheta\in \Theta:\; \max_{u\in\mathbb{B}^{|\cY|}} u^\top \cp(\ex) -\E_{\sF_{\tilde\gamma}}[h_{\eY_\vartheta}(u)|\ex]=0,\, \ex\text{-a.s.}\bigg\} \label{eq:SIR:incomplete_info:1} \\ &=\bigg\{\vartheta\in \Theta:\; u^\top \cp(\ex) \le \E_{\sF_{\tilde\gamma}}[h_{\eY_\vartheta}(u)|\ex],\,\forall u\in D, \ex\text{-a.s.}\bigg\},\label{eq:SIR:incomplete_info:2} \\ &= \bigg\{\vartheta\in \Theta:\; \sP(\ey\in K|\ex)\le \sT_{\eY_{\vartheta}(\ex,\eps)}(K;\sF_{\tilde\gamma})\,\forall K\subset\cY,\, \ex\text{-a.s.}\bigg\} \label{eq:SIR:incomplete_info:0}, \end{align} [[/math]]

with [math]D=\{u=[u_1,\dots,u_{|\cY|}]^\top:u_i\in\{0,1\},i=1,...,|\cY|\} [/math], [math]\vartheta=[d_1,d_2,b_1,b_2,\tilde\gamma][/math], and [math]\sT_{\eY_{\vartheta}(\ex,\eps)}(K;\sF_{\tilde\gamma})[/math] the probability that [math]\{\eY_\vartheta(\ex,\eps)\cap K\neq \emptyset\}[/math] implied when [math]\eps\sim\sF_{\tilde\gamma}[/math], [math]\ex[/math]-a.s.

Show Proof

The result in \eqref{eq:SIR:incomplete_info:1} follows by the same argument as in the proof of Theorem SIR-. Next I show equivalence of the conditions

[[math]] \begin{align*} (i)&u^\top\cp(\ex)\le\E_{\sF_{\tilde\gamma}}[h_{\eY_\vartheta}(u)|\ex]\forall u\in\mathbb{B}^{|\cY|}, \\ (ii)&u^\top\cp(\ex)\le\E_{\sF_{\tilde\gamma}}[h_{\eY_\vartheta}(u)|\ex]\forall u\in D. \end{align*} [[/math]]

By the positive homogeneity of the support function, condition [math](i)[/math] is equivalent to [math]\cp(\ex)\le\E_{\sF_{\tilde\gamma}}[h_{\eY_\vartheta}(u)|\ex]\forall u\in\R^{|\cY|}[/math], which implies condition [math](ii)[/math]. Next I show that condition [math](ii)[/math] implies condition [math](i)[/math]. As explained before, the set [math]\eY_\theta[/math], and hence also its convex hull [math]\conv(\eY_\theta)[/math], can take on only a finite number of realizations. Let [math]Y_1,\dots,Y_m[/math] be convex compact sets in the simplex of dimension [math]|\cY|-1[/math] equal to the possible realizations of [math]\conv(\eY_\theta)[/math], and let [math]\varpi_1(\ex),\dots,\varpi_m(\ex)[/math] denote the probability of each of these realizations conditional on [math]\ex[/math]. Then by Theorem 2.1.34 in , [math]\E_{\sF_{\tilde\gamma}}(\eY_\theta|\ex)=\sum_{j=1}^m Y_j\varpi_j(\ex)[/math]. By the properties of the support function (see, e.g., ), [math]h_{\E_{\sF_{\tilde\gamma}}(\eY_\theta|\ex)}(u) =\sum_{j=1}^m \varpi_j(\ex)h_{Y_j}(u)[/math]. For each [math]j=1,...,m,[/math] the vertices of [math]Y_j[/math] are a subset of the vertices of the [math](|\cY|-1)[/math]-dimensional simplex. Hence the supporting hyperplanes of [math]Y_j,j=1,...,m[/math], are a subset of the supporting hyperplanes of that simplex, which in turn are obtained through its support function evaluated in directions [math]u\in D[/math]. Finally, I show equivalence with the result in \eqref{eq:SIR:incomplete_info:0}. Because the vertices of [math]Y_j[/math] are a subset of the vertices of the [math](|\cY|-1)[/math]-dimensional simplex, each direction [math]u\in D[/math] determines a set [math]K_u\subset \cY[/math]. Given the choice of [math]u[/math], the value of [math]u^\top\ey(\et)[/math] equals one if [math]\ey(\et)\in K_u[/math] and zero otherwise. Hence, condition \eqref{eq:SIR:incomplete_info:2} reduces to

[[math]] \begin{align*} \sP(\ey\in K_u|\ex) = u^\top \cp(\ex) &\le \E_{\sF_{\tilde\gamma}}[h_{\eY_\vartheta}(u)|\ex] = \E_{\sF_{\tilde\gamma}}\left[\sup_{\ey(\et)\in\eY_\vartheta}u^\top\ey(\et)|\ex\right] \\ &= \E_{\sF_{\tilde\gamma}}[\one(\eY_\vartheta\cap K_u\neq \emptyset)|\ex]=\sT_{\eY_{\vartheta}(\ex,\eps)}(K_u;\sF_{\tilde\gamma}). \end{align*} [[/math]]

Observing that the collection [math]D[/math] comprises the [math]2^{|\cY|}[/math] vectors with entries equal to either 1 or 0, and that these determine all possible subsets [math]K_u[/math] of [math]\cY[/math], yields condition \eqref{eq:SIR:incomplete_info:0}.

■

One can use the same argument as in the proof of Theorem SIR-, to show that the Aumann expectation/support function characterization of the sharp identification region in Theorem SIR- coincides with the characterization based on the capacity functional in Theorem SIR-, when only pure strategies are allowed for. This shows that in this class of models, the capacity functional based characterization is a special case of the Aumann expectation/support function based one. study what is the identification power of equilibrium also in the case of static entry games with incomplete information. They show that in the presence of multiple equilibria, assuming Bayesian Nash behavior yields more informative regions for the parameter vector [math]\theta[/math] than assuming only rational behavior, but at the price of a higher computational cost. propose a procedure to test for the sign of the interaction effects (which here I have assumed to be non-positive) in discrete simultaneous games with incomplete information and (possibly) multiple equilibria. As a by-product of this procedure, they also provide a test for the presence of multiple equilibria in the DGP. The test does not require parametric specifications of players' payoffs, the distributions of their private signals, or the equilibrium selection mechanism. Rather, the test builds on the commonly invoked assumption that players' private signals are independent conditional on observed states. introduces an important class of models with flexible information structure. Each player is assumed to have a vector of payoff shifters unobservable by the researcher composed of elements that are private information to the player, and elements that are known to all players. The results of reported in this section apply to this set-up as well.

Auction Models with Independent Private Values

An Inference Approach Robust to Bidding Behavior Assumptions

study what can be learned about the distribution of valuations in an open outcry English auction where symmetric bidders have independent private values for the object being auctioned. The standard theoretical model , called ‘`button auction" model, posits that each bidder holds down a button while the object’s price rises continuously and exogenously, releasing it (in the dominant strategy equilibrium) when it reaches her valuation or all her opponents have left. In this case, the distribution of bidder's valuation can be learned exactly. show that much can be learned about the distribution of valuations, even allowing for the fact that real-life auctions may depart from this stylized framework, as in the following identification problem. \begin{IP}[Incomplete Auction Model with Independent Private Values]\label{IP:auction} For a given auction with [math]n \lt \infty[/math] participating bidders, let [math]\ev_i\sim\sQ,i=1,\dots,n,[/math] be bidder [math]i[/math]'s valuation for the object being auctioned and assume that [math]\ev_i\independent \ev_j[/math] for all [math]i\neq j[/math]. Assume that the support of [math]\sQ[/math] is [math][\underline{v},\bar{v}][/math] and that each bidder knows her own valuation but not that of her opponents. Let the auctioneer set a minimum bid increment [math]\delta\in [0,\bar{v})[/math], and for simplicity suppose there is no reserve price. Suppose the researcher observes order statistics of the bids, [math]\vec{\eb}_n\equiv(\eb_{1:n},\dots,\eb_{n:n})\sim\sP[/math] in [math]\R^n_+[/math], with [math]\eb_{i:n}[/math] the [math]i[/math]-th lowest of the [math]n[/math] bids. Assume that: (1) Bidders do not bid more than they are willing to pay; (2) Bidders do not allow an opponent to win at a price they are willing to beat. In the absence of additional information, what can the researcher learn about [math]\sQ[/math]? |}}

A realization of the model predicted ordered bids [math]\eB(\vec{\ev}_n)[/math] in \eqref{eq:RCS_auction} for [math]n=3,\vec{\ev}_n=v^0,\delta=0[/math].

The model in Identification Problem delivers set valued predictions because given valuations [math](\ev_1,\dots,\ev_n)[/math], the two fundamental assumptions about bidder's behavior yield

[[math]] \begin{align} \vec{\eb}_n \in \eB(\vec{\ev}_n)\equiv\left[\left\{\prod_{i=1}^{n-1}[\underline{v},\ev_{i:n}]\right\}\times [\ev_{n-1:n}-\delta,\ev_{n:n}]\right]\cap V_n,\label{eq:RCS_auction} \end{align} [[/math]]

where [math]\vec{\ev}_n\equiv(\ev_{1:n},\dots,\ev_{n:n})[/math] denotes the vector of order statistics of the valuations, and [math]V_n=\{v\in\R^n:\underline{v}\le v_1\le v_2\le\dots\le v_n\le \bar{v}\}[/math]. Figure provides a stylized depiction of a realization of this set for [math]\vec{\ev}_n=v^0[/math] when there are three bidders ([math]n=3[/math]), [math]\underline{v}=0[/math], and [math]\delta=0[/math]. In words, [math]\eB(\vec{\ev}_n)[/math] collects the model predicted values of ordered bids. The fact that [math]\eb_{i:n}\le \ev_{i:n}[/math] for all [math]i[/math] results from assumption (1): since each bidder bids at most an amount equal to her valuation, the [math]i[/math]-th highest bid cannot exceed the [math]i[/math]-th highest valuation . The fact that [math]\eb_{n:n}\ge \ev_{n-1,n}-\delta[/math] follows immediately from assumption (2) . The fact that [math]\vec{\eb}_n[/math] has to lie in [math]V_n[/math] follows because it is a vector of ordered bids. Why does this set-valued prediction hinder point identification? The reason is that the distribution of the observable data relates to the model structure in an incomplete manner. Define a bidding rule [math]\sB(\eb_{1:n},\dots,\eb_{n:n}|\ev_{1:n},\dots,\ev_{n:n})[/math] to be a conditional joint distribution for the order statistics of the bids conditional on the order statistics of the valuations. Then, for a given realization of the valuations [math]\ev_{1:n}=v_1,\dots,\ev_{n:n}=v_n[/math], the model requires that the support of [math]\sB(\cdot|v_1,\dots,v_n)[/math] is in [math]B(\vec{v})[/math] as defined in \eqref{eq:RCS_auction} with [math]\ev_{1:n}=v_1,\dots,\ev_{n:n}=v_n[/math], but imposes no other restriction on it. Hence, the model implied joint distribution of ordered bids is

[[math]] \begin{align} \sM_{1,\dots,n:n}(\cdot;\sB,\sQ)\equiv\int \sB(\cdot|v_1,\dots,v_n)\sQ_{1,\dots,n:n}(dv_1,\dots,dv_n),\label{eq:model:impl_sel_mech_auction} \end{align} [[/math]]

where [math]\sQ_{1,\dots,n:n}[/math] is the joint distribution of order statistics of the valuations implied by [math]\sQ[/math]. Since the bidding rule [math]\sB[/math] is left completely unspecified (other than requiring it to be a valid joint conditional probability distribution with support in [math]\eB[/math]), one can find multiple pairs [math](\sB ,\sQ)[/math] satisfying the assumptions of Identification Problem, such that [math]\sM_{1,\dots,n:n}(\cdot;\sB,\sQ)=\sG_{1,\dots,n:n}(\cdot)[/math], with [math]\sG_{1,\dots,n:n}[/math] the observed joint CDF of the order statistics of the bids associated with [math]\sP[/math]. propose to use simple and tractable implications of the model to learn features of [math]\sQ[/math]. Recall that with i.i.d. valuations, the distribution of each order statistic uniquely determines [math]\sQ(v)[/math], with [math]\sQ(v)\equiv\sQ(\ev\le v)[/math] for any [math]v\ge\underline{v}[/math], through:

[[math]] \begin{align} \sQ(v)=\sq_{\cB}(\sQ_{i:n}(v);i,n-i+1),\label{eq:HT:beta} \end{align} [[/math]]

where [math]\sQ_{i:n}[/math] is the CDF of [math]\ev_{i:n}[/math] and [math]\sq_{\cB}(\cdot;i,n-i+1)[/math] is the quantile function of a Beta-distributed random variable with parameters [math]i[/math] and [math]n-i+1[/math]. Using this, their Lemmas 1 and 3 yield, respectively,

[[math]] \begin{align} \sQ(v) &\le \min_{n,i}\sq_{\cB}(\sG_{i:n}(v);i,n-i+1),\forall v\in[\underline{v},\bar{v}],\label{eq:HT_upper}\\ \sQ(v) &\ge \max_{n}\sq_{\cB}(\sG_{n:n}(v-\delta);i,n-i+1),\forall v\in[\underline{v},\bar{v}],\label{eq:HT_lower} \end{align} [[/math]]

where, for any [math]v\ge\underline{v}[/math], [math]\sG_{i:n}(v)\equiv\sP(\eb_{i:n}\le v)[/math] denotes the observed CDF of [math]\eb_{i:n}[/math] for [math]i=1,\dots,n[/math].

Key Insight: The model and analysis put forward by trade point identification of the distribution of valuation under stringent assumptions on the bidding rule, for a robust inference approach that yields informative bounds under weak and widely credible assumptions on bidding behavior. Remarkably, ‘`nothing is lost" due to the use of their robust approach: point identification is recovered when the standard assumptions of the button auction model hold. This is because in the dominant strategy equilibrium the top losing bidder exits at her valuation, followed immediately by the winning bidder. Hence, [math]\eb_{n-1:n}=\ev_{n-1:n}=\eb_{n:n}[/math] and [math]\delta=0[/math], so that the upper and the lower bound in \eqref{eq:HT_upper}-\eqref{eq:HT_lower} coincide and point identify the distribution of valuations.

also provide sharp bounds on the optimal reserve price, which I do not discuss here. However, they leave open the question of whether the collection of CDFs satisfying \eqref{eq:HT_upper}-\eqref{eq:HT_lower} yields the sharp identification region for [math]\sQ[/math]. As discussed in Sections Selectively Observed Data-Interval Data, pointwise bounds on the CDF deliver tubes of admissible CDFs that in general yield outer regions on the CDF of interest. But in this identification problem, the issue of sharpness is even more subtle, and therefore addressed in the following subsection.

Before moving on to that discussion, I note that the work of spurred a rich literature applying partial identification analysis to the study of auction models. studies first price sealed bid auctions with equilibrium behavior, where affiliated valuations prevent --in the absence of parametric restrictions on the distribution of the model primitives-- point identification of the model. He derives bounds on seller revenue under various counterfactual scenarios on reserve prices and auction formats. also studies first price sealed bid auctions with equilibrium behavior, but relaxes the independence assumptions on symmetric valuations by requiring it to hold only conditional on unobserved heterogeneity. He derives bounds on various functionals of the distributions of interest, including the mean bid and mean valuation. analyze second price auctions with correlated private values. In this case, the distribution of valuations is not point identified even under the assumptions of the button auction model . Nonetheless, show that interesting functionals of it (seller profits and bidder surplus) can be bounded, if one assumes that transaction prices are determined by the second highest valuation and imposes some restrictions on the joint distribution of the number of bidders and distribution of the valuations. studies a related model of second-price ascending auctions with arbitrary dependence in bidders’ private values. She provides partial identification results for the joint distribution of values for any subset of bidders under various assumptions about what data the researcher observes. While in her framework the highest bid is never observed, she considers the case where only the winner's identity and the winning price are observed, and the case where all the identities and all the bids except for the highest bid are known. She also investigates the informational content of assuming positive dependence in bidders' values. are concerned with nonparametric identification of a two-stage entry and bidding game. Potential bidders are assumed to have private valuations and observe private signals before deciding whether to enter the auction. The dependence between signals and valuations is only minimally restricted. Hence, even with some excluded instruments that affect selection into the auction, the model primitives are only partially identified. The authors derive bounds on these primitives, and provide conditions under which point identification is restored. provide partial identification results in private value and common value auctions under weak restrictions on the information available to the bidders. Their approach leverages a result in yielding an equivalence between distributions of valuations that obey the restrictions imposed by a Bayesian Correlated Equilibrium and those that obey the restrictions imposed by Bayesian Nash Equilibrium under some information structure. Such equivalence is particularly helpful because the set of Bayesian Correlated Equilibria can be characterized through linear programming, so that the sharp identification region provided by is given by the collection of parameter vectors [math]\vartheta[/math] for which a linear program is feasible. Related results leveraging the linear structure of correlated equilibria in the context of entry games include , , and .

Characterization of Sharpness through Random Set Theory

bounds exploit the information contained in the marginal CDFs [math]\sG_{i:n}[/math] for each [math]i[/math] and [math]n[/math]. However, in Identification Problem additional information can be extracted from the joint distribution of ordered bids. obtain the sharp identification region [math]\idr{\sQ}[/math] using random set methods (Artstein's characterization in Theorem) applied to a quantile function representation of the order statistics. Here I provide an equivalent characterization that uses equation \eqref{eq:RCS_auction} directly, and which has not appeared in the literature before. Let [math]\cT[/math] denote the space of probability distributions with support on [math][\underline{v},\bar{v}][/math], so that [math]\sQ\in\cT[/math]. For a candidate distribution [math]\tilde{\sQ}\in\cT[/math], let [math]\tilde{\sQ}_{1,\dots,n:n}[/math] denote the implied distribution of order statistics of [math]n[/math] i.i.d. random variables distributed [math]\tilde{\sQ}[/math]. Let [math]\tilde{\eB}[/math] be a random closed set defined as in \eqref{eq:RCS_auction} with respect to order statistics of i.i.d. random variables with distribution [math]\tilde{\sQ}[/math]. For a given set [math]K\in\cK[/math], with [math]\cK[/math] the collection of compact subsets of [math]\R^n[/math], let [math]\sT_{\tilde\eB}(K;\tilde{\sQ})[/math] denote the probability of the event [math]\{\tilde\eB\cap K\neq \emptyset\}[/math] implied by [math]\tilde{\sQ}[/math].

Theorem (Distribution of Valuations in Incomplete Auction Model with Independent Private Values)

Under the assumptions of Identification Problem, the sharp identification region for [math]\sQ[/math] is

[[math]] \begin{align} \label{eq:SIR:auction} \idr{\sQ}= \left\{\tilde{\sQ}\in\cT: \sP(\vec{\eb}_n\in K) \le \sT_{\tilde\eB}(K;\tilde{\sQ}) \forall K\in\cK \right\}. \end{align} [[/math]]

Show Proof

The sharp identification region for [math]\sQ[/math] is given by the collection of probability distributions [math]\tilde{\sQ}\in\cT[/math] for which one can find a bidding rule [math]\sB(\cdot|\cdot)[/math] with support in [math]\tilde{\eB}[/math] a.s. such that [math]\sG_{1,\dots,n:n}(\cdot)=\sM_{1,\dots,n:n}(\cdot;\sB,\tilde{\sQ})[/math]. Here [math]\sM_{1,\dots,n:n}(\cdot;\sB,\tilde{\sQ})[/math] is defined as in \eqref{eq:model:impl_sel_mech_auction} with [math]\tilde{\sQ}[/math] replacing [math]\sQ[/math]. Take a distribution [math]\tilde{\sQ}[/math] satisfying this definition of sharpness. Then there exists a selection of [math]\tilde{\eB}[/math] determined by the bidding rule associated with [math]\tilde{\sQ}[/math], such that its distribution matches that of [math]\vec{\eb}_n[/math]. But then Theorem implies that the inequalities in \eqref{eq:SIR:auction} hold. Conversely, take [math]\tilde{\sQ}[/math] satisfying the inequalities in \eqref{eq:SIR:auction}. Then, by Theorem, [math]\vec{\eb}_n[/math] and [math]\tilde{\eB}[/math] can be realized on the same probability space as random elements [math]\vec{\eb}_n^\prime[/math] and [math]\tilde{\eB}^\prime[/math], [math]\vec{\eb}_n\edis \vec{\eb}_n^\prime[/math], [math]\tilde{\eB}\edis\tilde{\eB}^\prime[/math], such that [math]\vec{\eb}_n^\prime \in \tilde{\eB}^\prime[/math] a.s. One can then complete the auction model with a bidding rule that picks [math]\vec{\eb}_n^\prime[/math] with probability [math]1[/math], and the result follows.

■

In \eqref{eq:SIR:auction}, [math]\sP(\vec{\eb}_n\in K)[/math] is determined by the joint distribution of the ordered bids and hence can be learned from the data. On the other side, [math]\sT_{\tilde\eB}(K;\tilde{\sQ})[/math] is a function of the model and [math]\tilde{\sQ}\in\cT[/math]. Hence, it can be computed using \eqref{eq:RCS_auction}, with [math]\tilde\eB[/math] defined with respect to order statistics of i.i.d. random variables with distribution [math]\tilde{\sQ}\in\sT[/math]. To gain insights in the characterization of [math]\idr{\sQ}[/math], consider for example the set [math]K=\{\prod_{i=1}^{n-1}(-\infty,+\infty)\}\times(-\infty,v][/math]. Plugging it in the inequalities in \eqref{eq:SIR:auction}, one obtains

[[math]] \begin{align*} \sG_{n:n}(v) \le \sQ_{n-1,n}(v),\text{for all } n, \end{align*} [[/math]]

which, using \eqref{eq:HT:beta}, yields \eqref{eq:HT_lower}. Similarly, plugging in the sets [math]K_j=\{\prod_{i=1}^{j-1}(-\infty,+\infty)\}\times[v,\infty)\times\{\prod_{j+1}^n(-\infty,+\infty)\}[/math], [math]j=1,\dots,n[/math], yields \eqref{eq:HT_upper}. So the inequalities proposed by are a subset of the inequalities yielding the sharp identification region in Theorem SIR-. More information can be obtained by using additional sets [math]K[/math]. For instance, the set [math]K=[v_1,\infty)\times[v_2,\infty)\times\{\prod_{i=1}^{n}(-\infty,+\infty)\}[/math], [math]v_2\ge v_1[/math], yields [math]\sP(\eb_{1:n}\ge v_1,\eb_{2:n}\ge v_2)\le \sQ_{1,2:n}([v_1,\infty)\times[v_2,\infty))[/math], which further restricts [math]\sQ[/math]. Numerous examples can be given. Characterization \eqref{eq:SIR:auction} is stated using inequality eq:domin-t for the collection of compact subsets of [math]\R^n[/math]. One can instead use the (equivalent) inequality eq:dom-c, and show that in fact it suffices to check it for a much smaller collection of sets, as shown by (see also ). Nonetheless, this collection remains extremely large.

Key Insight: Random set theory and partial identification -- continued As stated in the Introduction, constructing the (random) set of model predictions delivered by the maintained assumptions is an exercise typically carried out in identification analysis, regardless of whether random set theory is applied. Indeed, for the problem studied in this section, put forward the set of admissible bids in \eqref{eq:RCS_auction}. With this set in hand, the tools of random set theory (in this case, Theorem) immediately deliver the sharp identification region of interest.

further generalize the analysis in this section by dropping the requirement of independent private values. This allows them, for example, to consider affiliated private values. They show that even in this significantly more complex context, the key behavioral restrictions imposed by to relate bids to valuations can be coupled with the use of random set theory, to characterize sharp identification regions.

Network Formation Models

Strategic models of network formation generalize the frameworks of single agents and multiple agents discrete choice models reviewed in Sections Discrete Choice in Single Agent Random Utility Models and Static, Simultaneous-Move Finite Games with Multiple Equilibria. They posit that pairs of agents (nodes) form, maintain, or sever connections (links) according to an explicit equilibrium notion and utility structure. Each individual's utility depends on the links formed by others (the network) and on utility shifters that may be pair-specific. One may conjecture that the results reported in Sections Discrete Choice in Single Agent Random Utility Models-Static, Simultaneous-Move Finite Games with Multiple Equilibria apply in this more general context too. While of course lessons can be carried over, network formation models present challenges that combined cannot be overcome without the development of new tools. These include the issue of equilibrium existence and the possibility of multiple equilibria when they exist, due to the interdependence in agents' choices (this problem was already discussed in Section Static, Simultaneous-Move Finite Games with Multiple Equilibria). Another challenge is the degree of correlation between linking decisions, which interacts with how the observable data is generated: one may observe a growing number of independent networks, or a growing number of agents on a single network. Yet another challenge, which substantially increases the difficulties associated with the previous two, is the combinatoric complexity of network formation problems. The purpose of this section is exclusively to discuss some recent papers that have made important progress to address these specific challenges and carry out partial identification analysis. For a thorough treatment of the literature on network formation, I refer to the reviews in , , , and . Depending on whether the researcher observes data from a single network or multiple independent networks, the underlying population of agents may be represented as a continuum or as a countably infinite set in the first case, or as a finite set in the second case. Henceforth, I denote generic agents as [math]i[/math], [math]j[/math], [math]k[/math], and [math]m[/math]. I consider static models of undirected network formation with non-transferable utility. The collection of all links among nodes forms the network, denoted [math]\ey[/math]. For any pair [math](i,j)[/math] with [math]i\neq j[/math], [math]\ey_{ij}=1[/math] if they are linked, and [math]\ey_{ij}=0[/math] otherwise ([math]\ey_{ii}=0[/math] for all [math]i[/math] by convention). The notation [math]\ey-\{ij\}[/math] denotes the network that results if a link present between nodes [math]i[/math] and [math]j[/math] is deleted, while [math]\ey+\{ij\}[/math] denotes the network that results if a link absent between nodes [math]i[/math] and [math]j[/math] is added. Denote agent [math]i[/math]'s payoff by [math]\bu_i(\ey,\ex,\epsilon)[/math]. This payoff depends on the network [math]\ey[/math] and the payoff shifters [math](\ex,\epsilon)[/math], with [math]\ex[/math] observable both to the agents and to the researcher, [math]\epsilon[/math] only to the agents, and [math](\ex,\epsilon)[/math] collecting [math](\ex_{ij},\epsilon_{ij})[/math] for all [math]i[/math] and [math]j[/math]. Following much of the literature, I employ pairwise stability as equilibrium notion: [math]\ey[/math] is a pairwise stable network if all linked agents prefer not to sever their links, and all non-existing links are damaging to at least one agent. Formally,

[[math]] \begin{align*} \forall(i,j):\ey_{ij}&=1,\bu_i(\ey,\ex,\epsilon)\ge \bu_i(\ey-\{ij\},\ex,\epsilon)\mathrm{and}\bu_j(\ey,\ex,\epsilon)\ge \bu_j(\ey-\{ij\},\ex,\epsilon),\\ \forall(i,j):\ey_{ij}&=0,\mathrm{if}\bu_i(\ey+\{ij\},\ex,\epsilon) \gt \bu_i(\ey,\ex,\epsilon)\mathrm{then}\bu_j(\ey+\{ij\},\ex,\epsilon) \lt \bu_j(\ey,\ex,\epsilon). \end{align*} [[/math]]

Under this equilibrium notion, if equilibria exist multiplicity is likely; see, among others, the examples in , , and . The model is therefore incomplete, because it does not specify how an equilibrium is selected in the region of multiplicity. For the same reasons as discussed in the context of finite games in Section Static, Simultaneous-Move Finite Games with Multiple Equilibria, partial identification results (unless one is willing to impose restrictions on the equilibrium selection mechanism). However, as I explain below, an immediate application of the identification analysis carried out there presents enormous practical challenges because there are [math]2^{n(n-1)/2}[/math] possible network configurations to be checked for stability (and the dimensionality of the space of unobservables is also very large). In what follows I consider two distinct frameworks that make different assumptions about the utility function and how the data is generated, and discuss what can be learned about the parameters of interest in these cases.

Data from Multiple Independent Networks

I first consider the case that the researcher observes data from multiple independent networks. I follow the set-up put forward by .

Identification Problem (Network Formation Model with Multiple Independent Networks)

Let there be [math]n\in\{2,3,\dots\},n \lt \infty[/math] agents, and let [math](\ex,\ey)\sim\sP[/math] be observable random variables in [math]\times_{j=1}^n\R^d\times\{0,1\}^{n(n-1)/2}[/math], [math]d \lt \infty[/math]. Suppose that [math]\ey[/math] is a pairwise stable network. For each agent [math]i[/math], let the utility function be known up to finite dimensional parameter vector [math]\delta\in\Delta\subset\R^p[/math], and given by

[[math]] \begin{multline} \bu_i(\ey,\ex,\epsilon;\delta)=\sum_{j=1}^n \ey_{ij}(f(\ex_i,\ex_j;\delta_1)+\epsilon_{ij})\\ +\delta_2\frac{\sum_{j=1}^n\sum_{k\neq i,k=1}^n\ey_{ij}\ey_{jk}}{n-2}+\delta_3\frac{\sum_{j=1}^n\sum_{k=j+1}^n\ey_{ij}\ey_{ik}\ey_{jk}}{n-2}\label{eq:utility:network:1} \end{multline} [[/math]]

with [math]f(\cdot,\cdot;\cdot)[/math] a continuous function of its arguments. Suppose that [math]\epsilon_{ij}[/math] are independent for all [math]i\neq j[/math] and identically distributed with CDF known up to parameter vector [math]\gamma\in\Gamma\subset\R^m[/math], denoted [math]\sF_\gamma[/math]. Assume that the support of [math]\sF_\gamma[/math] is [math]\R[/math], that [math]\sF_\gamma[/math] is absolutely continuous with respect to Lebesgue measure, and continuously differentiable with respect to [math]\gamma\in\Gamma[/math]. Let [math]\Theta=\Delta\times\Gamma[/math]. Assume that the researcher observes a random sample of networks and observable payoff shifters drawn from [math]\sP[/math]. In the absence of additional information, what can the researcher learn about [math]\theta\equiv[\delta_1\delta_2\delta_3\gamma][/math]?

analyzes this problem. She establishes equilibrium existence provided that [math]\delta_2\ge 0[/math] and [math]\delta_3\ge 0[/math] . Given payoff shifters [math](\ex,\epsilon)[/math] and parameters [math]\vartheta\equiv[\tilde\delta_1\tilde\delta_2\tilde\delta_3\tilde\gamma]\in\Theta[/math], let [math]\eY_\vartheta(\ex,\epsilon)[/math] denote the collection of pairwise stable networks implied by the model. It is easy to show that [math]\eY_\vartheta(\ex,\epsilon)[/math] is a random closed set as in Definition. The networks in [math]\eY_\vartheta(\ex,\epsilon)[/math] are [math]n\times n[/math] symmetric adjacency matrices with diagonal elements equal to zero and off diagonal elements in [math]\{0,1\}[/math]. To ease notation, I omit [math]\eY_\vartheta[/math]'s dependence on [math](\ex,\epsilon)[/math] in what follows. Under the assumption that [math]\ey[/math] is a pairwise stable network, at the true data generating value of [math]\theta\in\Theta[/math], one has

[[math]] \begin{align} \ey\in\eY_\theta\mathrm{a.s.} \label{eq:y_in_Y_network_multiple} \end{align} [[/math]]

Equation \eqref{eq:y_in_Y_network_multiple} exhausts the modeling content of Identification Problem. Theorem can be leveraged to extract its empirical content from the observed distribution [math]\sP(\ey,\ex)[/math]. Let [math]\cY[/math] be the collection of [math]n\times n[/math] symmetric matrices with diagonal elements equal to zero and all other entries in [math]\{0,1\}[/math], so that [math]|\cY|=2^{n(n-1)/2}[/math]. For a given set [math]K\subset\cY[/math], let [math]\sT_{\eY_{\vartheta}}(K;\sF_\gamma)[/math] denote the probability of the event [math]\{\eY_\vartheta\cap K\neq \emptyset\}[/math] implied when [math]\epsilon\sim\sF_\gamma[/math], [math]\ex[/math]-a.s.

Theorem (Structural Parameters in Network Formation Models with Multiple Independent Networks)

Under the assumptions of Identification Problem, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align} \idr{\theta}=\{\vartheta\in\Theta:\sP(\ey\in K|\ex)\le \sT_{\eY_{\vartheta}}(K;\sF_{\tilde\gamma})\,\forall K\subset\cY, \, \ex\text{-a.s.}\}.\label{eq:SIR:networks:1} \end{align} [[/math]]

Show Proof

Follows from similar arguments as for the proof of Theorem.

■

The characterization of [math]\idr{\theta}[/math] in Theorem SIR- is new to this chapter. While technically it entails a finite number of conditional moment inequalities, in practice their number can be prohibitive as it can be as large as [math]2^{2^{n(n-1)/2}}-2[/math]. Even using only a subset of the inequalities in \eqref{eq:SIR:networks:1} to obtain an outer region, for example applying the insights in , may not be practical (with [math]n=20[/math], [math]|\cY|\approx 10^{57}[/math]). Moreover, computation of [math]\sT_{\eY_{\vartheta}}(K;\sF_\gamma)[/math] may require (depending on the set [math]K[/math]) evaluation of rather complex integrals. To circumvent these challenges, proposes to analyze network formation through subnetworks. A subnetwork is the restriction of a network to a subset of the agents (i.e., a subset of nodes and the links between them). For given [math]A\subseteq\{1,2,\dots,n\}[/math], let [math]\ey^A=\{\ey_{ij}\}_{i,j\in A, i\neq j}[/math] be the submatrix in [math]\ey[/math] with rows and columns in [math]A[/math], and let [math]\ey^{-A}[/math] be the remaining elements of [math]\ey[/math] after [math]\ey^A[/math] is deleted. With some abuse of notation, let [math](\ey^A,\ey^{-A})[/math] denote the composition of [math]\ey^A[/math] and [math]\ey^{-A}[/math] that returns [math]\ey[/math]. Recall that [math]\eY_\vartheta\equiv\eY_\vartheta(\ex,\epsilon)[/math], and let

[[math]] \begin{align*} \eY_{\vartheta}^A=\{\ey^A\in\{0,1\}^{|A|}:\exists \ey^{-A}\in\{0,1\}^{|-A|}\mathrm{suchthat}(\ey^A,\ey^{-A})\in\eY_{\vartheta}\} \end{align*} [[/math]]

be the collection of subnetworks with rows and columns in [math]A[/math] that can be part of a pairwise stable network in [math]\eY_\vartheta[/math]. Let [math]\ex^A[/math] denote the subset of [math]\ex[/math] collecting [math]\ex_{ij}[/math] for [math]i,j\in A[/math]. For a given [math]y^A\in\{0,1\}^{|A|}[/math], let [math]\sC_{\eY_{\vartheta}^A}(y^A;\sF_\gamma)[/math] and [math]\sT_{\eY_{\vartheta}^A}(y^A;\sF_\gamma)[/math] denote, respectively, the probability of the events [math]\{\eY_\vartheta^A=\{y^A\}\}[/math] and [math]\{\{y^A\}\in\eY_\vartheta^A\}[/math] implied when [math]\epsilon\sim\sF_\gamma[/math], [math]\ex[/math]-a.s. The first event means that only the subnetwork [math]y^A[/math] is part of a pairwise stable network, while the second event means that [math]y^A[/math] is a possible subnetwork that is part of a pairwise stable network but other subnetworks may be part of it too. provides the following outer region for [math]\theta[/math] by adapting the insight in to subnetworks. In the theorem I abuse notation compared to Table by introducing a superscript, [math]A[/math], to make explicit the dependence of the outer region on it. \begin{OR}[Subnetworks-based Outer Region on Structural Parameters in Network Formation Models with Multiple Independent Networks] \label{OR:networks:1} Under the assumptions of Identification Problem, for any [math]A\subseteq\{1,2,\dots,n\}[/math], an [math]A[/math]-dependent outer region for [math]\theta[/math] is

[[math]] \begin{align} \mathcal{O}^A_\sP[\theta]=\{\vartheta\in\Theta:\sC_{\eY_{\vartheta}^A}(y^A;\sF_{\tilde\gamma})\le\sP(\ey^A=y^A|\ex^A)\le \sT_{\eY_{\vartheta}^A}(y^A;\sF_{\tilde\gamma})\,\forall y^A\subset\cY^A, \, \ex^A\text{-a.s.}\},\label{eq:OR:networks:1} \end{align} [[/math]]

where [math]\cY^A[/math] is the collection of [math]|A|\times|A|[/math] symmetric matrices with diagonal elements equal to zero and all other elements in [math]\{0,1\}[/math] so that [math]|\cY^A|=2^{|A|(|A|-1)/2}[/math]. \end{OR} \begin{proof} Let [math]\eu(\tilde\ey|\eY_\vartheta)[/math] be a random variable in the unit simplex in [math]\R^{n(n-1)/2}[/math] which assigns to each possible pairwise stable network [math]\tilde\ey[/math] that may realize given [math](\ex,\epsilon)[/math] and [math]\vartheta\in\Theta[/math] the probability that it is selected from [math]\eY_\vartheta[/math]. Given [math]y\in\cY[/math], denote by [math]\sM(y|\ex)[/math] the model predicted probability that the network realizes equal to [math]y[/math]. Then the model yields

[[math]] \begin{align} \sM(y|\ex)&=\int\eu(y| Y_\vartheta)d\sF_\gamma=\int_{y\in Y_\vartheta,| Y_\vartheta|=1}d\sF_\gamma+\int_{y\in Y_\vartheta,| Y_\vartheta|\ge 2}\eu( y| Y_\vartheta)d\sF_\gamma.\label{eq:model:distrib:network:1} \end{align} [[/math]]

The model implied distribution for subnetwork [math]\tilde\ey^A[/math] is obtained by taking the marginal of expression \eqref{eq:model:distrib:network:1} with respect to [math]\tilde\ey^{-A}[/math]

[[math]] \begin{align} \sM(y^A|\ex)&=\sum_{y^{-A}}\sM((y^A,y^{-A})|\ex)= \int_{y^A\in Y_\vartheta^A,| Y_\vartheta^A|=1}d\sF_\gamma+\int_{y^A\in Y_\vartheta^A,| Y_\vartheta^A|\ge 2}\sum_{y^{-A}}\eu((y^A,y^{-A})| Y_\vartheta)d\sF_\gamma.\label{eq:model:distrib:subnetwork:1} \end{align} [[/math]]

Replacing [math]\eu[/math] in \eqref{eq:model:distrib:subnetwork:1} with zero and one yields the bounds in \eqref{eq:OR:networks:1}. \end{proof} further assumes that the selection mechanism [math]\eu(\tilde\ey|\eY_\vartheta)[/math] is invariant to permutations of the labels of the players. Under this condition and the maintained assumptions on [math]\epsilon[/math], she shows that the inequalities in \eqref{eq:OR:networks:1} are invariant under permutations of labels, so subnetworks in any two subsets [math]A,A'\subseteq\{1,2,\dots,n\}[/math] with [math]|A|=|A'|[/math] and [math]\ex^A=\ex^{A'}[/math] yield the same inequalities for all [math]y^A=y^{A'}[/math]. It is therefore sufficient to consider subnetwork [math]A[/math] and the inequalities in \eqref{eq:OR:networks:1} associated with it. Leveraging this result, proposes an outer region obtained by looking at unlabeled subnetworks of size [math]|A|\le\bar{a}[/math] and given by

[[math]] \begin{align*} \outr{\theta}=\bigcap_{|A|\le\bar{a}}\mathcal{O}^A_\sP[\theta]. \end{align*} [[/math]]

As long as the subnetworks are chosen to be small, e.g., [math]|A|\le 2,3,4[/math], the inequalities in \eqref{eq:OR:networks:1} can be computed even if the network is large. shows that the inequalities in \eqref{eq:OR:networks:1} remain informative as [math]n[/math] grows. This fact highlights the importance of working with subnetworks. One could have applied the insight of directly to the full network by setting [math]\eu[/math] equal to zero and to one in \eqref{eq:model:distrib:network:1}. The resulting bounds, however, would vanish to zero as [math]n[/math] grows and become uninformative for [math]\theta[/math]. The characterization in Theorem OR- can be refined to obtain a smaller region, adapting the results in to subnetworks. The size of this refined region is weakly decreasing in [math]|A|[/math]. However, the refinement does not yield [math]\idr{\theta}[/math] because it is applied only to subnetworks.

Key Insight: At the beginning of this section I highlighted some key challenges to inference in network formation models. Identification Problem bypasses the concern on the dependence among linking decisions through the independence assumption on [math]\epsilon_{ij}[/math] and the presumption that the researcher observes data from multiple independent networks, which allows for identification of [math]\sP(\ey,\ex)[/math]. takes on the remaining challenges by formally establishing equilibrium existence and allowing for unrestricted selection among multiple equilibria. In order to overcome the computational complexity of the problem, she puts forward the important idea of inference based on subnetworks. While of course information is left on the table, the approach remains feasible even with large networks.

considers a framework similar to the one laid out in Identification Problem. He assumes non-negative externalities, and shows that in this case the set of pairwise stable equilibria is a complete lattice with a smallest and a largest equilibrium. He then uses moment functions that are monotone in the pairwise stable network (so that they take their extreme values at the smallest and largest equilibria), to obtain moment conditions that restrict [math]\theta[/math]. Examples of the moment functions used include the proportion of pairs with a link, the proportion of links belonging to traingles, and many more (see ). considers unilateral and bilateral directed network formation games, still under a sampling framework where the researcher observes many independent networks. The equilibrium notion that she uses is pure strategy Nash. She assumes that the payoff that player [math]i[/math] receives from forming link [math]ij[/math] is allowed to depend on the number of additional players forming a link pointing to [math]j[/math], but rules out other spillover effects. Under this assumption and some regularity conditions, shows that the network formation game can be decomposed into local games (i.e., games whose sets of players and strategy profiles are subsets of the network formation game's ones), so that the network formation game is in equilibrium if and only if each local game is in equilibrium. She then obtains a characterization of [math]\idr{\theta}[/math] using elements of random set theory.

Data From a Single Network

When the researcher observes data from a single network, extra care has to be taken to restrict the dependence among linking decisions. This can be done in various ways (see, e.g., ). Here I consider a framework proposed by .

Identification Problem (Network Formation Model with a Single Network)

Let there be a continuum of agents [math]j\in\cI=[0,\mu][/math], with [math]\mu \gt 0[/math] their total measure, who choose whom to link to based on a utility function specified below. Let [math]y:\cI\times\cI\to\{0,1\}[/math] be an adjacency mapping with [math]y_{jk}=1[/math] if nodes [math]j[/math] and [math]k[/math] are linked, and [math]y_{jk}=0[/math] otherwise. Assume that only connections up to distance [math]\bar{d}[/math] affect utility and that preferences are such that agents never choose to form more than a total of [math]\bar{l}[/math] links. To simplify exposition, let [math]\bar{d}=2[/math]. Let each agent [math]j[/math] be endowed with characteristics [math]\ex_j\in\cX[/math], with [math]\cX[/math] a finite set in [math]\R^p[/math], that are observable to the researcher. Additionally, let each agent [math]j[/math] be endowed with [math]\bar{l}\times|\cX|[/math] preference shocks [math]\epsilon_{j\ell}(x)\in\R,\ell=1,\dots,\bar{l},x\in\cX[/math], that are unobservable to the researcher and correspond to the possible direct connections and their characteristics. Suppose that the vector of preference shocks is independent of [math]\ex[/math] and has a distribution known up to parameter vector [math]\gamma\in\Gamma\subset\R^m[/math], denoted [math]\sQ_\gamma[/math]. Let [math]\cI(j)=\{k:y_{jk}=1\}[/math]. Assume that agents with characteristics and preference shocks [math](x,e)[/math] value links according to the utility function

[[math]] \begin{multline} \bu_j(y,x,e)=\sum_{k\in\cI(j)}(f(x_j,x_k)+e_{j\ell(k)}(x_k))\\ +\delta_1\left|\bigcup_{k\in\cI(j)}\cI(k)-\cI(j)-\{j\}\right| +\delta_2\sum_{k\in\cI(j)}\sum_{m\in\cI(j):m \gt k}y_{km}-\infty\one(|\cI(k)| \gt \bar{l})\label{eq:utility:network:2} \end{multline} [[/math]]

Assume that the network [math]\ey[/math] formed by agents with characteristics and shocks [math](\ex,\epsilon)[/math] is pairwise stable. Let [math]\Theta\equiv\Upsilon\times\Delta\times\Gamma[/math], with [math]\Upsilon[/math] the parameter space for [math]\cf\equiv\{f(x,w):x\in\cX,w\in\cX\}[/math]. In the absence of additional information, what can the researcher learn about [math]\theta\equiv[\cf\delta_1\delta_2\gamma][/math]?

Identification Problem enforces dimension reduction through the restrictions on depth and degree (the bounds [math]\bar{d}[/math] and [math]\bar{l}[/math]), so that it is applicable to frameworks with networks that have limited degree distribution (e.g., close friendships network, but not Facebook network). It also requires that individual identities are irrelevant. This substantially reduces the richness of unobserved heterogeneity allowed for and the dimensionality of the space of unobservables. While the latter feature narrows the domain of applicability of the model, it is very beneficial to obtain a tractable characterization of what can be learned about [math]\theta[/math], and yields equilibria that may include isolated nodes, a feature often encountered in networks data. study Identification Problem focusing on the payoff-relevant local subnetworks that result from the maintained assumptions. These are distinct from the subnetworks used by : whereas looks at subnetworks formed by arbitrary individuals and whose size is chosen by the researcher on the base of computational tractability, look at subnetworks among individuals that are within a certain distance of each other, as determined by the structure of the preferences. On the other hand, analysis does not require that agents have a finite number of types nor bounds the number of links that they may form. To characterize the local subnetworks relevant for identification analysis in their framework, propose the concepts of network type and preference class. A network type [math]t=(a,v)[/math] describes the local network up to distance [math]\bar{d}[/math] from the reference node. Here [math]a[/math] is a square matrix of size [math]1+\bar{l}\sum_{d=1}^{\bar{d}}(\bar{l}-1)^{d-1}[/math] that describes the local subnetwork that is utility relevant for an agent of type [math]t[/math]. It consists of the reference node, its direct potential neighbors ([math]\bar{l}[/math] elements), its second order neighbors ([math]\bar{l}(\bar{l}-1)[/math] elements), through its [math]\bar{d}[/math]-th order neighbors ([math]\bar{l}(\bar{l}-1)^{\bar{d}-1}[/math] elements). The other component of the type, [math]v[/math], is a vector of length equal to the size of [math]a[/math] that contains the observable characteristics of the reference node and her alters. The bounds [math]\bar{d}[/math] and [math]\bar{l}[/math] enforce dimension reduction by bounding the number of network types. The partial identification approach of depends on this number, rather than on the number of agents. For example, the number of moment inequalities is determined by the number of network types, not by the number of agents. As such, the approach yields its highest dividends for dimension reduction in large networks. Let [math]\cT[/math] denote the collection of network types generated from a preference structure [math]\bu[/math] and set of characteristics [math]\cX[/math]. For given realization [math](x,e)[/math] of the observable characteristics and preference shocks of a reference agent, and for given [math]\vartheta\in\Theta[/math], define the collection of network types for which no agent wants to drop a link by

[[math]] \begin{align*} H_\vartheta(x,e)=\{(a,v)\in\cT:v_1=x\mathrm{and}\bu(a,v,e)\ge \bu(a_{-\ell},v,e)\forall\ell=1,\dots,\bar{l}\}, \end{align*} [[/math]]

where [math]a_{-\ell}[/math] is equal to the local adjacency matrix [math]a[/math] but with the [math]\ell[/math]-th link removed (that is, it sets the [math](1,\ell+1)[/math] and [math](\ell+1,1)[/math] elements of [math]a[/math] equal to zero). Because [math](\ex,\epsilon)[/math] are random vectors, [math]\eH_\vartheta\equiv H_\vartheta(\ex,\epsilon)[/math] is a random closed set as per Definition. This random set takes on a finite number of realizations (equal to the possible subsets of [math]\cT[/math]), so that its distribution is completely determined by the probability with which it takes on each of these realizations. A preference class [math]H\subset\cT[/math] is one of the possible realizations of [math]\eH_\vartheta[/math] for some [math]\vartheta\in\Theta[/math]. The model implied probability that [math]\eH_\vartheta=H[/math] is given by

[[math]] \begin{align} \sM(H|\ex;\vartheta)\equiv\sQ_{\tilde\gamma}(\epsilon:\eH_\vartheta=H|\ex).\label{eq:model:prediction:network:class} \end{align} [[/math]]

Observation of data from one network allows the researcher, under suitable restrictions on the sampling process, to learn the distribution of network types in the data (type shares), denoted [math]\sP(t)[/math]. For example, in a network of best friends with [math]\bar{l}=1[/math] and [math]\bar{d}=2[/math], and [math]\cX=\{x^1,x^2\}[/math] (e.g., a simplified framework with only two possible races), agents are either isolated or in a pair. Network types are pairs for the agents' race and the best friend's race (with second element equal zero if the agent is isolated). Type shares are the fraction of isolated blacks, the fraction of isolated whites, the fraction of blacks with a black best friend, the fraction of whites with a black best friend, and the fraction of whites with a white best friend. The preference classes for a black agent are [math]H^1(b,e)=\{(b,0)\}[/math], [math]H^2(b,e)=\{(b,0),(b,b)\}[/math], [math]H^3(b,e)=\{(b,0),(b,w)\}[/math], [math]H^4(b,e)=\{(b,0),(b,w),(b,b)\}[/math] (and similarly for whites). In each case, being alone is part of the preference class, as there are no links to sever. In the second class the agent has a preference for having a black friend, in the third class for a white friend, and in the last class for a friend of either race. It is easy to see that the model is incomplete, as for a given realization of [math]\epsilon[/math] it makes multiple predictions on the agent's preference type. propose to map the distribution of preference classes into the observed distribution of preference types in the data through the use of allocation parameters, denoted [math]\alpha_H(t)\in[0,1][/math]. These are distinct from but play the same role as a selection mechanism, and they represent a candidate distribution for [math]t[/math] given [math]\eH_\vartheta=H[/math]. The model, augmented with them, implies a probability that an agent is of network type [math]t[/math]:

[[math]] \begin{align} \sM(t;\vartheta,\alpha)=\frac{1}{\mu}\sum_{H\subset\cT}\mu_{v_1(t)}\sM(H|v_1(t);\vartheta)\alpha_H(t),\label{eq:model:prediction:network:2} \end{align} [[/math]]

where [math]\mu_{v_1(t)}[/math] is the measure of reference agents with characteristics equal to the second component of the preference type [math]t[/math], [math]\ex=v_1(t)[/math], and [math]\alpha\equiv\{\alpha_H(t):t\in \cT, H\subset\cT\}[/math].

provide a characterization of an outer region for [math]\theta[/math] based on two key implications of pairwise stability that deliver restrictions on [math]\alpha[/math]. They also show that under some additional assumptions, this characterization yields [math]\idr{\theta}[/math] . Here I focus on their more general result. The first implication that they use is that existing links should not be dropped:

[[math]] \begin{align} t\notin H\Rightarrow\alpha_H(t)=0.\label{eq:networks:2:PS1} \end{align} [[/math]]

The condition in \eqref{eq:networks:2:PS1} is embodied in [math]\bar\alpha\equiv\{\alpha_H(t):t\in H, H\subset\cT\}[/math]. The second implication is that it should not be possible to establish mutually beneficial links among nodes that are far from each other. Let [math]t^\prime[/math] and [math]s^\prime[/math] denote the network types that are generated if one adds a link in networks of types [math]t[/math] and [math]s[/math] among two nodes that are at distance at least [math]2\bar{d}[/math] from each other and each have less than [math]\bar{l}[/math] links. Then the requirement is

[[math]] \begin{align} \left(\sum_{H\subset\cT}\mu_{v_1(t)}\sM(H|v_1(t);\vartheta)\alpha_H(t)\one(t^\prime\in H)\right)\left(\sum_{H\subset\cT}\mu_{v_1(s)}\sM(H|v_1(s);\vartheta)\alpha_H(s)\one(s^\prime\in H)\right)=0\label{eq:networks:2:PS2} \end{align} [[/math]]

In words, if a positive measure of agents of type [math]t[/math] prefer [math]t^\prime[/math] (i.e., [math]\alpha_H(t) \gt 0[/math] for some [math]H[/math] such that [math]t^\prime\in H[/math]), there must be zero measure of type [math]s[/math] individuals who prefer [math]s^\prime[/math], because otherwise the network is unstable. show that the conditions in \eqref{eq:networks:2:PS2} can be embodied in a square matrix [math]q[/math] of size equal to the length of [math]\bar{\alpha}[/math]. The entries of [math]q[/math] are constructed as follows. Let [math]H[/math] and [math]\tilde{H}[/math] be two preference classes with [math]t\in H[/math] and [math]s\in\tilde{H}[/math]. With some abuse of notation, let [math]q_{\alpha_H(t),\alpha_{\tilde{H}}(s)}[/math] denote the element of [math]q[/math] corresponding to the index of the entry in [math]\bar\alpha[/math] equal to [math]\alpha_H(t)[/math] for the row, and to [math]\alpha_{\tilde{H}}(s)[/math] for the column. Then set [math]q_{\alpha_H(t),\alpha_{\tilde{H}}(s)}(\vartheta)=\one(t^\prime\in H)\one(s^\prime\in\tilde{H})[/math]. It follows that this element yields the term [math]\big(\alpha_H(t)\one(t^\prime\in H)\big)\big(\alpha_{\tilde{H}}(s)\one(s^\prime\in \tilde{H})\big)[/math] in the quadratic form [math]\bar{\alpha}^\top q \bar{\alpha}[/math]. As long as [math]\mu_{v_1(\cdot)}[/math] and [math]\sM(\cdot|\ex;\vartheta)[/math] in \eqref{eq:model:prediction:network:class} are strictly positive, this term is equal to zero if and only if condition \eqref{eq:networks:2:PS2} holds for types [math]t[/math] and [math]s[/math]. With this background, Theorem OR- below provides an outer region for [math]\theta[/math]. The proof of this result follows from the arguments laid out above (see ). \begin{OR}[Outer Region on Parameters of a Network Formation Model with a Single Network] \label{OR:networks:2} Under the assumptions of Identification Problem,

[[math]] \begin{align} \outr{\theta}=\left\{\vartheta\in\Theta: \left(\begin{tabular}{rl} \ltmath\gt\min_{\bar{\alpha}} \bar{\alpha}^\top q \bar{\alpha}[[/math]]

& \\ s.t. & [math]\sM(t;\vartheta,\bar{\alpha})=\sP(t)\forallt\in\cT[/math] \\

& [math]\sum_{t\in H}\bar\alpha_H(t)=1\forall H\subset \cT[/math] \\ 
& [math]\alpha_H(t)\ge 0\forall t\in H,\forall H\subset \cT[/math]  

\end{tabular} \right)=0 \right\}.\label{eq:OR:networks:2} \end{align} </math> \end{OR} The set in \eqref{eq:OR:networks:2} does not equal [math]\idr{\theta}[/math] in all models allowed for in Identification Problem because condition \eqref{eq:networks:2:PS2} does not embody all implications of pairwise stability on non-existing links. While the optimization problem in \eqref{eq:OR:networks:2} is quadratic, it is not necessarily convex because [math]q[/math] may not be positive definite. Nonetheless, the simulations reported by suggest that [math]\outr{\theta}[/math] can be computed rapidly, as least for the examples they considered.

Key Insight: At the beginning of this section I highlighted some key challenges to inference in network formation models. When data is observed from a single network, as in Identification Problem, proposal to base inference on local networks achieves two main benefits. First, it delivers consistently estimable features of the game, namely the probability that an agent belongs to one of a finite collection of network types. Second, it achieves dimension reduction, so that computation of outer regions on [math]\theta[/math] remains feasible even with large networks and allowing for unrestricted selection among multiple equilibria.

Further Theoretical Advances and Empirical Applications

In order to discuss the partial identification approach to learning structural parameters of economic models in some level of detail while keeping this chapter to a manageable length, I have focused on a selection of papers. In this section I briefly mention several other excellent theoretical contributions that could be discussed more closely, as well as several empirical papers that have applied partial identification analysis of structural models to answer a wide array of questions of substantive economic importance.\medskip

and propose to embed revealed preference-based inequalities into structural models of both demand and supply in markets where firms face discrete choices of product configuration or of location. Revealed preference arguments are a trademark of the literature on discrete choice analysis. and use these arguments to leverage a subset of the model's implications to obtain easy-to-compute moment inequalities. For example, in the context of entry games such as the ones discussed in Section Static, Simultaneous-Move Finite Games with Multiple Equilibria, they propose to base inference on the implication that a player enters the market if and only if (s)he expects to make non-negative profits. This condition can be exploited even when players have heterogeneous (unobserved to the researcher) information sets, and it implies that the expected profits for entrants should be non-negative. Nonetheless, the condition does not suffice to obtain moment inequalities that include only observed payoff shifters and preference parameters. This is because the expected value of unobserved payoff shifters for entrants is not equal to zero, as the group of entrants is selected. The authors require the availability of valid (monotone) instrumental variables to solve this problem (see Section Treatment Effects with and without Instrumental Variables for uses of instrumental variables and monotone instrumental variables in partial identification analysis of treatment effects). Interesting features of their approach include that the researcher does not need to solve for the set of equilibria, nor to require that the distribution of unobservable payoff shifters is known up to finite dimensional parameter vector. Moreover, the same basic ideas can be applied to single agent models (with or without heterogeneous information sets). A shortcoming of the method is that the set of parameter vectors satisfying the moment inequalities may be wider than the sharp identification region under the maintained assumptions.

The breadth of applications of the approach proposed by and is vast. For example, uses it to model the formation of the hospital networks offered by US health insurers, and and use it to obtain bounds on firm fixed costs as an input to modeling product choices in the movie industry and in the US video game industry, respectively. estimates the effects of Wal-Mart's strategy of creating a high density network of stores. While the close proximity of stores implies cannibalization in sales, Wal-Mart is willing to bear it to achieve density economies, which in turn yield savings in distribution costs. His results suggest that Wal-Mart substantially benefits from high store density. measure the effects of chain economies, business stealing, and heterogeneous firms' comparative advantages in the discount retail industry. estimate a model of strategic voting and quantify the impact it has on election outcomes. As in other models analyzed in this section, the one they study yields multiple predicted outcomes, so that partial identification methods are required to carry out the empirical analysis if one does not assume a specific selection mechanism to resolve the multiplicity. They estimate their model on Japanese general-election data, and uncover a sizable fraction of strategic voters. They also estimate that only a small fraction of voters are misaligned (voting for a candidate other than their most preferred one). studies whether the rapid removal from the market for personal computers of existing central processing units upon creation of new ones through innovation reduces surplus. He finds that a limited group of price-insensitive consumers enjoys the largest share of the welfare gains from innovation. A policy that kept older technologies on the shelf would allow for the benefits from innovation to reach price-sensitive consumers thanks to improved access to mobile computing, but total welfare would not increase because consumer welfare gains would be largely offset by producer losses. analyze hospital referrals for labor and birth episodes in California in 2003, for patients enrolled with six health insurers that use, to a different extent, incentives to referring physicians groups to reduce hospital costs (capitation contracts). The aim is to learn whether enrollees with high-capitation insurers tend to be referred to lower-priced hospitals (ceteris paribus) compared to other patients with same-severity conditions, and whether quality of care was affected. Their model allows for an insurer-specific preference function that is additively separable in the hospital price paid by the insurer (which is allowed to be measured with error), the distance traveled, and plan and severity-specific hospital fixed effects. Importantly, unobserved heterogeneity entering the preference function is not assumed to be drawn from a distribution known up to finite dimensional parameter vector. The results of the empirical analysis indicate that the price paid by insurers to hospitals has an impact on referrals, with higher elasticity to price for insurers whose physicians groups are more highly capitated. study how the information that potential exporters have to predict the profits they will earn when serving a foreign market influences their decisions to export. They propose a model where the researcher specifies and observes a subset of the variables that agents use to form their expectations, but may not observe other variables that affect firms' expectations heterogeneously (across firms and markets, and over time). Because only a subset of the variables entering the firms' information set is observed, partial identification results. They show that, under rational expectations, they can test whether potential exporters know and use specific variables to predict their export profits. They also use their model's estimates to quantify the value of information. studies the implications of the \$85 billion automotive industry bailout in 2009 on the commercial vehicle segment. He finds that had Chrysler and GM been liquidated (or aquired by a major competitor) rather than bailed out, the surviving firms would have experienced a rise in profits high enough to induce them to introduce new products.

A different use of revealed preference arguments appears in the contributions of , , , , , , , and many others. For example, proposes a method to partially identify income-leisure preferences and to evaluate the associated effects of tax policies. He starts from basic revealed-preference analysis performed under the assumption that individuals prefer more income and leisure, and no other restriction. The analysis shows that observing an individual's time allocation under a status quo tax policy yields bounds on his allocation that may or may not be informative, depending on how the person allocates his time under the status quo policy and on the tax schedules. He then explores what more can be learned if one additionally imposes restrictions on the distribution of income-leisure preferences, using the method put forward by . One assumption restricts groups of individuals facing different choice sets to have the same distribution of preferences. The other assumption restricts this distribution to a parametric family. build on and expand 's framework to evaluate the effect of Connecticut's Jobs First welfare reform experiment on women' labor supply and welfare participation decisions.

propose a method to learn features of households' risk preferences in a random utility model that nests expected utility theory plus a range of non-expected utility models. They allow for unobserved heterogeneity in preferences (that may enter the utility function non-separably) and leave completely unspecified their distribution. The authors use revealed preference arguments to infer, for each household, a set of values for its unobserved heterogeneity terms that are consistent with the household's choices in the three lines of insurance coverage. As their core restriction, they assume that each household's preferences are stable across contexts: the household's utility function is the same when facing distinct but closely related choice problems. This allows them to use the inferred set valued data to partially identify features of the distribution of preferences, and to classify households into preference types. They apply their proposed method to analyze data on households' deductible choices across three lines of insurance coverage (home all perils, auto collision, and auto comprehensive). Their results show that between 70 and 80 percent of the households make choices that can be rationalized by a model with linear utility and monotone, quadratic, or even linear probability distortions. These probability distortions substantially overweight small probabilities. By contrast, fewer than 40 percent can be rationalized by a model with concave utility but no probability distortions.

propose a method to carry out demand analysis while allowing for general forms of unobserved heterogeneity. Preferences and linear budget sets are assumed to be statistically independent (conditional on covariates and control functions). show that for continuous demand, average surplus is generally not identified from the distribution of demand for a given price and income, and therefore propose a partial identification approach. They use bounds on income effects to derive bounds on average surplus. They apply the bounds to gasoline demand, using data from the 2001 U.S. National Household Transportation Survey.

Another strand of empirical applications pertains to the analysis of discrete games. use the method they develop, described in Section An Inference Approach Robust to the Presence of Multiple Equilibria, to study market structure in the US airline industry and the role that firm heterogeneity plays in shaping it. Their findings suggest that the competitive effects of each carrier increase in that carrier's airport presence, but also that the competitive effects of large carriers (American, Delta, United) are different from those of low cost ones (Southwest). They also evaluate the effect of a counterfactual policy repealing the Wright Amendment, and find that doing so would see an increase in the number of markets served out of Dallas Love.

proposes a model of static entry that extends the one in Section Static, Simultaneous-Move Finite Games with Multiple Equilibria by allowing individuals to have flexible information structures, where players's payoffs depend on both a common-knowledge unobservable payoff shifter, and a private-information one. His characterization of [math]\idr{\theta}[/math] is based on using an unrestricted selection mechanism, as in and . He applies the model to study the impact of supercenters such as Wal-Mart, that sell both food and groceries, on the profitability of rural grocery stores. He finds that entry by a supercenter outside, but within 20 miles, of a local monopolist's market has a smaller impact on firm profits than entry by a local grocer. Their entrance has a small negative effect on the number of grocery stores in surrounding markets as well as on their profits. The results suggest that location and format-based differentiation partially insulate rural stores from competition with supercenters.

A larger class of information structures is considered in the analysis of static discrete games carried out by . They allow for all information structures consistent with the players knowing their own payoffs and the distribution of opponents' payoffs. As solution concept they adopt the Bayes Correlated Equilibrium recently developed by . Also with this solution concept multiple equilibria are possible. The authors leave completely unspecified the selection mechanism picking the equilibrium played in the regions of multiplicity, so that partial identification attains. use the random sets approach to characterize [math]\idr{\theta}[/math]. They apply the method to estimate a model of entry in the Italian supermarket industry and quantify the effect of large malls on local grocery stores. provide partial identification results (and Bayesian inference methods) for semiparametric dynamic binary choice models without imposing distributional assumptions on the unobserved state variables. They carry out an empirical application using 's model of bus engine replacement. Their results suggest that parametric assumptions about the distribution of the unobserved states can have a considerable effect on the estimates of per-period payoffs, but not a noticeable one on the counterfactual conditional choice probabilities. use the random sets approach to partially identify and estimate dynamic discrete choice models with serially correlated unobservables, under instrumental variables restrictions. They extend two-step dynamic estimation methods to characterize a set of structural parameters that are consistent with the dynamic model, the instrumental variables restrictions, and the data. uses the random sets approach and a network formation model, to learn about Italian firms' incentives for having their executive directors sitting on the board of their competitors.

use the method described in Section Unobserved Heterogeneity in Choice Sets and/or Consideration Sets to partially identify the distribution of risk preferences using data on deductible choices in auto collision insurance. They posit an expected utility theory model and allow for unobserved heterogeneity in households' risk aversion and choice sets, with unrestricted dependence between them. Motivation for why unobserved heterogeneity in choice sets might be an important factor in this empirical framework comes from the earlier analysis of and novel findings that are part of contribution. They show that commonly used models that make strong assumptions about choice sets (e.g., the mixed logit model with each individual's choice set assumed equal to the feasible set, and various models of choice set formation) can be rejected in their data. With regard to risk aversion, their key finding is that their estimated lower bounds are significantly smaller than the point estimates obtained in the related literature. This suggests that the data can be explained by expected utility theory with lower and more homogeneous levels of risk aversion than it had been uncovered before. This provides new evidence on the importance of developing models that differ in their specification of which alternatives agents evaluate (rather than or in addition to models focusing on how they evaluate them), and to data collection efforts that seek to directly measure agents' heterogeneous choice sets .

study the effect of pre-vote deliberation on the decisions of US appellate courts. The question of interest is weather deliberation increases or reduces the probability of an incorrect decision. They use a model where communication equilibrium is the solution concept, and only observed heterogeneity in payoffs is allowed for. In the model, multiple equilibria are again possible, and the authors leave the selection mechanism completely unspecified. They characterize [math]\idr{\theta}[/math] through an optimization problem, and structurally estimate the model on US Courts of Appeal data. compare the probability of making incorrect decisions under the pre-vote deliberation mechanism, to that in a counterfactual environment where no deliberation occurs. The results suggest that there is a range of parameters in [math]\idr{\theta}[/math], for which judges have ex-ante disagreement of imprecise prior information, for which deliberation is beneficial. Otherwise deliberation leads to lower effectiveness for the court.

propose a test for the hypothesis of rational expectations for the case that one observes only the marginal distributions of realizations and subjective beliefs, but not their joint distribution (e.g., when subjective beliefs are observed in one dataset, and realizations in a different one, and the two cannot be matched). They establish that the hypothesis of rational expectations can be expressed as testing that a continuum of moment inequalities is satisfied, and they leverage the results in to provide a simple-to-compute test for this hypothesis. They apply their method to test for and quantify deviations from rational expectations about future earnings, and examine the consequences of such departures in the context of a life-cycle model of consumption.

estimate the demand for health insurance under the Affordable Care Act using data from California. Methodologically, they use a discrete choice model that allows for endogeneity in insurance premiums (which enter as explanatory variables in the model) and dispenses with parametric assumptions about the unobserved components of utility leveraging the availability of instrumental variables, similarly to the framework presented in Section Endogenous Explanatory Variables. The authors provide a characterization of sharp bounds on the effects of changing premium subsidies on coverage choices, consumer surplus, and government spending, as solutions to linear programming problems, rendering their method computationally attractive.

Another important strand of theoretical literature is concerned with partial identification of panel data models. consider a dynamic random effects probit model, and use partial identification analysis to obtain bounds on the model parameters that circumvent the initial conditions problem. considers a fixed effect panel data model where he imposes a conditional quantile restriction on time varying unobserved heterogeneity. Differencing out inequalities resulting from the conditional quantile restriction delivers inequalities that depend only on observable variables and parameters to be estimated, but not on the fixed effects, so that they can be used for estimation. obtain bounds on average and quantile treatment effects in nonparametric and semiparametric nonseparable panel data models. provide partial identification results in linear panel data models when censored outcomes, with unrestricted dependence between censoring and observable and unobservable variables. Their results are derived for two classes of models, one where the unobserved heterogeneity terms satisfy a stationarity restriction, and one where they are nonstationary but satisfy a conditional independence restriction. provides a method to partially identify state dependence in panel data models where individual unobserved heterogeneity needs not be time invariant. study semiparametric multinomial choice panel models with fixed effects where the random utility function is assumed additively separable in unobserved heterogeneity, fixed effects, and a linear covariate index. The key semiparametric assumption is a group stationarity condition on the disturbances which places no restrictions on either the joint distribution of the disturbances across choices or the correlation of disturbances across time. propose a within-group comparison that delivers a collection of conditional moment inequalities that they use to provide point and partial identification results. proposes a related method, where partial identification relies on the observation of individuals whose outcome changes in two consecutive time periods, and leverages shape restrictions to reduce the number of between alternatives comparisons needed to determine the optimal choice.

General references

Molinari, Francesca (2020). "Microeconometrics with Partial Identification". arXiv:2004.11751 [econ.EM].