The curse of high dimensions

label{Ch-INTRO} Mathematically, data is a subset [math]A\subseteq\mathbb{R}^d[/math] where the dimension [math]d[/math] is typically a very large number. Concrete examples are as follows. \smallskip

A greyscale picture with [math]320\times240[/math] pixel can be described by [math]75\,500[/math] numbers between [math]0[/math]\,(=white) and [math]1[/math]\,(=black) and this gives a vector in [math]\mathbb{R}^{75\,500}[/math].
The current Oxford dictionary counts [math]273\,000[/math] English words. An arbitrary English text can be seen as a vector in [math]\mathbb{R}^{273\,000}[/math] where each entry is the number of occurrences of each word in the text.
Netflix has approximately [math]3\,500[/math] movies and [math]200[/math] million registered users. Each user can give a rating from one to five stars for each movie. We can represent each user by her/his rating vector in [math]\mathbb{R}^{3\,500}[/math] containing in each entry the user's rating or a zero if the movie has not been rated. Alternatively, we can represent each movie by a vector in [math]\mathbb{R}^{200\,000\,000}[/math] containing in each entry the ratings of the corresponding user.
Amazon offers [math]353[/math] million items for sale. We can represent any of its customers as an element of [math]\mathbb{R}^{353\,000\,000}[/math] by counting the amount of purchases per product.
The human genome has approximately [math]10\,000[/math] genes, so every of the 9 billion humans can be considered as a point in [math]\mathbb{R}^{10\,000}[/math].
When doing medical diagnostic tests, we can represent a subject by the vector containing her/his results. These can include integers like antibody counts, real numbers like temperature, pairs of real numbers like blood pressure, or binary values like if a subject has tested positive or negative for a certain infection.
Facebook has [math]2.7[/math] billion users. If we name the users [math]1,2,3,\dots[/math], we can represent user [math]j[/math] in [math]\mathbb{R}^{2\,700\,000\,000}[/math] by a vector containing a one in the [math]i[/math]-th entry if [math]i[/math] and [math]j[/math] are friends and a zero if they are not.

\smallskip Given such a high-dimensional data set [math]A[/math], classical tasks to analyze the data, or make predictions based on it, involve to compute distances between data points. This can be for example

the classical euclidean distance (or any other [math]p[/math]-norm),
a weighted metric that, e.g., in 6.\ weights every medical information differently,
a distance that is not even a metric like for instance the cosine similarity.

Related tasks are then to determine the k-nearest neighbors within the data set [math]A[/math] of a given point [math]x\in\mathbb{R}^d[/math], to cover the set via [math]A\subseteq\cup_{b\in B}\B_r(b)[/math] or [math]A\subseteq\Gamma(B)[/math] with [math]B\subset A[/math] as small as possible, to find a cluster structure, to determine and fit a distribution function, or to detect a more complicated hidden pattern in the set. \smallskip From the perspective of classical undergraduate courses like Real Analysis, Linear Algebra and Measure Theory, the space [math]\mathbb{R}^d[/math], endowed with euclidean norm, appears well understood: Distances, balls, convex hulls, minimization problems, matrices and volume are well studied in finite dimensions. However, if [math]d[/math] is very large, we are faced with the following two obstructions. Firstly, the computation of the aforementioned quantities can be unfeasable in view of the sheer amount of data. Secondly, natural (and very intuitive!) probability distributions such as the uniform distribution [math]\mathcal{U}(B)[/math] on the hypercube [math]B=[-1,1]^d[/math] or unit ball [math]B=\B_1(0)\subseteq\mathbb{R}^d[/math] or the Gaussian distribution [math]\mathcal{N}(0,1)[/math] in [math]d[/math] dimensions, display several very counterintuitive effects if [math]d[/math] is large. This strongly affects methods that would help to overcome the first obstruction (e.g., drawing a random sample instead of using the whole data set) and has also to be taken into account if we are given empirical data which is subject to errors or noise that we wish to model by a certain probability distribution. \smallskip We begin by recalling the following definition. \begin{dfn}\label{DFN-DISTR} Let [math](\Omega,\Sigma,\P)[/math] be a probability space, let [math]B\subseteq\mathbb{R}[/math] be a Borel set and let [math]X\colon\Omega\rightarrow\mathbb{R}^d[/math] be a random vector.

We say that [math]X[/math] is uniformly distributed on [math]B\subseteq\mathbb{R''^d[/math]} if
[[math]] \P\bigl[X\in A\bigr] = {\medfrac{\lambda^d(A\capB)}{\lambda^d(B)}} [[/math]]
holds for every Borel set [math]A\subseteq\mathbb{R}^d[/math]. We write [math]X\sim\mathcal{U}(B)[/math] in this case and note that below we will focus on the cases of the hypercube [math]B=[-1,1]^d[/math] and the (closed) unit ball [math]B=\Bbar_1(0)=\{x\in\mathbb{R}^d\:;\:\|x\|_2\leqslant1\}[/math]. In the latter case we can as well drop the closure since [math]\{x\in\mathbb{R}^d\:;\:\|x\|_2=1\}[/math] has measure zero.
We say that [math]X[/math] is (spherically) Gaussian distributed with mean zero and variance [math]\sigma \gt 0[/math], if
[[math]] \P[X\in A] = {\medfrac{1}{(2\pi\sigma^2)^{d/2}}} \int_A\exp\bigl({-\medfrac{\|x\|^2}{2\sigma^2}}\bigr)\dd\lambda^d(x) [[/math]]
holds for every Borel set [math]A\subseteq\mathbb{R}^d[/math]. We write [math]X\sim\mathcal{N}(0,\sigma^2,\mathbb{R}^d)[/math] in this case and note that a straightforward computation (see Proposition) shows that [math]X=(X_1,\dots,X_d)\sim\mathcal{N}(0,\sigma^2,\mathbb{R}^d)[/math] holds if and only if [math]X_i\sim\mathcal{N}(0,\sigma^2,\mathbb{R}^1)[/math] holds for all [math]i=1,\dots,d[/math].

\end{dfn}

We start now with the case of the [math]d[/math]-dimensional hypercube [math]H_d:=\{(x_1,\dots,x_d)\in\mathbb{R}^d\:;\:x_i\in[-1,1] \text{ for all } 1\leqslant i\leqslant d\}[/math]. Not surprisingly, [math]H_d[/math] is a compact and absolutely convex set. Consider now the ‘corner’ [math]e=(1,1,\dots,1)\in H_d[/math]. Then

[[math]] \|e\|_2=\sqrt{1^2+1^2+\cdots+1^2}=\sqrt{d}\xrightarrow{d\rightarrow\infty}\infty [[/math]]

and this will hold for ‘more and more corners’ when [math]d[/math] increases. In particular, the mutual distance between ‘many’ corners increases with [math]d[/math]. On the other hand, if we pick two points [math]e_i=(0,\dots,0,1,0,\dots,0)[/math] and [math]f_j=(0,\dots,0,1,0,\dots,0)[/math] in the middle of two different ‘faces’ then their distances

[[math]] \|e_i-e_j\|_2=\sqrt{1^2+1^2}=\sqrt{2} [[/math]]

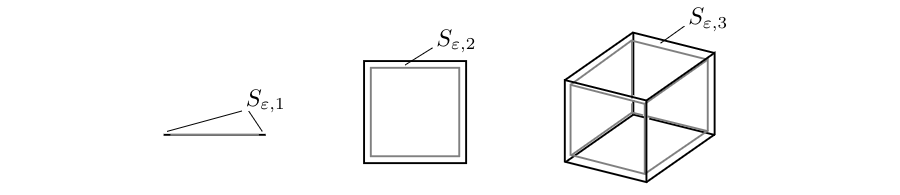
remains constant. This is in particular true for opposite faces, where [math]\|e_i-(-e_i)\|_2=2[/math]. The aforementioned computations paint a picture in which we could imagine the hypercube as an object where the corners ‘spike out’ whereas the centers of the faces stay at constant distance to each other. If distances behave non homogeneously, then we should be prepared that volume is distributed inhomogeneous, too. To see this, let [math]0 \lt \epsilon \lt 1[/math] and consider the subset

[[math]] S_{\epsilon,d}=H_d\backslash{}(1-\epsilon)H_d [[/math]]

of [math]H_d[/math] which can be thought of an [math]\epsilon[/math]-thin outer shell of the hypercube. \begin{center} \begin{picture}(300,65)(0,0)

\put(40,20){

} \put(124,8){

} \put(208,0){

}

\end{picture} \begin{fig}[math]S_{\epsilon,d}[/math] for [math]d=1,2,3[/math].\end{fig} \end{center} Since [math](1-\epsilon)H_d=[-1+\epsilon,1-\epsilon]^d[/math] is a cuboid, we can easily compute

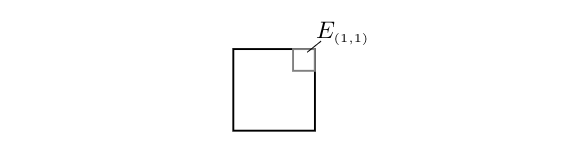
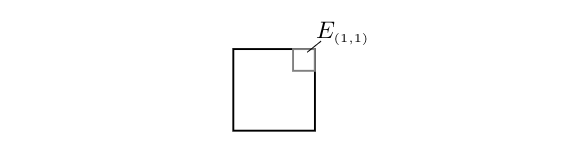
[[math]] \medfrac{\lambda^d(S_{\epsilon,d})}{\lambda^d(H_{d})}=\medfrac{\lambda^d(H^d)-\lambda^d((1-\epsilon)H_d)}{\lambda^d(H_{d})}=\medfrac{2^d-((2(1-\epsilon))^d}{2^d}=1-(1-\epsilon)^d\xrightarrow{d\rightarrow\infty}1 [[/math]]

for [math]0 \lt \epsilon \lt 1[/math]. This means that most of the volume of the hypercube is located close to its surface. Let us mention that the same holds true if we consider the hypercube [math][0,1]^d[/math] with side length one. Then for its volume we get [math]\lambda^d([0,1]^d)=1[/math] and the volume in the [math]\epsilon[/math]-thick shell equals [math]\lambda^d([0,1]^d\backslash[\epsilon,1-\epsilon]^d)=1-(1-2\epsilon)^d[/math] which again converges to [math]1[/math]. So also here most of the volume lies in an [math]\epsilon[/math]-thin shell below its surface. On the other hand not much of the volume can be located close to the corners: Consider the corner [math]e=(e_1,\dots,e_d)[/math] with [math]e_i\in\{1,-1\}[/math] of [math]H_d=[-1,1]^d[/math]. Then we consider

[[math]] E_{e}:=\{x\in\mathbb{R}^d\:;\: x_i\in[1-\epsilon,1] \text{ if } e_i=1 \text{ and } x_i\in[-1,-1+\epsilon] \text{ if } e_i=-1 \} [[/math]]

that is a cube with side length [math]\epsilon[/math] sitting in the [math]e[/math]-th corner of [math]H_d[/math] \begin{center}

\nopagebreak[4]

\begin{fig}[math]E_{(1,1)}\subseteq H_d[/math] for [math]d=2[/math].\end{fig} \end{center} and observe that [math]\lambda^d(E_e)=\epsilon^d[/math]. We put [math]0 \lt \epsilon \lt 1/2[/math] and since there are [math]2^d[/math] corners [math]e[/math] in [math]H_d[/math], we get that the volume in all the corners

[[math]] 2^d\cdot \epsilon^d =(2\epsilon)^d\xrightarrow{d\rightarrow\infty}0 [[/math]]

tends to zero. So we may think of the volume of [math]H_d[/math] being located close below the surface and around the middle points of the faces. The following pictures summarize the three different ways to look at the hypercube in high dimensions. We advise the reader however to be careful as all three pictures show of course a 2-dimensional cube and are only meant to visualize different effects that take place in high dimensions. \begin{center} \begin{picture}(350,110)(0,0)

\put(20,45){

}

\put(10,20.5){\begin{minipage}{90pt}\scriptsize The hypercube is compact and convex. \end{minipage}}

\put(136,42){

}

\put(122,10){\begin{minipage}{105pt}\scriptsize Distances between corners grow with the dimension, while distances between fa\-ces remain constant. \end{minipage}}

\put(263,45){

File:Tikz4e65d727.png

}

\put(250,15.5){\begin{minipage}{100pt}\scriptsize The volume concentrates at the surface and in the middle of the faces. \end{minipage}} \end{picture}\nopagebreak[4] \begin{fig}Three ways to think of the high-dimensional\vspace{-3pt}\\hypercube in terms of geometry and topology, metric and measure.\end{fig} \end{center} If we intepret the last of our above findings in terms of a random variable [math]X\sim\mathcal{U}(H_d)[/math], then it means that [math]X[/math] attains with high probability values close to the surface and close to the middle of the faces. Conversely, this means that every method that draws random points from the hypercube will neglect its corners and its interior. So if we for example are given a data set inside [math]H_d[/math] and want to compute a predictor function [math]H_d\rightarrow\mathbb{R}[/math] then we need a a very large sample to do so. Indeed, the volume of [math]H_d[/math] grows exponentially in [math]d[/math] so if we, e.g., want to partition [math]H_d[/math] into smaller cubes with fixed volume we will need exponentially many such cubes. Furthermore, if we knew that our data is uniformly distributed then all the data will gather together at the regions indicated above. If we now sample for instance two points then the odds that they are each close to the middle of different (and not opposite) faces are high. The right picture above suggests that we may expect that the angle between any two randomly chosen points will be approximately [math]90^{\circ}[/math]. Experiments suggest moreover, that the distance of two points chosen at random is close to [math]\sqrt{\scalebox{0.8}{[/math]\frac32[math]}d}[/math].

\smallskip The above effect is commonly referred to as the curse of high dimensions. Indeed, classical data analysis methods relying, e.g., on [math]k[/math]-nearest neighbor search, or cosine similarity, can apparently not anymore be applied effectively, if all mutual distances and angles between data points coincide! We will see below that this effect is not restricted to the hypercube, but appears also for the unit ball [math]\Bbar_1(0)[/math] and on the whole space [math]\mathbb{R}^d[/math] which we will study now.

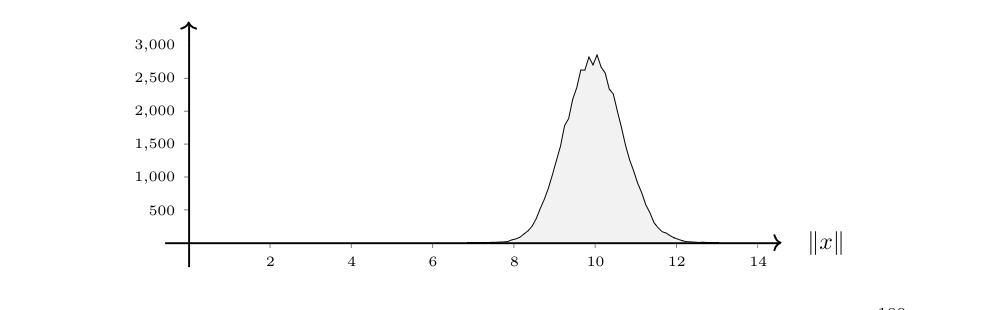
\medskip For this, let us consider points drawn at random from [math]\mathbb{R}^d[/math] with respect to a Gaussian distribution with mean zero and variance one. As we mentioned in Definition(ii), the latter formalizes as a random vector [math]X\colon\Omega\rightarrow\mathbb{R}^d[/math] whose coordinates are independent normal random variables. Therefore it is very easy (see Problem) to generate such random points in a simulation and compute angles and norms. If we do so, we detect an effect similar to what we just above observed for the hypercube. We get that the norms of all random points in dimension 100 are close to 10.

\begin{center}

\nopagebreak[4]

\begin{fig}\label{FIG-1}Distributions of the norm of 50\,000 random points [math]x\sim\mathcal{N}(0,1,\mathbb{R}^{100})[/math].\end{fig} \end{center} If we run the experiment for different dimensions [math]d[/math] and each time compute the average over the norms then we see that the latter turn out to be close to [math]\sqrt{d}[/math]. Moreover, we see that the variances seem to be bounded by a constant independent of the dimension.

\begin{center} \begin{tabular}{crrrrrrrrrr} \toprule [math]d[/math] & 1 & 10 & 100 & 1\,000 & 10\,000 & 100\,000 & 1\,000\,000 \\ \midrule [math]\frac{1}{n}{\displaystyle\Bigsum{i=1}{n}}\|x^{\scriptscriptstyle(i)}\|[/math] & 0.73 & 3.05 & 10.10 & 31.61 & 100.03 & 316.21 & 1000.03 \\ [math]\sqrt{d}[/math] & 1.00 & 3.16 & 10.00 & 31.62 & 100.00 & 316.22 & 1000.00 \\ Variance & 0.33 & 0.48 & 0.54 & 0.45 & 0.52 & 0.36 & 0.44 \\ \bottomrule \end{tabular}\nopagebreak[4] \begin{tab}\label{TAB-1}Average norms of [math]n=100[/math] random points [math]x^{\scriptscriptstyle(i)}\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math].\end{tab} \end{center} We leave it as Problem to carry out the experiments and replicate Figure and Table. From the theoretical point of view, if we use that [math]X\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math] has independent coordinates [math]X_i\sim\mathcal{N}(0,1)[/math] for [math]i=1,\dots,d[/math], we can compute expectations and variances directly. Since we do not know a priori how the root function interacts with the expectation, we start considering the norm squared. We then get

[[math]] \begin{equation}\label{EXP-NORM-SQUARED} \begin{array}{rl} \E(\|X\|^2) &= \E\bigl(X_1^2+\cdots+X_d^2\bigr) = \E(X_1^2)+\cdots+\E(X_d^2)\\ &= \E\bigl((X_1-\E(X_1))^2\bigr)+\cdots+\E\bigl((X_d-\E(X_d))^2\bigr)\\ &= \V(X_1)+\cdots+\V(X_d)= d \end{array} \end{equation} [[/math]]

which corroborates that [math]\E(\|X\|)[/math] should be close to [math]\sqrt{d}[/math] for large [math]d[/math]. Also, the variance of the norm squared can be computed directly, namely via

[[math]] \begin{equation}\label{VAR-NORM-SQUARED} \begin{array}{rl} \V(\|X\|^2) &=\V(X_1^2)+\cdots+\V(V_d^2) = d\cdot\V(X_1^2)=d\cdot\bigl(\E(X_1^4)-\E(X_1^2)^2\bigr)\\ & =d\cdot\bigl(\medfrac{1}{\sqrt{2\pi}}{\displaystyle\int_{\mathbb{R}}}x^4\exp(-x^2/2)\dd x-\V(X_1)\bigr)\\ &= (3-1)d= 2d. \end{array} \end{equation} [[/math]]

Without the square we get the following result which confirms and quantifies the picture that we got in the experiments, namely that Gaussian random vectors will have norm close to [math]\sqrt{d}[/math] and that their distribution does not spread out if [math]d[/math] increases.

Theorem

(i) We start with the following equality

[[math]] \|X\|-\sqrt{d} = \medfrac{\|X\|^2-d}{2\sqrt{d}}-\medfrac{(\|X\|^2-d)^2}{2\sqrt{d}(\|X\|+\sqrt{d})^2}=:S_d-R_d [[/math]]

which follows from [math]\|X\|^2-d=(\|X\|-\sqrt{d})(\|X\|+\sqrt{d})[/math]. Next we use \eqref{VAR-NORM-SQUARED} and [math]\|X\|\geqslant0[/math] to estimate

[[math]] 0\leqslant \E(R_d) \leqslant \medfrac{\E((\|X\|^2-d)^2)}{2d^{3/2}}=\medfrac{\V(\|X\|^2)}{2d^{3/2}}=\medfrac{2d}{2d^{3/2}}=\medfrac{1}{\sqrt{d}} [[/math]]

which shows that [math]\E(R_d)\rightarrow0[/math] for [math]d\rightarrow\infty[/math]. As [math]\E(\|X\|^2)=d[/math] we have [math]\E(S_n)=0[/math] and thus we get

[[math]] |\E(\|X\|-\sqrt{d})|=|\E(S_d-R_d)|=|-\E(R_d)|\leqslant\medfrac{1}{\sqrt{d}} [[/math]]

as claimed. \smallskip (ii) For the variance we obtain

[[math]] \begin{align*} \V(\|X\|) &= \V(\|X\|-\sqrt{d}) = \E\bigl((\|X\|-\sqrt{d})^2\bigr) - \bigl(\E(\|X\|-\sqrt{d})\bigr)^2\\ &\leqslant \E\bigl((\|X\|-\sqrt{d})^2\bigr)= \E\bigl(\|X\|^2 - 2\|X\|\sqrt{d} + d\bigr)\\ & = \E(\|X\|^2) - 2\sqrt{d}\E(\|X\|) +d= 2d -2\sqrt{d}\E\bigl(\|X\| -\sqrt{d} +\sqrt{d}\bigr)\\ & = 2\sqrt{d}\E(R_d) \leqslant 2 \end{align*} [[/math]]

which establishes (ii).

Show Proof

{{{4}}}

■

Let us now consider the mutual distance between two independent random vectors [math]X,Y\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math]. For the squared distance we can compute directly

[[math]] \begin{align*} \E(\|X-Y\|^2) & = \Bigsum{i=1}d\E\bigl((X_i-Y_i)^2\bigr)\\ &= \Bigsum{i=1}d \E(X_i^2)+2\E(X_i)\E(Y_i)+\E(Y_i^2)\\ & = \Bigsum{i=1}d (1+2\cdot0\cdot0+1) = 2d \end{align*} [[/math]]

which suggests that [math]\|X-Y\|[/math] will be close to [math]\sqrt{2d}[/math]. This is again underpinned by experiments, see Table, and we leave it as Problem to repeat the experiments. \begin{center} \begin{tabular}{crrrrrrrrr} \toprule [math]d[/math] & 1 & 10 & 100 & 1\,000 & 10\,000 & 100\,000 \\ \midrule [math]\frac{1}{n(n-1)}{\displaystyle\Bigsum{i\not=j}{}}\|x^{\scriptscriptstyle(i)}-x^{\scriptscriptstyle(j)}\|[/math] & 1.06 & 4.41 & 14.05 & 44.65 & 141.50 & 447.35 \\ [math]\sqrt{2d}[/math] & 1.41 & 4.47 & 14.14 & 44.72 & 141.42 & 447.21 \\ Variance & 0.74 & 1.10 & 0.92 & 0.89 & 0.96 & 1.08 \\ \bottomrule \end{tabular}\nopagebreak[4] \begin{tab}\label{TAB-3x}Average pairwise distances of [math]n=100[/math] random points [math]x^{\scriptscriptstyle(i)}\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math].\end{tab} \end{center} We leave it as Problem to adapt our proof of Theorem to establish the following result on the distances without square.

Theorem

This can be proved exactly as Theorem.

Show Proof

{{{4}}}

■

To see what is happening to the angles of random points we can now make use of the fact that we know already that [math]\E(\|X\|^2)=\E(\|Y\|^2)=d[/math] and [math]\E(\|X-Y\|^2)=2d[/math] holds. From this we get the next result.

Theorem

{{{3}}}

Show Proof

{{{4}}}

■

Also the statements of Theorem can be underpinned by experiments, see Table and Problem.

\begin{center} \begin{tabular}{crrrrrrrrrr} \toprule [math]d[/math] & 1 & 10 & 100 & 1\,000 & 10\,000 & 100\,000 \\ \midrule [math]\frac{1}{n(n-1)}{\displaystyle\Bigsum{i\not=j}{\phantom{n}}}\langle{}x^{\scriptscriptstyle(i)},x^{\scriptscriptstyle(j)}\rangle[/math] & -0.01 & 0.05 & -0.20 & 0.69 & 0.91 & 4.07 \\ Variance & 0.76 & 9.83 & 107.23 & 1\,022.83 & 9\,798.55 & 101\,435.71 \\ \bottomrule \end{tabular} \begin{tab}\label{TAB-3}Average scalar product of [math]n=100[/math] random points [math]x^{\scriptscriptstyle(i)}\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math].\end{tab} \end{center} The above means that the distribution of the scalar products spreads out for large [math]d[/math]. If we however consider the normalized scalar products [math]\langle{}\frac{x}{\|x\|},\frac{y}{\|y\|}\rangle{}[/math], then the experiments suggest that average and variance tend to zero as [math]d\rightarrow\infty[/math], see Problem. \medskip Working with the expectation describes what happens ‘in average’ and the variance allows to judge roughly the error we make if we reduce to considering the expectation. In the sequel we will, instead of working with expectation and variance, present explicit estimates for [math]\P\bigl[\bigl|\|X\|-\sqrt{d}\bigr|\geqslant\epsilon\bigr][/math] and [math]\P\bigl[\bigl|\langle{}X,Y\rangle{}\bigr|\geqslant\epsilon\bigr][/math] whenever [math]X,Y\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math]. Moreover, we will get similar results for [math]X,Y\sim\mathcal{U}(\B_1(0))[/math] and establish the following table \begin{center} \begin{tabular}{clll}

      \toprule
      \phantom{i}Distribution \phantom{x}& [math]\|X\|[/math] & [math]\|X-Y\|[/math] & [math]\langle X,Y\rangle[/math] \\
      \midrule
      [math]X,Y\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math]\phantom{x} &\phantom{[math]\sum^{T^T}[/math]}[math]\hspace{-5pt}\approx\sqrt{d}[/math] & \phantom{[math]\sum^{T^{T^T}}[/math]}[math]\approx\sqrt{2d}[/math]& \phantom{[math]\sum^{T^{T^T}}[/math]}[math]\approx0[/math]\\
      [math]X,Y\sim\mathcal{U}(\operatorname{B}_1(0))[/math]\phantom{x} &\phantom{[math]\sum^{T^{T^T}}[/math]}\hspace{-6pt}[math]\approx1[/math] & \phantom{[math]\sum^{T^{T^T}}[/math]}[math]\approx\sqrt{2}[/math]& \phantom{[math]\sum^{T^{T^T}}[/math]}[math]\approx0[/math]\\
      \bottomrule
      \end{tabular}\begin{tab}Values of norm and scalar product that will be\vspace{-3pt}\\attained in high dimensions ‘with high probability.’\end{tab}
      \end{center}

in which we mean, e.g., by [math]\|X\|\approx\sqrt{d}[/math], that the probability that [math]\|X\|-\sqrt{d}[/math] is larger than some threshold can be estimated by an expression that is small if the dimension is large enough. In the ideal case the threshold is a constant [math]\epsilon \gt 0[/math] that we can choose arbitrarily and the bound for the probability depends only on [math]d[/math]. We will see however that sometimes both expressions depend on [math]\epsilon[/math] and [math]d[/math]. In these cases we have to be careful when we want to consider [math]\epsilon\rightarrow0[/math] or [math]d\rightarrow\infty[/math]. Avoiding limits in this context\,---\,sometimes referred to as ‘non-asymptotic analysis’\,---\,will lead to theorems that guarantee that for almost all points of a data set [math]A[/math], e.g., more than [math](1-1/n)[/math]--fraction of them, some property holds, or that for every point of the data set a property holds with high probability, e.g., greater or equal to [math]1-1/n[/math]. Here, [math]n[/math] can for example depend on [math]\#A[/math] or on [math]d[/math].

\section*{Problems}

General references

Wegner, Sven-Ake (2024). "Lecture Notes on High-Dimensional Data". arXiv:2101.05841 [math.FA].