Taylor Series

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

Taylor Series.

The subject of Section 7 was the function defined by a given power series. In contrast, in this section we start with a given function and ask whether or not there exists a power series which defines it. More precisely, if [math]f[/math] is a function containing the number [math]a[/math] in its domain, then does there exist a power series [math]\sum_{i=0}^\infty a_i (x - a)^i[/math] with nonzero radius of convergence which defines a function equal to [math]f[/math] on the interval of convergence of the power series? If the answer is yes, then the power series is uniquely determined. Specifically, it follows from Theorem (7.4), page 526, that [math]a_i = \frac{1}{i!} f^{(i)}(a)[/math], for every integer [math]i \geq 0[/math]. Hence

[[math]] \begin{eqnarray*} f(x) &=& \sum_{i=0}^\infty \frac{1}{i!} f^{(i)}(a)(x - a)^i \\ &=& f(a) + f'(a)(x - a) + \frac{1}{2!} f''(a)(x - a)^2 + \cdots, \end{eqnarray*} [[/math]]

for every [math]x[/math] in the interval of convergence of the power series. Let [math]f[/math] be a function which has derivatives of every order at [math]a[/math]. The power series [math]\sum_{i=0}^\infty \frac{1}{i!} f^{(i)}(a)(x - a)^i[/math] is called the Taylor series of the function [math]f[/math] about the number [math]a[/math]. The existence of this series, whose definition is motivated by the preceding paragraph, requires only the existence of every derivative [math]f^{(i)}(a)[/math]. However, the natural inference that the existence of the Taylor series for a given function implies the convergence of the series to the values of the function is false. In a later theorem we shall give an additional condition which makes the inference true. Two examples of Taylor series are the series for [math]e^x[/math] and the series for [math]\ln(1 + x)[/math] developed in Example 1 of Section 7. The value of a convergent infinite series can be approximated by its partial sums. For a Taylor series [math]\sum_{i=0}^\infty \frac{1}{i!} f^{(i)}(a)(x-a)^i[/math], the nth partial sum is a polynomial in [math](x-a)[/math], which we shall denote by [math]T_n[/math]. The definition is as follows: Let [math]n[/math] be a nonnegative integer and [math]f[/math] a function such that [math]f^{(i)}(a)[/math] exists for every integer [math]i = 0, . . ., n[/math]. Then the [math]n[/math]th Taylor approximation to the function [math]f[/math] about the number [math]a[/math] is the polynomial [math]T_n[/math] given by

[[math]] \begin{equation} \begin{array}{ll} T_n(x) &= \sum_{i=0}^n \frac{1}{i!} f^{(i)}(a)(x-a)^i \\ &= f(a) + f'(a)(x-a) + \cdots + \frac{1}{n!} f^{(n)}(a)(x-a)^n , \end{array} \label{eq9.8.1} \end{equation} [[/math]]

for every real number [math]x[/math]. For each integer [math]k = 0, . . ., n[/math], direct computation of the [math]k[/math]th derivative at [math]a[/math] of the Taylor polynomial [math]T_n[/math] shows that it is equal to [math]f^{(k)}(a)[/math]. Thus we have the simple but important result:

Theorem

The [math]n[/math]th Taylor approximation [math]T_n[/math] to the function [math]f[/math] about a satisfies

[[math]] T_n^{(k)}(a) = f^{(k)}(a), \;\;\;\mathrm{for each}\; k = 0, . . ., n. [[/math]]

Example

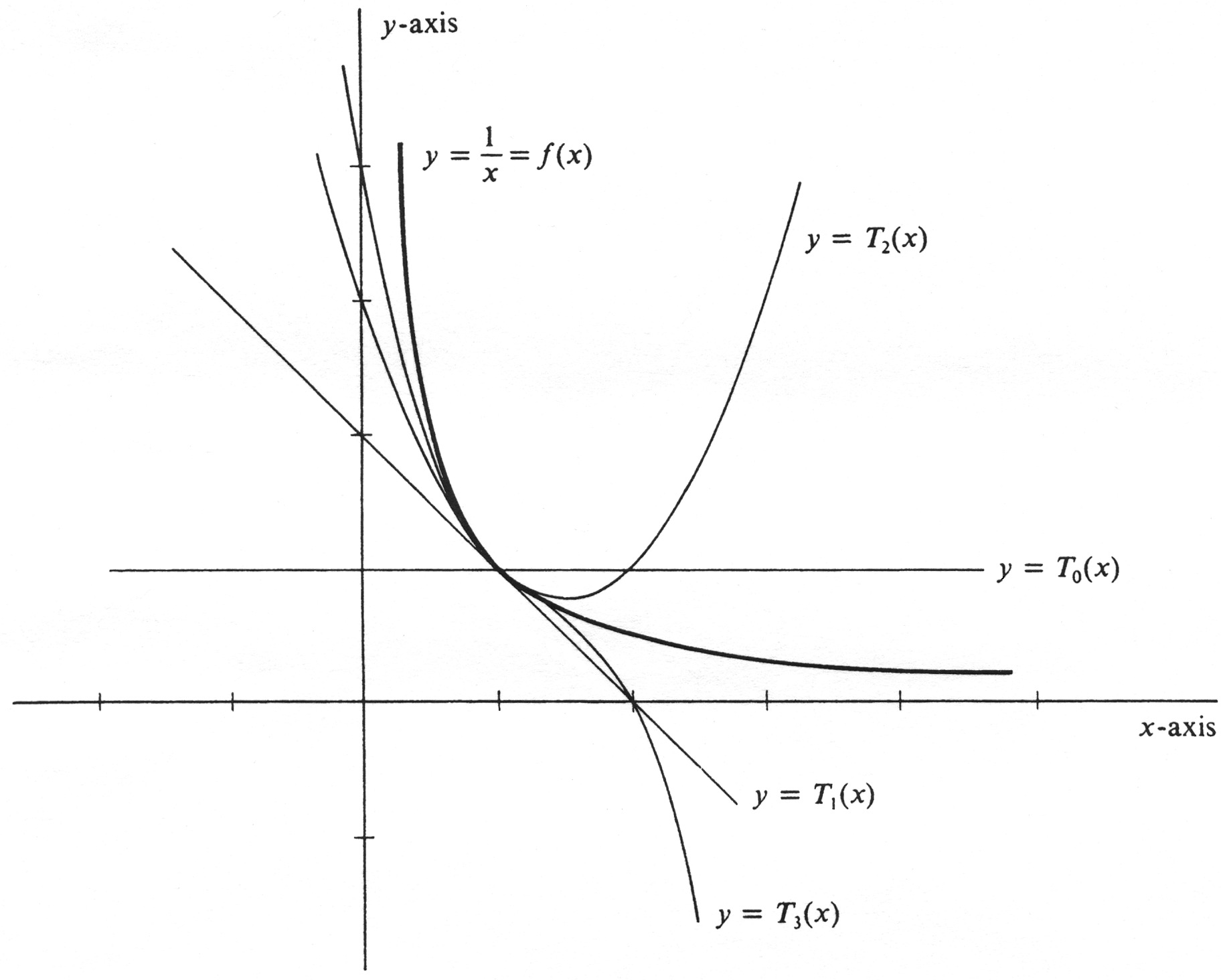
Let [math]f[/math] be the function defined by [math]f(x) = \frac{1}{x}[/math]. For [math]n[/math] = 0, 1, 2, and 3, compute the Taylor polynomial [math]T_n[/math] for the function [math]f[/math] about the number 1, and superimpose the graph of each on the graph of [math]f[/math]. The derivatives are:

[[math]] \begin{eqnarray*} f (x) &=& -\frac{1}{x^2}, \;\;\;\mbox{whence}\; f'(1) = -1, \\ f' (x) &=& \frac{2}{x^3}, \;\;\;\;\;\mbox{whence}\; f''(1)= 2, \\ f''' (x) &=& -\frac{6}{x^4} \;\;\;\;\mbox{whence}\; f'''(1) = - 6. \end{eqnarray*} [[/math]]

From the definition in (1), we therefore obtain

[[math]] \begin{eqnarray*} T_0(x) &=& f(1) = 1, \\ T_1(x) &=& 1 - (x - 1), \\ T_2(x) &=& 1 - (x - 1) + (x - 1)^2, \\ T_3(x) &=& 1 - (x - 1) + (x - 1)^2 - (x - 1)^3. \end{eqnarray*} [[/math]]

These equations express the functions [math]T_n[/math] as polynomials in [math]x - 1[/math] rather than as polynomials in [math]x[/math]. The advantage of this form is that it exhibits most clearly the behavior of each approximation in the vicinity of the number 1. Each one can, of course, be expanded to get a polynomial in [math]x[/math]. If we do this, we obtain

[[math]] \begin{eqnarray*} T_0(x) &=& 1, \\ T_1(x) &=& -x + 2, \\ T_2(x) &=& x^2 - 3x + 3,\\ T_3(x) &=& -x^3 + 4x^2 - 6x + 4. \end{eqnarray*} [[/math]]

The graphs are shown in Figure 10. The larger the degree of the approximating polynomial, the more closely its graph “hugs” the graph of [math]f[/math] for values of [math]x[/math] close to 1.

File:Guide c5467 scanfig9 10.png

The basic relation between a function [math]f[/math] and the approximating Taylor polynomials [math]T_n[/math] will be presented in Theorem (8.3). In proving it, we shall use the following lemma, which is an extension of Rolle's Theorem (see pages 111 ancl 112).

Theorem

Let [math]F[/math] be a function with the property that the [math](n + 1)[/math]st derivative [math]F^{(n+1)}(t)[/math] exists for every [math]t[/math] in a closed interval [math][a, b][/math], where [math]a \lt b[/math]. If

\item[i]] [math]F^{i}(a) = 0, \;\;\;\mathrm{for}\; i = 0, 1, . . ., n, \;\mathrm{and} [/math] \item[(ii)] [math]F(b)= 0,[/math]

then there exists [math]a[/math] real number [math]c[/math] in the open interval [math](a, b)[/math] such that [math]F^{(n+1)}(c) = 0[/math].

Show Proof

The idea of the proof is to apply Rolle's Theorem over and over again, starting with [math]i = 0[/math] and finishing with [math]i = n[/math]. (In checking the continuity requirements of Rolle's Theorem, remember that if a function has a derivative at a point, then it is continuous there.) A proof by induction on [math]n[/math] proceeds as follows: If [math]n = 0[/math], the result is a direct consequence of Rolle's Theorem. We must next prove from the assumption that if the lemma is true for [math]n = k[/math], then it is also true for [math]n = k + 1[/math]. Thus we assume that there exists a real number [math]c[/math] in the open interval [math](a, b)[/math] such that [math]F^{(k+1)}(c) = 0[/math] and shall prove that there exists another real number [math]c'[/math] in [math](a, b)[/math] such that [math]F^{(k+2)}(c') = 0[/math]. The hypotheses of (8.2) with [math]n = k + 1[/math] assure us that [math]F^{(k+2)}(t)[/math] exists for every [math]t[/math] in [math][a, b][/math] and that [math]F^{(k+1)}(a) = 0[/math]. The function [math]F^{(k +1)}[/math] satisfies the premises of Rolle's Theorem, since it is continuous on [math][a, c][/math], differentiable on [math](a, c)[/math], and [math]F^{(k+1)}(a) = F^{(k+1)}(c) = 0[/math]. Hence there exists a real number [math]c'[/math] in [math](a, c)[/math] with the property that [math]F^{(k+2)}(c') = 0[/math]. Since [math](a, c)[/math] is a subset of [math](a, b)[/math], the number [math]c'[/math] is also in [math](a, b)[/math], and this completes the proof.

■

We come now to the main theorem of the section:

TAYLOR'S THEOREM

Let [math]f[/math] be a function wifh the property that the [math](n + 1)[/math]st derivative [math]f^{(n+1)}(t)[/math] exists for every [math]t[/math] in the closed interval [math][a, b][/math], where [math]a \lt b[/math]. Then there exists a real number [math]c[/math] in the open interval [math](a, b)[/math] such that

[[math]] f(b) = \sum_{i=0}^n \frac{1}{i!} f^{(i)}(a)(b - a)^i + R_n, [[/math]]

where

[[math]] R_n = \frac{1}{(n +1)!} f^{(n+1)}(c)(b - a)^{n+1} . [[/math]]

Using the approximating Taylor polynomials, we can write the conclusion of this theorem equivalently as

[[math]] \begin{equation} f(b) = T_n(b) + \frac{1}{(n + 1)!} f^{(n+1)}(c)(b-a)^{n+1} . \label{eq9.8.2} \end{equation} [[/math]]

Note that the particular value of [math]c[/math] depends not only on the function [math]f[/math] and the numbers [math]a[/math] and [math]b[/math] but also on the integer [math]n[/math].

Show Proof

Let the real number [math]K[/math] be defined by the equation

[[math]] f(b) = T_n(b) + K(b - a)^{n+1}. [[/math]]

The proof of Taylor's Theorem is completed by showing that

[[math]] K = \frac{1}{(n + 1)!} f^{(n+1)}(c), [[/math]]

for some real number [math]c[/math] in [math](a, b)[/math]. For this purpose, we define a new function [math]F[/math] by setting

[[math]] F(t) = f(t) - T_n(t) - K(t - a)^{n+1}, [[/math]]

for every [math]t[/math] in [math][a, b][/math]. From the equation which defines [math]K[/math] it follows at once that

[[math]] f (b) - T_n(b) - K(b - a)^{n+1} = 0, [[/math]]

and hence that [math]F(b) = 0[/math]. In computing the derivatives of the function [math]F[/math], we observe that any derivative of [math]K(t-a)^{n+1}[/math] of order less than [math]n + 1[/math] will contain a factor of [math]t - a[/math], and therefore

[[math]] \frac{d^i}{dt^i} K(t-a)^{n+1}|_{t=a} = 0, \;\;\;\mbox{for}\; i = 0, ... , n. [[/math]]

Since [math]f^{i}(a) = T_n^{(i)}(a)[/math], for every integer [math]i = 0, . . ., n[/math], [see (8.1)], we conclude that

[[math]] F^{i} (a) = f^{i}(a) - T_n^{(i)}(a) - 0 = 0, \;\;\; i = 0,...,n. [[/math]]

Hence, by Lemma (8.2), there exists a real number [math]c[/math] in [math](a, b)[/math] such that

[[math]] F^{(n+1)} (c) = 0. [[/math]]

Finally, we compute [math]F^{(n+1)}(t)[/math] for an arbitrary [math]t[/math] in [math][a, b][/math]. Since the degree of the polynomial [math]T_n[/math] is at most [math]n[/math], its [math](n + 1)[/math]st derivative must be zero. Moreover, the [math](n + 1)[/math]st derivative of [math]K(t - a)^{n+1}[/math] is equal to [math](n + 1)!K[/math]. Hence

[[math]] F^{(n+1)}(t) = f^{(n+1)} (t) - (n + 1)! K. [[/math]]

Letting [math]t = c[/math], we obtain

[[math]] 0 = F^{(n+1)}(c) = f^{(n+1)} (c) - (n + 1)! K, [[/math]]

from which it follows that [math]K = \frac{1}{(n+1)!} f^{(n+1)}(c)[/math]. This completes the proof.

■

It has been assumed in the statement and proof of Taylor's Theorem that [math]a \lt b[/math]. However, if [math]b \lt a[/math], the same statement is true except that the [math](n + 1)[/math]st derivative exists in [math][b, a][/math] and the number [math]c[/math] lies in [math](b, a)[/math]. Except for the obvious modifications, the proof is identical to the one given. Suppose now that we are given a function [math]f[/math] such that [math]f^{(n+1)}[/math] exists at every point of some interval [math]I[/math] containing the number [math]a[/math]. Since Taylor's Theorem holds for any choice of [math]b[/math] in [math]I[/math] other than [math]a[/math], we may regard [math]b[/math] as the value of a variable. If we denote the variable by [math]x[/math], we have:

ALTERNATIVE FORM OF TAYLOR'S THEOREM

If [math]f^{(n+1)}(t)[/math] exists for every [math]t[/math] in an interval [math]I[/math] containing the number [math]a[/math], then, for every [math]x[/math] in [math]I[/math] other than [math]a[/math], there exists a real number [math]c[/math] in the open interval with endpoints [math]a[/math] and [math]x[/math] such that

[[math]] f(x) = f(a) + f'(a)(x-a) + \cdots + \frac{1}{n!} f^{(n)}(a)(x-a)^n + R_n, [[/math]]

where

[[math]] R_n = \frac{1}{(n+1)!} f^{(n+1)} (c) (x - a)^{n+1} . [[/math]]

The conclusion of this theorem is frequently called Taylor's Formula and [math]R_n[/math] is called the Remainder. As before, using the notation for the approximating Taylor polynomials, we can write the formula succinctly as

[[math]] \begin{equation} f(x) = T_n(x) + R_n . \label{eq9.8.3} \end{equation} [[/math]]

Example

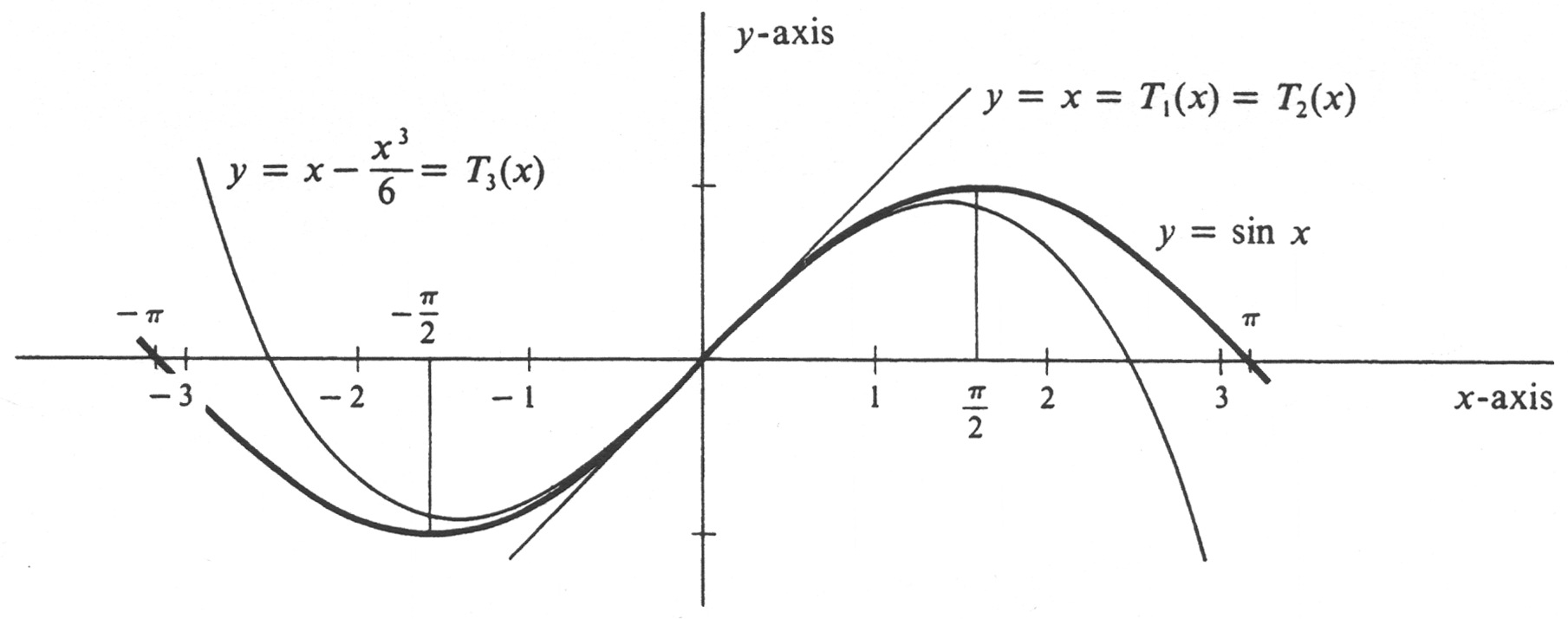
(a) Compute Taylor's Formula with the Remainder where [math]f(x) = \sin x, a = 0[/math], and [math]n[/math] is arbitrary. (b) Draw the graphs of [math]\sin x[/math] and of the polynomials [math]T_n(x)[/math], for [math]n[/math] = 1, 2, and 3. (c) Prove that, for every real number [math]x[/math],

[[math]] \sin x = \sum_{i=1}^\infty (-1)^{i-1} \frac{x^{2i-1}}{(2i - 1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots . [[/math]]

The first four derivatives are given by

[[math]] \begin{eqnarray*} \frac{d}{dx} \sin x &=& \cos x, \\ \frac{d^2}{dx^2} \sin x &=& -\sin x, \\ \frac{d^3}{dx^3} \sin x &=& -\cos x,\\ \frac{d^4}{dx^4} \sin x &=& \sin x. \end{eqnarray*} [[/math]]

Thus the derivatives of [math]\sin x[/math] follow a regular cycle which repeats after every fourth derivation. In general, the even-order derivatives are given by

[[math]] \frac{d^{2i}}{dx^{2i}} \sin x = (-1)^i \sin x, \;\;\; i= 0, 1,2,\cdots , [[/math]]

and the odd-order derivatives by

[[math]] \frac{d^{2i-1}}{dx^{2i-1}} \sin x = (-1)^{i-1} \cos x, \;\;\; i = 1, 2, 3, \cdots . [[/math]]

If we set [math]f(x) = \sin x[/math], then

[[math]] \begin{array}{ll} f^{(2i)}(0) = (-1)^i \sin 0 = 0, & \;\;\; i = 0, 1, 2, .... \\ f^{(2i-1)}(0) = (-1)^{i-1} \cos 0 = (-1)^{i-1},& \;\;\; i = 1, 2, 3, .... \end{array} [[/math]]

Hence the [math]n[/math]th Taylor approximation is the polynomial

[[math]] T_n(x) = \sum_{i=0}^n \frac{1}{i!} f^{(i)} (0)x^i, [[/math]]

in which the coefficient of every even power of [math]x[/math] is zero. To handle this alternation, we define the integer [math]k[/math] by the rule

[[math]] \begin{equation} k = \left \{ \begin{array}{ll} \frac{n}{2}, \;\;\; &\mathrm{if}~n~\mathrm{is~even,} \\ \frac{n + 1}{2}, \;\;\; &\mathrm{if}~n~\mathrm{is~odd.} \end{array} \right . \label{eq9.8.4} \end{equation} [[/math]]

It then follows that

[[math]] \begin{equation} T_n(x) = \sum_{i=1}^k \frac{1}{(2i -1)!} (-1)^{i - 1} x^{2i - 1} = \sum_{i=1}^k (-1)^{i- 1} \frac{x^{2i - 1}}{(2i - 1)!} . \label{eq9.8.5} \end{equation} [[/math]]

[If [math]n = 0[/math], we have the exception [math]T_0(x) = 0[/math].] For the remainder, we obtain

[[math]] \begin{equation} \begin{array}{ll} R_n &= \frac{1}{(n+1)!} f^{(n + 1)} (c) x^{n+1} \\ &= \left \{ \begin{array}{ll} \frac{x^{n+1}}{(n+1)!} & (-1)^k \cos c, \;\;\;\mathrm{if}~n~\mathrm{is~even}, \\ \frac{x^{n+1}}{(n+1)!} & (-1)^k \sin c, \;\;\;\mathrm{if}~n~\mathrm{is~odd}, \end{array} \right . \end{array} \label{eq9.8.6} \end{equation} [[/math]]

for some real number [math]c[/math] (which depends on both [math]x[/math] and [math]n[/math]) such that [math]|c| \lt |x|[/math]. The Taylor formula for [math]\sin x[/math] about the number 0 is therefore given by

[[math]] \sin x = \sum_{i=1}^k (-1)^{i-1} \frac{x^{2i-1}}{(2i-1)!} + R_n , [[/math]]

where [math]k[/math] is defined by equation (4), and the remainder [math]R_n[/math] by (6). For part (b), the approximating polynomials [math]T_1, T_2,[/math] and [math]T_3[/math] can be read directly from equation (5) [together with (4)]. We obtain

[[math]] \begin{eqnarray*} T_1(x) &=& x, \\ T_2(x) &=& x, \\ T_3(x) &=& x - \frac{x^3}{3!} = x - \frac{x^3}{6} . \end{eqnarray*} [[/math]]

Their graphs together with the graph of [math]\sin x[/math] are shown in Figure 11.

File:Guide c5467 scanfig9 11.png

To prove that [math]\sin x[/math] can be defined by the infinite power series given in (c), we must show that, for every real number [math]x[/math],

[[math]] \begin{eqnarray*} \sin x &=& \lim_{n \rightarrow \infty} T_n(x) \\ &=& \lim_{k \rightarrow \infty} \sum_{i=1}^k (-1)^{i-1} \frac{x^{2i-1}}{(2i-1)!} , \end{eqnarray*} [[/math]]

where [math]k[/math] is the integer defined in (4). Since [math]\sin x = T_n(x) + R_n[/math], an equivalent proposition is

[[math]] \lim_{n \rightarrow \infty} R_n = 0 . [[/math]]

To prove the latter, we use the important fact that the absolute values of the functions sine and cosine are never greater than 1. Hence, in the expression for [math]R_n[/math] in (6), we know that [math]|\cos c| \leq 1[/math] and [math]|\sin c| \leq 1[/math]. It therefore follows from (6) that

[[math]] |R_n| \leq \frac{|x|^{n+1}}{(n+1)!}. [[/math]]

It is easy to show by the Ratio Test [see Problem 4(b), page 510] that [math]\lim_{n \rightarrow \infty} \frac{|x|^{n+1}}{(n+1)!} = 0[/math]. Hence [math]\lim_{n \rightarrow \infty} R_n = 0[/math], and we have proved that

[[math]] \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots . [[/math]]

The form of the remainder in Taylor's Theorem provides one answer to the question posed at the beginning of the section, which, briefly stated, was: When can a given function be defined by a power series? The answer provided in the following theorem is obtained by a direct generalization of the method used to establish the convergence of the Taylor series for [math]\sin x[/math].

Theorem

Let [math]f[/math] be a function which has derivatives of every order at every point of an interval [math]I[/math] containing the number [math]a[/math]. If the derivatives are uniformly bounded on [math]I[/math], i.e., if there exists a real number [math]B[/math] such that [math]|f^{(n)}(t)| \leq B[/math], for every integer [math]n \geq 0[/math] and every [math]t[/math] in [math]I[/math], then

[[math]] f(x) = \sum_{i=0}^\infty \frac{1}{i!} f^{(i)}(a)(x - a)^i, [[/math]]

for every real number [math]x[/math] in [math]I[/math].

Show Proof

Since [math]f(x) = T_n(x) + R_n[/math] [see Theorem (8.4) and formula (3)], we must prove that [math]f(x) = \lim_{n \rightarrow \infty} T_n(x)[/math], or, equivalently, that [math]\lim_{n \rightarrow \infty} R_n = 0[/math]. Generally speaking, the number [math]c[/math] which appears in the expression for the remainder [math]R_n[/math] will be different for each integer [math]n[/math] and each [math]x[/math] in [math]I[/math]. But since the number [math]B[/math] is a bound for the absolute values of all derivatives of [math]f[/math] everywhere in [math]I[/math], we have [math]|f^{(n+1)}(c)| \leq B[/math]. Hence

[[math]] \begin{eqnarray*} |R_n| &=& \Big|\frac{1}{(n+1)!} f^{(n+1)} (c) (x-a)^{n+1}\Big|\\ &=& \frac{|x - a|^{n+1}}{(n+1)!}|f^{(n+1)} (c)| \leq \frac{|x - a|^{n+1}}{(n+1)!} B. \end{eqnarray*} [[/math]]

However [see Problem 4(b), page 510],

[[math]] \lim_{n \rightarrow \infty} \frac{|x - a|^{n+1}}{(n+1)!} B = 0 \cdot B = 0, [[/math]]

from which it follows that [math]\lim_{n \rightarrow \infty} R_n = 0[/math]. This completes the proof.

■

It is an important fact, referred to at the beginning of the section, that the convergence of the Taylor series to the values of the function which defines it cannot be inferred from the existence of the derivatives alone. In Theorem (8.5), for example, we added the very strong hypothesis that all the derivatives of [math]f[/math] are uniformly bounded on [math]I[/math]. The following function defined by

[[math]] f(x)= \left \{ \begin{array}{ll} 0 & \;\;\;\mbox{if}\; x = 0 ,\\ e^{-1/x^2} & \;\;\;\mbox{if}\; x \neq 0 , \end{array} \right. [[/math]]

has the property that [math]f^n(x)[/math] exists for every integer [math]n \geq 0[/math] and every real number [math]x[/math]. Moreover, it can be shown that [math]f^n(0) = 0[/math], for every [math]n \geq 0[/math]. It follows that the Taylor series about 0 for this function is the trivial power series [math]\sum_{i=0}^\infty 0 \cdot x^i[/math]. This series converges to 0 for every real number [math]x[/math], and does not converge to [math]f(x)[/math], except for [math]x = 0[/math]. When a Taylor polynomial or series is computed about the number zero, as in Example 2, there is a tradition for associating with it the name of the mathematician Maclaurin instead of that of Taylor. Thus the Maclaurin series for a given function is a power series in [math]x[/math], and is simply the special case of the Taylor series in which [math]a = 0[/math]. Suppose that, for a given [math]n[/math], we replace the values of a function [math]f[/math] by those of the [math]n[/math]th Taylor approximation to the function about some number [math]a[/math]. How good is the resulting approximation? The answer depends on the interval (containing [math]a[/math]) over which we wish to use the values of the polynomial [math]T_n[/math]. Since [math]f(x) - T_n(x) = R_n[/math], the problem becomes one of finding a bound for [math]|R_n|[/math] over the interval in question.

Example

(a) Compute the first three terms of the Taylor series of the function [math]f(x) = (x +1)^{1/3}[/math] about [math]x = 7[/math]. That is, compute

[[math]] T_2(x) = f(7) + f'(7)(x-7) + \frac{1}{2!} f''(7)(x-7)^2 . [[/math]]

(b) Show that [math]T_2(x)[/math] approximates [math]f(x)[/math] to within [math]\frac{5}{3^4 \cdot 2^8} = 0.00024[/math] (approximately) for every [math]x[/math] in the interval [7, 8]. Taking derivatives, we get

[[math]] \begin{eqnarray*} f'(x) &=& \frac{1}{3} (x + 1)^{-2/3} = \frac{1}{3(x+1)^{2/3}}, \\ f''(x) &=& - \frac{2}{9}(x + 1)^{-5/3} = -\frac{2}{9(x+1)^{5/3}}, \\ f'''(x) &=& \frac{2 \cdot 5}{9 \cdot 3} (x + 1)^{-8/3} = \frac{2 \cdot 5}{3^3(x + 1 )^{8/3}} . \end{eqnarray*} [[/math]]

Hence

[[math]] \begin{eqnarray*} f(7) &=& 8^{1/3} = 2,\\ f'(7) &=& \frac{1}{3 \cdot 2^2} = \frac{1}{12},\\ f''(7) &=& -\frac{2}{9 \cdot 2^5} = - \frac{1}{3^2 \cdot 2^4} = - \frac{1}{144} , \end{eqnarray*} [[/math]]

and the polynomial approximation to [math]f(x)[/math] called for in (a) is therefore

[[math]] T_2(x) = 2 + \frac{1}{12}(x-7) - \frac{1}{288}(x - 7)^2 . [[/math]]

For part (b), we have [math]|f(x)-T_2(x)| = |R_2|[/math] and

[[math]] R_2 = \frac{1}{3!} f'''(c)(x-7)^3, [[/math]]

for some number [math]c[/math] which is between [math]x[/math] and 7. To obtain a bound for [math]|R_2|[/math] over the prescribed interval [7, 8], we observe that in that interval the maximum value of [math](x - 7)[/math] occurs when [math]x = 8[/math] and the maximum value of [math]|f'''|[/math] occurs when [math]x = 7[/math]. Hence

[[math]] |R_2| \leq \frac{1}{3!} If'''(7)| |8 - 7|^3 . [[/math]]

Since [math]f'''(7) = \frac{2 \cdot 5}{3^3 \cdot 2^8}[/math], we get

[[math]] |R_2| \leq \frac{1}{3 \cdot 2} \frac{2 \cdot 5}{3^3 \cdot 2^8} \cdot 1^3 = \frac{5}{3^4 \cdot 2^8} [[/math]]

Hence for every [math]x[/math] in the interval [7, 8], the difference in absolute value between [math](x + 1)^{1/3}[/math] and the quadratic polynomial [math]T_2(x)[/math] is less than 0.00025.

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.