Permutations

[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

Many problems in probability theory require that we count the number of ways that a particular event can occur. For this, we study the topics of permutations and combinations. We consider permutations in this section and combinations in the next section. Before discussing permutations, it is useful to introduce a general counting technique that will enable us to solve a variety of counting problems, including the problem of counting the number of possible permutations of [math]n[/math] objects.

Counting Problems

Consider an experiment that takes place in several stages and is such that the number of outcomes [math]m[/math] at the [math]n[/math]th stage is independent of the outcomes of the previous stages. The number [math]m[/math] may be different for different stages. We want to count the number of ways that the entire experiment can be carried out.

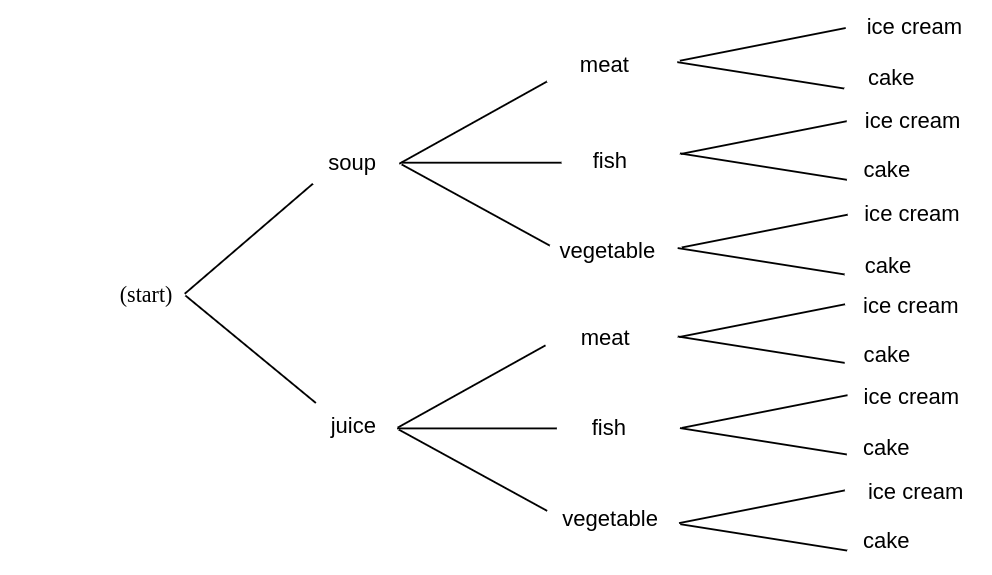
Example You are eating at Émile's restaurant and the waiter informs you that you have (a) two choices for appetizers: soup or juice; (b) three for the main course: a meat, fish, or vegetable dish; and (c) two for dessert: ice cream or cake. How many possible choices do you have for your complete meal? We illustrate the possible meals by a tree diagram shown in Figure. Your menu is decided in three stages---at each stage the number of possible choices does not depend on what is chosen in the previous stages: two choices at the first stage, three at the second, and two at the third. From the tree diagram we see that the total number of choices is the product of the number of choices at each stage. In this examples we have [math]2 \cdot 3 \cdot 2 = 12[/math] possible menus. Our menu example is an example of the following general counting technique.

Tree for your menu.

A Counting Technique

A task is to be carried out in a sequence of [math]r[/math] stages. There are [math]n_1[/math] ways to carry out the first stage; for each of these [math]n_1[/math] ways, there are [math]n_2[/math] ways to carry out the second stage; for each of these [math]n_2[/math] ways, there are [math]n_3[/math] ways to carry out the third stage, and so forth. Then the total number of ways in which the entire task can be accomplished is given by the product [math]N = n_1 \cdot n_2 \cdot \ldots \cdot n_r[/math].

Two-stage probability assignment.

Tree Diagrams

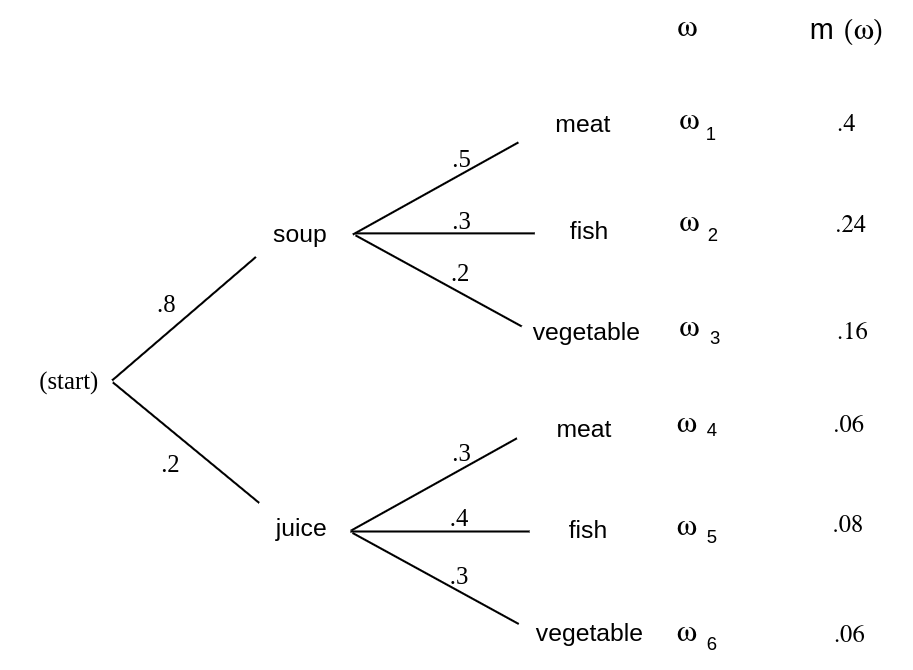
It will often be useful to use a tree diagram when studying probabilities of events relating to experiments that take place in stages and for which we are given the probabilities for the outcomes at each stage. For example, assume that the owner of \'Emile's restaurant has observed that 80 percent of his customers choose the soup for an appetizer and 20 percent choose juice. Of those who choose soup, 50 percent choose meat, 30 percent choose fish, and 20 percent choose the vegetable dish. Of those who choose juice for an appetizer, 30 percent choose meat, 40 percent choose fish, and 30 percent choose the vegetable dish. We can use this to estimate the probabilities at the first two stages as indicated on the tree diagram of Figure. We choose for our sample space the set [math]\Omega[/math] of all possible paths [math]\omega = \omega_1[/math], [math]\omega_2, \ldots, \omega_6[/math] through the tree. How should we assign our probability distribution? For example, what probability should we assign to the customer choosing soup and then the meat? If 8/10 of the customers choose soup and then 1/2 of these choose meat, a proportion [math]8/10 \cdot 1/2 = 4/10[/math] of the customers choose soup and then meat. This suggests choosing our probability distribution for each path through the tree to be the product of the probabilities at each of the stages along the path. This results in the probability distribution for the sample points [math]\omega[/math] indicated in Figure. (Note that [math]m(\omega_1) + \cdots + m(\omega_6) = 1[/math].) From this we see, for example, that the probability that a customer chooses meat is [math]m(\omega_1) + m(\omega_4) = .46[/math].

We shall say more about these tree measures when we discuss the concept of conditional probability in Chapter \ref{chp 4}. We return now to more counting problems. Example Columbus, Ohio, who have the same three initials. Assuming that each person has three initials, there are 26 possibilities for a person's first initial, 26 for the second, and 26 for the third. Therefore, there are [math]26^3 = 17,76[/math] possible sets of initials. This number is smaller than the number of people living in Columbus, Ohio; hence, there must be at least two people with the same three initials.

We consider next the celebrated birthday problem---often used to show that naive intuition cannot always be trusted in probability.

Birthday Problem

Example How many people do we need to have in a room to make it a favorable bet (probability of success greater than 1/2) that two people in the room will have the same birthday? Since there are 365 possible birthdays, it is tempting to guess that we would need about 1/2 this number, or 183. You would surely win this bet. In fact, the number required for a favorable bet is only 23. To show this, we find the probability [math]p_r[/math] that, in a room with [math]r[/math] people, there is no duplication of birthdays; we will have a favorable bet if this probability is less than one half. Assume that there are 365 possible birthdays for each person (we ignore leap years). Order the people from 1 to [math]r[/math]. For a sample point [math]\omega[/math], we choose a possible sequence of length [math]r[/math] of birthdays each chosen as one of the 365 possible dates. There are 365 possibilities for the first element of the sequence, and for each of these choices there are 365 for the second, and so forth, making [math]365^r[/math] possible sequences of birthdays. We must find the number of these sequences that have no duplication of birthdays. For such a sequence, we can choose any of the 365 days for the first element, then any of the remaining 364 for the second, 363 for the third, and so forth, until we make [math]r[/math] choices. For the [math]r[/math]th choice, there will be [math]365 - r + 1[/math] possibilities. Hence, the total number of sequences with no duplications is

[[math]] 365 \cdot 364 \cdot 363 \cdot \ldots \cdot (365 - r + 1)\ . [[/math]]

Thus, assuming that each sequence is equally likely,

[[math]] p_r = \frac{365 \cdot 364 \cdot \ldots \cdot (365 - r + 1)}{365^r}\ . [[/math]]

We denote the product

[[math]] (n)(n-1)\cdots (n - r +1) [[/math]]

by [math](n)_r[/math] (read “[math]n[/math] down [math]r[/math],” or “[math]n[/math] lower [math]r[/math]”). Thus,

[[math]] p_r = \frac{(365)_r}{(365)^r}\ . [[/math]]

The program Birthday carries out this computation and prints the probabilities for [math]r = 20[/math] to 25. Running this program, we get the results shown in Table

Birthday problem.

Number of people	Probability that all birthdays aredifferent
20	.5885616
21	.5563117
22	.5243047
23	.4927028
24	.4616557
25	.4313003

As we asserted above, the probability for no duplication changes from greater than one half to less than one half as we move from 22 to 23 people. To see how unlikely it is that we would lose our bet for larger numbers of people, we have run the program again, printing out values from [math]r = 10[/math] to [math]r = 100[/math] in steps of 10. We see that in a room of 40 people the odds already heavily favor a duplication, and in a room of 100 the odds are overwhelmingly in favor of a duplication.

Birthday problem.

Number of people	Probability that all birthdays aredifferent
10	.8830518
20	.5885616
30	.2936838
40	.1087682
50	.0296264
60	.0058773
70	.0008404
80	.0000857
90	.0000062
100	.0000003

We have assumed that birthdays are equally likely to fall on any particular day. Statistical evidence suggests that this is not true. However, it is intuitively clear (but not easy to prove) that this makes it even more likely to have a duplication with a group of 23 people. (See Exercise to find out what happens on planets with more or fewer than 365 days per year.)

We now turn to the topic of permutations.

Permutations

Definition

Let [math]A[/math] be any finite set. A permutation of [math]A[/math] is a one-to-one mapping of [math]A[/math] onto itself.

To specify a particular permutation we list the elements of [math]A[/math] and, under them, show

where each element is sent by the one-to-one mapping. For example, if [math]A = \{a,b,c\}[/math] a possible permutation [math]\sigma[/math] would be

[[math]] \sigma = \pmatrix{ a & b & c \cr b & c & a \cr}. [[/math]]

By the permutation [math]\sigma[/math], [math]a[/math] is sent to [math]b[/math], [math]b[/math] is sent to [math]c[/math], and [math]c[/math] is sent to [math]a[/math]. The condition that the mapping be one-to-one means that no two elements of [math]A[/math] are sent, by the mapping, into the same element of [math]A[/math]. We can put the elements of our set in some order and rename them 1, 2, \ldots, n</math>. Then, a typical permutation of the set [math]A =\{a_1,a_2,a_3,a_4\}[/math] can be written in the form

[[math]] \sigma = \pmatrix{ 1 & 2 & 3 & 4 \cr 2 & 1 & 4 & 3 \cr}, [[/math]]

indicating that [math]a_1[/math] went to [math]a_2[/math], [math]a_2[/math] to [math]a_1[/math], [math]a_3[/math] to [math]a_4[/math], and [math]a_4[/math] to [math]a_3[/math]. If we always choose the top row to be 1 2 3 4 then, to prescribe the permutation, we need only give the bottom row, with the understanding that this tells us where 1 goes, 2 goes, and so forth, under the mapping. When this is done, the permutation is often called a rearrangement of the [math]n[/math] objects 1, 2, 3, \ldots, n</math>. For example, all possible permutations, or rearrangements, of the numbers [math]A = \{1,2,3\}[/math] are:

[[math]] 123,\ 132,\ 213,\ 231,\ 312,\ 321\ . [[/math]]

It is an easy matter to count the number of possible permutations of [math]n[/math] objects. By our general counting principle, there are [math]n[/math] ways to assign the first element, for each of these we have [math]n - 1[/math] ways to assign the second object, [math]n - 2[/math] for the third, and so forth. This proves the following theorem.

Theorem

The total number of permutations of a set [math]A[/math] of [math]n[/math] elements is given by [math]n \cdot (n~-~1) \cdot (n - 2) \cdot \ldots \cdot 1[/math].

It is sometimes helpful to consider orderings of subsets of a given set. This prompts the following definition.

Definition

Let [math]A[/math] be an [math]n[/math]-element set, and let [math]k[/math] be an integer between 0 and [math]n[/math]. Then a [math]k[/math]-permutation of [math]A[/math] is an ordered listing of a subset of [math]A[/math] of size [math]k[/math].

Using the same techniques as in the last theorem, the following result is easily proved.

Theorem

The total number of [math]k[/math]-permutations of a set [math]A[/math] of [math]n[/math] elements is given by [math]n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n - k + 1)[/math].

Factorials

The number given in Theorem is called [math]n[/math] factorial, and is denoted by [math]n![/math]. The expression 0! is defined to be 1 to make certain formulas come out simpler. The first few values of this function are shown in Table. The reader will note that this function grows very rapidly.

Values of the factorial function.

[math]n[/math]	[math]n![/math]
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800

The expression [math]n![/math] will enter into many of our calculations, and we shall need to have some estimate of its magnitude when [math]n[/math] is large. It is clearly not practical to make exact calculations in this case. We shall instead use a result called Stirling's formula. Before stating this formula we need a definition.

Definition

Let [math]a_n[/math] and [math]b_n[/math] be two sequences of numbers. We say that [math]a_n[/math] is asymptotically equal to [math]b_n[/math], and write [math]a_n \sim b_n[/math], if

[[math]] \lim_{n \to \infty} \frac{a_n}{b_n} = 1\ . [[/math]]

Example [math]a_n/b_n = 1 + 1/\sqrt n[/math] and this ratio tends to 1 as [math]n[/math] tends to infinity, we have [math]a_n \sim b_n[/math].

Theorem

(Stirling's Formula)\label{thm 3.3} The sequence [math]n![/math] is asymptotically equal to

[[math]] n^ne^{-n}\sqrt{2\pi n}\ . [[/math]]

The proof of Stirling's formula may be found in most analysis texts. Let us verify this approximation by using the computer. The program StirlingApproximations prints [math]n![/math], the Stirling approximation, and, finally, the ratio of these two numbers. Sample output of this program is shown in Table. Note that, while the ratio of the numbers is getting closer to 1, the difference between the exact value and the approximation is increasing, and indeed, this difference will tend to infinity as [math]n[/math] tends to infinity, even though the ratio tends to 1. (This was also true in our Example where [math]n + \sqrt n \sim n[/math], but the difference is [math]\sqrt n[/math].)

Stirling approximations to the factorial function.

[math]n[/math]	[math]n![/math]	Approximation	Ratio
1	1	.922	1.084
2	2	1.919	1.042
3	6	5.836	1.028
4	24	23.506	1.021
5	120	118.019	1.016
6	720	710.078	1.013
7	5040	4980.396	1.011
8	40320	39902.395	1.010
9	362880	359536.873	1.009
10	3628800	3598696.619	1.008

Generating Random Permutations

We now consider the question of generating a random permutation of the integers between 1 and [math]n[/math]. Consider the following experiment. We start with a deck of [math]n[/math] cards, labelled 1 through [math]n[/math]. We choose a random card out of the deck, note its label, and put the card aside. We repeat this process until all [math]n[/math] cards have been chosen. It is clear that each permutation of the integers from 1 to [math]n[/math] can occur as a sequence of labels in this experiment, and that each sequence of labels is equally likely to occur. In our implementations of the computer algorithms, the above procedure is called RandomPermutation.

Fixed Points

There are many interesting problems that relate to properties of a permutation chosen at random from the set of all permutations of a given finite set. For example, since a permutation is a one-to-one mapping of the set onto itself, it is interesting to ask how many points are mapped onto themselves. We call such points fixed points of the mapping.

Let [math]p_k(n)[/math] be the probability that a random permutation of the set [math]\{1, 2, \ldots, n\}[/math] has exactly [math]k[/math] fixed points. We will attempt to learn something about these probabilities using simulation. The program FixedPoints uses the procedure RandomPermutation to generate random permutations and count fixed points. The program prints the proportion of times that there are [math]k[/math] fixed points as well as the average number of fixed points. The results of this program for 500 simulations for the cases [math]n = 10[/math], 20, and 30 are shown in Table.

Fixed point distributions.

Number of fixed points	Fraction of permutations
	n = 10	n = 20	n = 30
0	.362	.370	.358
1	.368	.396
2	.202	.164
3	.052	.060
4	.012	.008
5	.004	.002	.002
Average number of fixed points	.996	.948
	1.042

Notice the rather surprising fact that our estimates for the probabilities do not seem to depend very heavily on the number of elements in the permutation. For example, the probability that there are no fixed points, when [math]n = 10,\ 20,[/math] or 30 is estimated to be between .35 and .37. We shall see later (see Example) that for [math]n \geq 10[/math] the exact probabilities [math]p_n(0)[/math] are, to six decimal place accuracy, equal to [math]1/e \approx .367879[/math]. Thus, for all practical purposes, after [math]n = 10[/math] the probability that a random permutation of the set [math]\{1, 2, \ldots, n\}[/math] has no fixed points does not depend upon [math]n[/math]. These simulations also suggest that the average number of fixed points is close to 1. It can be shown (see Example) that the average is exactly equal to 1 for all [math]n[/math].

More picturesque versions of the fixed-point problem are: You have arranged the books on your book shelf in alphabetical order by author and they get returned to your shelf at random; what is the probability that exactly [math]k[/math] of the books end up in their correct position? (The library problem.) In a restaurant [math]n[/math] hats are checked and they are hopelessly scrambled; what is the probability that no one gets his own hat back? (The hat check problem.) In the Historical Remarks at the end of this section, we give one method for solving the hat check problem exactly. Another method is given in Example.

Records

Here is another interesting probability problem that involves permutations. Estimates for the amount of measured snow in inches in Hanover, New Hampshire, in the ten years from 1974 to 1983 are shown in Table.

Snowfall in Hanover.

Date	Snowfall in inches
1974	75
1975	88
1976	72
1977	110
1978	85
1979	30
1980	55
1981	86
1982	51
1983	64

Suppose we have started keeping records in 1974. Then our first year's snowfall could be considered a record snowfall starting from this year. A new record was established in 1975; the next record was established in 1977, and there were no new records established after this year. Thus, in this ten-year period, there were three records established: 1974, 1975, and 1977. The question that we ask is: How many records should we expect to be established in such a ten-year period? We can count the number of records in terms of a permutation as follows: We number the years from 1 to 10. The actual amounts of snowfall are not important but their relative sizes are. We can, therefore, change the numbers measuring snowfalls to numbers 1 to 10 by replacing the smallest number by 1, the next smallest by 2, and so forth. (We assume that there are no ties.) For our example, we obtain the data shown in Table.

Ranking of total snowfall.

Houses	7
Cats	49
Mice	343
Wheat	2401
Hekat	16807
	19607

This gives us a permutation of the numbers from 1 to 10 and, from this permutation, we can read off the records; they are in years 1, 2, and 4. Thus we can define records for a permutation as follows:

Definition

Let [math]\sigma[/math] be a permutation of the set [math]\{1, 2, \ldots, n\}[/math]. Then [math]i[/math] is a record of [math]\sigma[/math] if either [math]i = 1[/math] or [math]\sigma(j) \lt \sigma(i)[/math] for every [math]j = 1,\ldots,\,i - 1[/math].

Now if we regard all rankings of snowfalls over an [math]n[/math]-year period to be equally likely (and allow no ties), we can estimate the probability that there will be [math]k[/math] records in [math]n[/math] years as well as the average number of records by simulation.

We have written a program Records that counts the number of records in randomly chosen permutations. We have run this program for the cases [math]n = 10[/math], 20, 30. For [math]n = 10[/math] the average number of records is 2.968, for 20 it is 3.656, and for 30 it is 3.960. We see now that the averages increase, but very slowly. We shall see later (see Example) that the average number is approximately [math]\log n[/math]. Since [math]\log 10 = 2.3[/math], [math]\log 20 = 3[/math], and [math]\log 30 = 3.4[/math], this is consistent with the results of our simulations.

As remarked earlier, we shall be able to obtain formulas for exact results of certain problems of the above type. However, only minor changes in the problem make this impossible. The power of simulation is that minor changes in a problem do not make the simulation much more difficult. (See Exercise for an interesting variation of the hat check problem.)

List of Permutations

Another method to solve problems that is not sensitive to small changes in the problem is to have the computer simply list all possible permutations and count the fraction that have the desired property. The program AllPermutations produces a list of all of the permutations of [math]n[/math]. When we try running this program, we run into a limitation on the use of the computer. The number of permutations of [math]n[/math] increases so rapidly that even to list all permutations of 20 objects is impractical.

Historical Remarks

Our basic counting principle stated that if you can do one thing in [math]r[/math] ways and for each of these another thing in [math]s[/math] ways, then you can do the pair in [math]rs[/math] ways. This is such a self-evident result that you might expect that it occurred very early in mathematics. N. L. Biggs suggests that we might trace an example of this principle as follows: First, he relates a popular nursery rhyme dating back to at least 1730:

	As I was going to St. Ives,
	I met a man with seven wives,
	Each wife had seven sacks,
	Each sack had seven cats,
	Each cat had seven kits.
	Kits, cats, sacks and wives,
	How many were going to St. Ives?

(You need our principle only if you are not clever enough to realize that you are supposed to answer one, since only the narrator is going to St. Ives; the others are going in the other direction!)

He also gives a problem appearing on one of the oldest surviving mathematical manuscripts of about 1650 B.C., roughly translated as:

Houses	7
Cats	49
Mice	343
Wheat	2401
Hekat	16807
	19607

The following interpretation has been suggested: there are seven houses, each with seven cats; each cat kills seven mice; each mouse would have eaten seven heads of wheat, each of which would have produced seven hekat measures of grain. With this interpretation, the table answers the question of how many hekat measures were saved by the cats' actions. It is not clear why the writer of the table wanted to add the numbers together. One of the earliest uses of factorials occurred in Euclid's proof that there are infinitely many prime numbers. Euclid argued that there must be a prime number between [math]n[/math] and [math]n! + 1[/math] as follows: [math]n![/math] and [math]n! + 1[/math] cannot have common factors. Either [math]n! + 1[/math] is prime or it has a proper factor. In the latter case, this factor cannot divide [math]n![/math] and hence must be between [math]n[/math] and [math]n! + 1[/math]. If this factor is not prime, then it has a factor that, by the same argument, must be bigger than [math]n[/math]. In this way, we eventually reach a prime bigger than [math]n[/math], and this holds for all [math]n[/math]. The “[math]n![/math]” rule for the number of permutations seems to have occurred first in India. Examples have been found as early as 300 B.C., and by the eleventh century the general formula seems to have been well known in India and then in the Arab countries. The hat check problem is found in an early probability book written by de Montmort and first printed in 1708. It appears in the form of a game called Treize. In a simplified version of this game considered by de Montmort one turns over cards numbered 1 to 13, calling out 1, 2, \ldots, 13 as the cards are examined. De Montmort asked for the probability that no card that is turned up agrees with the number called out.

This probability is the same as the probability that a random permutation of 13 elements has no fixed point. De Montmort solved this problem by the use of a recursion relation as follows: let [math]w_n[/math] be the number of permutations of [math]n[/math] elements with no fixed point (such permutations are called derangements). Then [math]w_1 = 0[/math] and [math]w_2 = 1[/math].

Now assume that [math]n \ge 3[/math] and choose a derangement of the integers between 1 and [math]n[/math]. Let [math]k[/math] be the integer in the first position in this derangement. By the definition of derangement, we have [math]k \ne 1[/math]. There are two possibilities of interest concerning the position of 1 in the derangement: either 1 is in the [math]k[/math]th position or it is elsewhere. In the first case, the [math]n-2[/math] remaining integers can be positioned in [math]w_{n-2}[/math] ways without resulting in any fixed points. In the second case, we consider the set of integers [math]\{1, 2, \ldots, k-1, k+1, \ldots, n\}[/math]. The numbers in this set must occupy the positions [math]\{2, 3, \ldots, n\}[/math] so that none of the numbers other than 1 in this set are fixed, and also so that 1 is not in position [math]k[/math]. The number of ways of achieving this kind of arrangement is just [math]w_{n-1}[/math]. Since there are [math]n-1[/math] possible values of [math]k[/math], we see that

[[math]] w_n = (n - 1)w_{n - 1} + (n - 1)w_{n -2} [[/math]]

for [math]n \ge 3[/math]. One might conjecture from this last equation that the sequence [math]\{w_n\}[/math] grows like the sequence [math]\{n!\}[/math].

In fact, it is easy to prove by induction that

[[math]] w_n = nw_{n - 1} + (-1)^n\ . [[/math]]

Then [math]p_i = w_i/i![/math] satisfies

[[math]] p_i - p_{i - 1} = \frac{(-1)^i}{i!}\ . [[/math]]

If we sum from [math]i = 2[/math] to [math]n[/math], and use the fact that [math]p_1 = 0[/math], we obtain

[[math]] p_n = \frac1{2!} - \frac1{3!} + \cdots + \frac{(-1)^n}{n!}\ . [[/math]]

This agrees with the first [math]n + 1[/math] terms of the expansion for [math]e^x[/math] for [math]x = -1[/math] and hence for large [math]n[/math] is approximately [math]e^{-1} \approx .368[/math]. David remarks that this was possibly the first use of the exponential function in probability. We shall see another way to derive de Montmort's result in the next section, using a method known as the Inclusion-Exclusion method.

Recently, a related problem appeared in a column of Marilyn vos Savant. Charles Price wrote to ask about his experience playing a certain form of solitaire, sometimes called “frustration solitaire.” In this particular game, a deck of cards is shuffled, and then dealt out, one card at a time. As the cards are being dealt, the player counts from 1 to 13, and then starts again at 1. (Thus, each number is counted four times.) If a number that is being counted coincides with the rank of the card that is being turned up, then the player loses the game. Price found that he rarely won and wondered how often he should win. Vos Savant remarked that the expected number of matches is 4 so it should be difficult to win the game.

Finding the chance of winning is a harder problem than the one that de Montmort solved because, when one goes through the entire deck, there are different patterns for the matches that might occur. For example matches may occur for two cards of the same rank, say two aces, or for two different ranks, say a two and a three.

A discussion of this problem can be found in Riordan. In this book, it is shown that as [math]n \rightarrow \infty[/math], the probability of no matches tends to [math]1/e^4[/math].

The original game of Treize is more difficult to analyze than frustration solitaire. The game of Treize is played as follows. One person is chosen as dealer and the others are players. Each player, other than the dealer, puts up a stake. The dealer shuffles the cards and turns them up one at a time calling out, “Ace, two, three,..., king,” just as in frustration solitaire. If the dealer goes through the 13 cards without a match he pays the players an amount equal to their stake, and the deal passes to someone else. If there is a match the dealer collects the players' stakes; the players put up new stakes, and the dealer continues through the deck, calling out, “Ace, two, three, ....” If the dealer runs out of cards he reshuffles and continues the count where he left off. He continues until there is a run of 13 without a match and then a new dealer is chosen.

The question at this point is how much money can the dealer expect to win from each player. De Montmort found that if each player puts up a stake of 1, say, then the dealer will win approximately .801 from each player.

Peter Doyle calculated the exact amount that the dealer can expect to win. The answer is:

26516072156010218582227607912734182784642120482136091446715371962089931
52311343541724554334912870541440299239251607694113500080775917818512013
82176876653563173852874555859367254632009477403727395572807459384342747
87664965076063990538261189388143513547366316017004945507201764278828306
60117107953633142734382477922709835281753299035988581413688367655833113
24476153310720627474169719301806649152698704084383914217907906954976036
28528211590140316202120601549126920880824913325553882692055427830810368
57818861208758248800680978640438118582834877542560955550662878927123048
26997601700116233592793308297533642193505074540268925683193887821301442
70519791882/
33036929133582592220117220713156071114975101149831063364072138969878007
99647204708825303387525892236581323015628005621143427290625658974433971
65719454122908007086289841306087561302818991167357863623756067184986491
35353553622197448890223267101158801016285931351979294387223277033396967
79797069933475802423676949873661605184031477561560393380257070970711959
69641268242455013319879747054693517809383750593488858698672364846950539
88868628582609905586271001318150621134407056983214740221851567706672080
94586589378459432799868706334161812988630496327287254818458879353024498
00322425586446741048147720934108061350613503856973048971213063937040515
59533731591.

This is .803 to 3 decimal places. A description of the algorithm used to find this answer can be found on his Web page. A discussion of this problem and other problems can be found in Doyle et al.

The birthday problem does not seem to have a very old history. Problems of this type were first discussed by von Mises. It was made popular in the 1950s by Feller's book.

Stirling presented his formula

[[math]] n! \sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n [[/math]]

in his work Methodus Differentialis published in 1730. This approximation was used by de Moivre in establishing his celebrated central limit theorem that we will study in Chapter. De Moivre himself had independently established this approximation, but without identifying the constant [math]\pi[/math]. Having established the approximation

[[math]] \frac{2B}{\sqrt n} [[/math]]

for the central term of the binomial distribution, where the constant [math]B[/math] was determined by an infinite series, de Moivre writes:

... my worthy and learned Friend, Mr. James Stirling, who had applied himself after me to that inquiry, found that the Quantity [math]B[/math] did denote the Square-root of the Circumference of a Circle whose Radius is Unity, so that if that Circumference be called [math]c[/math] the Ratio of the middle Term to the Sum of all Terms will be expressed by [math]2/\sqrt{nc}\,[/math]...

General references

Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.