Ergodic Markov Chains

A second important kind of Markov chain we shall study in detail is an ergodic Markov chain, defined as follows.

Definition

A Markov chain is called an ergodic chain if it is possible to go from every state to every state (not necessarily in one move).

In many books, ergodic Markov chains are called irreducible.

Definition

A Markov chain is called a regular chain if some power of the transition matrix has only positive elements.

In other words, for some [math]n[/math], it is possible to go from any state to any state in exactly [math]n[/math] steps. It is clear from this definition that every regular chain is ergodic. On the other hand, an ergodic chain is not necessarily regular, as the following examples show.

Example Let the transition matrix of a Markov chain be defined by

		[math]1[/math] [math]2[/math]
[math]\mat{P} =\,\,[/math]	[math]\begin{array}{c c c c} 1\\ 2\\ \end{array}[/math]	[math]\begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}[/math]

Then is clear that it is possible to move from any state to any state, so the chain is ergodic. However, if [math]n[/math] is odd, then it is not possible to move from state 0 to state 0 in [math]n[/math] steps, and if [math]n[/math] is even, then it is not possible to move from state 0 to state 1 in [math]n[/math] steps, so the chain is not regular.A more interesting example of an ergodic, non-regular Markov chain is provided by the Ehrenfest urn model.

Example Recall the Ehrenfest urn model (Example).

The transition matrix for this example is

		[math]0[/math][math]1[/math] [math]2[/math] [math]3[/math] [math]4[/math]
[math]\mat{P}=\,\,[/math]	[math]\begin{array}{c c c c} 0\\ 1 \\ 2\\ 3\\ 4 \end{array}[/math]	[math]\begin{pmatrix} 0 & 1 & 0 & 0 & 0 \\ 1/4 & 0 & 3/4 & 0 & 0 \\ 0 & 1/2 & 0 & 1/2 & 0 \\ 0 & 0 & 3/4 & 0 & 1/4 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix}[/math]

In this example, if we start in state 0 we will, after any even number of steps, be in either state 0, 2 or 4, and after any odd number of steps, be in states 1 or 3. Thus this chain is ergodic but not regular.

Regular Markov Chains

Any transition matrix that has no zeros determines a regular Markov chain. However, it is possible for a regular Markov chain to have a transition matrix that has zeros. The transition matrix of the Land of Oz example of Introduction has [math]p_{NN} = 0[/math] but the second power [math]\mat{P}^2[/math] has no zeros, so this is a regular Markov chain.

An example of a nonregular Markov chain is an absorbing chain. For example, let

[[math]] \mat{P} = \pmatrix{ 1 & 0 \cr 1/2 & 1/2 \cr} [[/math]]

be the transition matrix of a Markov chain. Then all powers of [math]\mat{P}[/math] will have a 0 in the upper right-hand corner.

We shall now discuss two important theorems relating to regular chains.

Theorem

Let [math]\mat{P}[/math] be the transition matrix for a regular chain. Then, as [math]n \to \infty[/math], the powers [math]\mat{P}^n[/math] approach a limiting matrix [math]\mat{W}[/math] with all rows the same vector [math]\mat{w}[/math]. The vector [math]\mat{w}[/math] is a strictly positive probability vector (i.e., the components are all positive and they sum to one).

In the next section we give two proofs of this fundamental theorem. We give here the basic idea of the first proof.

We want to show that the powers [math]\mat{P}^n[/math] of a regular transition matrix tend to a matrix with all rows the same. This is the same as showing that [math]\mat{P}^n[/math] converges to a matrix with constant columns. Now the [math]j[/math]th column of [math]\mat{P}^n[/math] is [math]\mat{P}^{n} \mat{y}[/math] where [math]\mat{y}[/math] is a column vector with [math]1[/math] in the [math]j[/math]th entry and 0 in the other entries. Thus we need only prove that for any column vector [math]\mat{y},\mat{P}^{n} \mat{y}[/math] approaches a constant vector as [math]n[/math] tend to infinity.

Since each row of [math]\mat{P}[/math] is a probability vector, [math]\mat{Py}[/math] replaces [math]\mat{y}[/math] by averages of its components. Here is an example:

[[math]] \pmatrix{1/2 & 1/4 & 1/4 \cr 1/3 & 1/3 & 1/3 \cr 1/2 & 1/2 & 0\cr} \pmatrix {1 \cr 2 \cr 3 \cr} = \pmatrix{1/2 \cdot 1+ 1/4 \cdot 2+ 1/4 \cdot 3\cr 1/3 \cdot 1+ 1/3 \cdot 2+ 1/3 \cdot 3\cr 1/2 \cdot 1+ 1/2 \cdot 2+ 0 \cdot 3\cr} =\pmatrix {7/4 \cr 2 \cr 3/2 \cr}\ . [[/math]]

The result of the averaging process is to make the components of [math]\mat{Py}[/math] more similar than those of [math]\mat{y}[/math]. In particular, the maximum component decreases (from 3 to 2) and the minimum component increases (from 1 to 3/2). Our proof will show that as we do more and more of this averaging to get [math]\mat{P}^{n} \mat{y}[/math], the difference between the maximum and minimum component will tend to 0 as [math]n \rightarrow \infty[/math]. This means [math]\mat{P}^{n} \mat{y}[/math] tends to a constant vector. The [math]ij[/math]th entry of [math]\mat{P}^n[/math], [math]p_{ij}^{(n)}[/math], is the probability that the process will be in state [math]s_j[/math] after [math]n[/math] steps if it starts in state [math]s_i[/math]. If we denote the common row of [math]\mat{W}[/math] by [math]\mat{w}[/math], then Theorem states that the probability of being in [math]s_j[/math] in the long run is approximately [math]w_j[/math], the [math]j[/math]th entry of [math]\mat{w}[/math], and is independent of the starting state.

Example Recall that for the Land of Oz example of Introduction, the sixth powerof the transition matrix [math]\mat{P}[/math] is, to three decimal places,

		[math]\mbox{R}[/math][math]\mbox{N}[/math] [math]\mbox{S}[/math]
[math]\mat{P}=\,\,[/math]	[math]\begin{array}{c c c c} \mbox{R} \\ \mbox{N}\\ \mbox{S} \end{array}[/math]	[math]\begin{pmatrix} .4 & .2 & .4 \\ .4 & .2 & .4 \\ .4 & .2 & .4\\ \end{pmatrix}[/math]

Thus, to this degree of accuracy, the probability of rain six days after a rainy day is the same as the probability of rain six days after a nice day, or six days after a snowy day. Theorem predicts that, for large [math]n[/math], the rows of [math]\mat{P}[/math] approach a common vector. It is interesting that this occurs so soon in our example.

Theorem

Let [math]\mat {P}[/math] be a regular transition matrix, let

[[math]] \mat{W} = \lim_{n \rightarrow \infty} \mat{P}^n\ , [[/math]]

let [math]\mat{w}[/math] be the common row of [math]\mat{W}[/math], and let [math]\mat{c}[/math] be the column vector all of whose components are 1. Then

[math]\mat{w}\mat{P} = \mat{w}[/math], and any row vector [math]\mat{v}[/math] such that [math]\mat{v}\mat{P} = \mat{v}[/math] is a constant multiple of [math]\mat{w}[/math].
[math]\mat{P}\mat{c} = \mat{c}[/math], and any column vector [math]\mat{x}[/math] such that [math]\mat{P}\mat{x} = \mat{x}[/math] is a multiple of [math]\mat{c}[/math].

Show Proof

To prove part (a), we note that from Theorem,

[[math]] \mat{P}^n \to \mat{W}\ . [[/math]]

Thus,

[[math]] \mat{P}^{n + 1} = \mat{P}^n \cdot \mat{P} \to \mat{W}\mat{P}\ . [[/math]]

But [math]\mat{P}^{n + 1} \to \mat{W}[/math], and so [math]\mat{W} = \mat{W}\mat{P}[/math], and [math]\mat{w} = \mat{w}\mat{P}[/math].

Let [math]\mat{v}[/math] be any vector with [math]\mat{v} \mat{P} = \mat{v}[/math]. Then [math]\mat{v} = \mat{v} \mat{P}^n[/math], and passing to the limit, [math]\mat{v} = \mat{v} \mat{W}[/math]. Let [math]r[/math] be the sum of the components of [math]\mat{v}[/math]. Then it is easily checked that [math]\mat{v}\mat{W} = r\mat{w}[/math]. So, [math]\mat{v} = r\mat{w}[/math].

To prove part (b), assume that [math]\mat{x} = \mat{P} \mat{x}[/math]. Then [math]\mat{x} = \mat{P}^n \mat{x}[/math], and again passing to the limit, [math]\mat{x} = \mat{W}\mat{x}[/math]. Since all rows of [math]\mat{W}[/math] are the same, the components of [math]\mat{W}\mat{x}[/math] are all equal, so [math]\mat{x}[/math] is a multiple of [math]\mat{c}[/math].

■

Note that an immediate consequence of Theorem is the fact that there is only one probability vector [math]\mat{v}[/math] such that [math]\mat{v}\mat{P} = \mat{v}[/math].

Fixed Vectors

Definition

A row vector [math]\mat{w}[/math] with the property [math]\mat{w}\mat{P} = \mat{w}[/math] is called a fixed row vector for [math]\mat{P}[/math]. Similarly, a column vector [math]\mat{x}[/math] such that [math]\mat{P}\mat{x} = \mat{x}[/math] is called a fixed column vector for [math]\mat{P}[/math].

Thus, the common row of [math]\mat{W}[/math] is the unique vector [math]\mat{w}[/math] which is both a fixed row vector for [math]\mat{P}[/math] and a probability vector. Theorem shows that any fixed row vector for [math]\mat{P}[/math] is a multiple of [math]\mat{w}[/math] and any fixed column vector for [math]\mat{P}[/math] is a constant vector.

One can also state Definition in terms of eigenvalues and eigenvectors. A fixed row vector is a left eigenvector of the matrix [math]\mat{P}[/math] corresponding to the eigenvalue 1. A similar statement can be made about fixed column vectors.

We will now give several different methods for calculating the fixed row vector [math]\mat{w}[/math] for a regular Markov chain.

Example By Theorem we can find the limiting vector [math]\mat{w}[/math] for the Land of Oz from the fact that

[[math]] w_1 + w_2 + w_3 = 1 [[/math]]

and

[[math]] \pmatrix{ w_1 & w_2 & w_3 } \pmatrix{ 1/2 & 1/4 & 1/4 \cr 1/2 & 0 & 1/2 \cr 1/4 & 1/4 & 1/2 \cr} = \pmatrix{ w_1 & w_2 & w_3 }\ . [[/math]]

These relations lead to the following four equations in three unknowns:

[[math]] \begin{eqnarray*} w_1 + w_2 + w_3 &=& 1\ , \\ (1/2)w_1 + (1/2)w_2 + (1/4)w_3 &=& w_1\ , \\ (1/4)w_1 + (1/4)w_3 &=& w_2\ , \\ (1/4)w_1 + (1/2)w_2 + (1/2)w_3 &=& w_3\ . \end{eqnarray*} [[/math]]

Our theorem guarantees that these equations have a unique solution. If the equations are solved, we obtain the solution

[[math]] \mat{w} = \pmatrix{ .4 & .2 & .4 }\ , [[/math]]

in agreement with that predicted from [math]\mat{P}^6[/math], given in Example.

To calculate the fixed vector, we can assume that the value at a particular state, say state one, is 1, and then use all but one of the linear equations from [math]\mat{w}\mat{P} = \mat{w}[/math]. This set of equations will have a unique solution and we can obtain [math]\mat{w}[/math] from this solution by dividing each of its entries by their sum to give the probability vector [math]\mat{w}[/math]. We will now illustrate this idea for the above example.

Example We set [math]w_1 = 1[/math], and then solve the first and second linear equations from [math]\mat{w}\mat{P} = \mat{w}[/math]. We have

[[math]] \begin{eqnarray*} (1/2) + (1/2)w_2 + (1/4)w_3 &=& 1\ , \\ (1/4) + (1/4)w_3 &=& w_2\ . \\ \end{eqnarray*} [[/math]]

If we solve these, we obtain

[[math]] \pmatrix{w_1&w_2&w_3} = \pmatrix{1&1/2&1}\ . [[/math]]

Now we divide this vector by the sum of the components, to obtain the final answer:

[[math]] \mat{w} = \pmatrix{.4&.2&.4}\ . [[/math]]

This method can be easily programmed to run on a computer.

As mentioned above, we can also think of the fixed row vector [math]\mat{w}[/math] as a left eigenvector of the transition matrix [math]\mat{P}[/math]. Thus, if we write [math]\mat{I}[/math] to denote the identity matrix, then [math]\mat{w}[/math] satisfies the matrix equation

[[math]] \mat{w}\mat{P} = \mat{w}\mat{I}\ , [[/math]]

or equivalently,

[[math]] \mat{w}(\mat{P} - \mat{I}) = \mat{0}\ . [[/math]]

Thus, [math]\mat{w}[/math] is in the left nullspace of the matrix [math]\mat{P} - \mat{I}[/math]. Furthermore, Theorem states that this left nullspace has dimension 1. Certain computer programming languages can find nullspaces of matrices. In such languages, one can find the fixed row probability vector for a matrix [math]\mat{P}[/math] by computing the left nullspace and then normalizing a vector in the nullspace so the sum of its components is 1.

The program FixedVector uses one of the above methods (depending upon the language in which it is written) to calculate the fixed row probability vector for regular Markov chains.

So far we have always assumed that we started in a specific state. The following theorem generalizes Theorem to the case where the

starting state is itself determined by a probability vector.

Theorem

Let [math]\mat{P}[/math] be the transition matrix for a regular chain and [math]\mat{v}[/math] an arbitrary probability vector. Then

[[math]] \lim_{n \to \infty} \mat{v} \mat{P}^n = \mat{w}\ , [[/math]]

where [math]\mat{w}[/math] is the unique fixed probability vector for [math]\mat{P}[/math].

Show Proof

By Theorem,

[[math]] \lim_{n \to \infty} \mat{P}^n = \mat {W}\ . [[/math]]

Hence,

[[math]] \lim_{n \to \infty} \mat {v} \mat {P}^n = \mat {v} \mat {W}\ . [[/math]]

But the entries in [math]\mat {v}[/math] sum to 1, and each row of [math]\mat {W}[/math] equals [math]\mat {w}[/math]. From these statements, it is easy to check that

[[math]] \mat {v} \mat {W} = \mat {w}\ . [[/math]]

■

If we start a Markov chain with initial probabilities given by [math]\mat{v}[/math], then the probability vector [math]\mat{v} \mat{P}^n[/math] gives the probabilities of being in the various states after [math]n[/math] steps. Theorem then establishes the fact that, even in this more general class of processes, the probability of being in [math]s_j[/math] approaches [math]w_j[/math].

Equilibrium

We also obtain a new interpretation for [math]\mat{w}[/math]. Suppose that our starting vector picks state [math]s_i[/math] as a starting state with probability [math]w_i[/math], for all [math]i[/math]. Then the probability of being in the various states after [math]n[/math] steps is given by [math]\mat {w} \mat {P}^n = \mat {w}[/math], and is the same on all steps. This method of starting provides us with a process that is called “stationary.” The fact that [math]\mat{w}[/math] is the only probability vector for which [math]\mat {w} \mat {P} = \mat {w}[/math] shows that we must have a starting probability vector of exactly the kind described to obtain a stationary process.

Many interesting results concerning regular Markov chains depend only on the fact that the chain has a unique fixed probability vector which is positive. This property holds for all ergodic Markov chains.

Theorem

For an ergodic Markov chain, there is a unique probability vector [math]\mat{w}[/math] such that [math]\mat {w} \mat {P} = \mat {w}[/math] and [math]\mat{w}[/math] is strictly positive. Any row vector such that [math]\mat {v} \mat {P} = \mat {v}[/math] is a multiple of [math]\mat{w}[/math]. Any column vector [math]\mat{x}[/math] such that [math]\mat {P} \mat {x} = \mat {x}[/math] is a constant vector.

Show Proof

This theorem states that Theorem is true for ergodic chains. The result follows easily from the fact that, if [math]\mat{P}[/math] is an ergodic transition matrix, then [math]\bar{\mat{P}} = (1/2)\mat {I} + (1/2)\mat {P}[/math] is a regular transition matrix with the same fixed vectors (see Exercise -- Exercise).

■

For ergodic chains, the fixed probability vector has a slightly different interpretation. The following two theorems, which we will not prove here, furnish an interpretation for this fixed vector.

Theorem

Let [math]\mat{P}[/math] be the transition matrix for an ergodic chain. Let [math]\mat {A}_n[/math] be the matrix defined by

[[math]] \mat {A}_n = \frac{\mat {I} + \mat {P} + \mat {P}^2 +\cdots + \mat {P}^n}{n + 1}\ . [[/math]]

Then [math]\mat {A}_n \to \mat {W}[/math], where [math]\mat{W}[/math] is a matrix all of whose rows are equal to the unique fixed probability vector [math]\mat{w}[/math] for [math]\mat{P}[/math].

If [math]\mat{P}[/math] is the transition matrix of an ergodic chain, then Theorem states that there is only one fixed row probability vector for [math]\mat{P}[/math]. Thus, we can use the same techniques that were used for regular chains to solve for this fixed vector. In particular, the program FixedVector works for ergodic chains.

To interpret Theorem, let us assume that we have an ergodic chain that starts in state [math]s_i[/math]. Let [math]X^{(m)} = 1[/math] if the [math]m[/math]th step is to state [math]s_j[/math] and 0 otherwise. Then the average number of times in state [math]s_j[/math] in the first [math]n[/math] steps is given by

[[math]] H^{(n)} = \frac{X^{(0)} + X^{(1)} + X^{(2)} +\cdots+ X^{(n)}}{n + 1}\ . [[/math]]

But [math]X^{(m)}[/math] takes on the value 1 with probability [math]p_{ij}^{(m)}[/math] and 0 otherwise. Thus [math]E(X^{(m)}) = p_{ij}^{(m)}[/math], and the [math]ij[/math]th entry of [math]\mat {A}_n[/math] gives the expected value of [math]H^{(n)}[/math], that is, the expected proportion of times in state [math]s_j[/math] in the first [math]n[/math] steps if the chain starts in state [math]s_i[/math]. If we call being in state [math]s_j[/math] success and any other state failure, we could ask if a theorem analogous to the law of large numbers for independent trials holds. The answer is yes and is given by the following theorem.

Theorem

(Law of Large Numbers for Ergodic Markov Chains) Let [math]H_j^{(n)}[/math] be the proportion of times in [math]n[/math] steps that an ergodic chain is in state [math]s_j[/math]. Then for any [math]\epsilon \gt 0[/math],

[[math]] P\Bigl(|H_j^{(n)} - w_j| \gt \epsilon\Bigr) \to 0\ , [[/math]]

independent of the starting state [math]s_i[/math].

We have observed that every regular Markov chain is also an ergodic chain. Hence, Theorem and Theorem apply also for regular chains. For example, this gives us a new interpretation for the fixed vector [math]\mat {w} = (.4,.2,.4)[/math] in the Land of Oz example. Theorem predicts that, in the long run, it will rain 40 percent of the time in the Land of Oz, be nice 20 percent of the time, and snow 40 percent of the time.

Simulation

We illustrate Theorem by writing a program to simulate the behavior of a Markov chain. SimulateChain is such a program. Example In the Land of Oz, there are 525 days in a year. We have simulated the weather for one year in the Land of Oz, using the program SimulateChain. The results are shown in Table.

     SSRNRNSSSSSSNRSNSSRNSRNSSSNSRRRNSSSNRRSSSSNRSSNSRRRRRRNSSS 
     SSRRRSNSNRRRRSRSRNSNSRRNRRNRSSNSRNRNSSRRSRNSSSNRSRRSSNRSNR
     RNSSSSNSSNSRSRRNSSNSSRNSSRRNRRRSRNRRRNSSSNRNSRNSNRNRSSSRSS
     NRSSSNSSSSSSNSSSNSNSRRNRNRRRRSRRRSSSSNRRSSSSRSRRRNRRRSSSSR
     RNRRRSRSSRRRRSSRNRRRRRRNSSRNRSSSNRNSNRRRRNRRRNRSNRRNSRRSNR
     RRRSSSRNRRRNSNSSSSSRRRRSRNRSSRRRRSSSRRRNRNRRRSRSRNSNSSRRRR
     RNSNRNSNRRNRRRRRRSSSNRSSRSNRSSSNSNRNSNSSSNRRSRRRNRRRRNRNRS
     SSNSRSNRNRRSNRRNSRSSSRNSRRSSNSRRRNRRSNRRNSSSSSNRNSSSSSSSNR
     NSRRRNSSRRRNSSSNRRSRNSSRRNRRNRSNRRRRRRRRRNSNRRRRRNSRRSSSSN
     SNS

Weather in the Land of Oz.
State	Times	Fraction
R	217	.413
N	109	.208
S	199	.379

We note that the simulation gives a proportion of times in each of the states not too different from the long run predictions of .4, .2, and .4 assured by Theorem. To get better results we have to simulate our chain for a longer time. We do this for 10,00 days without printing out each day's weather. The results are shown in Table. We see that the results are now quite close to the theoretical values of .4, .2, and .4.

Comparison of observed and predicted frequencies for the Land of Oz.
State	Times	Fraction
R	4010	.401
N	1902	.19
S	4088	.409

Examples of Ergodic Chains

The computation of the fixed vector [math]\mat{w}[/math] may be difficult if the transition matrix is very large. It is sometimes useful to guess the fixed vector on purely intuitive grounds. Here is a simple example to illustrate this kind of situation.

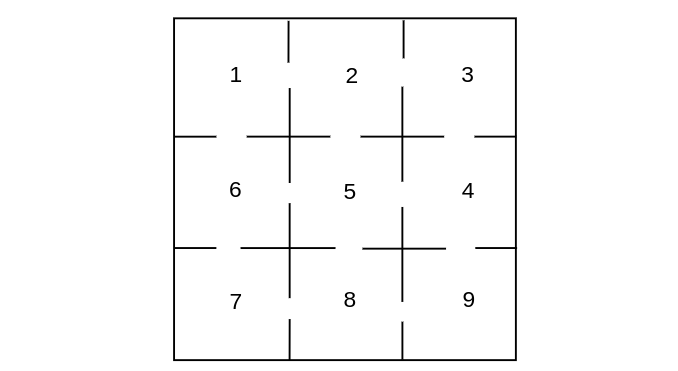
Example A white rat is put into the maze of Figure. There are nine compartments with connections between the compartments as indicated. The rat moves through the compartments at random. That is, if there are [math]k[/math] ways to leave a compartment, it chooses each of these with equal probability. We can represent the travels of the rat by a Markov chain process with transition matrix given by

		[math]1[/math][math]2[/math] [math]3[/math] [math]4[/math] [math]5[/math] [math]6[/math] [math]7[/math] [math]8[/math] [math]9[/math]
[math]\mat{P}=\,\,[/math]	[math]\begin{array}{c c c c} 1 \\ 2\\ 3\\ 4\\ 5\\ 6\\ 7\\ 8\\ 9 \end{array}[/math]	[math]\begin{pmatrix} 0 & 1/2 & 0 & 0 & 0 & 1/2 & 0 & 0 & 0 \\ 1/3 & 0 & 1/3 & 0 & 1/3 & 0 & 0 & 0 & 0 \\ 0 & 1/2 & 0 & 1/2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 1/3 & 0 & 0 & 0 & 1/3 \\ 0 & 1/4 & 0 & 1/4 & 0 & 1/4 & 0 & 1/4 & 0 \\ 1/3 & 0 & 0 & 0 & 1/3 & 0 & 1/3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1/2 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 0 & 1/3 & 0 & 1/3 & 0 & 1/3 \\ 0 & 0 & 0 & 1/2 & 0 & 0 & 0 & 1/2 & 0 \end{pmatrix}[/math]

That this chain is not regular can be seen as follows: From an odd-numbered state the process can go only to an even-numbered state, and from an even-numbered state it can go only to an odd number. Hence, starting in state [math]i[/math] the process will be alternately in even-numbered and odd-numbered states. Therefore, odd powers of [math]\mat{P}[/math] will have 0's for the odd-numbered entries in row 1. On the other hand, a glance at the maze shows that it is possible to go from every state to every other state, so that the chain is ergodic.

To find the fixed probability vector for this matrix, we would have to solve ten equations in nine unknowns. However, it would seem reasonable that the times spent in each compartment should, in the long run, be proportional to the number of entries to each compartment. Thus, we try the vector whose [math]j[/math]th component is the number of entries to the [math]j[/math]th compartment:

[[math]] \mat {x} = \pmatrix{ 2 & 3 & 2 & 3 & 4 & 3 & 2 & 3 & 2}\ . [[/math]]

It is easy to check that this vector is indeed a fixed vector so that the unique probability vector is this vector normalized to have sum 1:

[[math]] \mat {w} = \pmatrix{ \frac1{12} & \frac18 & \frac1{12} & \frac18 & \frac16 & \frac18 & \frac 1{12} & \frac18 & \frac1{12} }\ . [[/math]]

Example We recall the Ehrenfest urn model of Example. The transition matrix for this chain is as follows:

		[math]0[/math][math]1[/math] [math]2[/math] [math]3[/math] [math]4[/math]
[math]\mat{P} =\,\,[/math]	[math]\begin{array}{c c c c} 0 \\ 1\\ 2\\ 3\\ 4 \end{array}[/math]	[math]\begin{pmatrix} .000 & 1.000 & .000 & .000 & .000\\ .250 & .000 & .750 & .000 & .000\\ .000 & .500 & .000 & .500 & .000 \\ .000 & .000 & .750 & .000 & .250\\ .000 & .000 & .000 &1.000 & .000 \end{pmatrix}[/math]

If we run the program FixedVector for this chain, we obtain the vector

	[math]0[/math][math]1[/math] [math]2[/math] [math]3[/math] [math]4[/math]
[math]\mat{w} =\,\,[/math]	[math]\begin{pmatrix} .0625 &.2500 &.3750 &.2500 &.0625 \end{pmatrix}[/math]

By Theorem, we can interpret these values for [math]w_i[/math] as the proportion of times the process is in each of the states in the long run. For example, the proportion of times in state 0 is .0625 and the proportion of times in state 1 is .375. The astute reader will note that these numbers are the binomial distribution 1/16, 4/16, 6/16, 4/16, 1/16. We could have guessed this answer as follows: If we consider a particular ball, it simply moves randomly back and forth between the two urns. This suggests that the equilibrium state should be just as if we randomly distributed the four balls in the two urns. If we did this, the probability that there would be exactly [math]j[/math] balls in one urn would be given by the binomial distribution [math]b(n,p,j)[/math] with [math]n = 4[/math] and [math]p = 1/2[/math].

General references

Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.