Auction Models with Independent Private Values

[math] \newcommand{\edis}{\stackrel{d}{=}} \newcommand{\fd}{\stackrel{f.d.}{\rightarrow}} \newcommand{\dom}{\operatorname{dom}} \newcommand{\eig}{\operatorname{eig}} \newcommand{\epi}{\operatorname{epi}} \newcommand{\lev}{\operatorname{lev}} \newcommand{\card}{\operatorname{card}} \newcommand{\comment}{\textcolor{Green}} \newcommand{\B}{\mathbb{B}} \newcommand{\C}{\mathbb{C}} \newcommand{\G}{\mathbb{G}} \newcommand{\M}{\mathbb{M}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\T}{\mathbb{T}} \newcommand{\R}{\mathbb{R}} \newcommand{\E}{\mathbb{E}} \newcommand{\W}{\mathbb{W}} \newcommand{\bU}{\mathfrak{U}} \newcommand{\bu}{\mathfrak{u}} \newcommand{\bI}{\mathfrak{I}} \newcommand{\cA}{\mathcal{A}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cD}{\mathcal{D}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cG}{\mathcal{G}} \newcommand{\cg}{\mathcal{g}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cO}{\mathcal{O}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cQ}{\mathcal{Q}} \newcommand{\cR}{\mathcal{R}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cU}{\mathcal{U}} \newcommand{\cu}{\mathcal{u}} \newcommand{\cV}{\mathcal{V}} \newcommand{\cW}{\mathcal{W}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cZ}{\mathcal{Z}} \newcommand{\sF}{\mathsf{F}} \newcommand{\sM}{\mathsf{M}} \newcommand{\sG}{\mathsf{G}} \newcommand{\sT}{\mathsf{T}} \newcommand{\sB}{\mathsf{B}} \newcommand{\sC}{\mathsf{C}} \newcommand{\sP}{\mathsf{P}} \newcommand{\sQ}{\mathsf{Q}} \newcommand{\sq}{\mathsf{q}} \newcommand{\sR}{\mathsf{R}} \newcommand{\sS}{\mathsf{S}} \newcommand{\sd}{\mathsf{d}} \newcommand{\cp}{\mathsf{p}} \newcommand{\cc}{\mathsf{c}} \newcommand{\cf}{\mathsf{f}} \newcommand{\eU}{{\boldsymbol{U}}} \newcommand{\eb}{{\boldsymbol{b}}} \newcommand{\ed}{{\boldsymbol{d}}} \newcommand{\eu}{{\boldsymbol{u}}} \newcommand{\ew}{{\boldsymbol{w}}} \newcommand{\ep}{{\boldsymbol{p}}} \newcommand{\eX}{{\boldsymbol{X}}} \newcommand{\ex}{{\boldsymbol{x}}} \newcommand{\eY}{{\boldsymbol{Y}}} \newcommand{\eB}{{\boldsymbol{B}}} \newcommand{\eC}{{\boldsymbol{C}}} \newcommand{\eD}{{\boldsymbol{D}}} \newcommand{\eW}{{\boldsymbol{W}}} \newcommand{\eR}{{\boldsymbol{R}}} \newcommand{\eQ}{{\boldsymbol{Q}}} \newcommand{\eS}{{\boldsymbol{S}}} \newcommand{\eT}{{\boldsymbol{T}}} \newcommand{\eA}{{\boldsymbol{A}}} \newcommand{\eH}{{\boldsymbol{H}}} \newcommand{\ea}{{\boldsymbol{a}}} \newcommand{\ey}{{\boldsymbol{y}}} \newcommand{\eZ}{{\boldsymbol{Z}}} \newcommand{\eG}{{\boldsymbol{G}}} \newcommand{\ez}{{\boldsymbol{z}}} \newcommand{\es}{{\boldsymbol{s}}} \newcommand{\et}{{\boldsymbol{t}}} \newcommand{\ev}{{\boldsymbol{v}}} \newcommand{\ee}{{\boldsymbol{e}}} \newcommand{\eq}{{\boldsymbol{q}}} \newcommand{\bnu}{{\boldsymbol{\nu}}} \newcommand{\barX}{\overline{\eX}} \newcommand{\eps}{\varepsilon} \newcommand{\Eps}{\mathcal{E}} \newcommand{\carrier}{{\mathfrak{X}}} \newcommand{\Ball}{{\mathbb{B}}^{d}} \newcommand{\Sphere}{{\mathbb{S}}^{d-1}} \newcommand{\salg}{\mathfrak{F}} \newcommand{\ssalg}{\mathfrak{B}} \newcommand{\one}{\mathbf{1}} \newcommand{\Prob}[1]{\P\{#1\}} \newcommand{\yL}{\ey_{\mathrm{L}}} \newcommand{\yU}{\ey_{\mathrm{U}}} \newcommand{\yLi}{\ey_{\mathrm{L}i}} \newcommand{\yUi}{\ey_{\mathrm{U}i}} \newcommand{\xL}{\ex_{\mathrm{L}}} \newcommand{\xU}{\ex_{\mathrm{U}}} \newcommand{\vL}{\ev_{\mathrm{L}}} \newcommand{\vU}{\ev_{\mathrm{U}}} \newcommand{\dist}{\mathbf{d}} \newcommand{\rhoH}{\dist_{\mathrm{H}}} \newcommand{\ti}{\to\infty} \newcommand{\comp}[1]{#1^\mathrm{c}} \newcommand{\ThetaI}{\Theta_{\mathrm{I}}} \newcommand{\crit}{q} \newcommand{\CS}{CS_n} \newcommand{\CI}{CI_n} \newcommand{\cv}[1]{\hat{c}_{n,1-\alpha}(#1)} \newcommand{\idr}[1]{\mathcal{H}_\sP[#1]} \newcommand{\outr}[1]{\mathcal{O}_\sP[#1]} \newcommand{\idrn}[1]{\hat{\mathcal{H}}_{\sP_n}[#1]} \newcommand{\outrn}[1]{\mathcal{O}_{\sP_n}[#1]} \newcommand{\email}[1]{\texttt{#1}} \newcommand{\possessivecite}[1]{\citeauthor{#1}'s \citeyear{#1}} \newcommand\xqed[1]{% \leavevmode\unskip\penalty9999 \hbox{}\nobreak\hfill \quad\hbox{#1}} \newcommand\qedex{\xqed{$\triangle$}} \newcommand\independent{\perp\!\!\!\perp} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\cov}{Cov} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\Sel}{Sel} \DeclareMathOperator{\Bel}{Bel} \DeclareMathOperator{\cl}{cl} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\essinf}{essinf} \DeclareMathOperator{\esssup}{esssup} \newcommand{\mathds}{\mathbb} \renewcommand{\P}{\mathbb{P}} [/math]

An Inference Approach Robust to Bidding Behavior Assumptions

study what can be learned about the distribution of valuations in an open outcry English auction where symmetric bidders have independent private values for the object being auctioned. The standard theoretical model , called “button auction” model, posits that each bidder holds down a button while the object’s price rises continuously and exogenously, releasing it (in the dominant strategy equilibrium) when it reaches her valuation or all her opponents have left. In this case, the distribution of bidder's valuation can be learned exactly. show that much can be learned about the distribution of valuations, even allowing for the fact that real-life auctions may depart from this stylized framework, as in the following identification problem.

Identification Problem (Incomplete Auction Model with Independent Private Values)

For a given auction with [math]n \lt \infty[/math] participating bidders, let [math]\ev_i\sim\sQ,i=1,\dots,n,[/math] be bidder [math]i[/math]'s valuation for the object being auctioned and assume that [math]\ev_i\independent \ev_j[/math] for all [math]i\neq j[/math]. Assume that the support of [math]\sQ[/math] is [math][\underline{v},\bar{v}][/math] and that each bidder knows her own valuation but not that of her opponents. Let the auctioneer set a minimum bid increment [math]\delta\in [0,\bar{v})[/math], and for simplicity suppose there is no reserve price. Suppose the researcher observes order statistics of the bids, [math]\vec{\eb}_n\equiv(\eb_{1:n},\dots,\eb_{n:n})\sim\sP[/math] in [math]\R^n_+[/math], with [math]\eb_{i:n}[/math] the [math]i[/math]-th lowest of the [math]n[/math] bids. Assume that: (1) Bidders do not bid more than they are willing to pay; (2) Bidders do not allow an opponent to win at a price they are willing to beat. In the absence of additional information, what can the researcher learn about [math]\sQ[/math]?

A realization of the model predicted ordered bids [math]\eB(\vec{\ev}_n)[/math] in \eqref{eq:RCS_auction} for [math]n=3,\vec{\ev}_n=v^0,\delta=0[/math].

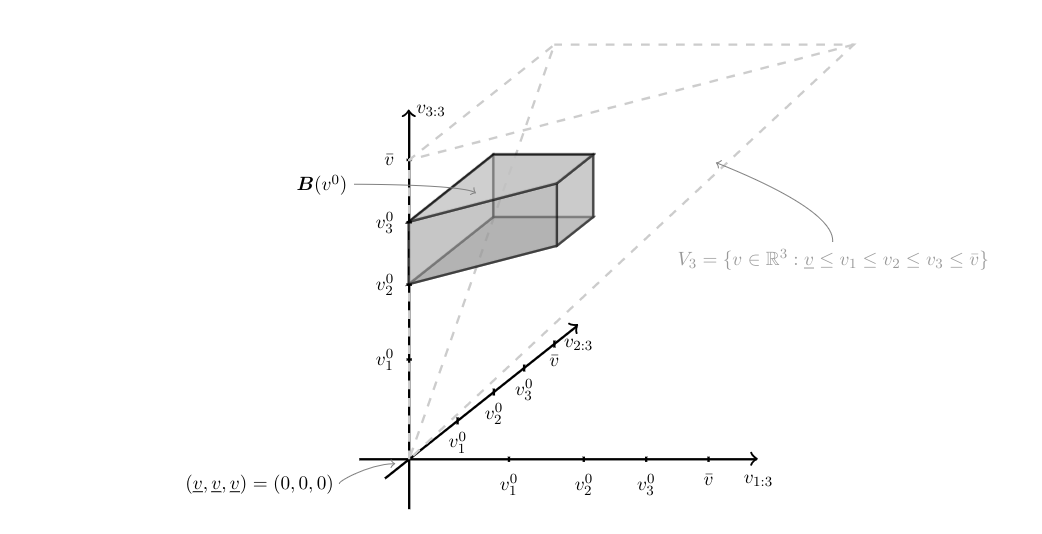
The model in Identification Problem delivers set valued predictions because given valuations [math](\ev_1,\dots,\ev_n)[/math], the two fundamental assumptions about bidder's behavior yield

[[math]] \begin{align} \vec{\eb}_n \in \eB(\vec{\ev}_n)\equiv\left[\left\{\prod_{i=1}^{n-1}[\underline{v},\ev_{i:n}]\right\}\times [\ev_{n-1:n}-\delta,\ev_{n:n}]\right]\cap V_n,\label{eq:RCS_auction} \end{align} [[/math]]

where [math]\vec{\ev}_n\equiv(\ev_{1:n},\dots,\ev_{n:n})[/math] denotes the vector of order statistics of the valuations, and [math]V_n=\{v\in\R^n:\underline{v}\le v_1\le v_2\le\dots\le v_n\le \bar{v}\}[/math]. Figure provides a stylized depiction of a realization of this set for [math]\vec{\ev}_n=v^0[/math] when there are three bidders ([math]n=3[/math]), [math]\underline{v}=0[/math], and [math]\delta=0[/math]. In words, [math]\eB(\vec{\ev}_n)[/math] collects the model predicted values of ordered bids. The fact that [math]\eb_{i:n}\le \ev_{i:n}[/math] for all [math]i[/math] results from assumption (1): since each bidder bids at most an amount equal to her valuation, the [math]i[/math]-th highest bid cannot exceed the [math]i[/math]-th highest valuation . The fact that [math]\eb_{n:n}\ge \ev_{n-1,n}-\delta[/math] follows immediately from assumption (2) . The fact that [math]\vec{\eb}_n[/math] has to lie in [math]V_n[/math] follows because it is a vector of ordered bids. Why does this set-valued prediction hinder point identification? The reason is that the distribution of the observable data relates to the model structure in an incomplete manner. Define a bidding rule [math]\sB(\eb_{1:n},\dots,\eb_{n:n}|\ev_{1:n},\dots,\ev_{n:n})[/math] to be a conditional joint distribution for the order statistics of the bids conditional on the order statistics of the valuations. Then, for a given realization of the valuations [math]\ev_{1:n}=v_1,\dots,\ev_{n:n}=v_n[/math], the model requires that the support of [math]\sB(\cdot|v_1,\dots,v_n)[/math] is in [math]B(\vec{v})[/math] as defined in \eqref{eq:RCS_auction} with [math]\ev_{1:n}=v_1,\dots,\ev_{n:n}=v_n[/math], but imposes no other restriction on it. Hence, the model implied joint distribution of ordered bids is

[[math]] \begin{align} \sM_{1,\dots,n:n}(\cdot;\sB,\sQ)\equiv\int \sB(\cdot|v_1,\dots,v_n)\sQ_{1,\dots,n:n}(dv_1,\dots,dv_n),\label{eq:model:impl_sel_mech_auction} \end{align} [[/math]]

where [math]\sQ_{1,\dots,n:n}[/math] is the joint distribution of order statistics of the valuations implied by [math]\sQ[/math]. Since the bidding rule [math]\sB[/math] is left completely unspecified (other than requiring it to be a valid joint conditional probability distribution with support in [math]\eB[/math]), one can find multiple pairs [math](\sB ,\sQ)[/math] satisfying the assumptions of Identification Problem, such that [math]\sM_{1,\dots,n:n}(\cdot;\sB,\sQ)=\sG_{1,\dots,n:n}(\cdot)[/math], with [math]\sG_{1,\dots,n:n}[/math] the observed joint CDF of the order statistics of the bids associated with [math]\sP[/math]. propose to use simple and tractable implications of the model to learn features of [math]\sQ[/math]. Recall that with i.i.d. valuations, the distribution of each order statistic uniquely determines [math]\sQ(v)[/math], with [math]\sQ(v)\equiv\sQ(\ev\le v)[/math] for any [math]v\ge\underline{v}[/math], through:

[[math]] \begin{align} \sQ(v)=\sq_{\cB}(\sQ_{i:n}(v);i,n-i+1),\label{eq:HT:beta} \end{align} [[/math]]

where [math]\sQ_{i:n}[/math] is the CDF of [math]\ev_{i:n}[/math] and [math]\sq_{\cB}(\cdot;i,n-i+1)[/math] is the quantile function of a Beta-distributed random variable with parameters [math]i[/math] and [math]n-i+1[/math]. Using this, their Lemmas 1 and 3 yield, respectively,

[[math]] \begin{align} \sQ(v) &\le \min_{n,i}\sq_{\cB}(\sG_{i:n}(v);i,n-i+1),\forall v\in[\underline{v},\bar{v}],\label{eq:HT_upper}\\ \sQ(v) &\ge \max_{n}\sq_{\cB}(\sG_{n:n}(v-\delta);i,n-i+1),\forall v\in[\underline{v},\bar{v}],\label{eq:HT_lower} \end{align} [[/math]]

where, for any [math]v\ge\underline{v}[/math], [math]\sG_{i:n}(v)\equiv\sP(\eb_{i:n}\le v)[/math] denotes the observed CDF of [math]\eb_{i:n}[/math] for [math]i=1,\dots,n[/math].

Key Insight: The model and analysis put forward by trade point identification of the distribution of valuation under stringent assumptions on the bidding rule, for a robust inference approach that yields informative bounds under weak and widely credible assumptions on bidding behavior. Remarkably, “nothing is lost” due to the use of their robust approach: point identification is recovered when the standard assumptions of the button auction model hold. This is because in the dominant strategy equilibrium the top losing bidder exits at her valuation, followed immediately by the winning bidder. Hence, [math]\eb_{n-1:n}=\ev_{n-1:n}=\eb_{n:n}[/math] and [math]\delta=0[/math], so that the upper and the lower bound in \eqref{eq:HT_upper}-\eqref{eq:HT_lower} coincide and point identify the distribution of valuations.

also provide sharp bounds on the optimal reserve price, which I do not discuss here. However, they leave open the question of whether the collection of CDFs satisfying \eqref{eq:HT_upper}-\eqref{eq:HT_lower} yields the sharp identification region for [math]\sQ[/math]. As discussed in Sections Selectively Observed Data-Interval Data, pointwise bounds on the CDF deliver tubes of admissible CDFs that in general yield outer regions on the CDF of interest. But in this identification problem, the issue of sharpness is even more subtle, and therefore addressed in the following subsection.

Before moving on to that discussion, I note that the work of spurred a rich literature applying partial identification analysis to the study of auction models. studies first price sealed bid auctions with equilibrium behavior, where affiliated valuations prevent --in the absence of parametric restrictions on the distribution of the model primitives-- point identification of the model. He derives bounds on seller revenue under various counterfactual scenarios on reserve prices and auction formats. also studies first price sealed bid auctions with equilibrium behavior, but relaxes the independence assumptions on symmetric valuations by requiring it to hold only conditional on unobserved heterogeneity. He derives bounds on various functionals of the distributions of interest, including the mean bid and mean valuation. analyze second price auctions with correlated private values. In this case, the distribution of valuations is not point identified even under the assumptions of the button auction model . Nonetheless, show that interesting functionals of it (seller profits and bidder surplus) can be bounded, if one assumes that transaction prices are determined by the second highest valuation and imposes some restrictions on the joint distribution of the number of bidders and distribution of the valuations. studies a related model of second-price ascending auctions with arbitrary dependence in bidders’ private values. She provides partial identification results for the joint distribution of values for any subset of bidders under various assumptions about what data the researcher observes. While in her framework the highest bid is never observed, she considers the case where only the winner's identity and the winning price are observed, and the case where all the identities and all the bids except for the highest bid are known. She also investigates the informational content of assuming positive dependence in bidders' values. are concerned with nonparametric identification of a two-stage entry and bidding game. Potential bidders are assumed to have private valuations and observe private signals before deciding whether to enter the auction. The dependence between signals and valuations is only minimally restricted. Hence, even with some excluded instruments that affect selection into the auction, the model primitives are only partially identified. The authors derive bounds on these primitives, and provide conditions under which point identification is restored. provide partial identification results in private value and common value auctions under weak restrictions on the information available to the bidders. Their approach leverages a result in yielding an equivalence between distributions of valuations that obey the restrictions imposed by a Bayesian Correlated Equilibrium and those that obey the restrictions imposed by Bayesian Nash Equilibrium under some information structure. Such equivalence is particularly helpful because the set of Bayesian Correlated Equilibria can be characterized through linear programming, so that the sharp identification region provided by is given by the collection of parameter vectors [math]\vartheta[/math] for which a linear program is feasible. Related results leveraging the linear structure of correlated equilibria in the context of entry games include , , and .

Characterization of Sharpness through Random Set Theory

bounds exploit the information contained in the marginal CDFs [math]\sG_{i:n}[/math] for each [math]i[/math] and [math]n[/math]. However, in Identification Problem additional information can be extracted from the joint distribution of ordered bids. obtain the sharp identification region [math]\idr{\sQ}[/math] using random set methods (Artstein's characterization in Theorem) applied to a quantile function representation of the order statistics. Here I provide an equivalent characterization that uses equation \eqref{eq:RCS_auction} directly, and which has not appeared in the literature before. Let [math]\cT[/math] denote the space of probability distributions with support on [math][\underline{v},\bar{v}][/math], so that [math]\sQ\in\cT[/math]. For a candidate distribution [math]\tilde{\sQ}\in\cT[/math], let [math]\tilde{\sQ}_{1,\dots,n:n}[/math] denote the implied distribution of order statistics of [math]n[/math] i.i.d. random variables distributed [math]\tilde{\sQ}[/math]. Let [math]\tilde{\eB}[/math] be a random closed set defined as in \eqref{eq:RCS_auction} with respect to order statistics of i.i.d. random variables with distribution [math]\tilde{\sQ}[/math]. For a given set [math]K\in\cK[/math], with [math]\cK[/math] the collection of compact subsets of [math]\R^n[/math], let [math]\sT_{\tilde\eB}(K;\tilde{\sQ})[/math] denote the probability of the event [math]\{\tilde\eB\cap K\neq \emptyset\}[/math] implied by [math]\tilde{\sQ}[/math].

Theorem (Distribution of Valuations in Incomplete Auction Model with Independent Private Values)

Under the assumptions of Identification Problem, the sharp identification region for [math]\sQ[/math] is

[[math]] \begin{align} \label{eq:SIR:auction} \idr{\sQ}= \left\{\tilde{\sQ}\in\cT: \sP(\vec{\eb}_n\in K) \le \sT_{\tilde\eB}(K;\tilde{\sQ}) \forall K\in\cK \right\}. \end{align} [[/math]]

Show Proof

The sharp identification region for [math]\sQ[/math] is given by the collection of probability distributions [math]\tilde{\sQ}\in\cT[/math] for which one can find a bidding rule [math]\sB(\cdot|\cdot)[/math] with support in [math]\tilde{\eB}[/math] a.s. such that [math]\sG_{1,\dots,n:n}(\cdot)=\sM_{1,\dots,n:n}(\cdot;\sB,\tilde{\sQ})[/math]. Here [math]\sM_{1,\dots,n:n}(\cdot;\sB,\tilde{\sQ})[/math] is defined as in \eqref{eq:model:impl_sel_mech_auction} with [math]\tilde{\sQ}[/math] replacing [math]\sQ[/math]. Take a distribution [math]\tilde{\sQ}[/math] satisfying this definition of sharpness. Then there exists a selection of [math]\tilde{\eB}[/math] determined by the bidding rule associated with [math]\tilde{\sQ}[/math], such that its distribution matches that of [math]\vec{\eb}_n[/math]. But then Theorem implies that the inequalities in \eqref{eq:SIR:auction} hold. Conversely, take [math]\tilde{\sQ}[/math] satisfying the inequalities in \eqref{eq:SIR:auction}. Then, by Theorem, [math]\vec{\eb}_n[/math] and [math]\tilde{\eB}[/math] can be realized on the same probability space as random elements [math]\vec{\eb}_n^\prime[/math] and [math]\tilde{\eB}^\prime[/math], [math]\vec{\eb}_n\edis \vec{\eb}_n^\prime[/math], [math]\tilde{\eB}\edis\tilde{\eB}^\prime[/math], such that [math]\vec{\eb}_n^\prime \in \tilde{\eB}^\prime[/math] a.s. One can then complete the auction model with a bidding rule that picks [math]\vec{\eb}_n^\prime[/math] with probability [math]1[/math], and the result follows.

■

In \eqref{eq:SIR:auction}, [math]\sP(\vec{\eb}_n\in K)[/math] is determined by the joint distribution of the ordered bids and hence can be learned from the data. On the other side, [math]\sT_{\tilde\eB}(K;\tilde{\sQ})[/math] is a function of the model and [math]\tilde{\sQ}\in\cT[/math]. Hence, it can be computed using \eqref{eq:RCS_auction}, with [math]\tilde\eB[/math] defined with respect to order statistics of i.i.d. random variables with distribution [math]\tilde{\sQ}\in\sT[/math]. To gain insights in the characterization of [math]\idr{\sQ}[/math], consider for example the set [math]K=\{\prod_{i=1}^{n-1}(-\infty,+\infty)\}\times(-\infty,v][/math]. Plugging it in the inequalities in \eqref{eq:SIR:auction}, one obtains

[[math]] \begin{align*} \sG_{n:n}(v) \le \sQ_{n-1,n}(v),\text{for all } n, \end{align*} [[/math]]

which, using \eqref{eq:HT:beta}, yields \eqref{eq:HT_lower}. Similarly, plugging in the sets [math]K_j=\{\prod_{i=1}^{j-1}(-\infty,+\infty)\}\times[v,\infty)\times\{\prod_{j+1}^n(-\infty,+\infty)\}[/math], [math]j=1,\dots,n[/math], yields \eqref{eq:HT_upper}. So the inequalities proposed by are a subset of the inequalities yielding the sharp identification region in Theorem SIR-. More information can be obtained by using additional sets [math]K[/math]. For instance, the set [math]K=[v_1,\infty)\times[v_2,\infty)\times\{\prod_{i=1}^{n}(-\infty,+\infty)\}[/math], [math]v_2\ge v_1[/math], yields [math]\sP(\eb_{1:n}\ge v_1,\eb_{2:n}\ge v_2)\le \sQ_{1,2:n}([v_1,\infty)\times[v_2,\infty))[/math], which further restricts [math]\sQ[/math]. Numerous examples can be given. Characterization \eqref{eq:SIR:auction} is stated using inequality eq:domin-t for the collection of compact subsets of [math]\R^n[/math]. One can instead use the (equivalent) inequality eq:dom-c, and show that in fact it suffices to check it for a much smaller collection of sets, as shown by (see also ). Nonetheless, this collection remains extremely large.

Key Insight: Random set theory and partial identification -- continued As stated in the Introduction, constructing the (random) set of model predictions delivered by the maintained assumptions is an exercise typically carried out in identification analysis, regardless of whether random set theory is applied. Indeed, for the problem studied in this section, put forward the set of admissible bids in \eqref{eq:RCS_auction}. With this set in hand, the tools of random set theory (in this case, Theorem) immediately deliver the sharp identification region of interest.

further generalize the analysis in this section by dropping the requirement of independent private values. This allows them, for example, to consider affiliated private values. They show that even in this significantly more complex context, the key behavioral restrictions imposed by to relate bids to valuations can be coupled with the use of random set theory, to characterize sharp identification regions.

General references

Molinari, Francesca (2020). "Microeconometrics with Partial Identification". arXiv:2004.11751 [econ.EM].